Generalizing the Alpha-Divergences and the Oriented Kullback–Leibler Divergences with Quasi-Arithmetic Means
Abstract
1. Introduction
1.1. Statistical Divergences and -Divergences
1.2. Divergences and Decomposable Divergences
1.3. Contributions and Paper Outline
2. The -Divergences Induced by a Pair of Strictly Comparable Weighted Means
2.1. The -Divergences
2.2. The Quasi-Arithmetic -Divergences
- the arithmetic mean (A): ,
- the geometric mean (G): , and
- the harmonic mean (H): .
2.3. Limit Cases of 1-Divergences and 0-Divergences
- and therefore . Let and in Equation (57). We have and , and the double inequality of Equation (57) becomesSince , , and , we get
- and therefore . Then, the double inequality of Equation (57) becomesThat is,since .
2.4. Generalized KL Divergences as Conformal Bregman Divergences on Monotone Embeddings
3. The Subfamily of Homogeneous -Power -Divergences for
4. Applications to Center-Based Clustering
4.1. Robustness of the Left-Sided Bregman Centroids
4.2. Robustness of Generalized Kullback–Leibler Centroids
| Algorithm 1: Generic seeding of k-means with divergence-based k-means++. |
| input: A finite set of n points, the number of cluster representatives , and an arbitrary divergence Output: Set of initial cluster centers Choose with uniform probability and  return |
5. Conclusions and Discussion
Funding
Conflicts of Interest
References
- Keener, R.W. Theoretical Statistics: Topics for a Core Course; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Basu, A.; Shioya, H.; Park, C. Statistical Inference: The Minimum Distance Approach; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing — An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Pardo, L. Statistical Inference Based on Divergence Measures; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Oller, J.M. Some geometrical aspects of data analysis and statistics. In Statistical Data Analysis and Inference; Elsevier: Amsterdam, The Netherlands, 1989; pp. 41–58. [Google Scholar]
- Amari, S. Information Geometry and Its Applications; Applied Mathematical Sciences; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Eguchi, S. Geometry of minimum contrast. Hiroshima Math. J. 1992, 22, 631–647. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cichocki, A.; Amari, S.i. Families of alpha-beta-and gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Amari, S.i. α-Divergence is Unique, belonging to Both f-divergence and Bregman Divergence Classes. IEEE Trans. Inf. Theory 2009, 55, 4925–4931. [Google Scholar] [CrossRef]
- Zhang, J. Divergence function, duality, and convex analysis. Neural Comput. 2004, 16, 159–195. [Google Scholar] [CrossRef]
- Hero, A.O.; Ma, B.; Michel, O.; Gorman, J. Alpha-Divergence for Classification, Indexing and Retrieval; Technical Report CSPL-328; Communication and Signal Processing Laboratory, University of Michigan: Ann Arbor, MI, USA, 2001. [Google Scholar]
- Dikmen, O.; Yang, Z.; Oja, E. Learning the information divergence. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 1442–1454. [Google Scholar] [CrossRef]
- Liu, W.; Yuan, K.; Ye, D. On α-divergence based nonnegative matrix factorization for clustering cancer gene expression data. Artif. Intell. Med. 2008, 44, 1–5. [Google Scholar] [CrossRef]
- Hellinger, E. Neue Begründung der Theorie Quadratischer Formen von Unendlichvielen Veränderlichen. J. Für Die Reine Und Angew. Math. 1909, 1909, 210–271. [Google Scholar] [CrossRef]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observation. Stud. Sci. Math. Hung. 1967, 2, 229–318. [Google Scholar]
- Qiao, Y.; Minematsu, N. A study on invariance of f-divergence and its application to speech recognition. IEEE Trans. Signal Process. 2010, 58, 3884–3890. [Google Scholar] [CrossRef]
- Li, W. Transport information Bregman divergences. Inf. Geom. 2021, 4, 435–470. [Google Scholar] [CrossRef]
- Li, W. Transport information Hessian distances. In Proceedings of the International Conference on Geometric Science of Information (GSI), Paris, France, 21–23 July 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 808–817. [Google Scholar]
- Li, W. Transport information geometry: Riemannian calculus on probability simplex. Inf. Geom. 2022, 5, 161–207. [Google Scholar] [CrossRef]
- Amari, S.i. Integration of stochastic models by minimizing α-divergence. Neural Comput. 2007, 19, 2780–2796. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Lee, H.; Kim, Y.D.; Choi, S. Non-negative matrix factorization with α-divergence. Pattern Recognit. Lett. 2008, 29, 1433–1440. [Google Scholar] [CrossRef]
- Wada, J.; Kamahara, Y. Studying malapportionment using α-divergence. Math. Soc. Sci. 2018, 93, 77–89. [Google Scholar] [CrossRef]
- Maruyama, Y.; Matsuda, T.; Ohnishi, T. Harmonic Bayesian prediction under α-divergence. IEEE Trans. Inf. Theory 2019, 65, 5352–5366. [Google Scholar] [CrossRef]
- Iqbal, A.; Seghouane, A.K. An α-Divergence-Based Approach for Robust Dictionary Learning. IEEE Trans. Image Process. 2019, 28, 5729–5739. [Google Scholar] [CrossRef]
- Ahrari, V.; Habibirad, A.; Baratpour, S. Exponentiality test based on alpha-divergence and gamma-divergence. Commun. Stat.-Simul. Comput. 2019, 48, 1138–1152. [Google Scholar] [CrossRef]
- Sarmiento, A.; Fondón, I.; Durán-Díaz, I.; Cruces, S. Centroid-based clustering with αβ-divergences. Entropy 2019, 21, 196. [Google Scholar] [CrossRef]
- Niculescu, C.P.; Persson, L.E. Convex Functions and Their Applications: A Contemporary Approach, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kolmogorov, A.N. Sur la notion de moyenne. Acad. Naz. Lincei Mem. Cl. Sci. His. Mat. Natur. Sez. 1930, 12, 388–391. [Google Scholar]
- Gibbs, A.L.; Su, F.E. On choosing and bounding probability metrics. Int. Stat. Rev. 2002, 70, 419–435. [Google Scholar] [CrossRef]
- Rachev, S.T.; Klebanov, L.B.; Stoyanov, S.V.; Fabozzi, F. The Methods of Distances in the Theory of Probability and Statistics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Vemuri, B.C.; Liu, M.; Amari, S.I.; Nielsen, F. Total Bregman divergence and its applications to DTI analysis. IEEE Trans. Med Imaging 2010, 30, 475–483. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the SODA ’07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 1027–1035. [Google Scholar]
- Bullen, P.S.; Mitrinovic, D.S.; Vasic, M. Means and Their Inequalities; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 31. [Google Scholar]
- Toader, G.; Costin, I. Means in Mathematical Analysis: Bivariate Means; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Cauchy, A.L.B. Cours d’analyse de l’École Royale Polytechnique; Debure frères: Paris, France, 1821. [Google Scholar]
- Chisini, O. Sul concetto di media. Period. Di Mat. 1929, 4, 106–116. [Google Scholar]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Nielsen, F. Generalized Bhattacharyya and Chernoff upper bounds on Bayes error using quasi-arithmetic means. Pattern Recognit. Lett. 2014, 42, 25–34. [Google Scholar] [CrossRef][Green Version]
- Nagumo, M. Über eine klasse der mittelwerte. Jpn. J. Math. Trans. Abstr. 1930, 7, 71–79. [Google Scholar] [CrossRef]
- De Finetti, B. Sul concetto di media. Ist. Ital. Degli Attuari 1931, 3, 369–396. [Google Scholar]
- Hardy, G.; Littlewood, J.; Pólya, G. Inequalities; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; The Regents of the University of California: Oakland, CA, USA, 1961; Volume 1. Contributions to the Theory of Statistics. [Google Scholar]
- Holder, O.L. Über einen Mittelwertssatz. Nachr. Akad. Wiss. Gottingen Math.-Phys. Kl. 1889, 44, 38–47. [Google Scholar]
- Bhatia, R. The Riemannian mean of positive matrices. In Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013; pp. 35–51. [Google Scholar]
- Akaoka, Y.; Okamura, K.; Otobe, Y. Bahadur efficiency of the maximum likelihood estimator and one-step estimator for quasi-arithmetic means of the Cauchy distribution. Ann. Inst. Stat. Math. 2022, 74, 1–29. [Google Scholar] [CrossRef]
- Kim, S. The quasi-arithmetic means and Cartan barycenters of compactly supported measures. Forum Math. Gruyter 2018, 30, 753–765. [Google Scholar] [CrossRef]
- Carlson, B.C. The logarithmic mean. Am. Math. Mon. 1972, 79, 615–618. [Google Scholar] [CrossRef]
- Stolarsky, K.B. Generalizations of the logarithmic mean. Math. Mag. 1975, 48, 87–92. [Google Scholar] [CrossRef]
- Jarczyk, J. When Lagrangean and quasi-arithmetic means coincide. J. Inequal. Pure Appl. Math. 2007, 8, 71. [Google Scholar]
- Páles, Z.; Zakaria, A. On the Equality of Bajraktarević Means to Quasi-Arithmetic Means. Results Math. 2020, 75, 19. [Google Scholar] [CrossRef]
- Maksa, G.; Páles, Z. Remarks on the comparison of weighted quasi-arithmetic means. Colloq. Math. 2010, 120, 77–84. [Google Scholar] [CrossRef]
- Zhang, J. Nonparametric information geometry: From divergence function to referential-representational biduality on statistical manifolds. Entropy 2013, 15, 5384–5418. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Generalizing Skew Jensen Divergences and Bregman Divergences with Comparative Convexity. IEEE Signal Process. Lett. 2017, 24, 1123–1127. [Google Scholar] [CrossRef]
- Kuczma, M. An Introduction to the Theory of Functional Equations and Inequalities: Cauchy’s Equation and Jensen’s Inequality; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nock, R.; Nielsen, F.; Amari, S.i. On conformal divergences and their population minimizers. IEEE Trans. Inf. Theory 2015, 62, 527–538. [Google Scholar] [CrossRef][Green Version]
- Ohara, A. Conformal flattening for deformed information geometries on the probability simplex. Entropy 2018, 20, 186. [Google Scholar] [CrossRef]
- Ohara, A. Conformal Flattening on the Probability Simplex and Its Applications to Voronoi Partitions and Centroids. In Geometric Structures of Information; Springer: Berlin/Heidelberg, Germany, 2019; pp. 51–68. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Zhang, J. On monotone embedding in information geometry. Entropy 2015, 17, 4485–4499. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. The dual Voronoi diagrams with respect to representational Bregman divergences. In Proceedings of the Sixth International Symposium on Voronoi Diagrams (ISVD), Copenhagen, Denmark, 23–26 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 71–78. [Google Scholar]
- Itakura, F.; Saito, S. Analysis synthesis telephony based on the maximum likelihood method. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan, 21–28 August 1968; pp. 280–292. [Google Scholar]
- Okamoto, I.; Amari, S.I.; Takeuchi, K. Asymptotic theory of sequential estimation: Differential geometrical approach. Ann. Stat. 1991, 19, 961–981. [Google Scholar] [CrossRef]
- Ohara, A.; Matsuzoe, H.; Amari, S.I. Conformal geometry of escort probability and its applications. Mod. Phys. Lett. B 2012, 26, 1250063. [Google Scholar] [CrossRef]
- Kurose, T. On the divergences of 1-conformally flat statistical manifolds. Tohoku Math. J. Second Ser. 1994, 46, 427–433. [Google Scholar] [CrossRef]
- Pal, S.; Wong, T.K.L. The geometry of relative arbitrage. Math. Financ. Econ. 2016, 10, 263–293. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Mahajan, M.; Nimbhorkar, P.; Varadarajan, K. The planar k-means problem is NP-hard. Theor. Comput. Sci. 2012, 442, 13–21. [Google Scholar] [CrossRef]
- Wang, H.; Song, M. Ckmeans.1d.dp: Optimal k-means clustering in one dimension by dynamic programming. R J. 2011, 3, 29. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J.; Lafferty, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory 2009, 55, 2882–2904. [Google Scholar] [CrossRef]
- Ronchetti, E.M.; Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Nielsen, F.; Nock, R. Total Jensen divergences: Definition, properties and clustering. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2016–2020. [Google Scholar]
- Eguchi, S.; Komori, O. Minimum Divergence Methods in Statistical Machine Learning; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]

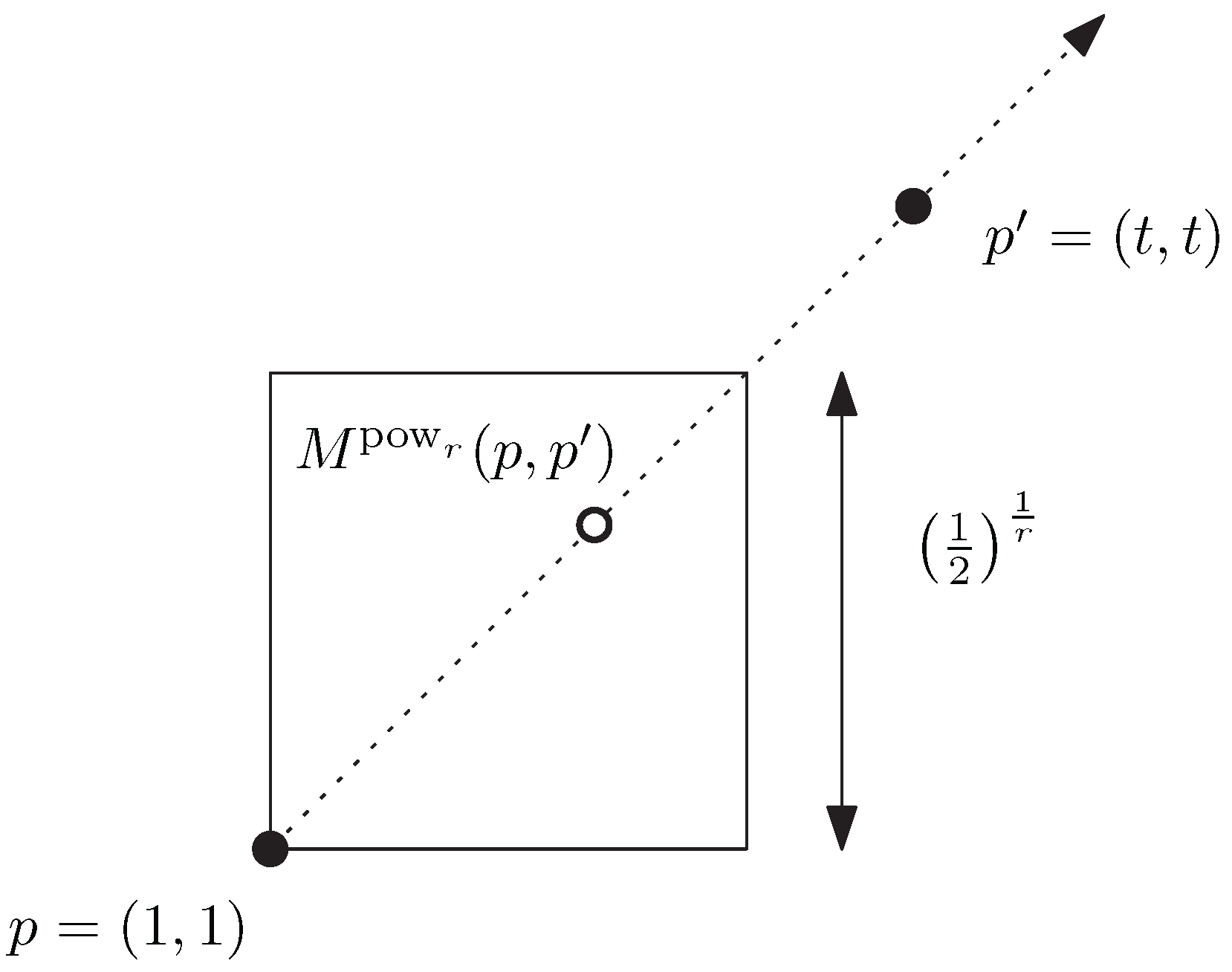
| Power Mean | |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F. Generalizing the Alpha-Divergences and the Oriented Kullback–Leibler Divergences with Quasi-Arithmetic Means. Algorithms 2022, 15, 435. https://doi.org/10.3390/a15110435
Nielsen F. Generalizing the Alpha-Divergences and the Oriented Kullback–Leibler Divergences with Quasi-Arithmetic Means. Algorithms. 2022; 15(11):435. https://doi.org/10.3390/a15110435
Chicago/Turabian StyleNielsen, Frank. 2022. "Generalizing the Alpha-Divergences and the Oriented Kullback–Leibler Divergences with Quasi-Arithmetic Means" Algorithms 15, no. 11: 435. https://doi.org/10.3390/a15110435
APA StyleNielsen, F. (2022). Generalizing the Alpha-Divergences and the Oriented Kullback–Leibler Divergences with Quasi-Arithmetic Means. Algorithms, 15(11), 435. https://doi.org/10.3390/a15110435









