Due to the complexity of the problem, the exact resolution approach will only be effective for small-sized instances. Therefore, in order to be able to handle larger instances of practical interest, we turn our attention toward heuristic approaches.
3.2.1. Greedy Constructive Heuristic
We begin with a greedy constructive heuristic based on a list algorithm.
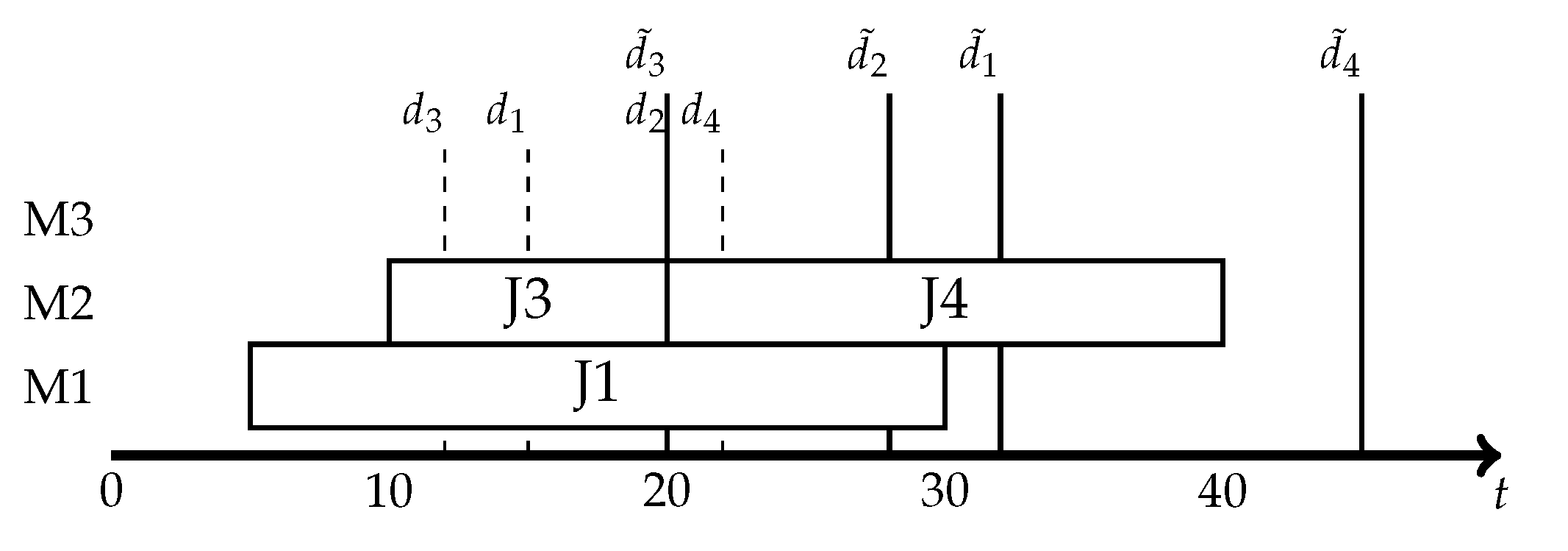
A solution to our problem will contain:
The starting times () and finish times () of jobs, ;
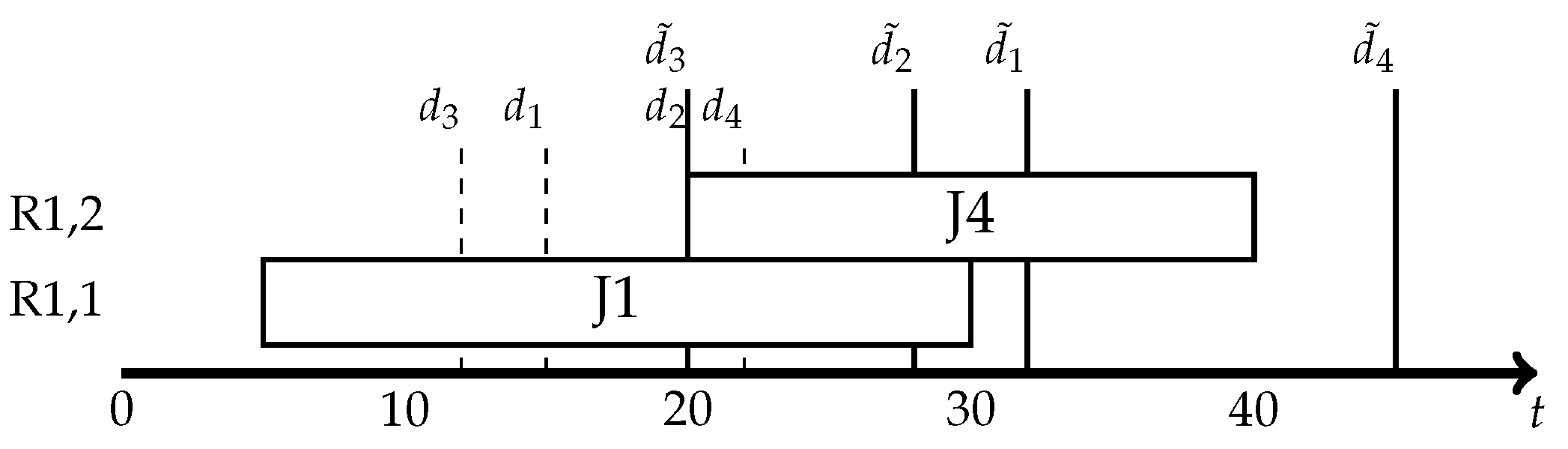
The starting times () and finish times () of machines, ;
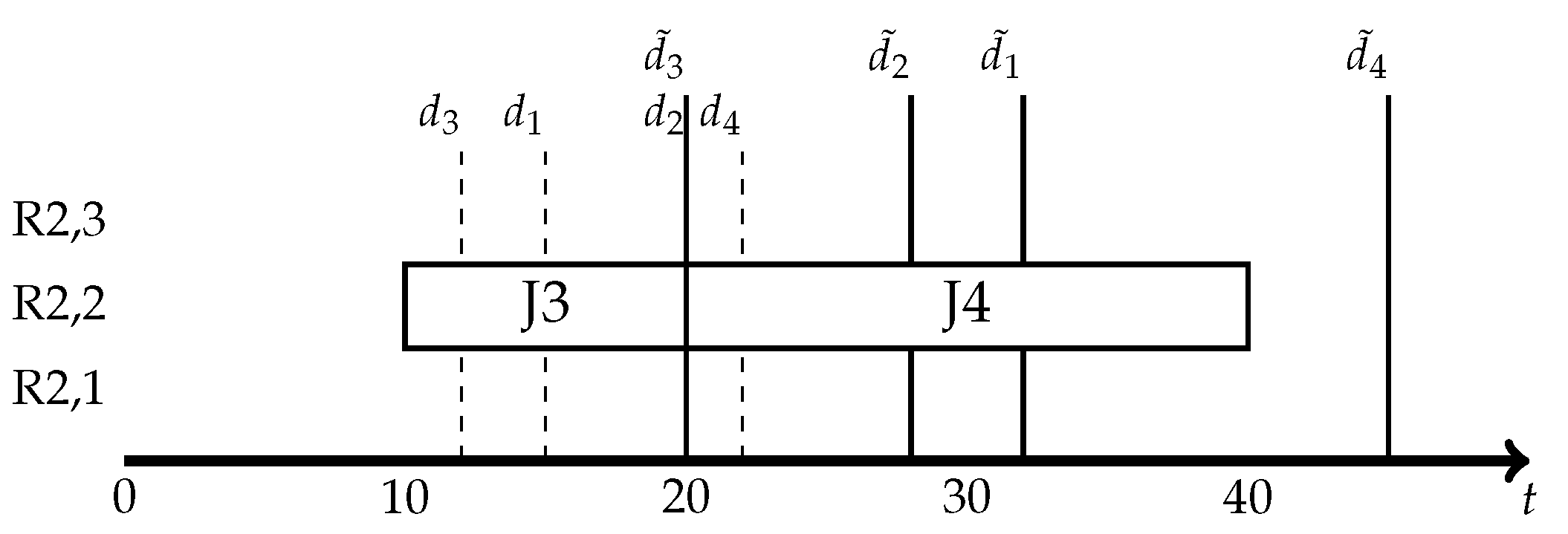
The starting times () and finish times () of resources, ;
The assignments of machines to jobs (), ;
The assignment of resources to jobs (), , .
Algorithm 1 illustrates the constructive heuristic.
| Algorithm 1: Greedy constructive heuristic |
![Algorithms 15 00433 i001 Algorithms 15 00433 i001]() |
We begin by initializing the solution S. It is initially empty, with its elements (, , , , , , , ) set to 0, i.e., 0 starting and completion times for all jobs, machines, and resources, as well as no assignments of jobs to machines and resources.
We then compute a first criterion in order to evaluate each job (line 2 of Algorithm 1, called by function ). This criterion consists of two sub-criteria:
The first sub-criterion is given as:
where
is the average processing time of task
j on all of the machines that can process it and
is the number of such machines.
If we were to order tasks in decreasing order of this sub-criterion, we would give priority to tasks with a high tardiness cost, small due date, and small average processing time.
The second sub-criterion is given as:
Ordering tasks in decreasing order of this sub-criterion gives priority to high-paying and high-penalty jobs.
We combine the two sub-criteria by normalizing the first and multiplying it with the second.
This first criterion is then used to sequence the jobs in decreasing order (line 3 of Algorithm 1).
For each job j in this order, we proceed to construct a sequence of machines to which it should be assigned. In order to construct this sequence, we first go through several steps.
We start by identifying the earliest starting date for job
j on each machine
i that can process it (line 5 of Algorithm 1):
where
A job j will start on machine i no earlier that the time needed to transport it to the machine and the time the machine and the resources that it requires become available.
When estimating the availability time of resources, we consider all resources and use to reduce this value to 0 if the resource type r is not required to process job j. For all needed resource types (), we estimate their available time and select the largest value, since they all need to be available throughout the duration of the job. For each resource type r, we look at all units of this resource () and select the one that would be available first using its complete date and adding a transport time if this resource was last used on a different machine than i.
Estimating whether a transport time is required is carried out using . If the last task using resource q of type r is performed on a different machine than i, then a transport time is required; otherwise, this time is set to 0.
We also record the resource units that were selected when constructing
using
(line 6 of Algorithm 1):
Using
and
, we then evaluate each machine
i using a second criterion (line 7 of Algorithm 1, called by function
), which is given as:
where
This criterion computes the net gain from selecting job j to be processed on machine i at time using its required resources . This criterion includes the selling price of the job (), its fixed costs (), the cost of transporting the job to the machine (), the renting cost of the machine while executing the job (), the idle time of renting the machine if it was used to process other jobs (), the renting cost of the required resources during the job processing but also during idle times for resources that have been used to process other jobs, and, finally, the tardiness costs.
Estimating the idle cost of machine i is carried out by checking whether is greater than 0, and, in this case, is equal to the cost of renting the machine per unit of time multiplied with the time between its latest complete date () and the estimated start date of job j ().
Estimating the idle cost of a resource r () is carried out in a similar way, considering the resource that should be selected in order to process job j.
Using the second criterion, we sequence the machines in decreasing order (line 8 of Algorithm 1). We then consider each machine from this list and select the first that does not lead the job to overshoot its deadline nor lead to a loss that is worse than if the job were not processed at all (line 10 of Algorithm 1). Once a machine fulfilling these conditions is found, we update the solution (line 11 of Algorithm 1) and jump to the next job (line 12 of Algorithm 1). If there is no machine that can fulfil these conditions, then the job is not processed.
3.2.2. Simulated Annealing
We consider a third heuristic for solving this problem: the simulated annealing procedure [
35].
This approach starts from an initial solution and then moves to close neighbors across multiple iterations. During each iteration, the neighboring solution replaces the current one if it improves the objective function. Non-improving solutions may also replace the previous solution with a probability that is proportional to the performance difference and taking into account a temperature parameter. This parameters is initially set to a high value and decreases at each iteration. High values increase the probability of accepting non-improving solutions, and low values do not. Therefore, the approach starts by exploring the search space and ends by intensifying its search.
The performance of the simulated annealing approach is heavily dependent on the choice of the initial temperature and the rate at which it decreases, also called an annealing schedule. Usually, the annealing schedule requires a significantly time-consuming tuning phase in order for the approach to perform well on a new problem.
Variants of this approach, where the annealing schedule adapts and requires no tuning, have been proposed, and we therefore consider one such approach here. Namely, we focus on the adaptive annealing schedule known as modified LAM [
36].
This adaptive simulated annealing (ASA) using the modified LAM annealing schedule is outlined in Algorithm 2.
| Algorithm 2: Adaptive simulated annealing using the modified LAM annealing schedule |
![Algorithms 15 00433 i002 Algorithms 15 00433 i002]() |
The algorithm starts by initializing the solution
S using the greedy constructive heuristic presented in
Section 3.2.1 (line 1). A copy is also generated in the form of
(line 2). The temperature parameter
T and an
parameter are both set to
(lines 3 and 4).
Throughout this algorithm, a solution of the problem is encoded using:
: the sequence of jobs;
: the assignment of machines to jobs;
: the assignment of resources to jobs.
For the initial solution, these elements correspond to those used by the constructive heuristic from
Section 3.2.1. In order to evaluate a solution, a decoding function that generates all of the elements of the solution (
,
,
,
,
,
,
,
) is used; however, for simplicity, we do not include these elements in the presentation of the algorithm. Initial values for the temperature and the acceptance rate are also set at this point.
We continue with the main loop of the algorithm (line 5 onward), which performs a preset number of iterations. Each iteration begins by generating a neighbor of solution . In our case, generating a neighbor of consists of applying, with equal probability, one of the following operators:
Swap two randomly selected jobs in ;
Randomly change the machine assignment of one randomly selected job in ;
Randomly change the resource assignment of one randomly selected job in .
Once a neighbor is generated, it is accepted as the new solution and replaces if it is better or if a randomly selected value between 0 and 1 is lower than (lines 7 and 8). Otherwise, the same solution will be used during the next iteration.
The
and
parameters correspond to the modified LAM annealing schedule from [
36], which the interested reader is referred to for further insight. Briefly speaking, this annealing schedule adapts the temperature so that the acceptance rate linearly decreases from 100% to 44% during the first 15% iterations of the algorithm, then fixes it at 44% during the following 50% iterations, while, for the remaining 35%, it drops linearly towards 0%.