Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contribution and Organization
2. WOA and SMA
2.1. WOA
- (1)
- Encircling prey
- (2)
- Spiral bubble-net feeding manoeuvre
- (3)
- Global exploration phase
2.2. SMA
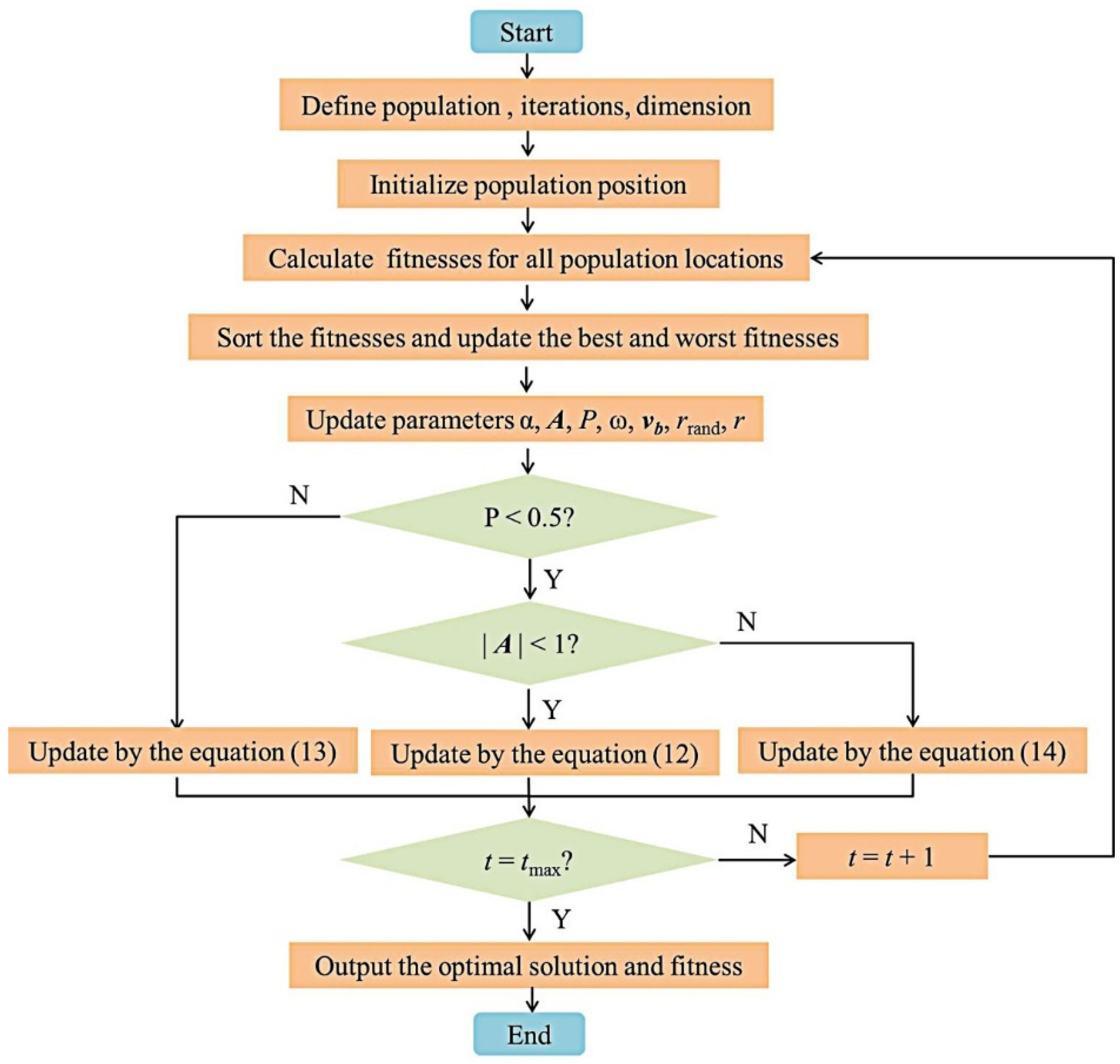
3. Slime Mould Whale Optimization Algorithm (SMWOA)
3.1. Principle of the SMWOA
- (1)
- In WOA, parameter a decreases linearly from 2 to 0, and cannot accurately reflect and adapt to the complex nonlinear search process. Therefore, the expression of parameter a in SMA is used to replace parameter a in original WOA.
- (2)
- To improve the flexibility and diversity of the search domain, the fitness weight representing each slime mould individual is introduced into the position updating strategy of WOA, which is helpful in reaching the optimal value quickly.
3.2. Computational Complexity
3.3. Performance Experiments of the SMWOA
4. Trajectory Optimization of Joints Based on SMWOA
4.1. Path Interpolation of Joints
4.2. Objective Function and Constraint Function
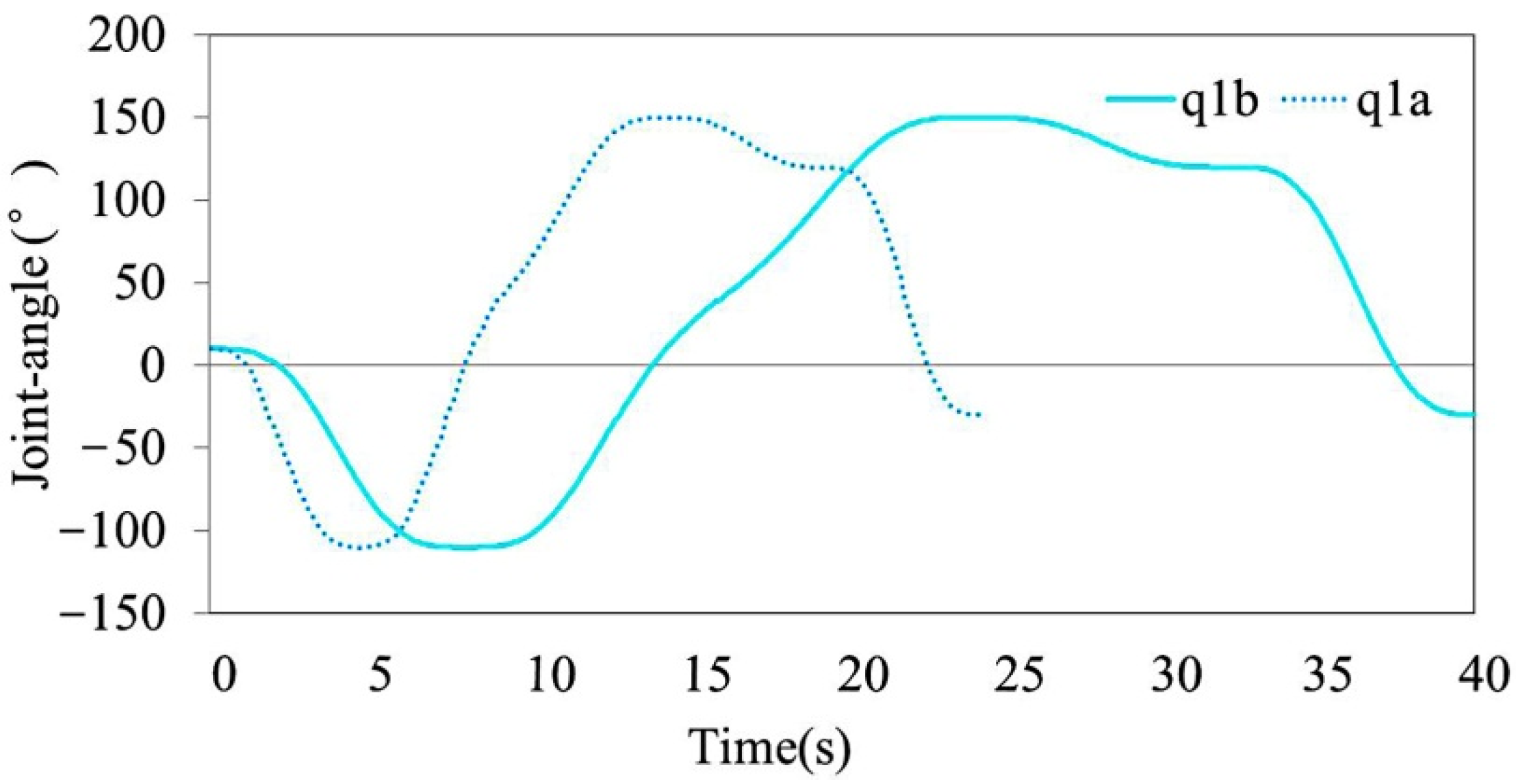
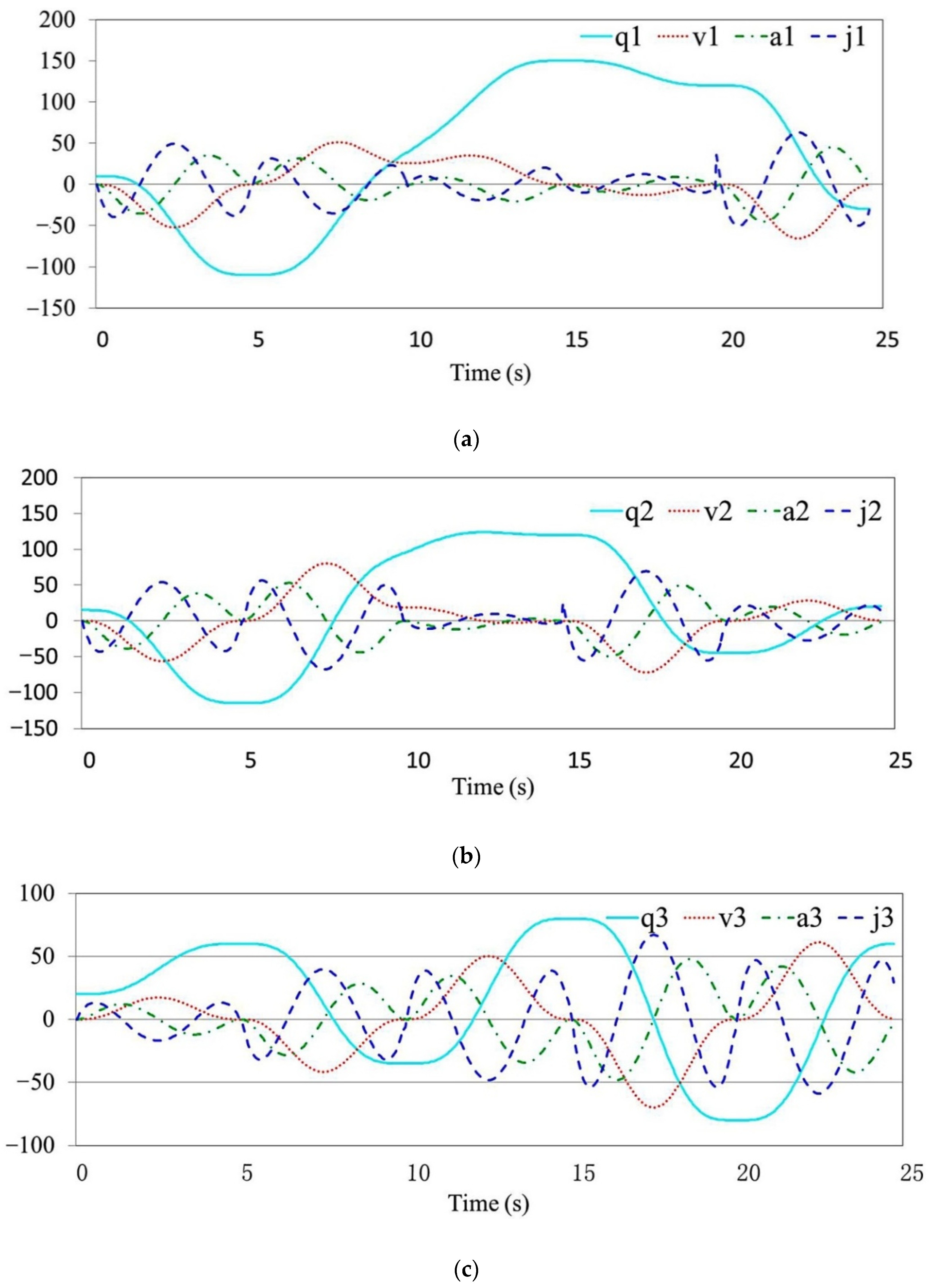
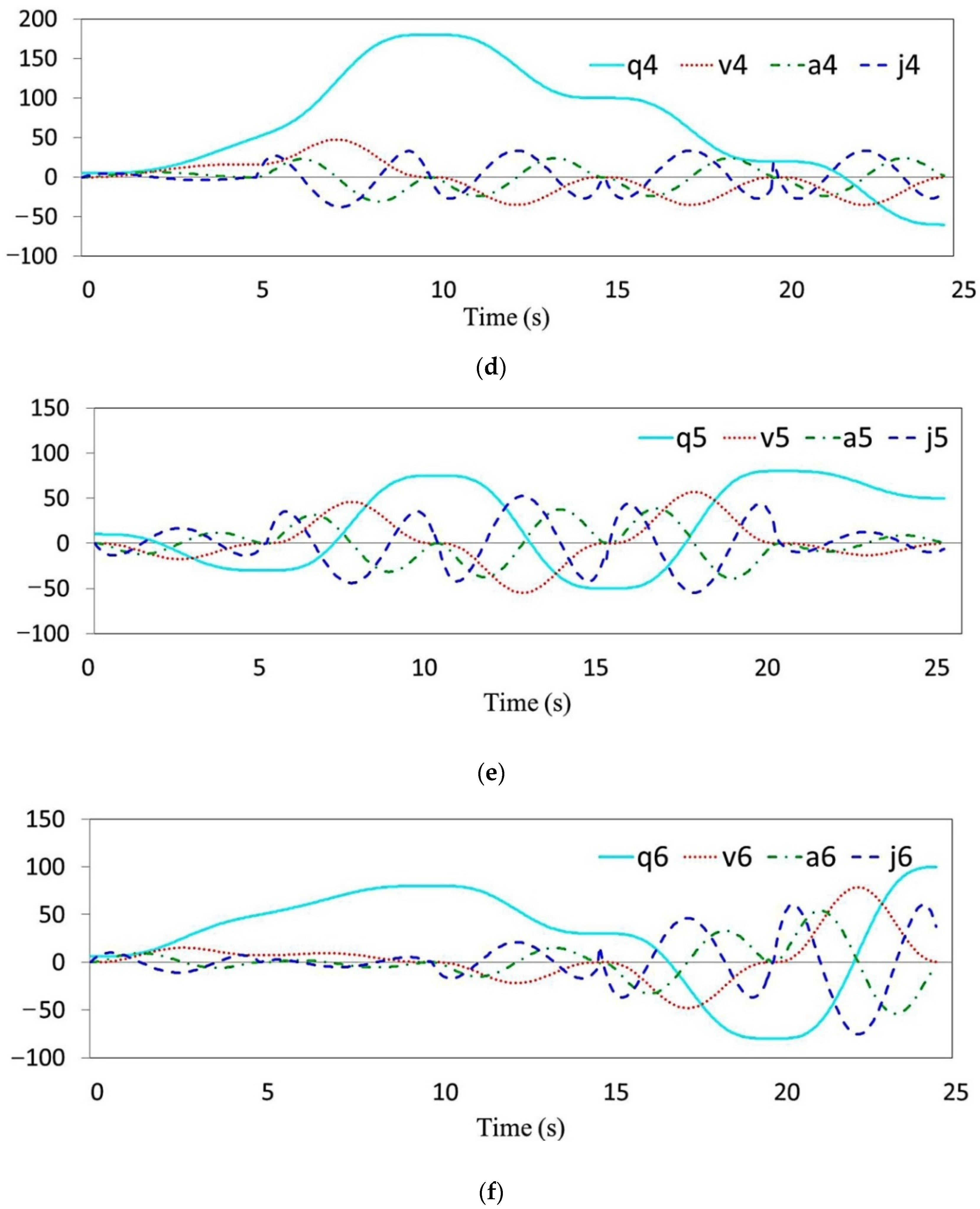
4.3. Optimal Experiment of Path Planning
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Psarommatis, F.; May, G.; Dreyfus, P.A.; Kiritsis, D. Zero defect manufacturing: State-of-the-art review, shortcomings and future directions in research. Int. J. Prod. Res. 2020, 58, 1–17. [Google Scholar] [CrossRef]
- Legnani, G.; Fassi, I.; Tasora, A.; Fusai, D. A practical algorithm for smooth interpolation between different angular positions. Mech. Mach. Theory 2021, 162, 104341. [Google Scholar] [CrossRef]
- Aggogeri, F.; Merlo, A.; Pellegrini, N. Active Vibration Control Development in Ultra-Precision Machining. J. Vib. Control 2021, 27, 790–801. [Google Scholar] [CrossRef]
- Borboni, A.; Aggogeri, F.; Elamvazuthi, I.; Incerti, G.; Magnani, P.L. Effects of profile interpolation in cam mechanisms. Mech. Mach. Theory 2020, 144, 103652. [Google Scholar] [CrossRef]
- Incerti, G. Modeling and simulation of a position-controlled servo-axis with elasticity and backlash in the transmission. Arch. Appl. Mech. 2017, 87, 633–645. [Google Scholar] [CrossRef]
- Liu, Z. Research and Simulation of Six-axis Industrial Robot Trajectory Planning Based on Robotics Toolbox. Mech. Eng. Autom. 2017, 3, 59–61. [Google Scholar]
- Rossi, C.; Savino, S. Robot trajectory planning by assigning positions and tangential velocities. Robot. Comput.-Integr. Manuf. 2013, 29, 139–156. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, X. Trajectory planning and simulation of six-DOF robot based on MATLAB. Manuf. Autom. 2014, 15, 95–97. [Google Scholar]
- Choi, T.; Park, C.; Do, H.; Park, D.; Kyung, J.; Chung, G. Trajectory correction based on shape peculiarity in direct teaching manipulator. Int. J. Control Autom. Syst. 2013, 11, 1009–1017. [Google Scholar] [CrossRef]
- Guo, T.Y.; Li, F.; Huang, K.; Zhang, F.Z.; Feng, Q. Application of Optimal Algorithm on Trajectory Planning of Mechanical Arm Based on B Spline Curve. In Applied Mechanic and Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2013; Volume 376, pp. 253–256. [Google Scholar]
- Yin, F.; Liang, Q.; Cheng, X.; Tao, Z. Research on Mechanical Arm Joint Space Trajectory Planning Algorithm Based on Optimal Time. Mach. Des. Res. 2017, 33, 12–15. [Google Scholar]
- Lian, L. Robot Joint Trajectory Planning Method Based on the Optimal Execution Time. Modul. Mach. Tool Autom. Manuf. Tech. 2018, 9, 57–60. [Google Scholar]
- Yang, Y.; Xu, H.; Li, S.; Zhang, L.; Yao, X. Time-optimal trajectory optimization of serial robotic manipulator with kinematic and dynamic limits based on improved particle swarm optimization. Int. J. Adv. Manuf. Technol. 2022, 120, 1253–1264. [Google Scholar] [CrossRef]
- Cheng, Q.; Hao, X.; Wang, Y.; Xu, W.; Li, S. Trajectory planning of transcranial magnetic stimulation manipulator based on time-safety collision optimization. Robot. Auton. Syst. 2022, 152, 104039. [Google Scholar] [CrossRef]
- Yu, X.; Dong, M.; Yin, W. Time-optimal trajectory planning of manipulator with simultaneously searching the optimal path. Comput. Commun. 2022, 181, 446–453. [Google Scholar] [CrossRef]
- Jing, Z.; Xijing, Z.; Xiaoling, M.; Xiao, W. Application of Improved Whale Optimization Algorithm in Time-Optimal Trajectory Planning of Manipulator. 2021. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?doi=10.13433/j.cnki.1003-8728.20200596 (accessed on 21 October 2021). [CrossRef]
- Hirakawa, A.R.; Kawamura, A. Trajectory generation for redundant manipulators under optimization of consumed electrical energy. In Proceedings of the Conference Record-IAS Annual Meeting (IEEE Industry Applications Society), San Diego, CA, USA, 6–10 October 1996; Volume 3, pp. 1626–1632. [Google Scholar]
- Uarg, D.P.; Kumar, M. Camera calibration and sensor fusion in an automated flexible manufacturing multi robot work cell. Proc. Am. Control Conf. 2002, 6, 4934–4939. [Google Scholar]
- Cheng, Q.; Xu, W.; Liu, Z.; Hao, X.; Wang, Y. Optimal Trajectory Planning of the Variable-Stiffness Flexible Manipulator Based on CADE Algorithm for Vibration Reduction Control. Front. Bioeng. Biotechnol. 2021, 9, 766495. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, C.; Wang, W.; Peng, B. Multi-objective trajectory planning based on SUMTNSGA-II. Comput. Eng. Des. 2015, 36, 3076–3081. [Google Scholar]
- Shi, X.; Fang, H.; Guo, W. Time-Energy-Jerk Optimal Trajectory Planning of Manipulators Based on Quintic NURBS. Mach. Des. Res. 2017, 33, 12–16. [Google Scholar]
- Shi, X.; Fang, H. Time-Energy-Jerk Optimal Planning of Industrial Robot Trajectories. Mach. Des. Manuf. 2018, 6, 254–257. [Google Scholar]
- Feng, B.; Liu, F.; Zheng, L. Optimal Motion Trajectory Planning of Robot Joint Space Based on Particle Swarm Optimization. Modul. Mach. Tool Autom. Manuf. Tech. 2018, 5, 1–4. [Google Scholar]
- Choubey, C.; Ohri, J. Optimal Trajectory Generation for a 6-DOF Parallel Manipulator Using Grey Wolf Optimization Algorithm. Robotica 2021, 39, 411–427. [Google Scholar] [CrossRef]
- Fu, Q.; Song, Y.; Wei, S.; Guo, L. Design of a kind of trajectory optimization algorithm for a manipulator based on genetic algorithm. Lect. Notes Electr. Eng. 2019, 529, 683–692. [Google Scholar]
- Zhao, J.; Zhu, X.; Song, T. Serial Manipulator Time-Jerk Optimal Trajectory Planning Based on Hybrid IWOA-PSO Algorithm. IEEE Access 2022, 10, 6592–6604. [Google Scholar] [CrossRef]
- Demir, G.; Vural, R.A. Heuristic Trajectory Planning of Robot Manipulator. In Proceedings of the 2021 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 16–18 November 2021; pp. 222–226. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- AbdelAziz, A.M.; Soliman, T.H.A.; Ghany, K.K.A.; Sewisy, A.A.E.M. A Pareto-Based Hybrid Whale Optimization Algorithm with Tabu Search for Multi-Objective Optimization. Algorithms 2019, 12, 261. [Google Scholar] [CrossRef]
- Ghoniem, R.M.; Alhelwa, N.; Shaalan, K. A Novel Hybrid Genetic-Whale Optimization Model for Ontology Learning from Arabic Text. Algorithms 2019, 12, 182. [Google Scholar] [CrossRef]
- Kotary, D.K.; Nanda, S.J.; Gupta, R. A many-objective whale optimization algorithm to perform robust distributed clustering in wireless sensor network. Appl. Soft Comput. 2021, 110, 107650. [Google Scholar] [CrossRef]
- Elaziza, M.A.; Oliva, D. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 17, 1843–1859. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Reda, M.; Karam, M.S.; Ripon, K.C.; Michael, J.R. An Efficient-Assembler Whale Optimization Algorithm for DNA Fragment Assembly Problem: Analysis and Validations. IEEE Access 2020, 8, 222144–222167. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, X.; Dai, R.; Chen, X.; Tan, S.; Xue, P. Kinematics Analysis and Palletizing Trajectory Planning of 6-DOF Robot. Mach. Tool Hydraul. 2021, 49, 33–37. [Google Scholar]

| Based Algorithm | Improved Algorithm | Interpolation Method |
|---|---|---|
| Particle swarm optimization (PSO) | PSO [10,23] | Quintic non-uniform rational B-spline curve (NURBS) |
| Cosine reduced-weight PSO [13] | Cubic polynomial | |
| Multi-objective PSO (MOPSO) [22] | Quintic B-spline curve | |
| Genetic algorithm (GA) | GA [15,25] | Cubic B-spline curve Fourth-fifth order polynomial |
| Adaptive Genetic Algorithm [11] | Cubic spline interpolation | |
| Ranking Adaptive Genetic Algorithm (RAGA) [14] | Quintic B-spline curve | |
| Combining genetic algorithm and adaptive simulated annealing algorithm [18] | Cubic polynomial | |
| SUMTNSUA-II [20] | Quintic B-spline curve | |
| Non-dominated sorting genetic algorithm with elitist strategy (NSGA-II) [21] | Quintic B-spline curve | |
| Whale optimization algorithm (WOA) | Improved WOA [16] | Quintic polynomial |
| IWOA-PSO [26] | Quintic B-spline curve |
| Functions | Expression | Dimension | Search Space | Optimal Value |
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | 0 | |
| Schwefel 2.22 | 30 | [−10, 10] | 0 | |
| Schwefel 1.12 | 30 | [−100, 100] | 0 | |
| Schwefel 2.21 | 30 | [−100, 100] | 0 | |
| Rosenbrock | 30 | [−30, 30] | 0 | |
| Rastrigin | 30 | [−5.12, 5.12] | 0 | |
| Ackley | 30 | [−32, 32] | 0 | |
| Alpine | [−10, 10] | 0 | ||
| Penalized 1.1 | 30 | [−50, 50] | 0 | |
| Penalized 1.2 | 30 | [−50, 50] | 0 | |
| Michalewicz | 2 | [−65.536, 65.536] | 1 | |
| Branin | 2 | [−5, 5] | 0.398 | |
| Goldstein-Price | 2 | [−2, 2] | 3 | |
| Hartmann-3D | 3 | [0, 1] | −3.86 | |
| Shekel 5 | 4 | [0, 10] | −10.1532 |
| Functions | Evaluation Indexes | SMWOA | WOA | PSO | GSA | DE | SMA |
|---|---|---|---|---|---|---|---|
| F1 | Avg | 0.00 × 100 | 7.91 × 10−74 | 3.72 × 100 | 1.23 × 10−18 | 1.78 × 10−92 | 2.74 × 10−108 |
| Std | 0.00 × 100 | 4.32 × 10−74 | 2.65 × 10−15 | 5.62 × 10−22 | 0.69 × 10−91 | 3.11 × 10−112 | |
| F2 | Avg | 3.57 × 10−67 | 1.86 × 10−49 | 2.05 × 10−1 | 6.46 × 10−10 | 3.09 × 10−1 | 3.75 × 10−24 |
| Std | 2.51 × 10−64 | 2.39 × 10−48 | 1.52 × 10−1 | 0.00 × 100 | 2.78 × 10−1 | 2.89 × 10−26 | |
| F3 | Avg | 3.72 × 10−82 | 4.31 × 10−6 | 3.89 × 10−3 | 1.13 × 10−3 | 3.74 × 10−5 | 2.25 × 10−45 |
| Std | 6.59 × 10−79 | 2.93 × 10−5 | 2.67 × 10−3 | 2.56 × 10−25 | 2.78 × 10−4 | 5.68 × 10−49 | |
| F4 | Avg | 2.58 × 10−16 | 7.25 × 10−12 | 4.56 × 10−8 | 7.86 × 10−10 | 3.72 × 10−14 | 2.74 × 10−23 |
| Std | 3.67 × 10−15 | 3.97 × 10−12 | 3.28 × 10−9 | 3.57 × 10−9 | 2.88 × 10−13 | 3.11 × 10−26 | |
| F5 | Avg | 2.75 × 10−33 | 2.79 × 101 | 4.52 × 102 | 2.36 × 101 | 3.74 × 100 | 3.75 × 10−24 |
| Std | 3.69 × 10−31 | 7.63 × 10−1 | 1.64 × 102 | 1.04 × 10−1 | 2.52 × 100 | 2.89 × 10−26 | |
| F6 | Avg | 5.04 × 10−29 | 1.06 × 10−21 | 1.29 × 102 | 2.32 × 101 | 5.27 × 10−3 | 0.00 × 100 |
| Std | 6.52 × 10−30 | 2.39 × 10−21 | 3.64 × 101 | 7.85 × 10−18 | 6.43 × 10−6 | 0.00 × 100 | |
| F7 | Avg | 6.54 × 10−28 | 5.39 × 10−15 | 3.77 × 10−3 | 6.32 × 10−8 | 4.47 × 10−4 | 2.74 × 10−26 |
| Std | 6.17 × 10−27 | 2.93 × 10−6 | 2.58 × 10−4 | 2.24 × 10−7 | 3.23 × 10−4 | 3.11 × 10−24 | |
| F8 | Avg | 6.24 × 10−39 | 1.26 × 10−2 | 5.79 × 10−1 | 3.58 × 100 | 3.78 × 10−2 | 3.75 × 10−24 |
| Std | 2.63 × 10−39 | 3.97 × 10−1 | 2.35 × 10−3 | 2.79 × 10−1 | 9.01 × 10−1 | 2.89 × 10−26 | |
| F9 | Avg | 4.37 × 10−15 | 3.05 × 10−3 | 5.69 × 100 | 1.32 × 100 | 7.63 × 10−1 | 2.25 × 10−15 |
| Std | 3.62 × 10−15 | 7.60 × 10−2 | 2.29 × 100 | 1.59 × 10−1 | 5.22 × 10−2 | 5.61 × 10−17 | |
| F10 | Avg | 2.47 × 10−10 | 8.97 × 100 | 3.74 × 100 | 5.22 × 10−1 | 3.24 × 10−1 | 2.74 × 10−8 |
| Std | 3.64 × 10−11 | 6.69 × 100 | 2.28 × 100 | 5.32 × 10−1 | 2.56 × 100 | 3.11 × 10−9 | |
| F11 | Avg | 1.80 × 100 | 3.76 × 100 | 1.89 × 100 | 4.59 × 100 | 2.58 × 100 | 1.75 × 100 |
| Std | 1.08 × 100 | 2.59 × 100 | 1.37 × 100 | 3.26 × 100 | 3.97 × 100 | 2.89 × 10−1 | |
| F12 | Avg | 0.42034 | 0.42718 | 0.41581 | 0.40278 | 0.39997 | 0.43669 |
| Std | 2.55 × 10−3 | 3.97 × 10−1 | 2.25 × 10−2 | 4.14 × 10−3 | 6.32 × 10−5 | 5.12 × 100 | |
| F13 | Avg | 3.00007 | 3.001 | 3.0019 | 3.0007 | 3.0022 | 3.00011 |
| Std | 1.36 × 10−4 | 7.62 × 10−1 | 1.39 × 100 | 2.67 × 10−2 | 2.63 × 101 | 1.05 × 10−3 | |
| F14 | Avg | −3.8563 | −3.8349 | −3.8498 | −3.8462 | −3.8547 | −3.8529 |
| Std | 3.23 × 10−7 | 5.92 × 10−2 | 7.68 × 10−6 | 3.29 × 10−5 | 6.12 × 10−8 | 2.86 × 10−6 | |
| F15 | Avg | −10.1337 | −8.2895 | −8.1933 | −8.0774 | −8.1324 | −10.1024 |
| Std | 3.24 × 10−3 | 2.73 × 100 | 4.63 × 100 | 4.89 × 100 | 5.79 × 101 | 1.41 × 10−2 | |
| p/h | 8.24 × 10−6/+ | 4.37 × 10−7/+ | 2.16 × 10−7/+ | 3.12 × 10−6/+ | 1.38 × 10−5/+ | ||
| Average ranking | 1.4000 | 3.9333 | 5.1333 | 4.6000 | 3.8000 | 2.1333 | |
| Total rank | 1 | 4 | 6 | 5 | 3 | 2 | |
| Nodes | Joints’ Positions | |||||
|---|---|---|---|---|---|---|
| θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | |
| 1 | 10 | 15 | 20 | 5 | 10 | 6 |
| 2 | −110 | −115 | 60 | 50 | −30 | 50 |
| 3 | 40 | 95 | −35 | 180 | 75 | 80 |
| 4 | 150 | 120 | 80 | 100 | −50 | 30 |
| 5 | 120 | −45 | -80 | 20 | 80 | −80 |
| 6 | −30 | 20 | 60 | −60 | 50 | 100 |
| Parameters | Constraints | |||||
|---|---|---|---|---|---|---|
| θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | |
| θmax (°) | 320 | 250 | 270 | 280 | 200 | 300 |
| ((°)/s) | 100 | 95 | 122 | 150 | 140 | 120 |
| ((°)/s2) | 245 | 245 | 475 | 475 | 500 | 500 |
| Algorithms | Time (s) | Total Time (s) | ||||
|---|---|---|---|---|---|---|
| h1 | h2 | h3 | h4 | h5 | ||
| SMA | 4.429 | 6.276 | 4.332 | 5.098 | 5.602 | 25.737 |
| WOA | 4.681 | 6.349 | 4.237 | 5.162 | 5.384 | 25.813 |
| SMWOA | 4.227 | 6.103 | 4.319 | 4.937 | 5.049 | 24.635 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yang, Q.; Wu, H.; Tan, S.; He, Q.; Wang, N.; Yang, X. Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm. Algorithms 2022, 15, 363. https://doi.org/10.3390/a15100363
Li X, Yang Q, Wu H, Tan S, He Q, Wang N, Yang X. Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm. Algorithms. 2022; 15(10):363. https://doi.org/10.3390/a15100363
Chicago/Turabian StyleLi, Xinning, Qin Yang, Hu Wu, Shuai Tan, Qun He, Neng Wang, and Xianhai Yang. 2022. "Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm" Algorithms 15, no. 10: 363. https://doi.org/10.3390/a15100363
APA StyleLi, X., Yang, Q., Wu, H., Tan, S., He, Q., Wang, N., & Yang, X. (2022). Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm. Algorithms, 15(10), 363. https://doi.org/10.3390/a15100363






