Abstract
Meta-analysis is an indispensable tool for synthesizing statistical results obtained from individual studies. Recently, non-Bayesian estimators for individual means were proposed by applying three methods: the James–Stein (JS) shrinkage estimator, isotonic regression estimator, and pretest (PT) estimator. In order to make these methods available to users, we develop a new R package meta.shrinkage. Our package can compute seven estimators (named JS, JS+, RML, RJS, RJS+, PT, and GPT). We introduce this R package along with the usage of the R functions and the “average-min-max” steps for the pool-adjacent violators algorithm. We conduct Monte Carlo simulations to validate the proposed R package to ensure that the package can work properly in a variety of scenarios. We also analyze a data example to show the ability of the R package.
1. Introduction
Meta-analysis is a tool for synthesizing statistical results obtained from individually published studies [1]. Meta-analyses have been employed in a variety of scientific studies [2,3,4,5], including studies on the influence of COVID-19 [6,7,8].
Usually, the goal of meta-analyses is to summarize individual studies to find some common effect [5,9]. The idea of estimating the common mean was originated from mathematical statistics and stratified sampling designs under fixed effect models (pp. 55–103 of [10,11,12,13]). In biostatistical methodologies, the estimation method based on random effect models [14] is popular. In either model, the goal of meta-analyses is usually to estimate the common mean by combining the estimators of individual means (Section 2.1).
In some scenarios, however, the goal of estimating the common mean is questionable. In these scenarios, meta-analyses can still be informative by looking at individual studies’ means (e.g., by a forest plot). Aside from these simple meta-analyses, Bayesian posterior means provide a more sophisticated summary of individual means in a meta-analysis [15,16,17,18,19].
Recently, Taketomi et al. [20] proposed non-Bayesian estimators of individual means by applying three methods: the James–Stein (JS) shrinkage estimator, isotonic regression estimator, and pretest (PT) estimator. Their frequentist estimators were shown to be superior to the individual studies’ estimators via decision theoretic criteria and Monte Carlo simulation experiments. These frequentist estimators also found their suitable applications to real data examples.
In this article, we propose a new R package meta.shrinkage in order to implement the frequentist estimators in [20]. Our package can calculate seven estimators (namely , ,, , , and ; see Section 3 for their definitions). We introduce this R package along with the usage of the R functions and the “average-min-max” steps for the pool-adjacent violators algorithm. We conduct Monte Carlo simulations to validate the proposed R package to ensure that the package can work properly in a variety of scenarios. We made the package freely available in the Comprehensive R Archive Network (CRAN): Available online: https://CRAN.R-project.org/package=meta.shrinkage (accessed on 14 November 2021).
This article is organized as follows. Section 2 gives the background, including a quick review of meta-analyses. Section 3 introduces the proposed R package. Section 4 conducts simulation studies to validate the proposed R package. Section 5 includes a data example to illustrate the proposed R package. Section 6 concludes the article with discussions. The appendices give the R code to reproduce the numerical results of this article.
2. Background
2.1. Meta-Analysis
This subsection reviews the basic concepts for meta-analysis.
To clarify the concepts, we introduce some notations and assumptions for a meta-analysis. Define as the number of studies, where stands for groups in the meta-analysis. For each , let be an estimator for a target estimand that is unknown. Let be a realized value of the random variable . We assume that the error is normally distributed so that , where is a known variance for the error distribution. Thus, is the mean of . The observed data are in this meta-analysis. We will not consider a setting where the variance is unknown [21,22], as this setting does not follow the framework of meta-analyses based on “summary data”. Without a loss of generality, we assume that corresponds to the null value.
Traditionally, the objective of meta-analyses is to estimate the common mean, denoted as . It is defined by the fixed effect model assumption of or the random-effects model assumption of for , where is the between-study variance. In this article, we assume neither, since the aforementioned models do not always fit the data at hand. For instance, if the studies have ordered means (e.g., ), the model is neither fixed nor random [20]. Indeed, many real meta-analyses have some covariates to systematically explain the reason for increasing means or decreasing means (see Section 5). In such circumstances, there is no general way to define the common mean . Below, we discuss what meta-analyses can do in the absence of the common mean.
2.2. Improved Estimation of Individual Means
Meta-analyses often display individual estimates along with their 95% confidence intervals (CIs): . Similarly, the funnel plot shows against (see [1,5,23,24] for these plots). These meta-analyses are possible without the assumptions of the fixed effect or random effect models. Therefore, looking at the individual estimates is a part of meta-analysis.
Taketomi et al. [20] pointed out the need for improving the individual estimates by shrinkage estimation methods [11,12,25,26]. They first regard as an estimator of . Then, they consider an estimator that improves upon in terms of the weighted mean square error (WMSE) criteria:
The above is called an improved estimator of . If “” in Equation (2) holds only for a restricted parameter space, is locally improved. Two locally improved estimators are relevant in this article. The first one is under ordered means, where the parameter space is restricted to . The second one is under the sparse normal means [27], where many values are zero (e.g., ).
The inverse variance weights in Equation (1) and (2) make it convenient to apply the classical decision theory [20]. Consequently, Taketomi et al. [20] were able to theoretically verify the (local) improvement of their estimators upon in terms of the WMSE. In practice, one may also be interested in the total MSE (TMSE) criterion, defined as [11,25], while the TMSE makes the theoretical analysis complex [11]. Section 4 will employ the TMSE criterion to assess the performance of all the improved estimators that will be introduced in the proposed R package.
Below, we introduce our R package, which can compute several improved estimators suggested by [20]. The goal of our package is to compute from that are the realized values for a random vector .
3. R Package meta.shrinkage
This section introduces our proposed R package meta.shrinkage, which can compute seven improved estimators for individual means, denoted as , , , , , , and . We will divide our explanations into four sections: Section 3.1 for and , Section 3.2 for , Section 3.3 for and , Section 3.4 for , and .
Before embarking on details, we explain the basic variables used in the package. Let be an estimate for under a known variance for . Thus, one needs to prepare to perform a meta-analysis. Accordingly, the input variables in the R console are two vectors:
- y: a vector for s;
- s: a vector for s.
Below is an example for the input variables for a dataset of in the R console.


This dataset comes from the data analysis of [20], in which gastric cancer data [28] was analyzed. The values for s are Cox regression estimates for the effect of chemotherapy on disease-free survival (DFS) for gastric cancer patients, and the values are the SEs.
3.1. James–Stein Estimator
The James–Stein (JS) estimator is defined as
This estimator is a variant from the primitive JS estimator [29], which was derived under homogeneous variances ( for ). The JS estimator reduces the WMSE by shrinking the vector toward . The degree of shrinkage is determined by the factor that typically takes its value from 0 (0% shrinkage) to 1 (100% shrinkage). In rare cases, it becomes greater than one (overshrinkage).
It was proven that has a smaller WMSE than when [20]. That is, Equations (1) and (2) hold. Thus, is an improve estimator without any restriction.
The positive-part JS estimator can further reduce the WMSE by avoiding the overshrinkage phenomenon of :
where .
In our R package, the function “js(.)” can compute and .
Below is the usage in the R console.

The values in the JS column are the shrunken values of y. The values are equivalent between the columns of JS and JS_plus because there is no overshrinkage.
3.2. Restricted Maximum Likelihood Estimators under Ordered Means
We consider the restricted maximum likelihood (RML) estimator when the individual means are ordered. Without loss of generality, we consider the increasing order . This indicates that belongs to . If there are such parameter constraints, they should be incorporated into the estimators in order to improve the estimation accuracy [20].
The RML estimator satisfying is calculated by
The above formula is called the pool-adjacent violators algorithm (PAVA). The computation requires the “average-min-max” steps (Figure 1). We developed an R function “rml(.)” in our R package to perform the matrix-based computation of Figure 1. This R function initially computes all the elements of the matrix (Figure 1). Then, it applies the command “max(apply(z, 1, min))”, where “1” indicates that “min” applies to the rows of the matrix “z”. This yields easy-to-understand code in the R program.
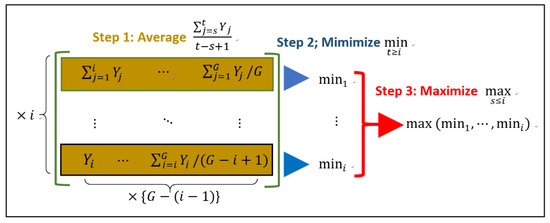
Figure 1.
The schematic diagram for implementing the pool-adjacent violators algorithm (PAVA) in the R function “rml(.)” in our R package.
To understand the reason why the matrix-based computation (Figure 1) is necessary, we give an example for calculating from a dataset . By setting and in Figure 1, the calculation for proceeds as follows:
The matrix in the preceding formula keeps four sub-averages of , including . Any one of the four components of the matrix can be . Hence, the matrix is necessary as well as sufficient to calculate . That aside, matrices are easy to manipulate in R.
The RML estimator gives a smaller WMSE than [20].
For theories and applications of the PAVA, we refer to [30,31,32,33,34]. We decided not to use the “pava(.)” function available in the R package “Iso” [33] to ensure the independence of our package from others. Nonetheless, we checked that “rml(.)” and “pava(.)” gave numerically identical results.
So far, we have assumed that the studies (i.e., ) are ordered to achieve . However, usually, the studies in a raw dataset may be arbitrarily ordered, and hence, one needs to find covariates to order the studies. For instance, one can use publication years if the values increase with them. More generally, we assume that there exists an increasing sequence of covariates () or a decreasing sequence of covariates () to achieve the order .
In our R package, the function “rml(.)” can compute . The function allows users to enter covariates when studies are not ordered. For instance, we enter the estimates (y), SEs (s), and the proportion of males (x) from the COVID-19 data with [7,20].

In this data, the estimates (y) are the log risk ratios (RRs) calculated from two-by-two contingency tables examining the association (mortality vs. hypertension). As found in the previous studies [7,20], there was a decreasing sequence of the proportion of males () that could achieve the order . Then, we have the following:


We see that the estimates are ordered, which is consistent with the prescribed order . By the option “test=TRUE”, one can test if the values are properly ordered by a sequence of covariates. Figure 2 shows the output including the LOWESS plot and a correlation test based on Kendall’s tau via “cor.test(x,y,method=“kendall”)”. The test confirmed that the means were ordered by a “decreasing” sequence (). We suggest the 10% significance level to declare the increasing or decreasing trend. In meta-analyses, 5% is too strict and not realistic since the number of studies is limited.
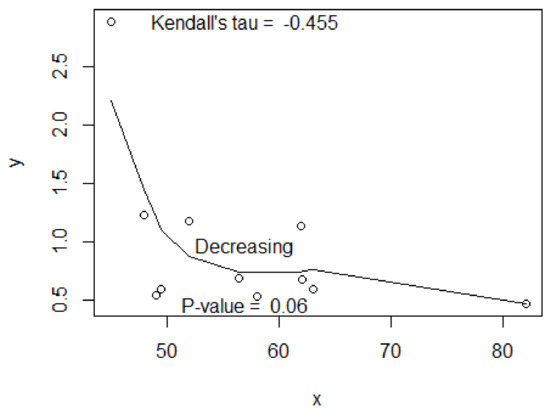
Figure 2.
The LOWLESS plot based on the estimates (y) and the proportions of males (x) from the COVID-19 data with 11 studies. Shown are Kendall’s tau and the test of no association between x and y.
3.3. Shrinkage Estimators under Ordered Means
The estimator introduced above (in Section 3.2) can be improved by the JS type shrinkage. Based on the idea of Chang [35], Taketomi et al. [20] proposed a JS-type estimator under the following order restriction:
where “RJS” stands for “restricted JS”, is the indicator function, where or if is true or false, respectively. Note that has a smaller WMSE than [20,35], meaning that gives more precise estimates than .
The RJS estimator can be further corrected by the following positive-part RJS estimator:
Consequently, has a smaller WMSE than [20].
In our R package, the function “rjs(.)” can compute and possibly with the aid of covariates.
For instance, one can analyze the COVID-19 data as follows:
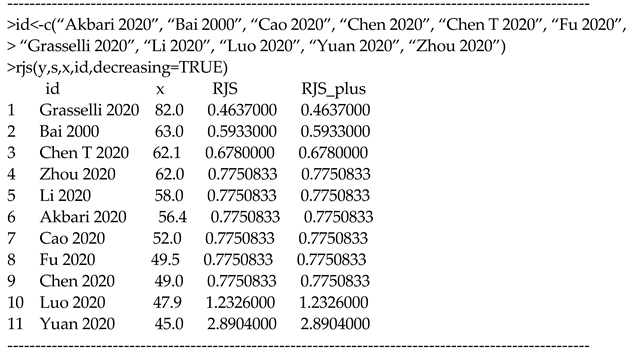

In the above commands, the input includes the optional argument “id” that signifies the leading authors and publication years of the 11 studies. We did so simply to make an informative output. If the input does not include this argument, the output shows the ordered sequence of 1, 2, …, 11 as shown in Section 3.2.
3.4. Estimators under Sparse Means
We now consider discrete shrinkage schemes by pre-testing vs. for . The idea was proposed by Bancroft [36], who developed pretest estimators (see also more recent works [20,37,38,39,40,41,42,43]). In the meta-analytic context, Taketomi et al. [20] adopted the general pretest (GPT) estimator of Shih et al. [41], which is defined as follows:
Here , , and is the upper pth quantile of for . To implement the GPT estimator, the values of , , and must be chosen. For any value of and , as well as a function , one can show that has smaller WMSE and TMSE values than , provided [20].
One may choose (50% shrinkage), as suggested by [20,41]. To facilitate the interpretability of the pretests, one may choose (5% level) and (10% level). The resultant estimator is
The special case of leads to the usual pretest (PT) estimator
In our R package, the function “gpt(.)” can compute and . The significance levels and the shrinkage parameter are flexibly chosen by the following arguments:
- alpha1: significance level for (0 < alpha1 < 1);
- alpha2: significance level for (0 < alpha2 < 1);
- q: degrees of shrinkage for (0 < q < 1).
If users do not specify them, the default values , , and will be realized. The following is an example:


The output shows that and lead to 0%, 50%, or 100% shrinkage of . The estimates of yield 0 for 12 studies, and the estimates of yield 0 for 10 studies.
4. Simulation: Validating the R Package
This technical section is devoted to the numerical verification of the proposed package via Monte Carlo simulation experiments. Users of the package may skip this section.
We conducted simulations to investigate the operating performance of the seven estimators implemented in the proposed R package (Section 3). Our simulation design added new scenarios to the original ones in [20]. Hence, the simulation not only added new knowledge on the performance of the seven estimators, but it also validated the proposed R package.
4.1. Simulation Design
We considered the four scenarios for the true parameters :
- Scenario (a):
- Ordered and non-sparse: ;
- Scenario (b):
- Ordered and sparse: ;
- Scenario (c):
- Unordered and non-sparse: ;
- Scenario (d):
- Unordered and sparse: ;
- Scenario (e):
- Ordered and non-sparse: ;
- Scenario (f):
- Ordered and sparse: .
These scenarios were not considered by our previous simulation studies [20].
We generated normally distributed data where was restricted (truncated) in , , as previously considered [20,44]. Using the data , we applied the proposed R package meta.shrinkage to compute , ,, , , , and for estimating . We examined how these estimators improved upon the standard estimator in terms of the TMSE and WMSE.
Our simulations were based on 10,000 repetitions using , where . Let be one of the seven estimators in the th repetition. To assess the TMSE, we computed it via the Monte Carlo average:
As the TMSE and WMSE gave the same conclusion, we reported on the former.
Appendix A provides the R code for the simulations, which can reproduce the results of the following section.
4.2. Simulation Results
Figure 3 compares the estimators , , ,, , , , and .
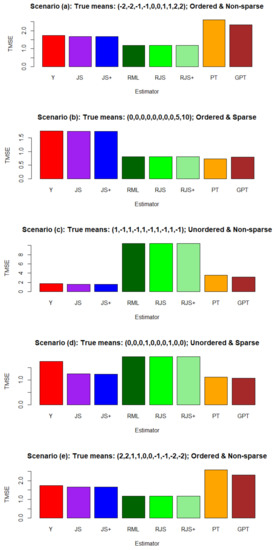
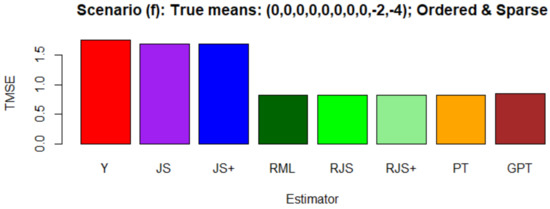
Figure 3.
Simulation results for the estimators , , ,, , , , and . Comparison is based on Monte Carlo average:.
In Scenarios (a) and (e), the smallest TMSE values were achieved by , , and , which appropriately accounted for the ordered means. Thus, these ordered mean estimators provided some advantages over the standard estimator . Here, users needed to specify the option “decreasing = FALSE” (Scenario (a)) or “decreasing = TRUE” (Scenario (e)) to capture the true ordering of the means. On the other hand, and produced unreasonably large TMSE values, since they wrongly imposed the sparse mean assumptions.
In Scenario (b), the smallest TMSE values were attained by followed by , as they took advantage of the sparse means. The TMSE values for , , and were also small by accounting for the ordered means. Hence, these pretest and restricted estimators produced significant advantages over the standard estimator .
In Scenario (c), and performed the best, but the advantage over was modest. In this scenario, , , and produced quite large TMSE values and performed the worst, since they wrongly assumed the ordered means. Additionally, and produced large TMSE values since they wrongly assumed the sparse means. This was the only scenario where the standard estimator was enough.
In Scenario (d), the smallest TMSE values were attained by , as it captured the sparse means. The performance of , , and was also good. On the other hand, , , and gave large TMSE values due to the unordered means.
In summary, our simulations demonstrated that the seven estimators implemented in the proposed R package exhibited desired operating characteristics. If the true means were ordered, the restricted estimators (, , and ) showed definite advantages over the standard estimator . In addition, the pretest estimators ( and ) produced the best performance under the sparse means. Finally, the JS estimators ( and ) modestly but uniformly improved upon across all the scenarios.
We therefore conclud that there are good reasons to apply the proposed R package to estimate in order to improve the accuracy of estimation.
5. Data Example
This section analyzes a dataset to illustrate the methods in the proposed package, demonstrating their possible advantages over the standard meta-analysis. Appendix B provides the R code, which can reproduce the following results.
We used the blood pressure dataset containing studies, where each study examined the effect of a treatment to reduce blood pressure. The dataset is available in the R package mvmeta. Available online: https://CRAN.R-project.org/package=mvmeta (accessed on 14 November 2021). Each study provided the treatment’s effect estimate on the systolic blood pressure (SBP) and the treatment’s effect on the diastolic blood pressure (DBP), as shown in Table 1. In the following analysis, we focus on the treatment’s effect estimates for the SBP and regard those for the DBP as covariates.

Table 1.
The 10 studies from the blood pressure data. Each study provided the treatment’s effect on the systolic blood pressure (SBP) and the treatment’s effect on the diastolic blood pressure (DBP).
We aimed to improve the individual treatment effects on the SBP by the methods in the R package meta.shrinkage. For this purpose, we utilized the covariate information to implement meta-analyses under ordered means (Section 3.2 and Section 3.3).
To apply the proposed methods, we changed the order of the 10 studies by the increasing order of the covariates (see the first column of Table 2). Under this order, we defined , where as the treatment effect estimates on the SBP (see in the second column of Table 2). Table 2 shows a good concordance between and the covariates; the smallest covariate (−7.87) yielded the smallest outcome (), and the largest covariate (−2.08) yielded the largest outcome (). However, the values of were not perfectly ordered.

Table 2.
The treatment effect estimates on the SBP based on the 10 studies from the blood pressure data. The 10 studies are ordered by the covariates (treatment effect estimates on the DBP).
We therefore considered the order-restricted estimators (, , and ) by imposing the assumption that the true treatment effects were ordered. Table 2 shows that these restricted estimators satisfied (see the fifth through the seventh columns of Table 2). Since it was reasonable to impose a concordance between the treatment effects on the SBP and DBP, these estimators may have been advantageous over the standard estimates (). In this data example, the JS estimators ( and ) were almost identical to the standard estimates . Hence, there would be little advantage to shrinkage in the JS estimators.
By the “rml(.)” function, we tested if the values were ordered by a sequence of covariates. Figure 4 shows a correlation-based test and the LOWESS plot. The test confirmed that the means were ordered by an increasing sequence (). The P-value was highly significant (p = 0.002). Therefore, we validated the assumption of ordered means.
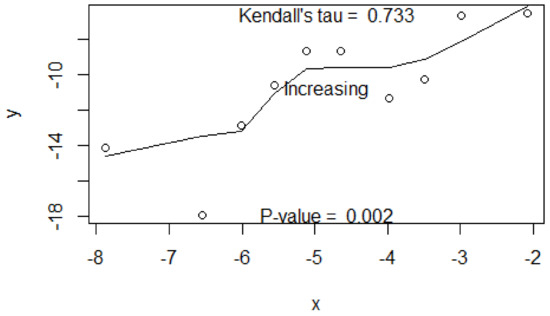
Figure 4.
The LOWLESS plot based on the treatment effect estimates on the SBP (y) and those on the DBP (x) from the blood pressure dataset with 10 studies. Shown are Kendall’s tau and the test of no association between x and y.
6. Conclusions and Future Extensions
This article introduced an R package meta.shrinkage (https://CRAN.R-project.org/package=meta.shrinkage (accessed on 15 November 2021)), which we made freely available on CRAN. It was first released on 19 November 2021 (version 0.1.0), following our original methodological article published on 20 October 2021 [20]. We hope that the timely release of our package facilitates the appropriate use of the proposed methods for interested readers. As the precision and reliability of the developed statistical methods are important, we conducted extensive simulation studies to validate the proposed R package (Section 4). We also analyzed a data example to show the ability of the R package (Section 5).
To implement isotonic regression in our R package, we proposed a matrix-based algorithm for the PAVA (Figure 1). This algorithm is easy to program in the R environment, where matrices are convenient to manipulate. However, if one tries to implement the PAVA in other programing environments, the matrix-based algorithm may be inefficient, especially for a meta-analysis with a very large number of studies. The number makes the proposed algorithm slow to compute the output. However, real meta-analyses rarely have more than 100 studies, so this issue may not arise at the practical level.
An extension of the present R packages to multiple responses is an important research topic. An example includes a meta-analysis of verbal and math test scores [45], consisting of two responses. A similar instance involves math and stat tests [44,46]. There is much room for meta-analyzing bivariate and multivariate responses [47,48,49,50,51,52,53,54,55,56]. Multivariate shrinkage estimators of multivariate restricted and unrestricted normal means, such as those in [57,58,59,60], can be considered for this extension.
The proposed R package can only handle normally distributed data; it cannot handle data that are non-normally distributed, asymmetrically distributed, or discrete-valued. To analyze such data, one should consider extensions of the meta-analysis methods in [20] toward asymmetric distributions for skewed or discrete response variables. Shrinkage and pretest estimators exist, such as [61] for the exponential distribution, [62] for the gamma distribution, and [63,64] for the Poisson distribution. Thus, meta-analytical applications of shrinkage estimators to asymmetric or non-normal models are relevant research directions.
We left a comparison of the estimators in our package with the Bayesian random-effects meta-analyses. For instance, the performance of the proposed estimators could be compared with the Bayesian posterior mean estimators, which could be computed from the bayesmeta package [15]. However, one needs to specify the prior mean and prior standard deviation to perform the Bayesian meta-analyses. Therefore, it remains unclear how to perform a fair comparison between the Bayesian and non-Bayesian estimators, as found in [65,66]. A carefully designed comparative study will be helpful for guiding users to apply two R packages: meta.shrinkage and bayesmeta.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/a15010026/s1.
Author Contributions
Conceptualization, N.T. and T.E.; methodology, N.T. and T.E.; data curation, N.T. and T.E.; writing, N.T., T.E., H.M. and Y.-T.C.; supervision, T.E., H.M. and Y.-T.C.; funding acquisition, H.M. and Y.-T.C. All authors have read and agreed to the published version of the manuscript.
Funding
Michimae H. is financially supported by JSPS KAKENHI Grant Number JP21K12127. Chang Y.T. is financially supported by JSPS KAKENHI Grant Number JP26330047 and JP18K11196.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the numerical results of the article are fully reproducible by the R code in the main text and appendices. The proposed R package is downloadable online from CRAN (https://CRAN.R-project.org/package=meta.shrinkage (accessed on 15 November 2021)) or from the “tar.gz” file from the article’s Supplementary Material.
Acknowledgments
The authors thank the two referees for their valuable suggestions that improved the article. We thank Alina Chen from the Algorithms Editorial Office for her offer to publish free of APC.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. R Code for Simulations
#install.packages(“meta.shrinkage”)
library(meta.shrinkage)
R = 10,000
Sa = “Scenario (a): True means: (−2,−2,−1,−1,0,0,1,1,2,2); Ordered & Non-sparse”
Sb = “Scenario (b): True means: (0,0,0,0,0,0,0,0,5,10); Ordered & Sparse”
Sc = “Scenario (c): True means: (1,−1,1,−1,1,−1,1,−1,1,−1); Unordered & Non-sparse”
Sd = “Scenario (d): True means: (0,0,0,1,0,0,0,1,0,0); Unordered & Sparse”
Se = “Scenario (e): True means: (2,2,1,1,0,0,−1,−1,−2,−2); Ordered & Non-sparse”
Sf = “Scenario (f): True means: (0,0,0,0,0,0,0,0,−2,−4); Ordered & Sparse”
Mu = c(−2,−2,−1,−1,0,0,1,1,2,2);nam = Sa
#Mu = c(0,0,0,0,0,0,0,0,5,10);nam = Sb
#Mu = c(1,−1,1,−1,1,−1,1,−1,1,−1);nam = Sc
#Mu = c(0,0,0,1,0,0,0,1,0,0);nam = Sd
#Mu = c(2,2,1,1,0,0,−1,−1,−2,−2);nam = Se
#Mu = c(0,0,0,0,0,0,0,0,−2,−4);nam = Sf
G = length(Mu)
Mu_y = Mu_js = Mu_jsp = matrix(NA,R,G)
Mu_rml = Mu_rjs = Mu_rjsp = matrix(NA,R,G)
Mu_pt = Mu_gpt = matrix(NA,R,G)
W = matrix(NA,R,G)
mu_y = mu_js = mu_jsp = rep(NA,R)
mu_rml = mu_rjs = mu_rjsp = rep(NA,R)
for(i in 1:R){
set.seed(i)
Chisq = rchisq(1000,df = 1)/4
s = sqrt(Chisq[(Chisq> = 0.009)&(Chisq< = 0.6)][1:G])
W[i,] = 1/s^2
y = rnorm(G,mean = Mu,sd = s)
Mu_y[i,] = y
Mu_js[i,] = js(y,s)$JS
Mu_jsp[i,] = js(y,s)$JS_plus
Mu_rml[i,] = rml(y)$RML
Mu_rjs[i,] = rjs(y,s)$RJS
Mu_rjsp[i,] = rjs(y,s)$RJS_plus
Mu_pt[i,] = gpt(y,s)$PT
Mu_gpt[i,] = gpt(y,s)$GPT
## for scenarios (e) and (f)
#Mu_rml[i,] = rev(rml(y,decreasing = TRUE)$RML)
#Mu_rjs[i,] = rev(rjs(y,s,decreasing = TRUE)$RJS)
#Mu_rjsp[i,] = rev(rjs(y,s,decreasing = TRUE)$RJS_plus)
}
Mu_mat = matrix(rep(Mu,R),nrow = R,ncol = G,byrow = TRUE)
TMSE_y = sum( colMeans((Mu_y-Mu_mat)^2) )
TMSE_js = sum( colMeans((Mu_js-Mu_mat)^2) )
TMSE_jsp = sum( colMeans((Mu_jsp-Mu_mat)^2) )
TMSE_rml = sum( colMeans((Mu_rml-Mu_mat)^2) )
TMSE_rjs = sum( colMeans((Mu_rjs-Mu_mat)^2) )
TMSE_rjsp = sum( colMeans((Mu_rjsp-Mu_mat)^2) )
TMSE_pt = sum( colMeans((Mu_pt-Mu_mat)^2) )
TMSE_gpt = sum( colMeans((Mu_gpt-Mu_mat)^2) )
TMSE = c(TMSE_y,TMSE_js,TMSE_jsp,TMSE_rml,
TMSE_rjs,TMSE_rjsp,TMSE_pt,TMSE_gpt)
barplot(TMSE,names.arg = c(“Y”,”JS”,”JS+”,”RML”,”RJS”,”RJS+”,”PT”,”GPT”),
col = c(“red”,”purple”,”blue”,”darkgreen”,”green”,
“lightgreen”,”orange”,”brown”),
main = nam,xlab = “Estimator”,ylab = “TMSE”)
Appendix B. R Code for the Data Example
#install.packages(“mvmeta”)
library(mvmeta)
#install.packages(“meta.shrinkage”)
library(meta.shrinkage)
data(hyp)
dat<-hyp
#-------------------
# JS estimator and JS_plus estimator
#-------------------
JS<-js(dat$sbp,dat$sbp_se)
id<-c(2,8,3,6,4,5,7,10,1,9)
dat1<-data.frame(“Y” = dat$sbp,”JS” = JS[,1],”JS_plus” = JS[,2],”id” = id)
dat1
dat2<-dat1[order(dat1$id,decreasing = T),]
#-------------------
# RML estimator
#-------------------
RML<-rml(dat$sbp,x = dat$dbp,id = dat$study,test = TRUE)
#-------------------
# RJS estimator and RJS+ estimator
#-------------------
RJS<-rjs(dat$sbp,dat$sbp_se,x = dat$dbp,id = dat$study)
res<-data.frame(“Study” = RML$id,”x”=RML$x,”Y” = dat2$Y,”JS” = dat2$JS
,”JS_plus” = dat2$JS_plus,”RML” = RML$RML
,”RJS” = RJS$RJS,”RJS_plus” = RJS$RJS_plus)
res
References
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kaiser, T.; Menkhoff, L. Financial education in schools: A meta-analysis of experimental studies. Econ. Educ. Rev. 2020, 78, 101930. [Google Scholar] [CrossRef] [Green Version]
- Leung, Y.; Oates, J.; Chan, S.P. Voice, articulation, and prosody contribute to listener perceptions of speaker gender: A systematic review and meta-analysis. J. Speech Lang. Hear. Res. 2018, 61, 266–297. [Google Scholar] [CrossRef] [PubMed]
- DerSimonian, R.; Laird, N. Meta-analysis in clinical trials revisited. Contemp. Clin. Trials 2015, 45, 139–145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleiss, J.L. Review papers: The statistical basis of meta-analysis. Stat. Methods Med. Res. 1993, 2, 121–145. [Google Scholar] [CrossRef]
- Batra, K.; Singh, T.P.; Sharma, M.; Batra, R.; Schvaneveldt, N. Investigating the psychological impact of COVID-19 among healthcare workers: A meta-analysis. Int. J. Environ. Res. Public Health 2020, 17, 9096. [Google Scholar] [CrossRef]
- Pranata, R.; Lim, M.A.; Huang, I.; Raharjo, S.B.; Lukito, A.A. Hypertension is associated with increased mortality and severity of disease in COVID-19 pneumonia: A systematic review, meta-analysis and meta-regression. J. Renin-Angiotensin-Aldosterone Syst. 2020, 21, 1470320320926899. [Google Scholar] [CrossRef]
- Wang, Y.; Kala, M.P.; Jafar, T.H. Factors associated with psychological distress during the coronavirus disease 2019 (COVID-19) pandemic on the predominantly general population: A systematic review and meta-analysis. PLoS ONE 2020, 15, e0244630. [Google Scholar] [CrossRef]
- Rice, K.; Higgins, J.P.; Lumley, T. A re-evaluation of fixed effect(s) meta-analysis. J. R. Stat. Soc. Ser. A 2018, 181, 205–227. [Google Scholar] [CrossRef]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Shinozaki, N.; Chang, Y.-T. Minimaxity of empirical Bayes estimators of the means of independent normal variables with unequal variances. Commun. Stat.-Theor. Methods 1993, 8, 2147–2169. [Google Scholar] [CrossRef]
- Shinozaki, N.; Chang, Y.-T. Minimaxity of empirical Bayes estimators shrinking toward the grand mean when variances are unequal. Commun. Stat.-Theor. Methods 1996, 25, 183–199. [Google Scholar] [CrossRef]
- Singh, H.P.; Vishwakarma, G.K. A family of estimators of population mean using auxiliary information in stratified sampling. Commun. Stat.-Theor. Methods 2008, 37, 1038–1050. [Google Scholar] [CrossRef]
- DerSimonian, R.; Laird, N. Meta-analysis in clinical trials. Control. Clin. Trials 1986, 7, 177–188. [Google Scholar] [CrossRef]
- Röver, C. Bayesian random-effects meta-analysis using the bayesmeta R package. J. Stat. Softw. 2020, 93, 1–51. [Google Scholar] [CrossRef]
- Raudenbush, S.W.; Bryk, A.S. Empirical bayes meta-analysis. J. Educ. Stat. 1985, 10, 75–98. [Google Scholar] [CrossRef]
- Schmid, C. Using bayesian inference to perform meta-analysis. Eval. Health Prof. 2001, 24, 165–189. [Google Scholar] [CrossRef] [PubMed]
- Röver, C.; Friede, T. Dynamically borrowing strength from another study through shrinkage estimation. Stat. Methods Med. Res. 2020, 29, 293–308. [Google Scholar] [CrossRef] [Green Version]
- Röver, C.; Friede, T. Bounds for the weight of external data in shrinkage estimation. Biom. J. 2021, 63, 1131–1143. [Google Scholar] [CrossRef]
- Taketomi, N.; Konno, Y.; Chang, Y.-T.; Emura, T. A Meta-Analysis for Simultaneously Estimating Individual Means with Shrinkage, Isotonic Regression and Pretests. Axioms 2021, 10, 267. [Google Scholar] [CrossRef]
- Shinozaki, N. A note on estimating the common mean of k normal distributions and the stein problem. Commun. Stat.-Theory Methods 1978, 7, 1421–1432. [Google Scholar] [CrossRef]
- Malekzadeh, A.; Kharrati-Kopaei, M. Inferences on the common mean of several normal populations under hetero-scedasticity. Comput. Stat. 2018, 33, 1367–1384. [Google Scholar] [CrossRef]
- Everitt, B. Modern Medical Statistics: A Practical Guide; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Lin, L. Hybrid test for publication bias in meta-analysis. Stat. Methods Med. Res. 2020, 29, 2881–2899. [Google Scholar] [CrossRef]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Shao, J. Mathematical Statistics; Springer: New York, NY, USA, 2003. [Google Scholar]
- van der Pas, S.; Salomond, J.-B.; Schmidt-Hieber, J. Conditions for posterior contraction in the sparse normal means problem. Electron. J. Stat. 2016, 10, 976–1000. [Google Scholar] [CrossRef]
- GASTRIC (Global Advanced/Adjuvant Stomach Tumor Research International Collaboration) Group. Role of chemotherapy for advanced/recurrent gastric cancer: An individual-patient-data meta-analysis. Eur. J. Cancer 2013, 49, 1565–1577. [Google Scholar] [CrossRef] [PubMed]
- James, W.; Stein, C. Estimation with quadratic loss. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; Volume 1, pp. 443–460. [Google Scholar]
- van Eeden, C. Restricted Parameter Space Estimation Problems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Li, W.; Li, R.; Feng, Z.; Ning, J. Semiparametric isotonic regression analysis for risk assessment under nested case-control and case-cohort designs. Stat. Methods Med. Res. 2020, 29, 2328–2343. [Google Scholar] [CrossRef] [PubMed]
- Robertson, T.; Wright, F.T.; Dykstra, R. Order Restricted Statistical Inference; Wiley: Chichester, UK, 1988. [Google Scholar]
- Turner, R. Pava: Linear order isotonic regression, Cran. 2020. Available online: https://CRAN.R-project.org/package=Iso (accessed on 14 November 2021).
- Tsukuma, H. Simultaneous estimation of restricted location parameters based on permutation and sign-change. Stat. Pap. 2012, 53, 915–934. [Google Scholar] [CrossRef]
- Chang, Y.-T. Stein-Type Estimators for Parameters Restricted by Linear Inequalities; Faculty of Science and Technology, Keio University: Tokyo, Japan, 1981; Volume 34, pp. 83–95. [Google Scholar]
- Bancroft, T.A. On biases in estimation due to the use of preliminary tests of significance. Ann. Math. Stat. 1944, 15, 190–204. [Google Scholar] [CrossRef]
- Judge, G.G.; Bock, M.E. The Statistical Implications of Pre-Test and Stein-Rule Estimators in Econometrics; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Khan, S.; Saleh, A.K.M.E. On the comparison of the pre-test and shrinkage estimators for the univariate normal mean. Stat. Pap. 2001, 42, 451–473. [Google Scholar] [CrossRef] [Green Version]
- Magnus, J.R. The traditional pretest estimator. Theory Probab. Its Appl. 2000, 44, 293–308. [Google Scholar] [CrossRef]
- Magnus, J.R.; Wan, A.T.; Zhang, X. Weighted average least squares estimation with nonspherical disturbances and an application to the Hong Kong housing market. Comput. Stat. Data Anal. 2011, 55, 1331–1341. [Google Scholar] [CrossRef]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. A class of general pretest estimators for the univariate normal mean. Commun. Stat.-Theory Methods 2021. [Google Scholar] [CrossRef]
- Shih, J.-H.; Lin, T.-Y.; Jimichi, M.; Emura, T. Robust ridge M-estimators with pretest and Stein-rule shrinkage for an intercept term. Jpn. J. Stat. Data Sci. 2021, 4, 107–150. [Google Scholar] [CrossRef]
- Kibria, B.G.; Saleh, A.M.E. Optimum critical value for pre-test estimator. Commun. Stat.-Simul. Comput. 2006, 35, 309–319. [Google Scholar] [CrossRef]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. Estimation of a common mean vector in bivariate meta-analysis under the FGM copula. Statistics 2019, 53, 673–695. [Google Scholar] [CrossRef]
- Gleser, L.J.; Olkin, L. Stochastically dependent effect sizes. In the Handbook of Research Synthesis; Russel Sage Foundation: New York, NY, USA, 1994. [Google Scholar]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. Copula-based estimation methods for a common mean vector for bivariate meta-analyses. Symmetry 2021, in press. [Google Scholar]
- Emura, T.; Sofeu, C.L.; Rondeau, V. Conditional copula models for correlated survival endpoints: Individual patient data meta-analysis of randomized controlled trials. Stat. Methods Med. Res. 2021, 30, 2634–2650. [Google Scholar] [CrossRef] [PubMed]
- Mavridis, D.; Salanti, G.A. practical introduction to multivariate meta-analysis. Stat. Methods Med. Res. 2013, 22, 133–158. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.; Xiang, L.; Wang, S. Semiparametric regression analysis of clustered survival data with semi-competing risks. Comput. Stat. Data Anal. 2018, 124, 53–70. [Google Scholar] [CrossRef]
- Peng, M.; Xiang, L. Correlation-based joint feature screening for semi-competing risks outcomes with application to breast cancer data. Stat. Methods Med. Res. 2021, 30, 2428–2446. [Google Scholar] [CrossRef]
- Riley, R.D. Multivariate meta-analysis: The effect of ignoring within-study correlation. J. R. Stat. Soc. Ser. A 2009, 172, 789–811. [Google Scholar] [CrossRef]
- Copas, J.B.; Jackson, D.; White, I.R.; Riley, R.D. The role of secondary outcomes in multivariate meta-analysis. J. R. Stat. Soc. Ser. C 2018, 67, 1177–1205. [Google Scholar] [CrossRef]
- Sofeu, C.L.; Emura, T.; Rondeau, V. A joint frailty-copula model for meta-analytic validation of failure time surrogate endpoints in clinical trials. BioMed. J. 2021, 63, 423–446. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, Y.; Maruo, K. Bivariate beta-binomial model using Gaussian copula for bivariate meta-analysis of two binary outcomes with low incidence. Jpn. J. Stat. Data Sci. 2019, 2, 347–373. [Google Scholar] [CrossRef] [Green Version]
- Kawakami, R.; Michimae, H.; Lin, Y.-H. Assessing the numerical integration of dynamic prediction formulas using the exact expressions under the joint frailty-copula model. Jpn. J. Stat. Data Sci. 2021, 4, 1293–1321. [Google Scholar] [CrossRef]
- Nikoloulopoulos, A.K. A vine copula mixed effect model for trivariate meta-analysis of diagnostic test accuracy studies accounting for disease prevalence. Stat. Methods Med. Res. 2017, 26, 2270–2286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karamikabir, H.; Afshari, M. Generalized Bayesian shrinkage and wavelet estimation of location parameter for spherical distribution under balance-type loss: Minimaxity and admissibility. J. Multivar. Anal. 2020, 177, 104583. [Google Scholar] [CrossRef]
- Bilodeau, M.; Kariya, T. Minimax estimators in the normal MANOVA model. J. Multivar. Anal. 1989, 28, 260–270. [Google Scholar] [CrossRef] [Green Version]
- Konno, Y. On estimation of a matrix of normal means with unknown covariance matrix. J. Multivar. Anal. 1991, 36, 44–55. [Google Scholar] [CrossRef] [Green Version]
- Karamikabir, H.; Afshari, M.; Lak, F. Wavelet threshold based on Stein’s unbiased risk estimators of restricted location parameter in multivariate normal. J. Appl. Stat. 2021, 48, 1712–1729. [Google Scholar] [CrossRef]
- Pandey, B.N. Testimator of the scale parameter of the exponential distribution using LINEX loss function. Commun. Stat.-Theory Methods 1997, 26, 2191–2202. [Google Scholar] [CrossRef]
- Vishwakarma, G.K.; Gupta, S. Shrinkage estimator for scale parameter of gamma distribution. Commun. Stat.-Simul. Comput. 2020. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Shinozaki, N. New types of shrinkage estimators of Poisson means under the normalized squared error loss. Commun. Stat.-Theory Methods 2019, 48, 1108–1122. [Google Scholar] [CrossRef]
- Hamura, Y. Bayesian shrinkage approaches to unbalanced problems of estimation and prediction on the basis of negative multinomial samples. Jpn. J. Stat. Data Sci. 2021. [Google Scholar] [CrossRef]
- Soliman, A.-A.; Abd Ellah, A.H.; Sultan, K.S. Comparison of estimates using record statistics from Weibull model: Bayesian and non-Bayesian approaches. Comput. Stat. Data Anal. 2006, 51, 2065–2077. [Google Scholar] [CrossRef]
- Rehman, H.; Chandra, N. Inferences on cumulative incidence function for middle censored survival data with Weibull regression. Jpn. J. Stat. Data Sci. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).