Abstract
This paper presents an algorithm for the fully automatic mesh generation for the finite element analysis of ships and offshore structures. The quality requirements on the mesh generator are imposed by the acceptance criteria of the classification societies as well as the need to avoid shear locking when using low degree shell elements. The meshing algorithm will be generating quadrilateral dominated meshes (consisting of quads and triangles) and the mesh quality requirements mandate that quadrilaterals with internal angles close to 90° are to be preferred. The geometry is described by a dictionary containing points, rods, surfaces, and openings. The first part of the proposed method consists of an algorithm to automatically clean the geometry. The corrected geometry is then meshed by the frontal Delaunay mesh generator as implemented in the gmsh package. We present a heuristic method to precondition the cross field of the fronatal quadrilateral mesher. In addition, the influence of the order in which the plates are meshed will be explored as a preconditioning step.
1. Introduction
This paper is concerned with automatic mesh generation in the process of the structural analysis of ships and off-shore structures. The ship structural analysis by the finite element method is governed by the acceptance criteria of the classification societies [1]. One of the possibilities to describe an input geometry, for a large class of such structures, is by the use of a dictionary of elements. The dictionaries which we will be considering in this paper consist of points, rods, surfaces, and openings. The points in the dictionary describe positions where the loads (for the finite element analysis) are going to be applied or the measurements are going to be taken. Rods describe the panel stiffeners or pillars. The set of surfaces will consist of three types of entities: web surfaces (parallelograms with one dimension much smaller than the other), regular surfaces (convex quadrilaterals defined by four co-planar nodes), and warped surfaces (closed loop surface defined by four corners which need not be co-planar) [2,3]. The preconditioning method which we are going to describe extends and improves the meshing algorithm from [4]. The algorithm from [4], called pyREMAKEmsh, is designed for the dictionaries that do not contain the warped surfaces. The present algorithm is extended to include the warped surfaces and also to improve the quality of the mesh by further preconditioning of the geometry. Our algorithm is intended for full automatic meshing of sections of ship structures (such as superstructures, decks, …) according to the rules of classification societies.
In a typical situation, a description of a geometry by a dictionary of elements contains many modeling inconsistencies such as overlapping plates or plates not in contact. Note that a stiffened panel as a constructive element is modeled by a plate (shell) in contact with a rod or a web surface. The constructed mesh should not contain any hanging nodes. However, it can happen, due to modeling inconsistency that e.g., a stiffener or a web surface does not overlap with a panel (model by a regular surface) which it is supposed to stiffen. Removing such modeling irregularities is fundamental both for the use of meshing algorithms which require that the surfaces are described as closed loop surfaces as well as by the subsequent finite element discretization procedures which require that there are no hanging nodes in the mesh [2,5]. The algorithm from [4] utilized boolean operations (with a tolerance) from Open CASCADE geometric kernel to solve this problem. The points in the dictionary represent locations where loads are applied or measurements are taken and so they need to be a part of the final mesh. This further complicates the meshing task. The requirements on a mesher are taken from ([6], Section 1.7) and can be summed up as:
- The elements with angles less than 45° and more than 135° should be avoided;
- In the high stress areas such as e.g., web surfaces, the use of triangular elements should be avoided.
- The use of triangular shell elements should be kept to the minimum.
- Quadrilateral shell elements with a high aspect ratio as well as distorted elements should be avoided—aspect ratio for quadrilaterals is to be kept close to 1 but should not exceed 3 for 4 node elements and should not exceed 5 for three node elements (triangles).
- Web surfaces should be modeled with at least four elements along the shorter dimension, and ideally with precisely four elements.
- The element size should be at least , where t is the thickness of the element.
Let us emphasize that classification societies use results of finite element analysis to accept or reject a ship’s design. The rules of the classification societies such as ([6], Section 1.7) specify the protocol for performing the sip structural analysis. This protocol includes restriction of the size and the type of finite element’s used and the bullet list provided above is a summary of the relevant requirements from the perspecive of a finite element mesh generator. Let us point out that an analysis which does not adhere to the classification rules such as [6] cannot lead to acceptance of the ships’ design and as such can incur severe opportunity costs on a user of a meshing tool. These requirements pose a challenge for implementing fully automatic meshing routines. Namely, these rules most often pose local linear constraints on the mesh and as such clash with the geometry optimization algorithms which search for globally optimal tessellations, see [5]. We relax those restrictions in order to accommodate more complex geometries typically encountered in ship structural analysis.
Let us briefly review the available results concerning fully automatic mesh generation for ship structural analysis. Meshes based on quadrilateral elements can either be generated directly by an advancing front algorithm, see [7] or by a hierarchical grid-based subdivision methods [8]. In this paper, we explore a third option, which is the construction of a quadrilateral dominated mesh by a recombination of triangular mesh [9,10]. An algorithm based on the preconditioned Blossom recombination approach [10] has been implemented in the pyREMAKEmsh algorithm presented in [4]. The method was designed for dictionaries which only contained co-planar plates. It was based on the control of the cross field, [11], using the insertion of virtual stiffeners. These stiffeners are used to split a plate with which they intersect but are not included in the dictionary as rod elements.
In this approach, it is necessary that the original triangular mesh be generated so that a recombination yields a regular quadrilateral mesh. Quadrilateral elements in gmsh are generated indirectly by the perfect matching algorithm based on the graph theoretic Blossom algorithm [10,12]. A default implementation starts from a standard Delaunay advancing front algorithm implemented in the metric. An important extension and improvement to the Blossom algorithm based quadrilateral mesh generation is realized by adapting the triangular advancing front mesher so that the generated triangular mesh can be efficiently matched into a regular quadrilateral mesh. It is achieved by modifying the advancing front Delaunay mesh generator with the change of norm from to the norm. It is a geometric fact that an equilateral triangle in the norm is in fact the right angle isosceles triangle, whereas an equilateral triangle in the (Euclidean) norm has internal angles equal to 60°, see [13]. With this change of norm, the triangles which are generated by the Delaunay algorithm will tend to be closer to right angle triangles and so will be amenable to good recombination into a regular quadrilateral mesh, see [13].
In this paper, we will present a geometry improvement algorithm which can tackle geometries containing warped plates. The algorithm is based on the processing pipeline which utilizes boolean operations in the 3D geometry kernel Open CASCADE to correct the geometry errors and to enforce local linear constraints. Furthermore, we will introduce a preprocessing step to make the results of the meshing algorithm repeatable and to control the mesh quality.
The makeup of the paper is as follows: We will first present materials and methods where we will describe the challenges and the necessary modifications to the algorithm necessary to be able to tackle warped plates. We will then present results of the applications of these algorithm to two characteristic examples from engineering practice. In the Discussion section, we will present statistical evaluation of the preprocessing algorithm.
2. Materials and Methods
Many modern quadrilateral meshing algorithms are designed around the notion of the cross field [11]. This is a heuristic function defined based on the geometry, and it models the preferred orientation of the mesh. For quadrilateral mesh generating algorithm, this is taken to be parallel to the boundaries of the domain. Frontal meshing algorithms propagate this cross field from the boundaries towards the interior of a surface. The new point is inserted in a mesh so that it forms an equilateral triangle with two nearest previously inserted nodes. In the quad oriented algorithm, one uses the norm, and so the equilateral triangle is actually isosceles with an angle close to the right-angle. These triangles can then be optimally matched into quadrilaterals using the graph theoretic approach which minimizes the measure of the departure of a quad (a pair of triangles) from regularity. Furthermore, the unmatched triangle will be pushed by the marching front to the boundary. In what follows, we will describe the basic properties of the algorithm and our method of imposing further line restriction on the mesh by the addition of the virtual stiffeners (rods) to the model. Let us note that full recombination of the mesh is not always desirable since it might lead to the reduced quality of the quadrilaterals. The Blossom and the simple recombination algorithms will leave some triangles in the mesh in the case when recombining all the triangles would lead to low quality quads (either by the aspect ratio or angle criterion). In such cases, to generate full-quad meshes, the full-quad recombination algorithm is used. The algorithm performs a subdivision of the elements, followed by the further recombination and smoothing. The smoothing is performed using the Lloyd’s algorithm, and then the whole sequence is repeated until all of the triangles have been matched [14]. We will employ the full recombination algorithm only in the case when the returned mixed mesh has more than triangles. Even then, we will return both meshes and raise the flag that the processing pipeline did not produce a mesh which meets all of the constraints. We will see that the fully recombined mesh forces the satisfaction of requirement for almost no triangles at the expense of reducing the quality of the quadrilateral mesh.
To this end, let us rigorously define the mesh quality measures which we will be using to check the compliance with the rules of the classification societies. For a quadrilateral q with internal angles , , we define the quality measure
This quality measure is equal to one for the perfect rectangle, and it is zero in the presence of angles which are less than zero or greater than the straight angle (a nonconvex quadrangle). Let now be the mixed tesselation consisting of quadrilaterals and triangles. The set is a disjoint union of the set of all quadrilaterals and the set of all triangles in the mesh. To define the stopping criterion, we introduce the following measures. Here, marks the cardinality of a finite set. The average for the tesselation is defined by
The percentage of quadrilaterals with angles between 80° and 100° in is marked with
and the measure of the portion of the elements in the mesh which are not triangles is defined as . Finally, we define the quantity as the percentage of irregular elements. Those are quadrilaterals with aspect ration larger than 3, quads with at least one angle less than 10° and more than 170°. Distorted triangles are triangles with aspect ratio 1:5 or more or with one internal angle less than 10° and more than 170°. The reason for introducing these further element categories is in the numerical analysis of the accuracy of the finite element approximation method when low degree shell elements are used. The accuracy can deteriorate quite rapidly when the internal angles of an element are far from the right angle. Some lower quality elements are unavoidable, as can be dictated by the description of the geometry. Subsequently, we utilize statistical indicators measuring precisely these classes of “degenerate” elements and use this to compare head to head the performance of two different algorithms or preconditioning variants on the same geometry.
The controls which we use to improve the control the number of nodes used to resolve circular boundaries and the resolution of the web surface. A hard constraint on the number of elements per smaller dimension of the web surface is at least four. To enforce this constraint, we split each of the web surfaces along the shorter dimension into four strips. We use the integer vector to denote the rule with which a web surface is split into strips. As a result, the web surface will be split into strips with height ratio :::.
Since Boolean operations are not defined for spline surfaces, the warped elements are appended at the end of the list of surfaces. These are to be distinguished from the web surfaces which are defined as regular parallelograms and are meshed first. Furthermore, it has been noted that the resulting mesh does depend on the order in which the surfaces have been meshed. To this end, we sort the regular surfaces, after Boolean operations, to correct the geometry that has been performed, according to the descending .
We compare the performance of an algorithm using this statistical criterion. Recall that there are hard constraints for which the elements should have internal angles between 45° and 135° and that we are allowed up to triangles in the mesh. We will relax this criterion in that we will measure the percentage of quadrilaterals in the mesh which satisfy this criterion. In addition, we will extend this into the target function which accounts for the regular quadrilaterals (having the internal angles between 80° and 100°) and the overall percentage of the mesh covered by quadrilaterals.
3. Results
In this section, we will present results of measuring the quality indicators for four geometries denoted by dictionaries with co-planar plates and and two dictionaries which also contain the warped plates and . The geometry is presented on Figure 1, whereas the geometries , and are presented in Figure 2 and Figure 3.
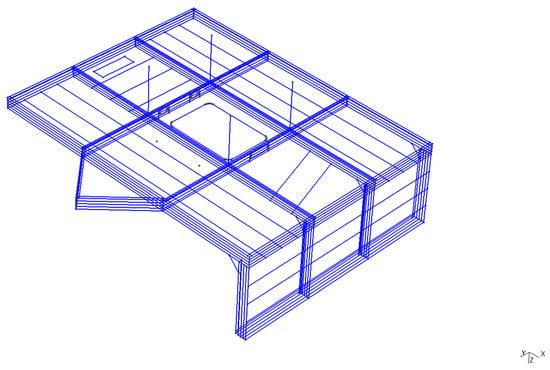
Figure 1.
Input dictionary describing the geometry. It consists of points, rods, and co-planar plates (convex quadrilaterals which are a subset of a plane).
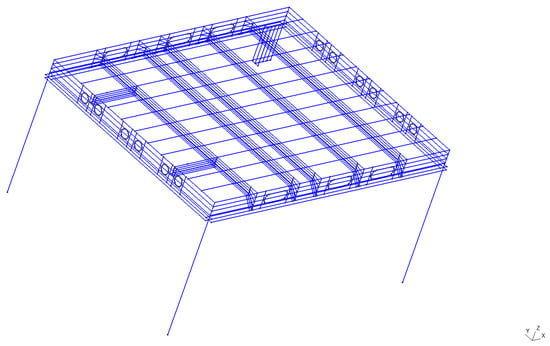
Figure 2.
Geometry .
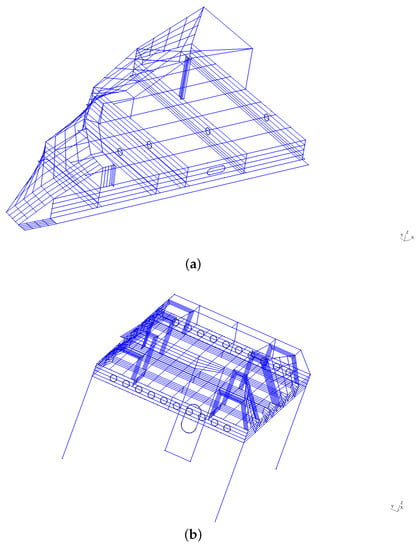
Figure 3.
Input geometries with warped plates in (a) and in (b).
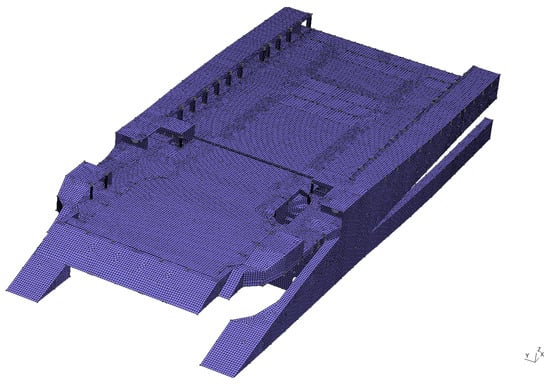
In Figure 4, we present a result of running the Algorithm 1 on the benchmark geometry . We se the hallmarks of an advancing front algorithm as well as an influence of the preiconditioning implemented as a variant of the virtual stiffener algorithm in order to control the local orientation of the quadrilaterals in the mesh (encoded in the cross-field function).

Figure 4.
Meshing using the preconditioned gmsh algorithm Packing for Parallelograms from [14].
The results of running the Algorithm 1 will be summarized in a table. We will also present details of some of the geometries. For instance, in the geometries from Figure 1 and Figure 2, we will be particularly concerned in the way in which the girders with holes have been resolved under the hard restriction of four elements per girder height. On the geometries with warped plates from Figure 3, we will concentrate on the effect of the cross-field—which will follow the warping of the plates—on the regularity of the mesh.
As a comparison, we present, exemplary, the results for the mesh produced by applying the full recombination algorithm. Our experiments on the five industry relevant geometries of varying complexities show that the number of triangles in the mesh is much smaller, but the number of regular quadrilaterals is reduced significantly and the overall number of elements can be almost double (see Table 1 and Table 2). In Figure 5b, we see that, even when the full recombination algorithm is used, preconditioning the geometry by virtual stiffeners and adapting the splitting of the web surface so that openings are in the two central strips limits the propagation of the effect of the smoothing algorithm, which reduced the number of triangles in the full recombination approach.
| Algorithm 1 Preconditioning the Packing for Parallelograms algorithm from [14] |
Require: A dictionary describing the geometry and the tolerance .
|

Table 1.
Quality measures for the studied geometries. Algorithm: Preconditioned algorithm Packing for Parallelograms.

Table 2.
Quality measures for the studied geometries. Algorithm: Full recombination combined with preconditioned Delaunay frontal meshing algorithm with smoothing.

Figure 5.
A comparison of the meshes for a web surface with openings from the geometry . We see that the full recombination algorithm produces an almost fully quadrilateral mesh, but the quality of the mesh, as measured by the SIGE indicator, for the full recombination algorithm is lower. In (a), we have the mesh generated by pyREMAKmsh and in (b) the fully recombined mesh.
Let us now compare the meshes generated by the preconditioned Packing for Parallelograms algorithm followed by a simple recombination as implemented in pyREMAKEmsh from [4] with the mesh obtained using the full recombination algorithm with smoothing [14,15]. We are comparing the meshes of the web surface with openings using the SIGE (signed inverse gradient error for the finite element solution) indicator from gmsh [3]. Elements marked by the lower SIGE indicator (color code from blue to green) do not meet the SIGE quality criterion. The elements marked in red are on the other hand of the highest quality.
4. Discussion and Conclusions
Let us now consider a more involved geometry describing a superstructure of a large yacht. This geometry will be denoted by and is depicted in Figure A1 and Figure A2. The generated mesh will have more than hundred thousand elements and we report the quality measures for the preconditioned recombination and the full recombination algorithms.
The geometry, together with details of the performance of two algorithms on the web surfaces, is presented in Figure 6.

Figure 6.
A comparison of the meshing algorithm on an example of a superstructure of a large yacht (geometry ). The details of the web surfaces are compared using the SIGE indicator. In (a), we have the mesh generated by pyREMAKmsh and in (b) the fully recombined mesh.
In order to emphasize the context of the mesh generation in ship structural analysis, let us emphasize that we are aiming for the coarsest mesh which satisfies the meshing rules posed by the classification societies. There are two reasons for this. One is the stability of the solution method which depends on the condition number of the finite element stiffness matrices which in turn deteriorate with aggressive mesh refinement. In other words, the element shape has much more adverse effects on the accuracy than the element size. The other is that there is a lower limit on the mesh size which is incurred by the material properties (thickness of the plates). Subsequently, the rules of the classification societies are to be interpreted as ingredients of the cost functions for the optimization and the quality measure of the mesh should further be penalized by the number of elements. This is precisely what we have achieved with our algorithm. We have chosen the combination of the algorithms (recombination and triangulation) together with the preconditioning steps (Boolean operations and virtual stiffeners) which optimize precisely such cost functions. A further argument for the preference of coarser meshes stems from the fact that we intend this algorithm to be used in the early stages of the design process when many design alternatives are tested, and this procedure allows for a cheep assessment if the proposed design adheres to the rules of the classification society. This design might be discarded later due to other reasons, so having to repeat only a cheap and reliable procedure is a big gain for a designers who might get to test more alternatives which are all conforming.
We see that the pyREMAKEmsh algorithm typically achieves the quality restrictions as posed by the classification societies. It should be noted that on challenging geometries smaller in size (containing web surfaces with many openings), it is possible that the preconditioned Packing for Parallelograms algorithm (as implemented in pyREMAKEmsh can have as many as triangles (geometries , and ). However, those triangles do not affect, as measured by the SIGE indicator, the high stress area adversely. On the other hand, the full recombination algorithm can achieve and almost exclusively quadrilateral mesh at the expense of a lower element quality. This can in particular be seen in Table 2 where the number of degenerate elements can be as high as . Furthermore, the SIGE criterion shows that these lower quality elements can be found in a high stress area such as web surfaces. In addition, in an example of a large geometry (120,000 elements for the pyREMAKEmsh algorithm and almost twice as many for the full recombination algorithm, see Table 3), we see that pyREMAKEmsh can produce the meshes with as few as less than 5% triangles. We also see that the running time of the triangulation algorithm seems to scale linearly, whereas the recombination algorithm can scale super linearly and the smoothing and full recombination algorithm is much more costly in terms of the running time. This further justifies our choice of the building blocks of the pyREMAKEmsh algorithm.

Table 3.
The mesh quality of the superstructure of a large yacht (geometry ).
Finally, let us note that the accuracy of the finite element solution for typical low degree shell elements can sometimes be reduced by more than when elements whose internal angles are far away from the right angle are used. This is the reason why we have opted to return both a fully recombined mesh as well as a preconditioned quadrilateral mesh with the warning flag raised. It will be future work to perform a full empirical parametric study of the relationship between the lowest angle in the mesh and the accuracy of the finite element approximation for various types of appropriate shell elements. In addition, a study of different (non standard) shell elements which might have a lesser dependence on the geometry of the mesh might prove to be a viable (albeit nonstandard) alternative.
Author Contributions
All three authors contributed equally to all segments of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported in part by EU Regional Development Funds under the project: KK.01.2.1.01.0124—Development of efficient methodology for finite element method based structural analysis of marine structures—REMAKE.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used for testing purposes as well as the code are available from github https://github.com/PMF-ZNMZR/pyREMAKEmsh (accessed on 13 November 2021).
Acknowledgments
The authors would like to thank the REMAKE project coordinator Bonum d.o.o team for help during preparation of an automatic meshing module and for providing the geometrical models which are relevant from an engineering perspective.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| SIGE | signed inverse gradient error for the finite element solution |
| web surface | a parallelogram with one dimension much smaller than the other |
| regular surface | quadrilateral defined by four co-planar corners |
| warped surfaces | generalized quadrilateral defined by four not co-planar corners |
References
- Nersesian, R.; Mahmood, S. International Association of Classification Societies: Handbook of Transnational Economic Governance Regimes; Brill|Nijhoff: Leiden, Belgium, 2009; pp. 765–774. [Google Scholar] [CrossRef]
- Hughes, O.; Paik, J.K. Ship Structural Analysis and Design; The Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 2010. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.2579 (accessed on 13 November 2021). [CrossRef]
- Grubišić, L.; Lacmanović, D.; Tambača, J. Automatic mesh generation for structural analysis in naval architecture. In Proceedings of the International Conference on Ships and Offshore Structures ICSOS 2021, Hamburg, Germany, 6–8 September 2021; Paper 13. p. 10. [Google Scholar]
- Jang, B.S.; Suh, Y.S.; Kim, E.K.; Lee, T.H. Automatic FE modeler using stiffener-based mesh generation algorithm for ship structural analysis. Mar. Struct. 2008, 21, 294–325. [Google Scholar] [CrossRef]
- DNVGL. DNVGL-CG-0127 CLASS GUIDELINE: Finite Element Analysis. 2020. Available online: https://rules.dnvgl.com/docs/pdf/DNVGL/CG/2020-08/DNVGL-CG-0127.pdf (accessed on 13 November 2021).
- Blacker, T.D.; Stephenson, M.B. Paving: A New Approach to Automated Quadrilateral Mesh Generation. Int. J. Numer. Methods Eng. 1991, 32, 811–847. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.1620320410 (accessed on 13 November 2021). [CrossRef]
- Baehmann, P.L.; Wittchen, S.L.; Shephard, M.S.; Grice, K.R.; Yerry, M.A. Robust, geometrically based, automatic two-dimensional mesh generation. Int. J. Numer. Methods Eng. 1987, 24, 1043–1078. [Google Scholar] [CrossRef]
- Pellenard, B.; Orbay, G.; Chen, J.; Sohan, S.; Kwok, W.; Tristano, J.R. QMCF: QMorph Cross Field-driven Quad-dominant Meshing Algorithm. Procedia Eng. 2014, 82, 338–350. [Google Scholar] [CrossRef] [Green Version]
- Remacle, J.F.; Lambrechts, J.; Seny, B.; Marchandise, E.; Johnen, A.; Geuzainet, C. Blossom-Quad: A non-uniform quadrilateral mesh generator using a minimum-cost perfect-matching algorithm. Int. J. Numer. Methods Eng. 2012, 89, 1102–1119. [Google Scholar] [CrossRef] [Green Version]
- Lévy, B.; Liu, Y. Lp Centroidal Voronoi Tessellation and Its Applications. ACM Trans. Graph. 2010, 29, 119. [Google Scholar] [CrossRef]
- Edmonds, J. Maximum matching and a polyhedron with 0,1-vertices. J. Res. Natl. Bur. Stand. Sect. B Math. Math. Phys. 1965, 69, 55–56. [Google Scholar] [CrossRef]
- Remacle, J.F.; Henrotte, F.; Carrier-Baudouin, T.; Béchet, E.; Marchandise, E.; Geuzaine, C.; Mouton, T. A frontal Delaunay quad mesh generator using the L∞ norm. Int. J. Numer. Methods Eng. 2013, 94, 494–512. [Google Scholar] [CrossRef]
- Baudouin, T.C.; Remacle, J.F.; Marchandise, E.; Henrotte, F.; Geuzaine, C. A frontal approach to hex-dominant mesh generation. Adv. Model. Simul. Eng. Sci. 2014, 1, 8. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi Tessellations: Applications and Algorithms. SIAM Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).