Fixed Point Results on Multi-Valued Generalized (α,β)-Nonexpansive Mappings in Banach Spaces

Abstract

In this paper, we provide and study the concept of multi-valued generalized $(\alpha ,\beta )$-nonexpansive mappings, which is the multi-valued version of the recently developed generalized $(\alpha ,\beta )$-nonexpansive mappings. We establish some elementary properties and fixed point existence results for these mappings. Moreover, a multi-valued version of the M-iterative scheme is proposed for approximating fixed points of these mappings in the weak and strong senses. Using an example, we also show that M-iterative scheme converges faster as compared to many other schemes for this class of mappings.

1. Introduction

We often denote the set of natural numbers by using the notation $\mathbb{N}$. Fixed point theory provides useful tools for solving different types of nonlinear problems, for which ordinary analytical methods fail. Fixed point theory for different types of single-valued mappings is now well-developed. One of the basic results, the Banach contraction theorem (BCT) [1], was successfully applied for finding the approximate solutions for many nonlinear problems that arise in the applied sciences. However, fixed point theory of multi-valued mappings is more difficult but more important than the corresponding theory of single-valued mappings (see, e.g., [2] and others). Thus, it is always desirable to study and extend the fixed point results for single-valued mappings to the case of multi-valued mappings. To study fixed point theory in the case of multi-valued mappings, we often need the following notion of distance—$(C,E)\to H(C,E)$, known as the Pompeiu Housdorff metric, which is defined by

$$H(C,E)=max\left\{\underset{c\in C}{sup}d(c,E),\underset{e\in E}{sup}d(C,e)\right\},\mathrm{for}\mathrm{each}C,E\in S\left(B\right).$$

where B is a subset of a Banach space and $S\left(B\right)$ is the set of all subsets of B. A subset E of X is said to be proximinal if, for all $x\in X$, there is an element $y\in E$ such that $\left|\right|x-y\left|\right|=d(x,E)$, where $d(x,E)=inf\left\{\left|\right|x-z\left|\right|:z\in E\right\}$. Throughout this paper, we use the notations $P_r\left(B\right)$ for the set of all proximinal subsets and $S_{cb}\left(B\right)$ for the set of all bounded and closed subsets of B. Suppose X is a Banach space and $\mathsf{Ø}\ne B\subseteq X$. Let $\mathbb{J}:B\to B$ and $p_{{}_0}\in B$. The point $p_0$ is regarded as a fixed point for $\mathbb{J}$ if $p_{{}_0}=\mathbb{J}\left(p_{{}_0}\right)$. On the other hand, if $\mathbb{J}:B\to S\left(B\right)$ is a multi-valued mapping and $p_0\in B$, the point $p_0$ is regarded as a fixed point (resp. an endpoint) for $\mathbb{J}$ if $p_{{}_0}\in \mathbb{J}\left(p_{{}_0}\right)$ (resp. $\mathbb{J}\left(p_0\right)=\left\{p_0\right\})$. The set of fixed point (resp. the set of endpoints) of $\mathbb{J}$ is often represented by $F_{ix}\left(\mathbb{J}\right)$ (resp. by $E_{nd}\left(\mathbb{J}\right)$).

Note that Nadler [3] proved the multi-version of BCP. In 1965, Browder [4] and Gohde [5] (cf. also Kirk [6] and others) provided a well-known result, which shows that, in a uniformly convex Banach space (UCBS) setting, nonexpansive selfmaps admit fixed points. The multi-valued version of these results are proved by Lim [7]. In 2008, Suzuki [8] suggested a condition on selfmaps, which he named condition (C) and proved that this condition is weaker than the concept of nonexpansive selfmaps. Very soon, Abkar and Eslamian [9] extended his concept to the case of multi-valued maps. In 2011, Aoyama and Kohsaka [10] defined and studied the notion of $\alpha$-nonexpansive selfmaps. These mappings also include nonexpansive maps. The multi-valued version of $\alpha$-nonexpansive mappings was introduced by Hajisharif [11]. In the year 2017, Pant and Shukla [12] studied the class of generalized $\alpha$-nonexpansive mappings and showed that this new class of maps properly included Suzuki maps [8] and partially included $\alpha$-nonexpansive maps due to Aoyama and Kohsaka [10]. Soon, Iqbal et al. [13] showed that their idea holds for the case of multi-valued mappings. In 2019, Pandey et al. [14] introduced the notion of $\beta$–Riech–Suzuki type nonexpansive selfmaps. Recently, Maldar et al. [15] obtained the multi-valued version of these maps. In 2020, Ullah et al. [16] defined generalized $(\alpha ,\beta )$-nonexpansive maps. These maps are very important because they included both of the classes due to Pant and Shukla [12] and Pandey et al. [14]. The purpose of the present work is to provide the multi-valued version of these maps and to study the related fixed point results.

After existence of fixed point for a mapping, it is natural to find the value of that fixed point. For this purpose, different iteration processes, i.e.,those of Mann [17], Ishikawa [18], Agarwal [19], SP [20], Abbas [21], Noor [22], CR [23], Normal-S [24], Thakur New [25] and M-iteration [26], etc., have been introduced. The approximating of a fixed point using an effective iterative technique is an important field of research. For instance, Khatoon and Uddin [27] studied Abbas’ iterative scheme for G-nonexpansive operators while Wairojjana [28] proved strong convergence of a certain scheme for variational inequalities problems. Moreover, different authors made claims about the convergence speed of their iteration processes: according to the authors in [19], the Agarwal iteration converges faster than Mann’s and has the same convergence speed as the Picard iteration. In [21], the author proved that the iteration process of Abbas converges faster than Agarwal’s. Similarly, according to Gursoy and Karakaya [29], the Picard-S iterative process is converge than the Picard, Ishikawa, Noor, SP, CR, Normal-S iteration processes. The author proved in [25] that the Thauker-New iterative process is fast in terms of convergence when compared to Picard, Mann, Ishikawa, Noor, Agarwal, and Abbas iteration processes for Suzuki generalized nonexpansive mappings. In 2018, Ullah and Arshad [26] proved that, compared to all the above mentioned iteration processes, newly introduced M-iteration processes have high speeds of convergence for Suzuki generalized nonexpansive mappings.

For multi-valued nonexpansive mappings, initially, Sastry and Babu [30] worked on the convergence of Mann and Ishikawa iterative processes in Hilbert spaces. Shehzad and Zegeye [31] (cf. also Song and Cho [32] and others) introduced $P_{\mathbb{J}}\left(a^{\prime }\right)=\{b^{\prime }\in \mathbb{J}\left(a^{\prime }\right):d(a^{\prime },\mathbb{J}{a}^{\prime })=\left|\right|a^{\prime }-b^{\prime }\left|\right|\}$ for multi-valued mappings $\mathbb{J}:B\to P\left(B\right)$ and also proved convergence of Ishikawa iteration process in a UCBS.

Consider a multi-valued mapping $\mathbb{J}:B\to P\left(B\right)$. Choose ${\alpha }_n,{\beta }_n,{\gamma }_n\in (0,1)$. We list here multi-valued versions of Noor [22], Picard–Mann [33], Abbas [21], and Picard-S [29], respectively, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\in B,\hfill \\ k_{n+1}=(1-{\alpha }_n)k_n+{\alpha }_n{v}_n,\hfill \\ l_n=(1-{\beta }_n)k_n+{\beta }_n{w}_n,\hfill \\ m_n=(1-{\gamma }_n)k_n+{\gamma }_n{u}_n,\hfill \end{array}\right.\end{array}$$

(1)

where $u_n\in P_{\mathbb{J}}\left(k_n\right)$, $w_n\in P_{\mathbb{J}}\left(m_n\right)$ and $v_n\in P_{\mathbb{J}}\left(l_n\right)$.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\in B,\hfill \\ k_{n+1}=v_n,\hfill \\ l_n=(1-{\alpha }_n)k_n+{\alpha }_n{u}_n,\hfill \end{array}\right.\end{array}$$

(2)

where $u_n\in P_{\mathbb{J}}\left(k_n\right)$ and $v_n\in P_{\mathbb{J}}\left(l_n\right)$.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\in B,\hfill \\ k_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_n{w}_n,\hfill \\ l_n=(1-{\beta }_n)u_n+{\beta }_n{w}_n,\hfill \\ m_n=(1-{\gamma }_n)k_n+{\gamma }_n{u}_n,\hfill \end{array}\right.\end{array}$$

(3)

where $u_n\in P_{\mathbb{J}}\left(k_n\right)$, $w_n\in P_{\mathbb{J}}\left(m_n\right)$ and $v_n\in P_{\mathbb{J}}\left(l_n\right)$.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\in B,\hfill \\ k_{n+1}=v_n,\hfill \\ l_n=(1-{\alpha }_n)u_n+{\alpha }_n{w}_n,\hfill \\ m_n=(1-{\beta }_n)k_n+{\beta }_n{u}_n,\hfill \end{array}\right.\end{array}$$

(4)

where $u_n\in P_{\mathbb{J}}\left(k_n\right)$, $w_n\in P_{\mathbb{J}}\left(m_n\right)$ and $v_n\in P_{\mathbb{J}}\left(l_n\right)$.

The multi-valued version of the M-iterative process reads as follows:

$$\left\{\begin{array}{c}{k}_1\in B,\hfill \\ k_{n+1}=v_n,\hfill \\ l_n=w_n,\hfill \\ m_n=(1-{\alpha }_n)k_n+{\alpha }_n{u}_n,\hfill \end{array}\right.$$

(5)

where $u_n\in P_{\mathbb{J}}\left(k_n\right)$, $w_n\in P_{\mathbb{J}}\left(m_n\right)$ and $v_n\in P_{\mathbb{J}}\left(l_n\right)$. Ullah et al. [34] used this scheme for finding fixed points of multi-valued $\alpha$-nonexpansive maps. Here, using (5), we will provide weak and strong convergence results for the class of multi-valued generalized $(\alpha ,\beta )$-nonexpansive mappings. The results will be supported by examples.

2. Preliminaries

Let B be a subset of a Banach space and $\mathbb{J}:B\to S\left(B\right)$. Then:

(i)

$\mathbb{J}$ is called nonexpensive if

$$H(\mathbb{J}{a}^{\prime },\mathbb{J}{b}^{\prime })\le \left|\right|a^{\prime }-b^{\prime }\left|\right|,\forall a^{\prime },b^{\prime }\in B.$$

(ii)

$\mathbb{J}$ is called quasi-nonexpensive if $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$ and

$$H(\mathbb{J}{a}^{\prime },\mathbb{J}{p}_{{}_0})\le \left|\right|a^{\prime }-p_{{}_0}\left|\right|,\forall p_{{}_0}\in F_{ix}and\forall a^{\prime }\in B\left(\mathbb{J}\right).$$

(iii)

$\mathbb{J}$ is called Suzuki generalized nonexpansive or endowed with condition $\left(C\right)$ if

$$\frac{1}{2}d(a^{\prime },\mathbb{J}{a}^{\prime })\le \left|\right|a^{\prime }-b^{\prime }\left|\right|\Rightarrow H(\mathbb{J}{a}^{\prime },\mathbb{J}{b}^{\prime })\le \left|\right|a^{\prime }-b^{\prime }\left|\right|,\forall a^{\prime },b^{\prime }\in B.$$

(iv)

$\mathbb{J}$ is called $\alpha$-nonexpensive if there exists $\alpha \in [0,1)$ such that $\forall a^{\prime },b^{\prime }\in B$,

$$H^2(\mathbb{J}{a}^{\prime },\mathbb{J}{b}^{\prime })\le \alpha d^2(a^{\prime },\mathbb{J}{b}^{\prime })+\alpha d^2(b^{\prime },\mathbb{J}{a}^{\prime })+(1-2\alpha )\left|\right|a^{\prime }-b^{\prime }{\left|\right|}^2.$$

(v)

$\mathbb{J}$ is called generalized $\alpha$-nonexpansive if $\alpha \in [0,1)$ exists such that $\forall a^{\prime },b^{\prime }\in B$,

$$\frac{1}{2}d(a,\mathbb{J}{a}^{\prime })\le \left|\right|a^{\prime }-b^{\prime }\left|\right|\Rightarrow$$

$$H(\mathbb{J}{a}^{\prime },\mathbb{J}{b}^{\prime })\le \alpha d(a^{\prime },\mathbb{J}{b}^{\prime })+\alpha d(b^{\prime },\mathbb{J}{a}^{\prime })+(1-2\alpha )\left|\right|a^{\prime }-b^{\prime }\left|\right|.$$

(vi)

$\mathbb{J}$ is called $\beta$-Reich–Suzuki type nonexpansive if $\beta \in [0,1)$ exists such that $\forall a^{\prime },b^{\prime }\in B$,

$$\frac{1}{2}d(a,\mathbb{J}{a}^{\prime })\le \left|\right|a^{\prime }-b^{\prime }\left|\right|\Rightarrow$$

$$H(\mathbb{J}{a}^{\prime },\mathbb{J}{a}^{\prime })\le \beta d(a^{\prime },\mathbb{J}{a}^{\prime })+\beta d(b^{\prime },\mathbb{J}{b}^{\prime })+(1-2\beta )\left|\right|a^{\prime }-b^{\prime }\left|\right|.$$

The single-valued example of a generalized $(\alpha ,\beta )$-nonexpansive selfmaps is the following.

Example 1.

If $\mathcal{B}=[0,\infty )$, then we may set

$$\mathbb{J}{r}^{\prime }=\left\{\begin{array}{c}0if{r}^{\prime }\le \frac{1}{2}\hfill \\ \frac{r^{\prime }}{2}if{r}^{\prime }>\frac{1}{2}.\hfill \end{array}\right.$$

If one chooses $\alpha =\beta =\frac{1}{4}$, then is easy to observe that $\mathbb{J}$ exceeds the class of generalized α-nonexpansive and β-Reich–Suzuki type selfmaps; however, with the help of triangular inequality, one can show that it is generalized $(\alpha ,\beta )$-nonexpansive.

Proposition 1

([31]).For a multi-valued mapping $\mathbb{J}:B\to P\left(B\right)$ and $P_{\mathbb{J}}\left(a^{\prime }\right)=\{b^{\prime }\in \mathbb{J}{a}^{\prime }:d(a^{\prime },\mathbb{J}{a}^{\prime })=\left|\right|a^{\prime }-b^{\prime }\left|\right|\}$. Then, the following conditions are equivalent:

(1)

$p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$,

(2)

$P_{\mathbb{J}}\left(p_{{}_0}\right)=\left\{p_{{}_0}\right\}$,

(3)

$p_{{}_0}\in F_{ix}\left(P_{\mathbb{J}}\right)$.

Further $F_{ix}\left(\mathbb{J}\right)=F_{ix}\left(P_{\mathbb{J}}\right)$.

Definition 1.

Let $\left\{k_n\right\}$ be a bounded sequence in X and B be a subset of X, then:

(1)

Asymptotic radius of $\left\{k_n\right\}$ at a point $x\in X$ is defined as

$$r(x,\left\{k_n\right\})=\underset{n\to \infty }{lim\; sup}\left|\right|k_n-x\left|\right|.$$

(2)

Asymptotic radius of $\left\{k_n\right\}$ with respect to B is defined as

$$r(x,B)=inf\{r(x,k_n):x\in B\}.$$

(3)

The asymptotic center of $\left\{k_n\right\}$ with respect to B is defined as

$$A(B,\left\{k_n\right\})=\{x\in B;r(x,\left\{k_n\right\})=r(B,\left\{k_n\right\})\}.$$

Lemma 1

([35]).Suppose that X is a UCBS. Consider a real sequence named $\left\{t_n\right\}$ in such a manner that $0<{inf}_{n\in \mathbb{N}}{t}_n\le {sup}_{n\in \mathbb{N}}{t}_n<1$. Now assume $\left\{a_n^{\prime }\right\}$ and $\left\{b_n^{\prime }\right\}$ are two sequences in X with the property that there exists a positive real umber h such that ${lim\; sup}_{n\to \infty }\left|\right|a_n^{\prime }\left|\right|\le h$, ${lim\; sup}_{n\to \infty }\left|\right|b_n^{\prime }\left|\right|\le h$ and ${lim}_{n\to \infty }\left|\right|(1-t_n)a_n^{\prime }+t_n{b}_n^{\prime }\left|\right|=h$. Then, ${lim}_{n\to \infty }\left|\right|a_n^{\prime }-b_n^{\prime }\left|\right|=0.$

Definition 2

([36]).Suppose $\mathsf{Ø}\ne B\subseteq X$, where X is a Banach space. Then, $\mathbb{J}:B\to P\left(B\right)$ satisfies condition $\left(I\right)$ if there exists a function $f:[0,\infty )\to [0,\infty )$ such that $f\left(0\right)=0$ and $f\left(r\right)>0$ for $r\in (0,\infty )$ and

$$d(a^{\prime },\mathbb{J}{a}^{\prime })\ge f\left(d(a^{\prime },F_{ix}\left(\mathbb{J}\right))\right)$$

for each $a^{\prime }\in B$.

Definition 3

([37]).Let X be a Banach space. The space X is said to be endowed with Opial’s condition if for any sequence $\left\{k_n\right\}\subset X$, with $k_n\rightharpoonup w$, it follows that

$$\underset{n\to \infty }{lim\; sup}\left|\right|k_n-w\left|\right|<\underset{n\to \infty }{lim\; sup}\left|\right|k_n-r^{\prime }\left|\right|,$$

where $r^{\prime }\in X$ and $r^{\prime }\ne w$.

Definition 4.

Consider a multi-valued mapping $\mathbb{J}:B\to P\left(B\right)$ and $\left\{k_n\right\}$ in B. The sequence $\left\{k_n\right\}$ is said to be an approximate fixed point sequence (shortly $a.f.p.s$) for $\mathbb{J}$ if $d(k_n,\mathbb{J}{k}_n)\to 0$ as $n\to \infty$.

Definition 5.

Suppose a multi-valued mapping $\mathbb{J}:B\to CB\left(B\right)$. Now one can say that $\mathbb{J}$ is demiclosed at $b\in B$ if for any sequence $\left\{k_n\right\}$ in B that is $k_n\rightharpoonup w$ for some $w\in B$ and $b_n\in \mathbb{J}\left(k_n\right),$$n\in \mathbb{N}$, which is strongly converges to b then we have $b\in \mathbb{J}\left(w\right)$.

3. Generalized ($\mathbf{\alpha },\mathbf{\beta }$)-Nonexpansive Multi-Valued Mapping

Definition 6.

Consider a multi-valued mapping $\mathbb{J}:B\to S\left(B\right)$. Then, $\mathbb{J}$ is called generalized ($\alpha ,\beta$)-nonexpansive if there exists two positive real constants $\alpha ,\beta$ with $\alpha +\beta <1$ and for all $a^{\prime },b^{\prime }\in B$, we have

$$\begin{array}{ccc}\hfill \frac{1}{2}d(a^{\prime },\mathbb{J}{a}^{\prime })& \le & \left|\right|a^{\prime }-b^{\prime }\left|\right|impliesthat\hfill \\ \hfill H(\mathbb{J}{a}^{\prime },\mathbb{J}{b}^{\prime })& \le & \alpha d(a^{\prime },\mathbb{J}{b}^{\prime })+\alpha d(b^{\prime },\mathbb{J}{a}^{\prime })+\beta d(a^{\prime },\mathbb{J}{a}^{\prime })+\beta d(b^{\prime },\mathbb{J}{b}^{\prime })+(1-\hfill \\ & & 2\alpha -2\beta \left)\right||a^{\prime }-b^{\prime }\left|\right|.\hfill \end{array}$$

Remark 1.

Obviously, the class of multi-valued generalized $(\alpha ,\beta )$-nonexpansive maps includes both the multi-valued generalized α-nonexpansive and multi-valued Riech–Suzuki type nonexpansive maps classes.

Lemma 2.

Suppose a Banach space X and $\mathsf{Ø}\ne B\subset X$ and also consider a multi-valued mapping $\mathbb{J}:B\to S_{cb}\left(B\right)$. If $\mathbb{J}$ is ($\alpha ,\beta$)-nonexpansive with a fixed point $p_0\in F_{ix}\left(\mathbb{J}\right)$ and satisfies the endpoint condition, then $\mathbb{J}$ is quasi-nonexpansive.

Proof. 

Assume that $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$. Then $\frac{1}{2}d(p_{{}_0},\mathbb{J}{p}_{{}_0})=0\le \left|\right|p_{{}_0}-b^{\prime }\left|\right|$ for any $b^{\prime }\in B$, so

$$\begin{array}{ccc}\hfill H(\mathbb{J}{b}^{\prime },\mathbb{J}{p}_0)& \le & \alpha d(b^{\prime },\mathbb{J}{p}_0)+\alpha d(p_0,\mathbb{J}{b}^{\prime })+\beta d(p_0,\mathbb{J}{p}_0)+\beta d(b^{\prime },\mathbb{J}{b}^{\prime })\hfill \\ & & +(1-2\alpha -2\beta )\left|\right|b^{\prime }-p_0\left|\right|\hfill \\ & \le & \alpha \left|\right|b^{\prime }-p_0\left|\right|+\alpha H(\mathbb{J}{p}_0,\mathbb{J}{b}^{\prime })+\beta \left(\right||b^{\prime }-p_0\left|\right|+H(\mathbb{J}{p}_0,\mathbb{J}{b}^{\prime }))\hfill \\ & & +(1-2\alpha -2\beta )\left|\right|b^{\prime }-p_0\left|\right|.\hfill \\ & \le & \alpha H(\mathbb{J}{b}^{\prime },\mathbb{J}{p}_0)+\beta H(\mathbb{J}{b}^{\prime },\mathbb{J}{p}_0)+(1-\alpha -\beta )\left|\right|b^{\prime }-p_0\left|\right|.\hfill \end{array}$$

This provides

$$(1-\alpha -\beta )H(\mathbb{J}{b}^{\prime },\mathbb{J}{p}_0)\le (1-\alpha -\beta )\left|\right|b^{\prime }-p_0\left|\right|.$$

Since $(1-\alpha -\beta )>0$, we obtain our desired result. □

Lemma 3.

Let B be a nonempty subset of a Banach space X and $\mathbb{J}:B\to S_{cb}\left(B\right)$ be a multi-valued mapping satisfying the endpoint condition. Then, $F_{ix}\left(\mathbb{J}\right)$ is closed provided that $\mathbb{J}$ is generalized ($\alpha ,\beta$)-nonexpansive.

Proof. 

Let $\left\{k_n\right\}\subseteq F_{ix}\left(\mathbb{J}\right)$ such that $k_n\to p_{{}_0}\in B$. Now

$$\frac{1}{2}d(k_n,\mathbb{J}{k}_n)=0\le \left|\right|k_n-p_{{}_0}\left|\right|.$$

Using Definition 6, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}d(k_n,\mathbb{J}{p}_{{}_0})& =& \underset{n\to \infty }{lim}H(\mathbb{J}{k}_n,\mathbb{J}{p}_{{}_0})\hfill \\ & \le & \underset{n\to \infty }{lim}[\alpha d(k_n,\mathbb{J}{p}_{{}_0})+\alpha d(p_{{}_0},\mathbb{J}{k}_n)+\beta d(k_n,\mathbb{J}{k}_n)+\beta d(p_{{}_0},\mathbb{J}{p}_{{}_0})\hfill \\ & & +(1-2\alpha -2\beta )\left|\right|k_n-p_{{}_0}\left|\right|]\hfill \\ & \le & \underset{n\to \infty }{lim}[\alpha d(k_n,\mathbb{J}{p}_{{}_0})+\beta d(p_{{}_0},\mathbb{J}{p}_{{}_0})+(1-\alpha -2\beta )\left|\right|k_n-p_{{}_0}\left|\right|]\hfill \\ & \le & \underset{n\to \infty }{lim}[\alpha d(k_n,\mathbb{J}{p}_{{}_0})+\beta \left|\right|k_n-p_{{}_0}\left|\right|+\beta d(k_n,\mathbb{J}{p}_{{}_0})+(1-\alpha -2\hfill \\ & & \beta \left)\right||k_n-p_{{}_0}\left|\right|]\hfill \\ & \le & \underset{n\to \infty }{lim}[\alpha d(k_n,\mathbb{J}{p}_{{}_0})+\beta d(k_n,\mathbb{J}{p}_{{}_0})+(1-\alpha -\beta )\left|\right|k_n-p_{{}_0}\left|\right|].\hfill \end{array}$$

The previous inequalities imply

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}d(k_n,\mathbb{J}{p}_{{}_0})& \le & \underset{n\to \infty }{lim}\left|\right|k_n-p_{{}_0}\left|\right|,\hfill \end{array}$$

because $0<(1-\alpha -\beta )<1$ and $\alpha ,\beta \in (0,1)$. So $p_{{}_0}\in \mathbb{J}\left(p_{{}_0}\right)$ and hence $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$. Thus, $F_{ix}\left(\mathbb{J}\right)$ is closed. □

4. Fixed Point Existence Results

Lemma 4.

Let B be a nonempty subset of a Banach space X and let $\mathbb{J}:B\to S_{cb}\left(B\right)$ be a generalized ($\alpha ,\beta$)-nonexpansive multi-valued mapping. In addition, let e and $r^{\prime }$ be elements in B for which $e\in \mathbb{J}{r}^{\prime }$. Then, the following inequalities holds:

(a)

$d(e,\mathbb{J}e)\le \left|\right|r^{\prime }-e\left|\right|$,

(b)

for every $s^{\prime }\in B$ we have either $\frac{1}{2}d(r^{\prime },\mathbb{J}{r}^{\prime })\le \left|\right|r^{\prime }-s^{\prime }\left|\right|$ or $\frac{1}{2}d(e,\mathbb{J}e)\le \left|\right|e-s^{\prime }\left|\right|$.

Proof. 

(a) Since $\frac{1}{2}d(r^{\prime },\mathbb{J}{r}^{\prime })\le \left|\right|r^{\prime }-e\left|\right|$ for any $e\in \mathbb{J}{r}^{\prime }$, we obtain

$$\begin{array}{ccc}\hfill H(\mathbb{J}{r}^{\prime },\mathbb{J}e)& \le & \alpha d(r^{\prime },\mathbb{J}e)+\alpha d(e,\mathbb{J}{r}^{\prime })+\beta d(r^{\prime },\mathbb{J}{r}^{\prime })+\beta d(e,\mathbb{J}e)+(1-\hfill \\ & & 2\alpha -2\beta \left)\right||r^{\prime }-e\left|\right|\hfill \\ & =& \alpha d(r^{\prime },\mathbb{J}e)+\beta d(r^{\prime },\mathbb{J}{r}^{\prime })+\beta d(e,\mathbb{J}e)+(1-2\alpha -2\beta )\left|\right|r^{\prime }-e\left|\right|\hfill \\ & \le & \alpha \left|\right|r^{\prime }-e\left|\right|+\alpha d(e,\mathbb{J}e)+\beta \left|\right|r^{\prime }-e\left|\right|+\beta d(e,\mathbb{J}{r}^{\prime })+\beta d(e,\mathbb{J}e)\hfill \\ & & +(1-2\alpha -2\beta )\left|\right|r^{\prime }-e\left|\right|\hfill \\ & \le & (\alpha +\beta )d(e,\mathbb{J}e)+(1-\alpha -\beta )\left|\right|r^{\prime }-e\left|\right|\hfill \end{array}$$

Since $e\in \mathbb{J}{r}^{\prime }$ and $(1-\alpha -\beta )>0$, we can write,

$$\begin{array}{ccc}\hfill d(e,\mathbb{J}e)& \le & (\alpha +\beta )d(e,\mathbb{J}e)+(1-\alpha -\beta )\left|\right|r^{\prime }-e\left|\right|\hfill \\ \hfill d(e,\mathbb{J}e)& \le & \left|\right|r^{\prime }-e\left|\right|,\hfill \end{array}$$

for any $e\in \mathbb{J}{r}^{\prime }$.

(b) Suppose to the contrary that for any $r^{\prime },s^{\prime }\in B$ and $e\in \mathbb{J}{r}^{\prime }$, we have

$$\begin{array}{cc}\frac{1}{2}d(r^{\prime },\mathbb{J}{r}^{\prime })\hfill & >\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \\ \frac{1}{2}d(e,\mathbb{J}e)\hfill & >\left|\right|e-s^{\prime }\left|\right|.\hfill \end{array}$$

(6)

From (6) and (a), we have

$$\begin{array}{ccc}\hfill \left|\right|a^{\prime }-e\left|\right|& \le & \left|\right|r^{\prime }-s^{\prime }\left|\right|+\left|\right|s^{\prime }-e\left|\right|\hfill \\ & <& \frac{1}{2}d(r^{\prime },\mathbb{J}{r}^{\prime })+\frac{1}{2}d(e,\mathbb{J}e)\hfill \\ & \le & \frac{1}{2}\left|\right|r^{\prime }-e\left|\right|+\frac{1}{2}\left|\right|r^{\prime }-e\left|\right|\hfill \\ & =& \left|\right|r^{\prime }-e\left|\right|,\hfill \end{array}$$

and a contradiction occurs. Hence, the result follows. □

Lemma 5.

Let B be a nonempty subset of a Banach space X and let $\mathbb{J}:B\to S_{cb}\left(B\right)$ be a generalized ($\alpha ,\beta$)-nonexpansive multi-valued mapping. Then,

$$d(r^{\prime },\mathbb{J}{s}^{\prime })\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)d(r^{\prime },\mathbb{J}{r}^{\prime })+\left|\right|r^{\prime }-s^{\prime }\left|\right|,\mathrm{for}{r}^{\prime },s^{\prime }\in B.$$

(7)

Proof. 

By Lemma 4, we have the following two cases:

Case 1. If $\frac{1}{2}d(r^{\prime },\mathbb{J}{r}^{\prime })\le \left|\right|r^{\prime }-s^{\prime }\left|\right|$, we have

$$\begin{array}{ccc}\hfill d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & d(r^{\prime },\mathbb{J}{r}^{\prime })+H(\mathbb{J}{r}^{\prime },\mathbb{J}{s}^{\prime })\hfill \\ & \le & d(r^{\prime },\mathbb{J}{r}^{\prime })+\alpha d(r^{\prime },\mathbb{J}{s}^{\prime })+\alpha d(b^{\prime },\mathbb{J}{r}^{\prime })+\beta d(r^{\prime },\mathbb{J}{r}^{\prime })+\beta \hfill \\ & & d(s^{\prime },\mathbb{J}{s}^{\prime })+(1-2\alpha -2\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ & \le & d(r^{\prime },\mathbb{J}{r}^{\prime })+\alpha d(r^{\prime },\mathbb{J}{s}^{\prime })+\alpha d(s^{\prime },\mathbb{J}{r}^{\prime })+\beta d(r^{\prime },\mathbb{J}{r}^{\prime })+\beta \hfill \\ & & \left|\right|r^{\prime }-s^{\prime }\left|\right|+\beta d(r^{\prime },\mathbb{J}{s}^{\prime })+(1-2\alpha -2\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

From the previous inequalities, we obtain

$$\begin{array}{ccc}\hfill (1-\alpha -\beta )d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & (1+\beta )d(r^{\prime },\mathbb{J}{r}^{\prime })+\alpha d(s^{\prime },\mathbb{J}{r}^{\prime })+\beta \left|\right|r^{\prime }-s^{\prime }\left|\right|+(1-2\alpha \hfill \\ & & -2\beta \left)\right||r^{\prime }-s^{\prime }\left|\right|\hfill \\ & \le & (1+\beta )d(r^{\prime },\mathbb{J}{r}^{\prime })+\alpha d(r^{\prime },\mathbb{J}{r}^{\prime })+\alpha \left|\right|r^{\prime }-s^{\prime }\left|\right|+\beta \left|\right|r^{\prime }-\hfill \\ & & s^{\prime }\left|\right|+(1-2\alpha -2\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ & \le & (1+\alpha +\beta )d(r^{\prime },\mathbb{J}{r}^{\prime })+(1-\alpha -\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

From the latter inequalities, we see

$$\begin{array}{ccc}\hfill d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & \left(\frac{1+\alpha +\beta }{1-\alpha -\beta }\right)d(r^{\prime },\mathbb{J}{r}^{\prime })+\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

The required result is proved.

Case 2. Let $\frac{1}{2}d(e,\mathbb{J}e)\le \left|\right|r^{\prime }-e\left|\right|$. Then, we see

$$\begin{array}{ccc}\hfill d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & \left|\right|r^{\prime }-e\left|\right|+d(e,\mathbb{J}e)+H(\mathbb{J}e,\mathbb{J}{s}^{\prime }),\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha d(e,\mathbb{J}{s}^{\prime })+\alpha d(s^{\prime },\mathbb{J}e)+\beta d(e,\mathbb{J}e)+\beta \hfill \\ & & d(s^{\prime },\mathbb{J}{s}^{\prime })+(1-2\alpha -2\beta )\left|\right|e-s^{\prime }\left|\right|\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|e-r^{\prime }\left|\right|+\alpha d(r^{\prime },\mathbb{J}{s}^{\prime })+\alpha \left|\right|s^{\prime }-e\left|\right|+\alpha \hfill \\ & & d(e,\mathbb{J}e)+\beta \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|s^{\prime }-r^{\prime }\left|\right|+\beta d(r^{\prime },\mathbb{J}{s}^{\prime })+(1\hfill \\ & & -2\alpha -2\beta \left)\right||e-s^{\prime }\left|\right|.\hfill \end{array}$$

Therefore, according to Lemma 4, we infer

$$\begin{array}{ccc}\hfill (1-\alpha -\beta )d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|s^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\beta \hfill \\ & & \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|r^{\prime }-s^{\prime }\left|\right|+(1-2\alpha -2\beta )\left|\right|e-s^{\prime }\left|\right|\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|s^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\beta \hfill \\ & & \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|e-s^{\prime }\left|\right|+(1-2\alpha -2\beta )\hfill \\ & & \left|\right|e-s^{\prime }\left|\right|\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|r^{\prime }-e\left|\right|+\beta \hfill \\ & & \left|\right|r^{\prime }-e\left|\right|+(1-\alpha -\beta )\left|\right|e-s^{\prime }\left|\right|\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|r^{\prime }-e\left|\right|+\beta \hfill \\ & & \left|\right|r^{\prime }-z\left|\right|+(1-\alpha -\beta )\left|\right|e-r^{\prime }\left|\right|+(1-\alpha -\beta )\left|\right|r^{\prime }-\hfill \\ & & s^{\prime }\left|\right|\hfill \\ & \le & 2\left|\right|r^{\prime }-e\left|\right|+\alpha \left|\right|r^{\prime }-e\left|\right|+\beta \left|\right|r^{\prime }-e\left|\right|+\left|\right|e-r^{\prime }\left|\right|+(1\hfill \\ & & -\alpha -\beta \left)\right||r^{\prime }-s^{\prime }\left|\right|\hfill \\ & \le & (3+\alpha +\beta )\left|\right|r^{\prime }-e\left|\right|+(1-\alpha -\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

As a consequence of the above inequalities, we obtain

$$\begin{array}{ccc}\hfill d(r^{\prime },\mathbb{J}{s}^{\prime })& \le & \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)\left|\right|r^{\prime }-e\left|\right|+\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

Therefore, since $e\in \mathbb{J}{r}^{\prime }$ and $\frac{1}{2}d(e,\mathbb{J}e)\le \left|\right|r^{\prime }-e\left|\right|$, we obtain

$$\begin{array}{c}\hfill d(r^{\prime },\mathbb{J}{s}^{\prime })\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)d(r^{\prime },\mathbb{J}{r}^{\prime })+\left|\right|r^{\prime }-s^{\prime }\left|\right|.\end{array}$$

Hence, in both cases the result is proved. □

For the fixed point existence result, the following lemmas are needed.

Lemma 6.

Consider a nonempty closed bounded subset B of a Banach space X and let $\mathbb{J}:B\to S_{cb}\left(B\right)$ be a generalized ($\alpha ,\beta$)-nonexpansive multi-valued mapping. Let $\left\{k_n\right\}$ be a bounded a.f.p.s for $\mathbb{J}$ in B. Then, $A(B,\left\{k_n\right\})$ is $\mathbb{J}$-invariant.

Proof. 

Let $s\in A(B,\left\{k_n\right\}).$ Since the mapping $\mathbb{J}$ satisfies (7), we obtain

$$\begin{array}{c}\hfill d(k_n,\mathbb{J}s)\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)d(k_n,\mathbb{J}{k}_n)+\left|\right|k_n-s\left|\right|.\end{array}$$

Now,

$$\begin{array}{ccc}\hfill r(\mathbb{J}s,\left\{k_n\right\})& =& \underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}s)\hfill \\ & \le & \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)\underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}{k}_n)+\underset{n\to \infty }{lim\; sup}\left|\right|k_n-s\left|\right|\hfill \\ & =& \underset{n\to \infty }{lim\; sup}\left|\right|k_n-s\left|\right|\hfill \\ & =& r(s,\left\{k_n\right\}).\hfill \end{array}$$

By definition of Asymptotic center we have, $\mathbb{J}s\in A(B,\left\{k_n\right\})$. Hence, $A(B,\left\{k_n\right\})$ is $\mathbb{J}$-invariant. □

Lemma 7.

Consider a nonempty closed convex and bounded subset B of a Banach space X and suppose $\left\{k_n\right\}$ is an a.f.p.s for $\mathbb{J}$ where $\mathbb{J}:B\to S_{cb}\left(B\right)$ is a generalized ($\alpha ,\beta$)-nonexpansive multi-valued mapping. Then

$$\underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}s)\le \underset{n\to \infty }{lim\; sup}\left|\right|k_n-s\left|\right|$$

for each $s\in B$.

Proof. 

Since $\mathbb{J}$ satisfies Equation (7), for any $s\in B$ we have

$$d(k_n,\mathbb{J}s)\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)d(k_n,\mathbb{J}{k}_n)+\left|\right|k_n-s\left|\right|.$$

Since $\left\{k_n^{\prime }\right\}$ is an a.f.p.s in B,

$$\underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}s)\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)\underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}{k}_n)+\underset{n\to \infty }{lim\; sup}\left|\right|k_n-s\left|\right|.$$

$$\underset{n\to \infty }{lim\; sup}d(k_n,\mathbb{J}s)\le \underset{n\to \infty }{lim\; sup}\left|\right|k_n-s\left|\right|,$$

for $s\in B$. □

Now, we prove the fixed point existence result.

Lemma 8.

Let X ba a Banach space and B ba a nonempty closed convex and bounded subset of X. Let $\mathbb{J}:B\to S_{cb}\left(B\right)$ be a generalized ($\alpha ,\beta$)-nonexpansive multi-valued mapping and for each approximate fixed point sequence $\left\{k_n\right\}\subset B$ for $\mathbb{J}$, the asymptotic center $A(B,\left\{k_n\right\})$ is nonempty and compact. Then, $\mathbb{J}$ has a fixed point.

Proof. 

Let $\left\{k_n\right\}$ be an a.f.p.s in the asymptotic center $A(B,\left\{k_n\right\})$. However, since this center is compact, there exists $\left\{k_{n_j}\right\}$ of $\left\{k_n\right\}$ such that

$$k_{n_j}\to p_{{}_0}\in A(B,\left\{k_n\right\}).$$

As Lemma 6 has an asymptotic center that is $\mathbb{J}$-invariant, $\mathbb{J}{p}_{{}_0}\in A(B,\left\{k_n\right\})$. Additionally, by Lemma 7, we have

$$\underset{n\to \infty }{lim\; sup}d(k_{n_j},\mathbb{J}{p}_{{}_0})\le \underset{n\to \infty }{lim\; sup}\left|\right|k_{n_j}-p_{{}_0}\left|\right|,$$

which implies that $p_{{}_0}\in \mathbb{J}{p}_{{}_0}.$ □

5. Convergence Results

Lemma 9.

Suppose that B be a nonempty closed and convex subset of UCBS X. Assume that $\mathbb{J}:B\to P_r\left(B\right)$ is a multi-valued mapping such that $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$. Additionally, assume that $P_{\mathbb{J}}$ is a generalized ($\alpha ,\beta$)-nonexpansive mapping. Suppose that $\left\{k_n\right\}$ is a sequence iteratively generated by (5) then for $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$, ${lim}_{n\to \infty }\left|\right|k_n-p_{{}_0}\left|\right|$ exists and ${lim}_{n\to \infty }d(k_n,P_{\mathbb{J}}\left(k_n\right))=0.$

Proof. 

If $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$ and $n\in \mathbb{N}$, then, by Lemmas 2 and (5), we have

$$\begin{array}{ccc}\hfill \left|\right|m_n-p_{{}_0}\left|\right|& \le & (1-{\alpha }_n)\left|\right|k_n-p_{{}_0}\left|\right|+{\alpha }_n\left|\right|u_n-p_{{}_0}\left|\right|\hfill \\ & \le & (1-{\alpha }_n)\left|\right|k_n-p_{{}_0}\left|\right|+{\alpha }_{n}H\left(P_{\mathbb{J}}\left(k_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right)\right)\hfill \\ & \le & (1-{\alpha }_n)\left|\right|k_n-p_{{}_0}\left|\right|+{\alpha }_n\left|\right|k_n-p_{{}_0}\left|\right|\hfill \\ & \le & \left|\right|k_n-p_{{}_0}\left|\right|.\hfill \end{array}$$

(8)

By the same token, we obtain

$$\begin{array}{ccc}\hfill \left|\right|l_n-p_{{}_0}\left|\right|& =& \left|\right|w_n-p_{{}_0}\left|\right|\hfill \\ & \le & H\left(P_{\mathbb{J}}\left(m_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right)\right)\hfill \\ & \le & \left|\right|m_n-p_{{}_0}\left|\right|,\hfill \end{array}$$

(9)

and also

$$\begin{array}{ccc}\hfill \left|\right|k_{n+1}-p_{{}_0}\left|\right|& =& \left|\right|v_n-p_{{}_0}\left|\right|\hfill \\ & \le & H\left(P_{\mathbb{J}}\left(l_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right)\right)\hfill \\ & \le & \left|\right|l_n-p_{{}_0}\left|\right|\hfill \\ & \le & \left|\right|m_n-p_{{}_0}\left|\right|\hfill \\ & \le & \left|\right|k_n-p_{{}_0}\left|\right|.\hfill \end{array}$$

Thus, $\left|\right|k_n-p_{{}_0}\left|\right|$ is bounded and nonincreasing, and so ${lim}_{n\to \infty }\left|\right|k_n-p_{{}_0}\left|\right|$ exists for $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$.

Next, we need to prove that

$$\underset{n\to \infty }{lim}\left|\right|k_n-u_n\left|\right|=0.$$

Suppose that

$$\underset{n\to \infty }{lim}\left|\right|k_n-p_{{}_0}\left|\right|=cwhere{p}_{{}_0}\in F_{ix}\left(\mathbb{J}\right).$$

(10)

We can easily obtain the following inequalities by using (5), (9), (8) and Lemma 2:

$$\left|\right|u_n-p_{{}_0}\left|\right|\le H(P_{\mathbb{J}}\left(k_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right))\le \left|\right|k_n-p_{{}_0}\left|\right|,$$

and

$$\left|\right|v_n-p_{{}_0}\left|\right|\le H(P_{\mathbb{J}}\left(l_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right))\le \left|\right|l_n-p_{{}_0}\left|\right|\le \left|\right|m_n-p_{{}_0}\left|\right|\le \left|\right|k_n-p_{{}_0}\left|\right|.$$

By taking the superior limit of the extreme expressions of the above two rows of inequalities and keeping in mind (10), we infer that

$$\underset{n\to \infty }{lim\; sup}\left|\right|u_n-p_{{}_0}\left|\right|\le c,$$

(11)

$$\underset{n\to \infty }{lim\; sup}\left|\right|v_n-p_{{}_0}\left|\right|\le c.$$

(12)

Then, it follows that

$$\begin{array}{ccc}\hfill \left|\right|k_{n+1}-p_{{}_0}\left|\right|& =& \left|\right|v_n-p_{{}_0}\left|\right|.\hfill \\ \hfill c& \le & \underset{n\to \infty }{lim\; inf}\left|\right|v_n-p_{{}_0}\left|\right|.\hfill \end{array}$$

(13)

By (12) and (13), we obtain

$$\underset{n\to \infty }{lim}\left|\right|v_n-p_{{}_0}\left|\right|=c.$$

From (5) and (9) we obtain,

$$\begin{array}{ccc}\hfill c& =& \underset{n\to \infty }{lim}\left|\right|v_n-p_{{}_0}\left|\right|\hfill \\ & \le & H(P_{\mathbb{J}}\left(l_n\right),P_{\mathbb{J}}\left(p_{{}_0}\right))\hfill \\ & \le & \left|\right|l_n-p_{{}_0}\left|\right|\hfill \\ & \le & \left|\right|m_n-p_{{}_0}\left|\right|\hfill \\ & \le & \left|\right|(1-{\alpha }_n)(k_n-p_{{}_0})+{\alpha }_n(u_n-p_{{}_0})\left|\right|\hfill \\ & \le & c.\hfill \end{array}$$

As a result, we obtain

$$\underset{n\to \infty }{lim}\left|\right|(1-{\alpha }_n)(u_n-p_{{}_0})+{\alpha }_n(k_n-p_{{}_0})\left|\right|=c.$$

(14)

Therefore, by (11), (10), (14) and Lemma 1, we have

$$\underset{n\to \infty }{lim}\left|\right|k_n-u_n\left|\right|=0.$$

Hence,

$$\underset{n\to \infty }{lim}d(k_n,P_{\mathbb{J}}\left(k_n\right))=0.$$

This completes the proof. □

Next, we are to prove convergence results.

Theorem 1.

Suppose that B be a nonempty compact and convex subset of UCBS X. Assume that $\mathbb{J}:B\to P_r\left(B\right)$ is a multi-valued mapping such that $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$. Additionally, assume that $P_{\mathbb{J}}$ be a generalized ($\alpha ,\beta$)-nonexpansive mapping. Then, a sequence $\left\{k_n\right\}$ defined as in (5) converges strongly to a fixed point of $\mathbb{J}$.

Proof. 

We have observed in Lemma 9 that

$$\underset{n\to \infty }{lim}d(k_n,P_{\mathbb{J}}\left(k_n\right))=0.$$

Due to compactness of B, there exists a subsequence $\left\{k_{n_j}\right\}$ of $\left\{k_n\right\}$ that converges to $p_{{}_0}\in B$. Since $P_{\mathbb{J}}$ is a generalized $(\alpha ,\beta )$-nonexpansive and the sequence $\left\{k_n\right\}$ satisfies (5), it follows that

$$d(k_{n_j},P_{\mathbb{J}}\left(p_{{}_0}\right))\le \left(\frac{3+\alpha +\beta }{1-\alpha -\beta }\right)d(k_{n_j},P_{\mathbb{J}}\left(k_{n_j}\right))+\left|\right|k_{n_j}-p_{{}_0}\left|\right|.$$

Since $F_{ix}\left(\mathbb{J}\right)=F_{ix}\left(P_{\mathbb{J}}\right)$, we obtain $p_{{}_0}\in \mathbb{J}\left(p_{{}_0}\right)$ as $i\to \infty$. As a result, $\left\{k_n\right\}$ converges strongly to $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)$. □

Proof of the theorem below is elementary, and hence is omitted.

Theorem 2.

Suppose that B is a nonempty closed convex subset of a UCBS X and let the multi-valued mapping $\mathbb{J}:B\to P_r\left(B\right)$ be such that the mapping $P_{\mathbb{J}}$ is generalized ($\alpha ,\beta$)-nonexpansive. Assume that $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$ and that the sequence $\left\{k_n\right\}$, which is iteratively generated as in (5), stisfies ${lim\; inf}_{n\to \infty }d(k_n,F_{ix}\left(\mathbb{J}\right))=0$. Then, this sequence converges strongly to a fixed point of $\mathbb{J}$.

Now, we use condition $\left(I\right)$ for establishing another strong convergence theorem.

Theorem 3.

Suppose that B is a nonempty closed convex subset of a UCBS X. Assume that the multi-valued mapping $\mathbb{J}:B\to P_r\left(B\right)$ satisfies condition $\left(I\right)$ and is such that $P_{\mathbb{J}}$ is a generalized ($\alpha ,\beta$)-nonexpansive mapping. If, moreover, $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$, then any sequence which is iteratively generated as in (5) converges strongly to a fixed point of $\mathbb{J}$.

Proof. 

Let the sequence $\left\{k_n\right\}$ be iteratively generated as in (5) and let $p_0\in F_{ix}\left(\mathbb{J}\right)$. In light of Lemma 9, since the sequence $\left|\right|k_n-p_{{}_0}\left|\right|$ is nonincreasing, the constant $c\ge 0$ defined by

$$c=\underset{n\to \infty }{lim}\left|\right|k_n-p_{{}_0}\left|\right|$$

(15)

exists.

It follows that for $c=0$, the proof is trivial. Therefore, we suppose that $c>0$. Now,

$$\begin{array}{ccc}\hfill \left|\right|k_{n+1}-p_{{}_0}\left|\right|& \le & \left|\right|k_n-p_{{}_0}\left|\right|\hfill \\ \hfill \underset{n\to \infty }{lim\; inf}\left|\right|k_{n+1}-p_{{}_0}\left|\right|& \le & \underset{n\to \infty }{lim\; inf}\left|\right|k_n-p_{{}_0}\left|\right|\hfill \\ \hfill d(k_{n+1},F_{ix}\left(\mathbb{J}\right))& \le & d(k_n,F_{ix}\left(\mathbb{J}\right)).\hfill \end{array}$$

As a result, ${lim}_{n\to \infty }d(k_n,F_{ix}\left(\mathbb{J}\right))$ exists. Additionally, according to Lemma 1, $F_{ix}\left(\mathbb{J}\right)=F_{ix}\left(P_{\mathbb{J}}\right)$. From Lemma 9, together with condition $\left(I\right)$, we then infer

$$\underset{n\to \infty }{lim}f\left(d(k_n,F_{ix}\left(\mathbb{J}\right))\right)\le \underset{n\to \infty }{lim}d(k_n,P_{\mathbb{J}}\left(k_n\right)).$$

Due to the nonincreasing nature of f and $f\left(0\right)=0$, we have

$$\underset{n\to \infty }{lim}d(k_n,F_{ix}\left(\mathbb{J}\right))=0.$$

The required result now follows from Theorem 2. □

Theorem 4.

Suppose that B is a nonempty closed convex subset of a UCBS X which satisfies Opial’s condition. Assume that $\mathbb{J}:B\to P_r\left(B\right)$ is a multi-valued mapping such that $F_{ix}\left(\mathbb{J}\right)\ne \mathsf{Ø}$ and is such that $P_{\mathbb{J}}$ is a generalized ($\alpha ,\beta$)-nonexpansive mapping. Additionally, let $I-P_{\mathbb{J}}$ be demiclosed with respect to zero. Then, any sequence $\left\{k_n\right\}$ iteratively generated as in (5) converges weakly to a fixed point of $\mathbb{J}$.

Proof. 

Let the sequence $\left\{k_n\right\}$ be iteratively generated as in (5) and let $p_{{}_0}\in F_{ix}\left(\mathbb{J}\right)=F_{ix}\left(P_{\mathbb{J}}\right)$ (see Lemma 1). Then, according to Lemma 9, $li{m}_{n\to \infty }\left|\right|k_n-p_{{}_0}\left|\right|$ exists. Since X is uniformly convex, it is reflexive. Therefore, there must exist a subsequence $\left\{k_{n_j}\right\}$ of $\left\{k_n\right\}$ that converges weakly to some $p_1\in B$. Additionally, $I-P_{\mathbb{J}}$ is demiclosed at zero, therefore $p_1\in F_{ix}\left(P_{\mathbb{J}}\right)=F_{ix}\left(\mathbb{J}\right)$. If the sequence $k_n$ does not weakly converg to $p_1$, then there must be a subsequence $\left\{k_{n_j}\right\}$ of $\left\{k_n\right\}$ such that $k_{n_j}\rightharpoonup p_2$ where $p_1\ne p_2$. Clearly, $p_2\in F_{ix}\left(P_{\mathbb{J}}\right)=F_{ix}\left(\mathbb{J}\right)$. By Opial’s property, we obtain

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\left|\right|k_n-p_1\left|\right|& =& \underset{j\to \infty }{lim}\left|\right|k_{n_j}-p_1\left|\right|\hfill \\ & <& \underset{j\to \infty }{lim}\left|\right|k_{n_j}-p_2\left|\right|\hfill \\ & =& \underset{n\to \infty }{lim}\left|\right|k_n-p_2\left|\right|\hfill \\ & <& \underset{j\to \infty }{lim}\left|\right|k_{n_j}-p_2\left|\right|\hfill \\ & =& \underset{j\to \infty }{lim}\left|\right|k_{n_j}-p_1\left|\right|\hfill \end{array}$$

and a contradiction occurs. Thus, the sequence $\left\{k_n\right\}$ converges weakly to a point in $F_{ix}\left(\mathbb{J}\right)$. □

6. Example

Example 2.

Let $X=R$ and $B=[0,\infty )$ and $\mathbb{J}:B\to C\left(B\right)$ be defined by,

$$\mathbb{J}\left(r^{\prime }\right)=\left\{\begin{array}{ll}\left(0\right)& if r^{\prime }\in [0,\frac{1}{1000}]=A\\ [0,\frac{r^{\prime }}{3}]& if r^{\prime }\in (\frac{1}{1000},\infty )-\left\{\frac{8}{5}\right\}=B\\ [0,\frac{7}{10}]& if r^{\prime }=\left\{\frac{8}{5}\right\}.\end{array}\right.$$

$\left(a\right)$ Then, we verify that $P_{\mathbb{J}}$ is generalized $(\alpha ,\beta )$-nonexpansive.

$\left(b\right)$ However, $P_{\mathbb{J}}$ is not α-nonexpansive.

Proof. 

$\left(a\right)$ If $r^{\prime }\in A$ then $P_{\mathbb{J}}\left(r^{\prime }\right)=\left\{0\right\}$ also if $r^{\prime }\in B$, then $P_{\mathbb{J}}\left(r^{\prime }\right)=\left\{\frac{r^{\prime }}{3}\right\}$ and if $r^{\prime }=\left\{\frac{3}{2}\right\}$ then $P_{\mathbb{J}}\left(r^{\prime }\right)=\left\{\frac{7}{10}\right\}$. Now we prove that $P_{\mathbb{J}}$ is $(\alpha ,\beta )$-nonexpansive for $\alpha =\frac{1}{4}$.

Case (1). 

When $r^{\prime },s^{\prime }\in A=[0,\frac{1}{1000}]$,

$$\begin{array}{ccc}\hfill H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime })=0& \le & \alpha d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\alpha d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\beta d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\beta d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })\hfill \\ & & +(1-2\alpha -2\beta )\left|\right|r^{\prime }-s^{\prime }\left|\right|.\hfill \end{array}$$

Case (2). 

When $r^{\prime },s^{\prime }\in B=[\frac{1}{1000},\infty )-\left\{\frac{8}{5}\right\}$,

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{1}{4}|r^{\prime }-\frac{s^{\prime }}{3}|+\frac{1}{4}|s^{\prime }-\frac{r^{\prime }}{3}|+\frac{1}{4}|r^{\prime }-\frac{r^{\prime }}{3}|+\frac{1}{4}|s^{\prime }-\frac{s^{\prime }}{3}|\hfill \\ \hfill & =\frac{1}{4}|\frac{s^{\prime }}{3}-r^{\prime }|+\frac{1}{4}|\frac{r^{\prime }}{3}-s^{\prime }|+\frac{1}{4}|\frac{r^{\prime }}{3}-r^{\prime }|+\frac{1}{4}|\frac{s^{\prime }}{3}-s^{\prime }|\hfill \\ \hfill & \ge \frac{1}{4}|\frac{4s^{\prime }}{3}-\frac{4r^{\prime }}{3}|+\frac{1}{4}|\frac{2r^{\prime }}{3}-\frac{2s^{\prime }}{3}|\hfill \\ \hfill & \ge \frac{1}{4}|\frac{6s^{\prime }}{3}-\frac{6r^{\prime }}{3}|\hfill \\ \hfill & =\frac{3}{2}\left|\frac{s^{\prime }-r^{\prime }}{3}\right|\hfill \\ \hfill & =\frac{3}{2}\left|\frac{r^{\prime }-s^{\prime }}{3}\right|\hfill \\ \hfill & \ge |\frac{r^{\prime }-s^{\prime }}{3}|=H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime }).\hfill \end{array}$$

Case (3). 

When $r^{\prime }\in A$ and, $s^{\prime }=\frac{8}{5}$,

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{1}{4}|r^{\prime }-\frac{7}{10}|+\frac{1}{4}|\frac{8}{5}|+\frac{1}{4}|\frac{7}{10}|+\frac{1}{4}\left|\frac{9}{10}\right|\hfill \\ \hfill & =\frac{1}{4}|\frac{7}{10}-r^{\prime }|+\frac{32}{40}\hfill \\ \hfill & =\frac{39}{40}-\frac{r^{\prime }}{4}\ge \frac{7}{10}=H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime }).\hfill \\ \end{array}$$

Case (4). 

When $r^{\prime }\in B$ and $s^{\prime }=\frac{8}{5}$,

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },r^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{1}{4}|r^{\prime }-\frac{7}{10}|+\frac{1}{4}|\frac{8}{5}-\frac{r^{\prime }}{3}|+\frac{1}{4}|r^{\prime }-\frac{r^{\prime }}{3}|+\frac{1}{4}|\frac{8}{5}-\frac{7}{10}|\hfill \\ \hfill & =\frac{1}{4}(r^{\prime }-\frac{7}{10})+\frac{1}{4}(\frac{8}{5}-\frac{r^{\prime }}{3})+\frac{1}{4}(r^{\prime }-\frac{r^{\prime }}{3})+\frac{1}{4}(\frac{8}{5}-\frac{7}{10})\hfill \\ \hfill & =\frac{r^{\prime }}{4}-\frac{7}{40}+\frac{2}{5}-\frac{r^{\prime }}{12}+\frac{r^{\prime }}{6}+\frac{9}{40}\hfill \\ \hfill & =\frac{2r^{\prime }}{3}+\frac{9}{20}\ge H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime }).\hfill \end{array}$$

Case (5). 

When $r^{\prime }\in A$ and $s^{\prime }\in B$,

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{1}{4}|r^{\prime }-\frac{s^{\prime }}{3}|+\frac{1}{4}|s^{\prime }|+\frac{1}{4}|r^{\prime }|+\frac{1}{4}|s^{\prime }-\frac{s^{\prime }}{3}|\hfill \\ \hfill & =\frac{1}{4}|r^{\prime }-\frac{s^{\prime }}{3}|+\frac{1}{4}|r^{\prime }|+\frac{5}{12}\left|s^{\prime }\right|.\hfill \end{array}$$

(16)

Here, we have two cases:

$$|r^{\prime }-\frac{s^{\prime }}{3}|=\left\{\begin{array}{cc}{r}^{\prime }-\frac{s^{\prime }}{3}\hfill & if{r}^{\prime }>\frac{s^{\prime }}{3}\hfill \\ \\ -r^{\prime }+\frac{s^{\prime }}{3}\hfill & if{r}^{\prime }\le \frac{s^{\prime }}{3}.\hfill \end{array}\right.$$

For the first case (i.e., $r^{\prime }>\frac{s^{\prime }}{3}$), (16) implies:

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{s^{\prime }}{3}+\frac{r^{\prime }}{2}\ge \frac{s^{\prime }}{3}=H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime }).\hfill \end{array}$$

For the second case (i.e., $r^{\prime }\le \frac{s^{\prime }}{3}$), (16) implies:

$$\begin{array}{cc}\hfill & \frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{s}^{\prime })+(1-\frac{2}{4}-\frac{2}{4})\left|\right|r^{\prime }-s^{\prime }\left|\right|\hfill \\ \hfill & =\frac{s^{\prime }}{2}\ge \frac{s^{\prime }}{3}=H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime }).\hfill \end{array}$$

Thus, $P_{\mathbb{J}}$ is a generalized $(\frac{1}{4},\frac{1}{4})$-nonexpansive mapping.

(b) On the other hand, for $r^{\prime }=1$ and $s^{\prime }=\frac{8}{5}$, we have

$$\frac{1}{2}d(r^{\prime },P_{\mathbb{J}}{r}^{\prime })=\frac{3}{10}<\frac{3}{5}=\left|\right|r^{\prime }-s^{\prime }\left|\right|.$$

However,

$$H(P_{\mathbb{J}}{r}^{\prime },P_{\mathbb{J}}{s}^{\prime })=\frac{7}{10}>\frac{69}{100}=\frac{1}{4}d(r^{\prime },P_{\mathbb{J}}{s}^{\prime })+\frac{1}{4}d(s^{\prime },P_{\mathbb{J}}{r}^{\prime })+(1-2\alpha )\left|\right|r^{\prime }-s^{\prime }\left|\right|.$$

Thus, $P_{\mathbb{J}}$ is not a generalized $(\frac{1}{4},\frac{1}{4})$-nonexpansive mapping.

Note that Figure 1 and Table 1 reflect the efficiency of the M-iteration process as compare to the other iteration processes in the case of multi-valued generalized $(\alpha ,\beta )$-nonexpansive mapping defined in Example 2.

Figure 1. Convergence behaviors of different iterative schemes to a fixed point $p_0=0$ of the map $\mathbb{J}$.

Table 1. Initial points influence on different iteration algorithms.

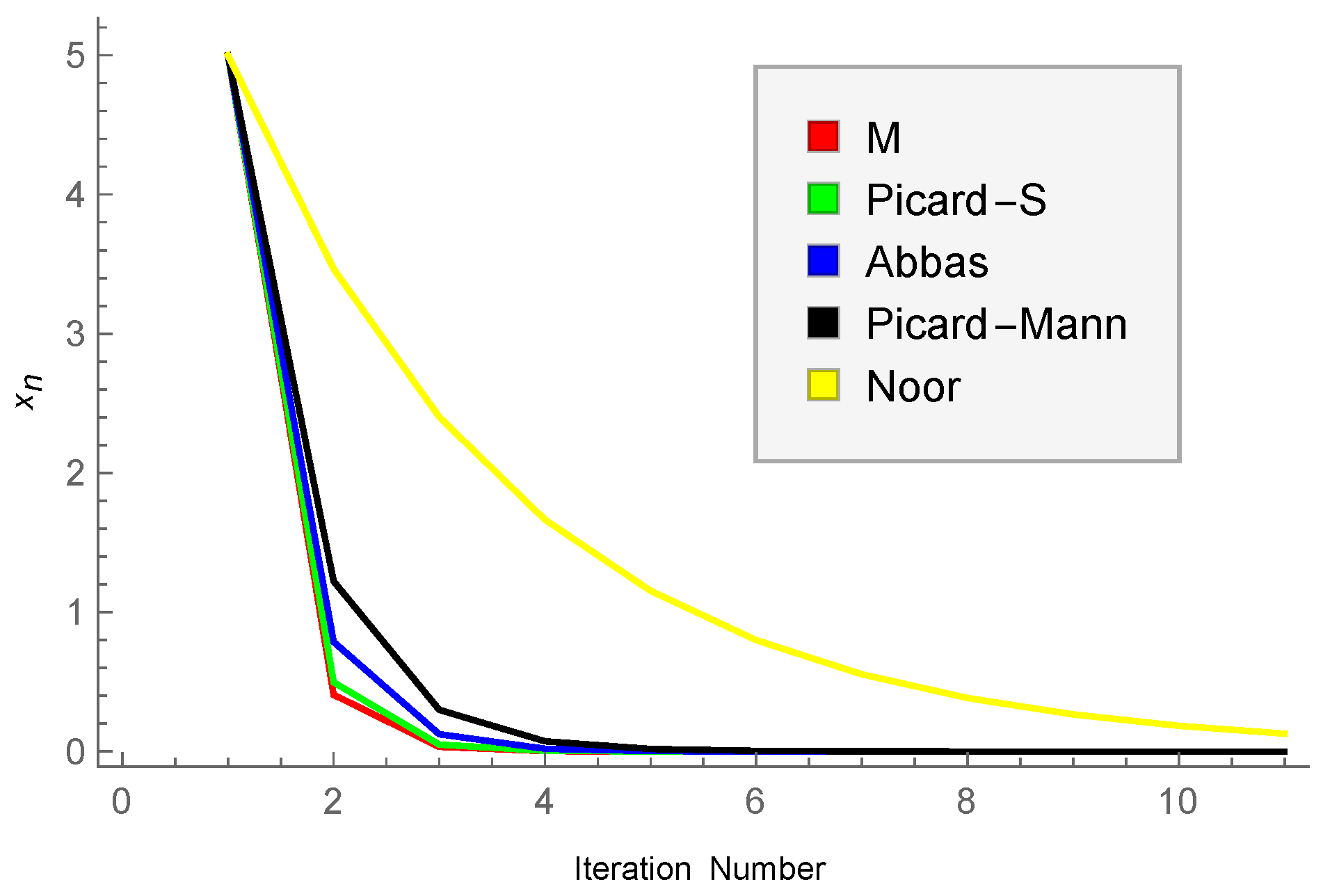
Number of Iterations Required to Obtain Fixed Point.
Initial Points	M-Iteration	Picard-S	Abbas	Picard–Mann	Noor
5	4	5	6	7	53
50	5	6	8	9	57
500	6	7	9	11	63
1200	7	7	10	11	66
2000	7	7	10	12	67

7. Conclusions

We have provided the multi-version of the generalized $(\alpha ,\beta )$-nonexpansive operators. Basic properties of these maps in a Banach space setting are established. For finding fixed points of these maps, we have provided the multi-valued version of the M-iteration and showed, by an example, that it is more effective than the other iterative schemes. Since multi-valued $(\alpha ,\beta )$-nonexpansive are more general than the multi-valued generalized $\alpha$-nonexpansive and multi-valued Reich–Suzuki type nonexpansive maps, we conclude that our main outcome improves and extends the corresponding results of Iqbal et al. [13] and Maldar et al. [15].