Abstract
Financial and commercial data are mostly represented in decimal format. To avoid errors introduced when converting some decimal fractions to binary, these data are processed with decimal arithmetic. Most processors only have hardwired binary arithmetic units. So, decimal operations are executed with slow software-based decimal arithmetic functions. For the fast execution of decimal operations, dedicated hardware units have been proposed and designed in FPGA. Decimal multiplication is found in most decimal-based applications and so its optimized design is very important for fast execution. In this paper two new parallel decimal multipliers in FPGA are proposed. These are based on a new decimal adder/subtractor also proposed in this paper. The new decimal multipliers improve state-of-the-art parallel decimal multipliers. Compared to previous architectures, implementation results show that the proposed multipliers achieve 26% better area and 12% better performance. Also, the new decimal multipliers reduce the area and performance gap to binary multipliers and are smaller for 32 digit operands.
1. Introduction
Financial and commercial applications like accounting, banking, tax calculation, insurance and currency conversion require a large amount of data computing. Therefore, they are typically executed in high-performance computing platforms. These applications run over large databases of numbers which, in many cases, are represented in decimal format [1]. The last revision of the IEEE standard for floating-point arithmetic [2] includes specific definitions and rules for decimal operations and three different formats: decimal 32, decimal 64 and decimal 128, with 7, 16 and 34 coefficient digits.
Most general-purpose processors only have binary arithmetic units. So, the fastest solution to run decimal operations would be to convert decimal numbers to binary before being processed and then convert the result to decimal. The problem is that not all decimal numbers can be represented exactly as binary numbers with a finite number of bits. So, to avoid errors created from binary calculation that could lead to unwanted result deviations [3,4], arithmetic operations must be done directly over decimal numbers [5]. Their calculations must follow the conventions of decimal arithmetic and must keep a word length enough to support the precision required by these applications. Current applications may need over 30 precision digits to represent exactly a large set of decimal values found in the databases of these applications [6].
Executing decimal operations with binary arithmetic hardware without converting data to binary requires software algorithms for decimal arithmetic. Several software libraries for decimal arithmetic are supported by Intel [7], ANSI C [8] and GCC [9]. Software-based decimal arithmetic is very slow compared to binary arithmetic implemented in hardware [5]. This is acceptable as long as the performance is not an application requirement. For example, commercial applications usually do not require high decimal arithmetic performance.
However, the fast increase of commercial and financial transactions requires fast decimal arithmetic computing to meet real-time requirements and exact computations. Some approaches to binary/decimal computing [5,10] were adopted for the design of processors with special units for decimal floating-point arithmetic, like the IBM eServer z900 [11], the IBM POWER6 [12] and the IBM z10 [13].
Since the set of applications taking advantage of these specialized units is somehow limited, most processors only include some kind of specific instructions to help in the execution of decimal operations performed in software. In this scenario, FPGAs (Field Programmable Gate Array) may be a good alternative for the execution of decimal arithmetic with dedicated hardware modules, like in many other applications [14,15]. Many financial applications already use FPGAs to speed-up the execution of their algorithms and so an hardware reprogrammable platform is already available. Besides, since logic in FPGAs is implemented with look-up tables, the gap between binary and decimal arithmetic is smaller than when implemented with ASIC (Application Specific Integrated Circuit).
Decimal multiplication is a fundamental arithmetic operation used in many applications and the design of other arithmetic functions. Therefore, fast decimal multipliers are important to obtain fast decimal-based applications. Two new methods for parallel decimal multiplication on FPGA with different tradeoffs between area and performance are proposed. The methods are based on a new decimal adder/subtractor.
The results obtained with the new decimal multipliers improve both the area and the performance of the best state-of-the-art decimal multipliers. Additionally, it reduces considerably the implementation gap between decimal and binary multipliers in FPGA.
This paper is organized as follows. Section 2 describes state-of-the-art of decimal multiplication. Section 3 introduces the decimal adder/subtractor. Section 4 describes the proposed decimal multipliers. Section 5 presents the results of the new decimal multipliers and compares the results with previous parallel decimal multipliers. Section 6 concludes the paper.
2. Related Work
Processors with dedicated decimal hardware multipliers implement them with iterative algorithms [16,17] to reduce the size of the arithmetic unit. However, iterative algorithms are slow compared to parallel implementations due to its iterative nature. for fast execution, parallel decimal multiplication consists of partial product generation for each multiplier digit followed by partial product addition. Partial product generation of a multiplication can be implemented with small digit by digit multipliers or N digit by multiplicand multipliers. A digit by digit multiplier can be implemented with logic or with look-up tables [18,19,20], for fast and compact design. However, given the quadratic number of digit by digit multipliers necessary to implement a multiplication, these solutions are viable only for small operand sizes. The proposal in [21] considered recoding of operands to simplify digit by digit multiplication for partial product generation. However, the performance and area of the decimal multiplier based on digit by digit multiplication is still worst than a multiplier with a partial product for each multiplier digit.
The approach followed to implement a multiplier is to determine the decimal multiples of the multiplier. A direct approach to a design a decimal multiplier based on multiples generates all multiples of the multiplicand. Then, selects the required multiples according to the multiplier digits. The generated multiples are then shifted and added to generate the final product. While simple, the method requires a large multiplexer with all multiplies for each multiplier digit and the generation of all multiples from A to 9A. Knowing that the generation of some multiples are not carry-free, this solution degrades the performance of the multiplier.
Therefore, authors started to consider only a limited set of multiples. In [22] only multiples A, 2A, 4A, 5A are used, since they can be generated without carry propagation (multiple 4A is generated from 2A in sequence as ). The other multiples are obtained by adding two of these multiples. Since multiple cannot be generated in a single carry-free step, it has been removed from the set of base multiples in [23]. The other multiples are obtained by adding a multiple from the set {0, 5X, 10X} and a multiple from the set {−2X, −X, 0, X, 2X}. For fast selection of multiples, digits of the multiplier are first recoded, but the solution requires a large multiplexer for each multiplier digit.
Since then, other sets of multiples and encodings were considered. In [24] two different decimal encodings (4221 and 5211) are used to generate and reduce the partial products with two different architectures. In one the architectures the multiplier is recoded into a signed-digit (SD) set [−5, 5], while in the other the multiplier is encoded as like in [23], where and . Signed-digit (SD) recoding of the multiplier in the set [−5, 5] was adopted by several authors for the implementation of a decimal multiplier [25,26]. The base architecture generates multiples {0, X, 2X, 3X, 4X, 5X}. These are selected for each partial product and the output is complemented to obtain the negative of the multiple. The partial products are then reduced with a partial product reduction module. Different representations are used to improve the generation of complements and the decimal addition. The radix-5 algorithm proposed in [24] was followed by [27] but using an hybrid 8421–5421 representation.
In [28] a decimal multiplier is proposed using a redundant decimal addition algorithm based on a weighted bit-set encoding. The method generates double BCD (Binary-Coded Decimal) numbers using decimal multiples 2X, 4X, and 5X. The redundant decimal adder is used to reduce the generated 2n BCD partial products to a redundant number in the range of [0, 15]. The final redundant product is then converted to BCD encoding.
The special case of constant decimal multiplication was considered in [29]. Constant decimal multiplication is widely used in economic and financial applications. The authors address this problem to design a solution with smaller area, power and delay compared to constant decimal multiplication implemented with a general decimal multiplier. The work proposes a new redundant digit set in {0, 18} and a 3:1 compressor. The results show an improvement in the area up to 89%.
Partial products are then added is a step known as partial product reduction using decimal adders. Partial product reduction can be designed with an adder tree or with a multioperand adder. An adder tree successively reduces pairs of partial products until a final result. Multioperand addition takes into account that multiple partials have to be reduced into a single value. In [30] three techniques were proposed for multioperand decimal addition. Two of the approaches consider speculative addition that speculates about BCD correction values which are corrected while adding the operands. The other technique uses a binary adder that produces a binary sum which is then corrected. This last technique achieved the best area-delay results. A mixed binary and BCD multioperand addition was proposed in [31]. Digits in a column are all added in binary, converted to decimal and finally added with decimal adders.
In [22,23] the adder tree is implemented with decimal carry look-ahead adders. In [32] partial products are recoded to 4221. This codification simplifies addition since it avoids he correction step. The method reduces three partial products to two equally weighted 4221 decimal digits. These two operands are then converted to BCD add added to generate the final result.
A different approach for decimal multiplication considers binary multipliers as the base arithmetic unit [33,34,35,36]. This permits using binary multipliers that are faster and may already be available in the system. Also, it implements both binary and decimal multiplication in a single module. The method first converts the BCD operands of the multiplication to binary. The converted operands are then multiplied using the binary multiplier. The binary product is then converted to BCD. The main drawback of the binary-based method is the large overhead introduced by the converters [35,37]. A balanced solution was proposed in [34] that subdivides the multiplier and the multiplicand into smaller blocks and applies the method to each of these sub-blocks. The partials are then aligned and added using decimal adders to generate the final product.
Most works on decimal multiplication target ASICs, but several architectures have been proposed for FPGA and coarse-grained reconfigurable computing [38]. Any of the previous architectures can be directly mapped to FPGA. However, a careful adaptation of the design leads to a more efficient architecture since logic functions in FPGAs are implemented with look-up tables. In [39] a parallel implementation of a multiplier was mapped in Virtex-4 FPGA from Xilinx. The architecture obtains the partial products using digit by digit multiplication with a binary multiplier followed by binary to BCD conversion [40]. The work in [41] described previously was mapped on a 6-input LUT FPGA.
A new optimization of the multiplication algorithm was considered in [42] where the application of the Karatsuba-Ofman algorithm reduces the area of the parallel decimal multipliers on FPGA at the cost of an increase in delay. A BCD multiplier using the atomic digit multiplier was proposed in [43]. The effort of the work is on the partial product reduction unit. The two-digit partial products of all digit multiplications are correctly aligned to generate the complete partial products. The partial products are then reduced with a mix of binary decimal compressors and decimal adders.
Recently, a new decimal multiplier [44] improved the area of the best previous decimal multipliers on FPGA by about 20%. The solution considers a new decimal adder based on a mixed BCD/excess-6 representation and a 5221 recoding of the multiplier digits. Partial products are obtained from the addition of a multiple in the set {0, 2X, 5X, 2X + 5X} and a multiple in the set {X, 2X}.
Two novel decimal multipliers on FPGA with different area/performance tradeoffs with both multipliers improving the area and performance of state-of-the-art multipliers are proposed. Both methods use a new adder/subtractor based on the excess-3 representation of multiples. Two different sets of multiples are considered: {0, X, 2X, 5X, 10X} and {2X, 4X, 5X}. Partial products are obtained by the addition or subtraction of two multiples of the sets. The method permits a very efficient generation of multiples, which considerably reduces the required resources. The area of the largest decimal multiplier is smaller than the area of an equivalent binary multiplier.
3. Decimal Adder/Subtractor
In [45] a decimal adder was proposed that considers an excess-6 representation to avoid carry propagation of addition. This adder is used in the proposed multipliers to implement the adder tree. It also serves as the base for a novel decimal adder/subtractor necessary for the design of the partial product generators. To better understand the new adder/subtractor, the decimal adder proposed in [45] is briefly described.
3.1. BCD/Excess-6 Adder
The fundamental idea of the adder proposed in [45] is to consider addition of one digit represented in BCD, w, and the other in excess-6 (BCD digit plus six), z. The result is correct if , but if then the result is in excess-6 and must be corrected by subtracting six to obtain a BCD number. The advantage of the method is that the carry out bit from each digit addition is always correct independently of whether the result as to be corrected or not. These avoids carry propagation to correct the result. The carry-out bit of each digit addition indicates if the result digit is BCD or excess-6. A carry out of 1 means that the digit is in BCD, while a carry-out of 0 means that the result is in excess-6 and must be corrected.
A generic decimal adder in which each of the operands can be independently represented in BCD or in excess-6 was designed in [45]. Each digit has an extra bit (isbcd) that specifies if the digit is represented in BCD (isbcd = 1) or excess-6 (isbcd = 0). Since the BCD/excess-6 adder needs one of the operands to be in BCD and the other in excess-6, the inputs may have to be converted accordingly. If both are represented in BCD, one of the operands must be converted to excess-6. If both are represented in excess6 then one must be converted to BCD.
The adjustment of the operands and their addition were designed with a single level of LUT-6 and the carry-chain of the FPGA. The expressions of the generate and propagate signals of a single digit adder are as follows [45]:
The generate signals are always
Signals wbcd and zbcd indicate whether the digits w and z are represented in BCD or in excess-6.
The addition of two decimal numbers whose digits are represented in BCD or excess-6 is implemented with a chain of single digit BCD/excess-6 adders.
3.2. BCD/Excess-6 Subtractor
BCD subtraction can be implemented with a similar approach. Considering two BCD digits, w and z, the subtraction is correct if , otherwise the result is in excess-6 and must be corrected by subtracting six to obtain a BCD number. The borrow out bit from each digit subtraction is always correct independently of whether the result as to be corrected or not. The borrow-out bit of each digit subtraction also informs if the result digit is BCD or excess-6, that is, a borrow out of 1 means that correction is needed.
Considering again the two BCD digits, w and z, the subtraction can be implemented with an adder as follows
where 9’z is the nine’s complement of z. Using the BCD/exccess-6 adder to execute this addition, we must add six to the equation:
From this equation, subtraction of two BCD digits, w − z, is accomplished by adding w with the 1’s complement of z, , plus one.
The decimal subtractor can be made generic with operands independently represented in BCD or in excess-6 specified by the input. In this case, the inputs have to be converted according to Table 1.

Table 1.
Functionality of a single digit BCD/excess-6 Subtraction.
Similar to the adder described in the previous Section, the subtraction of two digits is implemented with the generate and propagate signals defined as follows
The generate signals are always
Considering two N-digit decimal numbers and with digits represented in BCD or excess-6, specified with the extra inputs and . The subtraction is implemented with a chain of N single digit BCD/excess-6 subtractors. The carry-in of the single digit BCD/excess-6 subtractor associated with the least significant digit is ’1’. The result is the decimal subtraction and the extra output .
3.3. BCD/Excess-6 Adder/Subtractor
From the designs of the generic adder and subtractor described in the previous Sections, a generic adder/subtractor circuit can be implemented considering an extra input, , that specifies if the operands are to be added () or subtracted (). The propagate signals of the circuit are a merge of the propagate signals of the adder and of the subtractor described previously, namely.
The generate signals are always
The propagate signals of the generic BCD/excess-6 adder are functions of only two inputs when , while in the generic BCD/excess-6 subtractor they are functions of only two inputs when .
In the case of the generic adder/subtractor circuit, not considering input , signals and are functions of two variables, while signals and are functions of 3 and 4 variables, independently of inputs and . Therefore, the complexity of the generic adder/subtractor has increased.
It is possible to reduce this complexity to only two variables as in the generic adder and generic subtractor using operands represented in excess-3. Considering two BCD digits, w and z, converted to excess-3 (add three), and , respectively. The addition of and is given by
This is the same to say that one of the operands in represented in BCD and the other in excess-6. In addition, when operands use different representations the propagate signals are only functions of two variables.
Considering the same two digits in excess-3, the subtraction of and is given by
This is the same to say that both operands are in BCD. In subtraction when operands use the same representation the propagate signals are only functions of two variables.
Hence, when the operands are represented in excess-3 the propagate signals of both operations are in the most simplified form as follows:
This property will allow the simplification of the multiplier to be described in the next Section.
The complete BCD/excess-6 adder/subtractor is implemented with a chain of N single-digit BCD/excess-6 adder/subtractors. The carry-in of the single-digit BCD/excess-6 adder/subtractor associated with the least significant digit is connected to the operation selector. The carry-in is ’0’ if the selected operation is addition, and ’1’ otherwise. The result is the decimal addition or subtraction and an extra output for each digit to specify if it is BCD or excess-6.
4. Decimal Multiplier
Considering two operands, A and B, with n decimal digits () and (), respectively, given by
The product of A × B is a number with 2n decimal digits () given by .
A decimal digit, , is coded with four bits according to expression
where is the bit of at position j and is the weight of bit determined by the codification.
The most common codification of a decimal digit is BCD (Binary-Coded Decimal) that adopts the weights of a pure binary representation (8421). However, several other representations have been considered in the literature, like (5421), (4221), (5221), (4311) and (3321). A representation is chosen as the one that optimizes a particular arithmetic algorithm. As observed in Section 3.3, we are particularly interested in the excess-3 code (see Table 2).

Table 2.
Representation of a decimal digit with excess-3.
In this paper, the design of the multipliers follows the algorithm of most previous approaches. Partial products are first generated and then reduced with a tree of decimal adders. Each partial product results from the multiplication of a multiplier digit by the multiplicand. The partial product is obtained by the addition or subtraction of two multiples of the multiplicand. This paper considers two different sets of multiples for the partial product generation that leads to different tradeoffs between delay and area. In the following, both methods for partial product generation are described.
4.1. Partial Product Generator—Method 1
Considering a multiplicand, A, and a multiplier B, one partial product is the result of the multiplication of a multiplier digit, , by the multiplicand. Since a digit varies between 0 and 9, the partial product corresponds to a multiple of A in the set {0, 1A, 2A, …, 8A, 9A}. To obtain these multiples, two subsets of multiples are considered: = {0, 5A, 10A} and = {0, A, 2A}. The advantage of these subsets of multiples is that they can be easily generated without carry propagation, as will be shown later.
From these, any multiple of the set {0, A, 2A, …, 8A, 9A} can be obtained from the addition or subtraction between multiples of each set as shown in Table 3.

Table 3.
Generation of multiples using subsets = {0, 5A, 10A} and = {0, A, 2A}.
The hardware design of the partial product generator includes one multiplexer to select the multiple from the subset , another multiplexer to select the second multiple from and one decimal adder/subtractor (see Figure 1).
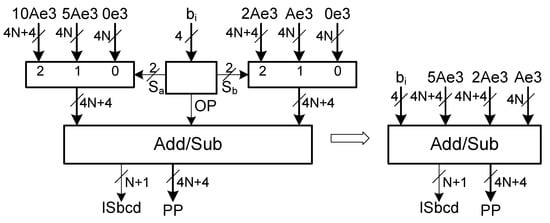
Figure 1.
Partial product generator for a single multiplier digit using subsets = {0, 5A, 10A} and = {0, A, 2A}.
Selectors and of the multiplexers, and operand selector are functions of the 4-bit multiplier digit, , as described in Table 4.

Table 4.
Generation of selectors in method 1.
The decimal adder/subtractor of the partial product generator is implemented as explained in Section 3.3 with multiples represented in excess-3. Therefore, propagate signals of the adder/subtractor are functions of three variables. Considering that the circuit is to be implemented in FPGAs with 6-input LUTs, there are three unused inputs in each LUT implementation of a propagate signal. So, the implementation of the partial product generator can be further optimized by merging the multiplexer of the subset {0, A, 2A} with the adder/subtractor (see Figure 2).
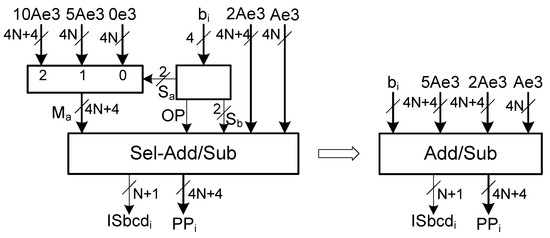
Figure 2.
Partial product generator for a single multiplier digit.
Block sums (op = 0) or subtracts (op = 1) the output of the multiplexer with one multiple in the set {0, A, 2A}, determined by selector {}. Considering the propagate and generate expressions of the BCD/excess-6 adder/subtractor with operands represented in excess-3, the expressions of the propagate and generate signals for a single digit of block are as follows:
where is a digit from the output of the multiplexer, . and are digits from multiples Ae3 and 2Ae3, respectively.
Connecting these propagate and generate signals with a carry chain provides the circuit for a single digit of block with a carry-in and a carry-out (see the implementation of a single digit in Figure 3).
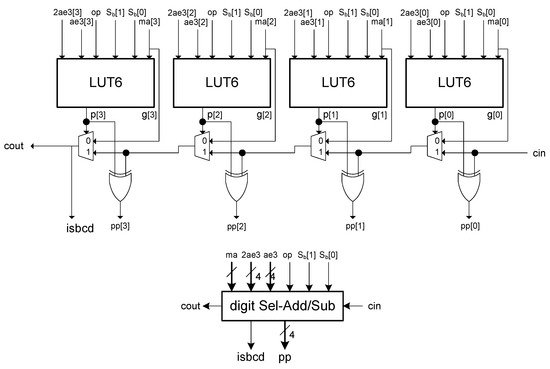
Figure 3.
Implementation for a single digit of block in method 1.
The complete partial product is obtained with a chain of these single-digit blocks. The generated partial products are in BCD/excess-6 format. Therefore, each partial product output consists of N + 1 BCD/excess-6 digits, , and N + 1 bits, , one for each digit, indicating if the digit is represented in BCD or excess-6.
The partial product generator produces all N partial products in parallel using N (single digit) partial product generators (see Figure 4).
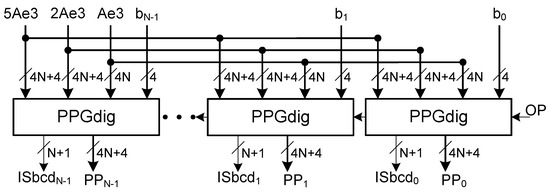
Figure 4.
Proposed partial product generator in method 1.
Each partial product generator receives one digit of operand B.
4.2. Partial Product Generator—Method 2
The second method to generate the partial product considers the following subsets of multiples: = {4A, 5A} and = {0, 2A, 4A}. The advantage of these subsets is that subset has only two multiples. The disadvantage is associated with the generation of multiple 4A as will be seen in the generation of multiples.
Similar to method 1, any multiple of the set {0, A, 2A, …, 8A, 9A} can be obtained from the addition or subtraction between multiples of each set as shown in Table 5.

Table 5.
Generation of multiples in method 2.
The architecture of the partial product circuit is similar to that designed for method 1, except that the multiplexer has only two inputs: 4A and 5A (see Figure 5).
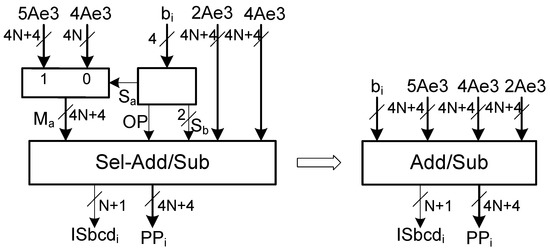
Figure 5.
Partial product generator for a single multiplier digit using subsets = {4A, 5A} and = {0, 2A, 4A}.
Selectors and , and operand selector are functions of the multiplier digit, , as described in Table 6.

Table 6.
Generation of selectors in method 2.
Also, to simplify the adder/subtractor of the partial product generator all multiples are represented in excess-3. Considering the equations of the propagate and generate expressions of the adder/subtractor with operands represented in excess-3, the expressions of the propagate and generate signals for a single digit of block are as follows:
Propagate and generate signals are interconnected with a carry chain to generate the circuit for a single digit of block with a carry-in and a carry-out (see the implementation of a single digit in Figure 6).
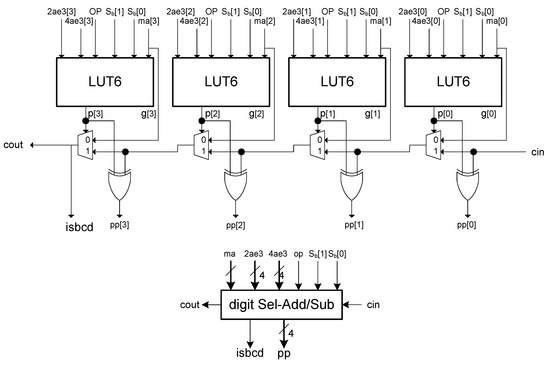
Figure 6.
Implementation for a single digit of block in method 2.
Similar to method 1, the complete partial product is obtained with a chain of these single-digit blocks. All N partial products are generated parallel with N partial product generators. The carry-in of the first module receives the signal.
4.3. Generation of Multiples
The generation of partial products with one of the previous method is based on the availability of multiples A, 2A, 4A, 5A and 10A of the multiplicand in excess-3, Ae3, 2Ae3, 4Ae3, 5Ae3 and 10Ae3, respectively. Multiple 10Ae3 is obtained from multiple Ae3 decimal shifted left one digit with the new least significant digit equal to three.
Considering a number with n digits, A = , where each digit has four bits, . Considering also the excess-3 of A, Ae3 = Y = , where each digit has four bits, . Each digit is obtained according to Table 7.

Table 7.
Digit in excess-3, .
Considering now the excess-3 of 2A, 2Ae3 = Y = , each digit is obtained according to Table 8.

Table 8.
Digit in excess-3, .
Multiple of digit is obtained according to the second column of Table 8. In this case, there is a carry out bit . However, since the least significant digit of is always zero then there is no carry propagation. However, multiple has always one at the least significant bit. So, is the addition of plus the carry out from , that is, it depends on and . The solution proposed in this paper, first determines all carries and then determines as a function of and , as described in Table 8.
The implementation of Y = 4Ae3 is based on multiple 2A. First, multiple B = 2A is determined according to the second column of Table 8. Then, multiple Y = 4Ae3 = 2Be3 is determined like multiple 2Ae3 described previously.
Considering the excess-3 of 5A, 5Ae3 = Y = , each digit is obtained according to Table 9.

Table 9.
Digit in excess-3, .
The multiple of one digit results in two digits. The most significant digit is in [0 to 4] and the least significant digit is in [0 or 5], depending if digit is even or odd, respectively. So, each digit depends on input digit and the least significant bit of digit , where . So, multiple 5A is generated in a single step without any carry propagation according to Table 9.
All multiple generators assume that the input number is in BCD. To be more generic, all multiple generators were designed with an extra input (isbcd) to specify if the number is in BCD or excess-6. With generic multiple generators, the multipliers are also generic permitting to interconnect several adders/subtractors or multipliers without having to convert the output to BCD.
4.4. Partial Product Reduction
Partial product reduction adds the N partial products {} with left shifted by i decimal places. Formally the addition of partial products is calculated according to Equation (17).
The multioperand addition is designed using an adder tree, similar to [44]. The tree has levels of adders. Each level i has adders, where level 0 is the first set of adders.
The complete partial product reduction tree for N operands of size N + 1 uses BCD/excess-6 single digit adders (digAdder). The critical path of the adder tree with N partials is given by digit adders plus carry chain bits.
4.5. BCD/Excess-6 to BCD Converter
The output of the partial product reduction is the product represented in BCD/excess-6 format, that is, some digits may be represented in BCD, while others may be represented in excess-6. Unless the output is the input of another decimal adder/subtractor or multiplier that accepts mixed BCD/excess-6 representations, the product has to be converted to BCD to be presented.
A digit of the product must be converted to BCD if isbcd is 0. The logical expressions to convert a BCD/excess-6 digit, to a BCD digit, are as follows:
The expressions are at most functions of four variables.
4.6. Architecture of the Two Versions of the Decimal Multiplier
The complete decimal multipliers include the multiples generators, the partial product generators and the partial product reduction (see Figure 7).
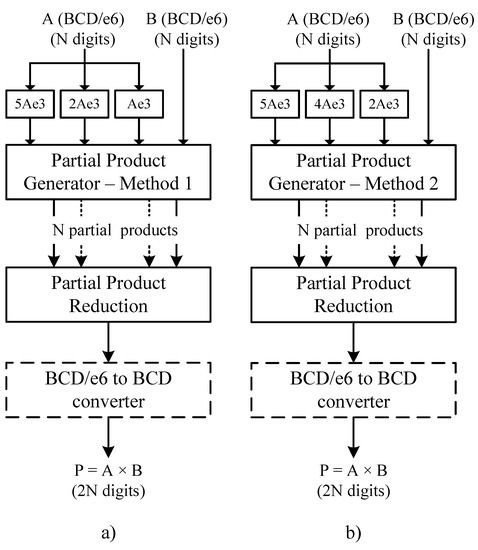
Figure 7.
Architecture fo the proposed decimal multipliers. (a) Decimal multiplier with method 1 and (b) decimal multiplier with method 2.
The output of the partial product reduction is in BCD/excess-6 format. A final BCD/excess-6 to BCD converter is required if the result in a pure BCD format is needed. The difference between both multipliers is the partial product generator and the required multiples. In Figure 7a, multiplier 1 uses the partial product generator based on multiples Ae3, 2Ae3, 5Ae3 and 10Ae3 (obtained directly from multiple Ae3), and in Figure 7b, multiplier 2 uses the partial product generator based on multiples 2Ae3, 4Ae3 and 5Ae3.
For an N × N decimal multiplier the theoretical area occupation of both decimal multipliers can be estimated (see Table 10).

Table 10.
Theoretical area of both decimal multipliers in number of LUT6.
There are two lines in the Table for the multiples generator: the first line is when the operands and the result are in BCD and the second line is when they are in BCD/excess-6 representation. In the last case, the final converter is not used.
The area of multiplier 1 with inputs and output represented in BCD is higher than multiplier 2. When inputs and output are represented in BCD/excess-6, multiplier 1 has an area higher than multiplier 2.
5. Results
All designs were described in VHDL and implemented in a Virtex-7 FPGA (-3 speed grade). The architecture was simulated, synthesized, placed and routed using Vivado 19.1 from Xilinx. The area of all implementations after place and route are presented in Table 11 and Table 12.

Table 11.
Logic area (LUTs) and delay (ns) of both multipliers with BCD inputs and output for different number of digits in a Virtex-7 FPGA, speed grade -3.

Table 12.
Logic area (LUTs) and delay (ns) of both multipliers with BCD/excess-6 inputs and output for different number of digits in a Virtex-7 FPGA, speed grade -3.
Multiplier 1 is the fastest while multiplier 2 is the smallest. These relations are determined by the multiples generators and the partial product generators. Multiplier 2 needs multiple that is harder to generate and has a critical path higher than the other multiples. This determines the higher critical path of the second multiplier. On the other side, the multiplexer of the partial product generator of multiplier 1 has three inputs. while the multiplexer of multiplier 2 has only two. This determines the smaller area of multiplier 2.
As can be observed from the results, multiplier 2 is 18% smaller than multiplier 1 for the 32 digit multiplier. This difference reduces for smaller multipliers. On the other side, multiplier 1 is 30% faster than multiplier 2 for the 2 digit multiplier. This difference reduces for larger multipliers (see Figure 8 and Figure 9).
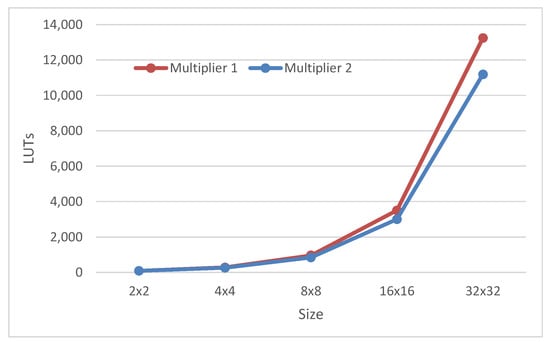
Figure 8.
Area variation of both multipliers.
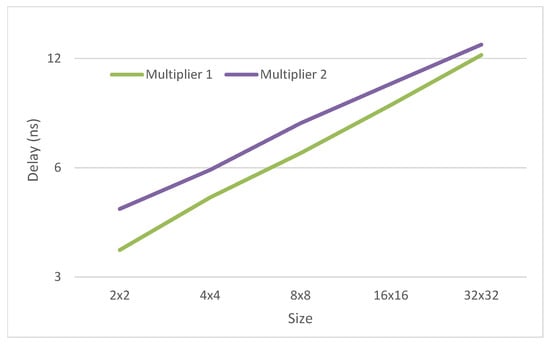
Figure 9.
Delay variation of both multipliers.
Multiples generator of multiplier 2 occupies more area than those of multiplier 1, but the partial generator is smaller in multiplier 2. Since the area of the partial product generators reduces faster, the difference of the area of the proposed multiplier 2 to the multiplier 1 increases with the size of the multipliers.
The difference in delay between the proposed multipliers is mostly due to the multiples generators. Therefore the absolute difference between both multipliers is almost constant. Therefore, the relative delay difference decreases with the size of the multipliers.
The results of the proposed multipliers were compared with state-of-the-art decimal multipliers implemented in FPGA [41,42,43,44], (see Table 13).

Table 13.
Comparison of the proposed decimal multipliers with state of the art works for different number of digits.
All designs consider registered inputs and outputs. The multiplier in [41] uses the final flip-flops to implement the final conversion from the internal representation to BCD. To register the outputs an extra level of LUTs is required. In our circuit, the extra level of LUTs implements both the converter and the register. In this reference, the decimal digit adder occupies five LUT, while our decimal adder occupies only four. For a fair comparison, the multiplier from [41] was redesigned and implemented with our decimal adder.
The decimal multiplier from [42] uses the Karatsuba-Offman algorithm to reduce the area at the cost of delay. The area reduction impact is higher for larger operands. However, even for the decimal multiplier, the proposed multiplier 1 achieves a similar area with a reduction of 34% in the delay. Multiplier 2 reduces the area by 15% for the multiplier with with a reduction of 28% in the delay. The improvements obtained with the proposed decimal multipliers are higher for smaller operands since the relative overhead of the Karatsuba-Offman algorithm is higher for smaller operands.
The proposed multiplier 1 is smaller (up to 14%) and faster than the previous best decimal multiplier from [44]. This is due to the reduction in the area of the partial product generator. The proposed multiplier 2 further improves the area of multiplier from [44] (up to 35%) and also the performance for the multipliers with operands of 16 and 32 digits.
The area of multiplier 2 was compared with the area of a binary multiplier of equivalent input operands generated for best speed with Xilinx Core Generator (see results in Table 14).

Table 14.
Comparison of the proposed decimal multipliers with state of the art works for different number of digits.
Small decimal multipliers are relatively expensive compared to the binary multiplier, but the proposed decimal multiplier 2 has an area only 4% higher than the area of the binary multiplier and the proposed decimal multiplier 2 is smaller than the binary multiplier. The area ratio reduction has to do with the overhead associated with the generation of the multiples which are amortized as the multiplier size increases. The delay of the decimal multiplier is always worse but the relative difference also decreases with the operand size for the same reasons.
6. Conclusions and Future Work
We have proposed a new decimal adder/subtractor and two new partial product generators for parallel decimal fixed-point multiplication on 6-input LUT FPGAs. The result was two decimal multipliers with different tradeoffs between area and performance.
The partial product generators are based on different sets of multiples, namely {2A, 5A, 10A} and {2A, 4A, 5A}. The first set of multiples is easier to generate but the partial product generator occupies more area than that using the second set of multiples. The inputs and output of the multipliers can be represented in BCD or BCD/excess6 formats.
The results were compared with the best state-of-art implementations of a parallel decimal multiplier in FPGA. One of the proposed multipliers achieves the best area and delay for all operand sizes, except the smallest one, , when compared to the state of-art. The second multiplier further improves the area but at the cost of an increase in delay. Compared to a binary multiplier, the larger multipliers have a comparable area, but the worst delay. Both area and delay ratios decrese with the operand size.
As future work, the proposed multiplier will be used to implement decimal floating-point multiplication and fused multiplication-addition.
Author Contributions
Conceptualization, M.P.V. and H.C.N.; methodology, M.P.V. and H.C.N.; software, M.P.V. and H.C.N.; validation, M.P.V. and H.C.N.; formal analysis, M.P.V. and H.C.N.; investigation, M.P.V. and H.C.N.; resources, M.P.V. and H.C.N.; data curation, M.P.V. and H.C.N.; writing—original draft preparation, M.P.V. and H.C.N.; writing—review and editing, M.P.V. and H.C.N.; visualization, M.P.V. and H.C.N.; supervision, M.P.V.; project administration, M.P.V.; funding acquisition, M.P.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with Reference UIDB/50021/2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsang, A.; Olschanowsky, M. A Study of Database 2 Customer Queries; Technical report; IBM Santa Teresa Laboratory: San Jose, CA, USA, 1991. [Google Scholar]
- IEEE Standards Committee. 754-2008 IEEE Standard for Floating-Point Arithmetic; IEEE: New York, NY, USA, 2008; pp. 1–58. [Google Scholar]
- Quinn, K. Ever had problems rounding offfigures? this stock exchange has. Wall Str. J. 1983, 202, 37. [Google Scholar]
- IBM Corporation. The Telco Benchmark. 2017. Available online: http://speleotrove.com/decimal/telcoSpec.html (accessed on 20 May 2020).
- Cowlishaw, M.F. Decimal floating-point: Algorism for Computers. In Proceedings of the 16th IEEE International Symposium on Computer Arithmetic, Santiago de Compostela, Spain, 15–18 June 2003; pp. 104–111. [Google Scholar]
- IBM Corporation. Decimal Arithmetic FAQ. 2007. Available online: http://speleotrove.com/decimal/decifaq1.html#needed (accessed on 20 May 2020).
- Cornea, M.; Anderson, C.; Harrison, J.; Tang, P.; Schneider, E.; Tsen, S. A software implementation of the IEEE 754R decimal floating-point arithmetic using the binary encoding format. In Proceedings of the IEEE 18th Symposium on Computer Arithmetic, Montpellier, France, 25–27 June 2007; pp. 29–37. [Google Scholar]
- ANSI CdecNumber Library v3.68. Available online: http://speleotrove.com/decimal/decnumber.html (accessed on 27 June 2021).
- GNU CCompiler Library. Available online: https://www.gnu.org/software/libc/ (accessed on 27 June 2021).
- Cornea, M.; Crawford, J. IEEE 754R Decimal Floating-Point Arithmetic: Reliable and Efficient Implementation for Intel Architecture Platforms. Intel Technol. J. 2007, 11, 91–94. [Google Scholar] [CrossRef]
- Busaba, F.; Krygowski, C.A.; Li, W.H.; Schwarz, E.M.; Carlough, S.R. The IBM z900 Decimal Arithmetic Unit. In Proceedings of the ASilomar Conference on Signals, Systems, Computers, Pacific Grove, CA, USA, 4–7 November 2001; pp. 1335–1339. [Google Scholar]
- Le, H.Q.; Starke, W.J.; Fields, J.S.; O’Connell, F.P.; Nguyen, D.Q.; Ronchetti, B.J.; Sauer, W.M.; Schwarz, E.M.; Vaden, M.T. IBM POWER6 microarchitecture. IBM J. Res. Dev. 2007, 51, 639–662. [Google Scholar] [CrossRef]
- Webb, C.F. IBM z10: The Next- Generation Mainframe Microprocessor. IEEE Micro 2008, 28, 19–29. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, D.; Wang, L. Convolution Accelerator Designs Using Fast Algorithms. Algorithms 2019, 12, 112. [Google Scholar] [CrossRef] [Green Version]
- Deabes, W. FPGA Implementation of ECT Digital System for Imaging Conductive Materials. Algorithms 2019, 12, 28. [Google Scholar] [CrossRef] [Green Version]
- Vestias, M.P.; Neto, H.C. Revisiting the Newton-Raphson Iterative Method for Decimal Division. In Proceedings of the 2011 21st International Conference on Field Programmable Logic and Applications, Chania, Greece, 5–7 September 2011; pp. 138–143. [Google Scholar] [CrossRef]
- Véstias, M.P.; Neto, H.C. Iterative decimal multiplication using binary arithmetic. In Proceedings of the 2011 VII Southern Conference on Programmable Logic (SPL), Cordoba, Argentina, 13–15 April 2011; pp. 257–262. [Google Scholar] [CrossRef]
- Larson, R.H. High-Speed Multiply Using Four Input Carry-Save Adder. IBM Tech. Discl. Bull. 1973, 16, 2053–2054. [Google Scholar]
- Ueda, T. Decimal Multiplying Assembly and Multiply Module. U.S. Patent 5,379,245, 3 January 1995. [Google Scholar]
- Castillo, E.; Lloris, A.; Morales, D.P.; Parrilla, L.; García, A.; Botella, G. A new area-efficient BCD-digit multiplier. Digit. Signal Process. 2017, 62, 1–10. [Google Scholar] [CrossRef]
- Erle, M.A.; Schwarz, E.M.; Schulte, M.J. Decimal Multiplication with Efficient Partial Product Generation. In Proceedings of the 17th IEEE Symposium on Computer Arithmetic, Cape Cod, MA, USA, 27–29 June 2005; pp. 21–28. [Google Scholar]
- Erle, M.A.; Schulte, M.J. Decimal multiplication via carry-save addition. In Proceedings of the 14th IEEE International Conference on Application Specific Systems, San Diego, CA, USA, 9–11 June 2003; pp. 348–358. [Google Scholar]
- Lang, T.; Nannarelli, A. A radix-10 combinational multiplier. In Proceedings of the IEEE 40th International Asilomar Conference on Signals, Systems, and Computers, Kos Island, Greece, 29 October–1 November 2006; pp. 313–317. [Google Scholar]
- Vázquez, A.; Antelo, E.; Montuschi, P. Improved Design of High-Performance Parallel Decimal Multipliers. IEEE Trans. Comput. 2010, 59, 679–693. [Google Scholar] [CrossRef]
- Gorgin, S.; Jaberipur, G. Sign-Magnitude Encoding for Efficient VLSI Realization of Decimal Multiplication. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2017, 25, 75–86. [Google Scholar] [CrossRef]
- Cui, X.; Dong, W.; Liu, W.; Swartzlander, E.E.; Lombardi, F. High Performance Parallel Decimal Multipliers Using Hybrid BCD Codes. IEEE Trans. Comput. 2017, 66, 1994–2004. [Google Scholar] [CrossRef]
- Zhu, M.; Jiang, Y.; Yang, M.; Chen, T. On High-Performance Parallel Decimal Fixed-Point Multiplier Designs. Comput. Electr. Eng. 2014, 40, 2126–2138. [Google Scholar] [CrossRef] [Green Version]
- Gorgin, S.; Jaberipur, G. A fully redundant decimal adder and its application in parallel decimal multipliers. Microelectron. J. 2009, 40, 1471–1481. [Google Scholar] [CrossRef]
- Hoseininasab, S.S.; Nikmehr, H. Architectures for multiple constant decimal multiplication. Comput. Electr. Eng. 2019, 75, 31–45. [Google Scholar] [CrossRef]
- Kenney, R.D.; Schulte, M.J. High Speed Multioperand Decimal Adders. IEEE Trans. Comput. 2005, 54, 953–963. [Google Scholar] [CrossRef] [Green Version]
- Dadda, L. Multioperand Parallel Decimal Adder: A Mixed Binary and BCD Approach. IEEE Trans. Comput. 2007, 56, 1320–1328. [Google Scholar] [CrossRef]
- Vázquez, A.; Antelo, E.; Montushi, P. A New Family of High-Performance Parallel Decimal Multipliers. In Proceedings of the IEEE 18th Symposium on Computer Arithmetic, Montpellier, France, 25–27 June 2007; pp. 195–204. [Google Scholar]
- Neto, H.; Véstias, M. Decimal Multiplier on FPGA using Embedded Binary Multipliers. In Proceedings of the International Conference on Field Programmable Logic and Applications, Dublin, Ireland, 27–31 August 2008; pp. 197–202. [Google Scholar]
- Véstias, M.; Neto, H. Parallel Decimal Multipliers using Binary Multipliers. In Proceedings of the IEEE 6th Southern Programmable Logic Conference, Pernambuco, Brazil, 24–26 March 2010; pp. 73–78. [Google Scholar]
- Fazlali, M.; Valikhani, H.; Timarchi, S.; Malazi, H.T. Fast Architecture for Decimal Digit Multiplication. Microprocess. Microsyst. 2015, 39, 296–301. [Google Scholar] [CrossRef]
- Mukkamala, S.; Rathore, P.; Peesapati, R. Decimal multiplication using compressor based-BCD to binary converter. Eng. Sci. Technol. Int. J. 2018, 21, 1–6. [Google Scholar] [CrossRef]
- Al-Khaleel, O.; Al-Qudah, Z.; Al-Khaleel, M.; Papachristou, C. High performance FPGA-based decimal-to-binary conversion schemes for decimal arithmetic. Microprocess. Microsystems 2013, 37, 287–298. [Google Scholar] [CrossRef]
- Emami, S.; Sedighi, M. An Optimized Reconfigurable Architecture for Hardware Implementation of Decimal Arithmetic. Comput. Electr. Eng. 2017, 63, 18–29. [Google Scholar] [CrossRef]
- Sutter, G.; Todorovich, E.; Bioul, G.; Vázquez, M.; Deschamps, J.P. FPGA Implementations of BCD Multipliers. In Proceedings of the IEEE International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 9–11 December 2009; pp. 36–41. [Google Scholar]
- Jaberipur, G.; Kaivani, A. Binary-coded decimal digit multipliers. IET Comput. Digit. Tech. 2007, 1, 377–381. [Google Scholar] [CrossRef] [Green Version]
- Vázquez, A.; de Dinechin, F. Efficient implementation of parallel BCD multiplication in LUT-6 FPGAs. In Proceedings of the 2010 International Conference on Field-Programmable Technology (FPT), Beijing, China, 8–10 December 2010; pp. 126–133. [Google Scholar]
- Véstias, M.; Neto, H. Parallel Decimal Multipliers and Squarers Using Karatsuba-Ofman’s Algorithm. In Proceedings of the 15th Euromicro Conference on Digital System Design, Cesme, Izmir, Turkey, 5–8 September 2012; pp. 782–788. [Google Scholar]
- Gao, S.; Al-Khalili, D.; Langlois, J.; Chabini, N. Efficient Realization of BCD Multipliers Using FPGAs. Int. J. Reconfigurable Comput. 2017, 2017, 2410408. [Google Scholar] [CrossRef]
- Véstias, M.P.; Neto, H.C. Improving the area of fast parallel decimal multipliers. Microprocess. Microsyst. 2018, 61, 96–107. [Google Scholar] [CrossRef]
- Neto, H.C.; Véstias, M.P. Decimal addition on FPGA based on a mixed BCD/excess-6 representation. Microprocess. Microsyst. 2017, 55, 91–99. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).