The Locating-Chromatic Number of Origami Graphs

Abstract

The locating-chromatic number of a graph combines two graph concepts, namely coloring vertices and partition dimension of a graph. The locating-chromatic number is the smallest k such that G has a locating k-coloring, denoted by ${\chi }_L\left(G\right)$. This article proposes a procedure for obtaining a locating-chromatic number for an origami graph and its subdivision (one vertex on an outer edge) through two theorems with proofs.

1. Introduction

The study of the partition dimension of connected graphs was introduced by Chartrand et al. [1,2] with the aim of finding a new method for attacking the problem of determining the metric dimension in graphs. The application of these metric dimensions can be seen in the navigation of a robot modeled by a graph [3,4], solving the problem of chemical data classification, and determining how to represent a set of chemical compounds in such a way that different compounds have different representations [5,6]. The concept of the locating-chromatic number was first introduced by Chartrand et al. in 2002, with two obtained graph concepts, namely coloring vertices and partition dimensions of a graph [7]. Finding the locating-chromatic number of a graph is one of the interesting (and un-completely solved) problems of graph theory. Let $G=(V,E)$ be a connected graph; the distance $d(x,y)$ between two of its vertices x and y is the length of the shortest path between them. Let c be a proper k-coloring of G with color $\{1,2,\dots ,k\}$, and $\mathrm{\Pi }=\{C_1,C_2,\dots ,C_k\}$ be a partition of $V\left(G\right)$ that is induced by the coloring c. The color code $c_{\mathrm{\Pi }}\left(v\right)$ of v is the ordered k-tuple $(d(v,C_1),d(v,C_2),\dots ,d(v,C_k)))$, where $d(v,C_i)=$ min $\{d(v,x):x\in C_i\}$ for any $i\in \{1,2,3,\dots ,k\}$. If all distinct vertices of G have distinct color codes, then c is called a k-locating coloring of G. The locating-chromatic number denoted by ${\chi }_L\left(G\right)$ is the smallest k such that G has a locating k-coloring. Let c be a locating k-coloring on graph $G(V,E)$. Furthermore, the locating-chromatic number has been determined for a few graph classes; for example, if $P_n$ is a path of order $n\ge 3$ then the locating-chromatic number is 3; for a cycle $C_n$ if $n\ge 3$ is odd, ${\chi }_L\left(C_n\right)=3$ was obtained, and if n is even, ${\chi }_L\left(C_n\right)=4$ was obtained; for a double star graph $\left(S_{a,b}\right)$, $1\le a\le b$ and $b\ge 2$, ${\chi }_L\left(S_{a,b}\right)=b+1$ was obtained. Let $\mathrm{\Pi }=\{S_1,S_2,\dots ,S_k\}$ be the partition of $V\left(G\right)$ induced by c. A vertex $v\in G$ is called a dominant vertex if $d(v,S_i)=1$, where $v\notin S_i$. Chartrand et al. characterized all graphs of order n with the locating-chromatic number $n-1$ [8].

The problem of determining the locating-chromatic number of any general graph is an NP-hard problem [9]. This means that to determine the locating-chromatic number of any given graph, we need a specific algorithm. In 2012, Baskoro and Purwasih proposed a procedure to obtain the locating-chromatic number of corona products of two graphs [9]. In 2014, Asmiati obtained the locating-chromatic number of a non-homogeneous amalgamation of stars [10]. Moreover, to determine the locating-chromatic number of disconnected graphs, graphs with dominant vertices and graphs of two components have been discussed in [11,12,13]. In 2019, the characterization of the locating chromatic number of powers of paths and a condition (sharp upper and lower bounds) for the locating chromatic number of powers of cycles were discussed [14] (see [15] for a discussion of the necessary and sufficient conditions for a pair of two specific start graphs to be an odd mean graph). Asmiati et al. determined the locating-chromatic number of some Petersen graphs; $P(n,1)$ four for odd $n\ge 3$ or five for even $n\ge 4$ were obtained [16], and in [17] results were obtained for certain barbell graphs. Syofyan et al. have succeed in determined the locating-chromatic number of homogeneous lobsters [18]. In [19], Asmiati obtained the locating-chromatic number for non-homogeneous caterpillar graphs and non-homogeneous firecracker graphs. Next, Irawan and Asmiati in 2018 determined the locating-chromatic number of subdivision firecrackers graphs [20] and in [21] obtained the certain operation of generalized Petersen graphs $sP(n,1)$. In 2014, Behtoei and Anbarloei determined the locating-chromatic number of the joining of two arbitrary graphs [22]. In addition to that, in this article we propose a procedure for obtaining the locating-chromatic number for an origami graph and its subdivision (one vertex on an outer edge). The following definition of an origami graph is taken from [23]. Let $n\in \mathbb{N}$ with $n\ge 3$. An origami graph $O_n$ is a graph with $V\left(O_n\right)=\{u_i,v_i,w_i:i\in \{1,\dots ,n\}\}$ and $E\left(O_n\right)=\{u_i{w}_i,u_i{v}_i,v_i{w}_i:i\in \{1,\dots ,n\}\}\cup \{u_i{u}_{i+1},w_i{u}_{i+1}:i\in \{1,\dots ,n-1\}\}\cup \{u_n{u}_1,w_n{u}_1\}$ (see Figure 1 for an example). Meanwhile, a subdivision of an origami graph $O_n^{\ast }$ is a graph with $V\left(O_n^{\ast }\right)=\{u_i,v_i,x_i,w_i:i\in \{1,\dots ,n\}\}$ and $E\left(O_n^{\ast }\right)=\{u_i{w}_i,u_i{v}_i,v_i{x}_i,x_i{w}_i:i\in \{1,\dots ,n\}\}\cup \{u_i{u}_{i+1},w_i{u}_{i+1}:i\in \{1,\dots ,n-1\}\}\cup \{u_n{u}_1,w_n{u}_1\}\}$ (see Figure 2 for an example).

2. Results and Discussions

Let c be a locating coloring in a connected graph G and $N\left(q\right)$ denote the set of neighbor of a vertex q in G. If p and q are distinct vertices of G such that $d(p,w)$ = $d(q,w)$ for all $w\in V\left(G\right)-\{p,q\}$, then $c\left(p\right)\ne c\left(q\right)$. In particular, if p and q are non-adjacent vertices such that $N\left(p\right)=N\left(q\right)$, then $c\left(p\right)\ne c\left(q\right)$ [7].

In the following subsection, the locating-chromatic number of origami graphs $O_n$ and their subdivisions called $O_n^{\ast }$ is described.

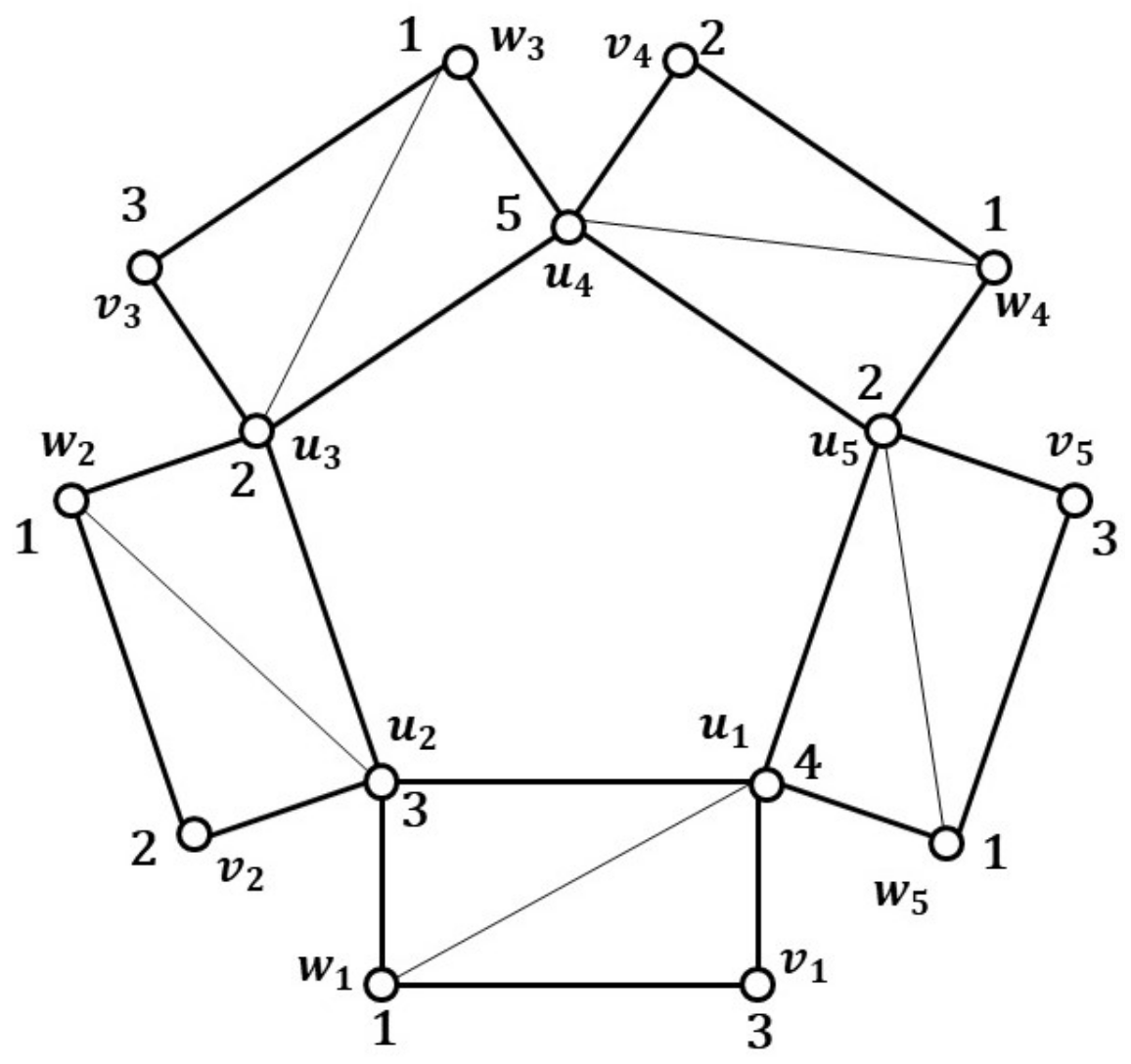
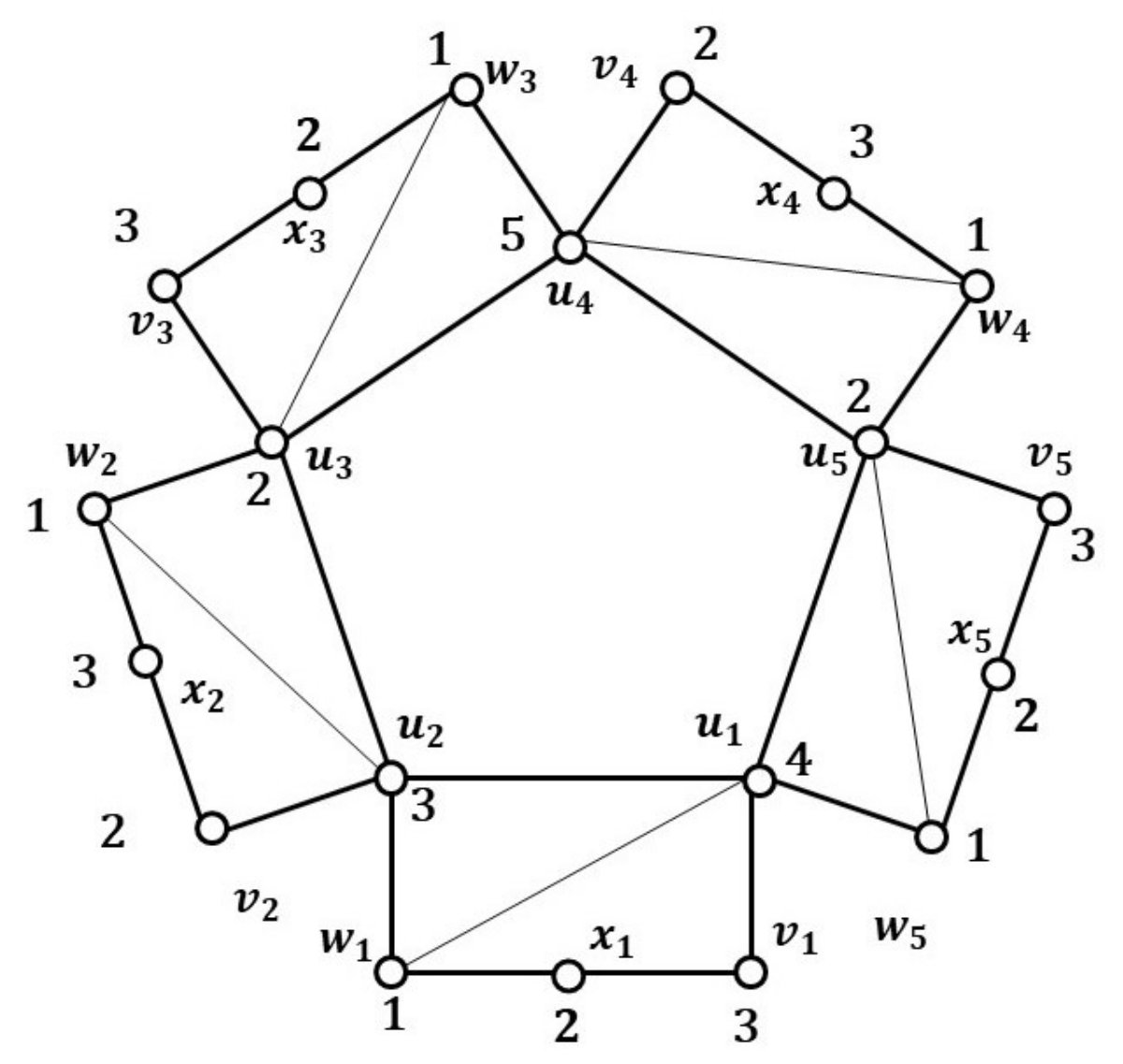
2.1. Locating-Chromatic Number of Origami Graphs

Theorem 1.

Let $O_n$ be an origami graph for $n\ge 3$. Then, the locating-chromatic number of $O_n$,

${\chi }_L\left(O_n\right)=\left\{\begin{array}{cc}4,\hfill & forn=3\hfill \\ 5,\hfill & otherwise.\hfill \end{array}\right.$

Proof. 

Let $n\in \mathbb{N}$ with $n\ge 3$. An origami graph $O_n$ is a graph with $V\left(O_n\right)=\{u_i,v_i,w_i:i\in \{1,\dots ,n\}\}$ and $E\left(O_n\right)=\{u_i{w}_i,u_i{v}_i,v_i{w}_i:i\in \{1,\dots ,n\}\}$∪$\{u_i{u}_{i+1},w_i{u}_{i+1}:i\in \{1,\dots ,n-1\}\}$∪$\{u_n{u}_1,w_n{u}_1\}$. Next, to prove the theorem, we consider the following two cases:

Case 1. 

${\chi }_L\left(O_3\right)=4$

First, we determine the lower bound of ${\chi }_L\left(O_3\right)$. In the origami graphs $O_n$ for $n\ge 3$, there are three adjacent vertices (complete graph with three vertices, denoted by $K_3$); we then need at least 3-locating coloring. Without loss of generality, we assign three colors for any $K_3$ in $O_n$ for $n\ge 3$, and then the three vertices are dominant vertices. As a result, if we use three colors it is not enough because there are more than one $K_3$ in $O_n$ for $n\ge 3$. Therefore, ${\chi }_L\left(O_3\right)\ge 4$.

Next, we determine the upper bound of ${\chi }_L\left(O_3\right)\le 4$. To show that 4 is an upper bound for the locating-chromatic number for the origami graph $O_3$ we describe a locating coloring c using four colors as follows:

• $c\left(u_i\right)=i,i=1,2,3.$
• $c\left(v_i\right)=\left\{\begin{array}{cc}2,\hfill & fori=1,3\hfill \\ 3,\hfill & fori=2.\hfill \end{array}\right.$
• $c\left(w_i\right)=4,i=1,2,3.$

The coloring c will create the partition $\mathrm{\Pi }$ on $V\left(O_3\right)$. We shall show that the color codes of all vertices in $O_3$ are different. We have: $c_{\mathrm{\Pi }}\left(u_1\right)=(0,1,1,1)$; $c_{\mathrm{\Pi }}\left(u_2\right)=(1,0,1,1)$; $c_{\mathrm{\Pi }}\left(u_3\right)=(1,1,0,1)$; $c_{\mathrm{\Pi }}\left(v_1\right)=(1,0,2,1)$; $c_{\mathrm{\Pi }}\left(v_2\right)=(2,1,0,1)$; $c_{\mathrm{\Pi }}\left(v_3\right)=(2,0,1,1)$; $c_{\mathrm{\Pi }}\left(w_1\right)=(1,1,2,0)$; $c_{\mathrm{\Pi }}\left(w_2\right)=(2,1,1,0)$; $c_{\mathrm{\Pi }}\left(w_3\right)=(1,1,1,0)$. Since the color codes of all vertices $O_3$ are different, c is a locating-chromatic coloring. Thus, ${\chi }_L\left(O_3\right)\le 4$.

Case 2. 

${\chi }_L\left(O_n\right)=5$, for $n\ge 4$

To determine the lower bound, we will show that four colors are not enough. For a contradiction, assume that there exists a 4-locating coloring c on $O_n$ for $n\ge 4$. We assign $\{c\left(u_i\right),c\left(v_i\right),c\left(w_i\right),c\left(u_{i+1}\right)\}=\{1,2,3,4\}$, where $c\left(v_i\right)\ne c\left(u_{i+1}\right)$ because $d(v_i,x)=d(u_{i+1},x)$, $x\in \{u_i,v_i\}$. Observe that, on $O_n$ for $n\ge 4$, there are n vertices $u_i$ whose degree is 5. As a result, at least two vertices $w_k,w_l$, $k\ne l$ have the same color codes, which is a contradiction. Therefore, ${\chi }_L\left(O_n\right)\ge 5$, for $n\ge 4$.

To show the upper bound for the locating-chromatic number of origami graphs $O_n$ for $n\ge 4$, let us differentiate some subcases.

Subcase 1. 

(Odd n), for $⌈\frac{n}{2}⌉$ odd, $n\ge 5$

Let c be a coloring of origami graph $O_n$, $⌈\frac{n}{2}⌉$ odd, and $n\ge 5$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n\right)$:

• $C_1=\left\{w_i\right|1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-1\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+3\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{u_{⌈\frac{n}{2}⌉+1}\right\}$.

For $⌈\frac{n}{2}⌉$ odd, the color codes of all the vertices of $V\left(O_n\right)$ are:

• $C_1=\left\{w_i\right|1\le i\le n\}$.

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,2,1,i,⌈\frac{n}{2}⌉-i+1).$$

For $2\le i\le ⌈\frac{n}{2}⌉,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,i,⌈\frac{n}{2}⌉-i+1).$$

For $i=⌈\frac{n}{2}⌉+1$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,2,n-i+1,i-⌈\frac{n}{2}⌉).$$

For $⌈\frac{n}{2}⌉+2\le i\le n,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,n-i+1,i-⌈\frac{n}{2}⌉).$$

$C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$.

For i odd, $3\le i\le ⌈\frac{n}{2}⌉,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,i-1,⌈\frac{n}{2}⌉-i+1).$$

For i odd, $⌈\frac{n}{2}⌉+2\le i\le n,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,n-i+1,i-⌈\frac{n}{2}⌉-1).$$

For i even, $2\le i\le ⌈\frac{n}{2}⌉-1,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,i,⌈\frac{n}{2}⌉-i+2).$$

For $i=⌈\frac{n}{2}⌉+1$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,3,n-i+2,1).$$

For i even, $⌈\frac{n}{2}⌉+3\le i\le n-1,n\ge 9$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,n-i+2,i-⌈\frac{n}{2}⌉).$$

$C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-1\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+3\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}.$

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,2,0,i,⌈\frac{n}{2}⌉).$$

For i odd, $3\le i\le ⌈\frac{n}{2}⌉,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,i,⌈\frac{n}{2}⌉-i+2).$$

For i odd, $⌈\frac{n}{2}⌉+2\le i\le n,n\ge 9$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,n-i+2,i-⌈\frac{n}{2}⌉).$$

For i even, $2\le i\le ⌈\frac{n}{2}⌉-1,n\ge 5$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,i-1,⌈\frac{n}{2}⌉-i+1).$$

For i even, $⌈\frac{n}{2}⌉+3\le i\le n-1,n\ge 9$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,n-i+1,i-⌈\frac{n}{2}⌉-1).$$

For $C_4=\left\{u_1\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_1\right)=(1,1,1,0,⌈\frac{n}{2}⌉-1).$$

For $C_5=\left\{u_{⌈\frac{n}{2}⌉+1}\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_{⌈\frac{n}{2}⌉+1}\right)=(1,1,2,⌈\frac{n}{2}⌉-1,0).$$

Since for n odd all vertices have different color codes, c is a locating coloring of origami graphs $O_n$, so that ${\chi }_L\left(O_n\right)\le 5$, for $⌈\frac{n}{2}⌉$ odd, $n\ge 5$.

Subcase 2. 

(Odd n), for $⌈\frac{n}{2}⌉$ even, $n\ge 7$.

Let c be a coloring of origami graph $O_n$, $⌈\frac{n}{2}⌉$ even, and $n\ge 7$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n\right)$ as follows:

• $C_1=\left\{w_i\right|1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-2\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+2\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{u_{⌈\frac{n}{2}⌉}\right\}$.

For $⌈\frac{n}{2}⌉$ even, the color codes of all the vertices of $V\left(O_n\right)$ are:

• $C_1=\left\{w_i\right|1\le i\le n\}.$

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,2,1,i,⌈\frac{n}{2}⌉-i).$$

For $2\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,i,⌈\frac{n}{2}⌉-i).$$

For $i=⌈\frac{n}{2}⌉$, we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,2,n-i+1,i-⌈\frac{n}{2}⌉+1).$$

For $⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,n-i+1,i-⌈\frac{n}{2}⌉+1).$$

$C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$.

For i odd, $3\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,i-1,⌈\frac{n}{2}⌉-i).$$

For i odd, $⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,n-i+1,i-⌈\frac{n}{2}⌉).$$

For i even, $2\le i\le ⌈\frac{n}{2}⌉-2,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,i,⌈\frac{n}{2}⌉-i+1).$$

For $i=⌈\frac{n}{2}⌉$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,3,i,i-⌈\frac{n}{2}⌉+1).$$

For i even, $⌈\frac{n}{2}⌉+3\le i\le n-1,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,n-i+2,i-⌈\frac{n}{2}⌉+1).$$

$C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-2\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+2\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}.$

For $i=1$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,2,0,i,⌈\frac{n}{2}⌉-i+1).$$

For i odd, $3\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,i,⌈\frac{n}{2}⌉-i+1).$$

For i odd, $⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,n-i+2,i-⌈\frac{n}{2}⌉+1).$$

For i even, $2\le i\le ⌈\frac{n}{2}⌉-2,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,i-1,⌈\frac{n}{2}⌉-i).$$

For i even, $⌈\frac{n}{2}⌉+2\le i\le n,n\ge 7$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,n-i+1,i-⌈\frac{n}{2}⌉).$$

$C_4=\left\{u_1\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_1\right)=(1,1,1,0,⌈\frac{n}{2}⌉-1).$$

$C_5=\left\{u_{⌈\frac{n}{2}⌉}\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_{⌈\frac{n}{2}⌉}\right)=(1,1,2,⌈\frac{n}{2}⌉-1,0).$$

Since for n odd all vertices have different color codes, c is a locating coloring of origami graphs $O_n$, so that ${\chi }_L\left(O_n\right)\le 5$, for $⌈\frac{n}{2}⌉$ even, $n\ge 7$.

Subcase 3. 

(even n), for $\frac{n}{2}$ odd, $n\ge 6$.

Let c be a coloring of origami graph $O_n$, $\frac{n}{2}$ odd, and $n\ge 6$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n\right)$:

• $C_1=\left\{w_i\right|1\le i\le \frac{n}{2}-1\}\cup \left\{w_i\right|\frac{n}{2}+1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{w_{\frac{n}{2}}\right\}$.

For $\frac{n}{2}$ odd, the color codes of all the vertices of $V\left(O_n\right)$ are:

$$C_1=\left\{w_i\right|1\le i\le \frac{n}{2}-1\}\cup \left\{w_i\right|\frac{n}{2}+1\le i\le n\}.$$

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,2,1,i,\frac{n}{2}-i+1).$$

For $2\le i\le \frac{n}{2}-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,i,\frac{n}{2}-i+1).$$

For $\frac{n}{2}+1\le i\le n,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,n-i+1,i-\frac{n}{2}+1).$$

$C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}.$

For i odd, $3\le i\le \frac{n}{2},n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,i-1,\frac{n}{2}-i+1).$$

For i odd, $\frac{n}{2}+2\le i\le n-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,n-i+1,i-\frac{n}{2}).$$

For i even, $2\le i\le \frac{n}{2}-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,i,\frac{n}{2}-i+2).$$

For i even, $\frac{n}{2}+1\le i\le n-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,n-i+2,i-\frac{n}{2}+1).$$

$C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}.$

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,3,0,i,\frac{n}{2}-i+2).$$

For i odd, $3\le i\le \frac{n}{2}-2,n\ge 10$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,i,\frac{n}{2}-i+2)$$

For $i=\frac{n}{2}$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(2,1,0,i,1).$$

For i odd, $\frac{n}{2}+2\le i\le n-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,n-i+2,i-\frac{n}{2}+1).$$

For i even, $2\le i\le \frac{n}{2}-1,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,i-1,\frac{n}{2}-i+1).$$

For i even, $\frac{n}{2}+1\le i\le n,n\ge 6$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,n-i+1,i-\frac{n}{2}).$$

For $C_4=\left\{u_1\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_1\right)=(1,2,1,0,\frac{n}{2}-i+1).$$

For $C_5=\left\{w_{\frac{n}{2}}\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(w_{\frac{n}{2}}\right)=(2,1,1,\frac{n}{2},0).$$

Since for n even all vertices have different color codes, c is a locating coloring of origami graphs $O_n$, so that ${\chi }_L\left(O_n\right)\le 5$, for $\frac{n}{2}$ odd, $n\ge 6$.

Subcase 4. 

(even n), for $\frac{n}{2}$ even, $n\ge 4$.

Let c be a coloring of origami graph $O_n$, $\frac{n}{2}$ even, and $n\ge 4$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n\right)$ as follows:

• $C_1=\left\{w_i\right|1\le i\le \frac{n}{2}\}\cup \left\{w_i\right|\frac{n}{2}+2\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{w_{\frac{n}{2}+1}\right\}$.

For $\frac{n}{2}$ even, the color codes of all the vertices of $V\left(O_n\right)$ are:

$C_1=\left\{w_i\right|1\le i\le \frac{n}{2}\}\cup \left\{w_i\right|\frac{n}{2}+2\le i\le n\}.$

For $i=1$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,2,1,i,\frac{n}{2}-i+2).$$

For $2\le i\le \frac{n}{2},n\ge 4$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,i,\frac{n}{2}-i+2).$$

For $\frac{n}{2}+2\le i\le n,n\ge 4$ we have:

$$c_{\mathrm{\Pi }}\left(w_i\right)=(0,1,1,n-i+1,i-\frac{n}{2}).$$

$C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}.$

For i odd, $3\le i\le \frac{n}{2}+1,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,i-1,\frac{n}{2}-i+2).$$

For i odd, $\frac{n}{2}+3\le i\le n-1,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,0,1,n-i+1,i-\frac{n}{2}-1).$$

For i even, $2\le i\le \frac{n}{2},n\ge 4$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,i,\frac{n}{2}-i+3).$$

For i even, $\frac{n}{2}+2\le i\le n,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,0,1,n-i+2,i-\frac{n}{2}).$$

$C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}.$

For $i=1$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,3,0,1,\frac{n}{2}+1).$$

For i odd, $3\le i\le \frac{n}{2}-1,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,i,\frac{n}{2}-i+3).$$

For $i=\frac{n}{2}+1$, we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(2,1,0,i,1).$$

For i odd, $\frac{n}{2}+3\le i\le n-1,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(v_i\right)=(1,1,0,n-i+2,i-\frac{n}{2}).$$

For i even, $2\le i\le \frac{n}{2},n\ge 4$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,i-1,\frac{n}{2}).$$

For i even, $\frac{n}{2}+2\le i\le n,n\ge 8$ we have:

$$c_{\mathrm{\Pi }}\left(u_i\right)=(1,1,0,n-i+1,i-\frac{n}{2}-1).$$

For $C_4=\left\{u_1\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(u_1\right)=(1,2,1,0,\frac{n}{2}).$$

For $C_5=\left\{w_{\frac{n}{2}}\right\}$, we have:

$$c_{\mathrm{\Pi }}\left(w_{\frac{n}{2}}\right)=(2,1,1,\frac{n}{2},0).$$

Since for n even all vertices have different color codes, c is a locating coloring of origami graphs $O_n$, so that ${\chi }_L\left(O_n\right)\le 5$, for $\frac{n}{2}$ even, $n\ge 4$. this completes the proof of Theorem 1. □

Note that Figure 1 is an example locating coloring for origami graph $O_5$.

2.2. Locating-Chromatic Number for Subdivision Outer Edge of Origami Graphs

Theorem 2.

Let $O_n^{\ast }$ be a subdivision outer edge of origami graphs for $n\ge 3$. Then the locating-chromatic number of $O_n^{\ast }$, ${\chi }_L\left(O_n^{\ast }\right)=\left\{\begin{array}{cc}4,\hfill & forn=3\hfill \\ 5,\hfill & otherwise.\hfill \end{array}\right.$

Proof. 

Let $O_n^{\ast }$, $n\ge 3$ be a subdivision of an origami graph; $O_n^{\ast }$ is a graph with $V\left(O_n^{\ast }\right)=\{u_i,v_i,x_i,w_i:i\in \{1,\dots ,n\}\}$ and $E\left(O_n^{\ast }\right)=\{u_i{w}_i,u_i{v}_i,v_i{x}_i,x_i{w}_i:i\in \{1,\dots ,n\}\}$∪$\{u_i{u}_{i+1},w_i{u}_{i+1}:i\in \{1,\dots ,n-1\}\}$∪$\{u_n{u}_1,w_n{u}_1\}$}. Next, to prove the theorem, we consider the following two cases:

Case A. 

${\chi }_L\left(O_3^{\ast }\right)=4$

First, we determine the lower bound of ${\chi }_L\left(O_3^{\ast }\right)$.

Without loss of generality, we assign $A=\{c\left(u_i\right),c\left(v_i\right),c\left(x_i\right),c\left(w_i\right),c\left(u_{i+1}\right)\}=\{1,2,3\}$. Then, there are three dominant vertices in A, while we still have vertices on other A that must be colored. As a result, there will be two vertices with the same color codes. Thus, ${\chi }_L\left(O_3^{\ast }\right)\ge 4$.

Next, we determine the upper bound of ${\chi }_L\left(O_3^{\ast }\right)\le 4$. To show that 4 is an upper bound for the locating-chromatic number for a subdivision outer edge of origami graph $O_3^{\ast }$, we describe a locating coloring c using four colors as follows:

$c\left(u_i\right)=i,i=1,2,3.$

$c\left(v_i\right)=\left\{\begin{array}{cc}2,\hfill & fori=1,3\hfill \\ 3,\hfill & fori=2.\hfill \end{array}\right.$

$c\left(w_i\right)=4,i=1,2,3.$

$c\left(x_i\right)=i,i=1,2,3.$

The coloring c will create the partition $\mathrm{\Pi }$ on $V\left(O_3^{\ast }\right)$. We shall show that the color codes of all vertices in $O_3^{\ast }$ are different. We have: $c_{\mathrm{\Pi }}\left(u_1\right)=(0,1,1,1)$; $c_{\mathrm{\Pi }}\left(u_2\right)=(1,0,1,1)$; $c_{\mathrm{\Pi }}\left(u_3\right)=(1,1,0,1)$; $c_{\mathrm{\Pi }}\left(v_1\right)=(1,0,2,2)$; $c_{\mathrm{\Pi }}\left(v_2\right)=(2,1,0,2)$; $c_{\mathrm{\Pi }}\left(v_3\right)=(2,0,1,2)$; $c_{\mathrm{\Pi }}\left(w_1\right)=(1,1,2,0)$; $c_{\mathrm{\Pi }}\left(w_2\right)=(2,1,1,0)$; $c_{\mathrm{\Pi }}\left(w_3\right)=(1,2,1,0)$. $c_{\mathrm{\Pi }}\left(x_1\right)=(0,1,3,1)$; $c_{\mathrm{\Pi }}\left(x_2\right)=(3,0,1,1)$; $c_{\mathrm{\Pi }}\left(x_3\right)=(2,1,0,1)$. Since the color codes of all vertices $O_3^{\ast }$ are different, c is a locating-chromatic coloring. Thus, ${\chi }_L\left(O_3^{\ast }\right)\le 4$.

Case B. 

${\chi }_L\left(O_n^{\ast }\right)=5$ for $n\ge 4$

Since a subdivision of origami graphs $O_n^{\ast }$ for $n\ge 4$ is obtained by origami graph $O_n$ with one added vertex in edge $v_i{w}_i$, we have ${\chi }_L\left(O_n^{\ast }\right)\ge 5$ for $n\ge 4$. The addition of one vertex on the outside does not reduce the number of colors needed because the number of the sets $B=\{c\left(u_i\right),c\left(v_i\right),c\left(w_i\right),c\left(u_{i+1}\right)\}$ is the same.

To show the upper bound for the locating-chromatic number for a subdivision outer edge of origami graph $O_n^{\ast }$ for $n\ge 4$, let us consider different subcases.

Subcase a. 

(odd n), for $⌈\frac{n}{2}⌉$ odd, $n\ge 5$.

Let c be a coloring for a subdivision outer edge of origami graph $O_n^{\ast }$, for $⌈\frac{n}{2}⌉$ odd, and $n\ge 5$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n^{\ast }\right)$:

• $C_1=\left\{w_i\right|1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$∪$\left\{x_i\right|$ for odd $i,1\le i\le n\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-1\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+3\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}$∪$\left\{x_i\right|$ for even $i,2\le i\le n-1\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{u_{⌈\frac{n}{2}⌉+1}\right\}$.

For for $⌈\frac{n}{2}⌉$ odd the color codes of all the vertices of $V\left(O_n^{\ast }\right)$ are:

$c_{\mathrm{\Pi }}\left(u_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,3\le i\le n,n\ge 5\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le ⌈\frac{n}{2}⌉-1,n\ge 5\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,⌈\frac{n}{2}⌉+3\le i\le n-1,n\ge 9\hfill \\ & \mathrm{for\; the\; fourth\; component},i=1\hfill \\ & \mathrm{for\; the\; fifth\; component},i=⌈\frac{n}{2}⌉+1\hfill \\ 2,\hfill & \mathrm{for\; the\; third\; component},i=⌈\frac{n}{2}⌉+1\hfill \\ i-1,\hfill & \mathrm{for\; the\; fourth\; component},2\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ n-i+1\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ ⌈\frac{n}{2}⌉-i,\hfill & \mathrm{for\; the\; fifth\; component},i=1\hfill \\ i-⌈\frac{n}{2}⌉-1,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ ⌈\frac{n}{2}⌉-i+1,\hfill & \mathrm{for\; the\; fifth\; component},2\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(v_i\right)=\left\{\begin{array}{cc}2,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 5\hfill \\ 0,\hfill & \text{for the second component},\mathrm{odd}i,1\le i\le n,n\ge 5\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n-1,n\ge 5\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ ⌈\frac{n}{2}⌉,\hfill & \mathrm{for\; the\; fifth\; component},i=1\hfill \\ ⌈\frac{n}{2}⌉-i+2,\hfill & \mathrm{for\; the\; fifth\; component},2\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ i-⌈\frac{n}{2}⌉,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(w_i\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 5\hfill \\ 2,\hfill & \mathrm{for\; the\; third\; component},i=⌈\frac{n}{2}⌉\mathrm{and}i=n\hfill \\ ⌈\frac{n}{2}⌉-i+1,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ i-⌈\frac{n}{2}⌉,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(x_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,1\le i\le n,n\ge 5\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n-1,n\ge 5\hfill \\ i+1,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ ⌈\frac{n}{2}⌉-i+2,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 5\hfill \\ i-⌈\frac{n}{2}⌉+1,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 5\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Since for n odd all vertices have different color codes, c is a locating coloring for subdivision of origami graph $O_n^{\ast }$, so that ${\chi }_L\left(O_n^{\ast }\right)\le 5$, for $⌈\frac{n}{2}⌉$ odd, $n\ge 5$.

Subcase b. 

(odd n), for $⌈\frac{n}{2}⌉$ even, $n\ge 7$.

Let c be a coloring for a subdivision outer edge of origami graph $O_n^{\ast }$, for $⌈\frac{n}{2}⌉$ even, and $n\ge 7$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n^{\ast }\right)$:

• $C_1=\left\{w_i\right|1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n-1\}$∪$\left\{x_i\right|$ for odd $i,1\le i\le n\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le ⌈\frac{n}{2}⌉-2\}$∪$\left\{u_i\right|$ for even $i,⌈\frac{n}{2}⌉+2\le i\le n-1\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n\}$∪$\left\{x_i\right|$ for even $i,2\le i\le n-1\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{u_{⌈\frac{n}{2}⌉}\right\}$.

For $⌈\frac{n}{2}⌉$ even, the color codes of all the vertices of $V\left(O_n^{\ast }\right)$ are:

$c_{\mathrm{\Pi }}\left(u_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,3\le i\le n,n\ge 7\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le ⌈\frac{n}{2}⌉-2,n\ge 7\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,⌈\frac{n}{2}⌉+2\le i\le n-1,n\ge 7\hfill \\ & \mathrm{for\; the\; fourth\; component},i=1\hfill \\ & \mathrm{for\; the\; fifth\; component},i=⌈\frac{n}{2}⌉\hfill \\ 2,\hfill & \mathrm{for\; the\; third\; component},i=⌈\frac{n}{2}⌉\hfill \\ i-1,\hfill & \mathrm{for\; the\; fourth\; component},2\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},\mathrm{odd}i,⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ ⌈\frac{n}{2}⌉-1,\hfill & \mathrm{for\; the\; fourth\; component},i=⌈\frac{n}{2}⌉\hfill \\ ⌈\frac{n}{2}⌉-i,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7\hfill \\ i-⌈\frac{n}{2}⌉,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(v_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{even}i,2\le i\le n-1,n\ge 7\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{odd}i,1\le i\le n,n\ge 7\hfill \\ 2,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 7\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 7\hfill \\ n-i+2\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ ⌈\frac{n}{2}⌉-i+1\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 7\hfill \\ i-⌈\frac{n}{2}⌉+1\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(w_i\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 7\hfill \\ 2,\hfill & \mathrm{for\; the\; third\; component},i=⌈\frac{n}{2}⌉-1\mathrm{and}i=n\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 7\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ ⌈\frac{n}{2}⌉-i,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7\hfill \\ i-⌈\frac{n}{2}⌉+1,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉\le i\le n,n\ge 7\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(x_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,1\le i\le n,n\ge 7\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n-1,n\ge 7\hfill \\ i+1,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le ⌈\frac{n}{2}⌉-1,n\ge 7\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},⌈\frac{n}{2}⌉\le i\le n,n\ge 7\hfill \\ ⌈\frac{n}{2}⌉-i+2,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le ⌈\frac{n}{2}⌉,n\ge 7\hfill \\ i-⌈\frac{n}{2}⌉+2,\hfill & \mathrm{for\; the\; fifth\; component},⌈\frac{n}{2}⌉+1\le i\le n,n\ge 7\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Since for n odd all vertices have different color codes, c is a locating coloring for a subdivision of the outer edge of origami graph $O_n^{\ast }$, so that ${\chi }_L\left(O_n^{\ast }\right)\le 5$, for $⌈\frac{n}{2}⌉$ even, $n\ge 7$.

Subcase c. 

(even n), for $\frac{n}{2}$ odd, $n\ge 6$.

Let c be a coloring for a subdivision outer edge of origami graph $O_n^{\ast }$, for $\frac{n}{2}$ odd, and $n\ge 6$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n^{\ast }\right)$:

• $C_1=\left\{w_i\right|1\le i\le \frac{n}{2}-1\}\cup \left\{w_i\right|\frac{n}{2}+1\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}$∪$\left\{x_i\right|$ for odd $i,1\le i\le n-1\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}$∪$\left\{x_i\right|$ for even $i,2\le i\le n\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{w_{\frac{n}{2}}\right\}$.

For $\frac{n}{2}$ odd, the color codes of all the vertices of $V\left(O_n^{\ast }\right)$ are:

$c_{\mathrm{\Pi }}\left(u_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,3\le i\le n-1,n\ge 6\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n,n\ge 6\hfill \\ & \mathrm{for\; the\; fourth\; component},i=1\hfill \\ 2,\hfill & \text{for the second component},i=1\hfill \\ i-1,\hfill & \mathrm{for\; the\; fourth\; component},2\le i\le \frac{n}{2},n\ge 6\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ \frac{n}{2}-i+1,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ i-\frac{n}{2},\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(v_i\right)=\left\{\begin{array}{cc}2,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 6\hfill \\ 0,\hfill & \text{for the second component},\mathrm{even}i,2\le i\le n,n\ge 6\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{odd}i,1\le i\le n-1,n\ge 6\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ \frac{n}{2}-i+2,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ i-\frac{n}{2}+1,\hfill & \mathrm{for\; component},\mathrm{fifth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(w_i\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for\; the\; first\; component},1\le i\le \frac{n}{2}-1,n\ge 6\hfill \\ & \mathrm{for\; the\; first\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ & \mathrm{for\; the\; fifth\; component},i=\frac{n}{2}\hfill \\ 2,\hfill & \mathrm{for\; the\; first\; component},i=\frac{n}{2}\hfill \\ & \text{for the second component},i=n\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ \frac{n}{2}-i+1,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ i-\frac{n}{2}+1,\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(x_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,1\le i\le n-1,n\ge 6\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n,n\ge 6\hfill \\ i+1,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ \frac{n}{2}-i+2,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2}-1,n\ge 6\hfill \\ i-\frac{n}{2}+2,\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+1\le i\le n,n\ge 6\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Since for n even all vertices have different color codes, c is a locating coloring for a subdivision of the outer edge of origami graph $O_n^{\ast }$, so that ${\chi }_L\left(O_n^{\ast }\right)\le 5$, for $\frac{n}{2}$ odd, $n\ge 6$.

Subcase d. 

(even n), for $\frac{n}{2}$ even, $n\ge 4$.

Let c be a coloring of subdivision origami graph $O_n^{\ast }$, for $\frac{n}{2}$ even, and $n\ge 4$; we make the partition $\mathrm{\Pi }$ of $V\left(O_n^{\ast }\right)$:

• $C_1=\left\{w_i\right|1\le i\le \frac{n}{2}\}\cup \left\{w_i\right|\frac{n}{2}+2\le i\le n\}$;
• $C_2=\left\{u_i\right|$ for odd $i,3\le i\le n-1\}$∪$\left\{v_i\right|$ for even $i,2\le i\le n\}$∪$\left\{x_i\right|$ for odd $i,1\le i\le n-1\}$;
• $C_3=\left\{u_i\right|$ for even $i,2\le i\le n\}$∪$\left\{v_i\right|$ for odd $i,1\le i\le n-1\}$∪$\left\{x_i\right|$ for even $i,2\le i\le n\}$;
• $C_4=\left\{u_1\right\}$;
• $C_5=\left\{w_{\frac{n}{2}+1}\right\}$.

For $\frac{n}{2}$ even the color codes of all the vertices of $V\left(O_n^{\ast }\right)$ are:

$c_{\mathrm{\Pi }}\left(u_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,3\le i\le n-1,n\ge 4\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n,n\ge 4\hfill \\ & \mathrm{for\; the\; fourth\; component},i=1\hfill \\ 2,\hfill & \text{for the second component},i=1\hfill \\ i-1,\hfill & \mathrm{for\; the\; fourth\; component},2\le i\le \frac{n}{2}+1,n\ge 4\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ \frac{n}{2},\hfill & \mathrm{for\; the\; fifth\; component},i=1\hfill \\ \frac{n}{2}-i+2,\hfill & \mathrm{for\; the\; fifth\; component},2\le i\le \frac{n}{2}+1,n\ge 4\hfill \\ i-\frac{n}{2}-1,\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(v_i\right)=\left\{\begin{array}{cc}2,\hfill & \mathrm{for\; the\; first\; component},1\le i\le n,n\ge 4\hfill \\ 0,\hfill & \text{for the second component},\mathrm{even}i,2\le i\le n,n\ge 4\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{odd}i,1\le i\le n-1,n\ge 4\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 4\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 4\hfill \\ \frac{n}{2}+i,\hfill & \mathrm{for\; the\; fifth\; component},i=1\hfill \\ \frac{n}{2}-i+3,\hfill & \mathrm{for\; the\; fifth\; component},2\le i\le \frac{n}{2}+1,n\ge 4\hfill \\ i-\frac{n}{2},\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(w_i\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for\; the\; first\; component},1\le i\le \frac{n}{2},n\ge 4\hfill \\ & \mathrm{for\; the\; first\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ & \mathrm{for\; the\; fifth\; component},i=\frac{n}{2}+1\hfill \\ 2,\hfill & \mathrm{for\; the\; first\; component},i=\frac{n}{2}+1\hfill \\ & \text{for the second component},i=n\hfill \\ i,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 4\hfill \\ n-i+1,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 4\hfill \\ \frac{n}{2}-i+2,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2},n\ge 4\hfill \\ i-\frac{n}{2},\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

$c_{\mathrm{\Pi }}\left(x_i\right)=\left\{\begin{array}{cc}0,\hfill & \text{for the second component},\mathrm{odd}i,1\le i\le n-1,n\ge 4\hfill \\ & \mathrm{for\; the\; third\; component},\mathrm{even}i,2\le i\le n,n\ge 4\hfill \\ i+1,\hfill & \mathrm{for\; the\; fourth\; component},1\le i\le \frac{n}{2},n\ge 6\hfill \\ n-i+2,\hfill & \mathrm{for\; the\; fourth\; component},\frac{n}{2}+1\le i\le n,n\ge 4\hfill \\ \frac{n}{2}-i+3,\hfill & \mathrm{for\; the\; fifth\; component},1\le i\le \frac{n}{2},n\ge 4\hfill \\ i-\frac{n}{2}+1,\hfill & \mathrm{for\; the\; fifth\; component},\frac{n}{2}+2\le i\le n,n\ge 4\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Since for n even all vertices have different color codes, c is a locating coloring for a subdivision outer edge of origami graph $O_n^{\ast }$, so that ${\chi }_L\left(O_n^{\ast }\right)\le 5$, for $\frac{n}{2}$ even, $n\ge 4$. This completes the proof of Theorem 2. □

Note that Figure 2 is an example locating coloring for a subdivision of the outer edge of origami graph $O_5^{\ast }$.

3. Conclusions

The proving steps of the two theorems we gave earlier show that the locating-chromatic number of origami graphs $O_n$, ${\chi }_L\left(O_n\right)$ is 4 for $n=3$ and 5 for $n\ge 4$; the same result holds for a subdivision of the outer edge of origami graph $O_n^{\ast }$. This research can be continued so as to determine the locating-chromatic number for some certain operations of origami graphs.