Efficient and Scalable Initialization of Partitioned Coupled Simulations with preCICE
Abstract
1. Introduction
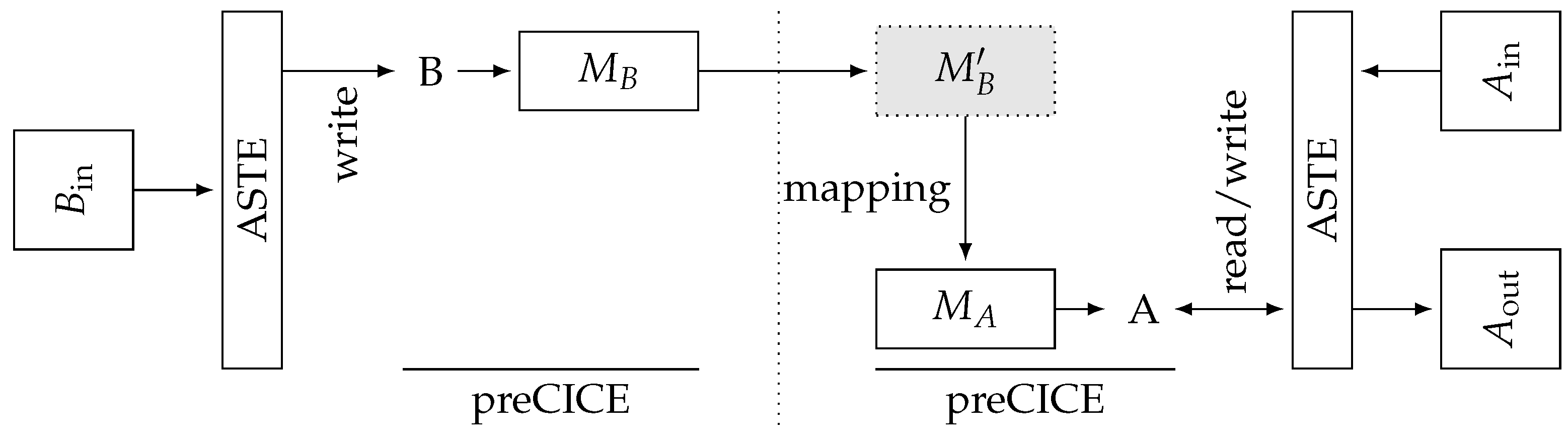
2. Two-Level Initialization
3. R-Tree-Based Mesh Filtering
- we fetch the k nearest primitives of degree m of vertex ,
- we sort them by ascending distance to ,
- we process the list of primitives and calculate interpolation weights for data interpolation from the primitive’s vertices to the projection point on the respective plain or line,we terminate and return the current primitive, if all weights are positive ,
- we return the nearest projection of degree of vertex u if no valid projection of degree m could be found.
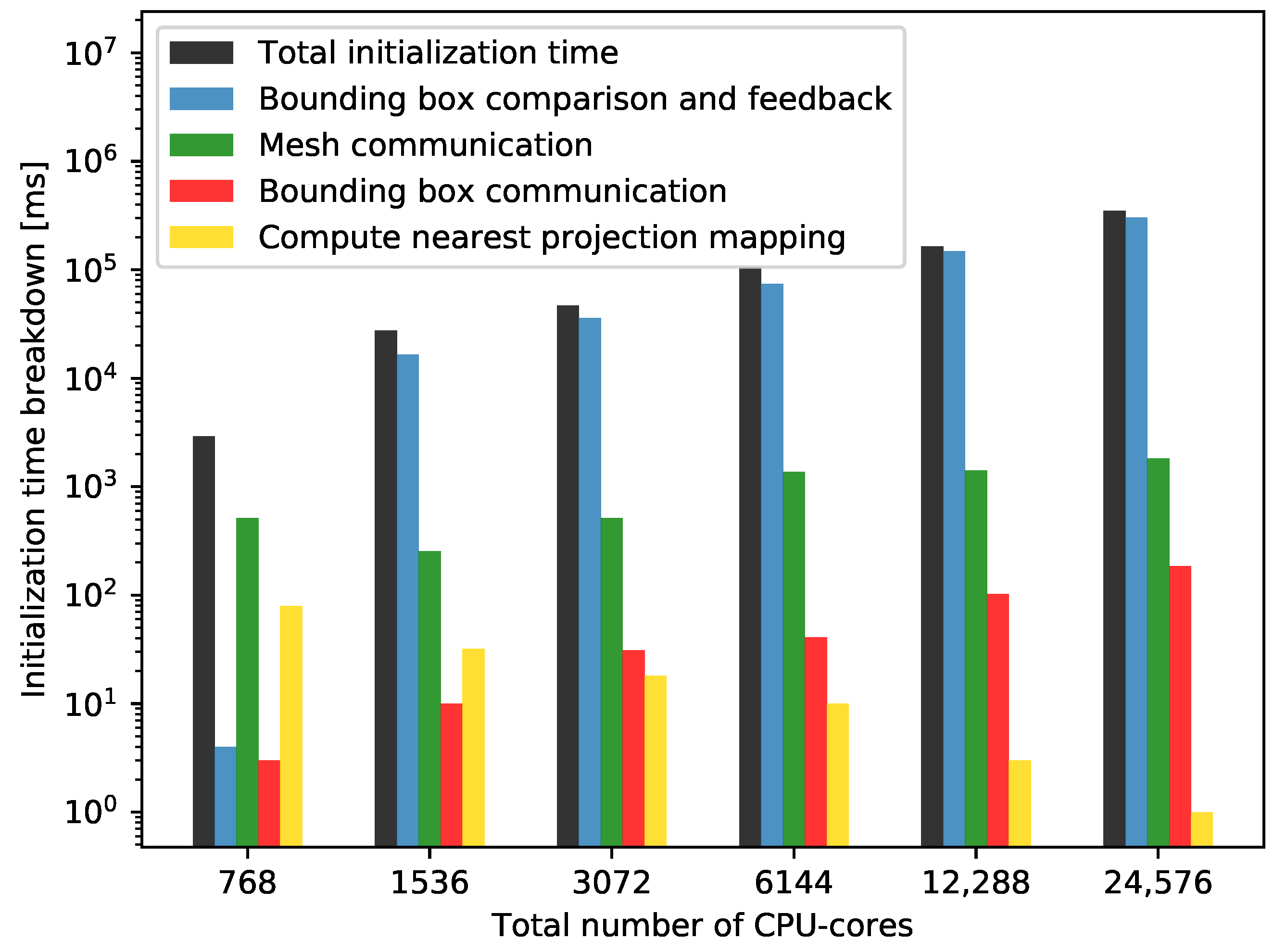
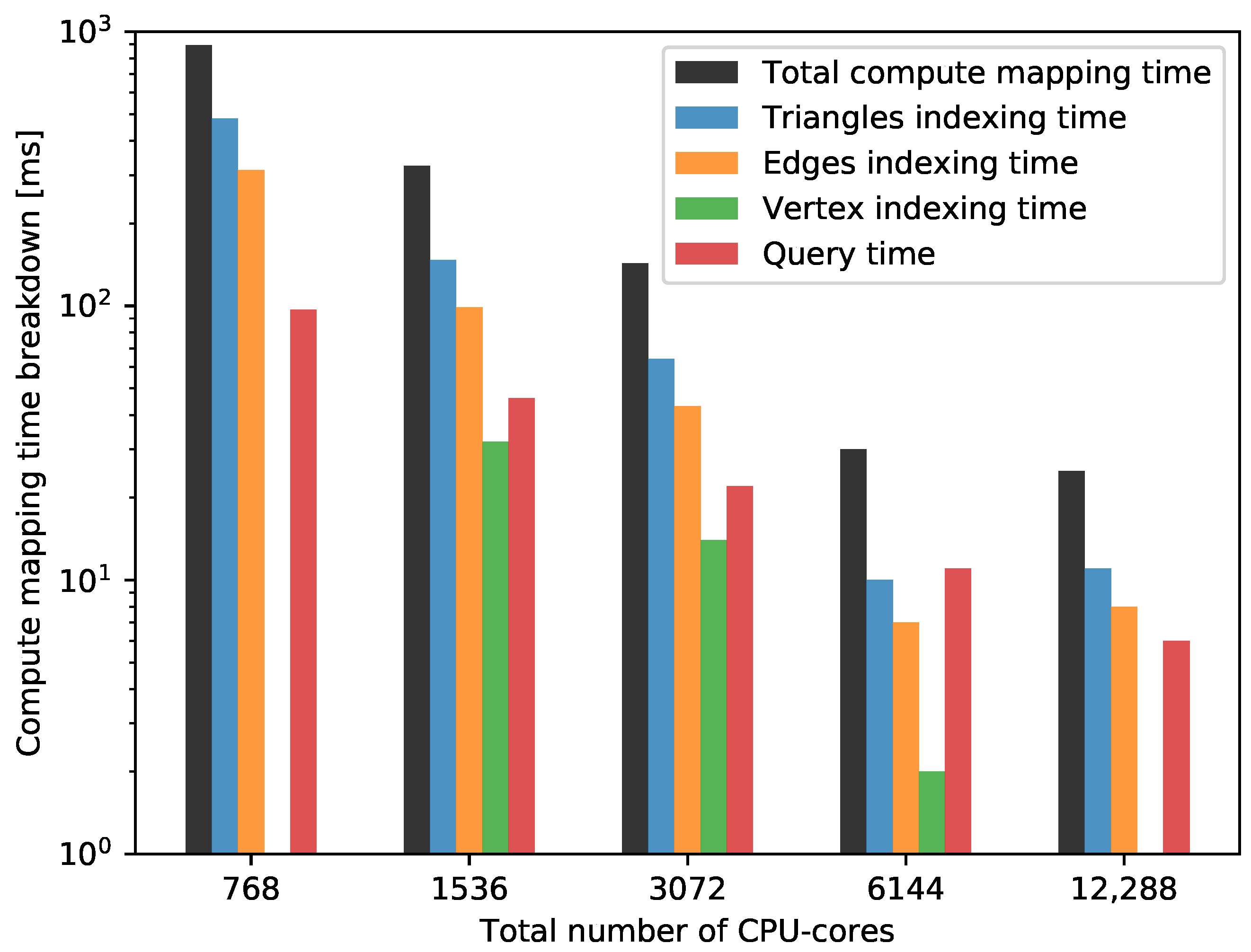
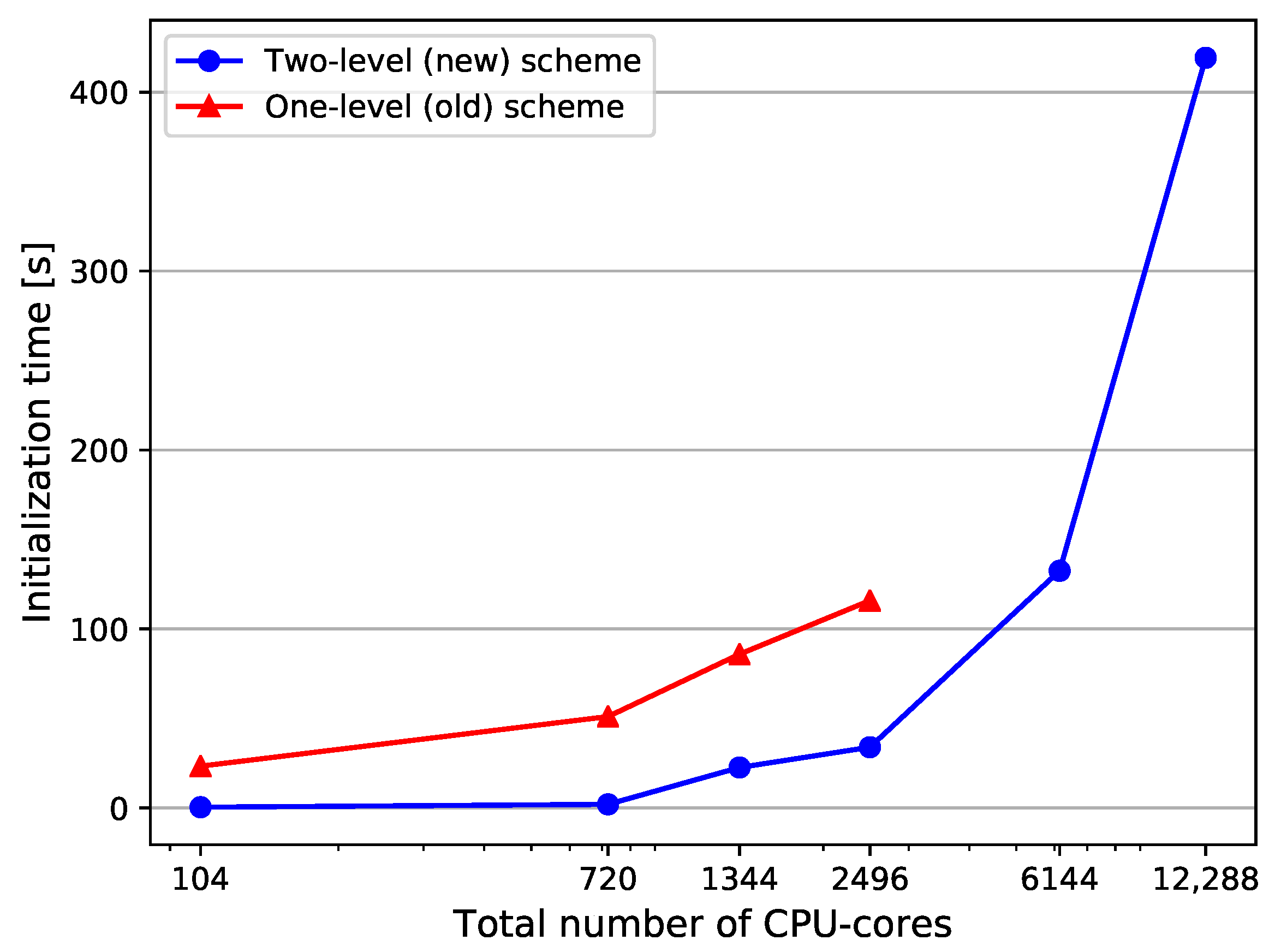
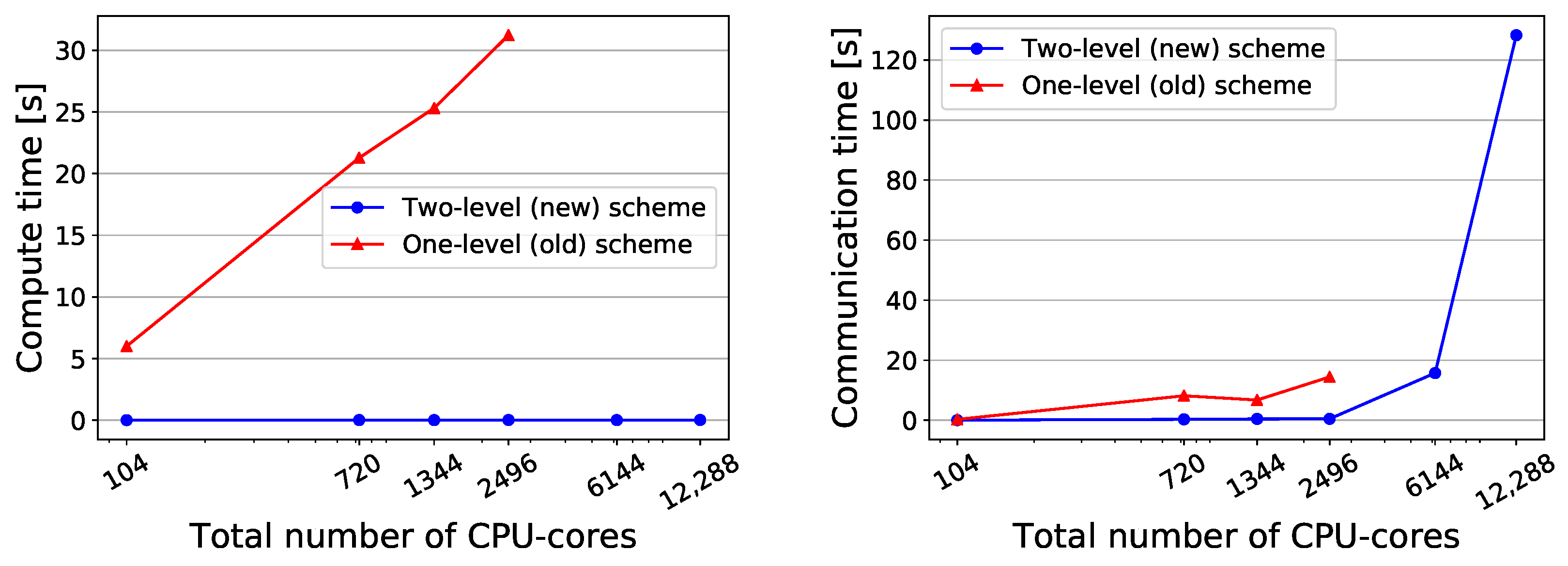
4. Performance Results
4.1. Test Case Description
4.2. Hardware Description
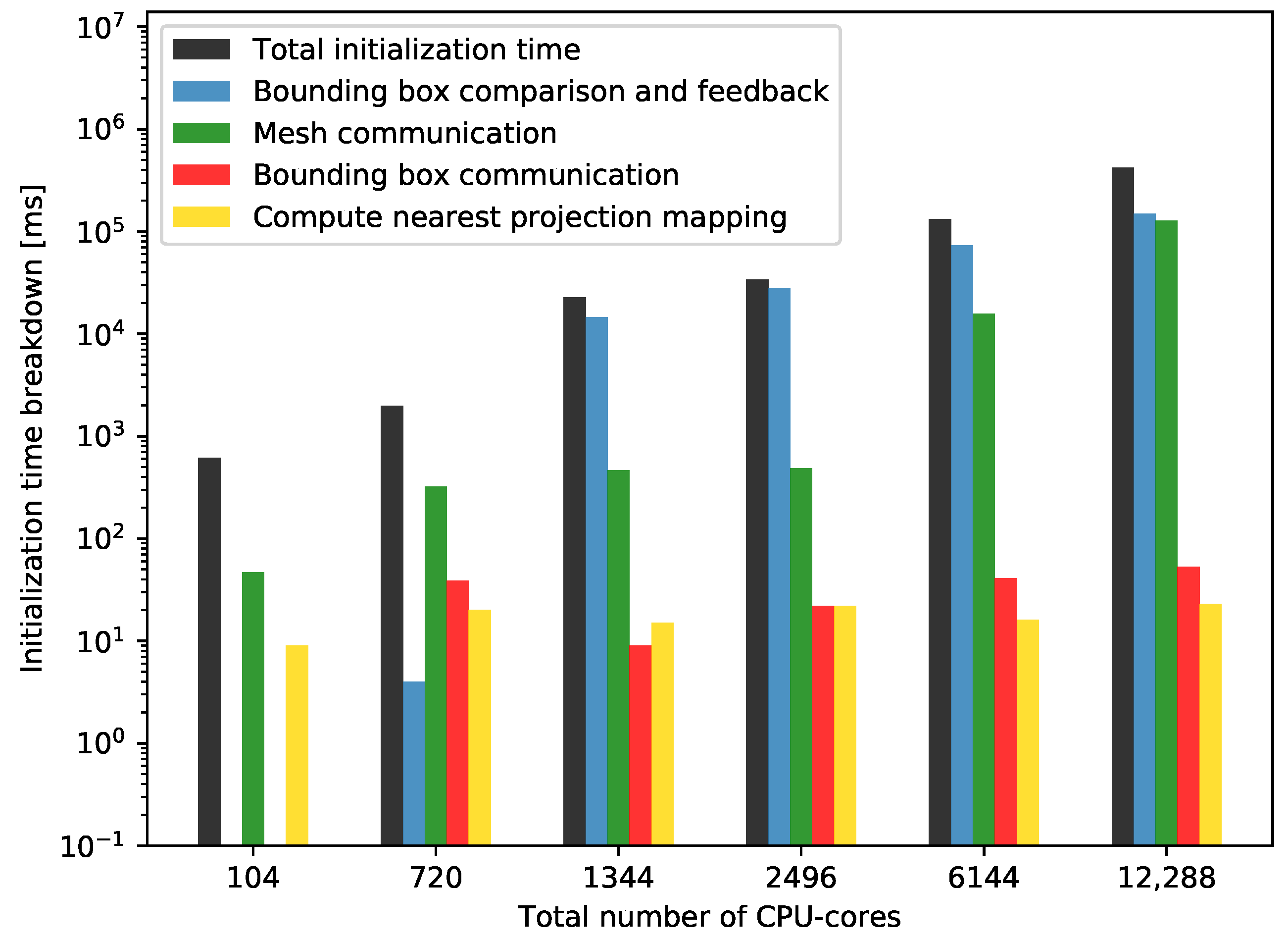
4.3. Performance Analysis
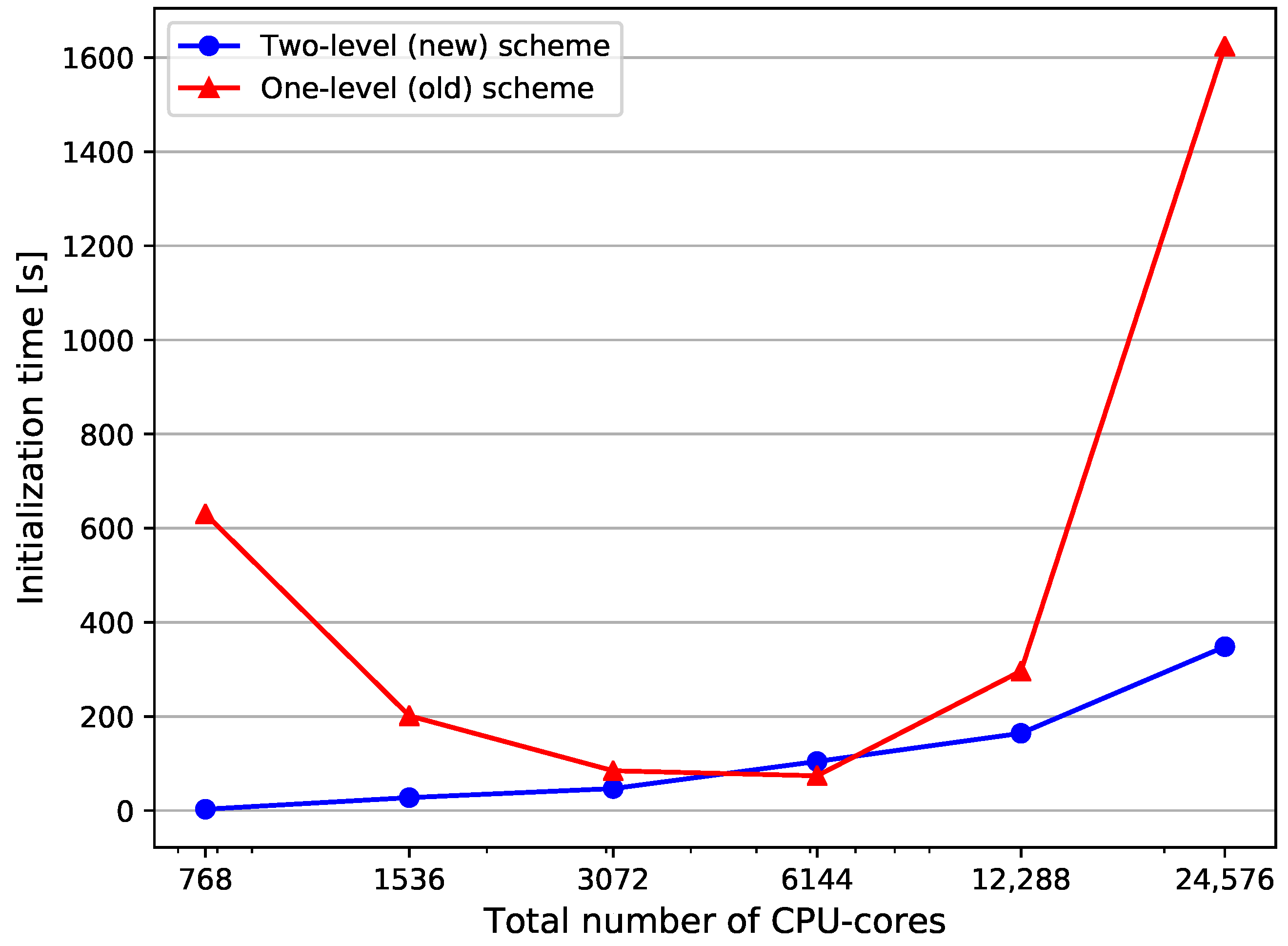
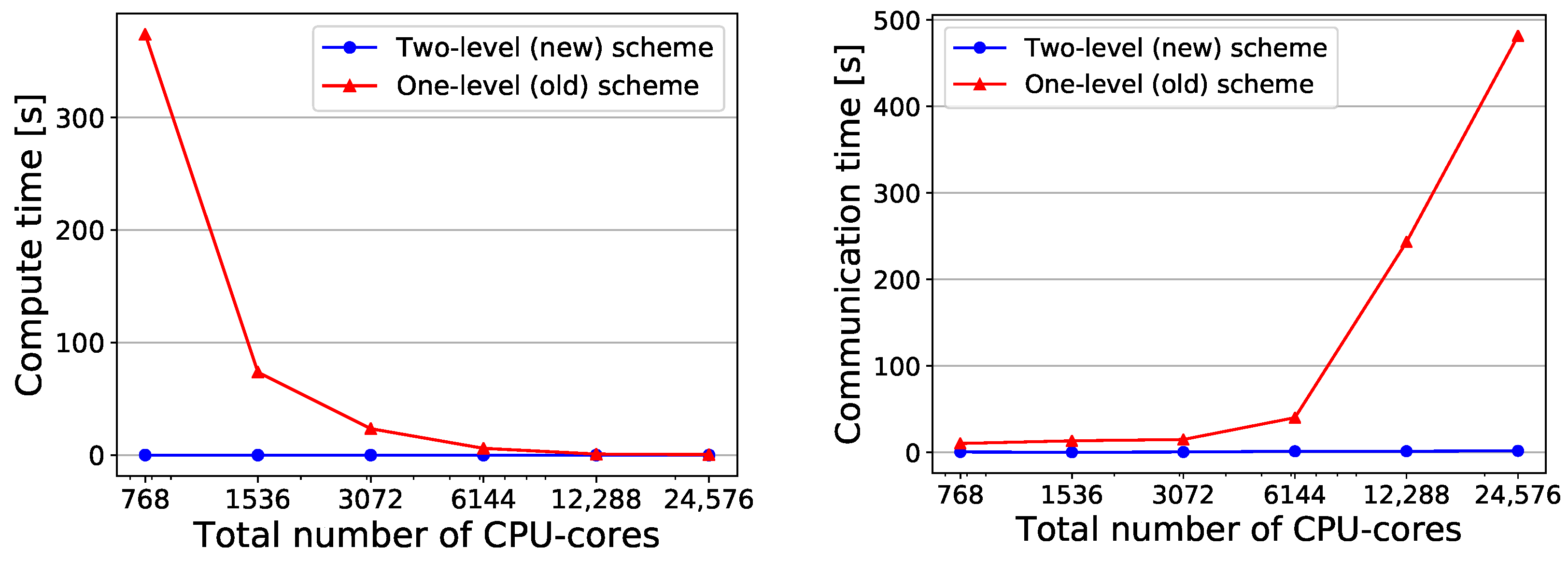
4.3.1. Strong Scaling
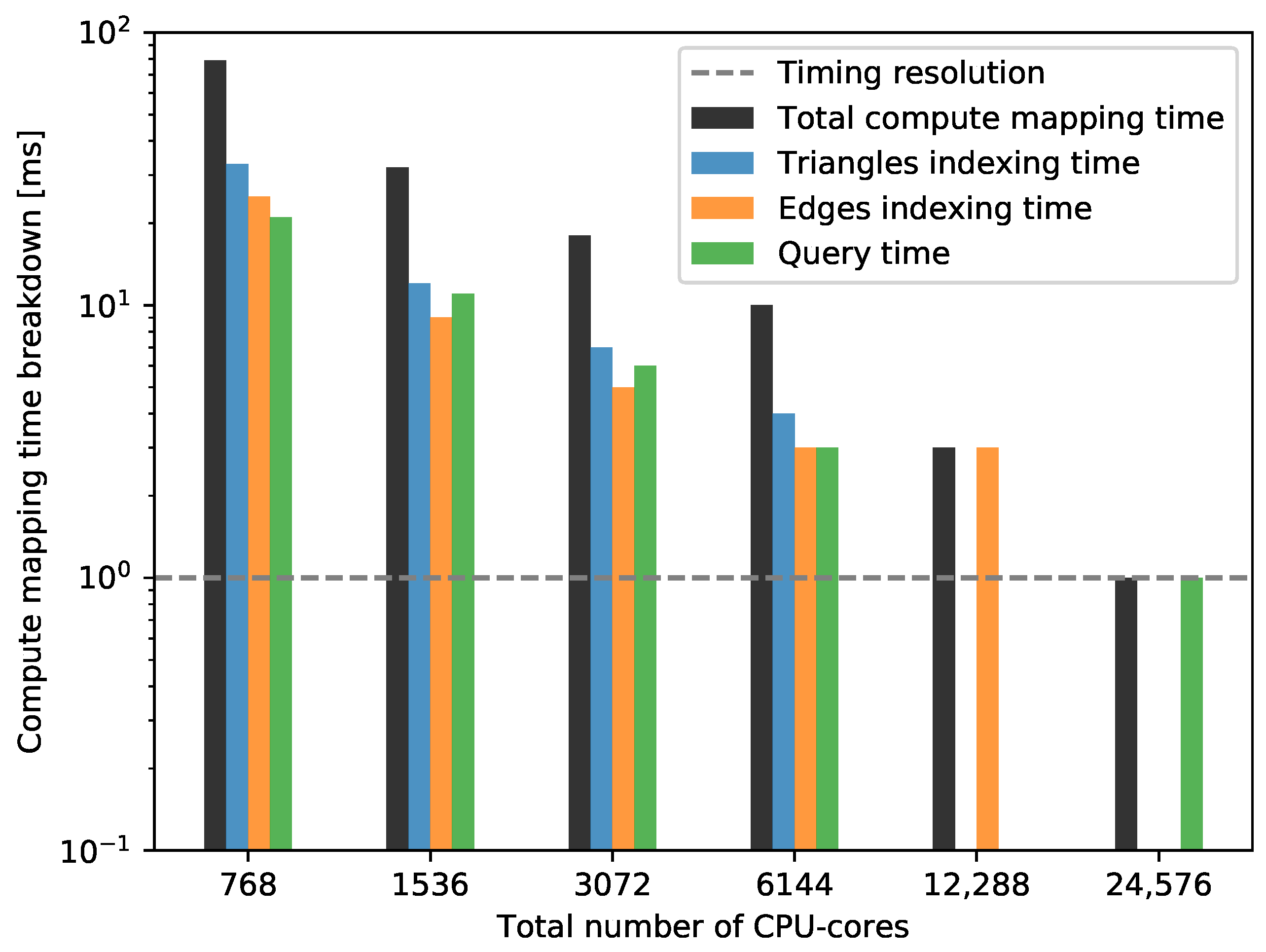
4.3.2. Weak Scaling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cinquegrana, D.; Vitagliano, P.L. Validation of a new fluid—Structure interaction framework for non-linear instabilities of 3D aerodynamic configurations. J. Fluids Struct. 2021, 103, 103264. [Google Scholar] [CrossRef]
- Naseri, A.; Totounferoush, A.; González, I.; Mehl, M.; Pérez-Segarra, C.D. A scalable framework for the partitioned solution of fluid–structure interaction problems. Comput. Mech. 2020, 66, 471–489. [Google Scholar] [CrossRef]
- Totounferoush, A.; Naseri, A.; Chiva, J.; Oliva, A.; Mehl, M. A GPU Accelerated Framework for Partitioned Solution of Fluid-Structure Interaction Problems. In Proceedings of the 14th WCCM-ECCOMAS Congress 2020, online, 11–15 January 2021; Volume 700. [Google Scholar]
- Jaust, A.; Weishaupt, K.; Mehl, M.; Flemisch, B. Partitioned coupling schemes for free-flow and porous-media applications with sharp interfaces. In Finite Volumes for Complex Applications IX—Methods, Theoretical Aspects, Examples; Klöfkorn, R., Keilegavlen, E., Radu, F.A., Fuhrmann, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 605–613. [Google Scholar] [CrossRef]
- Revell, A.; Afgan, I.; Ali, A.; Santasmasas, M.; Craft, T.; de Rosis, A.; Holgate, J.; Laurence, D.; Iyamabo, B.; Mole, A.; et al. Coupled hybrid RANS-LES research at the university of manchester. ERCOFTAC Bull. 2020, 120, 67. [Google Scholar]
- Bungartz, H.J.; Lindner, F.; Mehl, M.; Scheufele, K.; Shukaev, A.; Uekermann, B. Partitioned fluid-structure-acoustics interaction on distributed data—Coupling via preCICE. In Software for Exascale Computing—SPPEXA 2013–2015; Bungartz, H.J., Neumann, P., Nagel, E.W., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Lindner, F.; Mehl, M.; Uekermann, B. Radial basis function interpolation for black-box multi-physics simulations. In Proceedings of the VII International Conference on Coupled Problems in Science and Engineering (CIMNE), Rhodes Island, Greece, 12–14 June 2017; pp. 50–61. [Google Scholar]
- Mehl, M.; Uekermann, B.; Bijl, H.; Blom, D.; Gatzhammer, B.; Zuijlen, A. Parallel coupling numerics for partitioned fluid-structure interaction simulations. Comput. Math. Appl. 2016, 71, 869–891. [Google Scholar] [CrossRef]
- Scheufele, K.; Mehl, M. Robust multisecant Quasi-Newton variants for parallel Fluid-Structure simulations—And other multiphysics applications. SIAM J. Sci. Comput. 2017, 39, S404–S433. [Google Scholar] [CrossRef]
- Haelterman, R.; Bogaers, A.; Uekermann, B.; Scheufele, K.; Mehl, M. Improving the performance of the partitioned QN-ILS procedure for fluid-structure interaction problems: Filtering. Comput. Struct. 2016, 171, 9–17. [Google Scholar] [CrossRef]
- Uekermann, B. Partitioned Fluid-Structure Interaction on Massively Parallel Systems. Ph.D. Thesis, Department of Informatics, Technical University of Munich, Munich, Germany, 2016. [Google Scholar] [CrossRef]
- Lindner, F. Data Transfer in Partitioned Multi-Physics Simulations: Interpolation and Communication. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2019. [Google Scholar] [CrossRef]
- Lindner, F.; Totounferoush, A.; Mehl, M.; Uekermann, B.; Pour, N.E.; Krupp, V.; Roller, S.; Reimann, T.; Sternel, D.C.; Egawa, R.; et al. ExaFSA: Parallel Fluid-Structure-Acoustic Simulation. In Software for Exascale Computing—SPPEXA 2016–2019; Springer: Cham, Switzerland, 2020; pp. 271–300. [Google Scholar] [CrossRef]
- Wolf, K.; Bayrasy, P.; Brodbeck, C.; Kalmykov, I.; Oeckerath, A.; Wirth, N. MpCCI: Neutral interfaces for multiphysics simulations. In Scientific Computing and Algorithms in Industrial Simulations; Springer: Cham, Switzerland, 2017; pp. 135–151. [Google Scholar] [CrossRef]
- Joppich, W.; Kürschner, M. MpCCI—A tool for the simulation of coupled applications. Concurr. Comput. Pract. Exp. 2006, 18, 183–192. [Google Scholar] [CrossRef]
- Slattery, S.; Wilson, P.; Pawlowski, R. The data transfer kit: A geometric rendezvous-based tool for multiphysics data transfer. In Proceedings of the International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering (M&C 2013), Sun Valley, ID, USA, 5–9 May 2013; pp. 5–9. [Google Scholar]
- Plimpton, S.J.; Hendrickson, B.; Stewart, J.R. A parallel rendezvous algorithm for interpolation between multiple grids. J. Parallel Distrib. Comput. 2004, 64, 266–276. [Google Scholar] [CrossRef]
- Duchaine, F.; Jauré, S.; Poitou, D.; Quémerais, E.; Staffelbach, G.; Morel, T.; Gicquel, L. Analysis of high performance conjugate heat transfer with the openpalm coupler. Comput. Sci. Discov. 2015, 8, 015003. [Google Scholar] [CrossRef]
- Tang, Y.H.; Kudo, S.; Bian, X.; Li, Z.; Karniadakis, G.E. Multiscale universal interface: A concurrent framework for coupling heterogeneous solvers. J. Comput. Phys. 2015, 297, 13–31. [Google Scholar] [CrossRef]
- Thomas, D.; Cerquaglia, M.L.; Boman, R.; Economon, T.D.; Alonso, J.J.; Dimitriadis, G.; Terrapon, V.E. CUPyDO-An integrated Python environment for coupled fluid-structure simulations. Adv. Eng. Softw. 2019, 128, 69–85. [Google Scholar] [CrossRef]
- De Boer, A.; van Zuijlen, A.; Bijl, H. Comparison of conservative and consistent approaches for the coupling of non-matching meshes. Comput. Methods Appl. Mech. Eng. 2008, 197, 4284–4297. [Google Scholar] [CrossRef]
- Boost. Boost Library. Available online: http://www.boost.org/ (accessed on 15 April 2021).
- Beckmann, N.; Kriegel, H.P.; Schneider, R.; Seeger, B. The R*-tree: An efficient and robust access method for points and rectangles. In Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data, Atlantic City, NJ, USA, 23–25 May 1990; pp. 322–331. [Google Scholar] [CrossRef]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
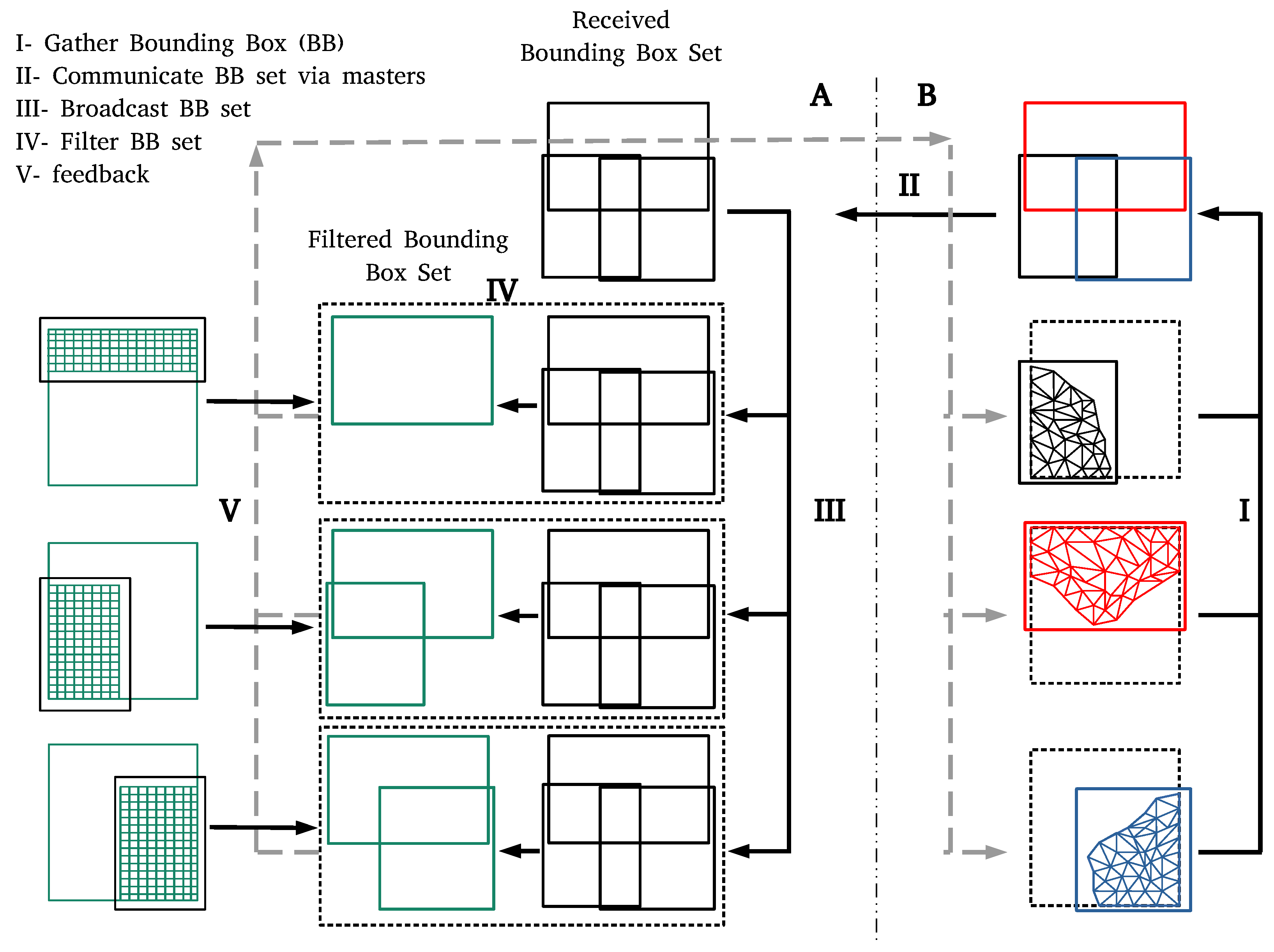
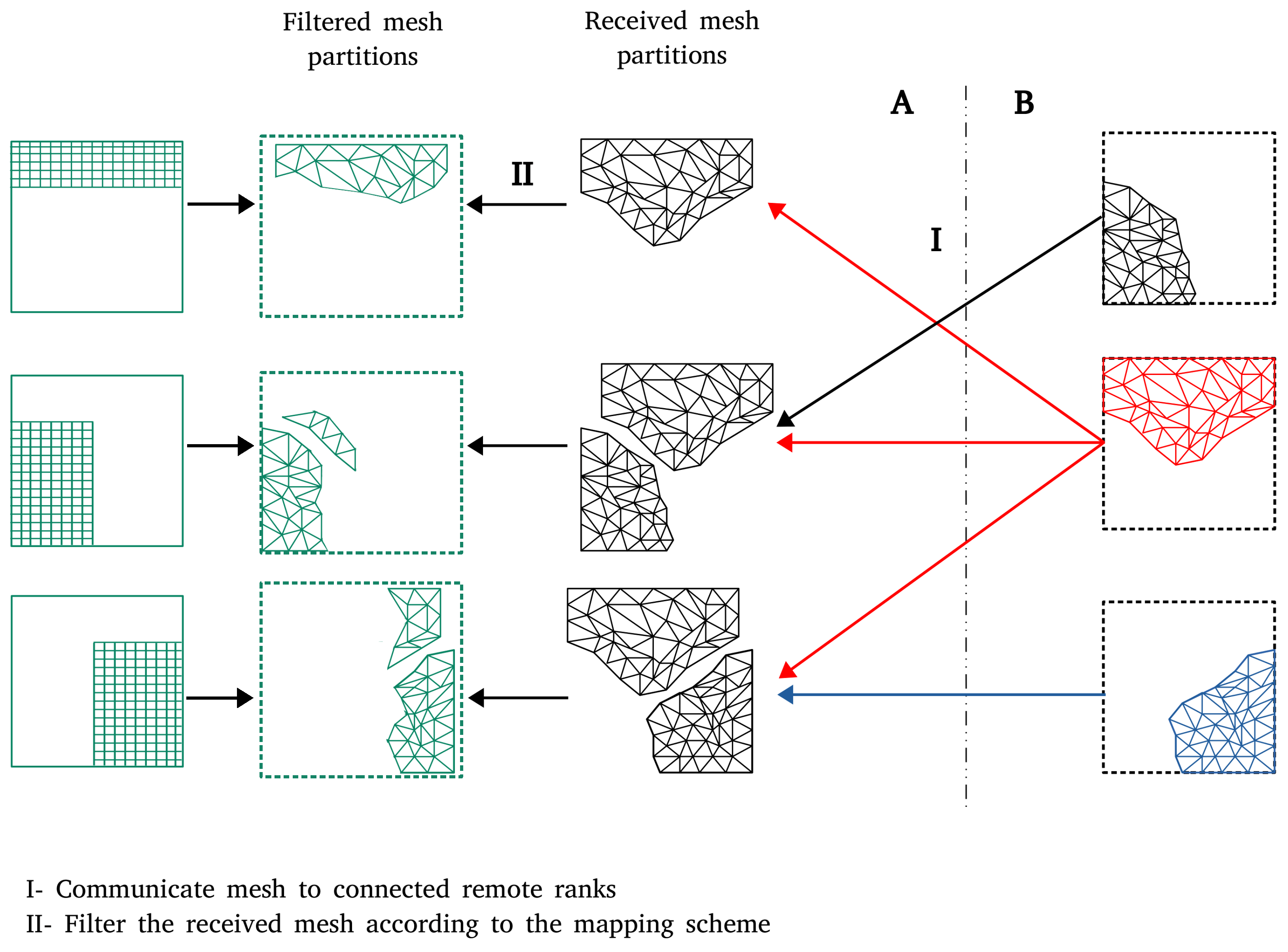
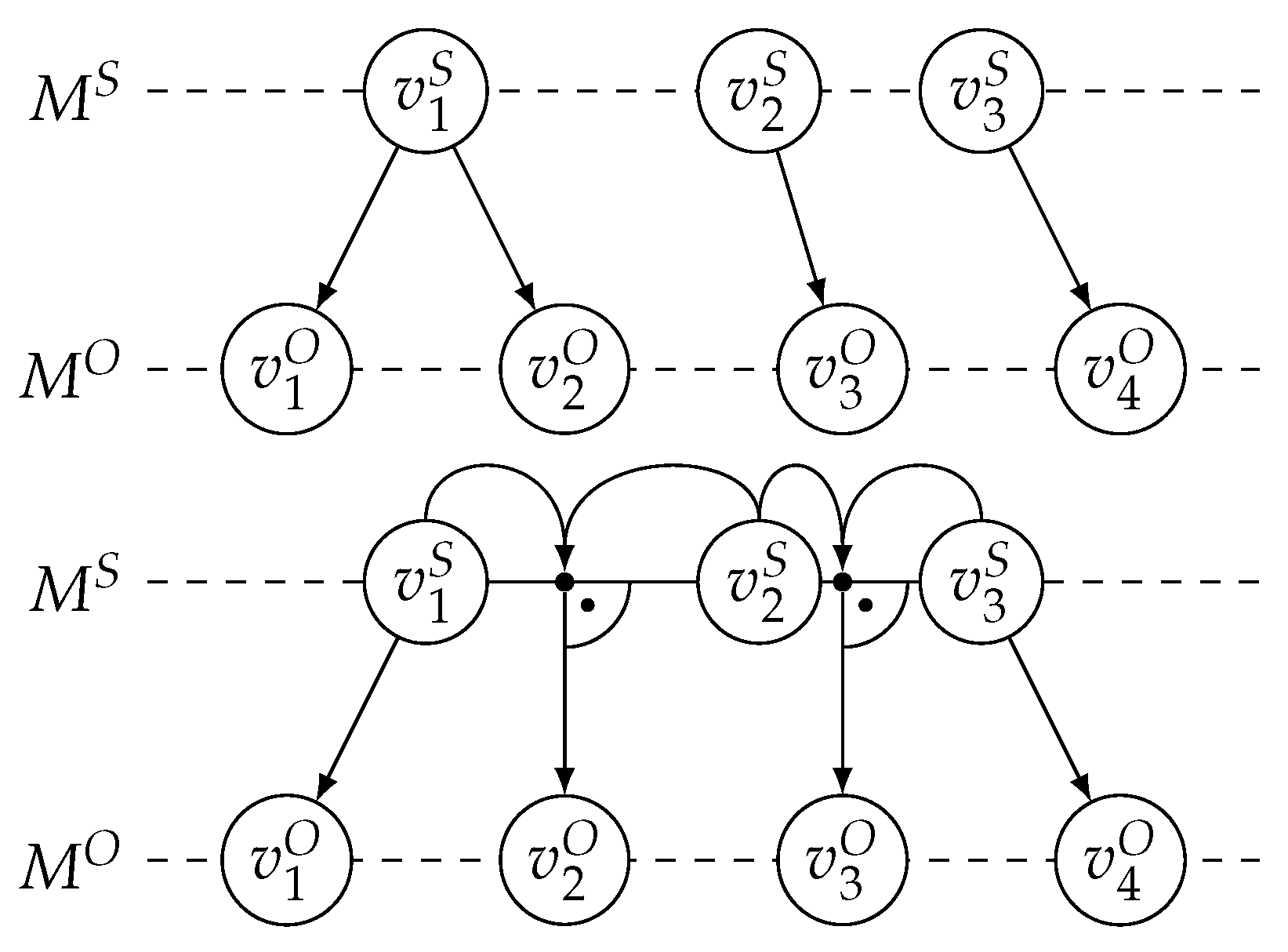
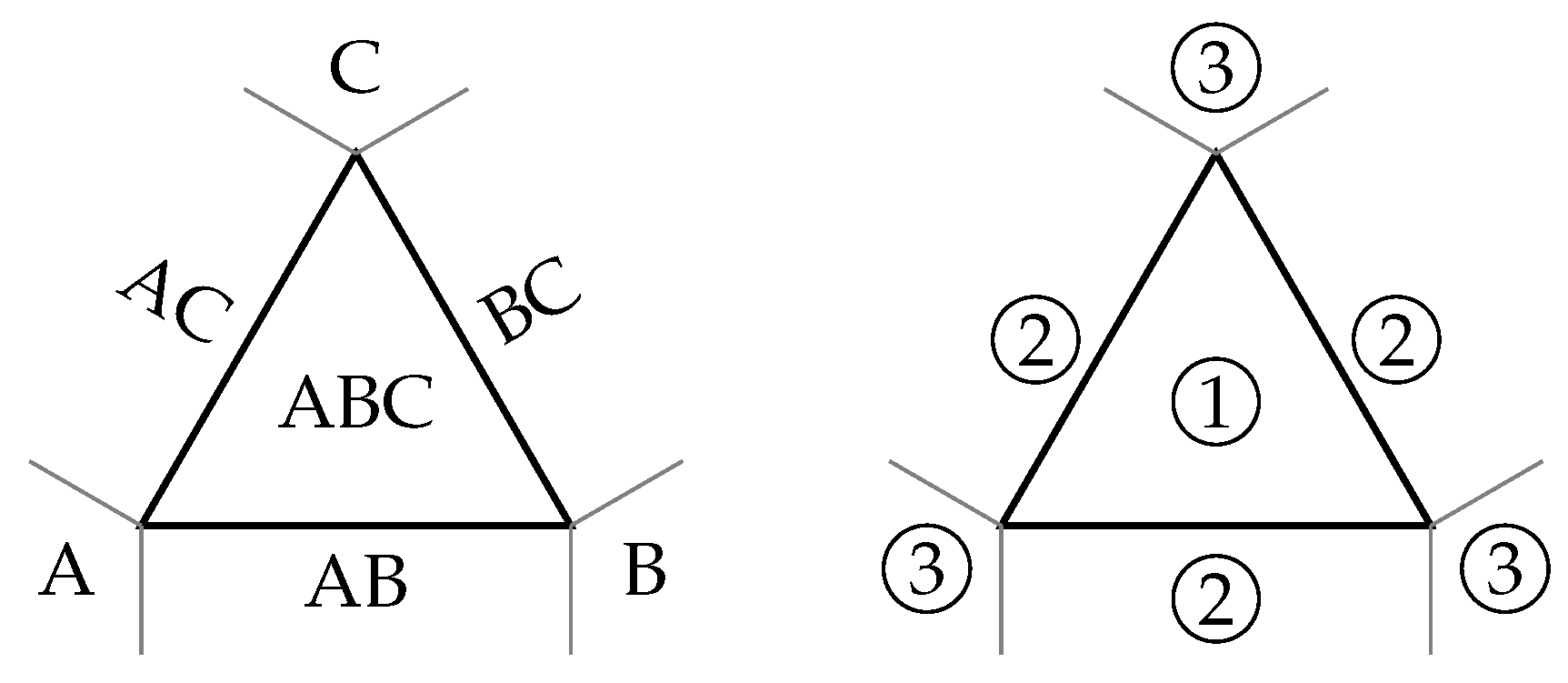


| Mesh ID | Mesh Width | Number of Vertices | Number of Triangles |
|---|---|---|---|
| M4 | 0.0005 | 628,898 | 1,257,391 |
| M5 | 0.0004 | 1,660,616 | 3,321,140 |
| M6 | 0.0003 | 2,962,176 | 5,924,260 |
| Cores | M4 | M6 | ||||
|---|---|---|---|---|---|---|
| Total | B | A | Lost Triangles | Rel [%] | Lost Triangles | Rel [%] |
| 768 | 192 | 576 | 44,244 | 3.52 | 90,195 | 1.52 |
| 1536 | 384 | 1152 | 62,003 | 4.93 | 154,358 | 2.61 |
| 3072 | 768 | 2304 | 86,085 | 6.85 | 246,937 | 4.17 |
| 6144 | 1536 | 4608 | 118,313 | 9.41 | 376,108 | 6.35 |
| 12,288 | 3072 | 9216 | 165,085 | 13.13 | 552,797 | 9.33 |
| 24,576 | 6144 | 18,432 | 230,556 | 18.34 | 797,042 | 13.45 |
| Mesh | Mesh | #Vertices | Cores | #Vertices per Core | |||
|---|---|---|---|---|---|---|---|
| ID | Width | Total | Total | B | A | B | A |
| M1 | 0.0025 | 25,722 | 104 | 26 | 78 | 989 | 330 |
| M2 | 0.0010 | 165,009 | 720 | 192 | 528 | 859 | 312 |
| M3 | 0.00075 | 330,139 | 1344 | 336 | 1008 | 982 | 328 |
| M4 | 0.0005 | 628,898 | 2496 | 624 | 1872 | 1007 | 336 |
| M5 | 0.0004 | 1,660,616 | 6144 | 1536 | 4608 | 1081 | 361 |
| M6 | 0.0003 | 2,962,176 | 12,288 | 3072 | 9216 | 964 | 321 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Totounferoush, A.; Simonis, F.; Uekermann, B.; Schulte, M. Efficient and Scalable Initialization of Partitioned Coupled Simulations with preCICE. Algorithms 2021, 14, 166. https://doi.org/10.3390/a14060166
Totounferoush A, Simonis F, Uekermann B, Schulte M. Efficient and Scalable Initialization of Partitioned Coupled Simulations with preCICE. Algorithms. 2021; 14(6):166. https://doi.org/10.3390/a14060166
Chicago/Turabian StyleTotounferoush, Amin, Frédéric Simonis, Benjamin Uekermann, and Miriam Schulte. 2021. "Efficient and Scalable Initialization of Partitioned Coupled Simulations with preCICE" Algorithms 14, no. 6: 166. https://doi.org/10.3390/a14060166
APA StyleTotounferoush, A., Simonis, F., Uekermann, B., & Schulte, M. (2021). Efficient and Scalable Initialization of Partitioned Coupled Simulations with preCICE. Algorithms, 14(6), 166. https://doi.org/10.3390/a14060166






