Abstract
The widespread use of automated decision processes in many areas of our society raises serious ethical issues with respect to the fairness of the process and the possible resulting discrimination. To solve this issue, we propose a novel adversarial training approach called GANSan for learning a sanitizer whose objective is to prevent the possibility of any discrimination (i.e., direct and indirect) based on a sensitive attribute by removing the attribute itself as well as the existing correlations with the remaining attributes. Our method GANSan is partially inspired by the powerful framework of generative adversarial networks (in particular Cycle-GANs), which offers a flexible way to learn a distribution empirically or to translate between two different distributions. In contrast to prior work, one of the strengths of our approach is that the sanitization is performed in the same space as the original data by only modifying the other attributes as little as possible, thus preserving the interpretability of the sanitized data. Consequently, once the sanitizer is trained, it can be applied to new data locally by an individual on their profile before releasing it. Finally, experiments on real datasets demonstrate the effectiveness of the approach as well as the achievable trade-off between fairness and utility.
1. Introduction
In recent years, the availability and the diversity of large-scale datasets, the algorithmic advancements in machine learning and the increase in computational power have led to the development of personalized services and prediction systems to such an extent that their use is now ubiquitous in our society. For instance, machine learning-based systems are now used in banking for assessing the risk associated with loan applications [1], in hiring system [2] and in predictive justice to quantify the recidivism risk of an inmate [3]. Despite their usefulness, the predictions performed by these algorithms are not exempt from biases, and numerous cases of discriminatory decisions have been reported over the last years.
For example, going back on the case of predictive justice, a study conducted by ProPublica showed that the recidivism prediction tool COMPAS, which is currently used in Broward County (Florida), is strongly biased against black defendants, by displaying a false positive rate twice as high for black persons than for white persons [4]. If the dataset exhibits strong detectable biases towards a particular sensitive group (e.g., an ethnic or minority group), the naïve solution of removing the attribute identifying the sensitive group prevents only direct discrimination. Indeed, indirect discrimination can still occur due to correlations between the sensitive attribute and other attributes.
In this paper, we propose a novel approach called GANSan (for Generative Adversarial Network Sanitizer) to address the problem of discrimination due to the biased underlying data. In a nutshell, our approach learns a sanitizer (in our case a neural network) transforming the input data in a way that maximize the following two metrics: (1) fidelity, in the sense that the transformation should modify the data as little as possible, and (2) non-discrimination, which means that the sensitive attribute should be difficult to predict from the sanitized data.
A typical use case might be one in which a company during its recruitment process offers to job applicants a tool to remove racial correlation in their data locally on their side before submitting their sanitized profile on the job application platform. If built appropriately, this tool would make the recruitment process of the company free from racial discrimination as it never had access to the original profile.
Another possible use case could be the recruitment process of referees for an amateur sports organization. In particular, in this situation, the selection should be primarily based on the merit of applicants, but at the same time, the institution might be aware that the data used to train a model to automatize this recruitment process might be highly biased according to race. In this example, the bias could be a result of the nature of the activity as well as the historical societal biases. In practice, approaches such as the Rooney Rule have been proposed and implemented to foster diversity for the recruitment of the coaches in the National Football League (NFL-USA) as well as in other industries. To address this issue, the institution could use our approach to sanitize the data before applying a merit-based recommendation algorithm to select the referee on the sanitized data.
Overall, our contributions can be summarized as follows.
- We propose a novel adversarial approach, inspired from Generative Adversarial Networks (GANs) [5], in which a sanitizer is learned from data representing the population. The sanitizer can then be applied on a profile in such way that the sensitive attribute is removed, as well as existing correlations with other attributes, while ensuring that the sanitized profile is modified as little as possible, preventing both direct and indirect discrimination. Thus, one of the main benefits of our approach is that the sanitization can be performed without having any knowledge regarding the tasks that are going to be conducted in the future on the sanitized data. In this sense, our objective is more generic than simply building a non-discriminating classifier, in the sense that we aim at debiasing the data with respect to the sensitive attribute.
- Another strength of our approach is that once the sanitizer has been learned, it can be used locally by an individual (e.g., on a device under their control) to generate a modified version of their profile that still lives in the same representation space, but from which it is very difficult to infer the sensitive attribute. In this sense, our method can be considered to fall under the category of randomized response techniques [6] as it can be distributed before being used locally by a user to sanitize their data. Thus, it does not require their true profile to be sent to a trusted third party. Of all of the approaches that currently exist in the literature to reach algorithmic fairness [7], we are not aware of any other work that has considered the local sanitization with the exception of [8], which focuses on the protection of privacy but could also be applied to enhance fairness.
- To demonstrate its usefulness, we have proposed and discussed four different evaluation scenarios and assessed our approach on real datasets for these four different scenarios. In particular, we carried out an empirical analysis of our approach to explain the behaviour of the sanitization process. In particular, we have analyzed the achievable trade-off between fairness and utility measured both in terms of the perturbations introduced by the sanitization framework but also with respect to the accuracy of a classifier learned on the sanitized data. However, we want to emphasize that in contrast to most of the previous works, once the dataset is sanitized it could be used for any other analysis tasks.
The outline of the paper is as follows. First, in Section 2, we introduce the system model before reviewing the background notions on fairness metrics.Afterward, in Section 3, we review the related work on methods for enhancing fairness belonging to the preprocessing approach like ours before describing GANSan in Section 4. Finally, we evaluate experimentally our approach in Section 5 before concluding in Section 6.
2. Preliminaries
In this section, we first present the system model used in this paper before reviewing the background notions on fairness metrics.
2.1. System Model
In this paper, we consider the generic setting of a dataset D composed of N records. Each record typically corresponds to the profile of the individual i and is made of d attributes, which can be categorical, discrete, or continuous. Amongst those, the sensitive attribute (e.g., gender, ethnic origin, religious belief, …) should remain hidden to prevent discrimination. In addition, the decision attribute Y is typically used for a classification task (e.g., accept or reject an individual for a job interview). The other attributes of the profile, which are neither nor , will be referred hereafter as .
For simplicity, in this work we restrict ourselves to the situations in which these two attributes are binary (i.e., and ). However, our approach can also be generalized to multi-valued attributes, although quantifying fairness for multi-valued attributes is much more challenging than for binary ones [9]. Our main objective is to prevent the possibility of inferring the sensitive attribute from the sanitized data. This objective is similar to the protection against membership inference, in which given a model and a set of records, consists in preventing the identification of records that were part of the training set [10,11,12,13]. In our context, it amounts to distinguish between the two groups generated by the values of S, which we will refer to as the sensitive group (for which ) and the privileged group (for which ).
2.2. Fairness Metrics
First, we would like to point out that there are many different definitions of fairness existing in the literature [7,14,15,16,17,18] and that the choice of the appropriate fairness metric is highly dependent on the context considered.
For instance, one natural approach for defining fairness is the concept of individual fairness [14], which states that individuals that are similar except for the sensitive attribute should be treated similarly (i.e., receive similar decisions). This notion relates to the legal concept of disparate treatment [19], which occurs if the decision process was made based on sensitive attributes. This definition is relevant when discrimination is caused by the decision process. Therefore, it cannot be used in the situation in which the objective is to directly redress biases in the data.
In contrast to individual fairness, group fairness relies on statistic of outcomes of the subgroups indexed by S and can be quantified in several ways, such as demographic parity [20] and equalized odds [21]. More precisely, the demographic parity corresponds to the absolute difference of rates of positive outcomes in the sensitive and privileged groups (for which, respectively, and ).:
while equalized odds is the absolute difference of odds in each subgroup:
in which refers to the prediction made on the decision attribute made by a trained classifier. Compared to the demographic parity, the equalized odds is more suitable when the base rates in both groups differ (). Other fairness metrics such as the calibration are also appropriate in the situation of different base rates. However, we will limit ourselves to equalized odds in this paper. Note that these definitions are agnostic to the cause of the discrimination and are based solely on the assumption that statistics of outcomes should be similar between subgroups.
In our work, we follow a different line of research by defining fairness in terms of the inability to infer S from other attributes [22,23]. This approach stems from the observation that it is impossible to discriminate based on the sensitive attribute if the latter is unknown and cannot be predicted from other attributes. Thus, our approach aims at sanitizing the data in such a way it should not be possible to infer the sensitive attribute from the sanitized data.
The inability to infer the attribute S can be measured by the accuracy of a predictor Adv trained to recover the hidden S (sAcc), as well as the balanced error rate (BER) introduced in [22] as the basis for the ϵ-fairness:
The BER captures the predictability of both classes and a value of can be considered optimal for protecting against inference in the sense that it means that the inferences made by the predictor are not better than a random guess. A dataset D, (A, A, Y) is said to be fair if for any classification algorithm , . The BER is more relevant than the accuracy of a classifier at predicting the sensitive attribute for datasets with imbalanced proportions of sensitive and privileged groups. Thus, a successful sanitization would lead to a significant drop of the accuracy while raising the BER close to its optimal value of .
3. Related Work
In recent years, many approaches have been developed to enhance the fairness of machine learning algorithms. Most of these techniques can be classified into three families of approaches, namely (1) the preprocessing approach [22,24,25,26] in which fairness is achieved by changing the characteristics of the input data (e.g., by suppressing undesired correlations with the sensitive attribute), (2) the algorithmic modification approach (also sometimes called constrained optimization) in which the learning algorithm is adapted to ensure that it is fair by design [27,28] and (3) the postprocessing approach that modifies the output of the learning algorithm to increase the level of fairness [21,29]. We refer the interested reader to [7] for a recent survey comparing the different fairness-enhancing methods. As our approach falls within the preprocessing approach, we will review afterward only the main methods of this category.
Among the seminal works in fairness enhancement, in [22] the authors have developed a framework that translates the conditional distributions of each of the datasets’ attributes by shifting them towards a median distribution. While this approach is straightforward, it does not take into account unordered categorical attributes as well as correlations that might arise due to a combination of attributes, which we address in this work. Zemel and co-authors [26] have proposed to learn a fair representation of data based on a set of prototypes, which preserves the outcome prediction accuracy and allows a faithful reconstruction of original profiles. Each prototype can equally identify groups based on sensitive attribute values. This technique has been one of the pioneering works in mitigating fairness by changing the representation space of the data.
However, for this approach to work, the definition of the set of prototypes (i.e., the number of prototypes and their characteristics) is highly critical. In particular, the number of prototypes influences the reconstruction quality. The higher the number of prototypes, the better the quality of the mapping. Indeed, each prototype can potentially capture a specific aspect of the data, but at the same time lower the demographic parity constraint since such specificity could help identify a particular group. In contrast, the smaller the number of prototypes, the more general the mapping, which lowers the quality of the reconstruction. Besides, the characteristics of the prototypes also have a significant impact on the quality of the mapping. Indeed, the prototypes live in the same space of the data and could typically act as representatives of the population. Thus, their choice should be balanced as the mapping relies on the distance between a particular record and the set of prototypes. For instance, having a set of prototypes closer to the privileged group will induce a lower quality of data reconstruction, especially on the privileged group, to compensate for their proximity with the set of prototypes. Indeed, the statistical constraints ensure that the mapping does not favour any of the groups.
Relying on the variational auto-encoder [30], Louizos and co-authors [25] have developed an approach to improve fairness by choosing a prior distribution independently of the group membership and removing differences across groups with the maximum mean discrepancy [31]. Recently, Creager, Madras, Jacobsen, Weis, Swersky, Toniann, and Zemel [32] have defined a preprocessing technique also based on variational auto-encoder, which consists in finding a representation in which a given number of sensitive attributes are independent of the rest of the data while maintaining an acceptable accuracy for the classification task considered. The approach is designed to handle more than one sensitive attribute and it does not require the sensitive attribute to be known at training time.
Our approach differs from these previous works by the design of the sanitization architecture, which does not rely on a careful choice of the prior distribution, thus leaving more flexibility on the choice of the mapping distribution. In addition to the lack of interpretability of the outputted representation, variational auto-encoders generally do not perform better than GANs [33].
In addition, several approaches have been explored to enhance fairness based on adversarial training.For instance, Edwards and Storkey [24] have trained an encoder to output a representation from which an adversary is unable to predict the group membership accurately, but from which a decoder can reconstruct the data and on which decision predictor still performs well. Madras, Creager, Pitassi, and Zemel [34] extended this framework to satisfy the equality of opportunities [21] constraint and explored the theoretical guarantees for fairness provided by the learned representation as well as the ability of the representation to be used for different classification tasks. Beutel, Chen, Zhao, and Chi [35] have studied how the choice of data affects fairness in the context of adversarial learning. One of the interesting results of their study is the relationship between demographic parity and the removal of the sensitive attribute, which demonstrates that learning a representation independent of the sensitive attribute with a balanced dataset (in terms of the sensitive and privileged groups) ensures demographic parity.
Zhang, Lemoine, and Mitchell [36] have designed a decision predictor satisfying group fairness by ensuring that an adversary is unable to infer the sensitive attribute from the predicted outcome. Afterward, Wadsworth, Vera, and Piech [37] have applied the latter framework in the context of recidivism prediction, demonstrating that it is possible to significantly reduce the discrimination while maintaining nearly the same accuracy as on the original data.
These approaches learn a fair classification mechanism by introducing the fairness constraints in the learning procedure. In contrast, the objective of our approach is to learn a sanitization framework transforming the input data to prevent the sensitive attribute from being inferred while maintaining the interpretability and utility of the data. The transformed dataset could be used for various purposes such as fair classification and other statistical analysis tasks, which is not possible for approaches that only enhance the fairness with respect to a specific classification task.
With respect to approaches generating a fair representation of the dataset, Sattigeri and co-authors [38] have developed a method to cancel out bias in high dimensional data using adversarial learning. Their approach has shown to be applicable on multimedia data, but they have not investigated the possibility of using it on tabular data, which has very different characteristics than multimedia data. Finally, McNamara, Ong, and Williamson [39] have investigated the benefits and drawbacks of fair representation learning. In particular, they demonstrated that techniques building fair representations restrict the space of possible decisions, hence providing fairness but also limiting the possible usages of the resulting data.
While these approaches are effective at addressing fairness, one of their common drawbacks is that they do not preserve the interpretability of the data. Notable exceptions in terms of interpretability are the methods FairGan [23] and its extension FairGan+ [40] proposed by Xu, Yuan, Zhang, and Wu. However, these methods have different objectives than ours as they aim at generating a dataset whose distributions are discrimination-free and such that those distributions are close to the original one, as well as training a fair classifier using the generated dataset. In fact, the generator in FairGan is trained to generate fair datasets from which a classifier can be learned to make fair decisions. These fair datasets globally follow the distribution of the original data, with the exception that the sensitive attribute cannot be inferred from it. FairGan+ extends FairGan by adding a predictor trained jointly with the generator of the fair dataset version to make fair predictions. The inference of the sensitive attribute from the predicted decision is also prevented with the introduction of an additional discriminator. While these approaches show interesting results, they cannot be used to sanitize new profiles in contrast to our approach. More precisely, GANSan enlarges the possible use cases by providing a sanitizer that can be used locally (i.e., on-the-fly) to protect the sensitive attribute of the user. This includes the fair classification investigated in FairGan+ and FairGan, but also other use cases.
In [41], Calmon, Wei, Vinzamuri, Ramamurthy, and Varshney have learned an optimal randomized mapping for removing group-based discrimination while limiting the distortion introduced at profiles and distributions levels to preserve utility. The approach requires the definition of penalty weights for any non-acceptable transformation, which can be complex to define as the relationship between attributes might not be fully understood. This makes the overall approach difficult to use in practice, especially on a dataset with a very large number of potential attribute-values combinations. Furthermore, the meaning of each of the given penalties might also be difficult to grasp and there could be a large number of non-acceptable transformations. Finally at the same time, the large number of constraints might not guarantee the existence of a solution satisfying them. Our approach is more generic and requires a smaller number of hyper-parameters.
Following a similar line of work, there is a growing body of research investigating the use of adversarial training to protect the privacy of individuals during the collection or disclosure of data. For instance, Feutry, Piantanida, Bengio, and Duhamel [42] have proposed an anonymization procedure based on the learning of three sub-networks: an encoder, an adversary, and a label predictor. The authors have ensured the convergence of these three networks during training by proposing an efficient optimization procedure with bounds on the probability of misclassification. Pittaluga, Koppal, and Chakrabarti [43] have designed a procedure based on adversarial training to hide a private attribute of a dataset.
While the aforementioned approaches do not consider the interpretability of the representation produced, Romanelli, Palamidessi, and Chatzikokolakis [8] have designed a mechanism to create a dataset preserving the original representation. More precisely, they have developed a method for learning an optimal privacy protection mechanism also inspired by GAN [44], which they have applied to location privacy. Here, the objective is to minimize the amount of information (measured by the mutual information) preserved between the sensitive attribute and the prediction made on the decision attribute by a classifier while respecting a bound on the utility of the dataset.
In addition, local sanitization approaches (also called randomized response techniques) have been investigated for the protection of privacy. More precisely, one of the benefits of local sanitization is that there is no need to centralize the data before sanitizing it, thus limiting the trust assumptions that an individual has to make on external entities when sharing their data. For instance, Wang, Hu, and Wu [45] have applied randomized response techniques achieving differential privacy during the data collection phase to avoid the need to have an untrusted party collecting sensitive information. Similar to our approach, the protection of information takes place at the individual level as the user can randomize their data before publishing it. The main objective is to produce a sanitized dataset in which global statistical properties are preserved, but from which it is not possible to infer the sensitive information of a specific user. In the line of work, Du and Zhan [46] have proposed a method for learning a decision tree classifier on this sanitized data. In the same local sanitization context, Osia, Shamsabadi, Sajadmanesh, Taheri, Katevas, Rabiee, Lane, and Haddadi [47] have proposed a hybrid approach to protect the user sensitive information. The idea consists of splitting the prediction model into two parts, the first one being run on the local device (i.e., end-user) while the second is executed on the entity (i.e., server) that requires the data. More precisely, the end-user runs the initial layer of the model and produces an output used by the server to make the final prediction. While this idea is partially similar to ours, there are important differences. For instance, as the user runs the initial model, their approach does not provide an unintelligible output to the user, even though such output contains minimal information about the sensitive attributes. Therefore, this is similar to the previously mentioned body of work that protects the sensitive attribute by changing the space of representation.
While these previous approaches protect the user information with limited impact on the data, none of these previous works have taken into account the fairness aspect. Thus, while our method also falls within the local sanitization approaches, in the sense that the sanitizer can be applied locally by a user, our initial objective is quite different as we aim at preventing the risk of discrimination. Nonetheless, at the same time, our method also protects against attribute inference with respect to the sensitive attribute. Table 1 provides a comparison of our approach with other methods from the state-of-the-art.

Table 1.
Comparative table of preprocessing methods for fairness enhancement in which Data Pub. refers to the ability to published the transformed dataset while Local San. concerns the ability to transform a profile on-the-fly. In addition, Simple P. indicates the number of hyper-parameters (the lower the better), Meaningful P. refer to the ease of comprehension and usage of the hyper-parameters to achieve a chosen objective, Dt. Compr. refers to whether or not the input data space is preserved.
4. Adversarial Training for Data Debiasing
As previously explained, removing the sensitive attribute is rarely sufficient to guarantee non-discrimination as correlations are likely to exist between other attributes and the sensitive one. In general, detecting and suppressing complex correlations between attributes is a difficult task.
To address this challenge, our approach GANSan relies on the modeling power of GANs to build a sanitizer that can cancel out correlations with the sensitive attribute without requiring an explicit model of those correlations. In particular, it exploits the capacity of the discriminator to distinguish the subgroups indexed by the sensitive attribute. Once the sanitizer has been trained, any individual can apply it locally on their profile before disclosing it. The sanitized data can then be safely used for any subsequent task.
4.1. Generative Adversarial Network Sanitization
High-level overview. Formally, given a dataset D, the objective of GANSan is to learn a function , called the sanitizer that perturbs individual profiles of the dataset D, such that a distance measure called the fidelity (in our case we will use the norm) between the original and the sanitized datasets (), is minimal, while ensuring that S cannot be recovered from . Our approach differs from classical conditional GAN [48] by the fact that the objective of our discriminator is to reconstruct the hidden sensitive attribute from the generator output, whereas the discriminator in classical conditional GAN has to discriminate between the generator output and samples from the true distribution.
Figure 1 presents the high-level overview of the training procedure, while Algorithm 1 describes it in detail.
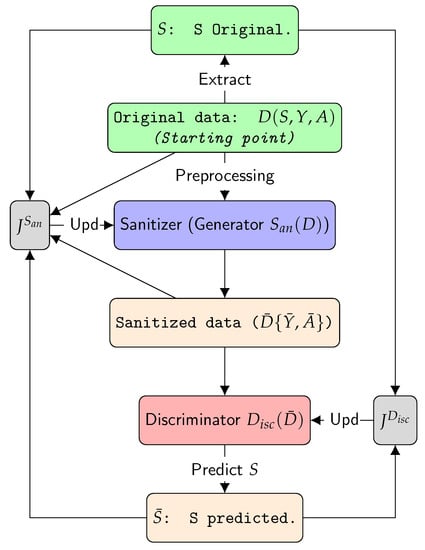
Figure 1.
Overview of the framework of GANSan. The objective of the discriminator is to predict S from the output of the sanitizer . The two objective functions that the framework aims at minimizing are, respectively, the discriminator and sanitizer losses, namely and .
The first step corresponds to the training of the sanitizer (Algorithm 1, Lines 7–17). The sanitizer can be seen as a generator similarly to standard GAN but with a different purpose. In a nutshell, it learns the empirical distribution of the sensitive attribute and generates a new distribution that concurrently respects two objectives: (1) finding a perturbation that will fool the discriminator in predicting S while (2) minimizing the damage introduced by the sanitization. More precisely, the sanitizer takes as input the original dataset D (including S and Y) plus some noise . The noise introduced is used to prevent the over-specialization of the sanitizer on the training set while making the reverse mapping of sanitized profiles to their original versions more difficult as the mapping will be probabilistic. As a result, even if the sanitizer is applied twice on the same profile, it can produce two different modified profiles.
The second step consists in training the discriminator for predicting the sensitive attribute from the data produced by the sanitizer (Algorithm 1, Lines 18–24). The rationale of our approach is that the better the discriminator is at predicting the sensitive attribute S, the worse the sanitizer is at hiding it and thus the higher the potential risk of discrimination. These two steps are run iteratively until convergence of the training.
| Algorithm 1GANSan Training Procedure |
|
| ▹ Initialization |
|
| ▹ Compute the reconstruction loss vector |
|
| ▹ compute the sensitive loss |
|
| ▹ concatenate the previously computed loss |
|
| ▹ Back-propagation using |
|
Training objective of GANSan. Let be the prediction of S by the discriminator (). Its objective is to accurately predict S, thus it aims at minimizing the loss . In practice in our work, we instantiate as the Mean Squared Error (MSE).
Given the hyperparameter representing the desired trade-off between the fairness and the fidelity, the sanitizer minimizes a loss combining two objectives:
in which is on the sensitive attribute. The term is due to the objective of maximizing the error of the discriminator (i.e., recall that the optimal value of the BER is ).
Concerning the reconstruction loss , we have first tried the classical Mean Absolute Error (MAE) and MSE losses. However, our initial experiments have shown that these losses produce datasets that are highly problematic in the sense that the sanitizer always outputs the same profile whatever the input profile, which protects against attribute inference but renders the profile unusable. Therefore, we had to design a slightly more complex loss function. More precisely, we chose not to merge the respective losses of these attributes (), yielding a vector of attribute losses whose components are iteratively used in the gradient descent. Hence, each node of the output layer of the generator is optimized to reconstruct a single attribute from the representation obtained from the intermediate layers. The vector formulation of the loss is as follows: and the objective is to minimize all its components. The details of the parameters used for the training are given in Section 5.1.
We want to point out that the sanitization process does not necessarily require the decision attribute as an input variable, thus while in this paper we chose to explicitly include it the sanitization can be carried out with or without this decision attribute.
4.2. Performance Metrics
The performance of GANSan will be evaluated by taking into account the fairness enhancement and the fidelity to the original data. With respect to fairness, we will quantify it primarily with the inability of a predictor , hereafter referred to as the adversary, in inferring the sensitive attribute (cf. Section 2) using its Balanced Error Rate (BER) [22] and its accuracy sAcc (cf., Section 2.2). We will also assess the fairness using metrics (cf. Section 2) such as demographic parity (Equation (1)) and equalized odds (Equation (2)).
To measure the fidelity between the original and the sanitized data, we have to rely on a notion of distance. More precisely, our approach does not require any specific assumption on the distance used, although it is conceivable that it may work better with some than others. For the rest of this work, we will instantiate by the -norm as it does not differentiate between attributes.
Note however that a high fidelity is a necessary but not a sufficient condition to imply a good reconstruction of the dataset. In fact, as mentioned previously early experiments showed that the sanitizer might find a “median” profile to which it will map all input profiles. Thus, to quantify the ability of the sanitizer to preserve the diversity of the dataset, we introduce the diversity measure, which is defined in the following way:
in which represent the kth attribute of the sanitized version of . While quantifies how different the original and the sanitized datasets are, the diversity measures how diverse the profiles are in each dataset. We will also provide a qualitative discussion of the amount of damage for a given fidelity and fairness to provide a better understanding of the qualitative meaning of the fidelity.
Finally, we evaluate the loss of utility induced by the sanitization by relying on the accuracy of prediction on a classification task. More precisely, the difference in between a classifier trained on the original data and one trained on the sanitized data can be used as a measure of the loss of utility introduced by the sanitization with respect to the classification task.
5. Experimental Evaluation
In this section, we describe the experimental setting used to evaluate GANSan as well as the results obtained.
5.1. Experimental Setting
Dataset description. We have evaluated our approach on two datasets that are classical in the fairness literature, namely the Adult Census Income as well as on German Credit. Both are available on the UCI repository (https://archive.ics.uci.edu/ml/index.php) (accessed on 20 November 2017). Adult Census reports the financial situation of individuals, with 45,222 records after the removal of rows with empty values. Each record is characterized by 15 attributes among which we selected the gender (i.e., male or female) as the sensitive one and the income level (i.e., over or below 50 K$) as the decision. German Credit is composed of 1000 applicants to a credit loan, described by 21 of their banking characteristics. Previous work [49] have found that using the age as the sensitive attribute by binarizing it with a threshold of 25 years to differentiate between old and young yields the maximum discrimination based on . In this dataset, the decision attribute is the quality of the customer with respect to their credit score (i.e., good or bad). Table 2 summarizes the distribution of the different groups with respect to S and Y. We will mostly discuss the results on Adult dataset in this section. However, the results obtained on German credit were quite similar.

Table 2.
Distribution of the different groups with respect to the protected attribute and the decision one for both the Adult Census Income and the German Credit datasets.
Datasets preprocessing. The preprocessing step consists in shaping and formatting the data such that it can be used by the neural network models. The first step consists in the one-hot encoding of categorical and numerical attributes with less than 5 values, followed by a scaling between 0 and 1.
Besides on Adult dataset, we need to apply a logarithm on columns - and - before any step because those attributes exhibit a distribution close to a Dirac delta [50], with the maximal values being, respectively, 9999 and 4356, and a median of 0 for both (respectively and of records have a value of 0). Since most values are equal to 0, the sanitizer will always nullify both attributes and the approach will not converge. Afterward, postprocessing steps consisting of reversing the preprocessing ones are performed in order to remap the generated data onto their original shape.
Models hyper-parameters.Table 3 details the structure of neural networks that have yielded the best results, respectively, on the Adult and German credit datasets. The training rate represents the number of times for which an instance is trained during a single iteration. For instance, for an iteration i, the discriminator is trained with records while the sanitizer is trained with records. The number of iterations is equal to: . Our experiments were run for a total of 40 epochs and the value of was varied using a geometric progression: . We refer the reader to Section 5.4 for a comparison of the execution time of our approach compared to other methods.

Table 3.
Hyper parameters of neural networks for Adult/German dataset.
Training process. We will evaluate GANSan using metrics such as the fidelity , the as well as the demographic parity (cf. Section 4.2). For this, we have conducted a 10-fold cross-validation during which the dataset is divided into ten blocks. During each fold, 8 blocks are used for the training, while another one is retained as the validation set and the last one as the test set.
We computed the and using the internal discriminator of GANSan and three external classifiers independent of the GANSan framework, namely Support Vector Machines (SVM) [51], Multilayer Perceptron (MLP) [52] and Gradient Boosting (GB) [53]. For all these external classifiers and all epochs, we report the space of achievable points with respect to the fidelity/fairness trade-off. Note that most approaches described in the related work (cf. Section 3) do not validate their results with independent external classifiers trained outside of the sanitization procedure. The fact that we rely on three different families of classifiers is not foolproof, in the sense that it might exist other classifiers that we have not tested that can do better, but it provides higher confidence in the strength of the sanitization than simply relying on the internal discriminator.
For each fold and each value of , we train the sanitizer during 40 epochs. At the end of each epoch, we save the state of the sanitizer and generate a sanitized dataset on which we compute the , and . Afterwards, is used to select the sanitized dataset that is closest to the “ideal point” (). More precisely, is defined as follows:
with referring to the minimum value of obtained with the external classifiers. For each value of , selects among the sanitizers saved at the end of each epoch, the one achieving the highest fairness in terms of for the lowest damage. We will use the three families of external classifiers for computing , and . We also used the same chosen sanitized test set to conduct a detailed analysis of its reconstruction’s quality ( and quantitative damage on attributes).
5.2. Evaluation Scenarios
Recall that GANSan takes as input the whole original dataset (including the sensitive and the decision attributes) and outputs a sanitized dataset (without the sensitive attribute) in the same space as the original one, but from which it is impossible to infer the sensitive attribute. In this context, the overall performance of GANSan can be evaluated by analyzing the reachable space of points characterizing the trade-off between the fidelity to the original dataset and the fairness enhancement. More precisely, during our experimental evaluation, we will measure the fidelity between the original and the sanitized data, as well as the , both in relation with the and , computed on this dataset.
However, in practice, our approach can be used in several situations that differ slightly from one another. In the following, we detail four scenarios that we believe are representing most of the possible use cases of GANSan. To ease the understanding, we will use the following notation: the subscript (respectively ) will denote the data in the training set (respectively test set). For instance, , , or represent, respectively, the attributes of the original training set (not including the sensitive and the decision attributes), the decision in the original training set, the attributes of the sanitized training set and the decision attribute in the sanitized training set. Table 4 describes the composition of the training and the testings sets for these four scenarios.

Table 4.
Scenarios envisioned for the evaluation of GANSan . Each set is composed of either the original attributes or their sanitized versions, coupled with either the original or sanitized decision.
Scenario 1: complete data debiasing. This setting corresponds to the typical use of the sanitized dataset, which is the prediction of a decision attribute through a classifier. The decision attribute is also sanitized as we assumed that the original decision holds information about the sensitive attribute. Here, we quantify the accuracy of prediction of as well as the discrimination represented by the demographic parity (Equation (1)) and equalized odds (Equation (2)).
Scenario 2: partial data debiasing.
In this scenario, similarly to the previous one, the training and the test sets are sanitized with the exception that the sanitized decision in both these datasets is replaced with the original one . This scenario is generally the one considered in the majority of papers on fairness enhancement [24,26,34], the accuracy loss in the prediction of the original decision between this classifier and another trained on the original dataset without modifications is a straightforward way to quantify the utility loss due to the sanitization.
Scenario 3: building a fair classifier. This scenario was considered in [23] and is motivated by the fact that the sanitized dataset might introduce some undesired perturbations (e.g., changing the education level from Bachelor to PhD). Thus, a third party might build a fair classifier but still apply it directly on the unperturbed data to avoid the data sanitization process and the associated risks. More precisely in this scenario, a fair classifier is obtained by training it on the sanitized dataset to predict the sanitized decision . Afterwards, this classifier is tested on the original data () by measuring its fairness through the demographic parity (Equation (1), Section 2). We also compute the accuracy of the fair classifier with respect to the original decision of the test set .
Scenario 4: local sanitization. The local sanitization scenario corresponds to the local use of the sanitizer by the individual himself. For instance, the sanitizer could be used as part of a mobile phone application providing individuals with a means to remove some sensitive attributes from their profile before disclosing them to an external entity. In this scenario, we assume the existence of a biased classifier, trained to predict the original decision on the original dataset . The user has no control over this classifier, but he is allowed nonetheless to perform the sanitization locally on their profile before submitting it to the existing classifier similarly to the recruitment scenario discussed in the introduction. This classifier is applied on the sanitized test set and its accuracy is measured with respect to the original decision as well as its fairness quantified by .
The local sanitization let the user chooses whether or not he wants to sanitize their data, which may lead to the situation in which some users decide not to apply the sanitization process on their data. We evaluate this setting in Section 5.3.1, in particular with respect to the amount of protection provided to users.
5.3. Experimental Results
General results on Adult.Figure 2 describes the achievable trade-off between fairness and fidelity obtained on Adult. First, we can observe that fairness improves when increased as expected. Even with (i.e., maximum utility with no focus on the fairness), we cannot reach a perfect fidelity to the original data as we get at most (cf. Figure 2). Increasing the value of from 0 to a low value such as provides a fidelity close to the highest possible (), but leads to a BER that is poor (i.e., not higher than ). Nonetheless, we still have a fairness enhancement, compared to the original data (, ).
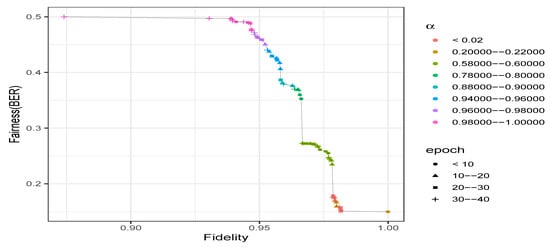
Figure 2.
Fidelity-fairness trade-off on Adult. Each point represents the minimum possible of all the external classifiers. The fairness improves with the increase of , a small value providing a low fairness guarantee while a high one causes greater damage to the sanitized data.
At the other extreme in which , the data is sanitized without any consideration of the fidelity. In this case, the is optimal as expected and the fidelity is lower than the maximum achievable (). However, slightly decreasing the value of , such as setting , allows the sanitizer to significantly remove the unwarranted correlations () with a cost of on fidelity ().
With respect to , the accuracy drops significantly when the value of increases (cf. Figure 3). GANSan renders the accuracy of predicting S from the sanitized set closer to the optimal values, which is the proportion of the privileged group in this case. However, it is nearly impossible to reach that ideal value, even at the extreme sanitization . Similarly to BER, slightly decreasing (from 1) by setting improves the sanitization while leading to a fidelity closer to the achievable maximum.
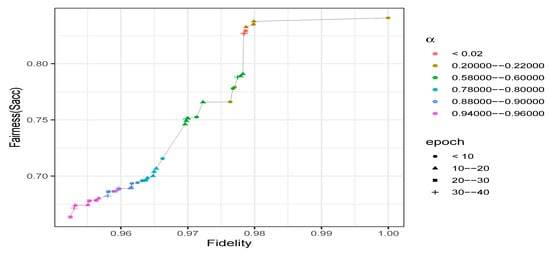
Figure 3.
Fidelity-fairness trade-off on Adult. Each point represents the minimum possible of all the external classifiers. decreases with the increase of , a small value providing a low fairness guarantee while a larger one usually introduced a higher damage. Remark that even with , a small damage is to be expected. Points whose (lower right) represent the on the original (i.e., unperturbed) dataset.
The quantitative analysis with respect to the diversity is shown in Figure 4. More precisely, the smallest drop of diversity obtained is , which is achieved when we set . Among all values of , the biggest drop observed is . The application of GANSan, therefore introduces an irreversible perturbation as observed with the fidelity. This loss of diversity implies that the sanitization reinforces the similarity between sanitized profiles as increases, rendering them almost identical or mapping the input profiles to a small number of stereotypes. When is in the range (i.e., complete sanitization), of categorical attributes have a proportion of modified records between and (cf. Figure 4).
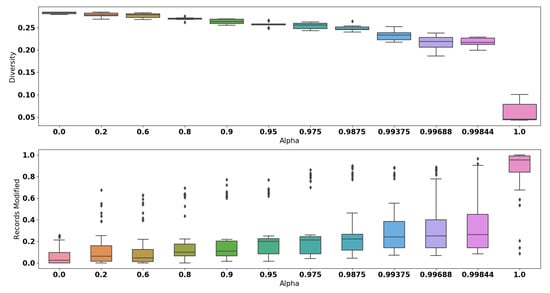
Figure 4.
Boxplots of the quantitative analysis of sanitized datasets selected using . These metrics are computed on the whole sanitized dataset. Modified records correspond to the proportion of records with categorical attributes affected by the sanitization.
For numerical attributes, we compute the relative change (RC) normalized by the mean of the original and sanitized values:
We normalize the RC using the mean (since all values are positives) as it allows us to handle situations in which the original values are equal to 0. With the exception of the extreme sanitization (), at least of records in the dataset have a relative change lower than for most of the numerical attributes. Selecting leads to of records being modified with a relative change less than (cf. Figure A1 in Appendix A).
General results on German.
Similarly to Adult, the protection increases with . More precisely (maximum reconstruction) achieves a fidelity of almost . The maximum protection of corresponds to a fidelity of and a sensitive accuracy value of .
We can observe on Figure 5 that most values are concentrated on the plateau, regardless of the fidelity and the value of . We believe this is due to the high disparity of the dataset. The fairness on German credit is initially quite high, being close to . Nonetheless, we can observe three interesting trade-offs on Figure 6, each located at a different shoulder of the Pareto front. These trade-offs are A (), B () and C (), each achievable with for the first one, and for the rest.
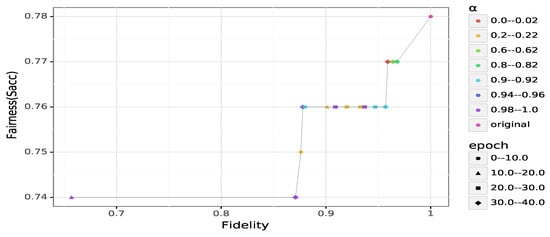
Figure 5.
Fidelity-fairness trade-off on German Credit. Each point represents the minimum possible of all the external classifiers.
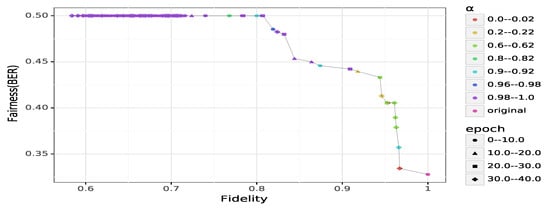
Figure 6.
Fidelity-fairness trade-off on German Credit.
We review the diversity and the sanitization induced damage on categorical attributes in Figure 7. As expected, the diversity decreases with alpha, rendering most profiles identical with . We can also observe some instabilities: higher values produce a shallow range of diversities (i.e., ) while smaller values have a higher range of diversities. Such instability is mainly explained by the size and the imbalance of the dataset, which does not allow the sanitizer to correctly learn the distribution (such phenomenon is common when training GANs with a small dataset). Nonetheless, most of the diversity results prove close to the original one, that is . The same trend is observed on the categorical attribute damage. For most values of , the median damage is below or equal to , meaning that we have to modify only two categorical columns in a record to remove unwanted correlations. For the numerical damage, most columns have a relative change lower than for more than of the dataset, regardless of the value of . Only columns Duration in month and Credit amount have a higher damage. This is due to the fact that these columns have a very large range of possible values compared to the other columns (33 and 921), especially for column Credit amount which also exhibits a nearly uniform distribution. Our reference points A, B and C have a median damage close to for A and for both B and C. The damage on categorical columns is also acceptable.
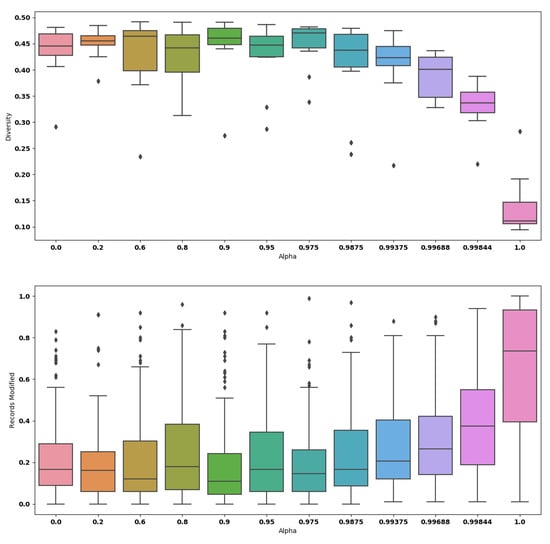
Figure 7.
Diversity and categorical damage on German.
To summarise our results, GANSan is able to maintain an important part of the dataset structure despite sanitization, making it usable for other analysis tasks. This is notably demonstrated by the lower damage and modifications, which preserve as much as possible of the original data values. Thus, results obtained on the sanitized dataset would therefore be close to those obtained on the original data, except on tasks involving the correlations with the sensitive attribute.
Nonetheless, at the individual level, some perturbations might have a more fundamental impact on some profiles than on others. Future work will investigate the relationship between the characteristics of a profile and the damage introduced. For the different scenarios investigated hereafter, we fixed the values of to and , which provides nearly a perfect level of sensitive attribute protection (respectively, and ) while leading to an acceptable damage on Adult ( and ). With respect to German, the results obtained for the different scenarios are analyzed and discussed in Appendix B.2.
Scenario 1: complete data debiasing. In this scenario, we observe that GANSan preserves the accuracy of the dataset. More precisely, it increases the accuracy of the decision prediction on the sanitized dataset for all classifiers (cf. Figure 8, Scenario S1),compared to the original one which is , and , respectively, for GB, MLP, and SVM. This increase can be explained by the fact that GANSan modifies the profiles to make them more coherent with the associated decision, by removing correlations between the sensitive attribute and the decision one. As a consequence, this sets the same decision to similar profiles in both the protected and the privileged groups. In fact, nearly the same distributions of decision attribute are observed before and after the sanitization but some record’s decisions are shifted ( of decision shifted in the sanitized whole set, of decision shifted in the sanitized sensitive group for ). Such decision shift could be explained by the similarity between those profiles to others with the opposite decisions in the original dataset. We also believe that the increase in accuracy is correlated with the drop of diversity. More precisely, if profiles become similar to each other, the decision boundary might be easier to find.
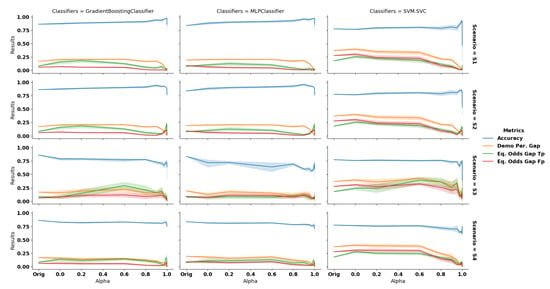
Figure 8.
Accuracy (blue), demographic parity gap (orange) and equalized odds gap (true positive rate in green and false positive rate in red) computed for scenarios 1, 2, 3 and 4 (top to bottom), with the classifiers GB, MLP and SVM (left to right) on Adult dataset. The greater the value of the better the fairness. Using only the sanitized data (S1, S2) increases the accuracy while a combination of the original () and sanitized data () decreases it.
The discrimination is reduced as observed through , and , which all exhibit a negative slope. When correlations with the sensitive attribute are significantly removed (), those metrics also significantly decrease. For , , , , and for GB; whereas as the original demographic parity gap and equalized odds gap are, respectively, , . The performances are improved further for . In this situation, the results obtained are, respectively, , , , and (cf., Table A1 and Table A2 in appendices for more details). In this setup, FairGan [23] achieves a BER of an accuracy of and a demographic parity of , while FairGan+ [40] reached a protection of BER of an accuracy of and a demographic parity of .
Scenario 2: partial data debiasing. Somewhat surprisingly, we observe an increase in accuracy for most values of alpha. The demographic parity also decreases while the equalized odds remains nearly constant (, green line on Figure 8). Table 5 compare the results obtained to other existing work from the state-of-the-art. We include the classifier with the highest accuracy (MLP) and the one with the lowest one (SVM).

Table 5.
Comparison on the basis of accuracy and demographic parity on Adult.
From these results, we can observe that GANSan outperforms the other methods in terms of accuracy, but the lowest demographic parity is achieved with FairGan+ [40] (). This is not surprising as this method is precisely tailored to reduce this metric. Our approach, as well as FairGan [23], do not perform well with the use of the original decisions (metric ). We believe that these poor performances are due to the fact that correlations with original decisions have been removed from the dataset, thus making the new predictions not aligned with the original ones. We also observe that the demographic parity has been improved and our method provides one of the best results on this metric. FairGan+ [36] and MUBAL [36] achieve the best results on the equalized odds metrics as they have been specifically tailored to tackle these metrics. Even though our method is not specifically constrained to mitigate the demographic parity, we can observe that it significantly improve it. Thus, while partial data debiasing is not the best application scenario for our approach as the original decision might be correlated with the sensitive attribute, it still mitigates its effect to some extent.
Scenario 3: building a fair classifier. The sanitizer helps to reduce discrimination based on the sensitive attribute, even when using the original data on a classifier trained on the sanitized one. As presented in the third row of Figure 8, as we force the system to completely remove the unwarranted correlations, the discrimination observed when classifying the original unperturbed data is reduced. On the other hand, the accuracy exhibits here the highest negative slope with respect to all the scenarios investigated. More precisely, we observe a drop of for the best classifier in terms of accuracy on the original set, which can be explained by the difference of correlations between A and Y and between and . As the fair classifiers are trained on the sanitized set ( and ), the decision boundary obtained is not relevant for A and Y.
FairGan [23], which also investigated this scenario, achieves and whereas our GB classifier achieves and for and and for .
Scenario 4: local sanitization. On this setup, we observe that the discrimination is lowered as the coefficient increases. Similarly to other scenarios, the larger the correlations with the sensitive attribute are removed, the higher the drop of discrimination as quantified by the , as well as , and the lower the accuracy on the original decision attribute. For instance, with GB we obtain , at and , for (the original values were and ). We have also evaluated the metric using sanitized decisions instead of the original ones We observed that the results significantly improve, especially for equalized odds. More precisely, the accuracy of GB increases to for , while the equalized odds varies from and (original decision) to and (sanitized decision). As explained in scenario S2, this suggests that correlations with the original decisions are not preserved by the sanitization process (DemoParity remains unchanged as they only involve the predicted decisions, which is independent of the ground truth).
Our observations highlights the possibility that GANSan can be used locally, thus allowing users to contribute to large datasets by sanitizing and sharing their information without relying on any third party, with the guarantee that the sensitive attribute GANSan has been trained for is removed.
The drop of accuracy due to the local sanitization is on GB ( with MLP). Thus, for applications requiring a time-consuming training phase, using GANSan to sanitize profiles without retraining the classifier seems to be a good compromise.
5.3.1. Effect of Mixed Data Composition
In the local sanitization scenario, the user could possibly decide to sanitize their data or publish it unmodified. In this section, we assess the amount of protection and fairness obtained when some users decide not to sanitize their data, resulting in a dataset composed of original and sanitized data. In fact, some users might believe that the sanitization would reduce the advantage due to their group membership and would not sanitize their data in consequence. More precisely, we consider the following settings:
- All. A random (i.e., regardless of their group membership) proportion of users did not use the sanitizer and instead submitted their profiles unmodified.
- Prt. All users of the privileged group sanitized their respective profiles while some others from the protected group published their original profiles.
- Prv. All members of the protected group deemed the application of the sanitization process useful while some users from the privileged group disregarded it. Thus, the dataset is composed of all sanitized profiles from the protected group and a mix of sanitized and original profiles from the privileged one.
For these settings, we varied the proportion p () of the original data composing each group (settings Prt and Prv) or composing the dataset (setting All). For instance, in setting with (), the dataset is composed of all of the protected group sanitized profiles, and of the privileged group data are unmodified.
For each sanitized profile, we have carried out experiments using both the original (Orig y) and the sanitized decisions (San y). The resulting dataset (mixed dataset ) is randomly split into a training and a testing set of size and of the total dataset. Furthermore, each experiment is repeated across the 10-fold cross-validation of the sanitization process. We computed the between a classifier trained on mixed data () and the same classifier trained on the sanitized data () to predict the decision: . We also computed the agreement obtained when training a classifier and predicting decisions using the mixed data and using the original one (). In a nutshell, the quantifies how much a classifier behaves similarly in different contexts, by looking at the proportion of data points that received the same predicted decision across all contexts. A high indicates that the impact on the original data is limited, in which case the sanitization neither hinders the performance of the predictor nor disadvantages a particular group.
As shown in Figure 9, agreements (second column of Figure 9) and (first column of Figure 9) are above for all proportions of mixed data, regardless of the decisions. More generally, we have observed that the use of original decisions (Orig y) results in a lower agreement than with sanitized ones (San y), because of the reduction of correlations between the data and the original decision. If original decisions are not transformed (by the sanitization) in relation to other attributes, they could still incorporate some form of unfairness (as observed with scenarios and ).
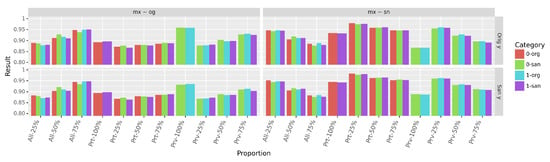
Figure 9.
Agreement results (mean) of Gradient Boosting (GB) trained to predict the sanitized decision attribute on Adult Dataset. z∼t (each column) refers to the agreement obtained when using GB, respectively, on data z and data t, respectively: . org denotes the original version while san corresponds to sanitized profiles in the mixed data. Top: data (mixed, sanitized, or original) with original decisions, bottom: data with sanitized decisions (except the original dataset). Note that the standard deviation is less than .
Sanitizing the privileged group data have the highest impact on both and since it is the largest group of the dataset. This impact is also more pronounced with the original decisions. As a consequence, the highest agreement overall is achieved at - with sanitized decisions ( and San y). The agreement is the lowest at proportion - when using the sanitized decisions and at proportion - when using original ones. These drops are explained by the fact that most original profiles have not been sanitized, as well as the reduction of correlations between the sanitized profiles and original decisions. In fact, the agreement is maximal at those identical proportions.
The high values of demonstrates that a classifier trained to predict decisions with the sanitized data and one trained on mixed data (as obtained with the local sanitization) behave similarly. Thus, we can expect both classifiers to achieve similar performances with respect to fairness metrics.
We report in Figure 10 the accuracy of predicting the sensitive attribute () on each group and each data version (original and sanitized). As expected, the small proportion of the protected group causes the accuracy to increase with the proportion p, especially when the profiles of the protected group are not sanitized - or when then sanitization is applied on randomly selected profiles (-).
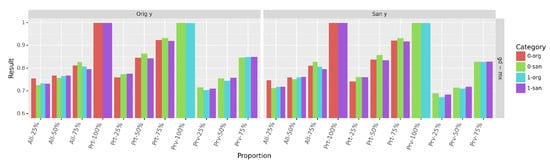
Figure 10.
Accuracy (mean) of Gradient Boosting (GB) trained to predict the sensitive attribute on Adult (mixed dataset). The accuracies on original data are both around for the protected and the privileged group regardless of the decision type. On the sanitized data, it is around for both groups using San y and around using Orig y. Note that the standard deviation is less than .
By looking at the classifier behavior on both the original and the sanitized parts of the mixed data, we can conclude that predicting the sensitive attribute could be viewed as two different operations: distinguishing the original from the sanitized profiles (which is easily performed as observed on proportions - and -) and distinguishing between the sanitized privileged and the sanitized protected profiles by leveraging on the additional information provided by the original profiles. We can also observe on Figure 10 that the impact of this additional information is highly dependent on the underlying distribution. For the same proportion p, keeping the original data from the privileged group (-) has a limited impact on the accuracy compared to the increase due to the original data from the protected one (-).
Figure 11 displays the values obtained. Similary to the accuracy, the decreases with the increase of the proportion of original profiles. The higher this sampling proportion, the easier the prediction of the sensitive attribute becomes as it consists in distinguishing original from sanitized profiles (column Miss Rt D.Vrs of Figure 11). From the miss prediction rate in each group (column Miss Rt Gp), we can see that the classifier tends to always predict the majority class when it cannot successfully distinguish between groups. Finally, we also observe the impact of the original decision, which contributes to the lowering of the BER values.
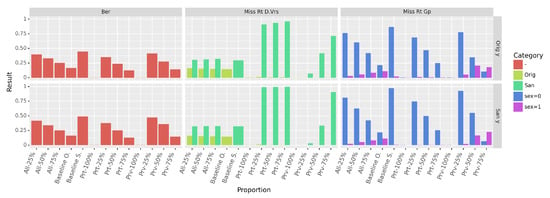
Figure 11.
BER and miss prediction rates of GB (trained to predict the sensitive attribute on Adult). From left to right: BER, miss prediction rate on the original and sanitized part of the mixed data, miss prediction rate per groups. The standard deviation for all computed results is below .
We have also evaluated the positive rate (), the true positives () and false positives () rates in each group (cf. Figure 12). The positive rate is used as the basis of the demographic parity () computation, while the true positives and false positives rates are used to compute the gap in equalized odds . The separate computation of these metrics allows us to observe the behavior of the classifier in each group.
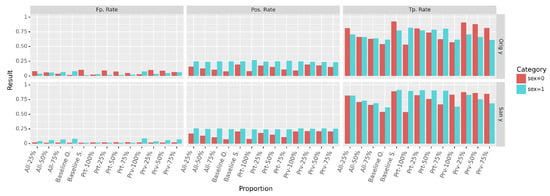
Figure 12.
(Left to right) False Positive rates, predicted Positive Rates and True Positive Rates obtained in each group with GB when predicting the decision attribute.
Figure 12 demonstrates that the best results are achieved when using only the sanitized data. The mixed data produces intermediate results that get worse with the increase of the original data proportion, rendering the mixed data closer to the original one. One notable effect is that the group from which the original data is preserved affects the results in the same direction. More precisely if the original data from the protected group is preserved, all the metrics in the protected group will become closer to their original unfair values. The same trend is observed in the privileged group. These effects are particularly observable on the Positive and the True Positive Rates.
We can relate these observations to our previous hypothesis about the prediction (of S or Y) on the mixed data that can be considered as two separate operations. The invariance to of the predicted positive rate in the privileged group can be explained by the fact that the sanitization process did not modify the amount of positive decision in the privileged group, but rather enhance the protected one (Baseline S.). Another interesting aspect is that the false positive rates in the protected group remained unchanged when using San y, while it varied with the proportion in the privileged data. In fact, as the false positive rate in the protected group did not change with the sanitization (Baseline O. and Baseline S.), we can expect the metric in the protected group not to be affected by the amount of sanitized data. With the original decision, the metric varies significantly in both groups. This can be explained by the fact that the transformation of the data is made without having the correct decision, reflecting, in consequence, the disagreement between the profile and the associated decision.
Finally, in Figure 13, we observe that the decision prediction accuracy is above for any chosen proportion.
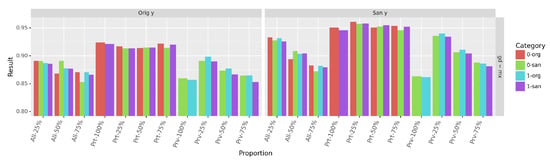
Figure 13.
Accuracy of decision prediction on Adult dataset. With the proportion, the value oscillates between the minimum corresponding to the original data (), and the maximum obtained using the complete sanitized set (). The standard deviation is below .
5.3.2. Decision Prediction Improvement Induced by the Sanitization
In Scenario S1—complete data debiasing, our results showed that the sanitization improves prediction of the decision. In addition to possible explanations (e.g., drop of diversity, the similarity between profiles), it suggests that the sanitization transforms the data such that all of the attributes-values are aligned with both the attribute distribution and the conditional distributions obtained by combining attributes. As an illustrative example, consider a dataset in which the profiles are composed of a binary sensitive attribute gender with values and , an attribute occupation and other attributes X which are identical for all profiles. Moreover, we assume that of profiles in the group have the value - for occupation, while the rest of the profiles have the value -. From this example, we can see that a classifier would predict the occupation attribute without difficulties if the attribute gender is included as the occupation is strongly correlated with the group membership. The sanitization process applied on this data would update the conditional distribution of occupation (since other attributes have identical values) by taking into account the predictability of the sensitive attribute (which should be reduced) and also aligning the value of attribute occupation with the distributions of other attributes. Thus, to prevent the inference of the sensitive attribute, the occupation values would be modified such that , while the alignment of the value would ensure that . The occupation would therefore be modified such that members of both groups and have the same decision. A similar, but more complex process could occur during the sanitization of data with higher and more complex distributions.
From this observation, if the decision attribute is strongly correlated with the sensitive attribute, the sanitization process would not necessarily result in a huge decrease of the accuracy in predicting the decision accuracy, even though the damage on the decision is significant. In other words, the sanitization transforms the data by removing correlations with the sensitive attribute, while correcting (based on the given data distributions) some distributions mismatch (as explained in our illustrative example) based on both the sensitive attribute and the characteristics of the dataset. The sanitization protocol does not take into account the semantic meaning of potential attribute-value combinations, but rather the alignment of conditional distributions.
To go one step further in our investigations, we considered the attribute relationship of the dataset Adult as the decision attribute, which is correlated with the sensitive attribute gender. In Table 6, we present the distribution of the attribute relationship as well as the conditional distributions in the dataset. We observed that the value Husband, which is predominant in the dataset, represents only the Male group. The Female group, is mostly identified with the values Wife and Unmarried, which represents almost of the dataset. In addition, the attributes Own-child and Not-in-family are most present in the Female group. Attributes relationship and gender are therefore correlated. We trained the Gradient Boosting (GB) classifier to predict the relationship attribute, which achieves an accuracy of on the original data. We observed that the precision and recall are especially high for the value husband, but are not significant for other values. The decision accuracy is, respectively, and in the Male and Female groups.

Table 6.
Original distributions of the attribute relationship. Gradient Boosting (GB) Recall () and Precision () when predicting the relationship values. Note that the classifier is trained without the sensitive attribute. Numerical values are given in percentage.
On the sanitized dataset, the accuracies and distributions are also computed and presented in Table 7. The value of attribute relationship are less associated with the gender. On the distribution of the attribute conditioned by the sensitive attribute, we observe a more balanced distribution of values in each group. The most discriminative value Husband is more balanced in both groups. We also observe that the values on the conditional distribution of the gender are more specific to each group. Nonetheless, the distribution is close to the dataset distribution of the same attribute ( and ). From a semantic perspective, at the time the data was collected, having a profile in the Female group associated with the value Husband might not be semantically meaningful, while from the distributional perspective, the sanitizer has aligned the profiles with their most appropriate values. As a consequence the accuracy of predicting the relationship increases from to ( and in, respectively, the Male and Female groups), even though the damage on that attribute is . We used the cosine and Euclidean (which is related to the MSELoss in our sanitization objective) distances to verify whether the profiles whose values have been changed to Husband are closer to other profiles in the Husband-group, as profiles from the latter group had not had their values changed by the sanitization (up to ). However, no particular trends were observed. This observation does not exclude the possibility that a higher-dimensional similarity metric might be used by the sanitization process. The damage of almost implies that using the original values as ground truth will cause a drop in the attribute prediction accuracy.

Table 7.
Sanitized distributions of the attribute relationship. Gradient Boosting (GB) Recall () and Precision () when predicting the relationship values. Note that the classifier is trained without the sensitive attribute. Numerical values are given in percentage.
To further demonstrate the possibility of alignment, we created a balanced synthetic dataset with the gender (values 0 and 1) as the sensitive attribute. This dataset is composed of three numerical columns (, and ), each sampled from a Gaussian distribution of and deviation . The decision () for each row is generated by taking the mean of the three numerical columns (), and is biased toward the group 0 by applying different thresholds: for group , a positive decision is obtained if while for , the positive decision is obtained if . On this synthetic dataset, the decision is correlated with the sensitive attribute, while others are kept identical. Our alignment hypothesis states that the decision attribute will be modified such that the decision threshold is identical for both groups, and such that the decision is obtained as a function of the other columns. By having a threshold independent of groups, the sanitized decision is not correlated with the sensitive attribute and having the decision as a function of other columns ensures that the transformation is not just a randomization process with limited distortions.
Our observations are presented in Figure 14, on which the sanitized dataset has the same protection () as the original one. Unexpectedly, the sanitization process did not modify the decision attribute but instead modified the attribute such that the attribute is a result of a function applied on other attributes, as well as the similarity of their conditional distributions as we expected (Figure 15). We can also observe that the original does not follow the same distribution as its sanitized counterpart. As a consequence, it would be difficult to train a classifier on one version to predict the other.
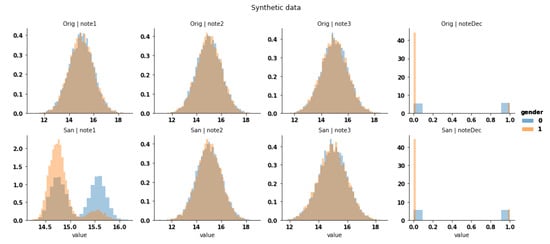
Figure 14.
Distribution of all attributes in the datasets. Top: Original data distribution, Bottom: Sanitized distributions. From left to right, attributes: , 2, 3 and the decision. The original data shows the similarity between distributions, but different decisions. The sanitizer aligned the distribution of such that it match the decision criteria, the sensitive attribute has not been hidden yet.
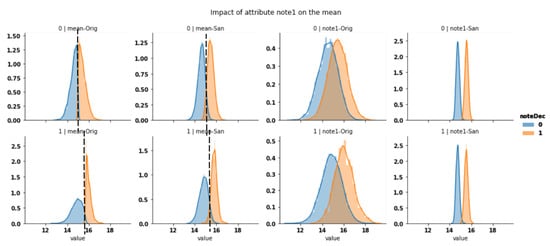
Figure 15.
Decision boundary based on the mean of all attributes on original (left-most) and sanitized (second left) for the group (top) and (bottom). The sanitization has modified the decision boundary of both groups, such that they are almost identical. The modification is only on attribute , which means that the decision attribute is not affected. Orig denotes the original distribution while refers to the sanitized one. The sanitized distribution of thus matches the decision boundary.
On a similar synthetic dataset in which we have augmented the discrimination (the threshold is increased for group and decreased for the other), we obtained similar observations about the alignment. In addition, attribute is rendered nearly identical for both groups (Figure 16). The state of is due to either the prevention of inference or the improper reconstruction which has not been completed yet.
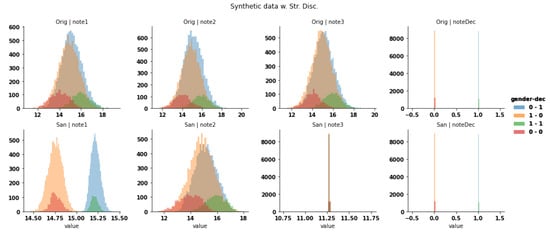
Figure 16.
Distribution of attributes on a synthetic dataset with stronger discrimination. The sanitization (bottom) starts with the alignment of some distributions () to match the decision criteria (), which is left untouched.
When pushed further on this dataset, the sanitization process triples the protection, by modifying all attributes such that the sensitive attribute is protected. The overall similarity of distributions is preserved while the deviation is reduced as shown in Figure 17.
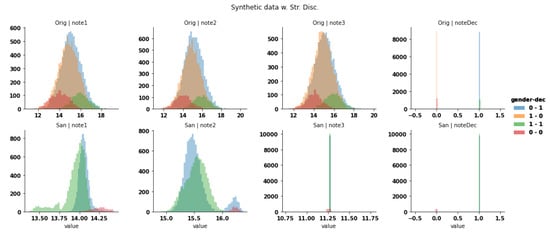
Figure 17.
Distribution of attributes on a synthetic dataset with increase protection of the sensitive attribute (from a BER of to almost ).
We believe that the alignment due to the sanitization explains the discordance between the sanitized decisions and the original ones.
5.4. Execution Time of GANSan
Using the available framework, we compared the execution of different approaches with ours. We used the Disparate Impact Remover (DIRM) [22] and Learning Fair Representation (LFR) [26] (with parameters ) from the framework AIF360 [54] and we implemented FairGan and GANSan using the framework Pytorch [55]. All of the time measurements were carried out on the same computer (Intel Core i7-8750H CPU @ 2.20 GHz with 30 Gi) using the dataset Adult Census. To accelerate the computation, we carried out our experiments on the Compute Canada platform [56], which offers more resources.
DIRM is the fastest to complete, only requiring 9.8 s while LFR needs s to complete. With respect to FairGan, we computed the time required to complete the computation of one epoch at the auto-encoding step ( s), the distribution learning ( s), and the fairness learning ( s) step. Overall, given the parameters used in their original research paper, FairGan requires about 16,960 s. GANSan requires s per epoch, leading to 18,414.8 s for 40 epochs, as used in our experiments. GANSan overhead is mainly due to the vectorized formulation of the loss function and also the larger size of the networks. In fact, the layers of our discriminator are, respectively, matrices of size for the first layer and for the subsequent ones until the last layer with size . The retained shape was the one we empirically found to provide good results while running in a reasonable amount of time. Using the same layers structure as FairGan, our approach runs in seconds per epoch (thus 6339 for all of 40 epochs).
6. Conclusions
In this work, we have introduced GANSan, a novel sanitization method inspired by GANs achieving fairness by removing the correlations between the sensitive attribute and the other attributes of the profile. Our experiments demonstrate that GANSan can prevent the inference of the sensitive attribute while limiting the loss of utility as measured in terms of the accuracy of a classifier learned on the sanitized data as well as by the damage on the numerical and categorical attributes. In addition, one of the strengths of our approach is that it offers the possibility of local sanitization, by only modifying the attributes as little as possible while preserving the space of the original data (thus preserving interpretability). As a consequence, GANSan is agnostic to subsequent use of data as the sanitized data is not tied to a particular task.
While we have relied on three different types of external classifiers for capturing the difficulty to infer the sensitive attribute from the sanitized data, it is still possible that a more powerful classifier exists that could infer the sensitive attribute with higher accuracy. Note that this is an inherent limitation of all the preprocessing techniques and not only our approach. Nonetheless, as future work, we would like to investigate other families of learning algorithms to complete the range of external classifiers. Finally, much work still needs to be done to assess the relationship between the different fairness notions, namely the impossibility of inference and the individual and group fairness.
Author Contributions
Conceptualization, U.A., F.B., S.G., R.C.N. and A.T.; methodology, F.B. and R.C.N.; software, F.B. and R.C.N.; validation, U.A. and R.C.N.; formal analysis, U.A., F.B., S.G., R.C.N. and A.T.; investigation, U.A., F.B. and R.C.N.; resources, S.G.; data curation, R.C.N.; writing—original draft preparation, U.A., R.C.N.; writing—review and editing, U.A., S.G., A.T.; visualization, U.A. and R.C.N.; supervision, S.G. and A.T.; project administration, S.G.; funding acquisition, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
Sébastien Gambs is supported by the Canada Research Chair program, a Discovery Grant (NSERC), the Legalia project (FQRNT) as well as a grant for the Office of the Privacy Commissioner (OPC) of Canada.
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs Publicly available datasets were analyzed in this study. This data can be found here: Adult Census (https://archive.ics.uci.edu/ml/datasets/adult accessed on 17 April 2020) and German Credit (https://archive.ics.uci.edu/ml/datasets/statlog+(german+credit+data) accessed on 17 April 2020).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Evaluation of Adult
This appendix is composed of supplementary results of the evaluation of the Adult dataset.
Appendix A.1. Numerical Attribute Damage
Figure A1 summarizes the numerical damage on Adult.
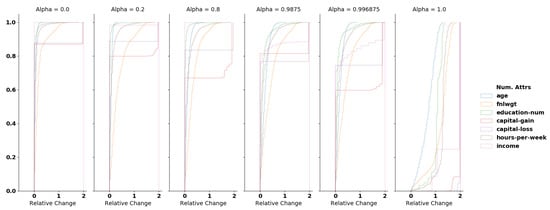
Figure A1.
Cumulative distribution of the relative change (x-axis) for numerical attributes, versus the ratio of records affected in the dataset (y-axis).
Appendix A.2. Evaluation of Group-Based Discrimination
Table A1 summarizes the results obtained in terms of discrimination for different fairness metrics while Table A2 presents the protection of the sensitive attribute for all classifiers. These results are obtained with both and .

Table A1.
Equalized odds and demographic parity on Adult.
Table A1.
Equalized odds and demographic parity on Adult.
| Clfs. | ||||||
|---|---|---|---|---|---|---|
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| Clfs. | ||||||
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| Clfs. | DemoParity | |||||
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||

Table A2.
Evaluation of GANSan ’s sensitive attribute protection on Adult.
Table A2.
Evaluation of GANSan ’s sensitive attribute protection on Adult.
| Clfs. | BER | sAcc | |||
|---|---|---|---|---|---|
| Baseline | Sanitized | Baseline | Sanitized | ||
| GB | |||||
| MLP | |||||
| SVM | |||||
| GB | |||||
| MLP | |||||
| SVM | |||||
Appendix A.3. Utility of GANSan
Table A3 summarizes the utility obtained when applying GANSan as measured in terms of the accuracy on the prediction of the decision attribute, as well as the fidelity and the diversity of the sanitized data on Adult.

Table A3.
Evaluation of GANSan ’s utility on adult Census.
Table A3.
Evaluation of GANSan ’s utility on adult Census.
| Clfs. | yAcc | |||||
|---|---|---|---|---|---|---|
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| GB | ||||||
| SVM | ||||||
| MLP | ||||||
| fid | diversity | |||||
| Baseline | Baseline | |||||
Appendix A.4. Qualitative Damage of GANSan on Adult
Table A4 and Table A5 shows the records that have been maximally and minimally damaged due to the sanitization.

Table A4.
Most damaged profiles for on the first and the fourth folds. Only the perturbed attributes are shown.
Table A4.
Most damaged profiles for on the first and the fourth folds. Only the perturbed attributes are shown.
| Attrs | Original | Fold 1 | Original | Fold 4 |
|---|---|---|---|---|
| age | 42 | 49.58 | 29 | 49.01 |
| workclass | State | Federal | Self-emp-not-inc | Without-pay |
| fnlwgt | 218,948 | 192,102.77 | 341,672 | 357,523.5 |
| education | Doctorate | Bachelors | HS-grad | Doctorate |
| education-num | 16 | 9.393 | 9 | 7.674 |
| marital-status | Divorced | Married-civ-spouse | Married-spouse-absent | Married-civ-spouse |
| occupation | Prof-specialty | Adm-Clerical | Transport-moving | Protective-serv |
| relationship | Unmarried | Husband | Other-relative | Husband |
| race | Black | White | Asian-Pac-Islander | Black |
| hours-per-week | 36 | 47.04 | 50 | 40.37 |
| native-country | Jamaica | Peru | India | Thailand |
| damage value | − | India | Thailand |

Table A5.
Minimally damaged profile, profile with damage at of the max at for the first fold.
Table A5.
Minimally damaged profile, profile with damage at of the max at for the first fold.
| Attrs | Original | Original | ||
|---|---|---|---|---|
| age | 49 | 49.4 | 35 | 29.768 |
| workclass | Federal-gov | Federal-gov | Private | Private |
| fnlwgt | 157569 | 193388 | 241998 | 179164 |
| education | HS-grad | HS-grad | HS-grad | HS-grad |
| education-num | 9 | 9.102 | 9 | 8.2765 |
| marital-status | Married-civ-spouse | Married-civ-spouse | Never-married | Never-married |
| occupation | Adm-Clerical | Adm-Clerical | Sales | Farming-fishing |
| relationship | Husband | Husband | Not-in-Family | Not-in-Family |
| race | White | White | White | White |
| capital-gain | 0 | 0 | 8.474 | 0 |
| capital-loss | 0 | 0 | 0 | 0 |
| hours-per-week | 46 | 44.67 | 40 | 42.434 |
| native-country | United-States | United-States | United-States | United-States |
| income | 0 | 0 | 1 | 0 |
Appendix B. Evaluation of German Credit
In this appendix, we will discuss the results obtained on German credit dataset.
Appendix B.1. Damage and Qualitative Analysis
Looking at the numerical attributes damage (Figure A2), we can observe that most columns have a relative change lower than for more than of the dataset, regardless of the value of . Only the attributes Duration in month and Credit amount have a higher damage. We believe this to be caused by the fact that these attributes have a large range of possible values compare to the other attributes (respectively 33 and 921), especially for attribute Credit amount, which also exhibits a nearly uniform distribution.
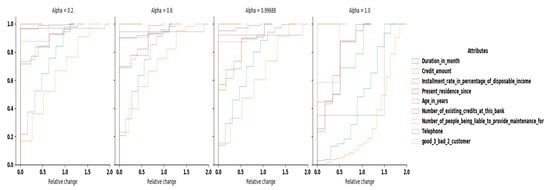
Figure A2.
Relative change.

Table A6.
Evaluation of GANSan ’s protection on test. Values for reference points A, B and C.
Table A6.
Evaluation of GANSan ’s protection on test. Values for reference points A, B and C.
| Classifier | Original | A: | B, C: |
|---|---|---|---|
| GB | |||
| MLP | |||
| SVM |
Appendix B.2. Evaluation Scenario, Other Fairness Metrics and Utilities
Figure A3 presents the results obtained on the different scenario investigated (S1: complete debiasing, S2: partial debiasing, S3: building a fair classifier, S4: local sanitization).
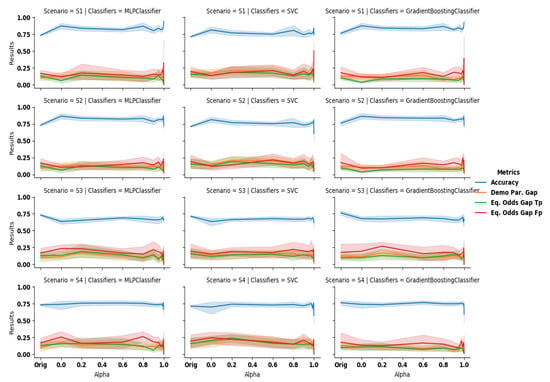
Figure A3.
Accuracy (blue), demographic parity gap (orange) and equalized odds gap (true positive rate in green and false positive rate in red) computed for scenarios 1, 2, 3 and 4 (top to bottom), with the classifiers GB, MLP and SVM (left to right) on german credit dataset.
First, we can observe that for all scenarios, the accuracy is mostly stable with the increase of for all classifiers. Thus, the sanitization does not significantly impact the quality of prediction, which is mostly around . This is higher than the ratio of the positive outcomes in the dataset. For scenarios S3 and S4, this observation contrast with the results obtained on Adult, in which the accuracy decreases with the increase of the protection coefficient.
Taking a closer look at the fairness metrics (cf., Figure A4), we can observe that DemoParity and have a negative slope, which increases with . However, is rather unstable, especially when .
S1: complete data debiasing. In this scenario, we observe that the sanitization makes the profiles in each decision group easily separable, which in turn improves the accuracy. The sanitization also reduces the risk of discrimination, similarly to the Adult dataset.
S2: partial data debiasing. Despite the fact that the sanitized and original decisions do not share the same distribution, the sanitization transformed the dataset in such way that it improves the classification performances of all classifiers. Nonetheless, the discrimination remains constant, which means that the original decision still preserves a certain amount of discrimination. This discrimination is to remove simply working on non-sensitive attributes alone, especially due to the small size of the dataset.
S3: building a fair classifier. Similarly to the results obtained on Adult, building a fair classifier by training it on sanitized data and testing it using unprocessed data have a higher impact on accuracy. In particular, we can observe a slight drop to the accuracy, from to almost for the first value of , before it remains stable across all . The decision boundaries learned by the fair classifier cannot be directly applied with success on another type of data as they do not share the same distribution. With respect to the fairness metrics, we observe two behaviors. More precisely, for the fairness metrics remain nearly constant in contrast to Adult in which they all seem to increase. However, the discrimination can be diminished when we set but not to the extreme end of the spectrum. More precisely, the increase for extreme values is due to the fact that the sanitization has almost completely perturbed the dataset, losing all of its structure. In addition, the dataset being highly imbalanced both on the sensitive attribute distribution as well as the decision one, all classifiers predict the majority class, which corresponds to the privileged group.
S4: local sanitization. For this scenario, the accuracy of the classifier is almost not affected by the sanitization while the discrimination is reduced. MLP provides the most unstable , but for all classifiers, we observe a reduction of and , which become more significant for higher values of (). This result is different from Adult, for which we have observed a negative slope. An in-depth analysis of such behaviour is left as future work.
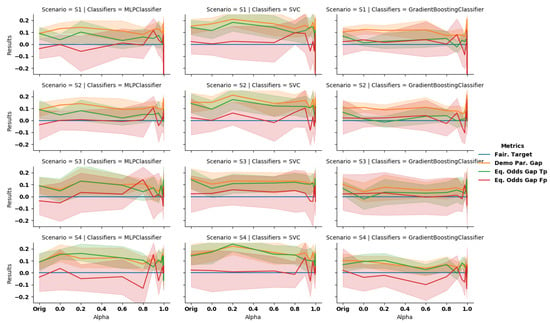
Figure A4.
Fairness metrics evaluated for different scenarios on the German credit dataset.
Table A7 summarizes the results obtained on these 4 scenarios for values of that correspond to points A and B.

Table A7.
GANSan quantitative results on german credit dataset.
Table A7.
GANSan quantitative results on german credit dataset.
| Classifier | ||||||
|---|---|---|---|---|---|---|
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| Classifier | ||||||
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| Classifier | DemoParity | |||||
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| Classifier | yAcc | |||||
| Baseline | S1 | S2 | S3 | S4 | ||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
| GB | ||||||
| MLP | ||||||
| SVM | ||||||
References
- Mahmoud, M.; Algadi, N.; Ali, A. Expert System for Banking Credit Decision. In Proceedings of the 2008 International Conference on Computer Science and Information Technology, Singapore, 29 August–2 September 2008. [Google Scholar]
- Faliagka, E.; Tsakalidis, A.; Tzimas, G. An integrated e-recruitment system for automated personality mining and applicant ranking. Internet Res. 2012, 22, 551–568. [Google Scholar] [CrossRef]
- Electronic Privacy Information Center. EPIC-Algorithms in the Criminal Justice System. 2016. Available online: https://epic.org/foia/doj/criminal-justice-algorithms (accessed on 17 April 2020).
- Angwin, J.; Larson, J.; Mattu, S.; Kirchner, L. Machine Bias. 2016. Available online: https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing (accessed on 17 April 2020).
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef]
- Friedler, S.A.; Scheidegger, C.; Venkatasubramanian, S.; Choudhary, S.; Hamilton, E.P.; Roth, D. A comparative study of fairness-enhancing interventions in machine learning. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 329–338. [Google Scholar]
- Romanelli, M.; Palamidessi, C.; Chatzikokolakis, K. Generating Optimal Privacy-Protection Mechanisms via Machine Learning. arXiv 2019, arXiv:1904.01059. [Google Scholar]
- Kearns, M.; Neel, S.; Roth, A.; Wu, Z.S. Preventing fairness gerrymandering: Auditing and learning for subgroup fairness. arXiv 2017, arXiv:1711.05144. [Google Scholar]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership inference attacks against machine learning models. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 3–18. [Google Scholar]
- Song, L.; Shokri, R.; Mittal, P. Membership inference attacks against adversarially robust deep learning models. In Proceedings of the 2019 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 23 May 2019; pp. 50–56. [Google Scholar]
- Salem, A.; Zhang, Y.; Humbert, M.; Berrang, P.; Fritz, M.; Backes, M. Ml-leaks: Model and data independent membership inference attacks and defenses on machine learning models. arXiv 2018, arXiv:1806.01246. [Google Scholar]
- Zhang, B.; Yu, R.; Sun, H.; Li, Y.; Xu, J.; Wang, H. Privacy for All: Demystify Vulnerability Disparity of Differential Privacy against Membership Inference Attack. arXiv 2020, arXiv:2001.08855. [Google Scholar]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 214–226. [Google Scholar]
- Joseph, M.; Kearns, M.; Morgenstern, J.H.; Roth, A. Fairness in learning: Classic and contextual bandits. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 325–333. [Google Scholar]
- Corbett-Davies, S.; Pierson, E.; Feller, A.; Goel, S.; Huq, A. Algorithmic decision making and the cost of fairness. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 797–806. [Google Scholar]
- Narayanan, A. Translation tutorial: 21 fairness definitions and their politics. In Proceedings of the ACM Conference on Fairness, Accountability, and Transparency (ACM FAccT), New York, NY, USA, 23–24 February 2018. [Google Scholar]
- Verma, S.; Rubin, J. Fairness Definitions Explained. In Proceedings of the 2018 IEEE/ACM International Workshop on Software Fairness (FairWare), Gothenburg, Sweden, 29 May 2018. [Google Scholar]
- Barocas, S.; Selbst, A.D. Big data’s disparate impact. Cal. L. Rev. 2016, 104, 671. [Google Scholar] [CrossRef]
- Berk, R.; Heidari, H.; Jabbari, S.; Kearns, M.; Roth, A. Fairness in criminal justice risk assessments: The state of the art. Sociol. Methods Res. 2018, 0049124118782533. [Google Scholar] [CrossRef]
- Hardt, M.; Price, E.; Srebro, N. Equality of opportunity in supervised learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3315–3323. [Google Scholar]
- Feldman, M.; Friedler, S.A.; Moeller, J.; Scheidegger, C.; Venkatasubramanian, S. Certifying and removing disparate impact. In Proceedings of the 21th ACM SIGKDD International Conference On Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 259–268. [Google Scholar]
- Xu, D.; Yuan, S.; Zhang, L.; Wu, X. FairGan: Fairness-aware Generative Adversarial Networks. arXiv 2018, arXiv:1805.11202. [Google Scholar]
- Edwards, H.; Storkey, A. Censoring representations with an adversary. arXiv 2015, arXiv:1511.05897. [Google Scholar]
- Louizos, C.; Swersky, K.; Li, Y.; Welling, M.; Zemel, R. The variational fair autoencoder. arXiv 2015, arXiv:1511.00830. [Google Scholar]
- Zemel, R.; Wu, Y.; Swersky, K.; Pitassi, T.; Dwork, C. Learning fair representations. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 325–333. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rogriguez, M.G.; Gummadi, K.P. Fairness constraints: Mechanisms for fair classification. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 962–970. [Google Scholar]
- Kamishima, T.; Akaho, S.; Asoh, H.; Sakuma, J. Fairness-aware classifier with prejudice remover regularizer. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Athens, Greece, 19–23 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 35–50. [Google Scholar]
- Kamiran, F.; Calders, T.; Pechenizkiy, M. Discrimination Aware Decision Tree Learning. In Proceedings of the 2010 IEEE International Conference on Data Mining, ICDM ’10, Sydney, Australia, 13–17 December 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 869–874. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.; Schölkopf, B.; Smola, A.J. A kernel method for the two-sample-problem. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 513–520. [Google Scholar]
- Creager, E.; Madras, D.; Jacobsen, J.H.; Weis, M.A.; Swersky, K.; Pitassi, T.; Zemel, R. Flexibly fair representation learning by disentanglement. arXiv 2019, arXiv:1906.02589. [Google Scholar]
- Jha, A.H.; Anand, S.; Singh, M.; Veeravasarapu, V. Disentangling factors of variation with cycle-consistent variational auto-encoders. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 805–820. [Google Scholar]
- Madras, D.; Creager, E.; Pitassi, T.; Zemel, R. Learning adversarially fair and transferable representations. arXiv 2018, arXiv:1802.06309. [Google Scholar]
- Beutel, A.; Chen, J.; Zhao, Z.; Chi, E.H. Data decisions and theoretical implications when adversarially learning fair representations. arXiv 2017, arXiv:1707.00075. [Google Scholar]
- Zhang, B.H.; Lemoine, B.; Mitchell, M. Mitigating Unwanted Biases with Adversarial Learning. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 805–820. [Google Scholar]
- Wadsworth, C.; Vera, F.; Piech, C. Achieving Fairness through Adversarial Learning: An Application to Recidivism Prediction. arXiv 2018, arXiv:1807.00199. [Google Scholar]
- Sattigeri, P.; Hoffman, S.C.; Chenthamarakshan, V.; Varshney, K.R. Fairness GAN. arXiv 2018, arXiv:1805.09910. [Google Scholar]
- McNamara, D.; Ong, C.S.; Williamson, R.C. Costs and benefits of fair representation learning. In Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, Honolulu, HI, USA, 27–28 January 2019; pp. 263–270. [Google Scholar]
- Xu, D.; Yuan, S.; Zhang, L.; Wu, X. FairGan+: Achieving fair data generation and classification through generative adversarial nets. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 1401–1406. [Google Scholar]
- Calmon, F.; Wei, D.; Vinzamuri, B.; Ramamurthy, K.N.; Varshney, K.R. Optimized pre-processing for discrimination prevention. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3992–4001. [Google Scholar]
- Feutry, C.; Piantanida, P.; Bengio, Y.; Duhamel, P. Learning anonymized representations with adversarial neural networks. arXiv 2018, arXiv:1802.09386. [Google Scholar]
- Pittaluga, F.; Koppal, S.; Chakrabarti, A. Learning privacy preserving encodings through adversarial training. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 791–799. [Google Scholar]
- Tripathy, A.; Wang, Y.; Ishwar, P. Privacy-preserving adversarial networks. arXiv 2017, arXiv:1712.07008. [Google Scholar]
- Wang, Y.; Wu, X.; Hu, D. Using Randomized Response for Differential Privacy Preserving Data Collection. In Proceedings of the EDBT/ICDT Workshops, Bordeaux, France, 15–18 March 2016; Volume 1558. [Google Scholar]
- Du, W.; Zhan, Z. Using randomized response techniques for privacy-preserving data mining. In Proceedings of the Ninth ACM SIGKDD International Conference On Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 505–510. [Google Scholar]
- Osia, S.A.; Shamsabadi, A.S.; Sajadmanesh, S.; Taheri, A.; Katevas, K.; Rabiee, H.R.; Lane, N.D.; Haddadi, H. A hybrid deep learning architecture for privacy-preserving mobile analytics. IEEE Internet Things J. 2020, 7, 4505–4518. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Kamiran, F.; Calders, T. Classifying without discriminating. In Proceedings of the 2009 2nd International Conference on Computer, Control and Communication, Karachi, Pakistan, 17–18 February 2009; pp. 1–6. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Number 27; Oxford University Press: Oxford, UK, 1981. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer perceptron and neural networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Bellamy, R.K.; Dey, K.; Hind, M.; Hoffman, S.C.; Houde, S.; Kannan, K.; Lohia, P.; Martino, J.; Mehta, S.; Mojsilovic, A.; et al. AI Fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias. arXiv 2018, arXiv:1810.01943. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems 2019 (NeurIPS 2019), Vancouver, BC, Canada, 4–9 December 2017; pp. 8024–8035. [Google Scholar]
- Baldwin, S. Compute Canada: Advancing computational research. J. Phys. Conf. Ser. 2012, 341, 012001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).