Abstract
This study presents a novel performance metric for feature selection algorithms that is unbiased and can be used for comparative analysis across feature selection problems. The baseline fitness improvement (BFI) measure quantifies the potential value gained by applying feature selection. The BFI measure can be used to compare the performance of feature selection algorithms across datasets by measuring the change in classifier performance as a result of feature selection, with respect to the baseline where all features are included. Empirical results are presented to show that there is performance complementarity for a suite of feature selection algorithms on a variety of real world datasets. The BFI measure is a normalised performance metric that can be used to correlate problem characteristics with feature selection algorithm performance, across multiple datasets. This ability paves the way towards describing the performance space of the per-instance algorithm selection problem for feature selection algorithms.
1. Introduction
There is no shortage of algorithms to solve popular, computationally difficult problems. As new approaches are discovered, the current state-of-the-art algorithms are improved upon. In some problem domains, the performance of new algorithms clearly dominates the performance of previous approaches. More often than not, however, new algorithms do not dominate the performance of earlier algorithms for all instances of a problem [1]. Performance complementarity amongst algorithms is the phenomenon where algorithms perform better on certain problem instances than on others. In a recent survey, Kerschke et al. [2] acknowledged performance complementarity for a variety of NP-hard optimisation and machine learning problems.
The feature selection problem has the goal of finding the smallest subset of all features that are the most relevant for a machine learning task. Feature selection is regarded as either a single objective or multi-objective combinatorial optimisation problem. There are a number of objectives to consider when selecting a feature selection algorithm depending on the application at hand, namely (1) simplicity, (2) stability, (3) number of reduced features, (4) classification accuracy, (5) storage and (6) computational requirements [3]. For this study, we consider the two primary objectives of classification accuracy and reducing the number of features.
This study takes both goals into account by formulating a single objective function for the feature selection problem in the context of classification. Multi-objective feature selection algorithms are not within the scope of this study.
A number of different algorithms have been proposed for solving the feature selection problem [3,4,5]. Chandrashekar and Sahin [3] showed that the performance of different feature selection techniques are often problem dependent and that the methods show vast disparity in their success ratios. They concluded that performance comparison for feature selection algorithms cannot be carried out using multiple datasets, since each underlying algorithm will behave differently for different datasets.
The per-instance algorithm selection problem considers the problem space, algorithm space, feature space and performance space of a class of problems [6]. The underlying performance measure of algorithms is a core component in automated algorithm selection [2] as represented by the performance space in the algorithm selection model. The baseline fitness improvement (BFI) measure is presented, which allows for performance comparison of feature selection algorithms across multiple datasets. The introduction of the BFI measure allows for the future development of landscape-aware algorithm selectors for feature selection.
An empirical performance evaluation is conducted, using six different feature selection algorithms applied to 29 different real world datasets. The performance complementarity phenomenon as it applies to feature selection algorithm performance, using the BFI measure and an algorithm ranking approach, is shown. The presence of performance complementarity for feature selection algorithms is necessary before the benefits of algorithm selection can be realised. The structural properties of the proposed BFI measure allows for performance comparisons across datasets. The ability to compare feature selection algorithm performance across datasets enables the development of algorithm selectors that are informed by characteristics of the underlying dataset and feature selection problem.
The following section gives an overview of the feature selection problem, feature selection algorithm performance evaluation and the algorithm selection problem. Section 3 describes the composition of the fitness function that is used in the study. Section 4 introduces the BFI measure, a new measure of feature selection algorithm performance. The robustness of the fitness function and BFI measure is evaluated in Section 5. The experimental setup is discussed in Section 6. Finally, the results obtained are discussed in Section 7 and the study is concluded in Section 8.
2. Background and Related Work
This section discusses the feature selection problem and provides an overview of the existing approaches to evaluate feature selection algorithm performance.
2.1. Feature Selection
The application of feature selection on a classification dataset ideally results in the smallest set of relevant features with respect to the classification task. Feature selection is applied as a pre-processing technique in order to reduce the dimensionality of a problem by removing redundant and irrelevant features. In addition, feature selection attempts to improve the performance of classification algorithms. By reducing the number of features, the classification model complexity is reduced which results in lower computational cost to construct and use the classification model. The probability for the classification model to overfit is reduced when using less, but relevant, features since the model is simpler and noise in the form of irellevant features is removed. Despite this advantage of simpler models, the dimensionality reduction in, and performance improvement objectives of, feature selection can often be in conflict with each other.
Feature irrelevance is misleading since two mutually exclusive features could be irrelevant, where the union of these features could be information rich with respect to the dependant variable [7]. The utilisation of a subset of relevant features, as opposed to the set of all features, has been shown to increase classifier performance, reduce computational complexity, and lead to a better understanding of the data for machine learning [3].
Feature selection algorithms can be categorised into three distinct categories, namely, filter, wrapper and embedded methods. This study exclusively focuses on filter and wrapper techniques. Filter methods [3] establish feature relevance based on information with respect to the dependent variable, using an information theoretic criterion such as correlation coefficient or mutual information. Wrapper methods [3] use subsets of features, for which a measure of the model performance is obtained per subset of features. Heuristic search is used by wrapper methods to determine the set of most relevant features, using the model accuracy as the objective function.
Choosing the most suitable feature selection algorithm for a given dataset is an unsolved problem. This is due to the lack of an underlying theoretical framework and a limited understanding of the nature of the feature selection problem [7].
2.2. Approaches to Evaluating Feature Selection Algorithm Performance
When new feature selection algorithms are proposed, justification has to be provided in the form of a performance comparison with other common feature selection algorithms. A common approach is to measure the performance of the underlying classifier after the feature selection algorithm has been applied. Classifier accuracy, i.e., counting the number of correctly classified instances vs. the number of incorrectly classified instances, is a popular approach [8,9,10,11]. Other accuracy measures have also been used to compare the performance of feature selection algorithms, such as the F-measure [12] and Cohen’s kappa statistic [13]. A disadvantage to using classifier accuracy alone as a performance measure for feature selection algorithms is that it makes it impossible to compare feature selection algorithms across datasets. This is because the classifier may not be well suited for the variety of classification tasks. What is needed is a way of quantifying the relative improvement gained by the feature selector. For example, a feature selection algorithm that increases classification accuracy on one problem from 50% to 70% should arguably be regarded as more successful than an algorithm that increases accuracy from 90% to 92%.
Attempts to measure the quality of the feature subset obtained by the application of feature selection algorithms have been made. Measures include feature redundancy [8] and the reduction in the number of features [12] amongst others.
There is no clear correct performance model for evaluating the performance of feature selection algorithms for the purpose of automatic algorithm selection [1].
2.3. Algorithm Selection
The algorithm selection problem is concerned with finding the best algorithm to use, assuming the availability of a number of alternative algorithms that may be applied to a specific instance of a problem [14]. An instance of a problem, in the context of the feature selection problem, is a classification dataset that feature selection algorithms are applied to. The per-instance algorithm selection problem [2] was first formulated as an abstract model consisting of a problem space, algorithm space, feature space and performance space [6]. The feature space of the algorithm selection model should not be confused with the feature space of the feature selection problem. The features describing the feature selection problem are the features that expose the various complexities of the problem. In order to avoid confusion, the features describing the feature selection problem are referred to as problem characteristics.
The per-instance algorithm selection problem assumes a set of instances I for a problem P, the set of measurable problem characteristics describing the problem instance , the set A of algorithms and a performance metric [2,14]. Given these essential components of the algorithm selection model, the objective of the per-instance algorithm selection model is to find the selection mapping, , to algorithm space A, where and such that the performance, , of the selected algorithm is maximised [14].
Given a set of features F in the feature selection domain, the feature selection problem is concerned with finding the best set of features such that the performance of the underlying classifier is maximised while minimising the number of features selected, i.e., . As an example, the algorithm selection model for the feature selection problem consists of P as the general feature selection problem, where I is a set of specific feature selection problems as applied to a specific classification dataset. Candidate problem characteristics may include characteristics such as the level of feature interdependence, the number of features and fitness landscape characteristics. A is the set of candidate feature selection algorithms. The interaction between the respective components of the algorithm selection model is illustrated in Figure 1.
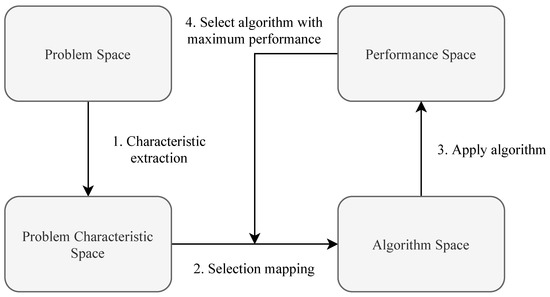
Figure 1.
Illustration of the algorithm selection model component interactions [6].
Performance complementarity is the phenomenon where there is no single algorithm that dominates the performance of all other algorithms on different instances of the same problem [2]. The per-instance algorithm selection problem is of particular importance when there is a high level of performance complementarity between the set of algorithms A on a set of problem instances I. The use of per-instance algorithm selectors shows promising opportunity to achieve better algorithm performance on problem instances for classification problems [15].
3. Fitness Function
A composite fitness function is used to measure the quality of a candidate solution in this study. The fitness function takes into account the two primary objectives of feature selection, namely, the maximisation of classifier performance and minimisation of the number of features used. In this study, a solution s to the feature selection problem is encoded as a binary string of length N (the number of features in the dataset), where 1 indicates inclusion and 0 indicates exclusion of the feature. The fitness function is formulated as
where is the classifier performance function and is a penalty function scaled exponentially on the number of features of the solution. The variables and are scaling constants. The intention of the scaling constants is to determine the priority of each feature selection objective respectively. The values of these scaling constants are determined in Section 5. The sensitivity of the scaling constants is examined in Section 7.
The fitness function in Equation (1) bears a resemblance to the Akaike information criterion (AIC) [16] for model selection. The AIC is formulated as
where k is the number of parameters to the model and is the likelihood function of the model. Lower AIC values are considered better where higher values for the fitness function in Equation (1) are considered better. Equation (1) and the AIC both consist of goodness of fit and penalty terms. The key difference between AIC and the fitness function in Equation (1) lies in the penalty terms. AIC uses a linear scale for the number of features selected, i.e., the value of k. Equation (1) uses an exponential scale. An exponential penalty scale is desirable for feature selection since the feature selection problem solution space has a size of , where N represents the number of features for the problem. The behaviour and intent of AIC is also different to that of the fitness function presented in Equation (1). The AIC establishes the quality of a model with respect to a collection of other candidate models: a many-to-many relationship. The fitness function in Equation (1) establishes the quality of a model with respect to the dimensionality of the problem on a per problem basis: a many-to-one relationship.
The performance of the classifier, , is measured using the F-measure [17]. The F-measure computes a score from the combination of the precision and recall accuracies of the model. The overall classifier performance is reported as the unweighted micro-average [18] of the F-measure.
A classifier has its own bias with regard to features that are considered useful to the classifier [19,20]. As a result of classifier bias, wrapper techniques will select different features for different classifiers on the same dataset [19]. A recent study by Bajer et al. [20] investigated the importance of the classifier for feature selection, concluding that the choice of classifier directly affects the computation cost and algorithm performance. The classic k-NN [21] using Euclidean distance, a simple non-stochastic classifier, is used as the underlying classifier to calculate . For this reason, although the performance results in the experiment of Section 7 cannot be generalised to other classifiers, the main result confirming the presence of performance complementarity should hold for other classifiers as well. The classifier implementation makes use of the Weka [22] library. k-NN is chosen as a classifier since it is a very simple algorithm that does not require excessive training. The best value for k is problem dependant. The focus of this study is on the evaluation of the feature selection algorithms, not of the underlying classifer. Therefore, k is arbitrarily chosen as .
The penalty function used in this study is an exponential function with respect to the number of features selected for a solution. The exponential scale penalty function is chosen since the feature selection search space also expands exponentially as the number of features increases. The range of the penalty function is desired to be the same as that of the classifier performance measure to be able to prioritise the feature selection objectives equally. To match the range of the F-measure (), the penalty function is designed to produce the value 1 when all the features are selected and the value 0 when one feature is selected and to grow exponentially, so that higher numbers of selected features are increasingly penalised. The penalty function is formulated as
where is the number of features selected and N is the total number of features available. The scaling constant () controls how aggressive the penalty function is, without changing the range of the function. Higher values of will provide relatively less aggressive penalties for lower numbers of features selected, and relatively more aggressive penalties for higher numbers of features selected. The value of is arbitrarily chosen as 10 for use in this study since it provides a reasonable trade off for the penalty severity between a low number of features and a high number of features. The penalty behaviour for and different values of is visualised in Figure 2. Figure 2 also shows the effect of applying a scaling constant of and .
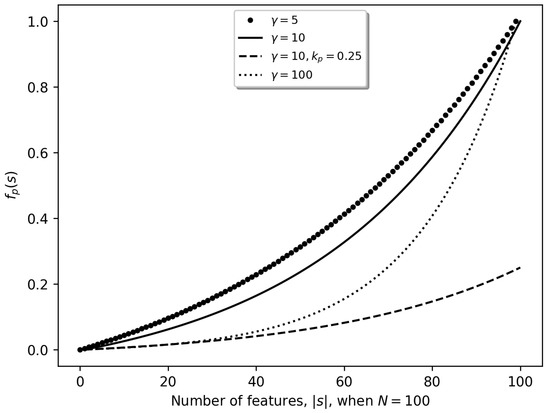
Figure 2.
Penalty function.
4. Baseline Fitness Improvement
The baseline solution of a problem is defined herein as the solution with all features selected, i.e., . The baseline fitness, , is the fitness of the baseline solution. The baseline fitness improvement (BFI) is a measure of the benefit gained by applying feature selection, relative to the baseline fitness of a problem. The BFI of a solution is calculated as
The BFI is interpreted as the potential gain of performing feature selection. The BFI measure also bears a resemblance to the AIC [16] for model selection. The fundamental difference in behaviour of the BFI and AIC lies in the interpretation of the individual metrics. The AIC establishes the quality of a model with respect to other models, whereas the BFI establishes the relative quality of a feature selection solution with respect to the baseline solution for a feature selection problem. A measure of algorithm performance, , alone is not representative of feature selection algorithm performance, but rather of the underlying classifier performance. Table 1 contains fictional algorithm performance, baseline fitness and the respective calculated BFI values to illustrate the differences in interpretation.

Table 1.
Artificial baseline fitness improvement (BFI) and performance.
Table 1 shows that a simple comparison of algorithm A for the two datasets using would lead one to believe that feature selection algorithm A performed better on dataset 1 than on dataset 2. Whilst it may be true that the underlying classifier performed better on dataset 1 than on dataset 2 with regard to classifier accuracy, it is not a true representation of the effectiveness of the feature selection algorithm. The BFI values show that algorithm A achieved a 0.4 improvement over the baseline fitness for both datasets. Therefore, the feature selection algorithm actually managed to improve the classification performance equally for the two datasets. In the absence of knowledge of the global optima of the problem, the baseline fitness acts as a universal reference point for real world feature selection problems. Therefore, the BFI can be used to assess the performance of a feature selection algorithm across datasets.
5. Fitness and BFI Robustness
An artificial dataset was constructed to test the robustness of the fitness function and BFI measure. The artificial dataset consists of 20 data instances, with four features each. The features and classes that are used in the artificial dataset are described in Table 2.

Table 2.
Artificial dataset features.
F1 is a unique ID that does not have any information to correlate with the class. F2 and F3 are completely correlated with the class, but offer completely redundant information. F4 is a sequence of zeros, exhibiting no information related to the class. Complete correlation means that the feature has discriminatory information with respect to the class, which will always result in correct classification if selected. Table 3 reports a truncated example of the artificial dataset.

Table 3.
Robustness artificial dataset excerpt.
The fitness function scaling constants, and , need to be determined in line with the importance of the feature selection objectives. In order to determine the correct scaling constants for the fitness function, a set of test cases was created. These test cases represent the priority we decided to give the individual feature selection objectives for the purposes of this study. Each test case has a set of requirements to be satisfied to pass:
- Test Case A. One irrelevant feature is selected, e.g., . This case should have a fitness lower than all other test cases since no relevant features are selected. Performance is therefore expected to be poor.
- Test Case B. All features are selected. This case should have a fitness greater than test case A. A solution with discriminatory information should perform better than a solution with no discriminatory information.
- Test Case C. One relevant feature is selected, e.g., or . This case should result in the highest fitness over all other test cases. This is the ideal solution, where a single feature can perfectly classify.
- Test Case D. Two relevant features, but one redundant, are selected, e.g., and . This case should have a fitness greater than test case A, but lower than test case C. The features are both correlated; therefore, it is expected to perform better than test case A where there are no relevant features. Redundant features are included; therefore, performance should be worse than the best case scenario in test case C.
- Test Case E. One irrelevant feature and one relevant feature are selected, e.g., and . This case should have a fitness greater than test case B and D but lower than test case C. This case should be better than test case B because it uses fewer features. This case contains a feature that is strongly correlated with the class and should therefore perform better than a solution with no relevant features as in test case A. One additional feature is considered than for test case C; therefore, it should be penalised more.
- Test Case F. A mix of one relevant, one redundant and one irrelevant feature, e.g., and . This case should have a fitness better than test case B and worse than test case E. One feature was removed in this test case in comparison to test case B. Therefore, this test case is expected to perform better than test case B. Since this test case includes more features than test case E, this test case should perform worse than test case E.
Setting the fitness scaling constants to and resulted in the fitness values as reported in Table 4. All of the test cases pass except for test cases A and B. The failure of test case B indicates that the scaling constants determine perfect classification, using all features, to be less fit than completely random classification using one bad feature (test case A).

Table 4.
Robustness results for , .
Table 5 shows the fitness values obtained for the artificial test where and . The penalty scaling constant is relaxed here, to set a balance where good classification will not be so harshly penalised in order to reduce the number of features. All test cases pass with these scaling constants.

Table 5.
Robustness results for , .
There may very well be other values for the scaling constants and that satisfy the robustness test cases that were presented in this section. These scaling constants are a representation of the feature selection objective priorities. Alternative values of and are considered in Section 7 to determine the effect of differing feature selection objective priorities, and how it relates to the performance of the suite of feature selection algorithms. The scaling constants for the fitness function are initially set as and for the analysis in Section 7.
6. Materials and Methods
This section describes the setup of the experimental study. A description of the classification datasets is provided. Thereafter, the applicable feature selection algorithms are discussed.
6.1. Datasets
The University of California, Irvine (UCI), Machine Learning Repository [23] hosts a variety of real world datasets that can be used for machine learning objectives. Twenty nine of these UCI repository classification datasets were used in this study and are summarised in Table 6.

Table 6.
Datasets.
Two limitations were imposed on the choice of datasets. The first limitation is that the number of features in a dataset must be greater than or equal to 10. This is done to emphasise the importance of the dimensionality reduction objective of feature selection. The minimum number of features is chosen as 10, since this allows for a sufficiently complex problem to be able to showcase the nuances of individual feature selection algorithms. The other limitation is to limit the number of data instances in the dataset to 800. This limitation is in place purely from a computational perspective, since the k-NN classification algorithm in use does not scale well with problems that have a large number of data instances.
6.2. Feature Selection Algorithms
This section describes the feature selection algorithms and the parameters that were used per algorithm. The feature selection algorithms that were used as benchmarks are listed in Table 7.

Table 7.
Feature selection algorithms.
AMSO and GAFS are two population-based, global search wrapper techniques. SBFS and SFFS are two simple local search wrapper techniques. PCFS and IGFS are two filter methods that do not consider the model accuracy (except to decide on the best number of features to select). These six algorithms all have very different approaches to solving the feature selection algorithm. RAND, a control method that randomly selects features, is included. A description of the individual algorithms follows.
Random Feature Selection (RAND). The random feature selection algorithm is not intended to work well. This feature selection algorithm is used as a control method. It is intended to be used as a sanity check to ensure that all other feature selection algorithms do indeed perform better than random. A binary string representation of a solution starts out with all features excluded. A random number between 0 and 1 is generated, drawn from a uniform distribution, for each feature in the set of all available features. A feature is included if the random number is greater than 0.5.
Adaptive Multi-Swarm Optimisation for Feature Selection (AMSO). The adapative multi-swarm optimisation for feature selection algorithm (AMSO) [24] was proposed for high-dimensional feature selection problems. AMSO starts by ranking available features in descending order, using any information theoretic criterion. This study also uses symmetrical uncertainty as an information theoretic criterion, as presented by Tran et al. [24]. The ordered list of features is then split by length for each sub-swarm. The motivation behind this is that particle swarm optimsation (PSO) will perform better with smaller search spaces. AMSO uses a competitive swarm optimiser approach to particle velocity updating [25]. The number of features considered in this study is substantially less than in the study where the algorithm was proposed. Therefore, all parameters were set as presented by Tran et al. [24], with the modification of the number of sub-swarms and population size. The population size was set to 50, and the number of sub-swarms to three. These parameters are more appropriate for problems with lower dimensions due to the particle lengths being significantly smaller for lower dimensionality problems. AMSO was chosen to be included due to its novelty and attention to dimensionality reduction. Since AMSO has a stochastic element, fitness is reported as the median over 30 independent runs of the algorithm.
Genetic Algorithm for Feature Selection (GAFS). The genetic algorithm for feature selection uses the classic genetic algorithm as described by Goldberg [26]. The Weka [22] implementation and default parameters were used. The parameters are:
- Population size: 20
- Number of generations: 20
- Crossover probability: 0.6
- Mutation probability: 0.033
Since the genetic algorithm has a stochastic element, fitness is reported as the median over 30 independent runs of the algorithm.
Generalised Sequential Backward Feature Selection (SBFS). The SBFS algorithm is used as implemented by the GreedyStepwise implementation in Weka [22]. The SBFS algorithm starts with an initial full set of features and sequentially removes a feature that results in better fitness. The process continues until there are no features that can be removed that will result in a better fitness than the current solution.
Generalised Sequential Forward Feature Selection (SFFS). The SFFS is used as implemented by the GreedyStepwise implementation in Weka [22]. The SFFS algorithm starts with an initial empty set of features and sequentially adds a feature that results in better fitness. The process continues until there are no features that can be added that will result in a better fitness than the current solution.
Pearson Correlation Coefficient Feature Selection (PCFS). The Pearson correlation coefficient is used to determine feature relevance. The implementation makes use of the Weka [22] library. Features are ranked based on relevance with respect to the class, in descending order.
One of the disadvantages of using information theoretic criteria is that the approach only assigns a measure of relevance to each feature. A method to determine the number of most relevant features is required. A simple linear combination approach is taken to evaluate the model accuracy for each combination. Given a list of ranked features in descending order, each linear combination of features is considered and the fitness of the solution is evaluated.
For example, let the set of all features sorted by decreasing relevance be . The following five solutions will be used to evaluate the model fitness: , , , , and . The feature set with the highest fitness value is selected as the number of features to use.
Information Gain Feature Selection (IGFS). The information-gain [27] information theoretic criterion is used to determine feature relevance. The implementation makes use of the Weka [22] library. Features are ranked based on relevance with respect to the class, in descending order. The same process of linear combination evaluation is followed as in the PCFS algorithm.
7. Results
This section reports the experimental results obtained by computing the BFI values for each dataset considered in Table 6. The set of feature selection algorithms are ranked and investigated to show performance complementarity across a variety of real world datasets.
Table 8 reports the BFI for each algorithm considered in this study, for each classification dataset. Algorithms RAND, AMSO and GAFS are stochastic in nature. The median and interquartile range of these stochastic algorithms are shown in Table 8. The expectation is that all of the feature selection algorithms perform better than random.

Table 8.
BFI results reported as medians for the first three stochastic algorithms (with interquartile ranges in parentheses) and as single values for the remaining deterministic algorithms.
Recall that higher BFI values are indicative of higher performance in terms of the two feature selection objectives. At a glance, it is clear that the control method, RAND, consistently performed worse than all other feature selection algorithms. There is no dataset where RAND performed better than any other feature selection algorithm. The control method is omitted in further analysis of these results.
The BFI values in Table 8 require further statistical analysis to be able to determine any meaningful performance difference for the set of stochastic feature selection algorithms. Table 8 contains two stochastic feature selection algorithms, namely, AMSO and GAFS. A two-tailed Mann–Whitney U test was conducted on the sample of fitness values for only these two stochastic algorithms over 30 independent runs. The null and alternative hypotheses for the Mann–Whitney U test are stated below:
Hypothesis 1 (H1).
the distributions of both BFI samples are equal.
Hypothesis 2 (H1).
the distributions of both BFI samples are not equal.
The null hypothesis was rejected for 20 datasets, i.e., the GAFS and AMSO algorithms did not have the same distribution of BFI values at a significance level of 0.05. The null hypothesis was not rejected for nine datasets, i.e., the GAFS and AMSO algorithms did have the same distribution of BFI values at a significance level of 0.05.
Table 9 reports a ranked list of feature selection algorithms, based on the BFI in Table 8, where 1 is the best and 6 is the worst performing algorithm. Table 9 contains two stochastic algorithms and four deterministic algorithms. The comparison between two algorithms’ performance to determine a rank obeys the following rules:

Table 9.
Algorithm performance rankings.
- Comparison between two stochastic algorithms: A Mann–Whitney U test is conducted to determine if the BFI sample distributions are equal. If the null hypothesis is rejected, the BFI median values are used to determine which algorithm performed better. Should the null hypothesis not be rejected, the algorithms are assigned the same rank.
- Comparison between a stochastic and deterministic algorithm: The BFI sample median for the stochastic algorithm is compared with the single BFI value of the deterministic algorithm. If the BFI value of the deterministic algorithm falls within the interquartile range of the stochastic algorithm BFI sample, then the algorithms are assigned the same rank.
- Comparison between two deterministic algorithms: The single BFI values are simply compared. Algorithms with the same BFI value are assigned the same rank.
Table 9 contains datasets where all algorithms resulted in the same rank (D2, D8 and D11). Since all algorithms performed equally for these cases, it does not make sense to include these datasets for analysis regarding best and worst performance. They are all ranked on the same level and therefore do not provide any information regarding the choice of the feature selection algorithm. Datasets where all algorithms resulted in the same ranks are pruned from further analysis.
Figure 3 summarises the distribution of the ranks for each algorithm in Table 9 and Figure 3 shows that all the algorithms did perform the best on at least one problem. The SFFS algorithm, according to Figure 3, was the only algorithm that performed the worst for at least one dataset. It is clear that there is no one algorithm that is the best for all scenarios. Algorithm GAFS has a denser distribution in the lower ranks in comparison to the other algorithms. GAFS performs effectively more often than other algorithms but is not infallible with regard to the best performance. Figure 3 provides valuable information regarding the distribution of algorithm ranks but does not consider algorithms that share a rank.
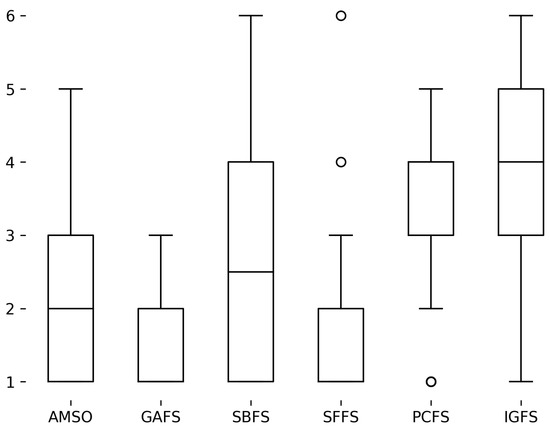
Figure 3.
Box plot of algorithm ranks.
The box plots in Figure 3 do not show the worst performing algorithm as rank 6 for scenarios where two or more distinct algorithms performed equally. As an example, should any two algorithms have been ranked on the same level then the worst rank for the specific dataset would be rank 5. Table 10 shows the number of times each algorithm was ranked as the lowest (best) and highest (worst) with respect to other candidate algorithms.

Table 10.
Best and worst algorithm counts.
These results are based on the penalty scaling constant of , and the classification scaling constant of . These scaling constants were determined in Section 5 as a result of sanity tests with regard to which feature selection objectives this study has considered as important. Table 10 clearly shows that all algorithms did perform the worst and the best for at least one dataset. Table 11 reports the results for using different values for the classification and penalty scaling constants. The same process was followed to produce the algorithm ranks in Table 11 as for Table 10.

Table 11.
Sensitivity of performance complementarity to objective function constants
Table 11 shows the relative performance of the six algorithms for different values of the objective function scaling constants, with reduced from 1 to 0 and with different values of (as denoted in the greyed rows). Considering the various different scaling constants under observation, it is clear that there is no one algorithm that reigns supreme. Only one combination of scaling constants, , , showed that the GAFS algorithm did not perform the worst for at least one dataset. The performance complementarity for feature selection algorithms in this study shows that choosing the best feature selection algorithm remains problem dependant.
8. Conclusions
The goal of this study was to propose a novel performance metric: the baseline fitness improvement (BFI) measure for feature selection algorithms, which is unbiased and can be used for comparative analysis across feature selection problems. The BFI is a normalised measure that allows performance comparison of algorithms across independent datasets, a critical component to the algorithm selection model.
Using BFI, the experimental results showed that there is no algorithm that is consistently the worst or the best. This observation remained valid for a variety of different scaling constants. All algorithms did perform the best for at least one problem.
The experimental analysis shows that there is performance complementarity for feature selection algorithms using BFI as the performance measure. Performance complementarity for feature selection algorithms is supported by other experiments carried out in the feature selection community [28].
The per-instance algorithm selection problem is of particular importance when there is a high level of performance complementarity between the set of algorithms A on a set of problem instances I. The use of per-instance algorithm selectors shows promising opportunity to achieve better algorithm performance on problem instances for classification problems [15]. The performance complementarity of feature selection algorithms encourages further research in automated algorithm selection for feature selection algorithms.
The experimental study in this paper was based on a set of 29 datasets with up to 148 features and 699 instances. In the era of big data, there are datasets that have many more features and instances. Further work could include experimentation on larger datasets to investigate the relative performance of different algorithms on large datasets and to confirm that performance complementarity still holds. Future work also includes using the BFI measure to determine the effect of fitness landscape characteristics on the performance of feature selection algorithms and to develop methods for landscape aware automated feature selection algorithm selection.
Author Contributions
Conceptualization, W.M., K.M.M. and A.P.E.; methodology, W.M., K.M.M. and A.P.E.; software, W.M.; validation, W.M.; formal analysis, W.M.; investigation, W.M.; writing—original draft preparation, W.M.; writing—review and editing, K.M.M. and A.P.E.; visualization, W.M.; supervision, K.M.M. and A.P.E. All authors have read and agreed to the published version of the manuscript.
Funding
The contribution to this research by K.M.M. was funded by the National Research Foundation of South Africa (Grant Number: 120837).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kotthoff, L. Algorithm selection for combinatorial search problems: A survey. In Data Mining and Constraint Programming; Springer: Berlin/Heidelberg, Germany, 2016; pp. 149–190. [Google Scholar]
- Kerschke, P.; Hoos, H.H.; Neumann, F.; Trautmann, H. Automated algorithm selection: Survey and perspectives. Evol. Comput. 2019, 27, 3–45. [Google Scholar] [CrossRef] [PubMed]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Zongker, D.; Jain, A. Algorithms for feature selection: An evaluation. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 2, pp. 18–22. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Rice, J.R. The algorithm selection problem. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 1976; Volume 15, pp. 65–118. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Zhao, Z.; Morstatter, F.; Sharma, S.; Alelyani, S.; Anand, A.; Liu, H. Advancing feature selection research. In ASU Feature Selection Repository; Arizona State University: Tempe, Arizona, 2010; pp. 1–28. [Google Scholar]
- Aha, D.W.; Bankert, R.L. A comparative evaluation of sequential feature selection algorithms. In Learning from Data; Lecture Notes in Statistics; Springer: Berlin/Heidelberg, Germany, 1996; Volume 112, pp. 199–206. [Google Scholar]
- Li, T.; Zhang, C.; Ogihara, M. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics 2004, 20, 2429–2437. [Google Scholar] [CrossRef] [PubMed]
- Bertolazzi, P.; Felici, G.; Festa, P.; Fiscon, G.; Weitschek, E. Integer programming models for feature selection: New extensions and a randomized solution algorithm. Eur. J. Oper. Res. 2016, 250, 389–399. [Google Scholar] [CrossRef]
- Mehri, M.; Chaieb, R.; Kalti, K.; Héroux, P.; Mullot, R.; Essoukri Ben Amara, N. A comparative study of two state-of-the-art feature selection algorithms for texture-based pixel-labeling task of ancient documents. J. Imaging 2018, 4, 97. [Google Scholar] [CrossRef]
- Mostert, W.; Malan, K.M.; Ochoa, G.; Engelbrecht, A.P. Insights into the feature selection problem using local optima networks. In Lecture Notes in Computer Science, Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization, Leipzig, Germany, 24–26 April 2019; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11452, pp. 147–162. [Google Scholar]
- Smith-Miles, K.A. Cross-disciplinary perspectives on meta-learning for algorithm selection. ACM Comput. Surv. 2009, 41, 1–25. [Google Scholar] [CrossRef]
- Lindauer, M.; Hoos, H.H.; Hutter, F.; Schaub, T. Autofolio: An automatically configured algorithm selector. J. Artif. Intell. Res. 2015, 53, 745–778. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; D. Reidel: Dordrecht, The Netherlands, 1986; Volume 81, p. 26853. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Van Asch, V. Macro-and Micro-Averaged Evaluation Measures [Basic Draft]; CLiPS: Antwerp, Belgium, 2013; Volume 49. [Google Scholar]
- Chrysostomou, K.; Chen, S.Y.; Liu, X. Combining multiple classifiers for wrapper feature selection. Int. J. Data Mining Model. Manag. 2008, 1, 91–102. [Google Scholar] [CrossRef]
- Bajer, D.; Dudjak, M.; Zorić, B. Wrapper-based feature selection: How important is the wrapped classifier? In Proceedings of the 2020 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 14–16 October 2020; pp. 97–105. [Google Scholar]
- Aha, D.; Kibler, D. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository; UCI: Irvine, CA, USA, 2013. [Google Scholar]
- Tran, B.; Xue, B.; Zhang, M. Adaptive multi-subswarm optimisation for feature selection on high-dimensional classification. In Proceedings of the Genetic and Evolutionary Computation Conference, ACM, Prague, Czech Republic, 13–19 July 2019; pp. 481–489. [Google Scholar]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2014, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hua, J.; Tembe, W.D.; Dougherty, E.R. Performance of feature-selection methods in the classification of high-dimension data. Pattern Recognit. 2009, 42, 409–424. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).