Abstract
The problem of classification for imbalanced datasets is frequently encountered in practical applications. The data to be classified in this problem are skewed, i.e., the samples of one class (the minority class) are much less than those of other classes (the majority class). When dealing with imbalanced datasets, most classifiers encounter a common limitation, that is, they often obtain better classification performances on the majority classes than those on the minority class. To alleviate the limitation, in this study, a fuzzy rule-based modeling approach using information granules is proposed. Information granules, as some entities derived and abstracted from data, can be used to describe and capture the characteristics (distribution and structure) of data from both majority and minority classes. Since the geometric characteristics of information granules depend on the distance measures used in the granulation process, the main idea of this study is to construct information granules on each class of imbalanced data using Minkowski distance measures and then to establish the classification models by using “If-Then” rules. The experimental results involving synthetic and publicly available datasets reflect that the proposed Minkowski distance-based method can produce information granules with a series of geometric shapes and construct granular models with satisfying classification performance for imbalanced datasets.
1. Introduction
As one of the key components of machine learning, fuzzy rule-based classifiers [1,2,3] explore the features of data by constructing fuzzy sets with strong generalization ability and extracting fuzzy rules with good interpretability. Compared with some traditional classification algorithms, such as decision trees [4,5], logistic regression [6], naive Bayes [7], neural networks [8], etc., fuzzy classifiers tend to consider both classification performance and interpretability of fuzzy rules when designing models. Fuzzy techniques are also combined with some classic classifiers to deal with human cognitive uncertainties in classification problems. Fuzzy decision trees [9] is a famous one of those, which have been proved as an efficient classification method in many areas [10,11,12]. Similarly, there are also some multiple classifier systems, such as fuzzy random forest [13] which are constructed by combining a series of fuzzy decision trees. However, when dealing with the data in practice, such as disease diagnosis [14], protection systems [15], nature disaster predictions [16] and financial problems [17], traditional fuzzy rule-based classifiers could not always extract fuzzy classification rules with good interpretability, which directly leads to the decrease of classification accuracy. This is mainly because the data in the real world often have the characteristic of imbalance [18,19], that is, the samples of a certain class (called the minority class) is far less than those of other classes (collectively called the majority class). Traditional fuzzy classifiers usually assume that the number of samples contained in each class in the dataset is similar, while the classification for imbalanced data focus on just two classes, viz., the minority class and the majority class.
To resolve the issue of classification for imbalanced data, some auxiliary methods have emerged. Data sampling is a common one of them, whose aim is to balance the dataset through increasing the sample size of the minority class (oversampling) or decreasing the sample sizes of majority classes (undersampling) before modeling. A famous oversampling method called “synthetic minority over-sampling technique (SMOTE)” is proposed by [20], where the minority class is oversampled through selecting the proper nearest neighbor samples from the minority class. In [21,22], the SMOTE part is modified before its first stage in which samples weight and k-means are added right before selecting nearest neighbor samples from the minority class of a dataset, respectively. Similarly, there are also a series of studies based on undersampling to help better deal with imbalanced data classification [23]. A number of fuzzy algorithms are combined with these data sampling techniques to handle imbalanced data classification issues. [24] presented a study in which the synergy between three fuzzy rule-based systems and preprocessing techniques (data sampling included) is analyzed in the issue of classification for imbalanced datasets. In [25], some new fuzzy decision tree approaches based on hesitant fuzzy sets are proposed to classify imbalanced datasets. An obvious advantage of the above-mentioned data balancing techniques is that they do not depend on the specific classifier and have good adaptability. However, the data are balanced with compromise, i.e., oversampling would increase the size of training set which may cause overfitting problems and undersampling would remove some useful samples from the training data. This is obviously contrary to the nature of data classification. In addition to the method of data sampling, another commonly used approach focuses on modifying the cost function of classification models so that the penalty weight of the misclassified minority samples in the cost function is greater than the one of the misclassified majority samples. The disadvantage is that there are no universally adequate standards to quantify the penalty weight of the misclassified minority samples.
The above-mentioned methods aim at improving the classification performance by adding some auxiliary methods, such as data sampling methods. However, interpretability is also a significant requirement when constructing classification models. As we all know, fuzzy rules or fuzzy sets constructed by fuzzy algorithms are usually highly interpretable which can reveal the structure of data. For example, the Takagi–Sugeno–Kang fuzzy classifier [26], a famous two-stage fuzzy classification model, obtains the antecedent parameters or initial structure characteristics through clustering algorithms [27,28]. However, when dealing with imbalanced datasets, the samples in the minority class may be treated as outliers or noise points or be completely ignored when applying clustering methods. This obviously affects the classification performance of imbalanced datasets. Thus, a fuzzy method considering both classification performance and interpretability should be constructed. Information granules are a concept worth considering.
Information granules [29] are entities composed of data with similar properties or functional adjacency which are the core concept in the field of granular computing (GrC) [30,31]. To a certain degree, an information granule is the indistinguishable minimum entity with explicit semantics which can depict data. This implies that data with similar numerical values can be arranged together and abstracted into an information granule with specific fuzzy semantics. This is consistent with the abstract process of building fuzzy sets around data. Since information granules can be built in different formalisms such as one-dimensional intervals, fuzzy sets, rough sets, and so on. Thus, in the view of high dimensionality and the special geometric structure of imbalanced datasets, we can construct two different collections of information granules to depict the characteristics of the majority class and the minority class [32], respectively. For instance, we can see clearly in Figure 1 that the hollow square-shape samples can be abstracted into a fuzzy set composing six cube-shaped information granules and the solid dot-shape ones can be abstracted into a fuzzy set containing only one cube-shaped information granule. Intuitively, the data is divided into two parts, i.e., the majority class is represented by a fuzzy set composed of six cubes and the minority one is represented by a fuzzy set composed of only one cube. This intuitive classification process demonstrates the principle of using information granules to classify imbalanced data. Therefore, the objective of this paper is to generate some information granules and then use them to form the fuzzy rules for the classification of imbalanced data. To achieve the objective, we proposed a Minkowski distance-based granular classification method. In our proposed method, the information granules in different Minkowski spaces are constructed based on a spectrum of Minkowski distance, which can well reveal the geometric structure of both the majority class and minority class of data. In other words, our approach aims at improving classification performance by exploring and understanding the geometric characteristics of imbalanced datasets, rather than just using some auxiliary methods. At the first stage of our Minkowski distance-based granular classification method, the imbalanced dataset is divided into two partitions in light of their class labels, viz., the majority class and the minority class. Each sample in each partition is considered a “spot” information granule. At the second stage, a series of bigger union information granules is constructed in each partition through using a Minkowski distance-based merging mechanism. The last stage aims at adjusting the radius of the overlapping information granules and building the granular description for each class of data by uniting the refined information granules contained by each corresponding partition. Subsequently, the granular Minkowski distance-based classification model for imbalanced datasets is constructed and two “If-Then” rules emerge to articulate the granular description for each partition and its minority or majority class label. Compared to the existing fuzzy classification methods for imbalanced datasets, this paper exhibits the following original aspects:
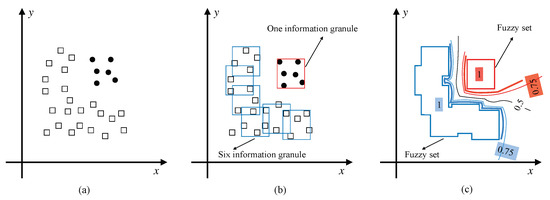
Figure 1.
(a) Two classes of imbalanced data; (b) Two classes of data covered by six information granules and one information granule, respectively; (c) Two fuzzy sets are formed for classification.
- The use of Minkowski distance provides an additional parameter for the proposed fuzzy granular classification algorithm, which helps to understand the geometric characteristics of imbalanced data from more perspectives.
- The constructed union information granules present various geometric shapes and contain different quantities of information granules, which can disclose the structural features of both majority classes and the minority class.
- The proposed Minkowski distance-based modeling method has an intuitive structure and a simple process, and there is no optimization or data preprocessing involved.
The rest of the paper is organized as follows. The representation of information granules, the Minkowski distance calculation and the merging mechanism between two information granules are introduced in Section 2. In Section 3, the Minkowski distance-based granular classification method is described in detail. The experiments on some imbalanced datasets are presented in Section 4. Section 5 concludes the whole paper.
2. Information Granules and Minkowski Distance
This section begins with a brief explanation of the Minkowski distance. Then a method of Minkowski distance representation of information granules is introduced. Finally, how to calculate the distance between two information granules and how to merge two information granules are introduced in detail.
2.1. Minkowski Distance
The distance between two points, i.e., and , in the n-dimensional real vector space is usually calculated by
This distance is the length of straight line between and , which is named Euclidean distance. However, the straight-line distance is not always applicable in my situations. As a result, Minkowski distance is considered. Here we still use two points, viz., and , and let them in space , the Minkowski distance is defined by
where p is a pivotal parameter. Obviously, the Minkowski distance is a set of distances determined by different values of p. Referring to (1), the Euclidean distance () is obtained when p equals 2. When we set p as 1, the Manhattan distance () is obtained, where the sum of the absolute values of the coordinate difference between and is calculated, says,
When p is equal to infinity, we obtain the Chebyshev distance (), viz.,
which means the greatest absolute value among all coordinate differences between and . Figure 2 presents a two-dimensional example. The length of the green oblique line represents the Euclidean distance, the length of the orange polyline is the Manhattan distance, and the length of the blue horizontal line is the Chebyshev distance, respectively.
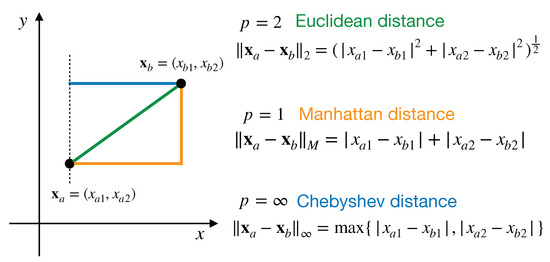
Figure 2.
Three typical Minkowski distances, i.e., Euclidean, Manhattan and Chebyshev distances.
2.2. The Representation of Information Granules
Clustering methods and a method called the principle of justifiable granularity [33] are usually used to transform data into information granules. In light of the unique distribution of imbalanced data, other methods should be considered for constructing and representing information granules. Since information granulation is a process of extracting knowledge from data by organizing close or similar data points. The organization of data points involves the calculation of the distances. Therefore, we use Minkowski distance to represent information granules. Assuming that there is a series of n-dimensional normalized data points, viz., , which are close to a fixed point, i.e., , the information granule generated on can be represented by
where the fixed point is the center of the information granule , is the predefined radius of , and means the Minkowski distance between and . The information granule can be treated as a hollow geometry, which covers the points whose distance to is within . For convenience, we represent the information granule simply with .
When we change the values of parameter p in (5), different geometric shapes of the corresponding information granules are produced. Specifically, when p equals 1, 2 and ∞ the Minkowski distance is determined as Manhattan, Euclidean and Chebyshev distances, respectively. Referring to (1), when the dimension (n) of points in is 2, 3 and higher values, the corresponding information granule appears in the form of a circle, a sphere, and hypersphere, respectively. Similarly, seeing (3), when p is set to 1, the geometric shapes of the constructed information granule would appear in the shape of a diamond, an octahedron and “hyper-diamond”. When p is set to ∞, the corresponding geometric shape of the corresponding information granule becomes a square, a cube and a hypercube. It is worth noting that when the parameter p of Minkowski distance is set as 2, 1 and ∞, the resulting information granules of different dimensions will appear as a series of corresponding regular shapes, see Figure 3. Given the above, the information granules constructed with Minkowski distance can be easily represented by two symbols, i.e., and , which effectively reduces the difficulty of presenting high-dimensional imbalanced data.
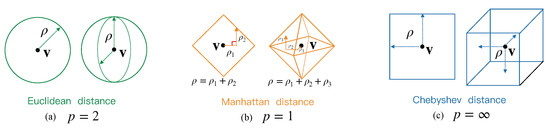
Figure 3.
The geometric shapes of 2-dimensional and 3-dimensional information granules with three Minkowski distances: (a) a circle and a sphere with Euclidean distance (), (b) a diamond and a octahedron with Manhattan distance (), (c) a square and a cube with Chebyshev distance ().
2.3. The Distance Measure and Merging Method between Information Granules
In the field of fuzzy granular classification, it is very necessary to study the location relationship of the constructed information granules in the Minkowski space. It is easy to know that the center and the radius determine the position and size (space occupation) of an information granule. Also, there is an important indicator to measure the location relationship of information granules, that is, the distance between information granules. In the Minkowski space, we anticipate the distance between two information granules, such as and , can be calculated by
where and are the centers, and are the corresponding radii.
In our proposed granular classification method, a point-to-granule and bottom-up model is constructed, which involves a process of merging method between information granules. For two information granules and , they can be merged into a bigger information granule , where
and are two points from the surface of both and owning the greatest Minkowski distance among others, which are calculated by
where is the unit vector in Minkowski space which records the direction from to , viz.,
For convenience, we take the information granules in space as an example and set the value of p as 2, 1 and ∞, respectively. Three couples of information granules are shown in Figure 4. Through the above-mentioned distance calculating and merging methods, for and in Figure 4a, the distance between them is and the information granule obtained by merging them is . For and in Figure 4b, the distance between them is and the information granule obtained by merging them is . For and in Figure 4c, the distance between them is and the information granule obtained by merging them is .
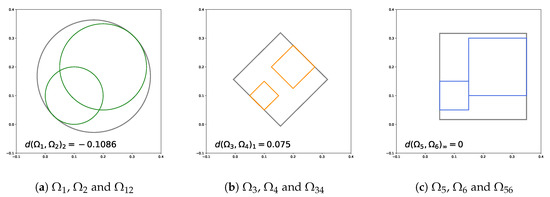
Figure 4.
The merger of three couples of information granules in space: (a) two overlapped granules merged into a bigger one (, →), (b) two isolated granules merged into a bigger one (, →), (c) two tangent granules merged into a bigger one (, →). The information granules obtained by merging each couple are represented in grey lines.
3. The Proposed Fuzzy Granular Classification Methods for Imbalanced Datasets Based on Minkowski Distance
In this section, the proposed Minkowski distance-based fuzzy granular classification method is detailed. To better demonstrate the modeling process, a normalized n-dimensional imbalanced dataset is used. Since is an imbalanced dataset, we partition it into two subsets, where all the sample in the majority class are grouped together into one subset, i.e., and the samples in rest minority class are grouped into another one, i.e., . and are the numbers of samples in and , respectively. The blueprint of the proposed three-stage classification method is shown in Figure 5.
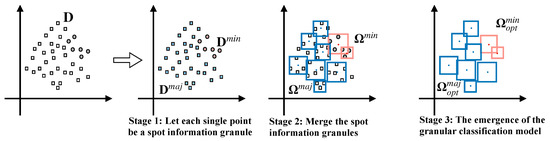
Figure 5.
The blueprint of the proposed fuzzy granular classification method based on Minkowski distance when p is set as ∞.
3.1. The Construction of Information Granules for Each Class
Considering the large difference between the quantities of samples in the majority class and the minority one for imbalanced datasets, it is unrealistic to use the same amount of information granules to capture the geometric characteristics of both majority and minority classes. It is a feasible option to construct two collections containing different quantities of granules to depict the structure of both two classes. Thus, the task of this section is to elaborate the process of constructing the corresponding collection of information granules on and .
Take the majority class as an example. Through the merging mechanism aforementioned in Section 2, a collection of information granules can be constructed by the following steps. At the beginning, each point in is regarded as a “spot” information granule whose radius equals zero and center is the point itself. Thus, we obtain the initial collection of , says, , where p is the Minkowski parameter. Next, the merging mechanism is conducted among these “spot” information granules in . Specially, the distances between any two information granules in collection are first calculated with (6) and the nearest pair of information granules and , are obtained. Then, we suppose that and are merged into a bigger information granule . Its radius, i.e., can be calculated by (8). Here, a key parameter is imported, that is, the radius threshold to adjust the size of the generated information granules. If this new radius is greater than the predefined , i.e., , the merging mechanism will not be executed and the two information granules and are maintained in collection . Otherwise, and are merged into with (7) and (8). Usually, when designing a granular model, a right value of is usually selected which makes . In this situation, the contents of the collection is updated by removing and and adding . So far, two “spot” information granules are merged into one new bigger one. After this, the above merging process can be repeated until the radius of the information granule obtained by merging any two information granules in is less than , which is represented in Algorithm 1.
| Algorithm 1: The Minkowski distance-based merging process for majority class subset . |
 |
Once the merging process is accomplished, a collection containing merged information granules is obtained, viz. . Through uniting all the elements in the collection , we obtain a “union information granule”, says, . For the minority subset , the corresponding union can also be obtained in the same way, says, . Since there is a big difference between the quantities of samples in and , the value of the radius threshold should be the same value when producing both and . In this way, by selecting appropriate values of radius threshold and Minkowski parameter p, the differences on the geometric structure and sample quantities can be capture by the two union information granules, and .
3.2. The Emergence and Evaluation of the Minkowski Distance-Based Fuzzy Granular Classification Model
Through the processing at the above two stages, the two union information granules, i.e., and , are produced to describe the key features of the majority class and minority class . Note that both and can depict the distribution and location of samples belonging to their corresponding classes, such as may occupy much more Minkowski space than , which indicates that the two unions are non-overlapping with each other. Therefore, before establishing the Minkowski distance-based classification model, the overlap between the two union information granules and should be eliminated.
If there is an overlap between and , there must be their element information granules are overlapping with each other. For instance, for from and from , if the Minkowski distance between their centers is lee than the sum of their radii, viz., , they are overlapped. In order to eliminate the overlap, we let and tangent to each other through scaling their radii into the half of the Minkowski distance between their centers,
In this way, we can eliminate all overlaps between two union information granules and and obtain two optimized ones, i.e., and . Thus they can be tagged with the corresponding majority class and minority class with “If-Then” rules. A Minkowski distance-based granular classification model containing two fuzzy rules are emerged, i.e.,
For a given test sample , we can calculate its activation levels versus the rule of majority class and the one of minority class in (13). Since the activation levels are usually determined by distances, those can be obtained by judging the position relation between the sample and union information granules, which can be considered by discussing the following three situations:
- (1)
- : In this situation, the sample is positioned within the boundary of the union information granule of majority class. We intuitively decide that the distance between the and is zero, viz.,
- (2)
- : In this situation, the sample is positioned within the boundary of union information granule of minority class. We intuitively decide that the distance between the and is zero, viz.,
- (3)
- and : In this situation, the sample locates in neither two union information granules. The Minkowski distance between the sample and a union information granule is determined with the minimum distance between and all information granules in and , i.e.,
Now the activation level of versus the majority class and can be obtained by calculating
respectively. After obtaining the activation levels of versus the two rules in (13), its class label can be determined by choosing the higher activation level, i.e., . A particular case, that is , means that is a boundary point which can be classified into both two classes.
Table 1 shows a confusion matrix of a two-class classification issue. In traditional classification algorithms, classification accuracy is often used as an evaluation index to quantify the performance of a classification model. According to Table 1, the classification accuracy can be calculated by

Table 1.
Confusion matrix for a two-class problem.
However, when facing imbalanced data sets, the samples in the minority class have little effect on the classification accuracy. Even if the classification model regards all samples as majority classes, the accuracy is still high. This means that it is difficult to well reflect the classification performance of the classifier on imbalanced data sets when using classification accuracy as the evaluation index alone. Thus, in this work, we consider the accuracy of each class and use the following geometric mean as the evaluation index.
4. Experiment Studies and Discussion
In this section, a series of experiments based on some synthetic and publicly available datasets are conducted. There are three purposes in this section: (1) verifying the feasibility of the proposed Minkowski distance-based method for imbalanced data classification, (2) exploring the impact of two key parameters, viz., the Minkowski parameter p and the radius threshold , on the results, (3) completing the comparison with some other methods for imbalanced data classification.
In order to obtain more rigorous experimental results, we first normalize the datasets used in the experiment before the experiment, viz., each attribute is normalized into a unit interval. As for the two parameters, the Minkowski parameter p is set as some certain values due to different datasets, i.e., , and the value of the radius threshold ranges from 0.02 to 0.12 with step 0.02. A fivefold cross-validation approach is considered for higher confidence results, where four of five partitions (80%) for training and the left one (20%) for testing. Reasonably, the five partitions for testing form the whole set. Thus the average result of the five partitions for each dataset is used.
4.1. Synthetic Datasets
Two synthetic datasets showing imbalanced characteristics and unique geometrical structures are used, see Figure 6. They are generated in the following way.
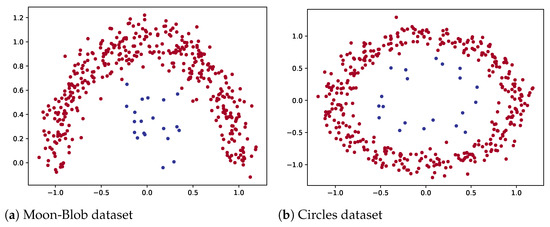
Figure 6.
The visualization of synthetic datasets involved in the experiments: (a) Moon-Blob dataset, (b) Circles dataset.
- (1)
- Moon-Blob dataset. This dataset contains 420 samples and two classes. One class, as the majority class, shows a shape of a moon and contains 400 samples. It is governed as follows:where ranges in and is a noise variable in a normal distribution . The samples of this Moon class are marked in red in Figure 6a. Another class, the minority class, shows a shape of a blob and contains 20 samples. The samples are randomly generated with regard to the normal distribution with the mean vector and the covariance matrix , which are marked in blue in Figure 6b.
- (2)
- Circles dataset. It is a two-dimensional dataset containing 420 samples with two classes. The majority class contains 400 samples, and governed as follows:The minority class contains 20 samples, and governed as follows:rangs in [0, ], and are scale factors and is s noise following a normal distribution . In Figure 6b, the majority class is represented in red points and the minority class is in blue.
The above two imbalanced datasets are generated to validate the feasibility of the Minkowski distance-based method. The experimental results on the two synthetic imbalanced datasets are presented in Table 2 and Table 3, where stands for the radius threshold, p stands for the parameter for calculating Minkowski distances, and the symbol contains the average value and the standard deviation of the geometric mean, referring to (17), delivered by the models on the testing sets. In individual tables, the results with the highest value of average value are highlighted in bold-face.

Table 2.
Experimental results () obtained by the corresponding classification models with different values of p and established on Moon-Blob dataset.

Table 3.
Experimental results () obtained by the corresponding classification models with different values of p and established on Circles dataset.
For Moon-Blob dataset, when the value of Minkowski parameter p equals 1 and the radius threshold is set as 0.10, the value of reaches its maximum, say, 94.54%. Refer to Figure 7a, we can see clearly that the majority class are exactly covered by the red diamond-shape information granules. The union information granule represents a moon shape just matching the original distribution of the samples in the majority class. In contrast, much less blue information granules are constructed for capturing the shape of the minority class. The corresponding classification decision boundary with and is presented in Figure 7b. The darker the color of an area in Figure 7b, the greater probability the samples in this area belong to the corresponding class. However, when and , the generated round-shape information granules do not cover the samples in majority class and minority class better than those with and , see Figure 7c. For Circles dataset, when the value of Minkowski parameter p is set as ∞ and the one of the radius threshold is set as 0.04, the value of reaches the maximum, say, 95.92%. It can be seen clearly that union information granules composed of red and blue cubes cover the samples of both majority and minority classes perfectly.

Figure 7.
(a) Diamond information granules on Moon-Blob dataset ( and ); (b) Decision boundaries on Moon-Blob dataset ( and ); (c) Circle information granules on Moon-Blob dataset ( and ); (d) Decision boundaries on Moon-Blob dataset ( and ); (e) Circle information granules on Circles dataset ( and ); (f) Decision boundaries on Circles dataset ( and );
Apparently, the configuration of Minkowski parameter p and the radius threshold dramatically affects the classification performance of the Minkowski distance-based granular models constructed by our proposed method. The main reason behind this is that p directly determines the geometric shape of the constructed information granules and determines the sizes. In detail, different imbalanced datasets have different sample distributions, which leads to the diversification of the geometric structure of datasets. The Minkowski parameter p used in our method enriches the geometric shapes of the constructed information granules. This enables the constructed granular classification models to explore the geometric structure of data from multiple perspectives and as accurately as possible, which helps to improve the classification performance. The radius threshold is the key parameter of this method to deal with imbalanced data. Since the minority class occupy tiny spaces, such as three blue diamonds in Figure 7a, transform the spaces occupied by the majority class into a union of some tiny space (similar to the ones occupied by the minority class). The proposed Minkowski distance-based granular classification method broadens the perspective of classification modeling, and also deftly solves the problem of too few samples in minority class in imbalanced data classification.
4.2. Publicly Available Datasets and Comparison with Other Methods
Twelve publicly available imbalanced datasets are considered from the KEEL repository (https://sci2s.ugr.es/keel/category.php?cat=clas). It is worth mentioning that the imbalanced datasets are obtained by splitting and reorganizing the “standard” datasets. Six of them are with low imbalanced ratio (the ratio of the number of samples in majority class to the one in minority class is less than 9) and the rest six are with a high imbalanced ratio (greater than 9). They are summarized in Table 4, where the names of datasets, the number of attributes, the number of samples and their imbalance ratio are presented.

Table 4.
Summary of publicly available imbalanced datasets from KEEL repository involved in the experiments.
The configuration of the relevant parameters on the publicly available datasets is as follows: for datasets with low imbalanced ratio, the Minkowski parameter p is set as 1 and the radius threshold is set as 0.08; for datasets with high imbalanced ratio, p is set as 2 and is set as 0.04. Other configurations of the two parameters are also used but no evident increases of the geometric mean (17) appear. In order to validate the performance of the model built by this Minkowski distance-based method, we conducted a comparative study based on the twelve publicly available datasets. In addition to the model established by this method, there are more classification models established by other fuzzy learning methods, which are Ichibushi et al.’s rule learning algorithms [2], Xu et al.’s E-algorithm on imbalanced dataset classification [34], the well-known C4.5 decision tree algorithm [35], and Fernández et al.’s hierarchical fuzzy rule-based classification model which adds a SMOTE preprocessing [36]. The experiment parameter set-up of these classifiers is shown in Table 5. Table 6 shows the corresponding comparison results (the average of with its associated standard deviation) for the test partitions of each classification method. In detail, by columns, we include the Ishibuchi et al.’s method (says, Ishibuchi), Xu et al.’s method (says, the E-Algorithm), the C4.5 algorithm, Fernández et al.’s method (says, Smote-HFRBCS) and our Minkowski distance-based method.

Table 5.
Configuration of the parameters of the selected four classifiers.

Table 6.
The comparison results obtained by implementing different classifiers on all datasets in terms of the average and standard deviation of .
In light of the values of , it is clear that the proposed Minkowski distance-based method can obtain higher values of geometric means than other methods on ten out of twelve datasets. Especially for the six datasets with a high imbalanced ratio, the models established by the proposed method perform much better referring to the mean result. This is because that the granular classification models in this paper is specially designed for the sample quantity, distribution and shapes of imbalanced datasets. The reason includes two aspects. One is that the union information granules constructed separately for the majority class and the minority one are capable of showing the difference between the two classes. In other words, the union information granule constructed for the majority class contains much more information granules and occupies more Minkowski space than those for the minority class, which ensures that the geometric characteristics of the two highly different classes can be captured separately. Another reason is that the information granules that make up each union information granule are produced based on Minkowski distance with various values of p, which results in the generated information granules having various geometric shapes. By adjusting the value of parameter p, we can explore the geometric structure of imbalanced data from different perspectives, and then achieve a more accurate capture of data features. In summary, the proposed Minkowski distance-based method shows some unique advantages over the other four classification methods in dealing with imbalanced datasets, which are shown in the following aspects. (i) The condition parts of the models constructed with our method are information granules, which can disclose the geometric characteristics of imbalanced datasets. (ii) The information granules constructed with different values of the Minkowski distance parameter p realize a multi-perspective description for both majority classes and minority classes of imbalanced datasets, which helps to improve the classification performance of the constructed models. (iii) The reasoning process of the granular classification models is based on the datasets themselves, which can achieve satisfactory classification performance without data preprocessing sampling or additional optimization methods.
5. Conclusions
In this paper, a Minkowski distance-based granular classification method for imbalanced datasets is presented. When compared with other classification methods in the field of imbalanced data classification, the proposed method aims at constructing information granules with multiple geometric shapes in Minkowski space. These information granules are capable of extracting key structure features from imbalanced data and establishing granular classification models with high performance and simple fuzzy rules. Some conclusions are listed as follows. (i) The granular models constructed by our Minkowski distance-based method perform better than three fuzzy rule-based classification methods and C4.5 decision tree method on imbalanced datasets, especially on those with high imbalanced ratio. (ii) Using different values of the Minkowski parameter p can result in union information granules in a series of geometric shapes; (iii) The radius threshold establishes a uniform size standard between the information granules constituting majority class and those constituting minority class, which ensures that the differences between the union information granule constructed on majority class and the one constructed on minority class only exist in the quantities of information granules they contain and the Minkowski space they occupy. (iv) The constructed granular models have clear structures, simple fuzzy rules, and no need for optimization methods and data sampling preprocess.
Author Contributions
Conceptualization, C.F.; methodology, C.F.; software, C.F.; validation, C.F., J.Y.; formal analysis, C.F., J.Y.; investigation, C.F.; resources, C.F., J.Y.; data curation, C.F.; writing–original draft preparation, C.F.; writing–review and editing, C.F.; visualization, C.F.; supervision, J.Y.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Chinese Central Universities under Grant DUT20LAB129.
Data Availability Statement
The data presented in this study are openly available in [https://sci2s.ugr.es/keel/category.php?cat=clas].
Acknowledgments
The author would like to thank the reviewers for their comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Nozaki, K.; Ishibuchi, H.; Tanaka, H. Adaptive fuzzy rule-based classification systems. IEEE Trans. Fuzzy Syst. 1996, 4, 238–250. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Yamamoto, T. Rule weight specification in fuzzy rule-based classification systems. IEEE Trans. Fuzzy Syst. 2005, 13, 428–435. [Google Scholar] [CrossRef]
- Jabari, S.; Zhang, Y. Very high resolution satellite image classification using fuzzy rule-based systems. Algorithms 2013, 6, 762–781. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Aitkenhead, M.J. A co-evolving decision tree classification method. Expert Syst. Appl. 2008, 34, 18–25. [Google Scholar] [CrossRef]
- Press, S.J.; Wilson, S. Choosing between logistic regression and discriminant analysis. J. Am. Stat. Assoc. 1978, 73, 699–705. [Google Scholar] [CrossRef]
- Rish, I. An empirical study of the naive Bayes classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; Volume 3, pp. 41–46. [Google Scholar]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Adamo, J.M. Fuzzy decision trees. Fuzzy Sets Syst. 1980, 4, 207–219. [Google Scholar] [CrossRef]
- Segatori, A.; Marcelloni, F.; Pedrycz, W. On distributed fuzzy decision trees for big data. IEEE Trans. Fuzzy Syst. 2017, 26, 174–192. [Google Scholar] [CrossRef]
- Xue, J.; Wu, C.; Chen, Z.; Van Gelder, P.H.A.J.M.; Yan, X. Modeling human-like decision-making for inbound smart ships based on fuzzy decision trees. Expert Syst. Appl. 2019, 115, 172–188. [Google Scholar] [CrossRef]
- Sardari, S.; Eftekhari, M.; Afsari, F. Hesitant fuzzy decision tree approach for highly imbalanced data classification. Appl. Soft. Comput. 2017, 61, 727–741. [Google Scholar] [CrossRef]
- Bonissone, P.; Cadenas, J.M.; Garrido, M.C.; Díaz-Valladares, R.A. A fuzzy random forest. Int. J. Approx. Reason. 2010, 51, 729–747. [Google Scholar] [CrossRef]
- Campadelli, P.; Casiraghi, E.; Valentini, G. Support vector machines for candidate nodules classification. Neurocomputing 1990, 68, 281–288. [Google Scholar] [CrossRef]
- Denning, D.E. An intrusion-detection model. IEEE Trans. Softw. Eng. 1987, 2, 222–232. [Google Scholar] [CrossRef]
- Asencio-Cortés, G.; Martínez-Álvarez, F.; Morales-Esteban, A.; Reyes, J. A sensitivity study of seismicity indicators in supervised learning to improve earthquake prediction. Knowl. Based Syst. 2016, 101, 15–30. [Google Scholar] [CrossRef]
- Sanz, J.A.; Bernardo, D.; Herrera, F.; Bustince, H.; Hagras, H. A compact evolutionary interval-valued fuzzy rule-based classification system for the modeling and prediction of real-world financial applications with imbalanced data. IEEE Trans. Fuzzy Syst. 2014, 23, 973–990. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Zhu, T.; Lin, Y.; Liu, Y. Synthetic minority oversampling technique for multiclass imbalance problems. Pattern Recognit. 2017, 72, 327–340. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Lin, W.C.; Tsai, C.F.; Hu, Y.H.; Jhang, J.S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409, 17–26. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; del Jesus, M.J.; Herrera, F. A study of the behaviour of linguistic fuzzy rule based classification systems in the framework of imbalanced data-sets. Fuzzy Sets Syst. 2008, 159, 2378–2398. [Google Scholar] [CrossRef]
- Ng, W.W.; Hu, J.; Yeung, D.S.; Yin, S.; Roli, F. Diversified sensitivity-based undersampling for imbalance classification problems. IEEE Trans. Cybern. 2014, 45, 2402–2412. [Google Scholar] [CrossRef] [PubMed]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Fu, C.; Lu, W.; Pedrycz, W.; Yang, J. Fuzzy granular classification based on the principle of justifiable granularity. Knowl. Based Syst. 2019, 170, 89–101. [Google Scholar] [CrossRef]
- Fu, C.; Lu, W.; Pedrycz, W.; Yang, J. Rule-based granular classification: A hypersphere information granule-based method. Knowl. Based Syst. 2020, 194, 105500. [Google Scholar] [CrossRef]
- Pedrycz, W. Knowledge-Based Clustering: From Data to Information Granules; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Pedrycz, W. Granular Computing: Analysis and Design of Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bargiela, A.; Pedrycz, W. Toward a theory of granular computing for human-centered information processing. IEEE Trans. Fuzzy Syst. 2008, 16, 320–330. [Google Scholar] [CrossRef]
- Meng, F.; Fu, C.; Shi, Z.; Lu, W. Granular Description of Data: A Comparative Study Regarding to Different Distance Measures. IEEE Access 2020, 8, 130476–130485. [Google Scholar] [CrossRef]
- Pedrycz, W.; Homenda, W. Building the fundamentals of granular computing: A principle of justifiable granularity. Appl. Soft. Comput. 2013, 13, 4209–4218. [Google Scholar] [CrossRef]
- Xu, L.; Chow, M.Y.; Taylor, L.S. Power distribution fault cause identification with imbalanced data using the data mining-based fuzzy classification E-algorithm. IEEE Trans. Power Syst. 2007, 22, 164–171. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan, M.B., Ed.; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1993. [Google Scholar]
- Fernández, A.; del Jesus, M.J.; Herrera, F. Hierarchical fuzzy rule based classification systems with genetic rule selection for imbalanced data-sets. Int. J. Approx. Reason. 2009, 50, 561–577. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).