Network Creation Games with Traceroute-Based Strategies †
Abstract
1. Introduction
1.1. The Standard Model for NCGs
1.2. Other Models for NCGs
1.3. Our New Local-View Models for NCGs
- ()
- Distance vector: in addition to his/her incident edges, each player u knows only the distances in between u and all the agents (this is the minimal knowledge needed by a player in order to compute her current cost).
- ()
- Shortest-Path Tree (SPT) view: each player u knows the edges of some SPT of rooted at u.
- ()
- Layered view: each player u knows the set of edges belonging to at least one SPT of rooted at u.
2. Convergence
2.1. Model
2.2. Models and
3. Complexity of Computing a Best Response
3.1. Model
3.2. Model
3.3. Model
4. Price of Anarchy
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fabrikant, A.; Luthra, A.; Maneva, E.; Papadimitriou, C.H.; Shenker, S. On a network creation game. In Proceedings of the ACM 22nd Symposium on Principles of Distributed Computing (PODC), Boston, MA, USA, 13–16 July 2003; pp. 347–351. [Google Scholar]
- Albers, S.; Eilts, S.; Even-Dar, E.; Mansour, Y.; Roditty, L. On Nash Equilibria for a Network Creation Game. ACM Trans. Econ. Comput. 2014, 2, 2:1–2:27. [Google Scholar] [CrossRef]
- Mihalák, M.; Schlegel, J.C. The price of anarchy in network creation games is (mostly) constant. Theory Comput. Syst. 2013, 53, 53–72. [Google Scholar] [CrossRef]
- Mamageishvili, A.; Mihalák, M.; Müller, D. Tree Nash equilibria in the network creation game. Internet Math. 2015, 11, 472–486. [Google Scholar] [CrossRef]
- Àlvarez, C.; Messegué, A. Network Creation Games: Structure vs Anarchy. arXiv 2017, arXiv:1706.09132. [Google Scholar]
- Àlvarez, C.; Messegué, A. On the Price of Anarchy for High-Price Links. In Proceedings of the Web and Internet Economics—15th International Conference (WINE 2019), New York, NY, USA, 10–12 December 2019; Caragiannis, I., Mirrokni, V.S., Nikolova, E., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2019; Volume 11920, pp. 316–329. [Google Scholar] [CrossRef]
- Demaine, E.D.; Hajiaghayi, M.T.; Mahini, H.; Zadimoghaddam, M. The Price of Anarchy in Network Creation Games. ACM Trans. Algorithms (TALG) 2012, 8, 13. [Google Scholar] [CrossRef]
- Bilò, D.; Lenzner, P. On the Tree Conjecture for the Network Creation Game. Theory Comput. Syst. 2020, 64, 422–443. [Google Scholar] [CrossRef]
- Alon, N.; Demaine, E.D.; Hajiaghayi, M.T.; Leighton, T. Basic network creation games. SIAM J. Discret. Math. 2013, 27, 656–668. [Google Scholar] [CrossRef][Green Version]
- Lenzner, P. Greedy selfish network creation. In International Workshop on Internet and Network Economics (WINE); Springer: Berlin/Heidelberg, Germany, 2012; pp. 142–155. [Google Scholar]
- Mihalák, M.; Schlegel, J.C. Asymmetric swap-equilibrium: A unifying equilibrium concept for network creation games. In International Symposium on Mathematical Foundations of Computer Science (MFCS); Springer: Berlin/Heidelberg, Germany, 2012; pp. 693–704. [Google Scholar]
- Laoutaris, N.; Poplawski, L.J.; Rajaraman, R.; Sundaram, R.; Teng, S. Bounded Budget Connection (BBC) games or how to make friends and influence people, on a budget. J. Comput. Syst. Sci. 2014, 80, 1266–1284. [Google Scholar] [CrossRef]
- Ehsani, S.; Fadaee, S.S.; Fazli, M.; Mehrabian, A.; Sadeghabad, S.S.; Safari, M.; Saghafian, M. A bounded budget network creation game. ACM Trans. Algorithms (TALG) 2015, 11, 34. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Proietti, G. Bounded-distance network creation games. ACM Trans. Econ. Comput. (TEAC) 2015, 3, 16. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. The max-distance network creation game on general host graphs. Theor. Comput. Sci. 2015, 573, 43–53. [Google Scholar] [CrossRef]
- Bilò, D.; Friedrich, T.; Lenzner, P.; Melnichenko, A. Geometric Network Creation Games. In Proceedings of the 31st ACM on Symposium on Parallelism in Algorithms and Architectures (SPAA 2019), Phoenix, AZ, USA, 22–24 June 2019; Scheideler, C., Berenbrink, P., Eds.; ACM: New York, NY, USA, 2019; pp. 323–332. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. Locality-based network creation games. In Proceedings of the 26th ACM on Symposium on Parallelism in Algorithms and Architectures (SPAA 2014), Prague, Czech Republic, 23–25 June 2014; Blelloch, G.E., Sanders, P., Eds.; ACM: New York, NY, USA, 2014; pp. 277–286. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. Locality-Based Network Creation Games. ACM Trans. Parallel Comput. 2016, 3, 6:1–6:26. [Google Scholar] [CrossRef]
- Bampas, E.; Bilò, D.; Drovandi, G.; Gualà, L.; Klasing, R.; Proietti, G. Network verification via routing table queries. J. Comput. Syst. Sci. 2015, 81, 234–248. [Google Scholar] [CrossRef]
- Beerliova, Z.; Eberhard, F.; Erlebach, T.; Hall, A.; Hoffmann, M.; Mihalák, M.; Ram, L.S. Network Discovery and Verification. IEEE J. Sel. Areas Commun. 2006, 24, 2168–2181. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. Network creation games with traceroute-based strategies. In International Colloquium on Structural Information and Communication Complexity (SIROCCO); Springer: Berlin/Heidelberg, Germany, 2014; pp. 210–223. [Google Scholar]
- Kawald, B.; Lenzner, P. On dynamics in selfish network creation. In Proceedings of the 25th ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), Montreal, QC, Canada, 23–25 July 2013; pp. 83–92. [Google Scholar]
- Chlebík, M.; Chlebíkova, J. Approximation hardness of dominating set problems. In European Symposium on Algorithms; Springer: Berlin/Heidelberg, Germany, 2004; pp. 192–203. [Google Scholar]
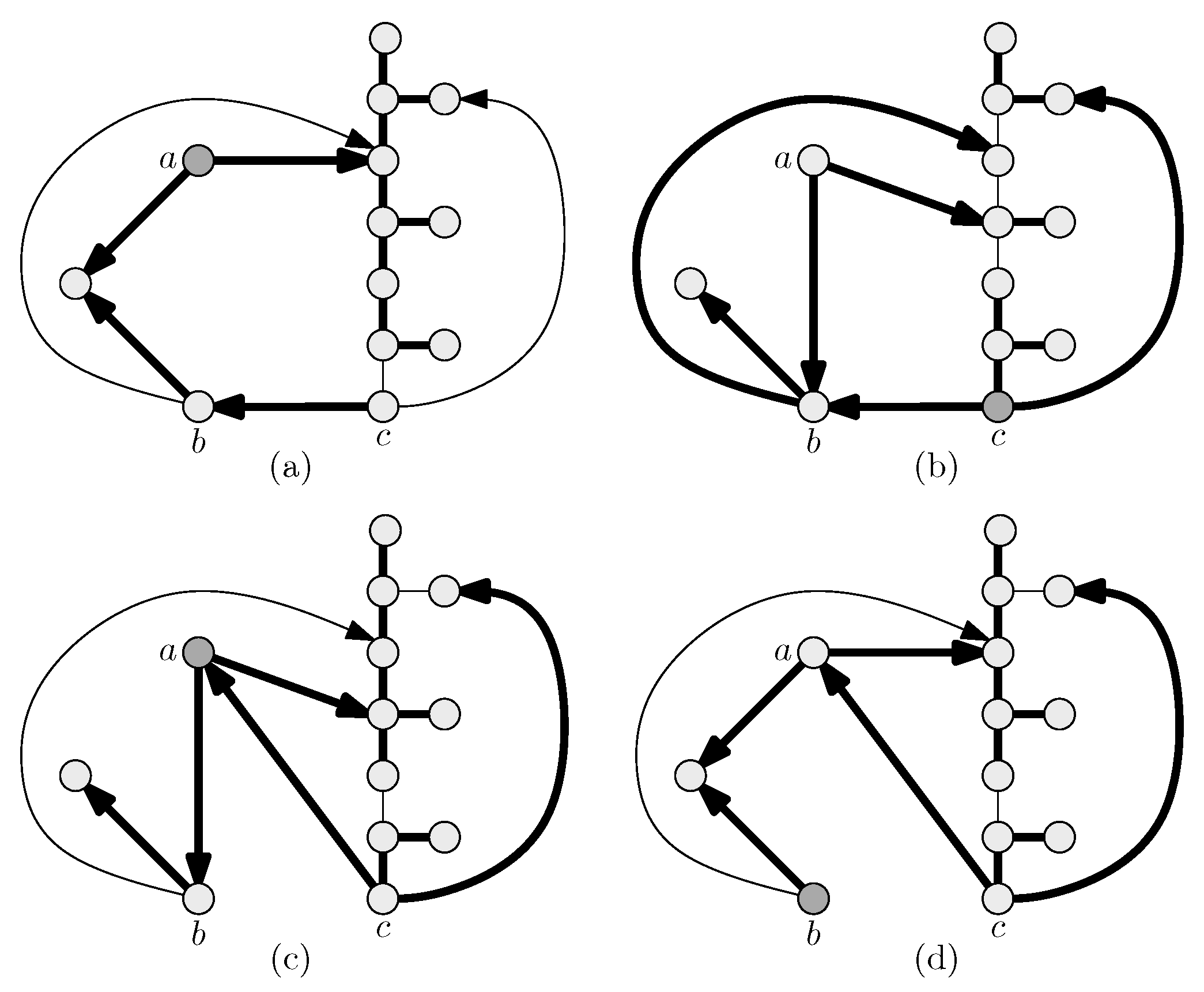
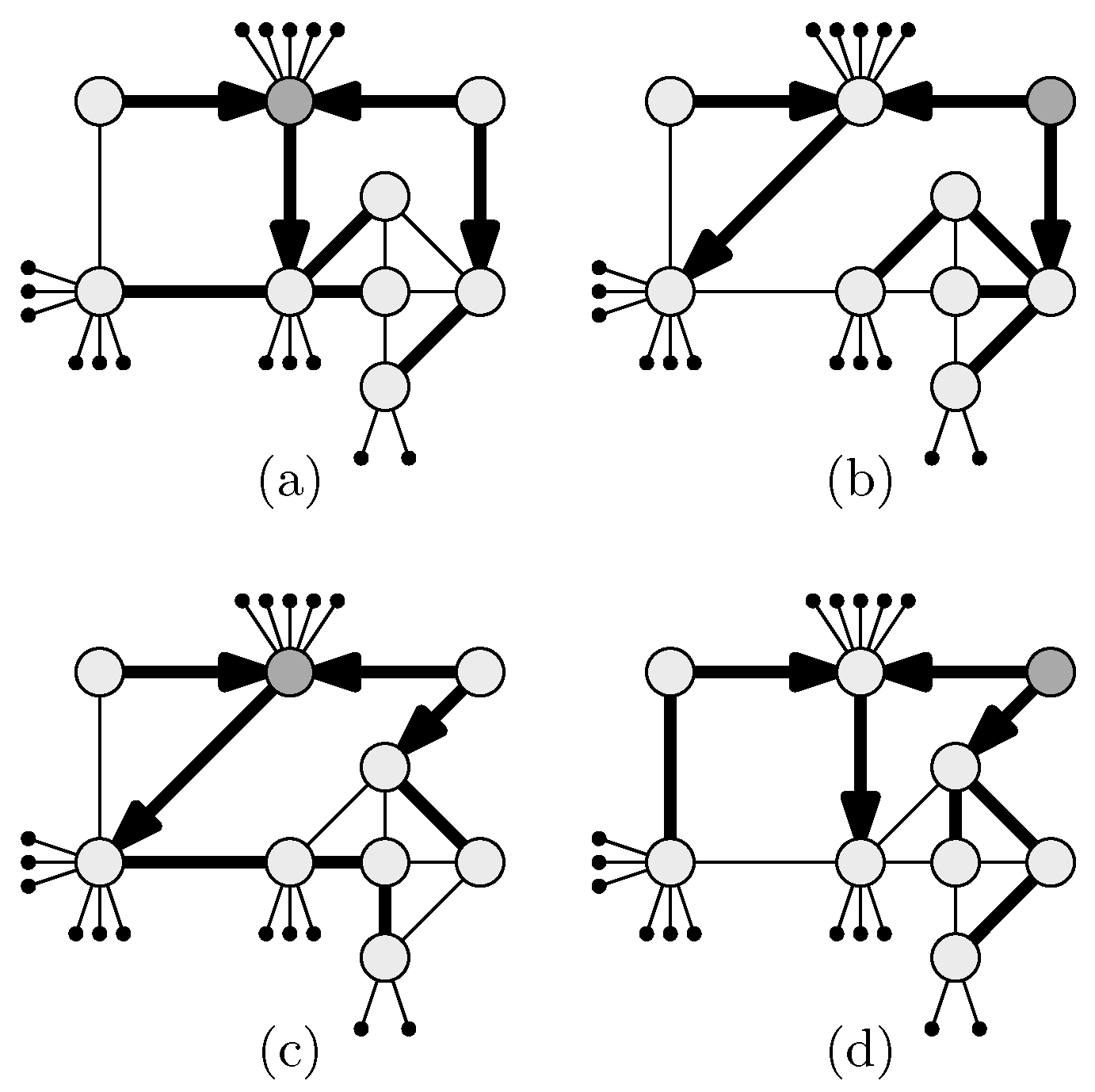
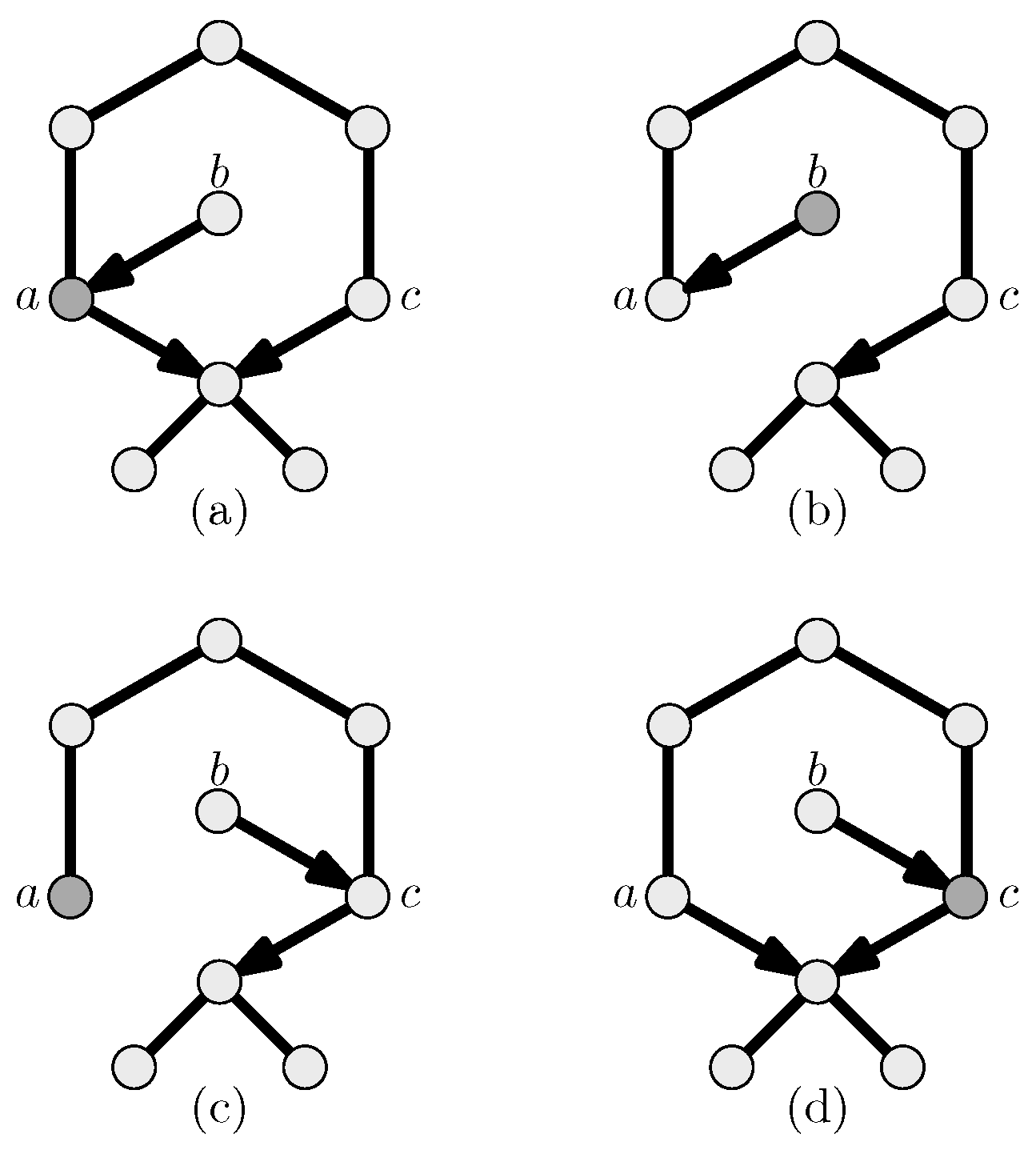
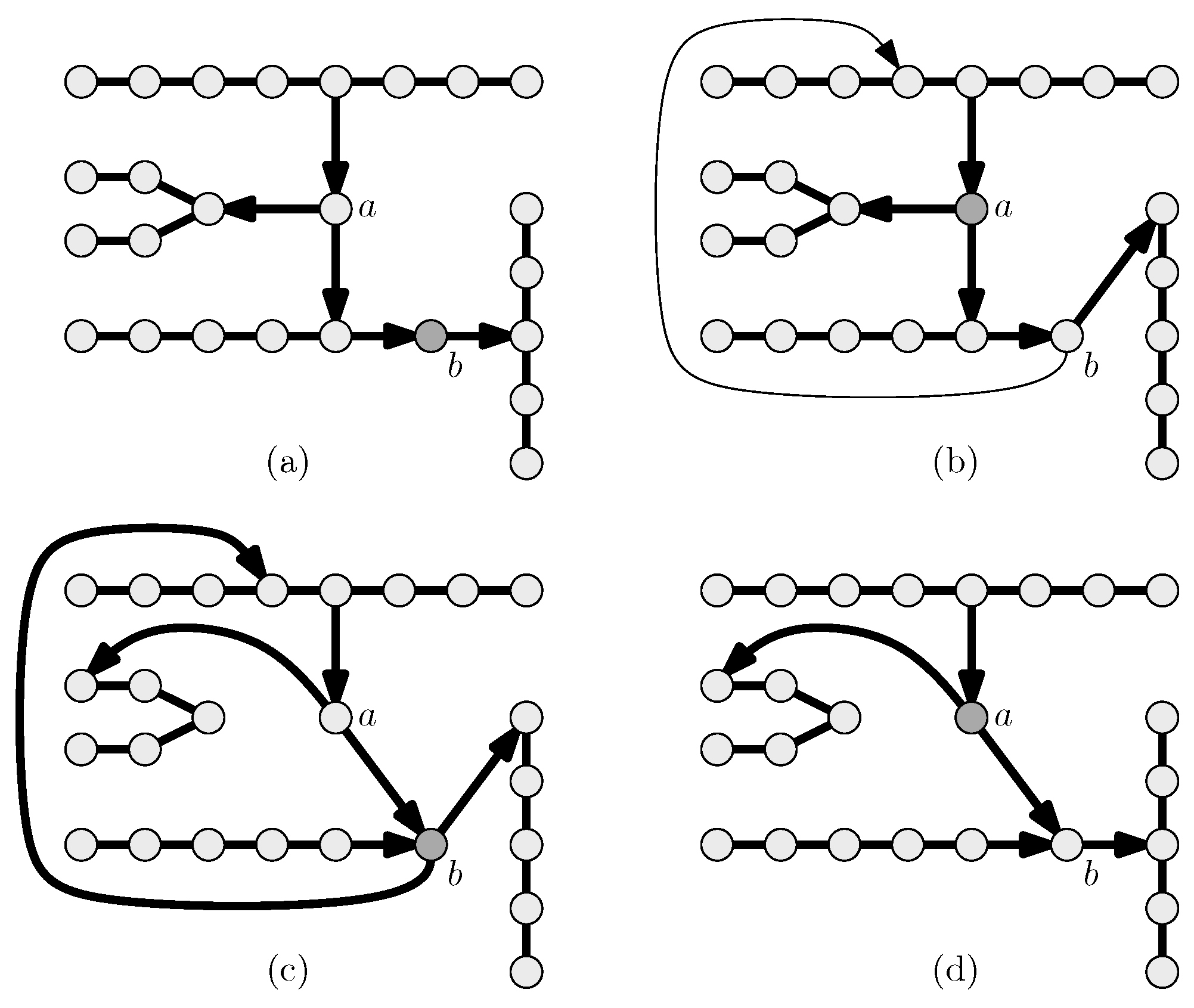
| Convergence | Best-Response Complexity | PoA | |
|---|---|---|---|
| Sum: Yes (∀ improving response dynamics (IRD)) Max: Yes (∀ IRD) | Sum: Open Max: Polynomial | Sum: Max: if if | |
| Sum: No (∃ best response dynamics (BRD) cycle) Max: No (∃ BRD cycle) | Sum: Polynomial Max: Polynomial | Sum: Max: if if | |
| Sum: No (∃ BRD cycle) Max: No (∃ BRD cycle) | Sum: NP-hard Max: NP-hard | Sum: Max: if if |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. Network Creation Games with Traceroute-Based Strategies. Algorithms 2021, 14, 35. https://doi.org/10.3390/a14020035
Bilò D, Gualà L, Leucci S, Proietti G. Network Creation Games with Traceroute-Based Strategies. Algorithms. 2021; 14(2):35. https://doi.org/10.3390/a14020035
Chicago/Turabian StyleBilò, Davide, Luciano Gualà, Stefano Leucci, and Guido Proietti. 2021. "Network Creation Games with Traceroute-Based Strategies" Algorithms 14, no. 2: 35. https://doi.org/10.3390/a14020035
APA StyleBilò, D., Gualà, L., Leucci, S., & Proietti, G. (2021). Network Creation Games with Traceroute-Based Strategies. Algorithms, 14(2), 35. https://doi.org/10.3390/a14020035






