Optimized Dissolved Oxygen Fuzzy Control for Recombinant Escherichia coli Cultivations
Abstract
:1. Introduction
2. Theory and Software
2.1. Fuzzy Theory
2.2. SUPERSYS_HCDC
2.3. Fuzzy Logic Toolbox
2.4. Artificial Neural Networks
3. Material and Methods
3.1. Escherichia Coli Cultivation Data for Simulations
3.2. Fuzzy Controller
3.3. Simulator
3.4. Fuzzy Controller Implementation in SUPERSYS_HCDC Program and E. coli Cultivation Test
3.4.1. Implementation of Fuzzy Controller
3.4.2. Bioreactor Experimental Set-Up
3.4.3. E. coli Strain and Culture Media
3.4.4. Bioreactor Cultivation
3.4.5. Analytical Methods
4. Results and Discussions
4.1. Simulation Results
4.2. DOC Fuzzy Controller Application in E. coli Cultivations
4.2.1. Initial Experiments
4.2.2. Adjustments in Princ1 and Princ2 Fuzzy Systems and Further E. coli Tests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Riesenberg, D. High-cell-density cultivation of Escherichia coli. Curr. Opin. Biotechnol. 1991, 2, 380–384. [Google Scholar] [CrossRef]
- Lee, S.Y. High cell-density culture of Escherichia coli. Trends Biotechnol. 1996, 14, 98–105. [Google Scholar] [CrossRef]
- Riesenberg, D.; Guthke, R. High-cell-density cultivation of microorganisms. Appl. Microbiol. Biotechnol. 1999, 51, 422–430. [Google Scholar] [CrossRef]
- Shiloach, J.; Fass, R. Growing, E. coli to high cell density—A historical perspective on method development. Biotechnol. Adv. 2005, 23, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Luli, G.W.; Strohl, W.R. Comparison of growth, acetate production, and acetate inhibition of Escherichia coli strains in batch and fed-batch fermentations. Appl. Environ. Microbiol. 1990, 56, 1004–1011. [Google Scholar] [CrossRef] [Green Version]
- Majewski, R.A.; Domach, M.M. Simple constrained-optimization view of acetate overflow in E. coli. Biotechnol. Bioeng. 1990, 35, 732–738. [Google Scholar] [CrossRef]
- Nakano, K.; Rischke, M.; Sato, S.; Märkl, H. Influence of acetic acid on the growth of Escherichia coli K12 during high-cell-density cultivation in a dialysis reactor. Appl. Microbiol. Biotechnol. 1997, 48, 597–601. [Google Scholar] [CrossRef]
- Phue, J.N.; Shiloach, J. Impact of dissolved oxygen concentration on acetate accumulation and physiology of E. coli BL21, evaluating transcription levels of key genes at different dissolved oxygen conditions. Metab. Eng. 2005, 7, 353–363. [Google Scholar] [CrossRef] [PubMed]
- O’Beirne, D.; Hamer, G. Oxygen availability and growth of Escherichia coli W3110: Dynamic responses to limitation and starvation. Bioprocess Eng. 2000, 23, 381–387. [Google Scholar] [CrossRef]
- O’Beirne, D.; Hamer, G. Oxygen availability and the growth of Escherichia coli W3110: A problem exacerbated by scale-up. Bioprocess Eng. 2000, 23, 487–494. [Google Scholar] [CrossRef]
- Eiteman, M.A.; Altman, E. Overcoming acetate in Escherichia coli recombinant protein fermentations. Trends Biotechnol. 2006, 24, 530–536. [Google Scholar] [CrossRef]
- Martin, T.W.; Couch, L.T. Fuzzy logic control of dissolved oxygen in a bio-reactor. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 8–11 September 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 936–940. [Google Scholar]
- Schmidell, W.; Lima, U.A.; Aquarone, E.; Borzani, W. Biotecnologia Industrial: Volume 2, 1st ed.; Edgard Blücher: São Paulo, Brazil, 2001; ISBN 9788578110796. [Google Scholar]
- Lee, S.C.; Hwang, Y.B.; Chang, H.N.; Chang, Y.K. Adaptive control of dissolved oxygen concentration in a bioreactor. Biotechnol. Bioeng. 1991, 37, 597–607. [Google Scholar] [CrossRef]
- Hsiao, J.; Ahluwali, M.; Kaufman, J.B.; Clem, T.R.; Shiloach, J. Adaptive Control Strategy for Maintaining Dissolved Oxygen Concentration in High Density Growth of Recombinant, E. coli. Ann. N. Y. Acad. Sci. 1992, 665, 320–333. [Google Scholar] [CrossRef] [PubMed]
- Akesson, M.; Hagander, P. Control of Dissolved Oxygen in Stirred Bioreactors. Technical Reports TFRT-7571. 1998, pp. 1–16. Available online: https://portal.research.lu.se/en/publications/control-of-dissolved-oxygen-in-stirred-bioreactors (accessed on 2 November 2021).
- Arevalo, H.; Sanchez, F.; Ruiz, F.; Guerrero, D.; Patino, D.; Almeciga-Diaz, C.J.; Rodriguez-Lopez, A. Gain-Scheduled Oxygen Concentration Control System for a Bioreactor. IEEE Lat. Am. Trans. 2018, 16, 2689–2697. [Google Scholar] [CrossRef]
- Chitra, M.; Pappa, N.; Abraham, A. Dissolved Oxygen Control of Batch Bioreactor using Model Reference Adaptive Control scheme. IFAC-Pap. 2018, 51, 13–18. [Google Scholar] [CrossRef]
- Mareels, I.M.Y.; Anderson, B.D.O.; Bitmead, R.R.; Bodson, M.; Sastry, S.S. Revisiting the Mit Rule for Adaptive Control. IFAC Proc. Vol. 1987, 20, 161–166. [Google Scholar] [CrossRef]
- Konstantinov, K.; Yoshida, T. Knowledge-Based Control of Fermentation Processes. Biotechnol. Bioeng. 1992, 39, 479–486. [Google Scholar] [CrossRef]
- Horta, A.C.L. Sistema Automático de Supervisão e Controle de Cultivos de Alta Densidade Celular de E.coli Recombinante. Doctoral Dissertation, Federal University of São Carlos, São Carlos, Brazil, 2011. [Google Scholar]
- Horta, A.C.L.; Da Silva, A.J.; Sargo, C.R.; Gonçalves, V.M.; Zangirolami, T.C.; De Campos Giordano, R. Robust artificial intelligence tool for automatic start-up of the supplementary medium feeding in recombinant E. coli cultivations. Bioprocess Biosyst. Eng. 2011, 34, 891–901. [Google Scholar] [CrossRef] [PubMed]
- Horta, A.C.L.; Silva, A.J.; Sargo, C.R.; Velez, A.M.; Gonzaga, M.C.; Giordano, R.C.; Gonçalves, V.M.; Zangirolami, T.C. A supervision and control tool based on artificial intelligence for high cell density cultivations. Braz. J. Chem. Eng. 2014, 31, 457–468. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. Fuzzy logic, neural networks, and soft computing. Commun. ACM 1994, 37, 77–84. [Google Scholar] [CrossRef]
- Akisue, R.A.; Horta, A.C.L.; de Sousa, R. Development of a Fuzzy System for Dissolved Oxygen Control in a Recombinant Escherichia coli Cultivation for Heterologous Protein Expression. In Computer Aided Chemical Engineering, Proceeding of the 28th European Symposium on Computer Aided Process Engineering, Graz, Austria, 10–13 June; Friedl, A., Klemeš, J.J., Radl, S., Varbanov, P.S., Wallek, T., Eds.; Elsevier B.V: Amsterdam, The Netherlands, 2018; Volume 43, pp. 1129–1134. [Google Scholar] [CrossRef]
- Noll, P.; Henkel, M. History and Evolution of Modeling in Biotechnology: Modeling & Simulation, Application and Hardware Performance. Comput. Struct. Biotechnol. J. 2020, 18, 3309–3323. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Logic and Approximate Reasoning. Synthese 1975, 30, 407–428. [Google Scholar]
- Zadeh, L.A. Fuzzy Logic. Comput. 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Belohlavek, R.; Dauben, J.W.; Klir, G.J. Fuzzy Logic and Mathematics, 1st ed.; Oxford University Press: Oxford, UK, 2017; Volume 1, ISBN 9780190200015. [Google Scholar]
- Gomide, F.A.C.; Gudwin, R.R. Modelagem, Controle, Sistemas e Lógica Fuzzy. SBA Control Automação 1994, 4, 97–115. [Google Scholar]
- Nelles, O. Nonlinear System Identification, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-642-08674-8. [Google Scholar]
- Kosko, B. Fuzzy Thinking the New Science of Fuzzy Logic, 1st ed.; Hyperion: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Zadeh, L.A. Fuzzy logic—A personal perspective. Fuzzy Sets Syst. 2015, 281, 4–20. [Google Scholar] [CrossRef]
- Horiuchi, J.I. Fuzzy modeling and control of biological processes. J. Biosci. Bioeng. 2002, 94, 574–578. [Google Scholar] [CrossRef]
- Horiuchi, J.I.; Kishimoto, M. Application of fuzzy control to industrial bioprocesses in Japan. Fuzzy Sets Syst. 2002, 128, 117–124. [Google Scholar] [CrossRef]
- Honda, H.; Kobayashi, T. Fuzzy control of bioprocess. J. Biosci. Bioeng. 2000, 89, 401–408. [Google Scholar] [CrossRef]
- Shioya, S.; Shimizu, K.; Yoshida, T. Knowledge-based design and operation of bioprocess systems. J. Biosci. Bioeng. 1999, 87, 261–266. [Google Scholar] [CrossRef]
- Nakamura, T.; Kuratani, T.; Morita, Y. Fuzzy Control Application to Glutamic Acid Fermentation. IFAC Proc. Vol. 1985, 18, 231–235. [Google Scholar] [CrossRef]
- Sousa, R.; Almeida, P.I.F. Design of a fuzzy system for the control of a biochemical reactor in fed-batch culture. Process Biochem. 2001, 37, 461–469. [Google Scholar] [CrossRef]
- Nucci, E.R.; Silva, R.G.; Gomes, T.C.; Giordano, R.C.; Cruz, A.J.G. A fuzzy logic algorithm for identification of the harvesting threshold during PGA production by Bacillus megaterium. Braz. J. Chem. Eng. 2005, 22, 521–527. [Google Scholar] [CrossRef]
- Borges, A.S.; Montano, I.D.C.; Sousa Junior, R.; Suarez, C.A.G. Automatic solids feeder using fuzzy control: A tool for fed batch bioprocesses. J. Process Control 2020, 93, 28–42. [Google Scholar] [CrossRef]
- Belchior, C.A.C.; Araújo, R.A.M.; Landeck, J.A.C. Dissolved oxygen control of the activated sludge wastewater treatment process using stable adaptive fuzzy control. Comput. Chem. Eng. 2012, 37, 152–162. [Google Scholar] [CrossRef]
- Huang, M.; Wan, J.; Wang, Y.; Ma, Y.; Zhang, H.; Liu, H.; Hu, Z.; Yoo, C.K. Modeling of a paper-making wastewater treatment process using a fuzzy neural network. Korean J. Chem. Eng. 2012, 29, 636–643. [Google Scholar] [CrossRef]
- Yang, T.; Qiu, W.; Ma, Y.; Chadli, M.; Zhang, L. Fuzzy model-based predictive control of dissolved oxygen in activated sludge processes. Neurocomputing 2014, 136, 88–95. [Google Scholar] [CrossRef]
- Piotrowski, R. Supervisory fuzzy control system for biological processes in sequencing wastewater batch reactor. Urban Water J. 2020, 17, 325–332. [Google Scholar] [CrossRef]
- Horta, A.C.L.; Zangirolami, T.C.; de Giordano, R.C.; Reis, G.B.; da Cruz, A.J.G.; de Jesus, C.D.F. SUPERSYS_HCDC—Programa de Computador Para Monitoramento e Controle de Biorreatores Para Cultivos; Instituto Nacional da Propriedade Industrial: Brasilia, Brazil, 2011. [Google Scholar]
- MathWorks. Fuzzy Logic Toolbox TM User ’s Guide, 29th ed.; MathWorks: Natick, MA, USA, 2016. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-Network-based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–683. [Google Scholar] [CrossRef]
- Howard, D.; Mark, B. Neural Network Toolbox Documentation. In Neural Network Tool, 4th ed.; MathWorks: Natick, MA, USA, 2004; p. 846. [Google Scholar]
- Beale, M.; Hagan, M.; Demuth, H. Neural Network ToolboxTM User’s Guide R2017b, 31st ed.; MathWorks: Natick, MA, USA, 2017. [Google Scholar] [CrossRef]
- Horta, A.C.L.; Sargo, C.R.; Da Silva, A.J.; De Carvalho Gonzaga, M.; Dos Santos, M.P.; Gonçalves, V.M.; Zangirolami, T.C.; De Campos Giordano, R. Intensification of high cell-density cultivations of rE. coli for production of S. pneumoniae antigenic surface protein, PspA3, using model-based adaptive control. Bioprocess Biosyst. Eng. 2012, 35, 1269–1280. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Fault Diagnosis Systems. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Carvalho, R.J.; Cabrera-Crespo, J.; Tanizaki, M.M.; Gonçalves, V.M. Development of production and purification processes of recombinant fragment of pneumococcal surface protein A in Escherichia coli using different carbon sources and chromatography sequences. Appl. Microbiol. Biotechnol. 2012, 94, 683–694. [Google Scholar] [CrossRef] [PubMed]
- Silva, G.G. Aspectos Morfológicos, Reológicos e Fisiológicos dos Cultivos de Eschericha coli Recombinante. Master’s Thesis, Federal University of São Carlos, São Carlos, Brazil, 2015. [Google Scholar]
- Sargo, C.R. Aperfeiçoamento de Cultivos de Alta Densidade Celular de rE.coli Utilizando Glicerol Como Fonte de Carbono. Master’s Thesis, Federal University of São Carlos, São Carlos, Brazil, 2011. [Google Scholar]
- De León, A.; Barba-De La Rosa, A.P.; Mayani, H.; Galindo, E.; Ramírez, O.T. Two Useful Dimensionless Parameters That Combine Physiological, Operational and Bioreactor Design Parameters for Improved Control of Dissolved Oxygen. Biotechnol. Lett. 2001, 23, 1051–1056. [Google Scholar] [CrossRef]
- De León-Rodríguez, A.; Galindo, E.; Ramírez, O.T. Design and Characterization of a One-Compartment Scale-down System for Simulating Dissolved Oxygen Tension Gradients. J. Chem. Technol. Biotechnol. 2010, 85, 950–956. [Google Scholar] [CrossRef]
- De León, A.; Hernández, V.; Galindo, E.; Ramírez, O.T. Effects of dissolved oxygen tension on the production of recombinant penicillin acylase in Escherichia coli. Enzyme Microb. Technol. 2003, 33, 689–697. [Google Scholar] [CrossRef]

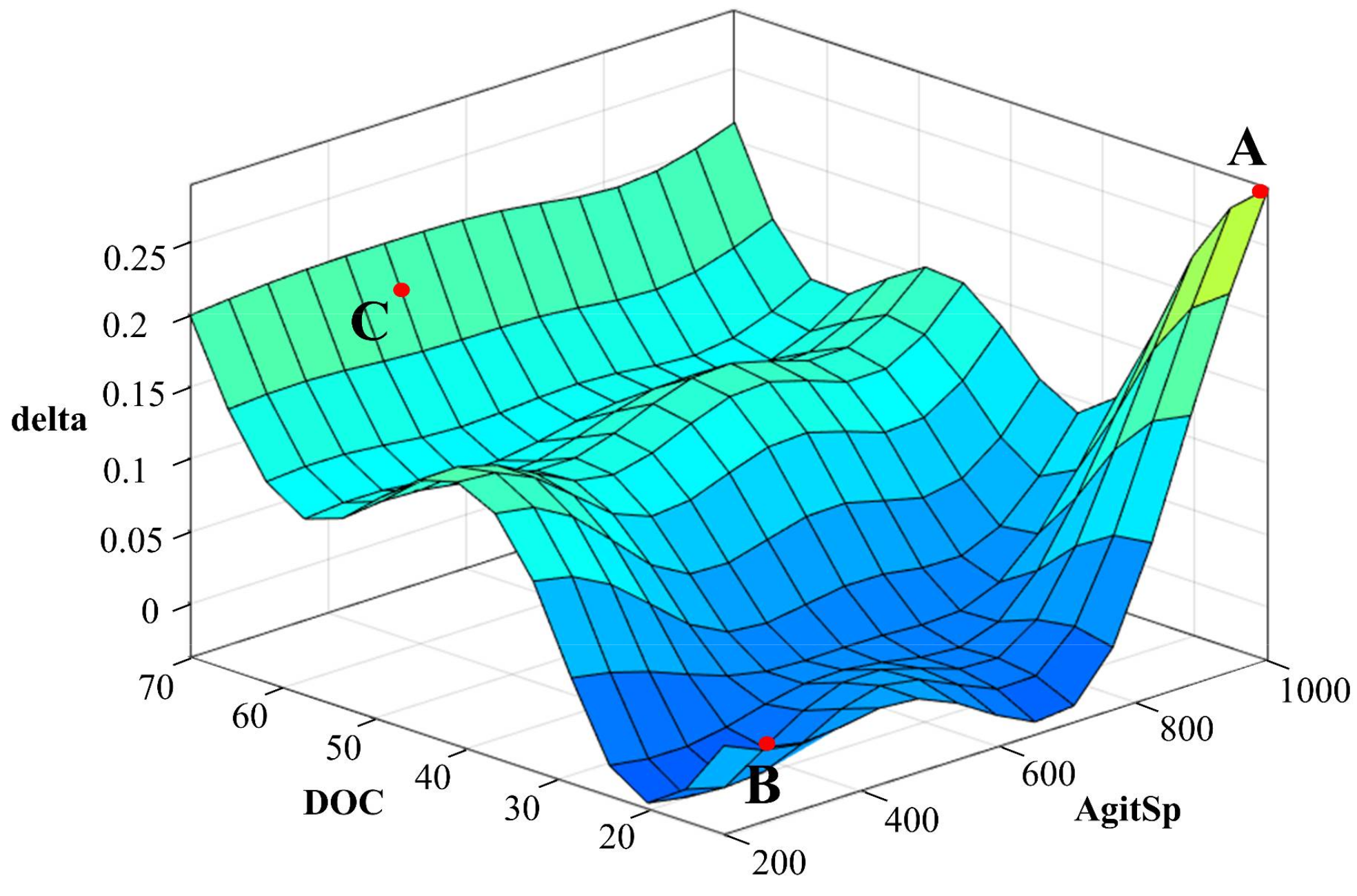
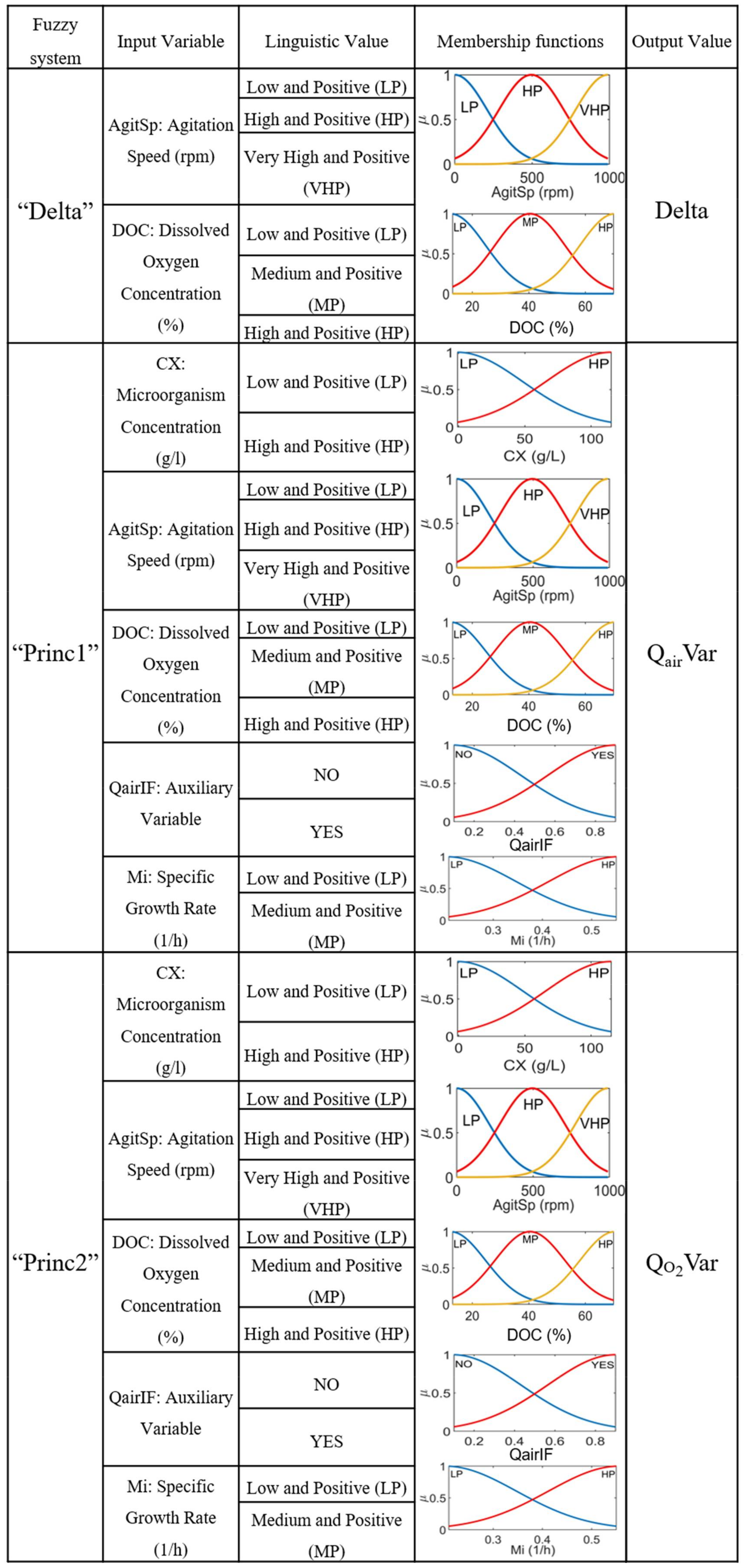
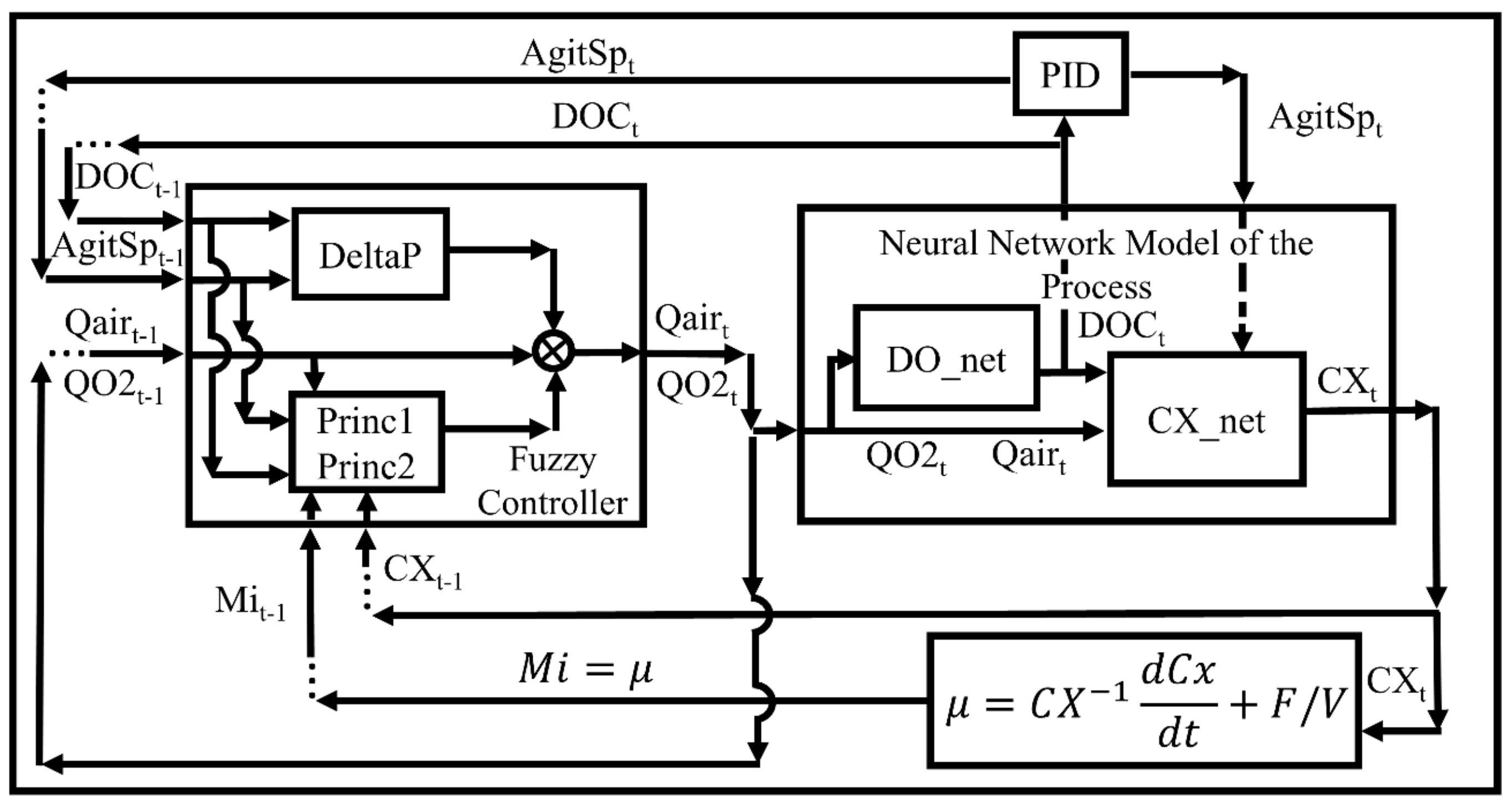
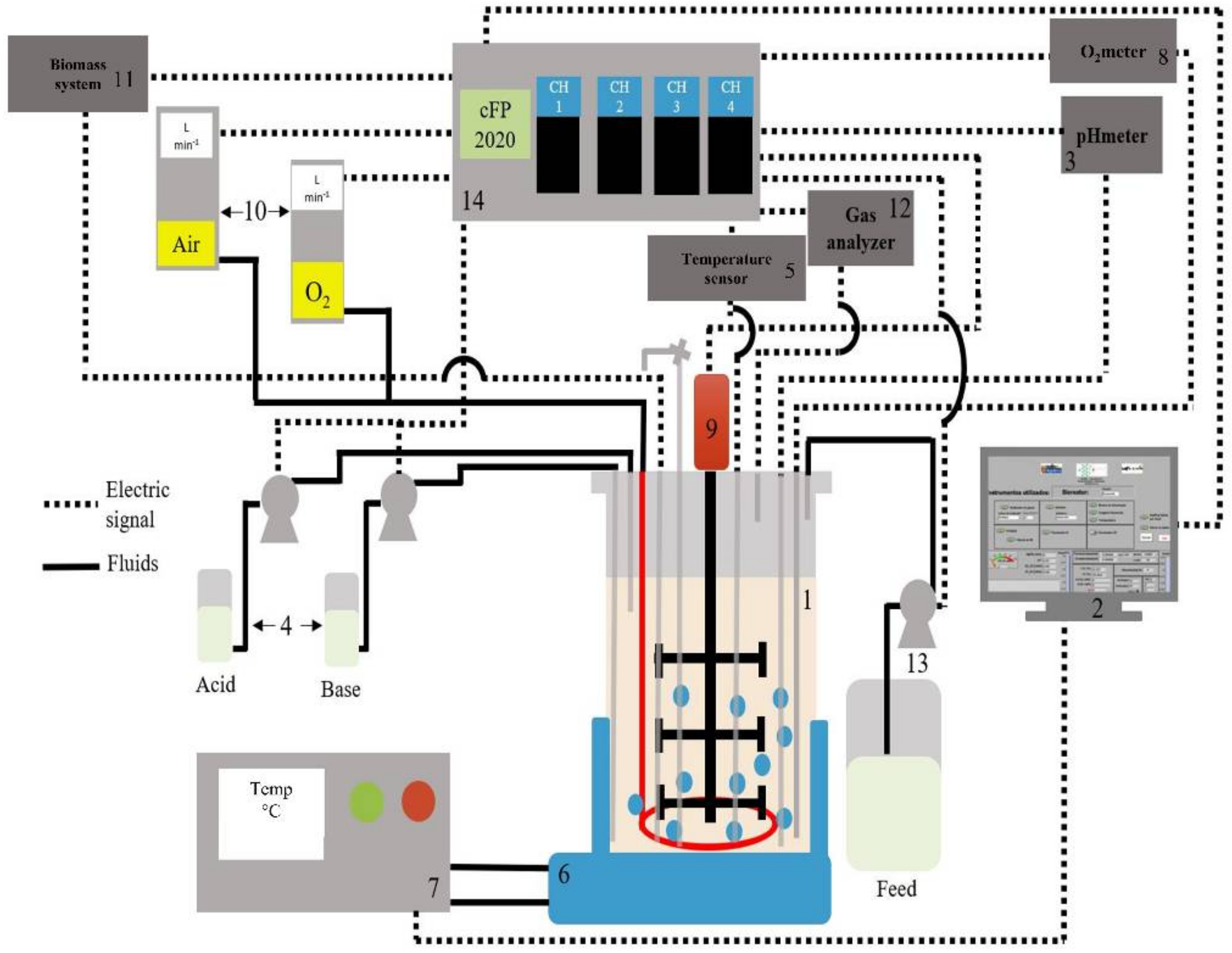
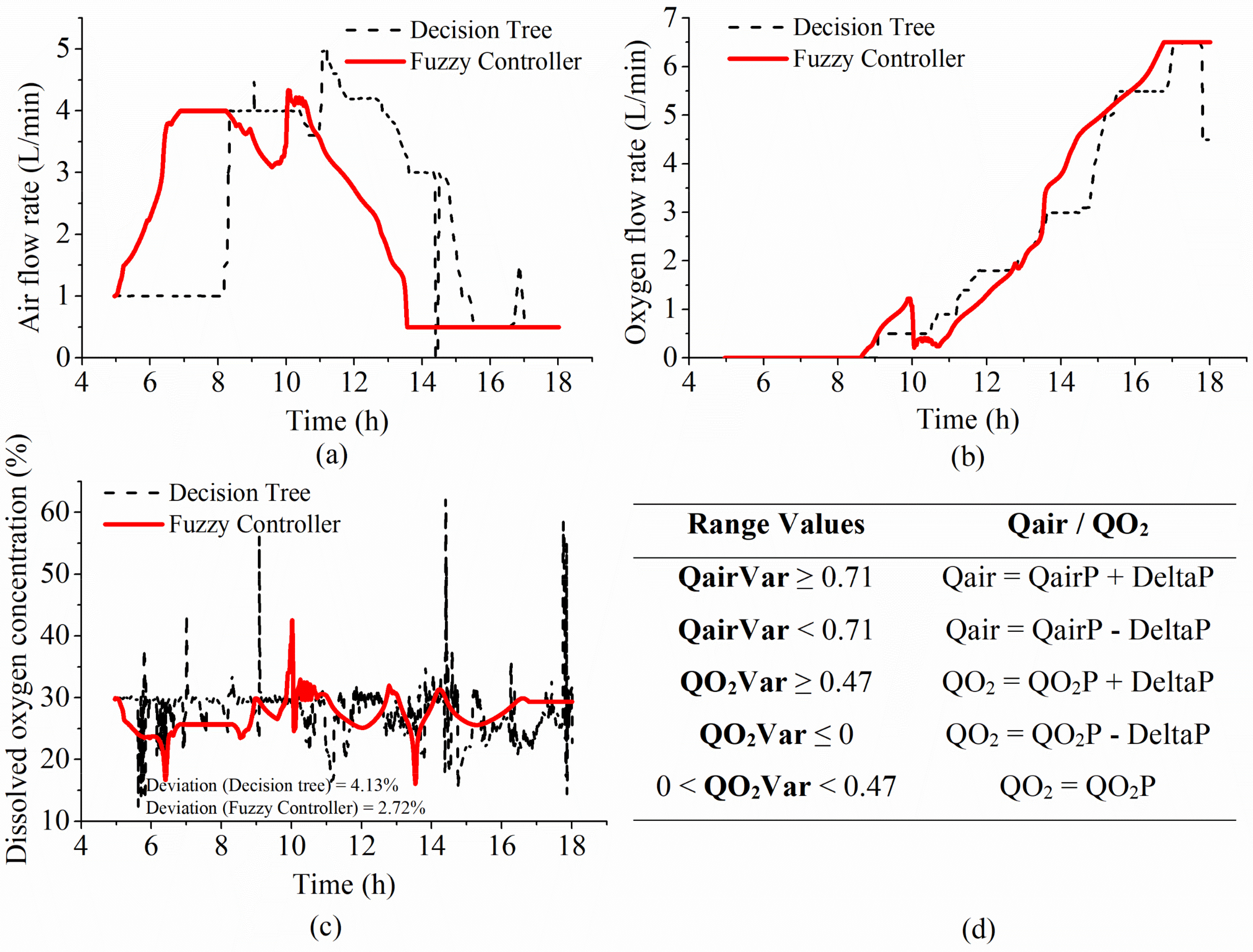
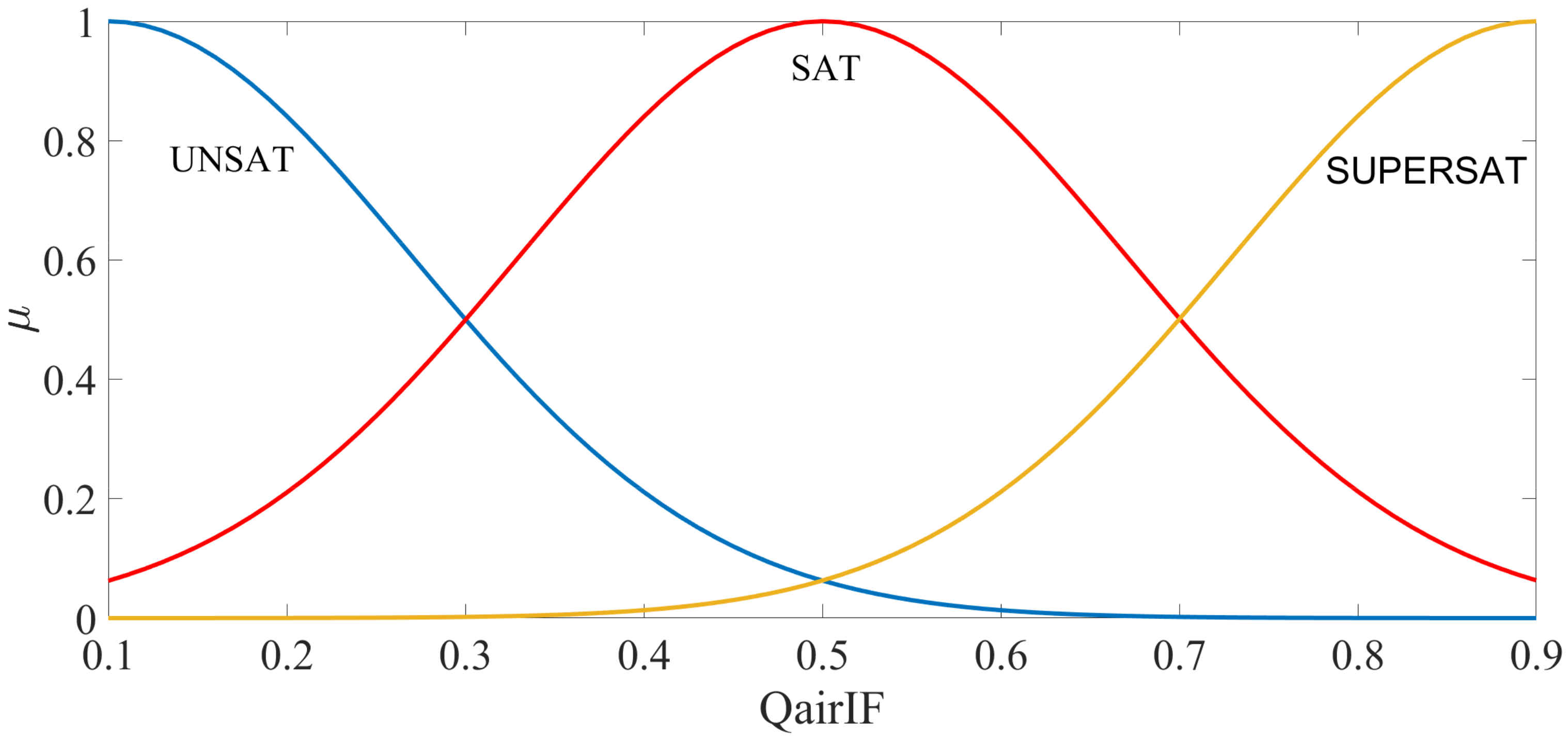
| Rule | AgitSp | DOC | Output (Delta) |
|---|---|---|---|
| 1 | LP | LP | F1 |
| 2 | LP | MP | F2 |
| 3 | LP | HP | F3 |
| 4 | HP | LP | F4 |
| 5 | HP | MP | F5 |
| 6 | HP | HP | F6 |
| 7 | VHP | LP | F7 |
| 8 | VHP | MP | F8 |
| 9 | VHP | HP | F9 |
| Function | a | b | c |
|---|---|---|---|
| F1 | −4.23 × 10−4 | −1.40 × 10−2 | 0.25 |
| F2 | −2.73 × 10−4 | 3.92 × 10−4 | 0.15 |
| F3 | 4.20 × 10−5 | 1.54 × 10−2 | −0.89 |
| F4 | −5.76 × 10−4 | 8.00 × 10−3 | 0.25 |
| F5 | 6.24 × 10−4 | 1.71 × 10−2 | 0.93 |
| F6 | 3.54 × 10−7 | 2.32 × 10−2 | −1.45 |
| F7 | 0.87 × 10−4 | 5.17 × 10−4 | −0.34 |
| F8 | 8.06 × 10−4 | 1.54 × 10−2 | −1.27 |
| F9 | 1.65 × 10−4 | 2.08 × 10−2 | −1.43 |
| Dataset | Phase | DO_net | CX_net | ||
|---|---|---|---|---|---|
| Samples | R 1 | Samples | R 1 | ||
| A16 | Training | 216 | 0.68 | 3681 | 1.00 |
| Validation | 47 | 0.59 | 789 | 1.00 | |
| Testing | 47 | 0.66 | 789 | 1.00 | |
| A12 | Training | 290 | 0.77 | 5160 | 0.98 |
| Validation | 62 | 0.72 | 1106 | 0.98 | |
| Testing | 62 | 0.63 | 1106 | 0.98 | |
| Rule | AgitSp | DO | QairIF | CX | Mi | Output |
|---|---|---|---|---|---|---|
| R1 | LP | LP | UNSAT | LP | LP | F1′ |
| R2 | LP | LP | UNSAT | LP | MP | F2′ |
| R3 | LP | LP | UNSAT | HP | LP | F3′ |
| R106 | VHP | HP | SUPERSAT | LP | MP | F106′ |
| R107 | VHP | HP | SUPERSAT | HP | LP | F107′ |
| R108 | VHP | HP | SUPERSAT | HP | MP | F108′ |
| Function | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| F1′ | 5.39 × 10−4 | −5.23 × 10−4 | 2.70 × 10−6 | 1.37 × 10−5 | 2.29 × 10−7 | 3.33 × 10−7 |
| F2′ | 5.37 × 10−4 | 3.25 × 10−5 | 2.68 × 10−6 | 1.36 × 10−5 | 3.31 × 10−7 | 2.68 × 10−6 |
| F3′ | 5.37 × 10−4 | −1.61 × 10−6 | 2.36 × 10−6 | 1.37 × 10−5 | 3.32 × 10−7 | 2.68 × 10−6 |
| F106′ | −1.72 × 10−3 | 2.48 × 10−2 | −1.67 × 10−6 | 1.97 × 10−4 | −8.36 × 10−7 | −1.74 × 10−6 |
| F107′ | 2.18 × 10−4 | −1.56 × 10−3 | 1.55 × 10−7 | 2.49 × 10−5 | 1.05 × 10−7 | 2.21 × 10−7 |
| F108′ | 9.69 × 10−5 | 9.37 × 10−5 | 8.00 × 10−8 | 1.05 × 10−5 | 4.67 × 10−8 | 9.79 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akisue, R.A.; Harth, M.L.; Horta, A.C.L.; de Sousa Junior, R. Optimized Dissolved Oxygen Fuzzy Control for Recombinant Escherichia coli Cultivations. Algorithms 2021, 14, 326. https://doi.org/10.3390/a14110326
Akisue RA, Harth ML, Horta ACL, de Sousa Junior R. Optimized Dissolved Oxygen Fuzzy Control for Recombinant Escherichia coli Cultivations. Algorithms. 2021; 14(11):326. https://doi.org/10.3390/a14110326
Chicago/Turabian StyleAkisue, Rafael Akira, Matheus Lopes Harth, Antonio Carlos Luperni Horta, and Ruy de Sousa Junior. 2021. "Optimized Dissolved Oxygen Fuzzy Control for Recombinant Escherichia coli Cultivations" Algorithms 14, no. 11: 326. https://doi.org/10.3390/a14110326
APA StyleAkisue, R. A., Harth, M. L., Horta, A. C. L., & de Sousa Junior, R. (2021). Optimized Dissolved Oxygen Fuzzy Control for Recombinant Escherichia coli Cultivations. Algorithms, 14(11), 326. https://doi.org/10.3390/a14110326







