New Approach for Radial Basis Function Based on Partition of Unity of Taylor Series Expansion with Respect to Shape Parameter

Abstract

Radial basis function (RBF) is gaining popularity in function interpolation as well as in solving partial differential equations thanks to its accuracy and simplicity. Besides, RBF methods have almost a spectral accuracy. Furthermore, the implementation of RBF-based methods is easy and does not depend on the location of the points and dimensionality of the problems. However, the stability and accuracy of RBF methods depend significantly on the shape parameter, which is primarily impacted by the basis function and the node distribution. At a small value of shape parameter, the RBF becomes more accurate, but unstable. Several approaches were followed in the open literature to overcome the instability issue. One of the approaches is optimizing the solver in order to improve the stability of ill-conditioned matrices. Another approach is based on searching for the optimal value of the shape parameter. Alternatively, modified bases are used to overcome instability. In the open literature, radial basis function using QR factorization (RBF-QR), stabilized expansion of Gaussian radial basis function (RBF-GA), rational radial basis function (RBF-RA), and Hermite-based RBFs are among the approaches used to change the basis. In this paper, the Taylor series is used to expand the RBF with respect to the shape parameter. Our analyses showed that the Taylor series alone is not sufficient to resolve the stability issue, especially away from the reference point of the expansion. Consequently, a new approach is proposed based on the partition of unity (PU) of RBF with respect to the shape parameter. The proposed approach is benchmarked. The method ensures that RBF has a weak dependency on the shape parameter, thereby providing a consistent accuracy for interpolation and derivative approximation. Several benchmarks are performed to assess the accuracy of the proposed approach. The novelty of the present approach is in providing a means to achieve a reasonable accuracy for RBF interpolation without the need to pinpoint a specific value for the shape parameter, which is the case for the original RBF interpolation.

1. Introduction

Over the past few decades, radial basis function (RBF) has attracted researchers’ attention as a method for interpolation, differentiation, and solving partial differential equations (PDEs). RBF-based methods have several advantages over the conventional methods including their ability to produce spectral accuracy [1] and their simplicity in implementation regardless of the problem’s dimension [2]. Their accuracy and stability are strongly predicated on the condition of the generated matrix. The improvement on the RBF can be classified into matrix solvers, shape parameter, and basis functions. In the following, a brief literature review of each methodology is provided.

As known, the preconditioning of a matrix improves the stability of the solver. So, dealing with the matrix solvers could improve the condition of the RBF matrix. There are several studies that investigated and evaluated the preconditioning of the RBF matrix [3,4,5,6,7,8,9,10,11,12]. Kansa et al. [11,12] used extended precision for the calculation in order to remove the computational singularity and enhance the condition of the interpolation matrix. Until now, the matrix solvers are not able to improve accuracy to the desired level.

The studies on the shape parameter can be categorized as modifying the shape parameter [13], using variable shape parameter [14,15,16,17], and finding optimal shape parameter [18,19,20,21,22,23,24,25]. Despite the success of identifying the optimal value of the shape parameter, the proposed methods are neither universal nor consistent. Furthermore, resolving different kinds of problems need fine-tuning. Consequently, the researchers investigated changing or transforming the RBFs to find a more general approach for a wide range of applications.

The modifications to the basis of the interpolant of the RBF can be classified into either single contributions [26,27,28,29,30,31] or classes of methods (pseudo-spectral radial basis function (RBF-PS) [32,33], finite difference radial basis function (RBF-FD) [23,34,35,36,37,38], partition of unity radial basis function (RBF-PU) [39,40,41], radial basis function using QR factorization (RBF-QR) [42,43,44,45,46], stabilized expansion of Gaussian radial basis function (RBF-GA) [47], rational radial basis function (RBF-RA) [48,49], and variably scaled kernels (VSK) [50,51,52,53]). Rashidinia et al. [30] proposed a stable algorithm for evaluating the interpolation matrix based on the eigen-function expansion of the Gaussian function. The accuracy and computation cost of the proposed method are verified for 1D and 2D cases. Yurova et al. [31] stabilized the Gaussian RBF by using the generating function of the Hermite polynomial. The proposed algorithm is found to be stable and can be generalized to higher dimensions. Fasshauer et al. [32,33] demonstrated that RBF could be interpreted in the framework of pseudo-spectral methods, which is more efficient than the regular (Kansa’s) RBF method for time-dependent PDEs. Tolstykh et al. [34] proposed the RBF interpolant with local supports, which is similar to the stencils of finite difference methods, and hence named RBF-FD. The method has reasonable accuracy and convergence. Wright et al. [35] combined the RBF-FD with the Hermite RBF interpolation to involve a smaller number of stencil nodes without sacrificing accuracy. Gonzalez-Rodriguez et al. [23,36] proposed an analytical formula for the RBF-FD weights to avoid the ill-condition in the computation of the RBF-FD weights. The formula is based on the semi-analytical computation of the Laurent series of the inverse of the RBF interpolation matrix. Flyer et al. [37] and Bayona et al. [38] observed that polyharmonic splines (PHS) padded with a polynomial provide a simple way to overcome stagnation error and produce good accuracy for interpolation and derivative approximation without the need for the shape parameter. The partition of unity interpolation approach is first used in the pioneer work of Shepard [54], where it is used to smoothly interpolate irregular data. Wendland [39] combined the partition of unity method with respect to space and RBF interpolation in order to form the RBF-PU method that can resolve large-scale scattered data problems. Cavoretto et al. [40] proposed a RBF-PU based method to suitably select variable shape parameters and sub-domain sizes that improve the accuracy by minimizing the error. Cavoretto et al. [41] used the RBF-PU with a stabilized weighted singular value decomposition (WSVD) basis. This algorithm is stable, accurate, and efficient given that it is local and has a stabilized basis. Fornberg et al. [42] proposed the RBF-QR method to eliminate ill-conditioning of the interpolation matrix for near-flat basis function. They applied the method for a particular case of points on a sphere surface. Fornberg et al. [43] compared different types of RBFs in the framework of RBF-QR to solve convective PDE over a wide range of shape parameter values. They found that the RBF-QR method is accurate and stable even for a shape parameter value approaching zero. Additionally, RBF-QR is extended and applied to two-dimensional problems [44]. Furthermore, RBF-QR is extended to work on an arbitrary node-set in 1D, 2D, and 3D problems [44]. Fasshauer et al. [45] offered a simpler algorithm for RBF-QR in arbitrary dimensions by using eigen-decomposition parametrized by the scale of the problem. Larsson et al. [46] extended RBF-QR to calculate the weights and differentiation matrix in order to solve PDEs. The proposed model has better accuracy and stability than the direct approach. Fornberg et al. [47] introduced the RBF-GA algorithm. The algorithm helps in numerically determining a well-conditioned basis utilizing the incomplete gamma function, which allows changing the basis without using infinite expansion. Based on the use of a rational approximation of a vector-valued function, the RBF-RA algorithm is adapted for a stable computation of the RBF interpolant when the shape parameter approaches zero [48,49].

In the current work, a novel approach for improving the accuracy of the RBF method is presented. Based on the novel approach, the Taylor series expansion is used to expand the RBF basis with respect to shape parameter around a predefined reference value to find a modified stable basis. According to the preliminary findings, this approach has weak coupling between shape parameter and distances near the reference shape parameter values. The further away the reference shape-parameter from the shape parameter, the weaker the coupling. In order to resolve this issue, the partition of unity with respect to the shape parameter is applied to the resultant equation. The current work uses PU with respect to the shape parameter, whereas previous literature works used it with respect to spatial coordinates. This modified approach improves accuracy and provides reliable and consistent results, even when the shape parameter approaches zero.

The paper is structured as follows. Section 2 explains using RBF for interpolation and approximating derivatives. In Section 3, the expansion of RBF using the Taylor series with respect to a fixed shape parameter value is introduced. Section 4 proposes applying the partition of unity approach to the Taylor series expansion of RBF. The results are discussed in Section 5. Finally, the conclusions are presented in Section 6.

2. Regular RBF Method

The conventional radial basis function method can be used to interpolate given $N$ data $f\left({\mathit{x}}_k\right)$ at ${\mathit{x}}_k$ locations by defining the interpolant function $I\left(x\right)$.

$$I\left(\mathit{x}\right)={\displaystyle {\displaystyle \sum }_{k=1}^N}{\alpha }_k\hspace{0.33em}\varphi \left(r\left(\mathit{x},{\mathit{x}}_k\right),\epsilon \right),$$

(1)

where $\varphi$ denotes the radial basis function, ${\alpha }_j$ are coefficients associated with each basis, and $\epsilon$ refers to the shape parameter. $r\left(\mathit{x},{\mathit{x}}_k\right)=\sqrt{\left(\mathit{x}-{\mathit{x}}_k\right)·\left(\mathit{x}-{\mathit{x}}_k\right)}$ signifies the distance between two points in space, as shown in Figure 1. Although the matrix generated from Gaussian RBF is ill-conditioned especially when the shape parameter approaches zero, the Gaussian radial basis function (i.e., Equation (2)) is selected in this work because it is one of the most accurate RBFs when used for approximation [43]. That is because it is strictly positive definite and infinitely differentiable [2]. In addition, it has the ability to evaluate its derivatives without the risk of dividing by zero.

$$\varphi \left(r,\epsilon \right)=exp\left(-{\epsilon }^2 r^2\right)$$

(2)

.

Coefficients ${\alpha }_j$ can be found by imposing the interpolation constraints (equating the interpolant at points ${\mathit{x}}_k$ to $f\left(\mathit{x}\right)$) on the interpolant:

$$I\left({\mathit{x}}_k\right)={\displaystyle {\displaystyle \sum }_{j=1}^N}{\alpha }_j\hspace{0.33em}\varphi \left(r\left({\mathit{x}}_k,{\mathit{x}}_j\right),\epsilon \right)=f\left({\mathit{x}}_k\right),$$

(3)

which results in the following system of equations:

$${\varphi }_{ij}{\alpha }_j=f\left({\mathit{x}}_i\right).$$

(4)

The matrix ${\varphi }_{ij}=\varphi \left(r\left({\mathit{x}}_i,{\mathit{x}}_j\right),\epsilon \right)$ is a symmetric square matrix, which represents the coefficients of a system of equations that can be solved for ${\alpha }_j$. The coefficients ${\alpha }_j$ are substituted in the interpolant (Equation (1)) to interpolate the given function $f\left(x\right)$ at any location $\mathit{x}$. Thereafter, the derivatives of the function $f$ can be approximated by taking the derivatives of the interpolant. For example, the first and second derivatives are presented in Equations (5) and (6), respectively.

$$\frac{\partial f\left(\mathit{x}\right)}{\partial x_{\alpha }}\approx \frac{\partial I\left(\mathit{x}\right)}{\partial x_{\alpha }}={\displaystyle {\displaystyle \sum }_{j=1}^N}{\alpha }_j\hspace{0.33em}\frac{\partial \varphi \left(r\left(\mathit{x},{\mathit{x}}_j\right),\epsilon \right)}{\partial x_{\alpha }}$$

(5)

$$\frac{{\partial }^{2}f\left(\mathit{x}\right)}{\partial x_{\alpha }\partial x_{\beta }}\approx \frac{{\partial }^{2}I\left(\mathit{x}\right)}{\partial x_{\alpha }\partial x_{\beta }}={\displaystyle {\displaystyle \sum }_{j=1}^N}{\alpha }_j\hspace{0.33em}\frac{{\partial }^2\varphi \left(r\left(\mathit{x},{\mathit{x}}_j\right),\epsilon \right)}{\partial x_{\alpha }\partial x_{\beta }}$$

(6)

In this section, it is shown that the interpolation and derivatives approximations depend on ${\alpha }_k$, which cannot be stably calculated when the shape parameter approaches zero because the matrix ${\varphi }_{ij}$ is ill-conditioned. A way to resolve this problem is proposed in the next section.

3. Taylor Series Radial Basis Function (RBF-TS)

The current authors argue that one of the reasons for the instability of RBF is the strong coupling between the shape parameter ($\epsilon$) and distances ($r$). As a first attempt to weaken this coupling, the basis function $\varphi$ and its derivatives are expanded with respect to shape parameter using the Taylor series around a reference shape parameter (${\epsilon }_0$):

$$\begin{gathered} \varphi \left(r,\epsilon \right)= \varphi \left(r,{\epsilon }_0\right)+{\left.\frac{\partial \varphi \left(r,\epsilon \right)}{\partial \epsilon }\right|}_{\epsilon ={\epsilon }_0}\left(\epsilon -{\epsilon }_0\right)+{\left.\frac{{\partial }^2\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^2}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^2}{2}+\cdots \\ ={\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^n\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^n}{n!} \end{gathered}$$

(7)

$$\begin{gathered} \frac{\partial \varphi \left(r,\epsilon \right)}{\partial x_{\alpha }}=\frac{\partial \varphi \left(r,{\epsilon }_0\right)}{\partial x_{\alpha }}+{\left.\frac{{\partial }^2\varphi \left(r,\epsilon \right)}{\partial \epsilon \partial x_{\alpha }}\right|}_{\epsilon ={\epsilon }_0}\left(\epsilon -{\epsilon }_0\right)+{\left.\frac{{\partial }^3\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^2\partial x_{\alpha }}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^2}{2}+\cdots \\ ={\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^{n+1}\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n\partial x_{\alpha }}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^n}{n!} \end{gathered}$$

(8)

$$\begin{gathered} \frac{{\partial }^2\varphi \left(r,\epsilon \right)}{\partial x_{\alpha }\partial x_{\beta }}=\frac{{\partial }^2\varphi \left(r,{\epsilon }_0\right)}{\partial x_{\alpha }\partial x_{\beta }}+{\left.\frac{{\partial }^3\varphi \left(r,\epsilon \right)}{\partial \epsilon \partial x_{\alpha }\partial x_{\beta }}\right|}_{\epsilon ={\epsilon }_0}\left(\epsilon -{\epsilon }_0\right)+{\left.\frac{{\partial }^4\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^2\partial x_{\alpha }\partial x_{\beta }}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^2}{2}+\cdots \\ ={\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^{n+2}\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n\partial x_{\alpha }\partial x_{\beta }}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^n}{n!} \end{gathered}$$

(9)

Figure 2 plots the log10 of the difference between RBF and its Taylor approximation to reveal the significant digits of the difference. For example, the value −10 indicates that both functions are identical up to 10 significant digits. In Figure 2, the rows from the top to the bottom represent RBF, first derivative, and second derivative with respect to $r$. On the other hand, columns from the left to the right denote the zeroth ($O=0$), first ($O=1$), and second ($O=2$) orders of truncation. As seen in Figure 2, the error increases as the difference between $\epsilon$ and ${\epsilon }_0$ increases, which implies that the Taylor series approximation deviates from RBF as $\epsilon$ moves away from ${\epsilon }_0$. The effect of truncation order on RBF and its derivatives can be deciphered from Figure 2 by comparing sub-figures across columns. It is found that the error decreases with the increasing truncation order or the decreasing order of the derivative. Regardless of the truncation order, the diagonal region of each graph is the region with minimum error; this is expected because $\epsilon$ and ${\epsilon }_0$ are almost identical in that region. Furthermore, the higher-order terms in the Taylor series become very small and negligible at the diagonal. In contrast, the error increases significantly away from the diagonals and the coupling between $r$ and $\epsilon$ becomes weak. Put succinctly, the coupling between $r$ and $\epsilon$ becomes weaker as $\epsilon$ deviates from ${\epsilon }_0$. This, in turn, implies that RBF-TS will drift considerably from Gaussian RBF.

The RBF-TS approach is tested for interpolation and approximation of derivatives (Section 5.1). It is shown that RBF-TS does not improve the accuracy where its accuracy depends on ${\epsilon }_0$. That is because of the nature of the Taylor series, which produces a reasonable approximation at and near ${\epsilon }_0$ and a bad approximation as $\epsilon$ moves away from ${\epsilon }_0$. Therefore, it is necessary to find a way to relatively strengthen the coupling when $\epsilon$ is away from ${\epsilon }_0$.

4. Partition of Unity for Taylor Series Radial Basis Function (RBF-TPU)

As evidenced in the previous section, the coupling between $r$ and $\epsilon$ becomes weak as $\epsilon$ moves away from ${\epsilon }_0$. In order to resolve this issue, $N_e$ different reference values of shape parameter (${\epsilon }_k$) are used, which help strengthen the coupling at ${\epsilon }_k$ values of the shape parameter.

$$\varphi \left(r,\epsilon \right)={\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^n\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_0\right)}^n}{n!}$$

(10)

This equation (i.e., Equation (10)) is identical to $\varphi$ at $\epsilon ={\epsilon }_k$ values. In order to find a proper approximation of $\varphi$ in between ${\epsilon }_k$ values, the set of equations (i.e., Equation (10) with different values of ${\epsilon }_k$) need to be somehow linked. This can be achieved by using the partition of unity approach with respect to the shape parameter, where each equation is weighted with an appropriate weight function ($w\left(\epsilon ,{\epsilon }_k\right)$). The results are summed over $k$.

$$\varphi \left(r,\epsilon \right){\displaystyle {\displaystyle \sum }_{k=1}^{N_e}}w\left(\epsilon ,{\epsilon }_k\right)={\displaystyle {\displaystyle \sum }_{k=1}^{N_e}}w\left(\epsilon ,{\epsilon }_k\right){\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^n\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_k\right)}^n}{n!}$$

(11)

Now, $\varphi$ could be isolated on the left-hand side by dividing both sides of Equation (11) by ${\displaystyle {{\displaystyle \sum }}_{k=1}^{N_e}}w\left(\epsilon ,{\epsilon }_k\right)$, which leads to a better approximation for $\varphi$ over a wider range of the shape parameter.

$$\varphi \left(r,\epsilon \right)={\displaystyle {\displaystyle \sum }_{k=1}^{N_e}}W\left(\epsilon ,{\epsilon }_k\right){\displaystyle {\displaystyle \sum }_{n=0}^O}{\left.\frac{{\partial }^n\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n}\right|}_{\epsilon ={\epsilon }_0}\frac{{\left(\epsilon -{\epsilon }_k\right)}^n}{n!},$$

(12)

where the partition weight ($W\left(\epsilon ,{\epsilon }_k\right)$) is expressed as follows:

$$W\left(\epsilon ,{\epsilon }_k\right)=\frac{w\left(\epsilon ,{\epsilon }_k\right)}{{\displaystyle {{\displaystyle \sum }}_{j=1}^{N_e}}w\left(\epsilon ,{\epsilon }_j\right)}.$$

(13)

It should be emphasized that the primary purpose of Equation (12) is to find a new basis that is not necessarily identical to the Gaussian basis. This new basis should have a weak dependency on the shape parameter and accuracy that is comparable to the Gaussian basis for the interpolation as well as the derivative approximation.

To use the new basis (Equation (12)), the considered range of shape parameter ($\epsilon$) should be divided into $N_e$ slightly overlapped sub-ranges, where non-negative weights for the partition of unity approximation ($w$) should be selected [55]. Regardless of the selected weight function, the sum of partition weights is one (${\displaystyle {{\displaystyle \sum }}_{k=1}^{N_e}}W\left(\epsilon ,{\epsilon }_k\right)=1$), which is where the name of the partition of unity comes from. In this work, two simple weight functions will be considered. The first and simplest weight function is $w=1$, which can be interpreted as averaging $\varphi$ over a given shape parameter range. Bell shape functions are generally chosen for a partition of unity approximation. They approximate cardinal condition (unity at the reference point and monotonically decreasing till approaches zero at neighbors), which is a desired property. This property makes the Gaussian function ($w\left(\epsilon ,{\epsilon }_0\right)=exp(-m\left(\epsilon -{\epsilon }_0{)}^2\right)$) a good candidate for the weight function. Hence, the Gaussian function is considered as a second weight function in this study. The $m$ parameter is introduced to control the width of the function. As $m$ approaches zero, the weight becomes flat and approaches one (the simplest weight). The compactly supported weight function can be emulated by changing the value $m$ in the weights.

The partition of unity approach can be applied to Equations (8) and (9) to find approximations of derivatives of $\varphi$.

$$\frac{\partial \varphi \left(r,\epsilon \right)}{\partial x_{\alpha }}=\hspace{1em}{\displaystyle {\displaystyle \sum }_{k=1}^{N_e}}W\left(\epsilon ,{\epsilon }_k\right){\displaystyle {\displaystyle \sum }_{n=0}^O}\frac{{\partial }^{n+1}\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n\partial x_{\alpha }}{|}_{\epsilon ={\epsilon }_k}\frac{{(\epsilon -{\epsilon }_k)}^n}{n!}$$

(14)

$$\frac{{\partial }^2\varphi \left(r,\epsilon \right)}{\partial x_{\alpha }\partial x_{\beta }}=\hspace{1em}{\displaystyle {\displaystyle \sum }_{k=1}^{N_e}}W\left(\epsilon ,{\epsilon }_k\right){\displaystyle {\displaystyle \sum }_{n=0}^O}\frac{{\partial }^{n+2}\varphi \left(r,\epsilon \right)}{\partial {\epsilon }^n\partial x_{\alpha }\partial x_{\beta }}{|}_{\epsilon ={\epsilon }_k}\frac{{(\epsilon -{\epsilon }_k)}^n}{n!}$$

(15)

Figure 3 illustrates the effect of the weight function; more specifically, Figure 3a shows the effect of the first weight function ($w=1$), while the second weight function is presented in the rest of the sub-figures for dif-ferent value of $m$ (i.e., Figure 3b for $m=0.01$, Figure 3c for $m=4$, and Figure 3d for $m=8$). In Figure 3, the arrangement of rows and columns of sub-figures is similar to that of Figure 2; however, there are two main differences. Firstly, the results are obtained from the partition of unity approximations (Equations (12), (14) and (15)) rather than the Tay-lor series. Secondly, the vertical axes in Figure 3 are the number of points to equally divide the ${\epsilon }_k$ range ($N_e$), as the partition of unity approximation is contingent on a range of ${\epsilon }_k$ values (taken as [0, 1]) instead of a single value (${\epsilon }_0$).

As shown in Figure 3a ($w=1$) and Figure 3b ($m=0.01$), the results are almost identical because $m$ is a very small value. The results can be confirmed analytically by taking the limit of $exp(-m\left(\epsilon -\epsilon {)}^2\right)$ as $m$ approaches zero, which results in one (the same weight as the one used for Figure 3a). The minimum error occurs at approximately $\epsilon =0.5$, which denotes the mean value of the considered range. This is expected as the weight is flat when $m$ is low, which causes the average value to show up in the middle of the range. The area of the middle region with the minimum error increases with an increase in the truncation order. This indicates that, as $O$ becomes higher, the present new basis and Gaussian RBF become identical.

Figure 3c ($m=4$) illustrates that the region with the lowest error is deviated from $\epsilon =0.5$, unlike the results of Figure 3b. The region is wider when compared with the results of the lower $m$ values. That is attributed to the weight, which becomes a narrow bell shape as $m$ increases. With a view to ascertaining this observation, the results for an even higher $m$ value ($m=8$) are plotted in Figure 3d. The figure shows an even larger accurate region and lower error than Figure 3c. These results indicate that the variable $m$ controls how the distances ($r$) and shape parameter ($\epsilon$) are related. Furthermore, these results do not reveal any significant change when $N_e$ is greater than 5, which is why $N_e=5$ is used in this study unless stated otherwise.

The present new bases are validated in the next section. In addition, they are used for the interpolation and derivative approximations and are compared to the Gaussian RBF.

5. Numerical Results

The results in this section will reveal both the capability and deficits of the proposed models. This can be achieved by testing the accuracy of interpolation and approximation of derivatives utilizing a model function. The following function and its derivative are used to benchmark the proposed model:

$$f\left(x\right)=\arctan \left(bx\right)+\frac{\sin \left(bx\right)}{b^2{x}^2+1}$$

(16)

$$\frac{\partial f\left(x\right)}{\partial x}=\frac{b}{b^2{x}^2+1}+\frac{b|\cos \left(bx\right)}{b^2{x}^2+1}-\frac{2|b^2|x|\sin \left(bx\right)}{{(b^2{x}^2+1)}^2}$$

(17)

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}f\left(x\right)}{\partial x^2}=& \hfill -\frac{b^2|\sin \left(bx\right)}{b^2{x}^2+1}+\frac{8|b^4|x^2\sin \left(bx\right)}{{(b^2{x}^2+1)}^3}\\ \hfill -& \hfill \frac{2|b^3|x+2|b^2|\sin \left(bx\right)+4b^3|x|\cos \left(bx\right)}{b^2{x}^2+1},\end{array}$$

(18)

where $b=\pi /4$. The range of [−1, 1] is considered for $x$ in this work.

5.1. General Comparison

In the previous sections, it was claimed that the proposed model improves accuracy and stability over a wider range of shape parameter. In order to verify this claim, the model function and its derivatives (Equations (16)–(18)) are approximated with 41 mesh points. The error of the approximations is calculated. To compare for a range of $\epsilon$ values, the norm of the error is considered to identify a single value for each case. Additionally, the log10 is applied to the norm to show the number of significant digits of the error. Accordingly, the final formula to calculate the error can be expressed as follows:

$$\log 10\left[norm\left(F_{approx}-F_{analytical}\right)\right],$$

(19)

where $F$ could be $f\left(x\right)$, $\partial f/\partial x$, or ${\partial }^{2}f/\partial x^2$.

The results of the conventional approach are plotted in Figure 4. It is noteworthy that the error increases as $\epsilon$ decreases. This is expected because, at low $\epsilon$, the generated matrix of the RBF is ill-conditioned, which has a negative effect on the accuracy. It is shown that the minimum interpolation error decreases for $\epsilon \ge 1.43$ when $\epsilon$ increases, while it is the opposite for the derivatives. This is a clear indication of the undesired Runge’s phenomenon, which affects the accuracy of the interpolation for any other locations set than the given one. In Figure 4, the symbols denote the results evaluated at different locations (the mid-points between nodes) than the one used for evaluating the interpolation coefficients. It is shown that the results of the derivatives are not affected by location. Meanwhile, the accuracy of the interpolation decreases when $\epsilon \ge 1.43$, which is consistent with the derivatives. The minimum errors of the derivatives are −5.37 and −3.58 for $\frac{\partial f}{\partial x}$ and $\frac{{\partial }^{2}f}{\partial x^2}$, respectively, which are located at $\epsilon \approx 1.43$. These results will act as reference results with which to compare

For the sake of comparison, RBF-TS is used to approximate the same function used in the conventional approach. The results are shown in Figure 5. To determine the effect of the truncation order on the accuracy, the sub-figures are compared column-wise. It can be deduced that the order of truncation does not have a significant effect on the accuracy as the results do not vary greatly when they are compared column-wise. In each sub-figure in Figure 5, the accuracy does not change significantly with $\epsilon$; however, it changes with ${\epsilon }_0$. This indicates that the chosen approach is unfeasible because it switches the dependency from $\epsilon$ to ${\epsilon }_0$. Nevertheless, it will give a chance to introduce another novel approach (i.e., RBF-TPU).

In RBF-TPU, the range of ${\epsilon }_k$ is fixed between [0, 1], because we are interested in the region of small $\epsilon$. However, the number of regular points to divide that range ($N_e$) is varied. The same model function is used as in RBF-TS and regular RBF. The results are plotted in Figure 6, which show that the accuracy does not change greatly with the truncation order or with $\epsilon$. Additionally, the achieved accuracy is almost the same as the maximum accuracy that was achieved with regular RBF in Figure 4. It is also found that $N_e$ has a negligible influence on accuracy. Subsequently, this model removes any dependency on $\epsilon$, which is considered to be an advantage. However, this model depends on ${\epsilon }_k$ through the range of ${\epsilon }_k$ and the constant ($m$) of the weight of partition of unity. The effect of these parameters is discussed in the next two subsections.

5.2. Effect of Varying $m$

The chosen weight for the partition of unity of the Taylor series is a bell-shaped Gaussian function. To control the width of the Gaussian function, a constant, called $m$, is introduced in the weight equation. In the previous results, the constant $m$ was kept fixed ($m=1$). In this section, the same benchmark will be performed again; however, $m$ will be varied instead of $N_e$. In order to ensure that the present new basis is as close as possible to the Gaussian basis, a minimum value of $N_e=5$ is selected, as shown in Section 4. The results of varying $m$ are depicted in Figure 7. Evidently, the accuracy is a function of $m$. In addition, the first ($O=1$) and second ($O=2$) truncation orders show inconsistent results at low $\epsilon$ values. In contrast, the zeroth truncation order ($O=0$) provides consistent and reliable results with reasonable accuracy.

It should be emphasized that the results of Figure 7 are repeated for different model functions, number of grid points, grid distributions, and $N_e$ values. However, it is not plotted because the results are not found to vary significantly. In other words, the previously mentioned parameters have a negligible effect on the accuracy. Subsequently, careful study of these results allows choosing proper values for $m$ and $\epsilon$ regardless of the given data or the problem. These values can be inferred from Figure 7. In brief, large values of $m$ and small values of $\epsilon$ should be chosen, and vice versa. In order to remove the dependency of the accuracy on $m$ and $\epsilon$, the range of ${\epsilon }_k$ should be investigated.

5.3. Effect of the Range of ${\epsilon }_k$

It is worth mentioning that, despite being invariant under the change of many parameters, the RBF-TPU results are affected drastically by the chosen interval for ${\epsilon }_k$. All the previous results are obtained with the interval of [0, 1]. It is observed that scaling down the interval will worsen the results. However, extending the interval to [−1, 1] improves the results by increasing the high accuracy region, as illustrated in Figure 8. It is shown that, for the studied ranges of $m$ and $\epsilon$, the errors of interpolation, first derivative, and second derivative approximations are roughly less than seven, four, and three significant digits, respectively. By examining the color-bar of Figure 8, the negligible fluctuation of the error becomes evident. For example, the maximum and minimum errors of interpolation are −7.1 and −7.3, which has a negligible fluctuation. Consequently, the accuracy is independent of $m$ and $\epsilon$ when using [−1, 1] as a range of ${\epsilon }_k$. Additionally, the accuracy remains the same as the maximum accuracy achieved with the regular RBF (Figure 4). Furthermore, it is shown in the previous section (Section 5.1) that the accuracy is independent of $N_e$. Hence, it can be concluded that the present basis (RBF-TPU), which is derived from the partition of unity with respect to shape parameter, yields accurate results that are independent of the shape parameter, $N_e$, and $m$. Notably, the optimization of the range of ${\epsilon }_k$ needs to be done once, after which the resulting range can be used for different problems.

5.4. Effect of Changing the Model Function, Mesh Size, and Mesh Distribution

The findings of the previous sections are summarized in

Table 1. Comparison of the minimum error for approximating derivatives (Equations (17) and (18)) between Gaussian radial basis function (RBF) and partition of unity for Taylor series RBF (RBF-TPU). The results of RBF-TPU are obtained from Figure 8.

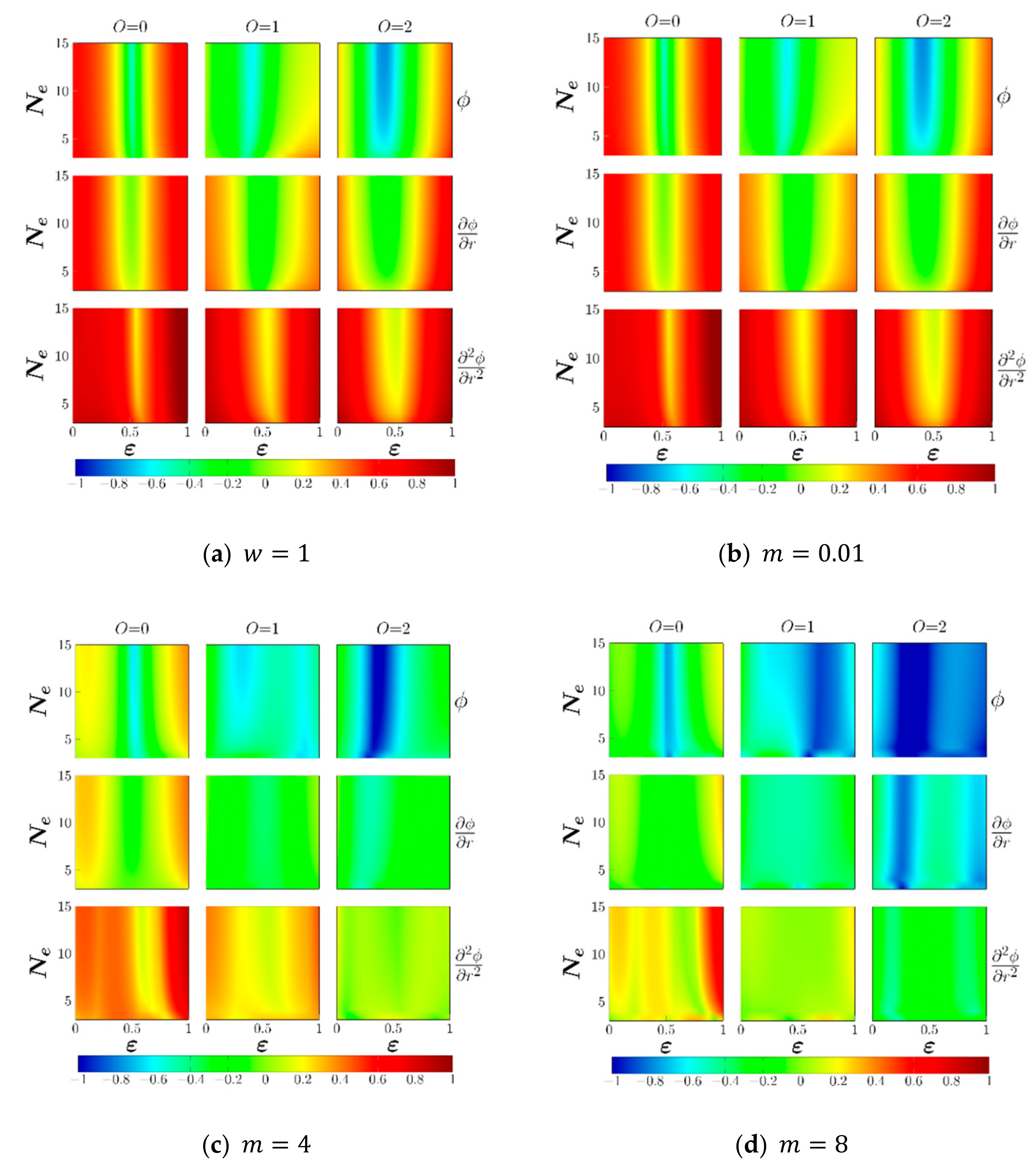
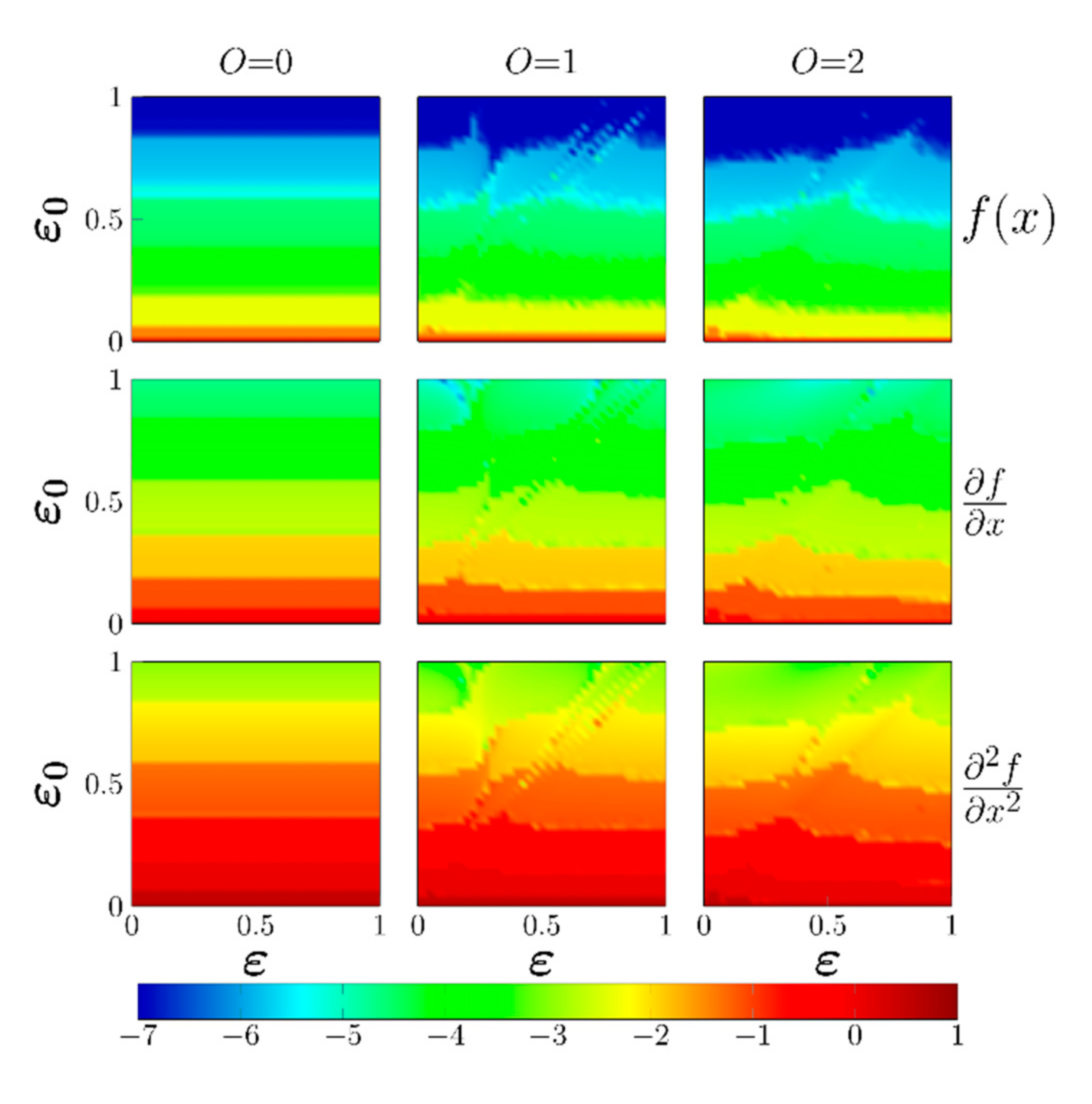
Model	Min log10[Norm(Error)]		Notes
	$\frac{\partial f}{\partial x}$	$\frac{{\partial }^{2}f}{\partial x^2}$
RBF	−5.37	−3.58	Depends on $\epsilon$ and has Runge’s phenomenon.
RBF-TPU	−4.70	−3.00	Does not depend on $\epsilon$, $m$, or $N_e$; once the range of ${\epsilon }_k$ is optimized, which should be done once.

. It is shown that RBF-TPU yields results that are comparable to those of Gaussian RBF, which are also independent of $\epsilon$, $N_e$, and $m$. However, the previous results are obtained for a single model function (i.e., Equation (21)), a single mesh size (21), and a single mesh distribution (Uniform). Importantly, these parameters should be varied to investigate the accuracy over a wider range of parameters so as to validate the optimality of the chosen range of ${\epsilon }_0$ ([−1, 1]). The mesh sizes of 21, 41, and 61 are considered, and uniform and stretched mesh distributions are also studied. The following formula is used to map a uniform mesh to a stretched one:

$$x=x_{min}+\left[\frac{\mathrm{erf}\left(2|\pi \frac{x-x_{min}}{x_{max}-x_{min}}-\pi \right)}{2|\mathrm{erf}\left(\pi \right)}+\frac{1}{2}\right]\left(x_{max}-x_{min}\right)$$

(20)

where $\mathrm{erf}$ denotes the error function, $x_{max}=1$, and $x_{min}=-1$.

A second model function is considered in addition to the first model function and its derivatives (Equations (21)–(23)).

$$f\left(x\right)=\frac{{(x^2-1)}^2}{\sqrt{x^2+1}}$$

(21)

$$\frac{\partial f}{\partial x}=\frac{3x^5+2x^3-5x}{{(x^2+1)}^{3/2}}$$

(22)

$$\frac{{\partial }^{2}f}{\partial x^2}=\frac{6x^6+15x^4+16x^2-5}{{(x^2+1)}^{5/2}}$$

(23)

RBF-TPU and Gaussian RBF are compared by varying the mesh size and mesh distribution for the two model functions. The results are depicted in

Table 2. Comparison of the minimum error for approximating derivatives between Gaussian RBF and RBF-TPU. The results of RBF-TPU are obtained from Figure 8. Note that “All” indicates the error is the same for all studied $\epsilon$ value.

Function	Mesh Distribution	Mesh Size	Method	Log10[Norm(Error)]		ε
				$\frac{\partial f}{\partial x}$	$\frac{{\partial }^{2}f}{\partial x^2}$	$\frac{\partial f}{\partial x}$	$\frac{{\partial }^{2}f}{\partial x^2}$
Equation (16)	Regular	21	RBF	−5.37	−3.58	1.43	1.10
			RBF-TPU	−4.70	−3.00	All	All
		41	RBF	−6.39	−4.43	1.35	1.35
			RBF-TPU	−5.01	−3.24	All	All
		61	RBF	−6.34	−4.46	1.33	1.33
			RBF-TPU	−5.01	−3.24	All	All
	Stretched (i.e., Equation (20))	21	RBF	−5.08	−4.18	1.18	1.18
			RBF-TPU	−4.14	−3.18	All	All
		41	RBF	−6.58	−4.66	1.35	1.35
			RBF-TPU	−4.98	−3.06	All	All
		61	RBF	−6.62	−4.46	1.35	1.35
			RBF-TPU	−4.85	−2.94	All	All
Equation (21)	Regular	21	RBF	−5.41	−3.46	1.35	1.35
			RBF-TPU	−3.86	−2.09	All	All
		41	RBF	−6.13	−4.48	1.33	1.33
			RBF-TPU	−4.29	−2.40	All	All
		61	RBF	−5.70	−3.77	1.35	1.30
			RBF-TPU	−4.20	−2.38	All	All
	Stretched (i.e., Equation (20))	21	RBF	−4.56	−3.14	1.15	1.10
			RBF-TPU	−3.80	−2.49	All	All
		41	RBF	−6.05	−4.63	1.33	1.33
			RBF-TPU	−4.38	−2.34	All	All
		61	RBF	−5.60	−3.63	1.30	1.30
			RBF-TPU	−4.14	−2.10	All	All

. For all cases reported in Table 2, the accuracy is independent of $m$ and $N_e$, which helps verify the results of the previous section. Table 2 illustrates that the accuracy of Gaussian RBF is maximum at a certain value of $\epsilon$; however, the accuracy of RBF-TPU is consistent over the studied range of $\epsilon$ ([0, 2]). Therefore, it can be concluded that the accuracy of RBF-TPU is always comparable to the maximum accuracy that is achieved with Gaussian RBF, although Gaussian RBF has a marginal better maximum accuracy at a certain $\epsilon$ value. This marginal difference is the price paid to achieve a consistent accuracy that is independent of the shape parameter.

5.5. Testing 2D Interpolation

In this section, the proposed RBF-TPU approach is assessed utilizing a 2D model function, where the following function and its derivatives are used:

$$f\left(x,y\right)={\left\{\sqrt{1+2\exp \left(-\frac{3}{2}\left(9\sqrt{x^2+y^2}-6\right)\right)}\right\}}^{-1}$$

(24)

$$\frac{\partial f\left(x,y\right)}{\partial x}=\frac{27x}{2\sqrt{x^2+y^2}}\exp \left(-\frac{3}{2}\left(9\sqrt{x^2+y^2}-6\right)\right)f^3\left(x,y\right)$$

(25)

$$\frac{\partial f\left(x,y\right)}{\partial y}=\frac{27y}{2\sqrt{x^2+y^2}}\exp \left(-\frac{3}{2}\left(9\sqrt{x^2+y^2}-6\right)\right)f^3\left(x,y\right)$$

(26)

The model function and its derivatives (i.e., Equations (24)–(26)) are approximated with 21 × 21 mesh points within the range of [−1, 1] for $x$ and $y$. This mesh size is selected as the mesh points have a negligible effect on accuracy, as seen in Table 2. The results of the conventional RBF approach are plotted in Figure 9. It can be observed that the results of the 2D model have a minimum error at a certain shape parameter value or in a narrow range of shape parameter values, similar to the case of 1D simulation (Figure 4). For regular mesh distribution, the minimum errors of the interpolation and derivatives are −0.707, 0.66, and 0.66 for $f$, $\frac{\partial f}{\partial x}$, and $\frac{\partial f}{\partial y}$, respectively, which are located approximately at $\epsilon \approx 0.95$. For the stretched mesh distribution, the minimum errors for $f$, $\frac{\partial f}{\partial x}$, and $\frac{\partial f}{\partial y}$ are −1.840, −0.260, and −0.260, respectively, and are located at $\epsilon \approx 3.6$. These results will act as reference results with which to compare. For RBF-TPU, the effects of $m$ and $\epsilon$ on the results of the 2D case are plotted in Figure 10. Similar to the case of 1D interpolation (see Figure 8), the error of RBF-TPU does not change significantly when changing $m$ and $\epsilon$. The results of the comparison between Gaussian RBF and RBF-TPU for the 2D case are tabulated in

Table 3. Comparison of the minimum error for approximating derivatives between Gaussian RBF and RBF-TPU for the 2D case (Equations (24)–(26)).

Mesh Distribution	Model	Min log10[Norm(Error)]
		$f$	$\frac{\partial f}{\partial x}$	$\frac{\partial f}{\partial y}$
Regular	RBF	−0.707	0.66	0.66
	RBF-TPU	−0.713	0.65	0.65
Stretched (i.e., Equation (20))	RBF	−1.840	−0.260	−0.260
	RBF-TPU	−1.117	0.132	0.145

. The average errors of interpolation and derivatives are −0.713, 0.65, and 0.65 for the regular mesh distribution and −1.117, 0.132, and 0.145 for the stretched mesh distribution. These results are consistent with the results obtained for the 1D case. Hence, it can be concluded that the present basis (i.e., RBF-TPU) yields accurate results for the 1D and 2D cases that are comparable to those of RBF interpolation and independent of the shape parameter, $N_e$, and $m$.

6. Conclusions

In this work, a proposal is made to apply the partition of unity approach to the Taylor series of RBF method in order to improve the basis of the method when using low shape parameter values ($\epsilon$). The Gaussian function is used as a weighting function for the partition of unity approximation and a constant referred to as $m$ is used to control the width of the Gaussian function. Subsequently, the effect of changing $m$ is presented. The obtained results from comparing the present basis and the Gaussian RBF reveal that, as $m$ approaches zero, the present basis approaches the mean value of Gaussian RBF over the reference shape parameter interval (${\epsilon }_0$). The proposed model is benchmarked and compared to a simple function. According to the results of this study, the proposed model has a good accuracy that is independent of $\epsilon$ and $N_e$ (the number of points to divide ${\epsilon }_0$ interval equally) when $m$ is constant. Meanwhile, the effect of varying $m$ instead of $N_e$ is also studied. The results indicate that $m$ and $\epsilon$ are inversely proportional to each other at a constant accuracy. The accuracy can be made independent of $m$ and $\epsilon$ by altering the interval of ${\epsilon }_0$. The results also reveal that an interval of [−1, 1] is an excellent choice because it produces accuracy that is comparable to the maximum accuracy of the Gaussian RBF and is also independent of $\epsilon$, $m$, and $N_e$. The main novelty of the current work is in introducing a way to get a reasonable accuracy using RBF interpolation without the need to pinpoint a specific value for the shape parameter.