Abstract
We consider the problem of utilizing the parcel locker network for the logistics solution in the metropolitan area. Two-echelon distribution systems are attractive from an economic standpoint, whereas the product from the depot can be distributed from or to intermediate facilities. In this case, the intermediate facilities are considered as locker facilities present in an accessible location in the vicinity of the final customers. In addition, the utilization of locker facilities can reduce the cost caused by the unattended deliveries. The problem is addressed as an optimization model that formulated into an integer linear programming model denoted as the two-echelon vehicle routing problem with locker facilities (2EVRP-LF). The objective is to minimize the cost of transportation with regards to the vehicle travelling cost, the intermediate facilities renting cost, and the additional cost to compensate the customer that needs to travel to access the intermediate facilities. Because of its complexity, a simulated annealing algorithm is proposed to solve the problem. On the other hand, the modelling approach can be conducted by generating two-phase optimization model approaches, which are the p-median problem and the capacitated vehicle routing problem. The results from both methods are compared in numerical experiments. The results show the effectiveness of 2EVRP-LF compared to the two-phase optimization. Furthermore, the simulated annealing algorithm showed an effective performance in solving 2EVRP-LF.
1. Introduction
E-commerce, also known as electronic commerce, refers to the buying and selling of goods or services using the Internet, and the transfer of money and data to execute these transactions. E-commerce sales worldwide amounted to 1.86 trillion US dollars and projected to grow to 4.48 trillion US dollars in 2021 [1]. The growth of e-commerce has evolved to make products easier to purchase through online retailers and marketplaces. Small businesses and large corporations have all benefited from e-commerce, which enables them to sell their goods and services at a scale that was not possible with traditional offline retail. Moreover, the growth of e-commerce is associated with an increasing number of packages delivered to individual customers. Thus, the last mile distribution plays a vital role in serving customers.
The last mile distribution are commonly used home delivery (HD) methods, and the packages are delivered directly to the recipients’ site. However, it is seen as a cost-ineffective approach for goods distribution. It is because this approach often met unfortunate condition such as heavy traffic and environmental issues, especially in the urban area. Therefore, the last mile distribution is regarded as the most expensive, most polluting, and the least efficient part of the e-commerce supply chain [2]. Moreover, there are occasional unattended deliveries that can raise the re-delivery cost.
Customer pickup (CP) is an option for the customers that is considered to be a less time-consuming and less costly process than the HD. In CP, customers are allowed to pick up or deliver the packages via intermediate facilities located nearby the customers’ home or office. The customer pickup locations are usually located in a public area that is easy to be accessed. A more traditional form of parcel locker is seen in the implementation of a reception box which is a fixed locker to receive a package that is installed outside a consumer’s home. Kämäräinen et al. [3] showed that the utilization of a reception box can reduce the cost of home delivery by 42%. Lemke et al. [4] found that 15% of the customer tends to have more intention to use the lockers if it is located near to their home.
Reverse logistics is a logistics network that consists of activities such as there are flows of product goes at least one step back in the supply chain. Business activities consist of moving goods from the customer to the retailer, the retailer to the distributor, and the distributor to the manufacturer. The purpose of those activities is varied from proper disposal at the end of the product life cycle, refurbish, product recall, to become a part of the green supply chain. These activities are beneficial for a company image which involved a trade-off with the cost required to support the process. Therefore, to unlock the full benefits of reverse logistics activities, the use of a parcel locker network needs to be further investigated.
Our proposed research concerns on how to conduct reverse logistics activities such as product return, refurbish, and product recall by utilizing parcel locker network. The problem is addressed as an optimization model that formulated into an integer linear programming model denoted as the two-echelon vehicle routing problem with locker facilities (2EVRP-LF). The objective is to minimize the cost of transportation with regards to the vehicle travelling cost to pick up the product from locker facilities/intermediate facilities, and the additional cost to compensate the customer that needs to travel to access the locker. Figure 1 shows the illustration of 2EVRP-LF.
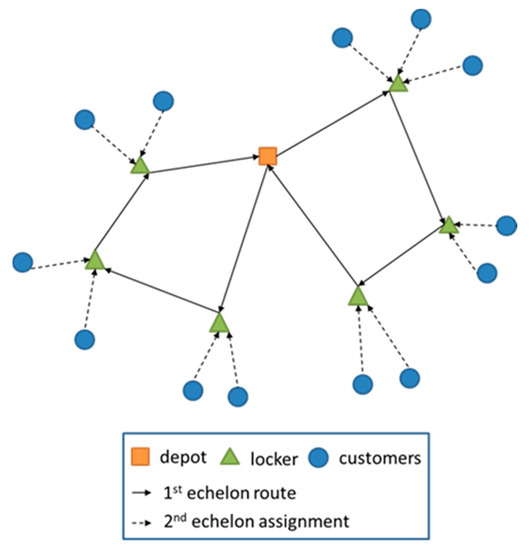
Figure 1.
The illustration of reverse logistics using parcel locker network facilities.
The remainder of this paper is organized as follows: In Section 2 we listed the literature review related to the study. Section 3 shows the formulation of the two-echelon VRP-LF model. We demonstrate the numerical experiments of this problem in Section 4. Finally, the conclusion and future research direction are discussed in Section 5.
2. Literature Review
In city logistics, direct delivery might be challenged by unexpected traffic and unattended delivery. This condition was one of the motivations for the introduction of two-echelon VRP (2E-VRP). Many studies are comparing the effectiveness of the HD approach using a single echelon strategy modelled as CVRP model to the CP approach of using two-echelon strategy.
The basic form of 2E-VRP is considered the two-echelon capacitated vehicle routing problem (2E-CVRP). The term was introduced by Perboli et al. [5]. The study proposed a mathematical model for the 2E-CVRP, which is based on the classical CVRP problem with the addition that the delivery from depot to customers is managed by routing and consolidating freight through intermediate depots. The nature of CVRP is an NP-Hard problem. Therefore, the 2E-CVRP as an extension of the CVRP is NP-hard [6].
Research conducted by Jepsen et al. [7] shows that the basic method used is the branch and cut algorithm in non-mathematical mathematical models that provides a strict lower limit for 2E-CVRP symmetrical. The computational results show that our algorithm is superior to the algorithm previously proposed in the literature, and we can complete 47 of 93 tests as an example of optimality in which 34 of them are solved for optimality for the first time. Santos et al. [8] developed Integer Programming formulation and two branch-and-price implementations for the Two-Echelon Capacitated Vehicle Routing Problem. One algorithm considers routes that satisfy the elementary conditions, while the other relaxes such constraints when pricing routes. Baldacci et al. [9] developed 2E-VRP through the addition of side constraints that function to derive valid lower bounds and an exact method that decomposes the 2E-CVRP into a limited set of multi depot capacitated vehicle routing problems. This research has quite a good impact on the 2E-VRP research area because it is able to offer an exact algorithm that is proven capable of solving 2E-VRP problems from journal sources before 2013. The research’s exact algorithm solved to optimality 144 out of the 153 instances from the literature and closed 97 of them for the first time. Sitek [10] in his paper presents a concept known as hybrid approach to modeling and optimization the 2E-VRP with integrating two environment of mathematical programing (MP) and constraint logic programming (CLP). There is also interesting research conducted by Soysal et al. [11] with a comprehensive MILP formulation for time-dependent two-echelon capacitated vehicle routing problem that accounts for vehicle type, traveled distance, vehicle speed, load, multiple time zones, and emissions. The paper offers insight on economies of environmentally friendly vehicle routing in 2E-VRP. The result shows the best solution is obtained from the use of the two-echelon distribution system.
Research on 2E-VRP continued to grow even from several previous studies, the application of metaheuristic, and applied in several other areas. Santos et al. [12] developed research in 2E-VRP from the previous research with a branch-and-cut-and-price for 2E-VRP. The algorithm tried reformulation based on q-routes that combines two important features. First, the symmetry issues observed in a formulation coming from a previous study of the problem that has been overcome. Second, it is strengthened with several classes of valid inequalities. Breunig et al. [13] in their paper addressed two optimization problems. The two-echelon routing problem and two-echelon location problem. The problems will be combined to produce itineraries to deliver goods to customers, with transit through intermediate facilities. The paper purposes hybrid metaheuristic approach which combines enumerative local search with destroy-and-repair principles, as well as some tailored operators to optimize the selections of intermediate facilities. Li et al. [14] conducted research with multi-echelon distribution strategy to minimize environmental impact as a consequence of logistic operations. The paper considered short-term tactical problem named two-echelon time-constrained vehicle routing problem (2E-TVRP) which was a little bit different from 2E-VRP. The result shows the scheduling provided by 2E-TVRP is promising to reduce the CO2 emissions per ton-kilometer of the linehaul-delivery system by adjusting the central depot location or developing the loaded-semitrailer demand among O-D pairs to eliminate empty-running of tractors. Eitzen et al. [15] applied 2E-VRP in transporting goods in urban logistics to reduce traffic congestion that might occur.
Wang et al. [16] in their research applied a metaheuristic approach based on variable neighborhood search (VNS) and integer programming to solve 2E-CVRP-E. The integer programing has a role to find better optimal result after VNS algorithm was applied. To validate its effectiveness, the metaheuristic first performs tests on 2E-CVRP instances and improves 13 current best-known solutions out of 234 instances. Wang et al. [17] proposed a genetic-algorithm-based (GA) approach to solve the 2E-CVRPSD. A simple encoding and decoding scheme, a modified route copy crossover operator, and a satellite-selection-based mutation operator are devised in this approach. The numerical results show that for all instances, the expected cost of the best 2E-CVRPSD solution found by the proposed approach is not greater than that of the best-known 2E-CVRP solution with an average relative gap of 2.57%. Therefore, the GA-based approach can find high-quality solutions for the 2E-CVRPSD. Liu et al. [18] formulated the problem as a mixed 0-1 linear program and proposed five families of valid inequalities to strengthen the model. Based on the model and the inequalities, we implement a branch-and-cut algorithm to solve the problem. The proposed branch-and-cut algorithm was evaluated on two classes of randomly generated instances. The computational results show that the five families of valid inequalities can substantially improve the lower bounds yielded by the LP relaxation of the model, and the branch-and-cut algorithm can solve more instances to optimality than CPLEX. We also conduct additional experiments to analyze the impacts of the grouping constraints on the problem and illustrate the differences between the 2E-CVRPGC and the 2E-CVRP. Sahraeian and Esmaeili [19] tried to minimize the total travel cost, customer waiting time, and carbon dioxide emission in 2E-CVRP with perishable food. The proposed model is a mixed-integer non-linear programming (MINLP). By applying some linearization methods, the MINLP model exchanged to a mixed-integer linear programming (MILP). This paper uses a non-dominated sorting genetic (NSGA-II) algorithm to solve the presented mathematical model. The related results would be compared with Lp-metric results in small-sized test problems and with multi-objective particle swarm optimization (MOPSO) algorithm in medium and large-sized test problems. In order to evaluate the quality of the solution sets, the results of two meta-heuristic algorithms are compared based on four comparison metrics in medium-sized problems. The obtained results indicate the efficiency of the NSGA-II algorithm.
Kitjacharoenchai et al. [20] introduced a new routing model that considers a synchronized truck-drone operation by allowing multiple drones to fly from a truck, serve one or multiple customers, and return to the same truck for a battery swap and package retrieval. The model addresses two levels (echelons) of delivery: primary truck routing from the main depot to serve assigned customers and secondary drone routing from the truck, which behaves like a moveable intermediate depot to serve other sets of customers. The model takes into account both trucks’ and drones’ capacities with the objective of finding optimal routes of both trucks and drones that minimizes the total arrival time of both trucks and drones at the depot after completing the deliveries. The problem can be solved by formulated mixed integer programming (MIP) for the small-size problem, and two efficient heuristic algorithms are designed to solve the large-size problems: Drone Truck Route Construction (DTRC) and Large Neighborhood Search (LNS). The development of 2E-VRP research shows if there is no research that combines the 2E-VRP problem with the locker facility. So that the research carried out in this paper will provide a good addition to research in the field of 2E-VRP.
The solution approach for solving 2E-CVRP consist of developing exact approaches, heuristic methods, or a combination of both. The exact approach commonly using column generation techniques such as branch and bound or branch and prices. Meanwhile, heuristics methods are mostly using metaheuristics such as GA, TS, and ALNS. Recent developments are combining exact approach and heuristics approach known as math-heuristics.
The use of two-echelon for parcel distribution is applied in many real-life problems. Therefore, there is an increasing number of distribution modelled using the two-echelon approaches shows in the literature. A survey regarding the overview of two-echelon distribution systems are presented in Cuda, Guastaroba, and Speranza [6]. Despite the use of the two-echelon on various type of application, to our knowledge, a model that considers the use of parcel locker facilities for reverse logistics using 2E-VRP based model is not available. Therefore, this study proposed the two-echelon vehicle routing problem with locker facilities for reverse logistics. One of the references used in the development of this research case was carried out by Deutsch and Golany [21]. This research focuses on the problem of designing a parcel locker network as a solution to the Logistics Last Mile Problem: choosing the optimal number, locations, and sizes of parcel lockers facilities. The objective is to maximize the total profit, consisting of the revenue from customers who use the service, minus the facilities’ fixed and operational setup costs, the discounts in the delivery costs for customers who need to travel in order to collect their parcels, and the loss of potential customers who are not willing to travel for service. Therefore, this study proposes a two-echelon vehicle routing problem with locker facilities for reverse logistics. This research tries to find the best solution to minimize the traveling cost and the discount given to the customer using the 2E-VRP model approach and the search for optimal solutions using a simulated annealing metaheuristic.
3. Two-Echelon Vehicle Routing Problem with Locker Facilities
The network structure of 2EVRP-LF consists of two-echelon distribution network; the first echelon comprises of Set M = {1 … |M|}, where m = 1 represent the depot, and the rest are intermediate facilities (locker facilities). The nodes in the first echelon are connected and associated with the distance. Csij represents distance travelled from node i to j where . The second echelon consists of the locker facilities and the customer node. The customer node are represented in set N = {1 … |N|} and also includes the distance between pairs of customers and lockers facilities represented as Ccij represent distance travelled from node i to j where . Each customer is associated with demand Dn where . The customer assignment in the second echelon is restricted to the parcel locker facility Qsm where . The routing decision in the first echelon is limited by the capacity of the available vehicle Qvv where v is one of the vehicles available represented in set V = {1 … |V|}. The models developed are using the decision variables as follows.
Decision variables
- Xi,j,v
- 1; if there is a route from i to j using vehicle v0; Otherwise
- Zi
- 1; if the locker i is opened0; Otherwise
- Si,j
- 1; if customer i is served by parcel locker j
- Qi
- Total amount of demand in parcel locker i
- ai,v
- Number of demand in parcel locker i using vehicle v
Objective
The objective function (1) minimizes the total system costs that consist of transportation cost for the first echelon and the cost occurred to compensate for additional distance travelled by the customers in the second echelon. Constraints (2) and (3) ensure that the locker opened are served once in the routing decision of the first echelon. Constraint (4) ensures the consecutive movement of vehicles in the first echelon. Constraints (5) and (6) ensure that a vehicle is starting and returning to the depot. Constraints (7) and (8) restrict the parcel capacity limits the total customers’ demand assigned to each parcel. Constraint (9) restricts a customer is served only by one locker facility. Constraint (10) ensures the flow continuity. Lastly, constraint (11) ensures that the demand being served at each vehicle does not exceed its capacity limit.
4. Simulated Annealing for Solving 2EVRP-LF
In this study, a simulated annealing (SA) algorithm is used to solve the proposed 2EVRP-LF. SA has been reported successfully to solve the VRP and its variants [22,23,24,25]. The main characteristic of SA that differs from the other approaches is the mechanism to allow exploration on worse solutions, even infeasible solutions with a small probability in order to escape from local optimal. The probability to accept worse solution is determined by a formula that considered the difference between solutions and parameter denoted as temperature. This section describes the detail component of implementing SA for 2EVRP-LF, including solution representation, parameters used, SA procedure, and neighborhood move.
4.1. Solution Representation
A solution is represented by a string of numbers consisting of intermediate facilities denoted by the set {1,2, …, |M|}, |V| − 1 dummy zeros represent the vehicle being used, and the set {|M|, … , |M| + |N|} represents the customers. Figure 2 shows the solution representation and the illustration of the solution associated with it. The mechanism to convert from the solution representation is described as follows. First of all, two lists are generated based on the solution, namely an intermediate facility list (IFL) and customer list (CL). IFL consists of the intermediate facilities and dummy zeros ordered by the sequence of its appearance in the solution. IFL represents the priority of visiting each intermediate facilities on each vehicle that is represented by the dummy zeros; take the example for the solution in Figure 2. The solution is generated based on data provided in Table 1 and Table 2. In this example, each intermediate facility has a capacity of 20. In addition, the demand associated with each customer is 10. It is also assumed that the vehicle capacity is 50. The solution list of {2,5,6,1,7,8,0,4,10,9,3} is broken down into IFL and CL. The IFL consists of {2,1,0,4,3}. Meanwhile, the CL consists of the priority list of customer ordered by the sequence of its appearance in the solution. In this example, CL consists of {5,6,7,8,10,9}. Based on these two list, we can assign the customer to the intermediate facility based on the order of IFL and CL. Also, we use the list in IFL to determine which IF is visited by the first vehicle, second vehicle, and so on. In this case, the first vehicle is visiting the intermediate facility 2 then intermediate facility 1. The intermediate facility 2 is only receiving a package from customer 5 and 6 because of the capacity constraint of the facility. While intermediate facility 1 is receiving a package from customer 7 and 8. Then, the next vehicle is assigned to visit intermediate facility 4 and 3. Intermediate facility 4 is assigned to receive a package from customer 10 and 9. However, intermediate facility 3 is not necessary as all customers have been served. Therefore, in this case intermediate facility 3 is not visited.
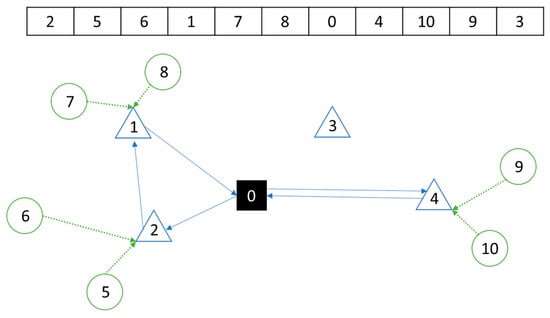
Figure 2.
Illustration of solution representation for 2EVRP-LF.

Table 1.
Illustration of input data for 2EVRP-LF.

Table 2.
Example of cost-matrix between nodes for 2EVRP-LF.
4.2. Parameters Used
The proposed SA algorithm requires four parameters: Iiter, T0, Tf, and alpha. Iiter denotes the number of iterations with which the search proceeds at a particular temperature. T0 represents the initial temperature. Tf is final temperature, and alpha is a coefficient used to control the speed of the cooling schedule.
4.3. SA Procedure
The proposed simulated annealing (SA) starts with an initial random solution. After the initial phase, the algorithm continues to improvement phase. The improvement phase tries to get a better solution than the initial phase by randomly choosing different neighborhood moves, such as swap, insertion, and reverse moves. At the beginning, the current temperature T is set to T0 and randomly generates initial solution denoted as X. The current best solution, Xbest, and the best objective function of X, denoted by Fbest, are set to be X and objective (X), respectively.
In the improvement phase a new solution Y is generated from the neighborhood of current solution X, N(X), and its objective function value is evaluated. Let Δ is equal to the difference between objective of Y and objective of X. If Δ is less than zero, then it means that Y is better than X, and therefore X is replaced by Y; otherwise, the probability of replacing X with Y is exp(Δ/T). Here, Xbest and Fbest record the current best solution and the best objective function value, correspondingly. The current temperature T decreases after Iiter using formula T = T*alpha. The algorithm terminates when the current temperature is lower than Tf.
4.4. Neighborhood
There are three neighborhood moves used in the proposed SA. They are swap, insert, and reverse. The swap neighborhood consists of exchanging the positions of two nodes in the solution. The insertion neighborhood consists of removing a node from it and inserting it after a random position j in the solution. The reverse move is performed by randomly choosing two nodes and reversing the order of the nodes between them.
5. Computational Experiments
The mathematical model solved using a commercial MILP solver, GUROBI, that coded on AMPL a mathematical programming language. The experiment was performed on a PC with specifications of Intel (R) Core (TM) i7 at 3.60 GHz, 16 Gb of RAM, and running on a 64-bit platform under Windows 10 Operating System. The computational experiments were conducted to show the improvement gained by considering 2EVRP-LF and the effectiveness of the proposed SA on solving 2EVRP-LF. The following sub-section describe the test instances, parameter settings, and computational results
5.1. Test Instances
The test instances are generated based on the CVRP dataset proposed by Augerat et al. (datasets A, B, and P), by Christofides and Eilon (for dataset E), by Fisher (for dataset F), and by Christofides, Mingozzi, and Toth (for dataset M). From those instances, a number of m randomly positioned parcel lockers are generated around the customers’ location. Therefore, the result from CVRP can be compared to the result of the first echelon distance travelled in 2EVRP-LF. Meanwhile, another approach is being tested to solve the problem. This approach consists of two steps commonly known as two phases optimization. The first step is optimizing the allocation of customers to the locker facility using an optimization approach which is modelled as the p-median problem. Then the result of the first phase optimization is used as an input for the second phase optimization. The second phase optimization is to generate vehicle routes to serve the demand at each locker facility. This phase is solved using a CVRP model.
The second experiment uses the proposed SA to solve the same instances. In this experiment a comparison between the results of SA with the results generated using exact solution is carried out. The purpose is to show the effectiveness of SA to solve 2EVRP-LF.
5.2. Parameter Settings
This study uses one-factor-at-a-time (OFAT) procedure for the parameter tuning that is shown to be effective to choose the parameter for the simulated annealing heuristics [23]. The OFAT procedure set one parameter sequentially at a time. In these experiment, each parameter has several option to choose as follows.
Iiter: 10 N, 25 N, 250 N
T0: 5, 25, 50
TF: 5, 0.5, 0.05
Alpha: 0.25, 0.5, 0.9
For example, as shown in Figure 3a, three parameter of Iiter were observed, meanwhile the other parameters were fixed at the same number. The experiment shows that parameter with Iiter is equal to 25 N provides the best objective function with acceptable computational time. Therefore, the selected parameter for Iiter is 25 N, where N represents the number of customers. Meanwhile, when observing T0, the result shows that the objective values of all three parameters were not much different. Therefore, computational time was used as the tie-breaker that ends up choosing T0 is equals to 5. The rest of the parameters use the same principle. After parameter tuning, it is decided that the parameter used for the experiments are T0 = 5, Tf = 0.05, Iiter =25N, and alpha = 0.9. The analysis on impact of each SA parameters on objective function and computational time is shown in Figure 3.
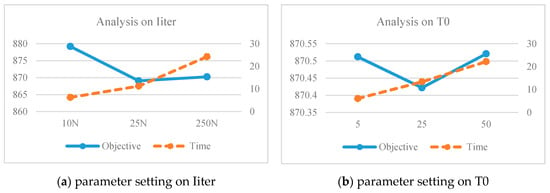
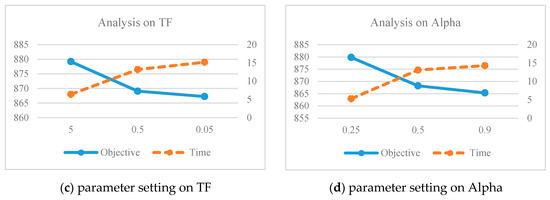
Figure 3.
SA parameters setting.
5.3. Computational Results
The numerical results for the first experiment are shown in Table 3. Columns 1–3 consist of the instance no, name, and a number of parcel locker facility in the corresponding instance. The following columns 4 and 5 are the objective and number of vehicle being used for the CVRP solution. The next columns are the results related to 2EVRP and 2Phases approaches. Those columns use header Echelon1 (objective value of the first echelon), Echelon2 (objective value of the first echelon), NV (number of the vehicle used for the routing in the first echelon), and the CPU solving time to obtain the results. The last two columns show the saving of routing cost using 2EVRP-LF compared to the CVRP and the comparison between the total cost of using 2EVRP-LF and 2Phases optimization approach.

Table 3.
Comparisons of VRP, 2EVRPLF using Gurobi, and 2EVRP-LF using the 2Phase approach.
The results show that using 2EVRP-LF can give benefits by having on average 70.4% less cost compared to conducting the last mile using HD concept or in this case modelled as CVRP. However, in order to make this saving the user needs to travel to the designated pickup station that on average is 2.623 times of the routing distance. Therefore, a common approach of using CP is to give some compensation to make it interesting to the customers to use the system. This compensation can use the saving obtained from the less routing cost in the first echelon. Further analysis shows that the two-phase optimization generates a worse solution compared to the 2EVRP-LF. The average difference between the two approaches is 18.95%. The situation is expected because the sub-optimal result is generated at each phase of the 2Phases approach. However, the 2EVRP-LF still has drawbacks in solving instances with a large number of m. This exposes the limitation of the solver to solve the problem which belongs to the class NP-hard problem.
The results from the second experiment, as shown in Table 4, are compared with the previous results of 2EVRPLF generated using GUROBI solver with the proposed SA. The results show that using SA the average distance travelled in the first and second echelon are 322.46 and 826.88, respectively. Furthermore, the average percentage different between GUROBI and SA shows that SA can give a better result with an average of 2.01%. The computational time of SA is also faster with the average of 2.57. As suspected earlier, exact solution approach such as using GUROBI has limitation on larger and more complex instances. It is indicated by the result that SA can better perform mostly on the instances where GUROBI was not able to generate the optimal solution. Meanwhile, for the result that already solved until optimality, the percentage difference is zero. Furthermore, Table 5 shows the detail experimental results of the 2EVRPLF dataset in terms of the best objective function found and the average computational results over five replications. The result description can be used by the future researchers to conduct and repeat the experiment.

Table 4.
Comparisons of 2EVRPLF using SA with exact solution approach.

Table 5.
Detail result of SA for 2EVRPLF.
6. Conclusions and Future Research Directions
This research proposes the two-echelon vehicle routing problem with locker facilities, which is an extension of 2E-CVRP. The problem is modelled as an integer linear programming problem. This 2E-VRPLF is used to represent the utilization of parcel networks facilities to conduct reverse logistics activities in the urban area. The strategy of using the locker facilities is also known as customer pickup strategy. Numerical examples are conducted to show the effectiveness of using CP compared to the home delivery strategy. It is shown that the use of CP based on 2E-VRPLF allows reducing the transportation cost by 70.4% with the average number of vehicles being 2-3 vehicles compared to the 6-7 vehicles used in the HD strategy. This saving can also be considered as the maximum compensation that can be given to the customer because the average travel distance of 2.623 times of the supplier’s travelled distance needs to be taken into consideration. Furthermore, the utilization of 2E-VRPLF is more effective than using the two-phase approach.
Furthermore, the experiment of using SA for solving 2E-VRPLF showed a promising result. The SA approach can provide a better result compared to solving the 2E-VRPLF using an exact solution approach such as using GUROBI solver. The computational time of using the SA approach is also reported to be faster. However, the computational result still needs to be experimented on a more complex problem that happen in practice or real-life.
As so many sophisticated metaheuristics are available, further research needs to investigate the use of heuristics or metaheuristics approach that enables to find a better solution. It is also interesting to explore a more practical consideration in the mathematical model such as time windows, pickup and delivery situation, and multiple depots. In addition, the implementation of two-echelon model might not only be applicable for the land transportation but also for sea transportation such as for maritime route optimization problems.
Author Contributions
Conceptualization, A.A.N.P.R.; methodology, A.A.N.P.R., P.J., A.C.K.; software, A.A.N.P.R.; validation, A.A.N.P.R., A.C.K.; formal analysis, A.A.N.P.R., P.J.; investigation, A.A.N.P.R., P.J.; resources, A.A.N.P.R.; data curation, A.A.N.P.R., P.J.; writing—original draft preparation, A.A.N.P.R.,P.J., A.C.K., S.F.P., R.N.; writing—review and editing, A.A.N.P.R., P.J., A.C.K., O.A.C.D; visualization, A.A.N.P.R., P.J., A.C.K.; supervision, S.F.P., R.N., O.A.C.D.; project administration, A.A.N.P.R., P.J.; funding acquisition, A.A.N.P.R., P.J., A.C.K., S.F.P., R.N., O.A.C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universitas Pertamina under UP-UISI 2019 collaboration grant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Statista Global Retail E-Commerce Market Size 2014—2021. Available online: https://www.statista.com/statistics/379046/worldwide-retail-e-commerce-sales/ (accessed on 3 October 2019).
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Characteristics of Innovations in Last-Mile Logistics-Using Best Practices, Case Studies and Making the Link with Green and Sustainable Logistics; Association for European Transport and Contributors: London, UK, 2009. [Google Scholar]
- Kämäräinen, V.; Saranen, J.; Holmström, J. The reception box impact on home delivery efficiency in the e-grocery business. Int. J. Phys. Distrib. Logist. Manag. 2001, 31, 414–426. [Google Scholar] [CrossRef]
- Lemke, J.; Iwan, S.; Korczak, J. Usability of the parcel lockers from the customer perspective–the research in Polish Cities. Transp. Res. Procedia 2016, 16, 272–287. [Google Scholar] [CrossRef]
- Perboli, G.; Tadei, R.; Vigo, D. The two-echelon capacitated vehicle routing problem: Models and math-based heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef]
- Cuda, R.; Guastaroba, G.; Speranza, M.G. A survey on two-echelon routing problems. Comput. Oper. Res. 2015, 55, 185–199. [Google Scholar] [CrossRef]
- Jepsen, M.; Spoorendonk, S.; Ropke, S. A branch-and-cut algorithm for the symmetric two-echelon capacitated vehicle routing problem. Transp. Sci. 2013, 47, 23–37. [Google Scholar] [CrossRef]
- Santos, F.A.; da Cunha, A.S.; Mateus, G.R. Branch-and-price algorithms for the two-echelon capacitated vehicle routing problem. Optim. Lett. 2013, 7, 1537–1547. [Google Scholar] [CrossRef]
- Baldacci, R.; Mingozzi, A.; Roberti, R.; Calvo, R.W. An exact algorithm for the two-echelon capacitated vehicle routing problem. Oper. Res. 2013, 61, 298–314. [Google Scholar] [CrossRef]
- Sitek, P. A hybrid approach to the two-echelon capacitated vehicle routing problem (2E-CVRP). In Recent Advances in Automation, Robotics and Measuring Techniques; Springer: Berlin/Heidelberg, Germany, 2014; pp. 251–263. [Google Scholar]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Bektaş, T. The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations. Int. J. Prod. Econ. 2015, 164, 366–378. [Google Scholar] [CrossRef]
- Santos, F.A.; Mateus, G.R.; da Cunha, A.S. A branch-and-cut-and-price algorithm for the two-echelon capacitated vehicle routing problem. Transp. Sci. 2015, 49, 355–368. [Google Scholar] [CrossRef]
- Breunig, U.; Schmid, V.; Hartl, R.F.; Vidal, T. A large neighbourhood based heuristic for two-echelon routing problems. Comput. Oper. Res. 2016, 76, 208–225. [Google Scholar] [CrossRef]
- Li, H.; Yuan, J.; Lv, T.; Chang, X. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems considering carbon dioxide emissions. Transp. Res. Part D Transp. Environ. 2016, 49, 231–245. [Google Scholar] [CrossRef]
- Eitzen, H.; Lopez-Pires, F.; Baran, B.; Sandoya, F.; Chicaiza, J.L. A Multi-Objective Two-Echelon Vehicle Routing Problem. An Urban Goods Movement Approach for Smart City Logistics. In Proceedings of the 2017 XLIII Latin American Computer Conference (CLEI), Cordoba, Argentina, 4–8 September 2017; pp. 1–10. [Google Scholar]
- Wang, K.; Shao, Y.; Zhou, W. Matheuristic for a two-echelon capacitated vehicle routing problem with environmental considerations in city logistics service. Transp. Res. Part D Transp. Environ. 2017, 57, 262–276. [Google Scholar] [CrossRef]
- Wang, K.; Lan, S.; Zhao, Y. A genetic-algorithm-based approach to the two-echelon capacitated vehicle routing problem with stochastic demands in logistics service. J. Oper. Res. Soc. 2017, 68, 1409–1421. [Google Scholar] [CrossRef]
- Liu, T.; Luo, Z.; Qin, H.; Lim, A. A branch-and-cut algorithm for the two-echelon capacitated vehicle routing problem with grouping constraints. Eur. J. Oper. Res. 2018, 266, 487–497. [Google Scholar] [CrossRef]
- Sahraeian, R.; Esmaeili, M. A multi-objective two-echelon capacitated vehicle routing problem for perishable products. J. Ind. Syst. Eng. 2018, 11, 62–84. [Google Scholar]
- Kitjacharoenchai, P.; Min, B.-C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598. [Google Scholar] [CrossRef]
- Deutsch, Y.; Golany, B. A parcel locker network as a solution to the logistics last mile problem. Int. J. Prod. Res. 2018, 56, 251–261. [Google Scholar] [CrossRef]
- Osman, I.H. Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Ann. Oper. Res. 1993, 41, 421–451. [Google Scholar] [CrossRef]
- Yu, V.F.; Redi, A.P.; Hidayat, Y.A.; Wibowo, O.J. A simulated annealing heuristic for the hybrid vehicle routing problem. Appl. Soft Comput. 2017, 53, 119–132. [Google Scholar] [CrossRef]
- Yu, V.F.; Purwanti, S.S.; Redi, A.P.; Lu, C.-C.; Suprayogi, S.; Jewpanya, P. Simulated annealing heuristic for the general share-a-ride problem. Eng. Optim. 2018, 50, 1178–1197. [Google Scholar] [CrossRef]
- Redi, A.A.N.P.; Maula, F.R.; Kumari, F.; Syaveyenda, N.U.; Ruswandi, N.; Khasanah, A.U.; Kurniawan, A.C. Simulated annealing algorithm for solving the capacitated vehicle routing problem: A case study of pharmaceutical distribution. J. Sist. Dan Manaj. Ind. 2020, 4, 41–49. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).