Any block preconditioner for a saddle-point linear system, like the one that we considered, can only yield scalable results if the preconditioners used to approximate the block and the Schur complement are scalable. Therefore, the main task is to find such suitable preconditioners for the two blocks involved.
5.1. Block Preconditioner
It is well known that Multigrid methods allow for obtaining scalable results for convection-diffusion problems. Our
block indeed represents a discretized convection-diffusion operator and, therefore, we expect to obtain scalable results while using a suitable Multigrid scheme. An accurate analysis of the scalability provided by Multigrid can be found, for instance, in [
23,
24].
The application of a Multigrid preconditioner is particularly easy in the case of diffusion-dominated problems, since even the very simple damped Jacobi smoother is able to produce optimal results. However, in the case of convection-dominated problems, the choice of the smoother is fundamental for obtaining satisfactory results. In these situations, it is necessary to use a more sophisticated smoother, like the Gauss–Seidel method, coupled with an adequate choice of the pattern used to apply it; this pattern should try to follow the convective flow as much as possible. In the case of complicated recirculating flows, it is not possible to generate a pattern that is able to do this and so different strategies must be employed. In [
2], the suggestion is to use multiple iterations of the Gauss-Seidel smoother, each one performed following a simple pattern. In particular, if the flow is recirculating and therefore has components both negative and positive in directions
x and
y, then there should be four patterns and they should sweep through the domain in both directions, going back and forth. Hence, one pattern will evolve in the
x direction, from the left to the right, another one from right to left. The same holds for the
y direction, yielding a total of four different smoothing patterns. An alternative using only one pattern in every direction is possible: this approach will be cheaper, but a single iteration will be less accurate. This option has been used, for instance, in [
13] when dealing with convection-diffusion problems.
One thing to remember is that, when multiple patterns are used for every smoothing iteration, they should be applied in opposite order in the pre- and post-smoothing phases. If in the pre-smoothing step, we apply first pattern A and then pattern B, then in the post smoothing phase we should apply first pattern B and then A.
The drawback of using multiple patterns is that some parts of the flow, which only have component of the velocity in one direction, do not need smoothing in the other direction. Thus, a lot of time is lost smoothing in directions that are not necessary. This is not a problem for convergence, since this excessive smoothing does not worsen the solution, but it is a problem for the computational time. Moreover, this approach does not exploit the separability of the block: indeed, the convection-diffusion operator consists of a block-diagonal matrix, with two identical blocks, one for direction x and one for y. This structure of the matrix can be exploited to obtain a more efficient implementation: indeed, when applying the preconditioner to a vector r, we can split this vector into and and apply to each of these components just the preconditioner for one of the diagonal blocks of matrix F. In this way, the dimensions of the matrices used are halved and, more importantly, we can choose to perform the smoothing only in the direction that we are considering. This means that when we apply the preconditioner to , we use Gauss–Seidel with a pattern that only evolves in the x direction. We do not expect more accurate solutions with this method, since applying extra smoothing does not create such a problem, but we expect to reduce the computational time required.
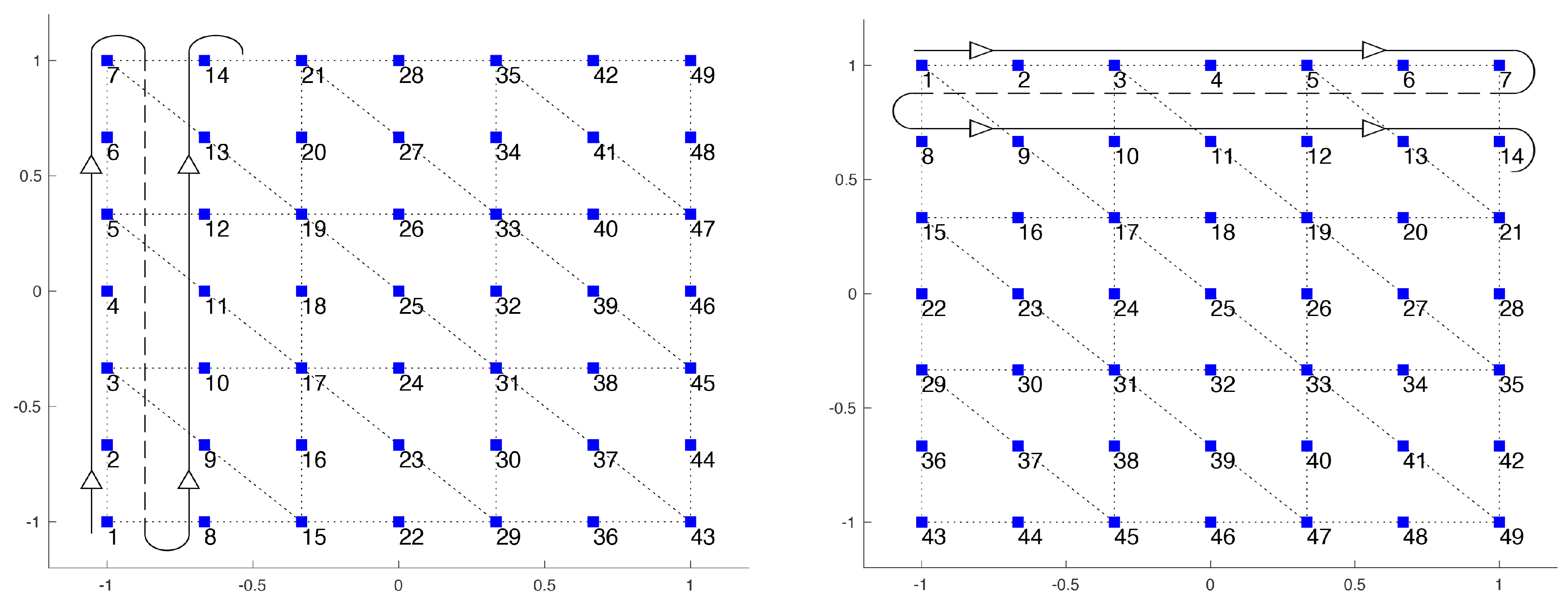
Two approaches are possible when applying one of the patterns in the smoothing phase. We can divide the pattern in groups and apply the smoother to all the nodes of every group simultaneously; for instance, if the pattern to be applied evolves in the x direction, then each group would be one of the vertical lines of nodes. In this way, the smoother updates all of the values for these nodes at once, which is the best approach possible. However, in this way, the linear system to be solved inside Gauss–Seidel is block triangular and not triangular. Alternatively, we can apply the smoother to every node individually; in this way, the system to be solved is triangular, but along every line, some nodes are updated before and some others later. We used the second approach, as the results were very similar, but the computational time was lower.
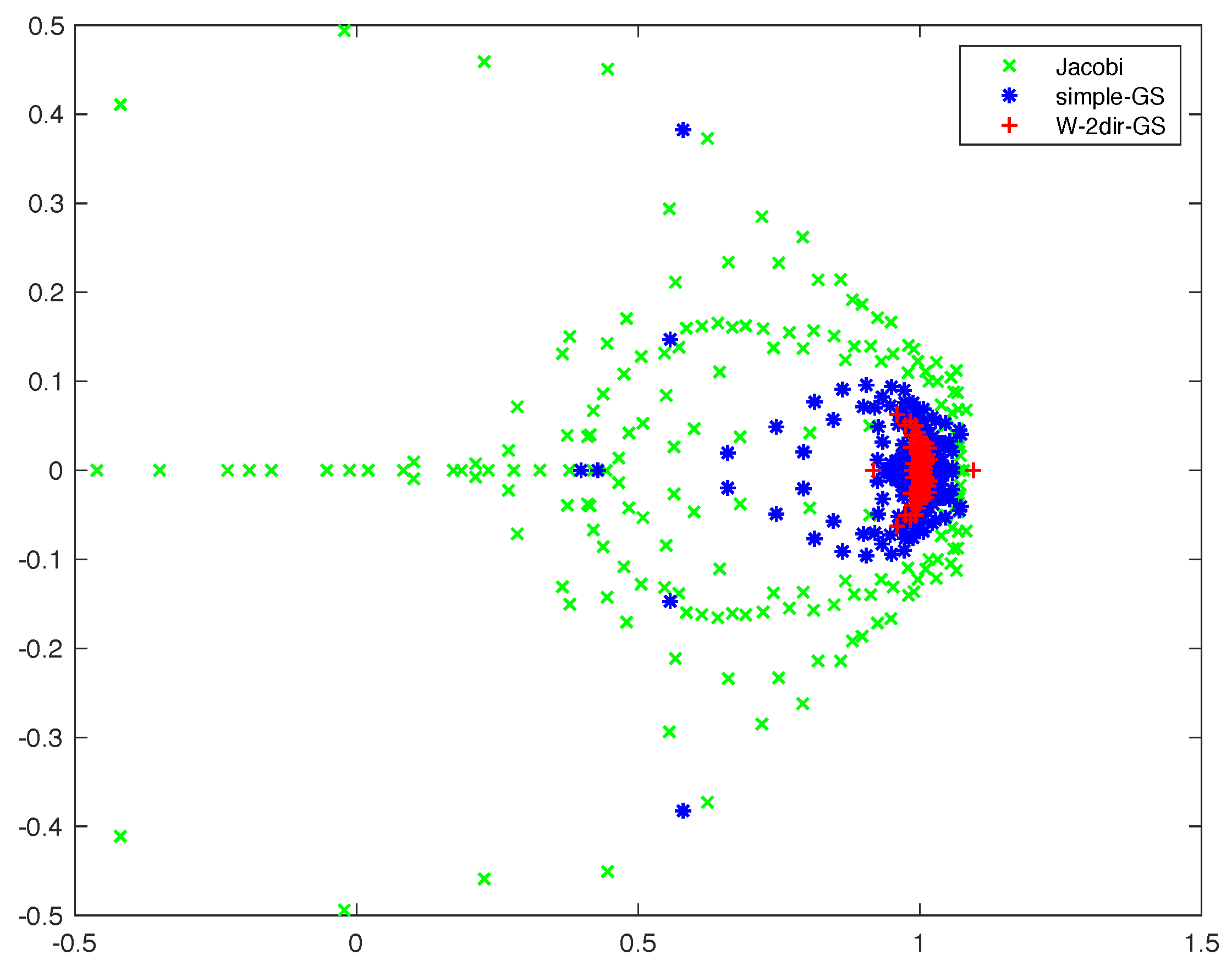
In the numerical experiments, we tested four different approaches, which are summarized in the following:
Jacobi, which identifies the Multigrid scheme using the simple damped Jacobi smoother.
simple-GS, which indicates the use of Gauss-Seidel with lexicographic ordering.
2dir-GS, which identifies the Gauss-Seidel smoother applied with two patterns, one for every direction.
split-GS, which indicates the new approach that exploits the structure of the block.
The patterns that are used in the last two approaches are shown in
Figure 2 for a small grid.
Besides the smoother, there are other aspects of the Multigrid preconditioner that must be treated with care when dealing with convection-dominated problems. Stabilization needs to be taken into account: when passing from one grid to the next, the matrix to be used in the following grid must be the exact matrix, with the accurate stabilization; the Galerkin coarse grid operator should be avoided, because the coarser grids need stabilization, while the fine ones may not need it. In our experiments, we used streamline diffusion stabilization.
The restriction and prolongation operators can be taken to be the natural ones, i.e., the ones obtained exploiting the values of the basis functions over the nodes of the discretizations. Finally, we need to choose the cycle to be used: a V-cycle would be cheaper, but it may need more iterations to obtain the same accuracy. We chose to use a W-cycle instead, which requires more computational effort, but more closely clusters the eigenvalues around one. However, as we shall see in the next section, the Multigrid method is also used by the Schur complement preconditioner. In that case, we made a different choice of cycle.
5.2. Schur Complement Preconditioner
Let us now focus on finding a scalable preconditioner for the Schur complement. In the case of diffusion-dominated problems, then the mass matrix or even a diagonal approximation of it can produce scalable results. Indeed, for the Stokes problem, which represents the limit case where convection is not present, the pressure mass matrix is spectrally equivalent to the Schur complement.
The difficult challenge is to find a scalable preconditioner in the case of convection-dominated problems. The first approaches used the mass matrix that was scaled by the viscosity. This choice, although very simple, does not yield scalable results in general. Therefore, more complicated preconditioners are necessary. We now summarize some of these alternatives.
5.2.1. PCD Preconditioner
The Pressure convection-diffusion (PCD) approach can be intuitively justified when considering the operator that the Schur complement represents: matrix is the discrete counterpart of the continuous operator , where represents the local wind (given by the solution of the previous iteration in the case of the Oseen problem). We can think of a preconditioner for the Schur complement as an approximation of the discrete version of the inverse of this operator: then, calling the convection-diffusion operator built in the pressure space and the corresponding Laplacian, we can assume that matrix is an approximation for . However, in the case of diffusion-dominated problems, and tend to coincide, yielding the identity matrix as preconditioner. Premultiplying by , the pressure mass matrix, we can assure that in this extreme case the preconditioner goes back to the known optimal alternative.
This preconditioner was proposed and derived formally in [
4] and studied thoroughly in [
25]. It provides a significant improvement with respect to the scaled mass matrix, keeping the computational cost low: matrices
and
are indeed smaller than
F and
L, making this preconditioner particularly efficient. However, the rate of convergence seems to suffer when
gets close to zero, even for simple problems. Moreover, matrix
is not used in the original problem and, thus, needs to be built at every Picard iteration; the proper boundary conditions to apply to it are not straightforward to choose and they do not necessarily coincide with the conditions applied to the original problem. An analysis of this issue can be found in [
14].
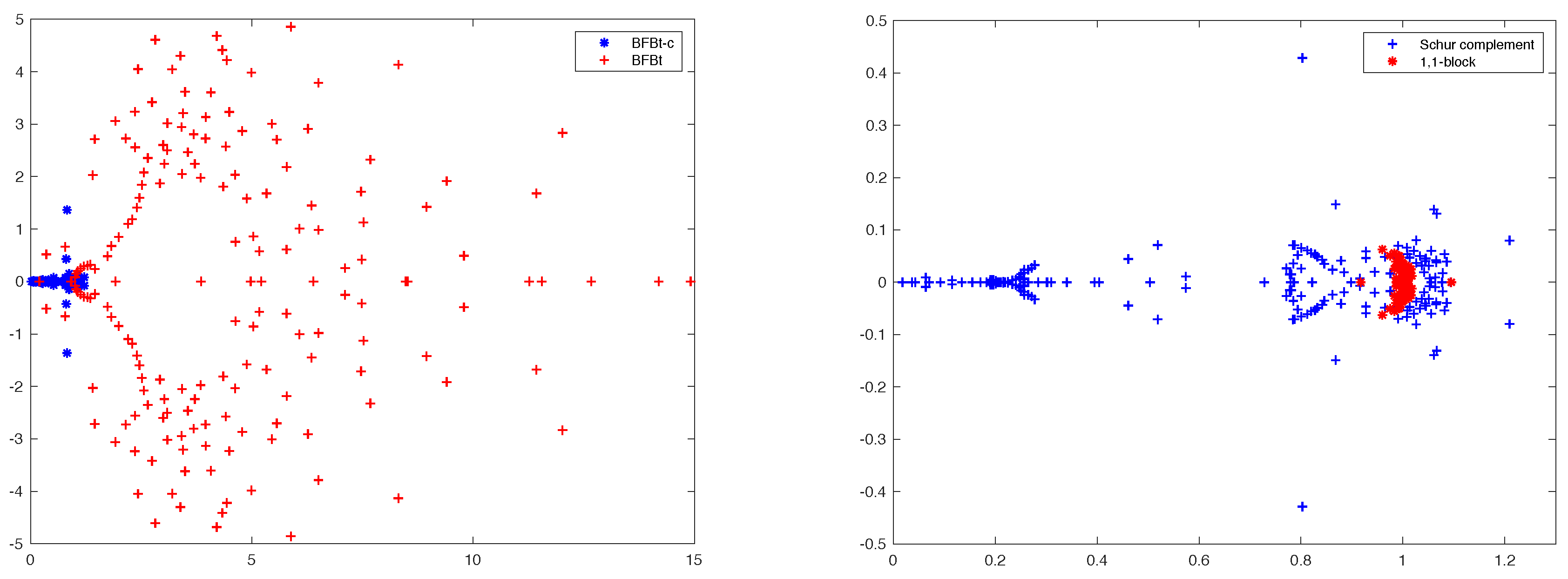
5.2.2. BFBt Preconditioner
A different preconditioner can be derived in a more algebraic way: in [
9], it is proved that, under the assumption that
, the exact inverse of the Schur complement is given by matrix
Hence, we can take
as a preconditioner for the Schur complement, even if the assumption does not hold in general. Further analysis showed that an improvement can be obtained when considering the scaled version
which, in the case of continuous pressure elements, simplifies to
where
is the velocity mass matrix, or an approximation of it. This preconditioner is clearly more expensive than the PCD, since it involves two applications of
and a product with matrix
F instead of
. However, most of the matrices used are already available and the additional boundary conditions to apply to
represent a less critical problem. Dependence on the mesh size and on the viscosity is observed, especially for complicated flows.
5.2.3. Commuted BFBt Preconditioner
An improvement to the BFBt preconditioner was proposed in [
14], where they analyzed the continuous counterpart of matrix (
18) and suggested to commute some of the operators involved, yielding the preconditioner
where
L is the diffusive part of matrix
F. This alternative is even more expensive than the previous one, since matrix
L is larger than
. On the positive side, all of the matrices are already available and there are no new boundary conditions to apply. Moreover, the inversion of matrix
L can be performed with the same Multigrid technique used to precondition matrix
F.
This last alternative is the one that has showed the best results in term of scalability, even if some dependence on the mesh size can still be observed for very low viscosities and complicated flows. It is also worth pointing out that, in the case of diffusion-dominated problems, this approach behaves decisively worse than PCD.
5.2.4. Augmented Lagrangian Approach
We briefly sketch a completely different approach from the ones previously presented: suppose modifying the
block of the original saddle-point linear system, so that the matrix becomes
where
is a parameter and
W is positive definite. The solution is not changed, but it is now possible to simplify the Schur complement and find a very efficient preconditioner. As shown in [
1], if
W is taken to be the pressure mass matrix, an optimal choice for
is simply
. However, this great efficiency in the Schur complement preconditioner is balanced by the need for a much more complicated Multigrid scheme for the new
block. In [
3], this approach was generalized to the three dimensional case and it was also pointed out that the highly specialized Multigrid scheme used depends on the choice of the discretization and it may not be possible to use this method with every such choice.
In our numerical experiments, we chose to use preconditioner (
19), since it is the one with the best chance of providing scalable results for a recirculating flow and since it does not involve matrices to be computed separately. Moreover, it exploits the same Multigrid that we used for the
block, which means that any improvement that we make there also has an impact on the Schur complement.
Some comments must be made regarding the Multigrid used to invert matrix L. We used the same strategy used for matrix F, with the following differences: since no convection is present, we found out that using the V cycle is sufficient to provide good results; we performed a larger number of cycles, since, in this case, we would like to obtain the exact inverse of L and not just a preconditioner. We maintained the approach of splitting matrix L, since this allows for saving computational time.