Abstract
A Sudoku puzzle often has a regular pattern in the arrangement of initial digits and it is typically made solvable with known solving techniques called strategies. In this paper, we consider the problem of generating such Sudoku instances. We introduce a rigorous framework to discuss solvability for Sudoku instances with respect to strategies. This allows us to handle not only known strategies but also general strategies under a few reasonable assumptions. We propose an exact method for determining Sudoku clues for a given set of clue positions that is solvable with a given set of strategies. This is the first exact method except for a trivial brute-force search. Besides the clue generation, we present an application of our method to the problem of determining the minimum number of strategy-solvable Sudoku clues. We conduct experiments to evaluate our method, varying the position and the number of clues at random. Our method terminates within 1 min for many grids. However, as the number of clues gets closer to 20, the running time rapidly increases and exceeds the time limit set to 600 s. We also evaluate our method for several instances with 17 clue positions taken from known minimum Sudokus to see the efficiency for deciding unsolvability.
1. Introduction
Sudoku is a popular number placement puzzle. In an ordinary Sudoku (Figure 1), given a partially completed grid, the goal is to fill in all empty cells with digits from 1 to 9 in such a way that each cell has a single digit, and each digit appears only once in every row, column, and subgrid.
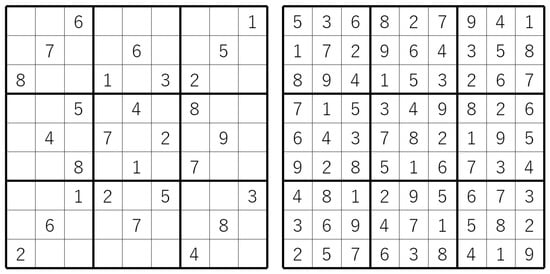
Figure 1.
Sudoku clues (left) and its solution (right).
Sudokus that appear in books, newspapers, and so on often have the following characteristics:
- The arrangement of initial digits (called clues) forms a regular pattern.
- The level of difficulty is moderate.
Regarding 1, for example, the left grid of Figure 1 has reflection symmetry on the two diagonal axes. It may also have the shape of a number, a letter, or a symbol. Regarding 2, completing Sudokus generally requires backtracking, which is amenable to computers. On the other hand, there is a set of techniques (called strategies) that humans use in solving Sudokus by hand [1]. Typically strategies are if-then rules: If a strategy is applicable to the current grid, then it might rule out digits as candidates or might determine digits as those to be finally placed. A strategy-solvable Sudoku is a partially completed grid that can be completed by applying strategies repeatedly. Here, the strategies must be selected from a set of predetermined ones. Since there is no need to guess, strategy-solvable Sudokus (at least for a few basic strategies) might be referred to as Sudokus having a moderate level of difficulty for humans.
Making new Sudoku instances having these characteristics is not an easy task. There is a public software (The generator of Zama and Sasano [2] http://www.cs.ise.shibaura-it.ac.jp/2016-GI-35/SudokuGenerator.tar.gz, accessed on 26 May 2020) that is able to generate Sudokus from a given set of clue positions so that they are solvable with some known strategies. However, it is still hard to generate those with 20 or less clues and those with around 45 or more clues. For such instances, there might be no other choice but to rely on human intelligence involving the intuition, the inspiration, and the experience of enthusiasts.
In this paper, we consider a method for determining Sudoku clues in specified positions such that all empty cells can be filled in with a specified set of strategies (see Figure 2).
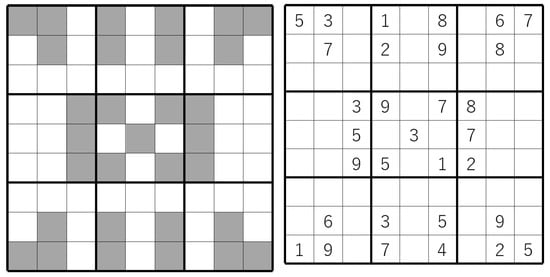
Figure 2.
Clue positions (left) and clues solvable with naked singles only (right).
Almost all Sudoku generators simply output proper Sudoku instances (i.e., partially completed grids having unique solutions). Clue arrangements and strategies necessary for solving are uncontrollable. To the best of our knowledge, the only exception is the generator of Zama and Sasano mentioned earlier. Their generator is based on the generate-and-test method, which repeats the following steps until the test is passed or the number of trials exceeds a predetermined limit:
- Generate clues in specified positions.
- Test whether all other cells are completed using specified strategies only.
A similar idea is also mentioned in [3,4]. Since the test step can be done quickly, the key is to devise a criterion for the generation step so that the number of trials is as small as possible.
Since the generate-and-test method examines only a limited portion of the vast search space, it has the drawbacks listed below:
- The lower the density of solutions (i.e., strategy-solvable clues) over the whole search space becomes, the harder it becomes to find a solution.
- If a set of clue positions happens to be not strategy-solvable, it is unable to recognize it no matter how much time passes.
- Even for a strategy-solvable set of clue positions, there is no guarantee for being able to find a solution in a finite amount of time.
To tackle these issues (in particular the last two), we consider it necessary to formulate the concept of strategy-solvability. It seems that strategy-solvability has been recognized intuitively, and no formal treatment has been given so far. In this paper, we introduce a rigorous framework to discuss solvability for Sudoku instances with respect to strategies and define the notion of strategy-solvable Sudoku clues. This allows us to handle not only known strategies but also general strategies under a few reasonable assumptions. We then propose an exact method for determining strategy-solvable Sudoku clues for a given set of clue positions that is solvable with a given set of strategies. The key is a reduction to a constraint satisfaction problem (CSP). Our method is able to benefit from the power of state-of-the-art CSP solvers. Pruning techniques of CSP solvers are expected to be effective for the first issue above. Moreover, as long as any complete CSP solver is utilized, it is guaranteed that if a set of clue positions is not strategy-solvable, our method eventually recognizes the unsolvability; otherwise, our method eventually finds strategy-solvable clues.
This is the first exact method except for a trivial brute-force search. As strategies allowed in completing Sudokus, this paper employs naked singles, hidden singles, and locked candidates [1], which are quite basic yet powerful enough to complete many Sudokus. Indeed, we have confirmed that the combination of the three strategies allows for solving as many as 37,373 of the 49,151 minimum Sudokus (i.e., Sudokus with 17 clues) collected by Gordon F. Royle [5]. Here we remark that our CSP formulation is almost independent of specific strategies. In order to allow other strategies, it is sufficient to formulate the corresponding logical constraints and add them with a minor modification of the strategy-independent part.
Besides the clue generation, we present an application of our method to the problem of determining the minimum number of Sudoku clues that are solvable with a given set of strategies. We demonstrate that our method is easily customized for this problem with a small modification in the CSP constraints. It is well-known that there is no proper Sudoku with 16 or less clues [6]. There are many Sudokus with 17 clues that are solvable with basic strategies such as hidden singles. Interestingly, this may not be the case for naked singles, arguably one of the most basic strategies, as we have confirmed that no grid solvable with only naked singles is included in the minimum Sudoku collection. This poses an open problem of whether there is a gap between the minimum numbers for strategy-solvable Sudokus and proper Sudokus. Our method will be useful in tackling this problem thanks to the ability of determining unsolvability.
We conduct experiments to compare our method with the generator of Zama and Sasano [2], using grids varying the position and the number of clues at random. From the results, we observe that our method terminates within 1 min for many instances, showing our method being stable in terms of running time. However, as the number of clues gets closer to 20, the running time rapidly increases and exceeds a time limit. On the other hand, the generator of Zama and Sasano can often find solutions much faster even with close to 20 clues, while the performance sharply deteriorates around 45 clues and exceeds the time limit for all grids with more clue positions. Perhaps this is due to the exponential blow-up of the search space (in other words, the exponential decline in the density of solutions). We also evaluate our method for several instances with 17 clue positions taken from known minimum Sudokus to see the efficiency for deciding unsolvability.
The main contributions of the present paper are to formulate the concept of strategy-solvability, to establish an exact method for the strategy-solvable Sudoku clues problem, and to demonstrate the flexibility of the CSP-based approach. It remains as future work to improve our method for less clues.
Unless otherwise noted, the size of the Sudoku is fixed to throughout the paper. This is simply for convenience and our method can be easily translated into general Sudokus on a grid.
The paper is organized as follows. Section 2 introduces necessary notations and terminology, and explains strategies. Section 3 formulates the concept of strategy-solvability and the strategy-solvable Sudoku clues problem. Section 4 proposes an exact method for the strategy-solvable Sudoku clues problem, and Section 5 presents two improvements for our method. Section 6 presents an application of the strategy-solvable minimum Sudoku problem. Section 7 presents experimental results. Section 8 summarizes related work. Section 9 concludes this paper.
2. Preliminaries
In this section we introduce necessary notations and terminology and explain strategies.
2.1. Notations and Terminology
For convenience, rows and columns are numbered from 0 to 8. A cell is denoted by the pair of a row index i and a column index j. The 9 subgrids of are called blocks. Rows, columns, and blocks are collectively called groups. A group is identified with the set of all cells in the group. By abuse of notation, we denote by the difference of a singleton from a group G.
Given a partially completed grid, the goal of a Sudoku puzzle is to fill in all empty cells with digits from 1 to 9 in such a way that:
- Each cell has a single digit; and
- Each digit appears only once in every group.
The completed grid is called a solution. A Sudoku is a convenient alias for a partially completed grid given as an initial grid. A Sudoku is proper if it has a unique solution. The occurrence of a digit in an initial grid is called a clue, and Sudoku clues are the clues in an initial grid. A cell in an initial grid to which some digit is designated to be placed as a clue is called a clue cell or a clue position.
2.2. Strategies
There is a set of techniques (called strategies) that humans use in solving Sudokus by hand [1]. Typically strategies are if-then rules: If a strategy is applicable to the current grid, then it might rule out digits as candidates or might determine digits as those to be finally placed. Throughout the following explanation, let n be a non-zero digit and be a cell.
A naked single is a strategy that places n in if no other candidate but n remains at . For example, let us look at the gray cell in the left grid of Figure 3. Since all digits but 5 appear in either group having , these digits must be ruled out and only 5 remains. Hence, 5 is placed in . Starting with the left grid of Figure 3, one can reach the right grid using only naked singles, but cannot proceed any more because of two or more candidates over all empty cells.
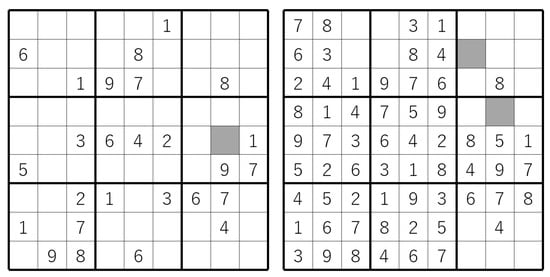
Figure 3.
Starting with the partially completed grid on the (left), one can reach the grid on the (right) using only naked singles but cannot proceed any more.
A hidden single is a strategy that places n in if there is a group G having such that no cell in has n as a candidate. For example, let us look at the right grid of Figure 3. For the row of index 1, we can observe that every cell in the row except for the gray cell does not have 7 as a candidate. Indeed, for any such cell, 7 already appears in another cell of the same column. Hence, a hidden single strategy determines 7 in . In this way, by applying hidden singles repeatedly, the grid can be completed.
Let be groups such that . A locked candidate is a strategy that rules out n over all cells in one difference set if no cell in the other difference set has n as a candidate. For example, let us look at the right grid of Figure 3. Let A be the column of index 7, and let B be the block adjacent, on the right, to the center block. No empty cell in has 3 as a candidate because for each such cell, there is another cell in the same row to which 3 is already placed. Hence, 3 is ruled out for all empty cells in . Because of this, 2 becomes a unique candidate at . It is determined as the digit at by a naked single. In this way, the grid can also be completed using locked candidates as well as naked singles.
Figure 4 is an example of a grid showing that locked candidates are independent of the combination of naked singles and hidden singles. Actually, none of the empty cells can be determined using naked singles and hidden singles, but if locked candidates are allowed in addition, then there is an empty cell that can be filled in.
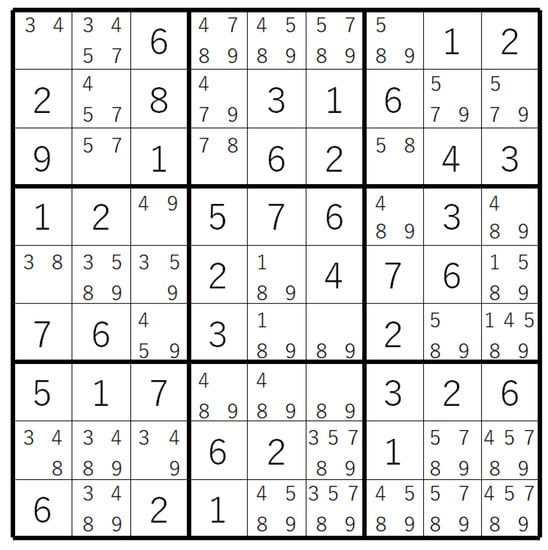
Figure 4.
Grid showing that locked candidates are independent of the combination of naked singles and hidden singles.
To see this, look at cell in Figure 4. All candidates except 5 are removed by applying locked candidates. Indeed, let A be the 6-th row and B be the block to which belongs. Since no cell in has and 9 as candidates, these digits are removed from candidates at , and only 5 remains. Hence, by applying naked singles to this cell, 5 is determined. In this way, this grid can be completed, which shows that locked candidates are independent of the combination of naked singles and hidden singles.
3. Formulation
Although some known strategies are introduced in the previous section and some solvable cases are explained using particular grids, there are still unclear points, such as what is a strategy in general and what operations are allowed for placing or ruling out digits. In this section, we thus introduce a rigorous framework to discuss solvability for Sudoku instances. This allows us to handle not only known strategies but also general strategies under a few reasonable assumptions. This also makes it clear that, for example, it is not allowed to temporarily place digits and then cancel them when a contradiction occurs. Such an inference would allow us to do backtracking, which nullifies the restriction of completion methods.
A state transition model of Sudoku is a tuple such that Q is the set of all possible states, R is a state transition relation, I is the set of initial states, and F is the set of final states. We will explain each component below. Figure 5 shows how a grid evolves as strategies are applied, which will be used as an example in the succeeding explanation.
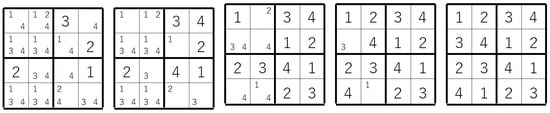
Figure 5.
Sequence of grids in a Sudoku, evolving from the left-most initial state to the right-most final state. Larger digits are determined ones and smaller digits are candidates.
A state of grid (or a state in short) is a pair of functions. The function f maps the set of cells to the set of digits, and means that if , then n is placed in ; otherwise, no digit is placed. The function g maps the set of cells to the powerset of the set of non-zero digits, and represents the set of all candidates at . Here, by abuse of notation, and denote and , respectively. All states must satisfy the conditions and below: for all cells and non-zero digits n,
- S1
- ,
- S2
- if there is a different non-zero digit from n such that or there is a different cell from with both in a common group such that .
We denote by Q the set of all states.
The antecedent of is a condition for digits n that can be safely ruled out whenever some digits are placed. Imposing ensures that all such digits are ruled out. This is simply to make all states have a type of normal form, and it would not deduce any wrong consequence as long as decisions for number placements are correct, such as not violating the properness. In Figure 5 we can observe that all grids are in “normal form”.
A state transition relation is a binary relation . The (or in infix notation) means that there are strategies by which q is changed to . We refer to q and as the source state and the target state of the transition, respectively. All state transitions must satisfy that for any cell and non-zero digit n, if holds in the source state, it does also in the target state; if holds in the source state, it does also in the target state. This simply means that once digits are placed or ruled out it cannot be cancelled afterward. We put one more assumption as follows. For any three states , , and with and , if , then . We consider this assumption not so strong. Indeed, many strategies, such as naked singles and hidden singles, decide to place digits by examining only candidates. For such strategies, suppose that is obtained from by applying all strategies applicable to . Then, if , no strategy applicable to remains, and cannot be changed any more, i.e., .
A state is an initial state if it satisfies the following: for all clue cells; for the other cells; and if and only if the antecedent of holds. The last condition ensures that for each clue cell, all digits but the determined one are ruled out; all digits that appear as candidates in a common group to some determined digit are ruled out; and—the only-if part—no other digits are ruled out. Notice that the only-if part is the most essential because the if part can be omitted thanks to . It is worth noting, that for non-initial states, this must not be assumed in general because of strategies for number removals such as locked candidates. For example, in the-left most grid of Figure 5, we can observe that all digits not designated to be ruled out by the antecedent of remain as candidates. We denote by I the set of all initial states.
A final state is a state such that digits are determined for all cells, that is, for all . We denote by F the set of all final states.
Definition 1.
Let be a state transition model of Sudoku. A state is strategy-solvable if there is a sequence of states such that , , and for all .
Definition 2.
Let be a state transition model of Sudoku. The strategy-solvable Sudoku clues problem (or SSC in short) is to determine whether there is a strategy-solvable state of .
Suppose that R is given as a logical formula that represents strategies and a set S of clue cells is also given. Consider Q, I, and F as the ones defined as described above. Sudoku clues are strategy-solvable if the initial state corresponding to the Sudoku clues is strategy-solvable with respect to . The strategy-solvable Sudoku clues problem is defined accordingly. If the output of the problem is yes, in practice we will also ask for generating strategy-solvable Sudoku clues.
Proposition 1.
Let be a state of grid. For any cells , in a common group, implies or .
Proof.
Suppose that , , and . Let . Applying , we obtain . Since , applying , we obtain for all . From both, follows, and this is contradictory to . □
Corollary 1.
Every final state represents a Sudoku solution.
Proof.
Let be a final state. Since f is a function, each cell must have a single digit. From Proposition 1 and , it follows that each digit appears once in every group. □
Notice that this corollary holds no matter what state transition relation is given.
Proposition 2.
Let R be a state transition relation. Let be a sequence of states such that for all . If for all , then .
Proof.
Let be the number of all triples such that . Clearly, . Hence . □
4. Our Method
In this section, we propose an exact method for the strategy-solvable Sudoku clues problem (SSC). As strategies allowed in completing Sudokus, this paper employs naked singles, hidden singles, and locked candidates, which are quite basic yet powerful enough to complete many Sudokus.
4.1. Overview
The key of our method is to encode a given SSC instance to an equivalent constraint satisfaction problem (CSP) instance and then to solve it using a generic CSP solver. For the CSP encoding, we introduce variables for representing states of grid and other auxiliary variables. Using such variables, we represent constraints for states, state transitions, particular strategies, and so on.
Any variable assignment that satisfies all such constraints substantially corresponds to a sequence of states with strategy-solvable, as characterized in Definition 1. Here, the initial state represents an assignment of digits to clue cells and the whole sequence represents a history of evolving grids and applied strategies, which eventually reaches a Sudoku solution. Hence, by applying a CSP solver to the encoded constraints, we eventually obtain strategy-solvable Sudoku clues, if they exist; otherwise, we eventually recognize the strategy-unsolvability of the clue cells, that is, no assignment of digits to the clue cells is strategy-solvable.
The details of our method are explained as follows. At first, we present constraints for a state transition framework, which is almost independent of particular strategies. As stated above, we introduce variables for representing states of grid and auxiliary variables. We then represent various constraints using such variables. After that, we shift to particular strategies. We present constraints for number placements and constraints for number removals. We finally provide the whole picture of our method as well as some remarks.
4.2. Constraints for a General State Transition Framework
We introduce variables for representing the states of a grid. We then present constraints for initial states, constraints for state transitions, and constraints for final states.
4.2.1. Variables
Let be a state of a grid in step , i.e., a state reachable from an initial state by k transitions. Let i and j be a row index and a column index, respectively. The integer variable encodes the value of at cell . In other words, takes 0 if no digit is placed in , and it takes a non-zero digit n if n is placed in . The Boolean variable encodes whether the set of candidates at cell includes a non-zero digit n. Here is true if and only if . We call variables of the forms and X-variables and Y-variables, respectively.
The remaining variables are Boolean variables of the form , which are used for auxiliary purposes. We call them Z-variables. Each Z-variable is introduced per particular condition for a number placement or a number removal. The parameter m is simply an identifier for distinguishing between a large number of particular conditions. We thus number all such conditions in an arbitrary order.
It is worth noting, that since X-variables and Y-variables have k in their parameters, we have to fix the maximum number of steps, K, in advance. In principle, it suffices to let . This is shown later. Since this is too large in practice, we will propose a practical method using a smaller K while keeping the exactness in Section 5.
4.2.2. Constraints for Initial States
The constraints for initial states are as follows. For all clue cells ,
and for the other cells ,
Here we would not explicitly impose any constraint on Y-variables in step 0 because such constrains can be derived from the constraints for Y-variables of an arbitrary step and the constraints for number removals.
4.2.3. Constraints for State Transitions
The constraints for state transitions represent how X-variables and Y-variables in the current grid are determined from the previous grid.
The constraint that allows us to determine a non-zero digit n at cell in step k is as follows.
Here, runs over all possible Z-variables that can derive the left-hand side. The only-if part means that if , then there must be evidence, i.e., some Z-variable is true. One such Z-variable is the case for which n is determined at in the previous step.
As noticed before, suppose that the parameter m is uniquely determined in order to distinguish the condition in the right-hand side from the other particular conditions for Z-variables. Hereafter we will follow the same implicit agreement whenever appears in constraints. The other Z-variables of Formula (3) will be detailed later according to particular cases. Note that as discussed in Section 3, in order for our assumption for state transitions to be met, it is sufficient to let be determined by only Y-variables in the previous step (except for Formula (4)).
The constraint that allows us to rule out a non-zero digit n as a candidate at cell in step k is as follows.
In the same way as X-variables, runs over all possible Z-variables that can derive the left-hand side. One such Z-variable is the case for which n is ruled out as a candidate at in the previous step.
The other Z-variables of Formula (5) will be detailed later according to particular cases.
4.2.4. Constraints for Final States
The constraints for final states are those that allow us to reject the current state as soon as it turns out that there is no chance to reach final states. There are three cases for the current state of a grid:
- All cells are completed.
- Some empty cells remain, and some candidates have been ruled out from the previous grid.
- Some empty cells remain, and no candidate has been ruled out from the previous grid.
Clearly the first case must be accepted. For the third case, our assumption of state transitions (see Section 3) implies that the current incomplete grid cannot be changed anymore. Hence, the third case must be rejected immediately. For the second case, since applicable strategies may remain for the current grid, the decision must be postponed to the next grid. The following formula is in charge of this filtration.
Suppose that the current grid is in step . The left-hand side means that no candidate has not been ruled out from the previous grid, and the right-hand side means that the current grid is completed. It is clear that this formula rejects only the third case among the three cases.
As announced earlier, we show here that is sufficient. Let be any sequence of states such that is an initial state and is the next state of for all k. The assumption for state transitions (see Section 3) ensures that once for some ; it follows that for all . From Proposition 2, the minimum with is bounded from above by 649. Therefore it suffices to let . Notice that is necessary in order to decide whether is a final state.
4.3. Constraints for Particular Number Placements
We explain particular cases for s in Formula (3).
4.3.1. Naked Singles
The right-hand side of the following formula is the condition for which a naked single allows us to determine a non-zero digit n at cell in step . Notice that in order for this to take effect, it is necessary that the following is registered to Formula (3).
The right-hand side means that all digits but n are ruled out as candidates at cell in the previous step. There are two cases: either only n remains as a candidate or no digit remains. Although a naked single is applicable only to the former case, there is no substantial problem. Because even if the latter case occurs, we obtain from Formulas (3) and (8), and we also obtain for any other digit in the same way, which is a contradiction.
4.3.2. Hidden Singles
The right-hand side of the following formula is the condition for which a hidden single allows us to determine a non-zero digit n at cell in step .
Here, let G be any group such that . There are three cases for G, and for each case the corresponding constraint must be generated from Formula (9). The right-hand side of Formula (9) does not exclude the case for which n is ruled out over all cells in G, but there is no substantial problem, just like in Formula (8).
4.4. Constraints for Particular Number Removals
We will now explain particular cases for s in Formula (5).
4.4.1. Conditions for States of a Grid
We have imposed the two conditions and on the states of a grid in order to reject states that violate the rules of a Sudoku puzzle. We introduce constraints corresponding to and . Unlike the other constraints, the constraints below determine a relation between X-variables and Y-variables in the same step.
The following formula corresponds to , which ensures that all cells have at least one candidate in all steps .
The following formula corresponds, in turn, to one of the two cases in the antecedent of , that is, a different digit from n is determined at cell .
Here, suppose that is registered in Formula (5). If the right-hand side of Formula (11) holds, then it follows from Formulas (5) and (11) that n is ruled out as a candidate at in the same step k, which is the consequent of .
The following formula corresponds to the other case in the antecedent of , that is, there is a different cell from with both in a common group G such that n is determined at .
Here, let G be any group such that . There are three cases for G, and for each case the corresponding constraint must be generated from Formula (12). Just like Formula (11), Formula (12) and Formula (5) imply that n is ruled out as a candidate at in the same step k, which is the consequent of .
4.4.2. Locked Candidates
The right-hand side of the following formula is the condition for which a locked candidate allows us to rule out a non-zero digit n at cell in step .
Here, let A and B be any groups such that and . For all possible combinations of A and B, the corresponding constraint must be generated from Formula (13). Notice that Formula (13) can be commonly used to deduce for all , by which the size of constraints can be largely reduced.
4.5. Remarks
We have presented a CSP encoding for the strategy-solvable Sudoku clues problem. That is, given a set of cells, there are clues for the cells such that the grid can be completed using naked singles, hidden singles, and locked candidates if and only if there is an assignment of X-variables, Y-variables, and Z-variables that satisfies all the constraints generated from Formulas (1)–(13). A satisfying assignment substantially corresponds to a sequence of states with strategy-solvable, as characterized in Definition 1. By applying a CSP solver to the encoded constraints, we eventually obtain strategy-solvable Sudoku clues, if they exist; otherwise, we eventually recognize the strategy-unsolvability of the clue cells, that is, no assignment of digits to the clue cells is strategy-solvable. The constraints for a general state transition framework are almost independent of particular strategies. The only connection is via Z-variables in Formulas (3) and (5). In order to include additional strategies, it is sufficient to model these strategies as logical formulas independently and then register new Z-variables for them to Formula (3) or Formula (5).
5. Two Improvements
In this section, we present two improvements to our method.
5.1. Reduction of Constraint Size
The biggest issue of our method is that there are hundreds of thousands of constraints. A simple way for reducing constraint size is to eliminate constraints concerning clue cells. For all clue cells, digits are determined in an initial state, and the determined digits do not change over all succeeding steps. Hence, all constraints necessary for clue cells in each step take the same values as those in the previous step. In the constraints for final states, there is no need to examine the values of X-variables and Y-variables for clue cells. However, we must not ignore the constraints for clue cells in step 0 corresponding to Formulas (10)–(12) because otherwise we could not reject initial states violating the rules of the Sudoku puzzle.
5.2. Incremental Approach
Our method requires to fix a maximum step size, K, in advance. Since it has a significant impact on constraint size, K needs to be as small as possible. However, for a small K, our method may return false clues. To see this, let us take a look at Figure 3. Suppose that the left grid is an initial state and the right grid is a state in step K. The right grid is not yet completed, but no constraint has been violated up to step K. Since there is no further step, our method returns the initial grid, even if only a naked single strategy is allowed. Notice that if the right grid was in step or less, our method would reject the initial grid (because the constraints for final states are violated).
We propose a practical method using a smaller K while keeping the exactness. A basic idea is to repeatedly apply our original method while incrementing K from an initial number until K exceeds a sufficiently large number . Algorithm 1 is a pseudo code for the method. Notice that once constraints become unsatisfiable, constraints with any lager maximum step size must be unsatisfiable.
| Algorithm 1 Incremental approach for the strategy-solvable Sudoku clues (SSC) |
| for to do |
| Generate constraints for a given SSC instance with maximum step K. |
| if the set of constraints is unsatisfiable then |
| return UNSAT |
| else if the grid in step K is completed then |
| return Sudoku clues in the initial grid. |
| end if |
| end for |
6. Application
Besides the clue generation, we present an application of our method to the problem of determining the minimum number of Sudoku clues that are solvable with a given set of strategies.
Our method is easily customized with a small modification as follows. Remove Formulas (1) and (2). Instead, introduce integer variables taking 0 or 1, , for all cells and the following formula.
Introduce the following formula for ensuring that the number of determined digits in step 0 is less than or equal to a threshold .
Here the summation runs over all variables .
In order to compute the minimum number, it is sufficient to repeatedly solve the modified constraints while decreasing one by one until the constraints become unsatisfiable.
7. Experiments
In this section, we conduct two experiments to evaluate our method.
7.1. Common Settings and Remarks
Our method uses Sugar version 2.3.3 [7,8] as a CSP solver and MiniSat version 2.0 [9,10] as a SAT solver internally invoked by Sugar. The maximum step size K is set to 30, and our method is applied only once (i.e., with no use of an incremental approach) because in preliminary experiments, we have confirmed that is sufficient for many instances including those used in these experiments (Note that the whole sequence of states returned by a CSP solver represents a history of evolving grids and applied strategies. To check that the initial state in the sequence is strategy-solvable, it suffices to check if the state in step K is a final state, that is, for all . To make doubly sure, all the results (initial grids) obtained by our method were verified using a separate program, which is made publicly available together with our implemented CSP encoder in our website. This verification program simply consists of selecting applicable strategies to the current grid from a set of predetermined strategies and applying them until the grid is completed or no applicable strategy exists). The computational environment is as follows:
- OS: Ubuntu 18.04.4 LTS
- Main memory: 16 GB
- CPU: Intel ® Core ™ i7-4600U 2.10GHz
The implementation of our method was checked for all possible arrangements of 3 and 4 clue positions for a Sudoku. These instances are so small that a naive brute force search can quickly decide. It was confirmed that the solvability results for our method completely coincide with those for the brute force search over all instances. Here all strategies allowed to be used are naked singles, hidden singles, and locked candidates. It turned out that there is no strategy-solvable instance with 3 clue positions, and there are exactly 704 strategy-solvable instances with 4 clue positions. It is worth noting, that all of the 704 instances are also solvable with naked singles only. Since there is no proper Sudoku with 3 clues, there is no gap between the minimum numbers of proper Sudokus and strategy-solvable Sudokus with naked singles.
The implementation of the CSP encoding part of our method, tools such as the brute force search program, and all instances used in the experiments are publicly available in our website (http://www.disc.lab.uec.ac.jp/toda/code/scg.html, accessed on 27 May 2020).
7.2. Running Time Comparison
We compared our CSP-based method (CSP) with the generator of Zama and Sasano [2] (ZS). The time limit was set to 600 s. In both methods, only naked singles, hidden singles, and locked candidates were allowed to be used. Although other strategies are implemented in the generator of Zama and Sasano, we restricted the program to the three strategies by modifying their program.
We made a total of 100 input instances (i.e., sets of cells) by repeating the following procedure: select a number n from 20 to 79 at random, and generate distinct n cells at random. Table 1 shows the distribution of input instances with respect to the number of clues. All instances are confirmed to be strategy-solvable.

Table 1.
Distribution of input instances with respect to the number of clues.
In preliminary experiments we confirmed that the brute force algorithm exceeded the time limit (600 s) for all instances. Moreover, the implementation of a naive generate-and-test method (Clues for specified positions were randomly generated and it was tested in a straightforward way whether the set of the clues is strategy-solvable. The “naive” means that no elaborated heuristic is used in the generation step) could solve only 4 instances within the time limit. As will be described in Section 8, the naive generate-and-test method falls into one of the four major methods for Sudoku clue generation (called a forward search), which admit both a strategy-solvability aspect and a geometric constraint aspect. Both codes are made publicly available on our website.
Figure 6 shows a cactus plot of running time comparison. Each point is plotted so that the x-coordinate is the number of instances solved within the time specified in the y-coordinate. The points for our method (CSP) and the generator of Zama and Sasano (ZS) are indicated with + and ×, respectively. The curve formed by the points for the same method shows an increase in the number of solved instances over time.
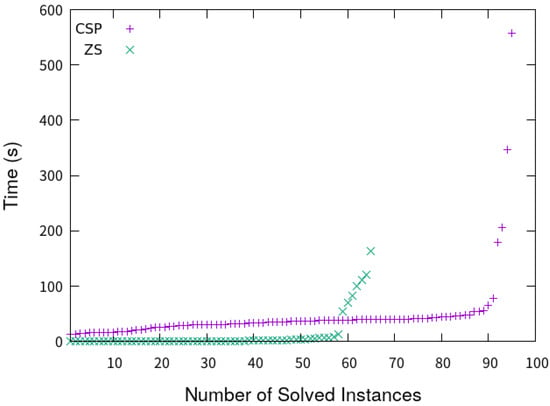
Figure 6.
Comparison of running time.
Our method solved 95 of a total of 100 instances within the time limit, while the generator of Zama and Sasano solved 65 instances. The curve of our method shows a linear increase up to around 90 in the x-axis, which indicates the number of solved instances. All such instances are solved within about 1 minute. The curve grows rapidly after 90. All instances taking more than 1 min including those exceeding the time limit have 25 or less cells.
On the other hand, the generator of Zama and Sasano can often find solutions much faster even in near 20 cells, as the curve of Zama–Sasano almost overlaps the x-axis up to near 60, which indicates the number of solved instances. The number of clue cells in such solved instances is 45 or less. After that, the performance drops significantly as the curve sharply increases. All instances with 50 or more cells cannot be solved within the time limit.
7.3. Evaluation on Unsolvability
To see the efficiency for deciding unsolvablity, we made instances that seem to be on the border between solvable cases and unsolvable cases by randomly selecting 30 minimum Sudokus from the collection of Gordon F. Royle [5] and extracting only clue positions, simply forgetting placed digits. In this experiment, all strategies allowed to be used were naked singles only. Note that although no grid solvable with naked singles was included in the collection, it is possible that changing digits in the same positions makes grids solvable.
Within 8 h, our method terminated for 14 of the 30 instances, and all of them were confirmed to be not strategy-solvable. Table A1 in the Appendix A shows the chosen minimum Sudokus and the running times. Although 10 instances took merely from 10 to 20 min, other instances took much more time. It is still unknown whether there are 17 clues solvable with naked singles only. This appears far from the settlement of the problem of the gap between the numbers of strategy-solvable Sudokus and proper Sudokus by a computer program, considering a large number of possible arrangements of 17 positions.
8. Related Work
There are several methods for sudoku clue generation [11]. As far as we are aware, most methods lack either a strategy-solvability aspect or a geometric constraint aspect, and they often aim at controlling the difficulty levels of the Sudoku instances to be generated. Since both aspects are at the heart of our present work, most methods are considered as intended to tackle different generation problems from ours. In the following, we briefly summarize them in terms of the differences from ours.
Known Sudoku generation methods are mainly classified into four types: a local search, a forward search, a backward search, and a logical modeling approach. The local search consists of starting with a partially-completed grid, which may be randomly generated or selected from known proper Sudoku instances, and then repeatedly searching neighbor grids by changing a portion of the current grid, such as relocating a few clue positions, removing a few clues, or replacing digits with different ones until a desired grid is found [12].
The forward search consists of repeatedly generating an initial grid (typically at random) and checking if it has a unique solution using Sudoku solvers. The checking step is sometimes done without verifying uniqueness in an exact sense. For example, Mantere and Koljonen used a Sudoku solver based on genetic algorithms [13]. In their method, an initial grid consists of randomly generated 20–50 clues and the check step is done in such a way that an initial grid is solved 10 times using their GA-based solver and it is checked if only one solution is obtained over the trials. Examples of other Sudoku solving methods include stochastic local searches, CSP solvers, and dancing links [14]. The generator of Zama and Sasano [2] falls into this group. Strategy-solvable Sudokus are guaranteed to be proper in an exact sense, and checking solvability can be done quickly, unlike checking properness. A similar idea is also mentioned in [3,4]. As far as we are aware, all known generators based on the forward search, with a few exceptions, do not take the strategy-solvability of Sudoku instances into consideration.
The backward search consists of starting with a completed grid and repeatedly eliminating digits so as not to violate properness; in other words, the resulting grid does not have distinct solutions [15]. Boothby et al. used inverse operations of some known strategies to eliminate digits and propose a constrained breadth search [16]. Their method admits a strategy-solvability aspect; however no known method based on the backward search can handle geometric constraints for an initial grid in the sense that no grid satisfying geometric constraints might appear during a search. Xue el al. used a Las Vegas algorithm to generate completed grids and used several operations (called dig-hole strategies) to eliminate digits.
The logical modeling approach consists of converting generation problems into equivalent constraints described in languages such as CSP (constraint satisfaction problem) and ASP (answer set programming), and to apply a generic solver to solve them. Our method falls into this group. Gebser provided an ASP encoding for proper Sudokus [17]. Fatemi el al. used a CSP encoding, but the constraints were simply those ensuring that grids do not violate Sudoku rules [18].
9. Conclusions
Sudokus that appear in books, newspapers, and so on often have a regular pattern in the arrangement of initial digits and are typically made so that all empty cells can be completed using some known techniques, called strategies. We formally defined the problem of generating such Sudoku instances by introducing the concept of strategy-solvability, which means that all empty cells can be filled in with digits using only a given set of strategies. We proposed an exact method for solving this problem. The key is to encode a given problem instance into an equivalent CSP instance and then solve it by applying a CSP solver.
There are a few existing researches, but all of them are based on the generate-and-test method, which repeatedly generates a set of clues and then tests whether it is strategy-solvable. There are some drawbacks, such as not being able to recognize that a specified set of cells is strategy-unsolvable.
To the best of our knowledge, our method is the first exact method except for the trivial brute-force search. Our method can eventually find strategy-solvable Sudoku clues if they exist, and otherwise our method can eventually recognize strategy-unsolvability. Besides the clue generation, we presented an application of our method to the problem of determining the minimum number of strategy-solvable Sudoku clues, demonstrating that our method is easily customized with a small modification.
We conducted experiments to compare our method with the generator of Zama and Sasano, using grids varying the positions and the numbers of clues at random. From the results we observed that our method terminated within 1 min for many grids, showing our method to be stable in terms of running time. However, as the number of clues got closer to 20, the running time rapidly increased and exceeded the time limit, which was set to 600 s. On the other hand, the generator of Zama and Sasano could often find solutions much faster even nearing 20 clues, while the performance sharply deteriorated around 45 clues and exceeded the time limit for all grids with more clue positions. We also evaluated our method for several instances with 17 clue positions taken from known minimum Sudokus to see the efficiency for deciding unsolvability. It remains for future work to improve our method for less clues.
Author Contributions
Conceptualization, K.N. and T.T.; methodology, K.N. and T.T.; software, T.T.; validation, T.T.; formal analysis, T.T.; investigation, K.N. and T.T.; resources, T.T.; data curation, T.T.; writing—original draft preparation, K.N. and T.T.; writing—review and editing, T.T.; visualization, T.T.; supervision, T.T.; project administration, T.T.; funding acquisition, T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI, Grant Number 17K17725.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The randomly chosen 30 minimum Sudokus and the running times (in s): each sequence of 9 digits is separated by a period, and such 9 sequences in each line represent the rows of a grid.
Table A1.
The randomly chosen 30 minimum Sudokus and the running times (in s): each sequence of 9 digits is separated by a period, and such 9 sequences in each line represent the rows of a grid.
| Grids | Time (s) |
|---|---|
| 090600000.000080300.000000010.060000800.000205000.000041000.000300702.401000000.500000000 | - |
| 050608000.300000070.000000000.000400601.700100500.200000000.061000000.000070020.000090000 | 926 |
| 000600370.801000000.000200000.070010060.000004500.200080000.060700000.000050800.000000000 | - |
| 005000060.000780000.000000000.200000407.001300000.000000800.000601030.040070000.580000000 | - |
| 031000000.000400006.000000200.600059000.000010030.400000000.000200800.050000010.700600000 | 1243 |
| 000000025.000601000.090000000.805000600.000020000.000000300.040250000.300000790.000800000 | 1255 |
| 600500300.000000010.000000000.000000596.010024000.000000000.704000800.000210000.300900000 | - |
| 000010600.050000030.000080000.700500020.000002000.008000000.530900000.000400807.000000100 | - |
| 000530800.700600000.400000000.100024000.000000630.000000000.050301000.000000042.080000000 | 1070 |
| 070060030.500400100.000000000.400501000.300000076.000800000.001000500.060020000.000000000 | - |
| 000700380.501000000.000200000.000000506.070400000.000000900.300056000.080010040.000000000 | - |
| 603001020.000800500.200000000.050040700.000003000.000200000.040750000.000000031.000000000 | 994 |
| 000030001.007500000.600000000.810002000.000600350.400000000.003000760.040080000.000000000 | - |
| 500300000.000000801.004000600.000600430.710000000.000500000.200000060.000078000.000010000 | 6564 |
| 080071000.000040600.000000000.040000008.000600010.200500000.603000500.500200000.000080000 | 1134 |
| 400000076.000081000.000000000.000630004.500000200.017000000.320400000.000000810.000000000 | - |
| 020540000.040000006.000000010.080700500.900020000.000006000.603000000.000300200.100000000 | 26,835 |
| 500060107.030200000.400000000.280000030.000007000.000010000.000800020.000400600.001000000 | - |
| 400010000.060000020.000000000.000500270.301400000.008000000.000600100.070002000.100000003 | - |
| 008000200.400050000.000600070.000082000.060000050.000300000.950100000.000000306.000000800 | - |
| 010000300.000042000.000090000.000800100.205000000.600000004.000310000.900000020.000700050 | 10,090 |
| 050000200.000700010.600080000.012000050.000600040.000030000.900000308.000001000.000000600 | 852 |
| 600050043.200000007.000400010.070200000.000060200.010000000.500000800.000730000.000000000 | - |
| 304050600.000200000.600000000.080000072.000031000.000000000.120700000.000000340.000000009 | 889 |
| 040000300.000072000.000010800.200000010.050700000.000050000.000800400.701000000.600300000 | - |
| 400080000.000500100.000000200.000034070.001000000.060000000.750000030.000001640.000200000 | 1021 |
| 000042500.100000070.000000000.400700000.000000208.000000650.025000000.000830000.060100000 | 869 |
| 600800000.000090500.000000020.025000700.090000300.000400001.100300008.000050060.000000000 | 849 |
| 200400000.000000031.000000007.000702500.301000000.900800000.080000400.000030090.070000000 | - |
| 007000010.400700000.000800030.200000400.000010000.000300000.000002709.530000000.080000600 | - |
References
- Davis, T. The Mathematics of Sudoku. 2020. Available online: http://www.geometer.org/mathcircles/sudoku.pdf (accessed on 26 May 2020).
- Zama, S.; Sasano, I. Technical Report 1, IPSJ SIG Technical Report, 2016-G1-35. 2016. Available online: http://id.nii.ac.jp/1001/00157936/ (accessed on 17 June 2020). (In Japanese).
- Maeda, K.; Okuno, H. Design and Implementation of Sudoku Puzzle Constructing Support System. In Proceedings of the 70th National Convention of IPSJ, Tsukuba, Japan, 13–15 March 2008; Volume 4ZH-4, pp. 799–800. (In Japanese). [Google Scholar]
- Stuart, A.C. Sudoku Creation and Grading. 2020. Available online: https://www.sudokuwiki.org/Sudoku_Creation_and_Grading.pdf (accessed on 17 June 2020).
- Royle, G.F. A Collection of 49,151 Distinct Sudoku Configurations with 17entries. 2020. Available online: https://staffhome.ecm.uwa.edu.au/~00013890/sudokumin.php (accessed on 26 May 2020).
- McGuire, G.; Tugemann, B.; Civario, G. There Is No 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem via Hitting Set Enumeration. Exp. Math. 2014, 23, 190–217. [Google Scholar] [CrossRef]
- Tramura, N. Sugar: A SAT-Based Constraint Solver. 2020. Available online: http://bach.istc.kobe-u.ac.jp/sugar/ (accessed on 26 May 2020).
- Tamura, N.; Banbara, M. Sugar: A CSP to SAT Translator Based on Order Encoding. 2008, pp. 65–69. Available online: http://bach.istc.kobe-u.ac.jp/papers/pdf/cpai06.pdf (accessed on 17 June 2020).
- Eén, N.; Sörensson, N. The MiniSat Page. 2020. Available online: http://minisat.se/ (accessed on 26 May 2020).
- Eén, N.; Sörensson, N. An Extensible SAT-solver. In Theory and Applications of Satisfiability Testing; Giunchiglia, E., Tacchella, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 502–518. [Google Scholar]
- De Kegel, B.; Haahr, M. Procedural Puzzle Generation: A Survey. IEEE Trans. Games 2020, 12, 21–40. [Google Scholar] [CrossRef]
- Contributors, W. Sudoku Solving Algorithms—Wikipedia The Free Encyclopedia. 2020. Available online: https://en.wikipedia.org/wiki/Sudoku_solving_algorithms (accessed on 17 June 2020).
- Mantere, T.; Koljonen, J. Solving, rating and generating Sudoku puzzles with GA. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 1382–1389. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, Volume 4, Fascicle 5: Mathematical Preliminaries Redux; Introduction to Backtracking; Dancing Links; Pearson Education: London, UK, 2019. [Google Scholar]
- Zambon, G. Sudoku Programming with C, 1st ed.; Apress: New York, NY, USA, 2015. [Google Scholar]
- Boothby, T.; Svec, L.; Zhang, T. Generating Sudoku Puzzles as an Inverse Problem. 2008. Available online: https://sites.math.washington.edu/~morrow/mcm/team2306.pdf (accessed on 17 June 2020).
- Gebser, M. gen sudoku.gringo. 2020. Available online: https://asparagus.cs.uni-potsdam.de/encoding/show/id/12739 (accessed on 17 June 2020).
- Fatemi, B.; Kazemi, S.M.; Mehrasa, N. Rating and Generating Sudoku Puzzles Based on Constraint Satisfaction Problems. Int. J. Comput. Inf. Eng. 2014, 8, 1811–1816. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).