1. Introduction
Atanassov [
1] introduced the notion Intuitionistic Fuzzy Set (IFS), which generalizes the notion of Fuzzy Set proposed by Zadeh [
2]. Based on the fact that IFS is appropriate for cases dealing with uncertainty and vagueness, many authors have applied them to decision making. In the case of multiple attribute decision making the operational laws of Intuitionistic Fuzzy Values (IFVs) propose an elementary and remarkable topic. Atanassov [
1,
3] introduced the basic operational laws and presented some of their properties. Beliakov et al. [
4] developed some operations by using additive generators of the product t-norm. Zhao and Wei [
5] proposed the intuitionistic fuzzy Einstein hybrid aggregation operators. Atanassov, Pasi and Yager [
6] contributed to the case of multi-criteria group decision making, with the attributes being intuitionistic fuzzy numbers and the corresponding weights being crisp numerical values; their method is applied in the context of public relations and mass communication. Wang and Li [
7] proposed the score function and the weighted score function methods. Ouyang and Pedrycz [
8] proposed a model for intuitionistic fuzzy multi- attributes decision making that deals with the degrees of membership and nonmembership individually that is applied in multiple criteria supplier selection problems. Tao et al. [
9] gave an intuitionistic fuzzy copula arithmetic aggregation operator in multi-attribute decision making. Liu and Li [
10], extended power Bonferroni mean to interval-valued intuitionistic fuzzy numbers and applied it to multiple attribute group decision making in the evaluation of air quality. Seikh and Mandal [
11], introduced intuitionistic fuzzy Dombi weighted averaging operator, intuitionistic fuzzy Dombi hybrid averaging operator, intuitionistic fuzzy Dombi weighted geometric operator, intuitionistic fuzzy Dombi ordered weighted geometric operator and intuitionistic fuzzy Dombi hybrid geometric operator. Xian, Guo and Chai [
12], introduced an intuitionistic fuzzy linguistic-induced generalized ordered weighted averaging operator and made an application about taking targeted measures in poverty alleviation (TPA). Shi, Yang and Xiao [
13], introduced the intuitionistic fuzzy power geometric Heronian mean operator and the weighted intuitionistic fuzzy power geometric Heronian mean operator. Zou, Chen and Fan [
14], introduced the improved intuitionistic fuzzy weighted geometric operator of intuitionistic fuzzy values. For further contributions, references are provided [
15,
16,
17,
18,
19,
20,
21,
22].
Näther [
23] states that copulas and t-norms often coincide. Nelsen [
24] and Alsina et al. [
25] contributed to the introduction and application of copulas. Beliakov et al. [
26], has set copulas as conjunctive functions. In addition, the selection of the most suitable conjunctive function and how to fit additive generators for Archimedean t-norms and Archimedean copulas is depicted in Näther [
23].
The present paper aims to investigate the intuitionistic fuzzy copula aggregation operators, with the combination of fuzzy negations, in order to develop multiple attribute decision making methods for IFVs. To accomplish that, the construction of novel operations for IFVs is essential. As a result, the combination of copulas and fuzzy negations [
27] produces new operations, which allow us to construct novel intuitionistic fuzzy Archimedean copula weighted arithmetic and geometric aggregation operations with the usage of arithmetic and geometric means.
As a result, the remainder of the paper is organized as follows.
Section 2 includes some basic concepts of copula theory, fuzzy negations and intuitionistic fuzzy sets and also our development on novel operations for IFVs with the combination of the above. The properties of the proposed operations are investigated. In
Section 3 we provide the new intuitionistic fuzzy Archimedean copula weighted arithmetic and geometric aggregation operators, including a further analysis of their properties. In
Section 4 we provide an algorithm to accomplish the multiple attribute decision making procedure. In
Section 5 we provide a practical example to materialize the application of the proposed approach. In the discussion section, the results of our work are explained thoroughly and are compared with previous studies. In
Section 7, we provide some concluding remarks and future research directions.
2. Preliminaries
This Section provides novel operations for IFVs, which are established through the concepts of copula, co-copula, Archimedean copula and fuzzy negations.
Sklar [
28] presented the concept of copula, as a mathematical tool to combine probability distributions, framing the dependence structure within random variables with the usage of their CDFs.
Definition 1. [
28]
A 2-dimensional copula is a function with domain and range , grounded and 2-increasing, i.e., satisfies the following boundary and monotonicity conditions:
where, and .
Below, the definition of co-copula is given, according to Cherubini et al.’s [
29] work:
Definition 2. [
29]
The co-copula of a copula is defined as: According to Nelsen [
24] the co-copula is not a copula, but may be constructed by the usage of a copula. Fréchet [
30] and Hoeffding [
31] introduced the Fréchet–Hoeffding [
24] bounds of copulas for any
At this point, the method follows the definition of Archimedean copulas, which may be constructed with significant ease and ensure some remarkable properties.
Definition 3. [
24]
Let be a continuous, strictly decreasing function on with and the pseudo-inverse of , which is defined as:Then,,corresponds to the conditions of Definition 1, henceis a copula andis called Archimedean copula.
In the case, whereis strictly increasing,and, then. In that caseis called strict generator andis called strict Archimedean copula.
In
Table 1, some Archimedean copulas are listed.
The study of the applications of copulas in fuzzy sets is of great importance, given that specific copulas are t-norms and specific co-copulas are t-conorms and vice versa. Moreover, Näther [
23] mentioned in his work that the combination of probabilistic information or fuzzy information hardly matters. Below, the Atanassov’s [
1] definition for Intuitionistic Fuzzy Sets is provided:
Definition 4. [
1]
Let be a reference set, an Intuitionistic Fuzzy Set (IFS) on is defined as:where, the functions and denote the degrees of membership and non-membership of the element to the set , respectively with:,,andis called degree of indeterminacy ofto. Additionally,is called Intuitionistic Fuzzy Value (IFV) and the set of all IFVs is.
Definition 5. [
32]
A decreasing function is called a fuzzy negation if and . A fuzzy negation is called: Strict, if it is strictly decreasing and continuous and Strong, if it is an involution, i.e., . Table 2, proposes two parametric families of fuzzy negations:
Moreover, the operations of IFVs in Tao et al.’s [
9] work, are being extended through the adaptation of fuzzy negations.
Definition 6. Letandbe two IFVs anda parameter.
- 1.
- 2.
- 3.
Scalar Multiplication operation - 4.
By replacing the
parameter with the appropriate value, the Tao et al.’s [
9] operations of IFVs are produced. Moreover, a further investigation is held for the properties of the proposed operations.
Theorem 1. Letandbe two IFVs anda real valued parameter. The novel operations of IFVs are closed or their values are also IFVs, i.e.,.
Proof of Theorem 1. We have
and
. Since
is strictly decreasing then:
Similarly, as
we get:
We add Equations (4) and (5) and we get:
Based on the fact that
is also strictly decreasing, we obtain:
Morover, by Definition 1, as
,
holds.
Thus, the result of the operation is:
As Equation (3) is concerned:
For
we get:
that holds.
For
we get:
that holds.
We assume that for
holds. Then for
:
Hence, by mathematical induction the proof is complete. The proofs that the rest of the operations belong to the set are similar.
Next we investigate the properties of the proposed operations: □
Theorem 2. Let,and real valued parametersthen:
Proof of Theorem 2. The cases 1 and 2 are obvious, because of Archimedean copulas and the corresponding co-copulas commutativity.
□
In order to achieve the derivation of different operations for IFVs, the usage of generator functions from
Table 1 and of fuzzy negations from
Table 2, is accomplished. Those operations are listed in
Table 3:
In the following Section, we propose the development of intuitionistic fuzzy Archimedean copula weighted arithmetic and geometric aggregation operators, which is achieved. Furthermore, the properties of those extended aggregation operators are investigated.
4. and Operators in MADM
In this section an algorithm for Multiple-Attribute Decision Making (MADM) with IFVs is introduced. Let
be the set of alternatives and
be the set of attributes, with a weighting vector
, with
and
. The intuitionistic fuzzy decision matrix
where
with
and
represent the degree that
satisfies
, such that
, with
i.e.,
In order to obtain the weighting vector of attributes, the modified maximizing deviations method for MADM with intuitionistic fuzzy information [
9] can be used. As MADM with intuitionistic fuzzy information is a procedure to end up with the best alternative
the comparison of IFVs is achieved by the following concept.
For any IFV
Chen and Tan [
33] proposed a score function
and Hong and Choi [
34] proposed an accuracy function
, i.e.,
and
, respectively. The larger the score is, the greater the IFV would be. In the case that the score function’s values for two IFVs are equal; the accuracy function can provide more specific result. Xu and Yager [
35], based on score and accuracy functions, gave a total order for IFVs.
Based on the above and inspired by MADM model in [
9], we derive the following algorithm.
| Algorithm 1 Multiple Attribute Decision Making Model |
| BEGIN |
| 1: Obtain the normalized intuitionistic fuzzy decision matrix, i.e., |
| . |
| 2: Determine the weighting vector of the attributes. |
| 3: Aggregate the IFVs using the proposed or |
| operators. |
| 4: Sort the options according to score function and accuracy function. |
| 5: Select the best alternative, by ranking the values of . |
| END |
In order to demonstrate the proposed method, we provide the following numerical example, which is adapted from Tao et al.’s [
9] work, in order to compare their method with the present extension of it.
5. A Practical Example for MADM with IFVs.
A research facility has arranged to purchase an electronic device. The people in charge, selected the four most appropriate models for further consideration, after the market research. Those are indicated as the four alternatives The evaluation of the alternatives is achieved by the consideration of five attributes by the decision maker (DM). Those attributes are listed as follows: the layout of the product (), the technical assistance (), the brand (), the price () and the quality of the product ().
- Step 1.
The normalized intuitionistic fuzzy decision matrix can be obtained as follows:
in which, the element
with
and
, represents the intuitionistic membership and non-membership degree of the i-th alternative that satisfies the j-th attribute.
- Step 2.
In the present work, we use Tao et al.’s [
9], modified maximizing deviations method, in order to derive the five weightings of the attributes, and since the numerical example is the same we get:
- Step 3.
The aggregated results are given by the usage of
and
operators and are listed in
Table 6 and
Table 7.
- Step 4.
The score function’s results for each alternative and for each type of
and
operators are listed in
Table 8 and
Table 9.
- Step 5.
The ranking of the alternatives is achieved and is depicted in
Table 10.
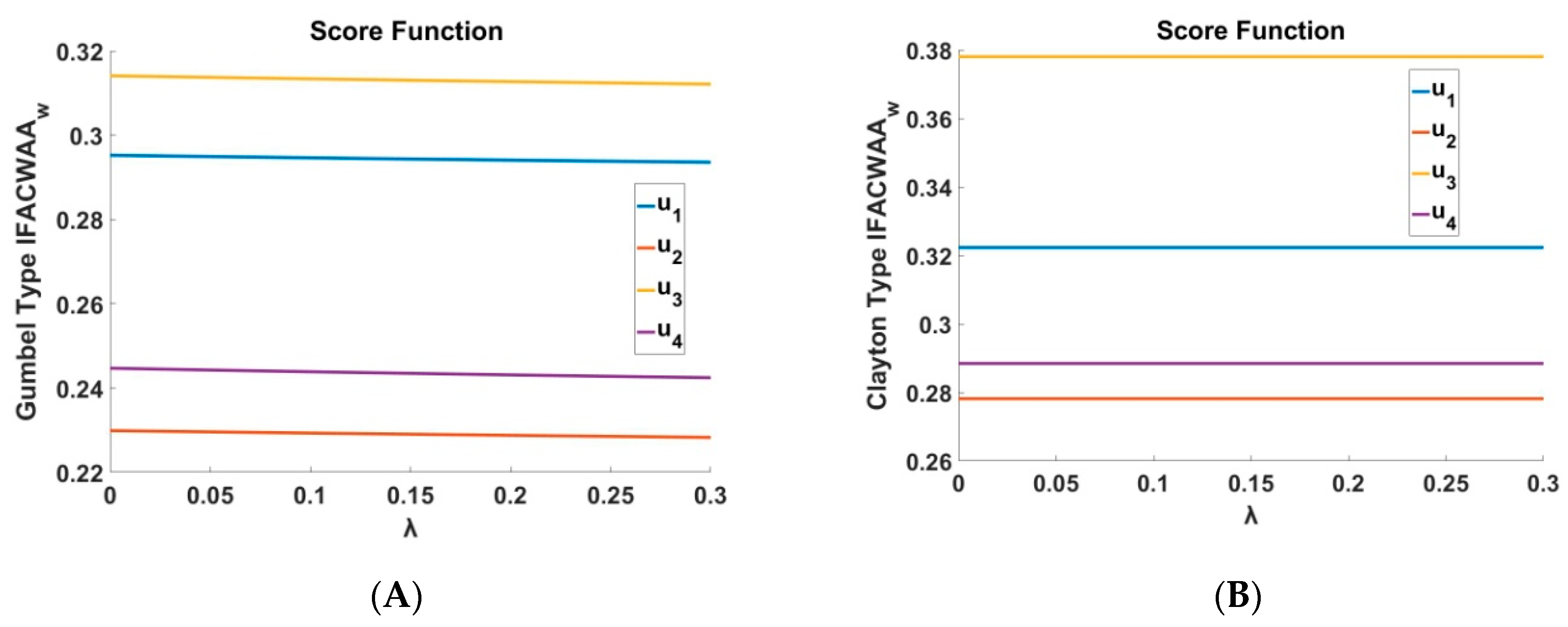
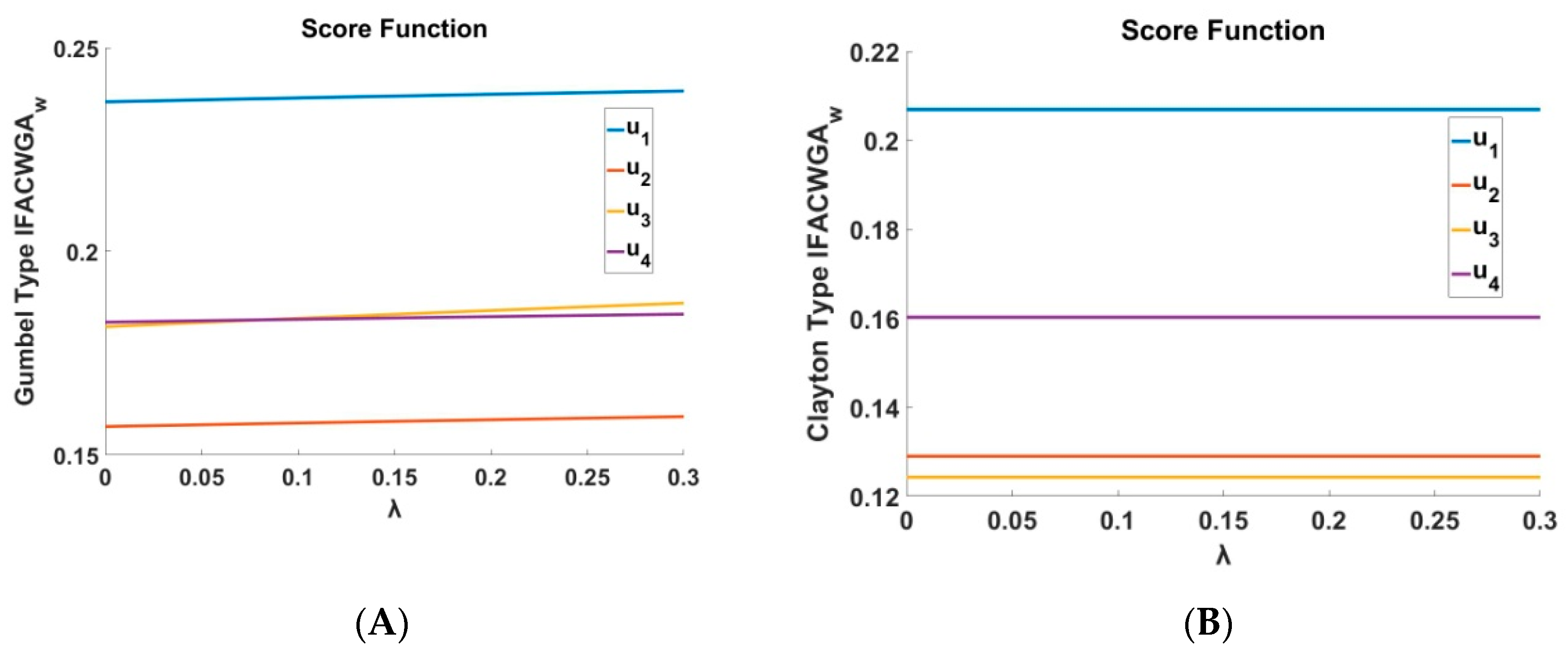
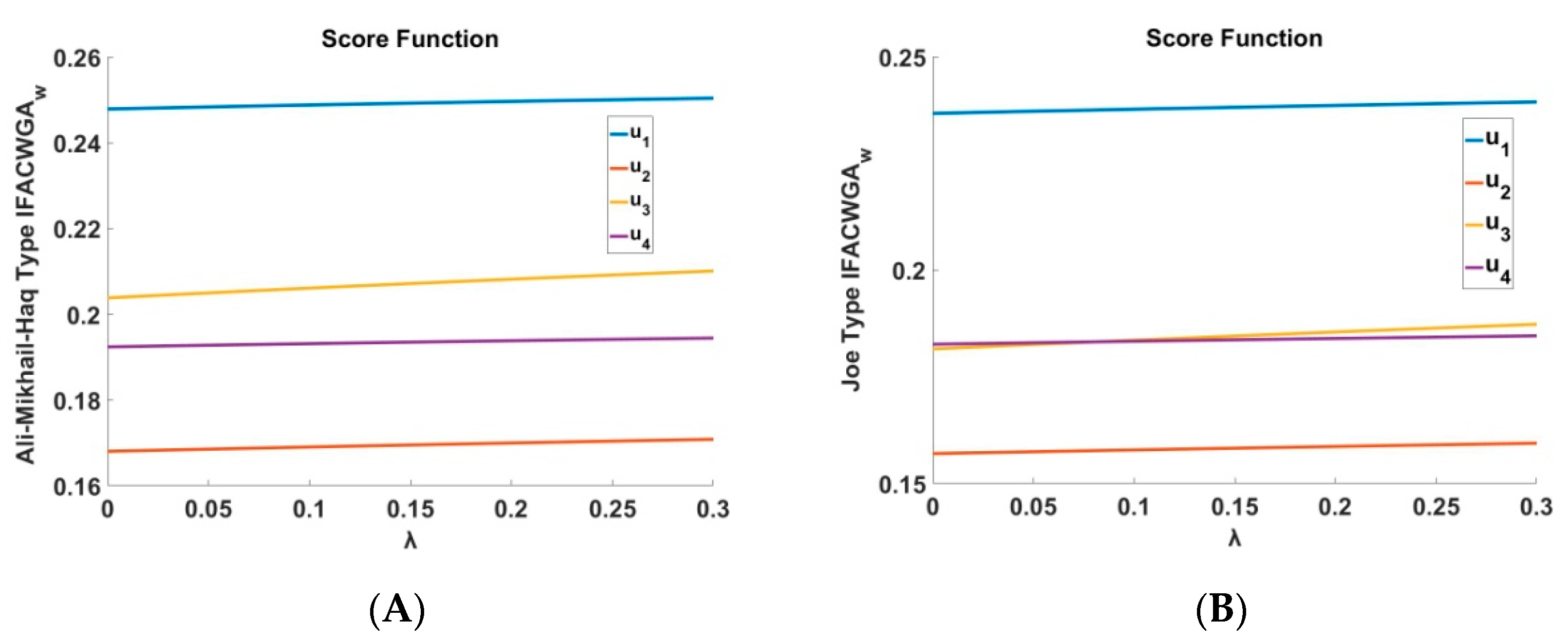
To illustrate the affection of
parameter in the procedure as
parameter is fixed to 1 (and -1 in Ali-Mikhail-Haq case) we utilized the following graphs that are depicted in
Figure 1 and
Figure 2 for the
and in
Figure 3 and
Figure 4 for the
.
6. Discussion
The present paper establishes specific novel operational laws of IFVs, as the generalization of the existing copula-based operational laws, with the contribution of fuzzy negations. Additionally, the paper provides the extension of the proposed operations to the arithmetic mean and to the geometric mean of IFVs.
First of all, the replacement of the
parameter with the numerical value zero in Sugeno class, or with the numerical value one in Yager class, in Definitions 6–8 and the corresponding tables (
Table 3,
Table 4 and
Table 5), provides us with the operation laws and the aggregation operators of Tao et al.’s [
9] work. As a result, the generalization of the existing operators by the proposed operational laws and the extension of the existing aggregation operators are verified. More specifically, the extension of the existing aggregation operators is based on the reform of the existing basic operational environment.
Regarding the provided practical example for MADM with IFVs, developed in order to point out the advantages and the flexibility of the proposed algorithm, we may call forth the following comparison with [
9].
To continue with the ranking of the alternatives in [
9], the usage of Gumbel-type aggregation operator suggests the third alternative (
) as the most adequate one. In addition, the Clayton-, Ali-Mikhail-Haq- and Joe-type of aggregation operators provides the same alternative, respectively, through the other three alternatives are developed with a different order. On the other hand, in our approach, as
Table 10 shows, there is no difference in the order of the four alternatives for each type of aggregation operator and, as a result, the order problem is distinguished.
In addition, in
Table 10, the order of the alternatives is provided, suggesting the usage of
operators for each copula type, which represents a new best alternative. Specifically, Gumbel-, Ali-Mikhail-Haq- and Joe-type aggregation results demonstrate that the most adequate alternative is
and
follows. The rest ranking remains the same with the
operators ranking. However, in the case of Clayton-type
ranking in respect of the three alternatives is totally different, through the first one remains
demonstrating the most adequate choice. This perspective may be considered reasonable, given that the parameter
does not affect, neither the membership degree, nor the nonmembership degree in the aggregation process and this fact may be observed in the Clayton-type score function’s plot.
Another remarkable fact about the proposed aggregation operators is that they provide two parameters affecting (in most cases) the results, suggesting more choices and flexibility for the decision makers. For the description of the affection of
parameter,
Figure 1,
Figure 2,
Figure 3 and
Figure 4 have been utilized, as
parameter is fixed to 1 (and -1 in the Ali-Mikhail-Haq case).
In
Figure 1, apparently the Gumbel- and Clayton-type of
operators suggest distinct score functions for each alternative, with
always representing the most adequate choice and
the least adequate one. The same holds for the Joe- and Ali-Mikhail-Haq-type of
operators, as it is depicted in
Figure 2. In
Figure 3, the Gumbel-type of
suggests
as the most adequate choice and
the least adequate one, through alternatives
and
that meet a crossover point. In
Figure 4, we may observe that Joe-type of
proposes the same alternatives, respectively, as the Gumbel-type approach, but also a crossover point for the alternatives
and
.
7. Conclusions
The paper cited the generalization of copula-based operations of Intuitionistic Fuzzy Values (IFVs) via fuzzy negations. Additionally, novel aggregation operators were produced from the new operations of IFVs, with their properties being further investigated. As a result, an algorithm is suggested, which may be utilized in Multiple Attribute Decision Making (MADM) processes.
The main advantage of our work is that the aggregation operators of IFVs provided in the suggested algorithm are univariate parametric, therefore various intuitionistic fuzzy Archimedean copula weighted arithmetic and geometric operators could be obtained, with each one potentially being more appropriate for the decision makers. Combined with the most appropriate copula [
23] for each MADM case, more specified aggregator operators would be provided to express more accurately a decision maker’s attitude.
In the future our aim is to combine the proposed operations with fuzzy negations via conic sections [
36], in order to produce modified families of aggregator operations of IFVs. Furthermore, we are willing to adapt the proposed operations, following the appropriate transformation, in other types of fuzzy sets, such as hesitant fuzzy sets [
37], and unbalanced linguistic term sets [
38] and neutrosophic sets [
39], in order to construct algorithms for multiple attribute decision making and multiple attribute group decision making.