1. Introduction
In the mathematical and computational field, model order reduction (MOR) is a technique for constructing efficient lower dimensional models for reducing the computational cost of large scale dynamical systems from partial differential equations (PDEs) in numerical simulation. Many modern mathematical models are useful for describing physical phenomena in real life. However, the process for solving the numerical solution of these mathematical models often has high computational complexity. To overcome this problem, A reduced order model can be used to approximate the original system while preserving the main properties and containing the important features of the original model.
This paper considers nonlinear partial differential equation called Allen–Cahn equation, which was first introduced by Cahn and Allen to describe the motion of anti-phase boundaries in metallic alloys [
1]. This equation is used in mathematical physics, to describe the process of phase separation. The Allen–Cahn equation has been widely used in many applications, such as image analysis [
2,
3], crystal growth [
4], and motion by mean curvature flow [
5]. In particular, it has become a basic model equation for the diffuse interface approach developed to study phase transitions and interfacial dynamics in material science [
6].
In a general model of Allen–Cahn equation used for describing phase transition in materials science, there is an important parameter called an “interaction length” [
5]. The change of this parameter can significantly affect the numerical solutions and the behavior of the phase transition. In particular, when this parameter becomes very small (approaching zero), there will be a sharp interface limit (the mean curvature flow). This work aims to construct low-dimensional models for Allen–Cahn equation with different values of this interaction length parameter by using model reduction approach with common projection bases that can be generated only once and reused for all various parameter values. In the mathematical and computational field, model order reduction (MOR) is a technique for constructing a low dimensional model that preserve the necessary information from the full discretized system, while saving computational time and storage. The advantage of a reduced model often lies in the decrease of simulation time and the provision accurate results when compared to the high dimensional system. There are many MOR techniques such as balance truncation [
7], Krylov subspace MOR methods [
8], projection based MOR [
9], and the Moment-matching method [
10]. This work uses proper orthogonal decomposition (POD) as a starting point for constructing reduced-order model for Allen–Cahn equation. POD approach generally gives high accurate reduced models with much smaller dimensions by generating a set of optimal basis that represents a given data set with minimum error. However, it cannot truly reduce the computational complexity of nonlinear term. We therefore employ the discrete empirical interpolation method (DEIM), as well as a modified Gappy POD (GPOD) for efficiently constructing reduced order systems.
POD is a popular method for model reduction, which was first proposed by Lumley [
11]. It is also known as Karhunen–Loéve decomposition [
12] or principal component analysis [
13]. It provides a technique for analyzing multidimensional data. This method constructs an orthonormal basis for representing the given data in a certain least squares optimal sense. The basic properties of the POD method have been studied in [
14] as it is applied to data compression and used as a model reduction technique for finite dimensional linear systems. Prajna [
15] purposed sufficient conditions for preserving stability in POD model reduction. POD has been widely applied in many application such as data analysis, data compression and model reduction in various fields of engineering and science. Applications of POD include image processing [
16], data compression, signal analysis [
17], turbulence modeling [
18], control of fluids [
19], electrical power grids [
20], and modeling and control of chemical reaction systems [
21,
22]. Noor et al. [
23] presented a reduced-basis technique and a computational algorithm within the context for analyzing nonlinear structure. Peterson [
24] demonstrated that the reduced basis method based on POD can efficiently approximate the solution of incompressible viscous flow. Ravindran [
25] demonstrated a reduced-order modeling approach using POD for simulation and control of incompressible flows. Gunzburger, Peterson, and Shadid [
26] focused on reduced order modeling of time-dependent PDEs with multiple parameters on POD approach to the reduced order model. Carlberg and Ferhat [
27] used a compact POD to compute a reduced basis for an optimization-oriented reduced order model and applied this to compute a reduced basis for model reduction of static systems [
28].
POD also has been used for various nonlinear dynamical systems. In [
29], POD has been used with global optimum search framework to construct a temporally-local reduced model for nonlinear parabolic PDEs. An adaptive framework for POD was introduced in [
30], when new snapshots are included for feedback control of dissipative nonlinear PDEs. In [
31], a modification of data ensemble revision approach was developed and used with adaptive POD framework to construct reduced order models for output feedback control of distributed processes. The notion of sparse POD has been introduced and successfully used for constructing reduced order models of nonlinear parabolic PDEs with moving boundaries [
32].
DEIM is a nonlinear technique for approximating nonlinear terms of a dynamical system to further decrease computational complexity of POD reduced systems. The DEIM approach was introduced in [
33], and approximates a nonlinear function by combining projection with interpolation. This approach is a discrete variant of the empirical interpolation method (EIM) [
34], which was originally described in a function space setting. The DEIM approximation was extended to nonlinear reduced models by localization (LDEIM) [
35]. There are other nonlinear techniques for approximating nonlinear terms, such as the Gauss–Newton with approximated tensors (GNAT) method [
36], the best points interpolation method [
37] and missing point estimation [
38]. There are many works combining a reduced model by POD with DEIM such as the photovoltaic module [
39], the shallow water equations model [
40], the Navier–Stokes equations [
41] and drift-diffusion equations [
42].
Gappy POD (GPOD) was first purposed by Everson and Sirovich [
43]. It has been used as an approach to restore incomplete data. Thanh, Damodaran, and Willcox [
44] presented this in the context of fluid dynamic application. Bos et al., [
45] presented this in the context of solving the numerical simulation of nonlinear system. Willcox [
46] extented GPOD to handle unsteady flow reconstruction problem. Lee and Mavris [
47] applied this method for various problems in aerospace engineering. Murray and Ukeiley [
48] used GPOD in the context of particle image velocimetry (PIV) data for subsonic cavity flow.
Remark 1. In this work, new contributions include:
A novel model reduction algorithm that improves the accuracy of the existing standard model reduction technique that combines the orthogonal decomposition (POD) and discrete empirical interpolation method (DEIM) by using a modification of GPOD that is based on least-squares approximation to the nonlinear term.
Comparison of computational complexity of the proposed method and the standard methods in both theoretical and numerical aspects.
Numerical experiments that demonstrate the accuracy and efficiency of the proposed method for solving the parametrized Allen–Cahn equation for both homogeneous and non-homogeneous boundary conditions with different types of initial conditions.
The remainder of this paper is organized as follow. In
Section 2, the general form of Allend-Cahn equation and its corresponding discretization are given.
Section 3 provides some background on POD and POD-DEIM approaches, as well as introduces the POD-GPOD approach. The accuracy and efficiency of the POD-GPOD framework are compared with the standard POD approach and POD-DEIM approach in
Section 4 for simulating the solution of parametrized Allen–Cahn equation. Finally, conclusion and remarks are discussed in
Section 5.
4. Numerical Results
This section presents the numerical tests that demonstrate the accuracy and efficiency of the resulting POD-GPOD approach on approximating the solution of the parametrized Allen–Cahn equation when compared with the standard POD and POD-DEIM approaches. It mainly considers 3 numerical tests. In
Section 4.1, we test these model reduction frameworks on Allen–Cahn equation with non-homogenious boundary conditions and square block initial condition. In
Section 4.2 and
Section 4.3, we test these model reduction approaches with various parameter values for two different initial conditions. In particular, we use only one basis for POD and one basis for DEIM or GPOD to construct several reduced systems for different parameter values that are not previously used in the snapshot sets. In all of these numerical experiments, we use the MATLAB program for solving the numerical solutions. The approximation error of the solution from each of these reduced systems is defined as
where
and
, respectively, are snapshot matrices from solving the FD full system and reduced system, which could be POD, POD-DEIM, or POD-GPOD reduced system.
4.1. Numerical Test 1 (Fixed Parameter): Non-Homogenious Boundary Conditions with Square Block Initial Data
In this subsection, we used a square block initial condition to test model reduction approaches for Allen–Cahn Equation (
1). The initial condition is defined by a piecewise constant function with value
a on wave crest and value
b on wave trough. We used the following inputs: internal point
in
, time steps
on
and
. We used a space step-size
, and time step-size
.
First, we selected wave crest
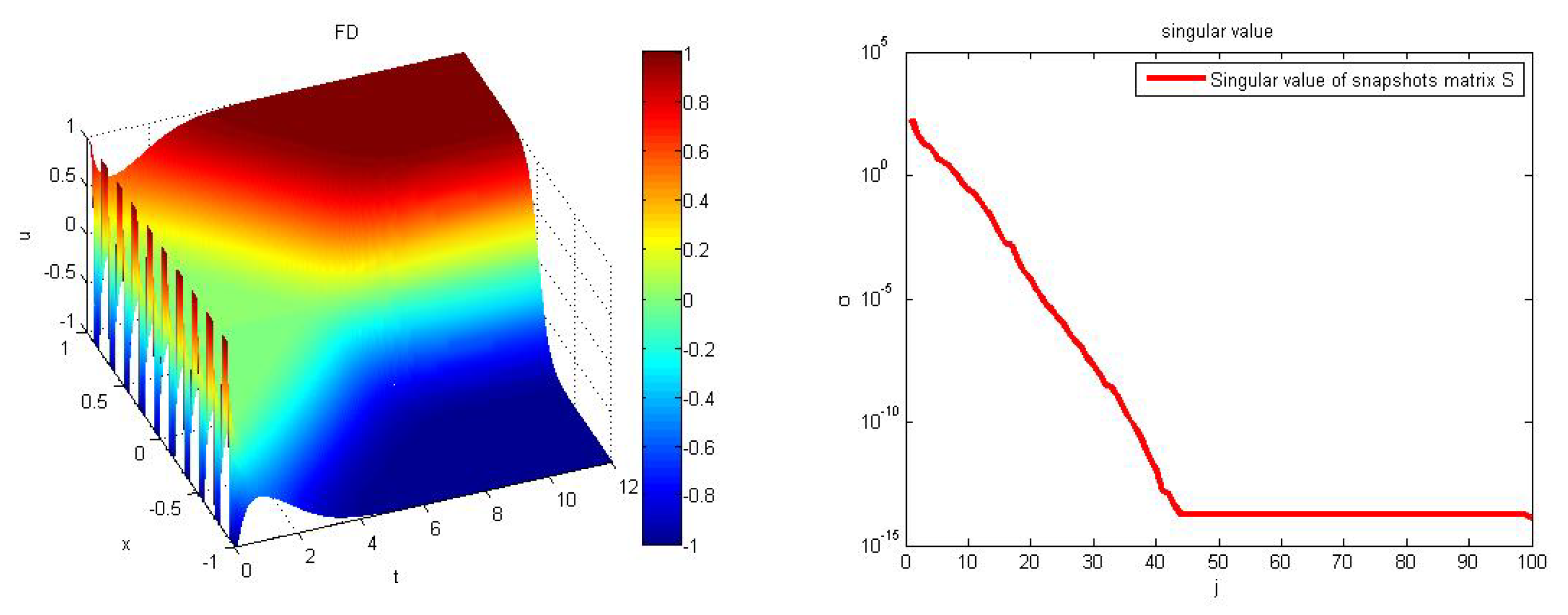
and wave trough
. We solved the numerical solution of the FD full system. When the time increases, the evolution of the Allen–Cahn equation still keeps the phase separation after long time calculation in the left plot of
Figure 1. From the right plot of
Figure 1, the decreasing of singular values of the snapshot matrix and then beginning to stabilize implies that solution information lies within a subspace whose dimension is significantly lower than the full dimension used in the discretization. That is, we can further reduce the dimensions of the full discretized system and still obtain accurate approximate solution.
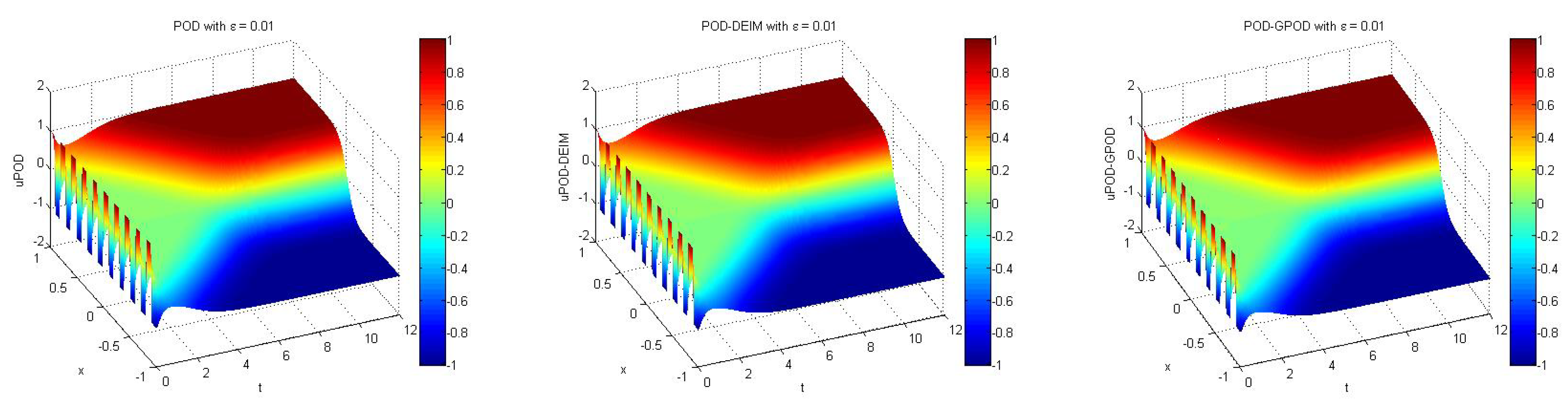
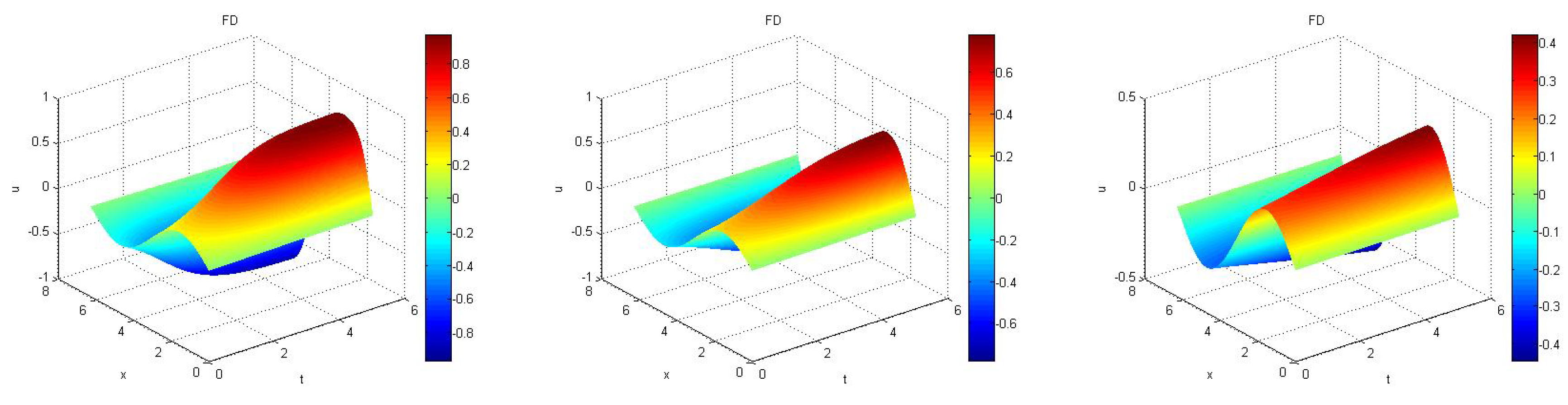
Next, we solved the numerical solution of the reduced system and used dimensions of POD basis
and DEIM basis
. We obtained the approximate evolution of phase function of Allen–Cahn equation from POD, and POD-DEIM approaches for time
to
as shown in the first two plots of
Figure 2. Finally, GPOD is used for reducing the complexity of the nonlinear term from the POD reduced system using a dimension of nonlinear basis
m that is less than the number of selected rows
q. The dimension of POD basis, nonlinear basis, and the number of selected rows in this numerical test are
and
respectively. We obtained the evolution of the phase function of Allen–Cahn equation by using POD-GPOD method for time
to
as shown in the last plot of
Figure 2. Notice that the approximations from both POD-DEIM and POD-GPOD seem to be visually indistinguishable from the original solution. More details on errors are given in
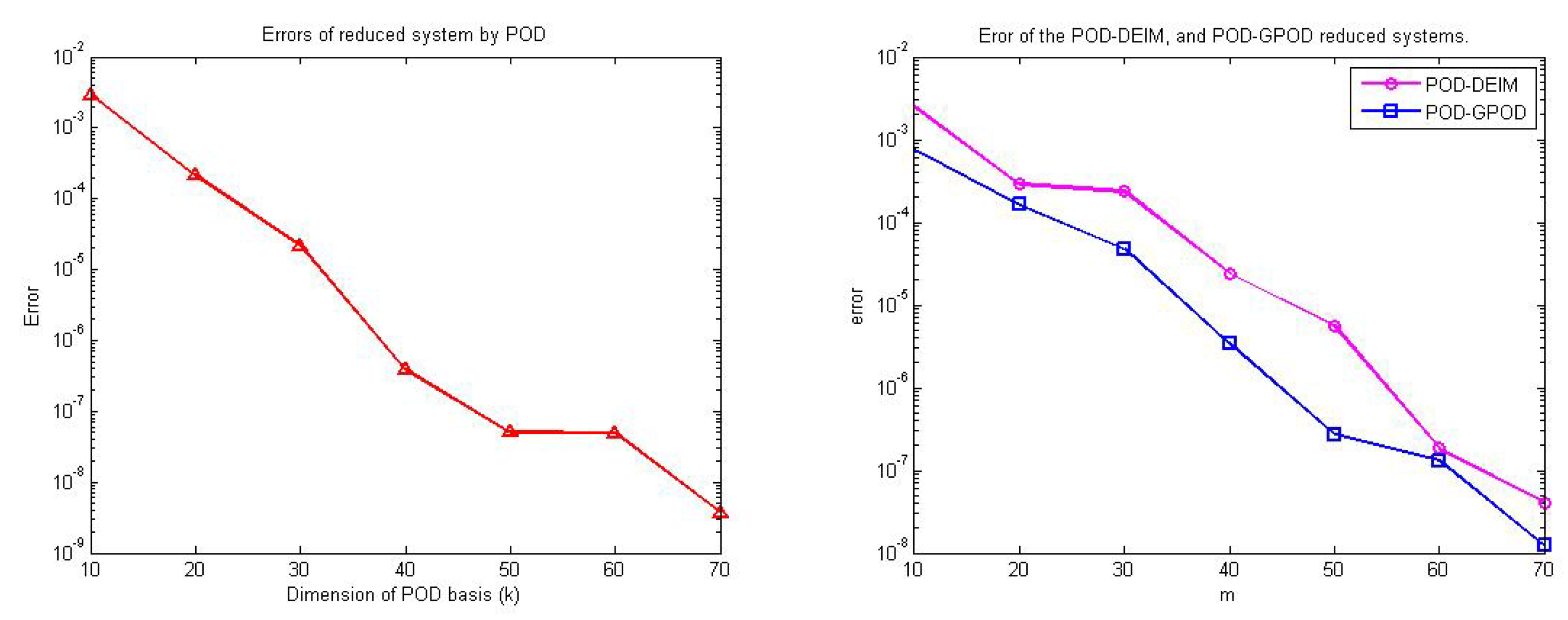
Table 2 and
Figure 3.
The runtime and error from (
21) are computed for POD-reduced system as shown in
Table 2 and for POD-DEIM and POD-GPOD reduced systems as shown in
Table 3 for different dimension
m of nonlinear basis, and number of selected rows
q.
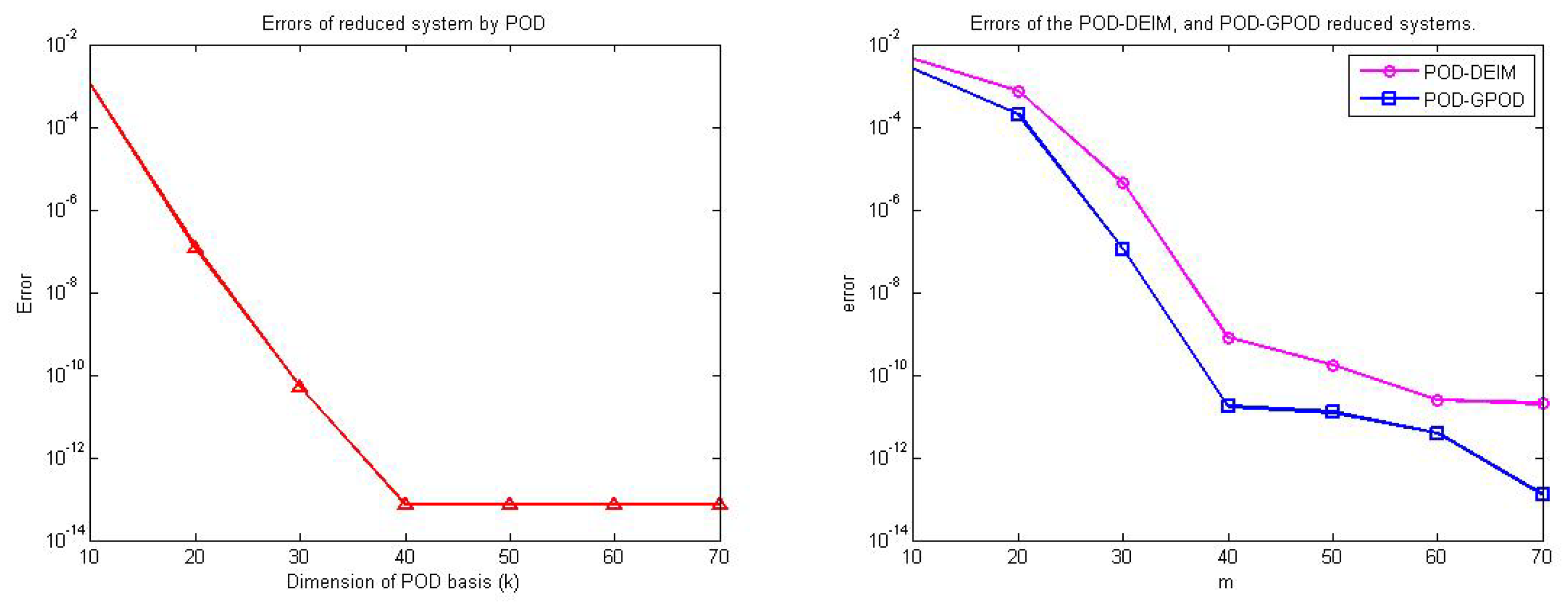
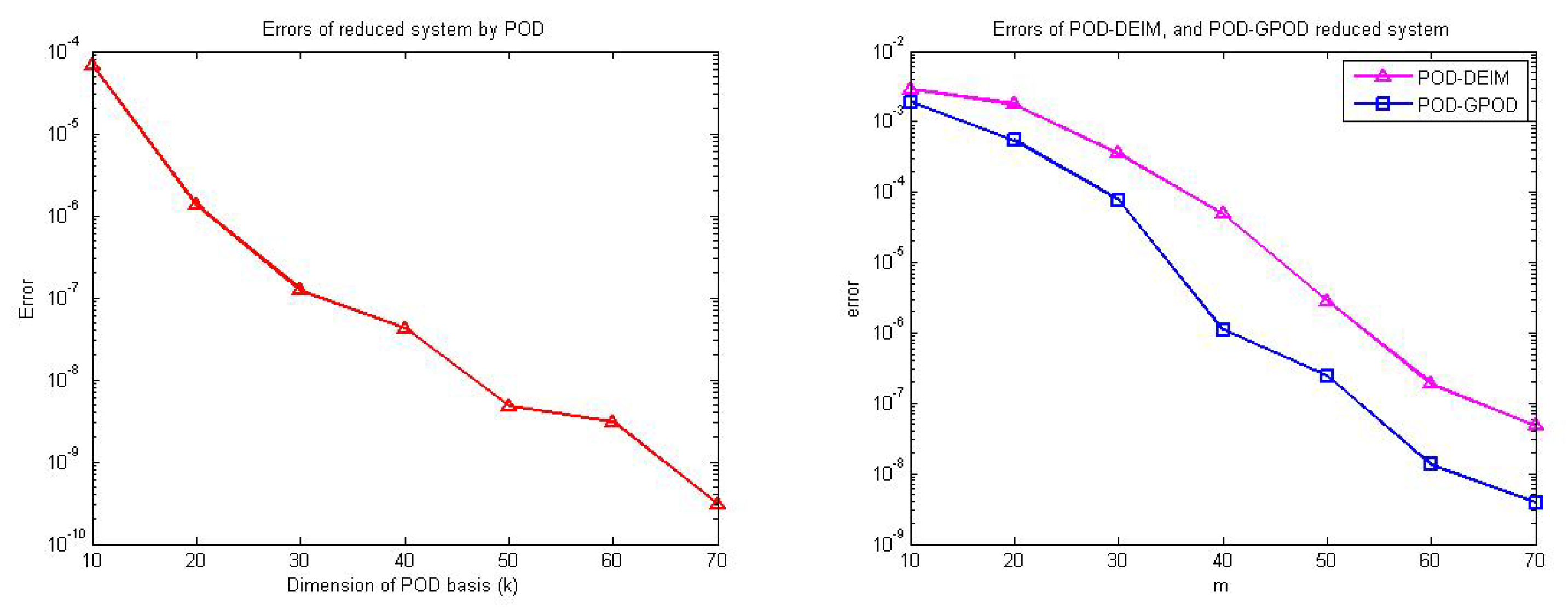
It can be observed in
Figure 3 that the error decreases as the dimension of POD increases as also shown in
Table 2. For a fixed POD dimension of
the error of POD-DEIM reduced system can be reduced by increasing the dimension of DEIM basis as shown in
Table 3 and
Figure 3. Similarly for POD-GPOD reduced system, when POD dimension is fixed to be
, the error can be decreased by increasing both the dimension of nonlinear basis and the number of selected rows as shown in
Table 3. From
Figure 3 and
Table 3, for each
m, the error of POD-GPOD approach is clearly smaller than the error of POD-DEIM approach.
Note that, from
Figure 3, although the accuracy of the POD approach is higher (less error) than the POD-DEIM and POD-GPOD approaches, the reduction of the simulation time seems to be far less than these last two approaches, as shown in
Table 2 and
Table 3. To compare the speedup of the reduced order approaches, the runtimes given in
Table 2 and
Table 3 are all scaled with the simulation time for the full-order system, which is considered to be 100%. From
Table 2, the runtime of POD approach is shown to be approximately 20–30% of the original full order system, i.e., around 3.3–5 times faster than the full order system, when the POD dimensions
are used. From
Table 3, the POD-DEIM approach used only 2.51–4.88% of the full order system’s runtime, i.e., roughly 20–40 time faster, when POD dimension
with DEIM dimension
are used. For POD-GPOD approach, as shown in the second part of
Table 3, the runtime is reduced to approximately 5.49–6.57% of the original system, i.e., roughly 15–19 times faster than the original system. This shows that DEIM and GPOD techniques can significantly speed-up the simulation time of POD approach with small trade-off on accuracy. Notice that POD-DEIM approach provides the fastest speedup, but it has slightly less accuracy than the others. As a result, the POD-GPOD approach is shown to balance between the accuracy and the computational speedup.
In the next two numerical experiments, we will consider Allen–Cahn equation with parameter variation for different initial conditions and boundary conditions.
4.2. Numerical Test 2 (Parameter Variation): Homogeneous Boundary Conditions
The goal of this section is to construct reduced systems that have different values of a given parameter by using one basis set for each POD, DEIM, and GPOD. We consider Allen–Cahn Equation (
1) with
the initial condition:
, and the homogeneous boundary conditions:
. In our numerical tests, the number of internal point is
in
, the number of time steps is
on
and
. We used a space step-size is
, time step-size is
and the basis sets used in POD and DEIM approximations were constructed from
snapshots.
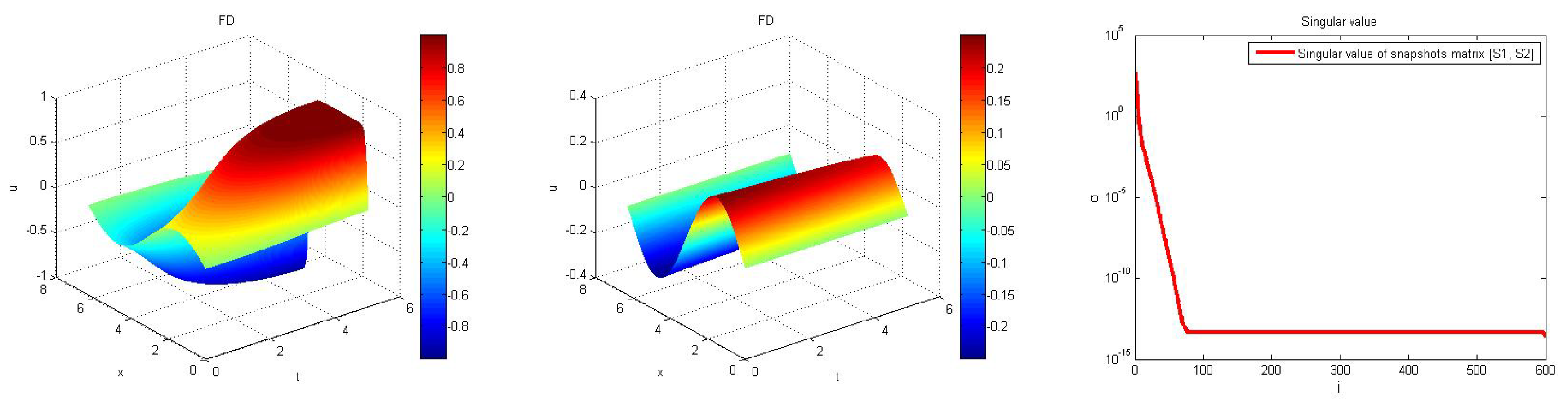
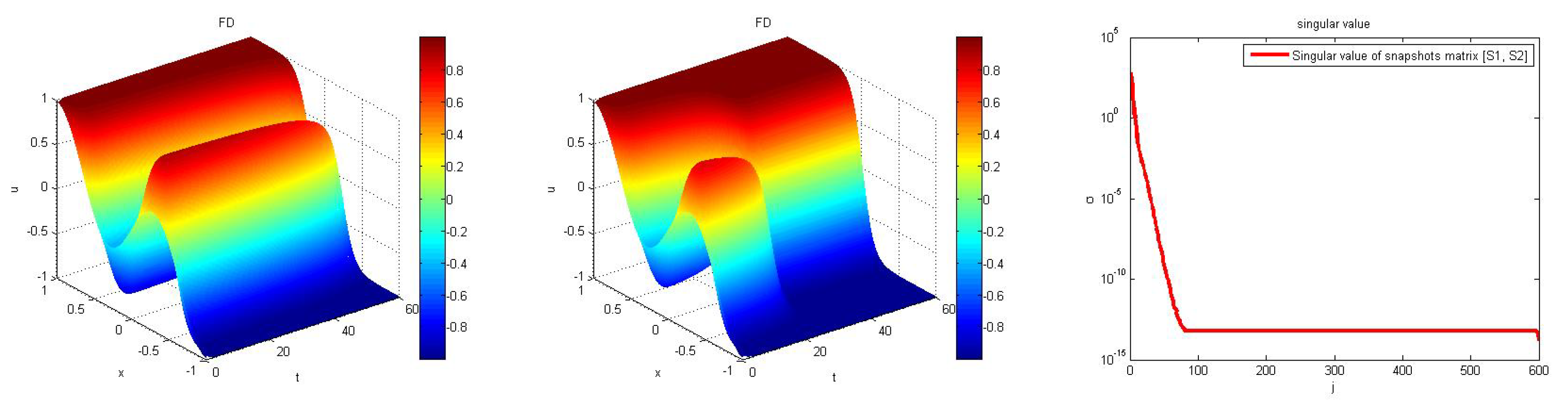
We used snapshots from the full systems with
and
, as shown in
Figure 4, respectively, to construct snapshot matrices
,
and
,
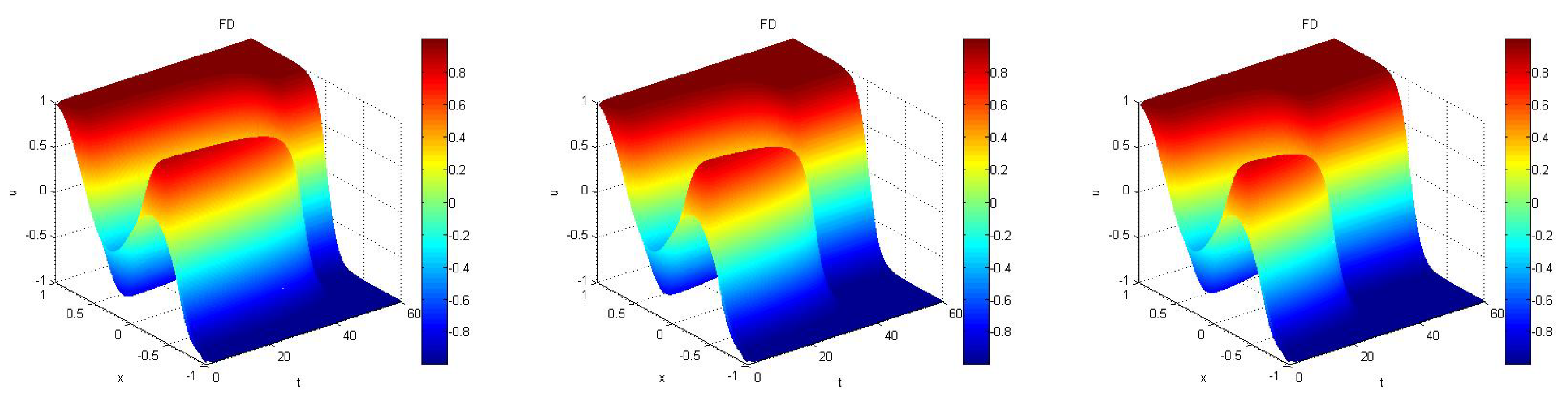
. These snapshot matrices were used to construct basis sets for constructing reduced models with different parameter values
i.e.,
as shown in
Figure 5. The singular values corresponding to the combined snapshot matrix
, which is used for computing POD basis, is shown in the last plot of
Figure 4. The combined nonlinear snapshot matrix
is used for constructing the basis for DEIM and GPOD approximations. Notice from the plots in
Figure 4 and
Figure 5 that the behaviors of the solutions are clearly different as the value of parameter
changes.
In
Table 4 and
Table 5, the average of errors from (
21) is given for POD, POD-DEIM, and POD-GPOD approaches with parameter variation
and
. The corresponding average runtimes given in these tables are scaled with the runtime of the full order system, whose average runtime is considered to be 100%. Note that in
Table 5, the dimension
k is fixed to be 50 with different dimension
m of nonlinear basis and different dimension
q of selected rows.
It can be observed that the decrease of the average error in
Figure 6 corresponds to the increase of dimension of POD basis, as also shown in
Table 4. At a fixed POD dimension of
the decrease of the average error corresponds to the increase of dimension of DEIM basis, as also shown in
Table 5. Similarly, at a fixed POD dimension of
the decrease of the average error corresponds to the increase of both dimension of nonlinear basis and the number of selected rows in POD-GPOD approach. In
Figure 6, the average error for the POD-GPOD reduced system is decreased more than the average error from the POD-DEIM reduced system. The average runtime of the reduced systems by POD approach was ranging between 39.37% to 46.91% of the average runtime of the full-order system, which is roughly 2.1–2.5 times speedup as shown in
Table 4.
The average runtime in
Table 4 shows that POD approach can speedup the simulation of the full-order model to roughly 2.1–2.5 times faster (using 39.37% to 46.91% of the average runtime for the full-order system). In
Table 5, the POD-DEIM approach and POD-GPOD approach are shown to give around 300–500 times and 240–255 times, respectively, for the speedups. Although GPOD seems to use more simulation time than DEIM, it has already reduced the runtime of the full-order system (more than 200 time speedup) and, more importantly, it can provide approximation with less error than DEIM around one order of magnitude when the dimension
.
Table 6 summarizes the accuracy and the scaled average computational time of the reduced systems when compared with the full-order system (the runtime of full-order system is normalized to be one), for a special case fixed dimensions
,
, and
.
4.3. Numerical Test 3 (Parameter Variation): Non-Homogeneous Boundary Conditions
This section considers parametrized Allen–Cahn Equation (
1) with non-homogeneous boundary conditions. We used
, with the initial condition:
, and the non-homogeneous boundary conditions:
. In this numerical tests, the number of internal points is in , the number of time steps is on and . We used a space step-size is , time step-size is . The value of parameter is varying in this numerical test.
We used snapshots from the full systems with
and
from time
to
, as shown in
Figure 7, to construct matrices of solution snapshots and nonlinear snapshots. The decay of singular values of the matrix of solution snapshots is shown in the last plot of
Figure 7. These snapshot matrices were used to construct basis sets for constructing reduced models of full systems with different parameter values
i.e.,
as shown in
Figure 8. Notice from
Figure 7 and
Figure 8 that the behaviors of the solutions are clearly different as the parameter changes, i.e., as the value of parameter
gets bigger, the solution reaches the steady state faster.
In
Table 7 and
Table 8, we present average runtimes and average errors from the parameter variation using
and
for POD, POD-DEIM, and POD-GPOD approaches, respectively. We computed the runtime and error from (4.1).
Table 8 shows the average error of the POD-GPOD reduced systems with POD basis of dimension
, where
m is the dimension of nonlinear basis, and
q is the number of selected rows.
The results in this section illustrate the same trends as in the previous numerical tests. From
Table 7 and
Table 8, the POD approach is more accurate, but it is much less efficient in term of computational time than the POD-DEIM and POD-GPOD approaches. From
Table 7, when the POD approach uses
, the average error is of order
and the average runtime is shown to be 32.957% of the full-order system, which is approximately three times faster than the full-order system. From
Table 8, when the POD-DEIM reduced system uses
and
, the average error is of order
and the average runtime is 0.191% of the full-order system, which is approximately 524 times faster than the full-order system. From
Table 8, when the POD-GPOD reduced system uses
,
and
, the the average error is of order
and the average runtime is 0.379% of the full-order system, which is approximately 264 times faster than the full-order system.
Figure 9 shows that the reduced systems become more accurate as the dimension
k for POD and dimension
m for DEIM increase. As in the previous numerical test, the second plot in
Figure 9 also demonstrates that the POD-GPOD reduced system is more accurate than the POD-DEIM reduced system for each fixed dimension
m.
Table 9 summarizes the accuracy and the scaled computational time of the reduced systems when compared with the full-order system. In
Table 9, the ratio of the average runtime of the full discretized system is normalized to be 1. It considers a special case fixed dimensions
,
, and
. These results demonstrate that GPOD can further improve the accuracy of the DEIM, while still substantially decrease the computational complexity of the nonlinear term of POD reduced system.