Binary Time Series Classification with Bayesian Convolutional Neural Networks When Monitoring for Marine Gas Discharges
Abstract
1. Introduction
2. Methods
2.1. Problem Formulation
2.2. Artificial Neural Network
2.3. Bayesian Neural Networks and Bayesian Parameter Estimation
2.4. Monte Carlo Dropout
2.5. Uncertainty Estimation in MC Dropout
2.6. Bayesian Decision Making
2.7. Decision Support in Environmental Monitoring under Uncertainty
| Algorithm 1 Algorithm for decision support in environmental monitoring under uncertainty |
| Input: |
| - Training set |
| - Unlabeled time series |
| - Number of realizations in posterior sampling T |
| - Number of classes C |
| - CCN model with weights |
| - Posterior summary function |
| - cost associated with taking action if the class is |
| 1 Optimize CNN model weights with MC dropout algorithm |
| Optimize BCNN model |
| 2 Generate posterior predictive distribution from optimized BCNN |
| Simulate T samples from the posterior distribution of the weights |
| Estimate posterior predictive distribution for all classes |
| Extract the posterior distribution for class with T samples |
| Approximate with e.g., (5) or (6) |
| 3. Make optimal decision based on posterior predictive distribution |
| Minimize the conditional risk. |
| return Optimal decision based on and cost function |
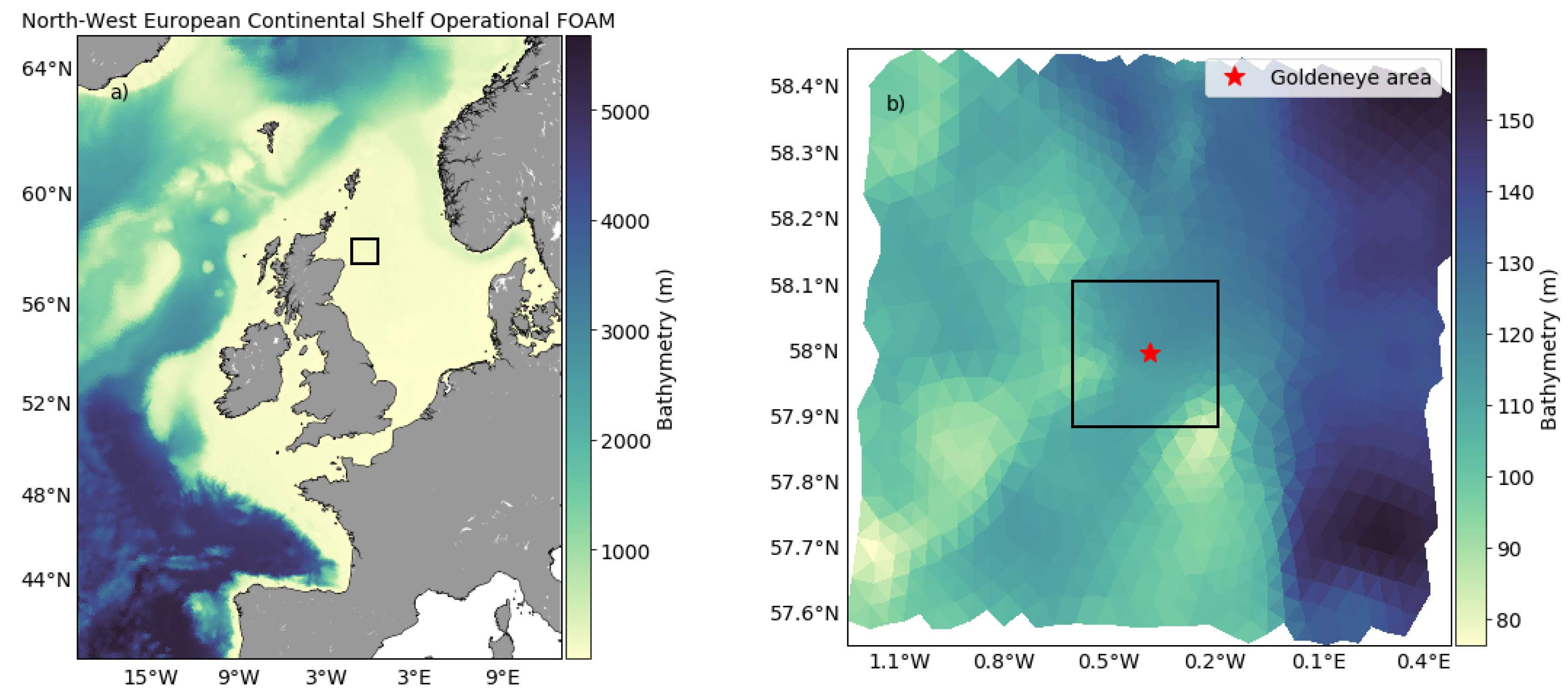
3. Case Study—Goldeneye CCS Site
3.1. Data
3.1.1. Description of Data Set
3.1.2. Preprocessing of Data
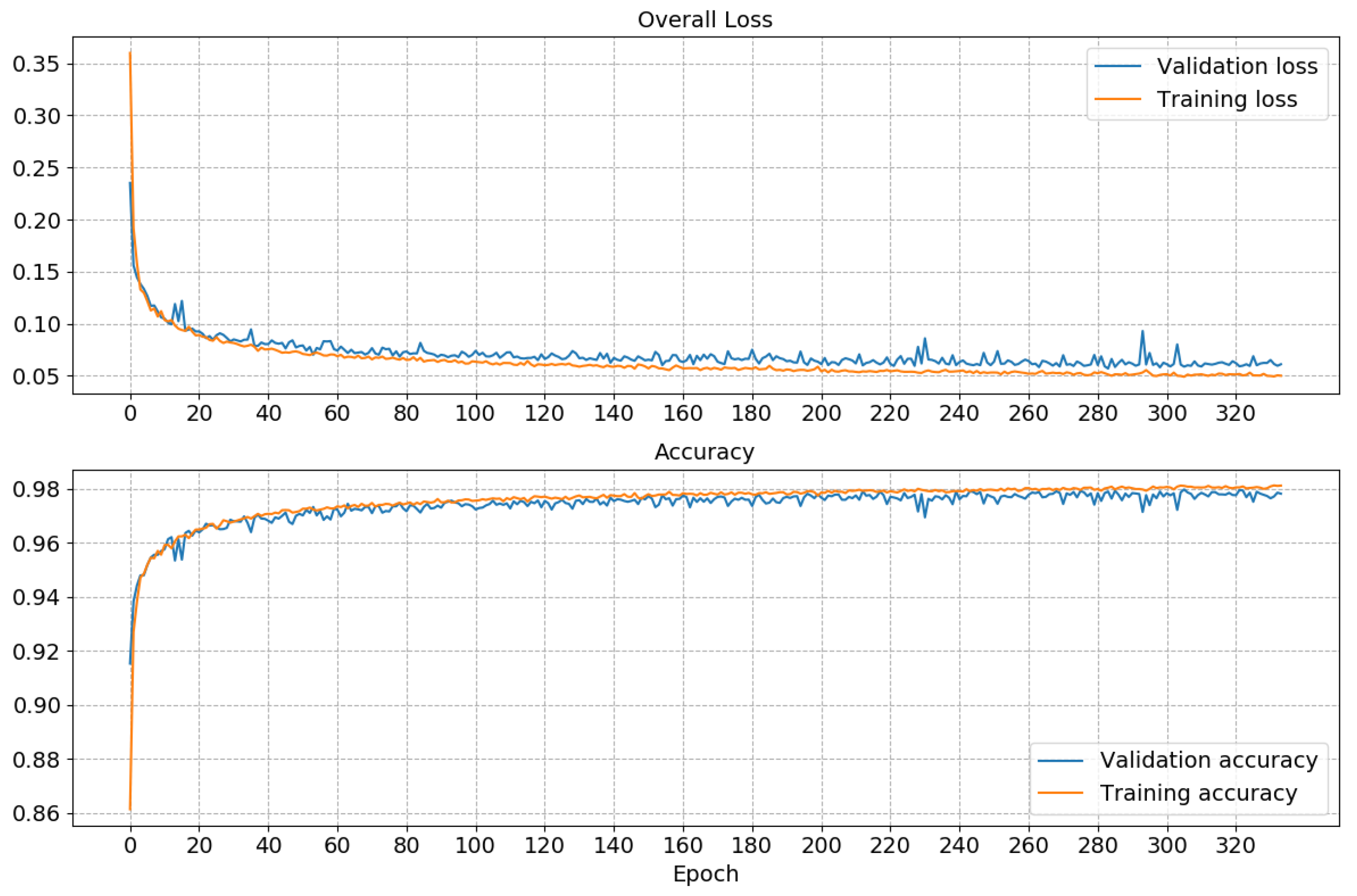
3.2. Model for TSC: Bayesian Convolutional Neural Networks
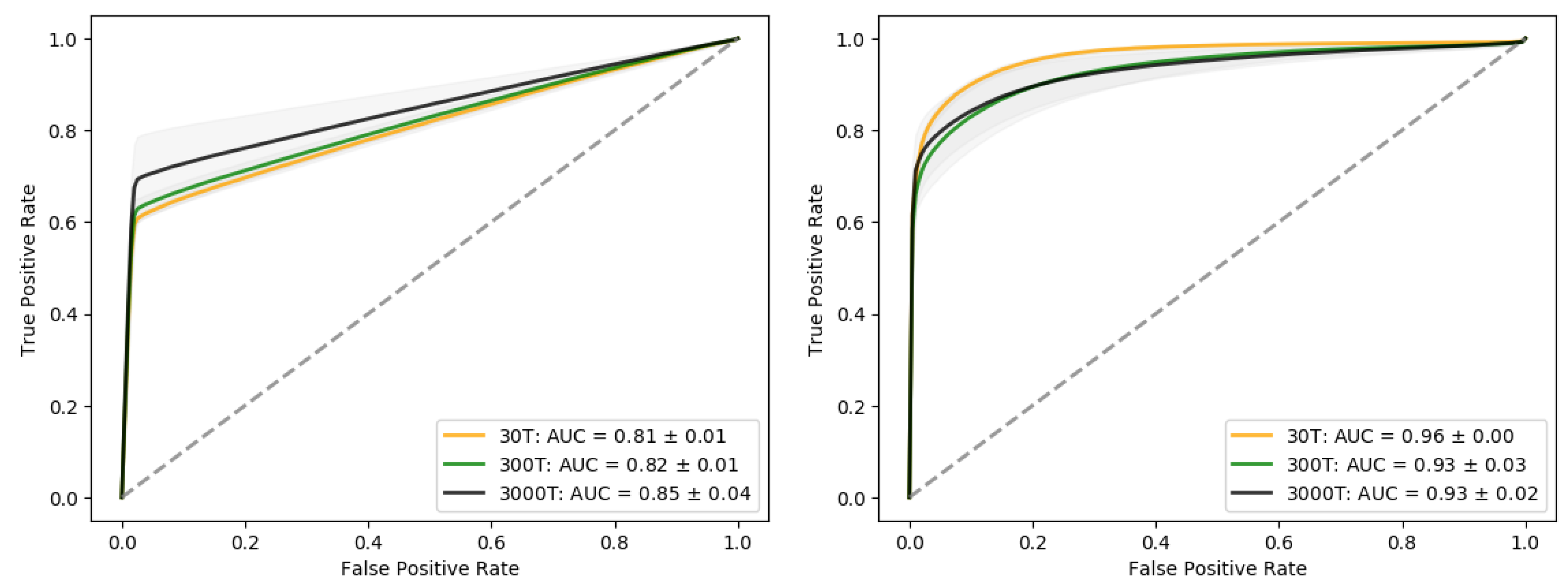
3.3. Performance of the Classifier
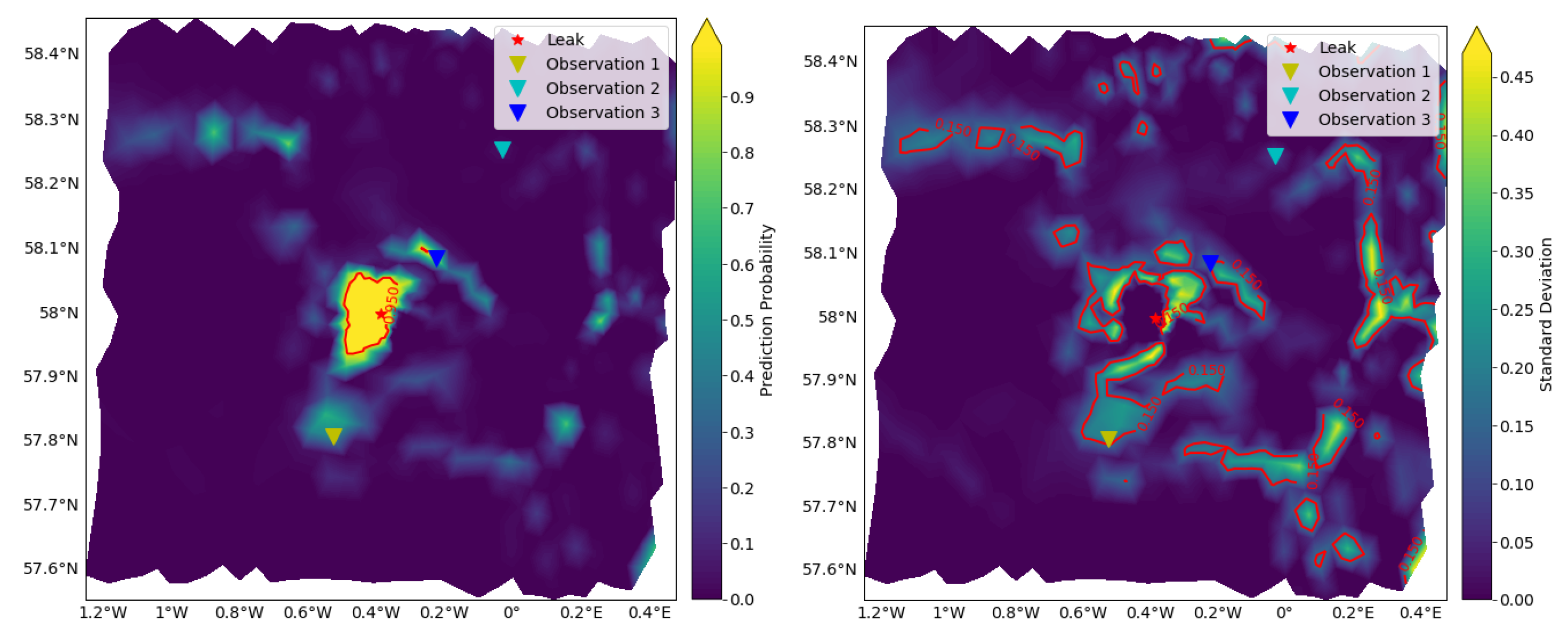
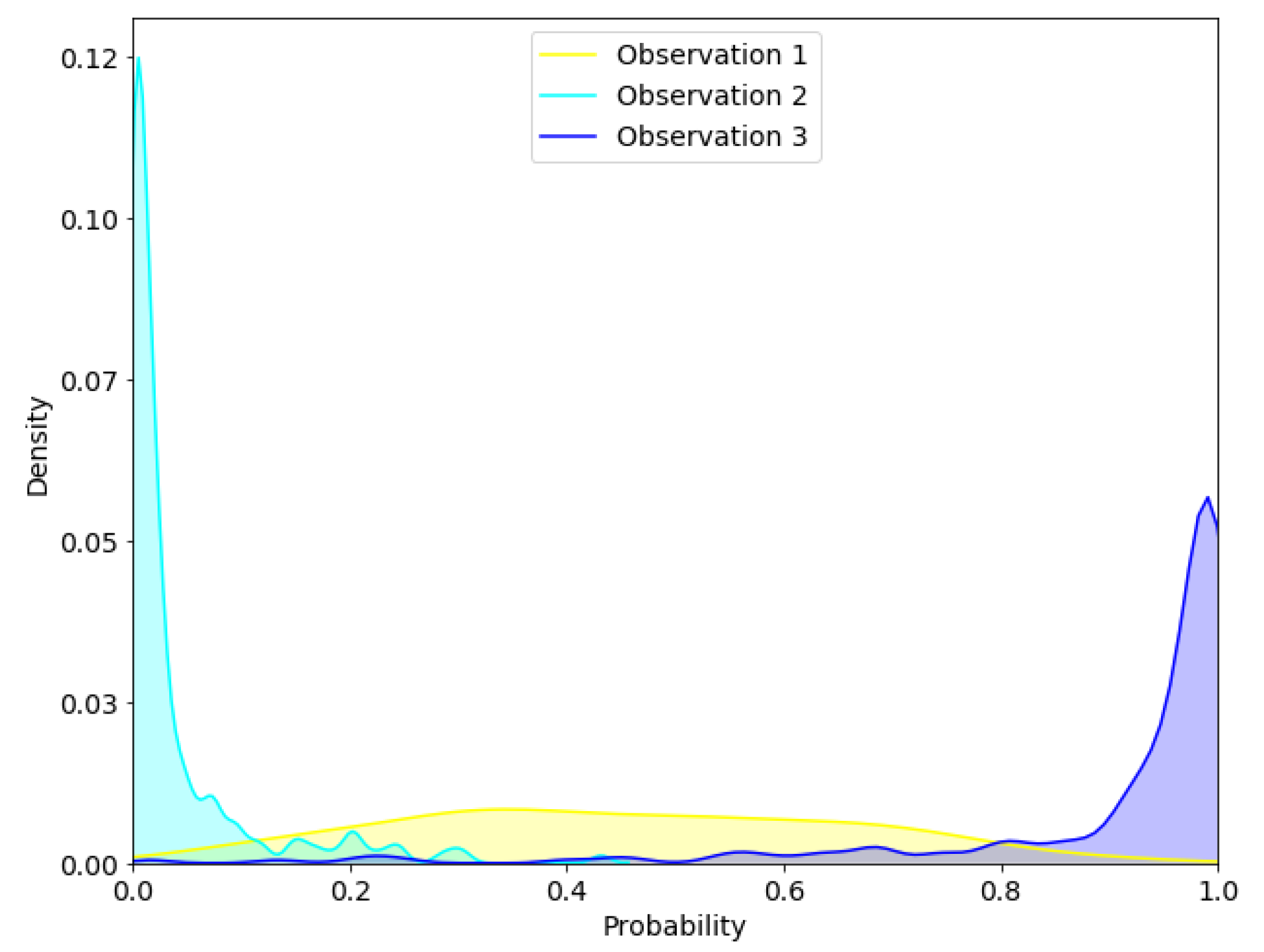
3.4. Approximated Predictive Mean and Uncertainty
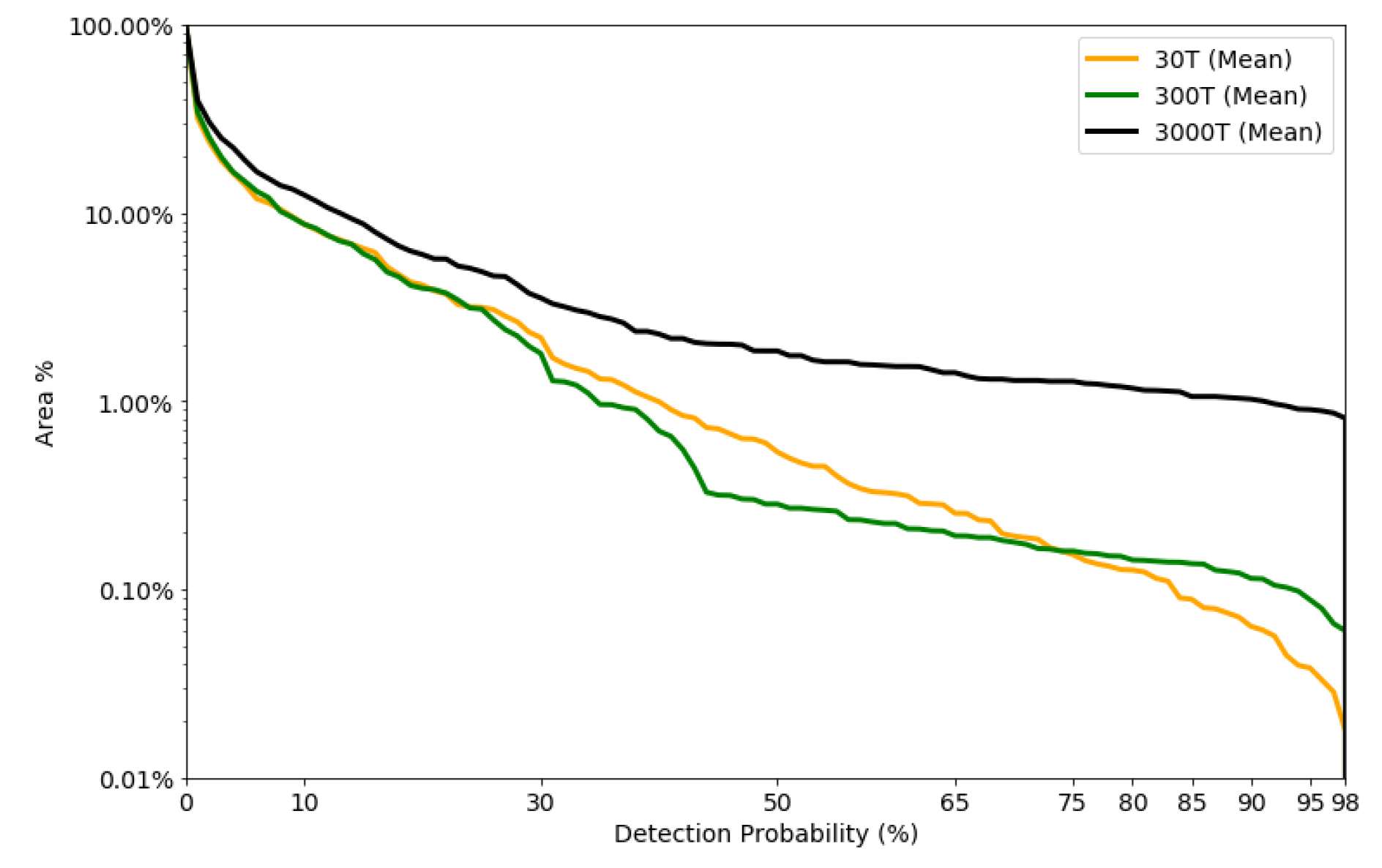
3.5. Detectable Area vs. Detection Probability
3.6. Sensitivity Analysis
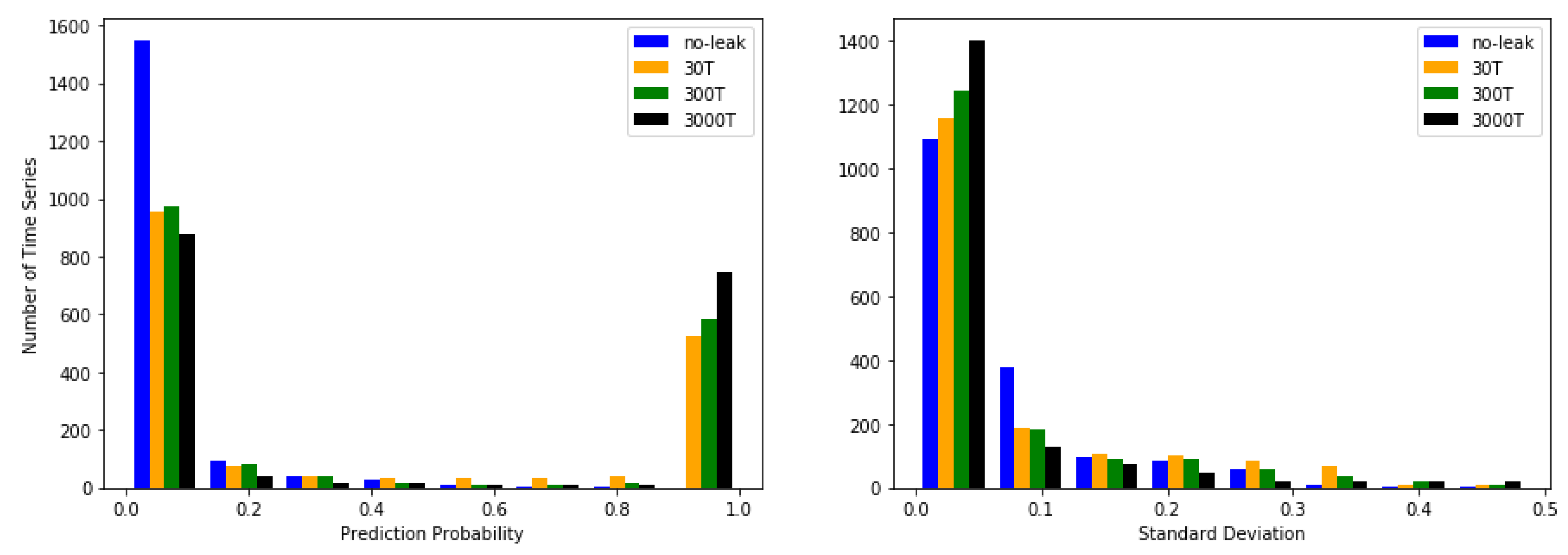
3.6.1. Reducing the Training Data Set
3.6.2. Adding Gaussian Noise the Test Data Set
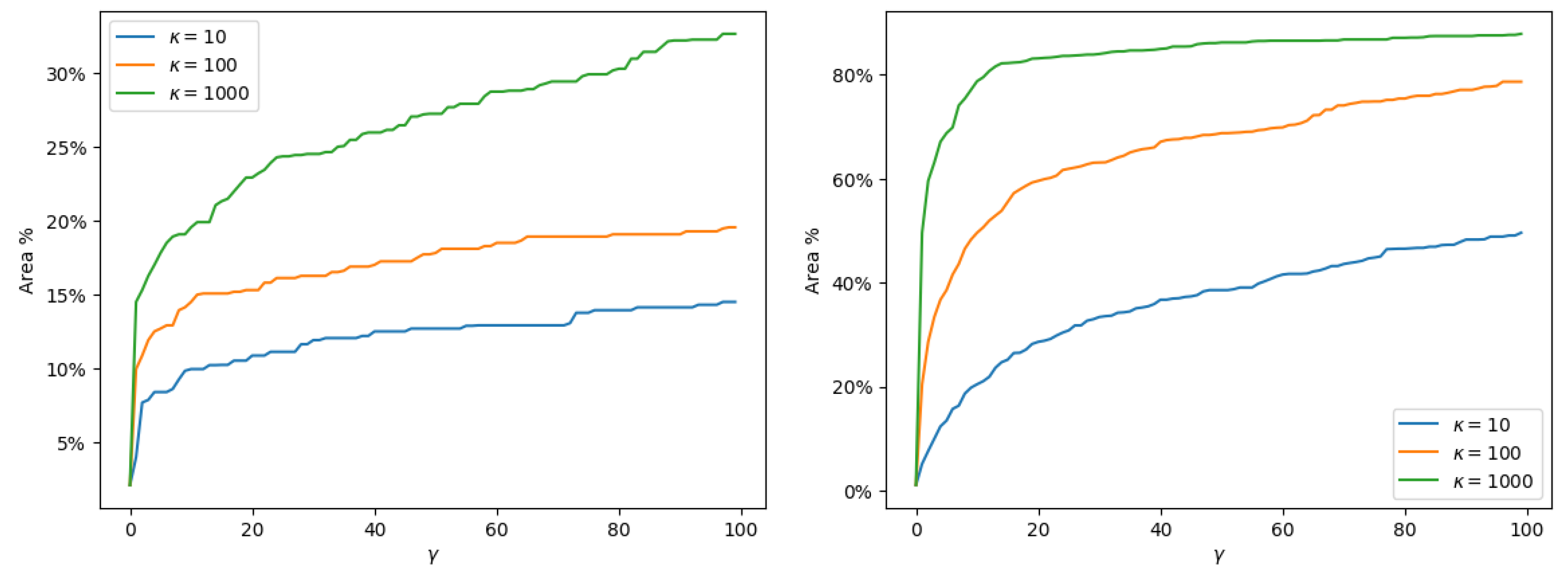
3.7. Making Decisions Based on BCNN Output with Varying Cost
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | Area Under the Curve |
| BCNN | Bayesian Convolutional Neural Network |
| CCS | Carbon Capture and Storage |
| CO | Carbon dioxide |
| CNN | Convolutional Neural Network |
| DOAJ | Directory of open access journals |
| DTW | Dynamic Time Warping |
| ERSEM | European Regional Seas Ecosystem Model |
| FVCOM | Finite-Volume Community Model |
| IOC | Intergovernmental Oceanographic Commission |
| KDE | Kernel Density Estimate |
| MAP | Maximum A Posteriori |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MC | Monte Carlo |
| MCMC | Markov Chain Monte Carlo |
| ReLu | REctified Linear Unit |
| RNN | Recurrent Neural Networks |
| ROC | Receiver Operating Characteristic |
| STEMM-CCS | Strategies for Environmental Monitoring of Marine Carbon Capture and Storage |
| TSC | Time Series Classification |
| UN | United Nations |
References
- Halpern, B.S.; Longo, C.; Hardy, D.; McLeod, K.L.; Samhouri, J.F.; Katona, S.K.; Kleisner, K.; Lester, S.E.; O’Leary, J.; Ranelletti, M.; et al. An index to assess the health and benefits of the global ocean. Nature 2012, 488, 615–620. [Google Scholar] [CrossRef] [PubMed]
- Domínguez-Tejo, E.; Metternicht, G.; Johnston, E.; Hedge, L. Marine Spatial Planning advancing the Ecosystem-Based Approach to coastal zone management: A review. Mar. Policy 2016, 72, 115–130. [Google Scholar] [CrossRef]
- Ali, A.; Thiem, Ø.; Berntsen, J. Numerical modelling of organic waste dispersion from fjord located fish farms. Ocean Dyn. 2011, 61, 977–989. [Google Scholar] [CrossRef]
- Hylland, K.; Burgeot, T.; Martínez-Gómez, C.; Lang, T.; Robinson, C.D.; Svavarsson, J.; Thain, J.E.; Vethaak, A.D.; Gubbins, M.J. How can we quantify impacts of contaminants in marine ecosystems? The ICON project. Mar. Environ. Res. 2017, 24, 2–10. [Google Scholar] [CrossRef] [PubMed]
- First, P.J. Global Warming of 1.5 ∘C an IPCC Special Report on the Impacts of Global Warming of 1.5 ∘C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change. Sustain. Dev. Efforts Eradicate Poverty 2019, 1, 1–22. [Google Scholar]
- Agency, I.E. Global Energy & CO2 Status Report; Technical Report; IEA: Paris, France, 2018. [Google Scholar]
- Bauer, S.; Beyer, C.; Dethlefsen, F.; Dietrich, P.; Duttmann, R.; Ebert, M.; Feeser, V.; Görke, U.; Köber, R.; Kolditz, O.; et al. Impacts of the use of the geological subsurface for energy storage: An investigation concept. Environ. Earth Sci. 2013, 70, 3935–3943. [Google Scholar] [CrossRef]
- Blackford, J.; Bull, J.M.; Cevatoglu, M.; Connelly, D.; Hauton, C.; James, R.H.; Lichtschlag, A.; Stahl, H.; Widdicombe, S.; Wright, I.C. Marine baseline and monitoring strategies for carbon dioxide capture and storage (CCS). Int. J. Greenh. Gas Control 2015, 38, 221–229. [Google Scholar] [CrossRef]
- Jones, D.; Beaubien, S.; Blackford, J.; Foekema, E.; Lions, J.; Vittor, C.D.; West, J.; Widdicombe, S.; Hauton, C.; Queirós, A. Developments since 2005 in understanding potential environmental impacts of {CO2} leakage from geological storage. Int. J. Greenh. Gas Control 2015, 40, 350–377. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, X. 10 challenging problems in data mining research. Int. J. Inf. Technol. Decis. Mak. 2006, 5, 597–604. [Google Scholar] [CrossRef]
- Esling, P.; Agon, C. Time-series data mining. ACM Comput. Surv. (CSUR) 2012, 45, 12. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [CrossRef] [PubMed]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series; KDD Workshop: Seattle, WA, USA, 1994; Volume 10, pp. 359–370. [Google Scholar]
- Ratanamahatana, C.A.; Keogh, E. Three myths about dynamic time warping data mining. In Proceedings of the 2005 SIAM International Conference on Data Mining, SIAM, Newport Beach, CA, USA, 21–23 April 2005; pp. 506–510. [Google Scholar]
- Bagnall, A.; Janacek, G. A run length transformation for discriminating between auto regressive time series. J. Classif. 2014, 31, 154–178. [Google Scholar] [CrossRef][Green Version]
- Smyth, P. Clustering Sequences with Hidden Markov Models. Available online: http://papers.nips.cc/paper/1217-clustering-sequences-with-hidden-markov-models.pdf (accessed on 1 June 2020).
- Williams, C.K.; Barber, D. Bayesian classification with Gaussian processes. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1342–1351. [Google Scholar] [CrossRef]
- James, G.M.; Hastie, T.J. Functional linear discriminant analysis for irregularly sampled curves. J. R. Stat. Soc. Ser. B 2001, 63, 533–550. [Google Scholar] [CrossRef]
- Hall, P.; Poskitt, D.S.; Presnell, B. A functional data—Analytic approach to signal discrimination. Technometrics 2001, 43, 1–9. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-series classification with COTE: The collective of transformation-based ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Lines, J.; Taylor, S.; Bagnall, A. Time Series Classification with HIVE-COTE: The Hierarchical Vote Collective of Transformation-Based Ensembles. ACM Trans. Knowl. Discov. Data 2018, 12. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 1–47. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time series classification using multi-channels deep convolutional neural networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; pp. 298–310. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Hüsken, M.; Stagge, P. Recurrent neural networks for time series classification. Neurocomputing 2003, 50, 223–235. [Google Scholar] [CrossRef]
- MacKay, D.J.C. A Practical Bayesian Framework for Backpropagation Networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Alendal, G.; Blackford, J.; Chen, B.; Avlesen, H.; Omar, A. Using Bayes Theorem to Quantify and Reduce Uncertainties when Monitoring Varying Marine Environments for Indications of a Leak. Energy Procedia 2017, 114, 3607–3612. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. arXiv 2015, arXiv:1505.05424. [Google Scholar]
- Shridhar, K.; Laumann, F.; Liwicki, M. A comprehensive guide to bayesian convolutional neural network with variational inference. arXiv 2019, arXiv:1901.02731. [Google Scholar]
- Leibig, C.; Allken, V.; Ayhan, M.S.; Berens, P.; Wahl, S. Leveraging uncertainty information from deep neural networks for disease detection. Sci. Rep. 2017, 7, 17816. [Google Scholar] [CrossRef] [PubMed]
- Abideen, Z.U.; Ghafoor, M.; Munir, K.; Saqib, M.; Ullah, A.; Zia, T.; Tariq, S.A.; Ahmed, G.; Zahra, A. Uncertainty Assisted Robust Tuberculosis Identification With Bayesian Convolutional Neural Networks. IEEE Access 2020, 8, 22812–22825. [Google Scholar] [CrossRef]
- Kendall, A.; Cipolla, R. Modelling uncertainty in deep learning for camera relocalization. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4762–4769. [Google Scholar]
- Malde, K.; Handegard, N.O.; Eikvil, L.; Salberg, A.B. Machine intelligence and the data-driven future of marine science. ICES J. Mar. Sci. 2019. [Google Scholar] [CrossRef]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Freeman, B.S.; Taylor, G.; Gharabaghi, B.; Thé, J. Forecasting air quality time series using deep learning. J. Air Waste Manag. Assoc. 2018, 68, 866–886. [Google Scholar] [CrossRef] [PubMed]
- Kiiveri, H.; Caccetta, P.; Campbell, N.; Evans, F.; Furby, S.; Wallace, J. Environmental Monitoring Using a Time Series of Satellite Images and Other Spatial Data Sets. In Nonlinear Estimation and Classification; Denison, D.D., Hansen, M.H., Holmes, C.C., Mallick, B., Yu, B., Eds.; Springer: New York, NY, USA, 2003; pp. 49–62. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest Monitoring Using Landsat Time Series Data: A Review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Blackford, J.; Artioli, Y.; Clark, J.; de Mora, L. Monitoring of offshore geological carbon storage integrity: Implications of natural variability in the marine system and the assessment of anomaly detection criteria. Int. J. Greenh. Gas Control 2017, 64, 99–112. [Google Scholar] [CrossRef]
- Siddorn, J.R.; Allen, J.I.; Blackford, J.C.; Gilbert, F.J.; Holt, J.T.; Holt, M.W.; Osborne, J.P.; Proctor, R.; Mills, D.K. Modelling the hydrodynamics and ecosystem of the North-West European continental shelf for operational oceanography. J. Mar. Syst. 2007, 65, 417–429. [Google Scholar] [CrossRef]
- Alendal, G.; Drange, H. Two-phase, near-field modeling of purposefully released CO2 in the ocean. J. Geophys. Res. Ocean. 2001, 106, 1085–1096. [Google Scholar] [CrossRef]
- Dewar, M.; Sellami, N.; Chen, B. Dynamics of rising CO2 bubble plumes in the QICS field experiment. Int. J. Greenh. Gas Control 2014. [Google Scholar] [CrossRef]
- Ali, A.; Frøysa, H.G.; Avlesen, H.; Alendal, G. Simulating spatial and temporal varying CO2 signals from sources at the seafloor to help designing risk-based monitoring programs. J. Geophys. Res. Ocean. 2016, 121, 745–757. [Google Scholar] [CrossRef]
- Blackford, J.; Alendal, G.; Avlesen, H.; Brereton, A.; Cazenave, P.W.; Chen, B.; Dewar, M.; Holt, J.; Phelps, J. Impact and detectability of hypothetical CCS offshore seep scenarios as an aid to storage assurance and risk assessment. Int. J. Greenh. Gas Control 2020, 95, 102949. [Google Scholar] [CrossRef]
- Vielstädte, L.; Karstens, J.; Haeckel, M.; Schmidt, M.; Linke, P.; Reimann, S.; Liebetrau, V.; McGinnis, D.F.; Wallmann, K. Quantification of methane emissions at abandoned gas wells in the Central North Sea. Mar. Pet. Geol. 2015, 68, 848–860. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Chen, C. An Unstructured-Grid, Finite-Volume Community Ocean Model: FVCOM User Manual; Sea Grant College Program, Massachusetts Institute of Technology: Cambridge, MA, USA, 2012. [Google Scholar]
- Butenschön, M.; Clark, J.; Aldridge, J.N.; Allen, J.I.; Artioli, Y.; Blackford, J.; Bruggeman, J.; Cazenave, P.; Ciavatta, S.; Kay, S.; et al. ERSEM 15.06: A generic model for marine biogeochemistry and the ecosystem dynamics of the lower trophic levels. Geosci. Model Dev. 2016, 9, 1293–1339. [Google Scholar]
- Hähnel, P.; Mareček, J.; Monteil, J.; O’Donncha, F. Using deep learning to extend the range of air pollution monitoring and forecasting. J. Comput. Phys. 2020, 408, 109278. [Google Scholar] [CrossRef]
- Ruthotto, L.; Haber, E. Deep neural networks motivated by partial differential equations. J. Math. Imaging Vis. 2019, 62, 1–13. [Google Scholar] [CrossRef]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Bayesian convolutional neural networks with Bernoulli approximate variational inference. arXiv 2015, arXiv:1506.02158. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Tibshirani, R.J.; Efron, B. An introduction to the bootstrap. Monogr. Stat. Appl. Probab. 1993, 57, 1–436. [Google Scholar]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cazenave, P.; Blackford, J.; Artioli, Y. Regional Modelling to Inform the Design of Sub-Sea CO2 Storage Monitoring Networks. In Proceedings of the 14th Greenhouse Gas Control Technologies Conference Melbourne, Melbourne, Australia, 21–26 October 2018; pp. 21–26. [Google Scholar]
- Riebesell, U.; Fabry, V.J.; Hansson, L.; Gattuso, J.P. Guide to Best Practices for Ocean Acidification Research and Data Reporting; Office for Official Publications of the European Communities: Brussels, Belgium, 2011.
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Baldi, P.; Sadowski, P. The dropout learning algorithm. Artif. Intell. 2014, 210, 78–122. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hvidevold, H.K.; Alendal, G.; Johannessen, T.; Ali, A.; Mannseth, T.; Avlesen, H. Layout of CCS monitoring infrastructure with highest probability of detecting a footprint of a CO2 leak in a varying marine environment. Int. J. Greenh. Gas Control 2015, 37, 274–279. [Google Scholar] [CrossRef]
- Greenwood, J.; Craig, P.; Hardman-Mountford, N. Coastal monitoring strategy for geochemical detection of fugitive CO2 seeps from the seabed. Int. J. Greenh. Gas Control 2015, 39, 74–78. [Google Scholar] [CrossRef]
- Hvidevold, H.K.; Alendal, G.; Johannessen, T.; Ali, A. Survey strategies to quantify and optimize detecting probability of a CO2 seep in a varying marine environment. Environ. Model. Softw. 2016, 83, 303–309. [Google Scholar] [CrossRef]
- Alendal, G. Cost efficient environmental survey paths for detecting continuous tracer discharges. J. Geophys. Res. Ocean. 2017, 122, 5458–5467. [Google Scholar] [CrossRef]
- Oleynik, A.; García-Ibáñez, M.I.; Blaser, N.; Omar, A.; Alendal, G. Optimal sensors placement for detecting CO2 discharges from unknown locations on the seafloor. Int. J. Greenh. Gas Control 2020, 95, 102951. [Google Scholar] [CrossRef]
- Botnen, H.; Omar, A.; Thorseth, I.; Johannessen, T.; Alendal, G. The effect of submarine CO2 vents on seawater: Implications for detection of subsea Carbon sequestration leakage. Limnol. Oceanogr. 2015, 60, 402–410. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Rajasegarar, S.; Moshtaghi, M.; Leckie, C.; Palaniswami, M.; Havens, T.C. Anomaly detection in environmental monitoring networks [application notes]. IEEE Comput. Intell. Mag. 2011, 6, 52–58. [Google Scholar] [CrossRef]
- Ahmad, H. Machine learning applications in oceanography. Aquat. Res. 2019, 2, 161–169. [Google Scholar] [CrossRef]




| Leak | No-Leak | # Time Series | Start/End | |
|---|---|---|---|---|
| Training Data | 75.8% | 24.2% | 116,659 | Start |
| Validation Data | 75.8% | 24.2% | 49,997 | Start |
| Test Data | 69.8% | 36.2% | 6944 | End |
| Scenario | Prediction Probability | Standard Deviation |
|---|---|---|
| 0T | 90.15 | 115.48 |
| 30T | 624.25 | 183.54 |
| 300T | 633.58 | 161.82 |
| 3000T | 773.77 | 153.94 |
| Leak | No-Leak | |
|---|---|---|
| Confirm () | ||
| Not Confirm () | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gundersen, K.; Alendal, G.; Oleynik, A.; Blaser, N. Binary Time Series Classification with Bayesian Convolutional Neural Networks When Monitoring for Marine Gas Discharges. Algorithms 2020, 13, 145. https://doi.org/10.3390/a13060145
Gundersen K, Alendal G, Oleynik A, Blaser N. Binary Time Series Classification with Bayesian Convolutional Neural Networks When Monitoring for Marine Gas Discharges. Algorithms. 2020; 13(6):145. https://doi.org/10.3390/a13060145
Chicago/Turabian StyleGundersen, Kristian, Guttorm Alendal, Anna Oleynik, and Nello Blaser. 2020. "Binary Time Series Classification with Bayesian Convolutional Neural Networks When Monitoring for Marine Gas Discharges" Algorithms 13, no. 6: 145. https://doi.org/10.3390/a13060145
APA StyleGundersen, K., Alendal, G., Oleynik, A., & Blaser, N. (2020). Binary Time Series Classification with Bayesian Convolutional Neural Networks When Monitoring for Marine Gas Discharges. Algorithms, 13(6), 145. https://doi.org/10.3390/a13060145





