A Fuzzy-Based Decision Support Model for Risk Maturity Evaluation of Construction Organizations
Abstract
1. Introduction
2. Literature Review
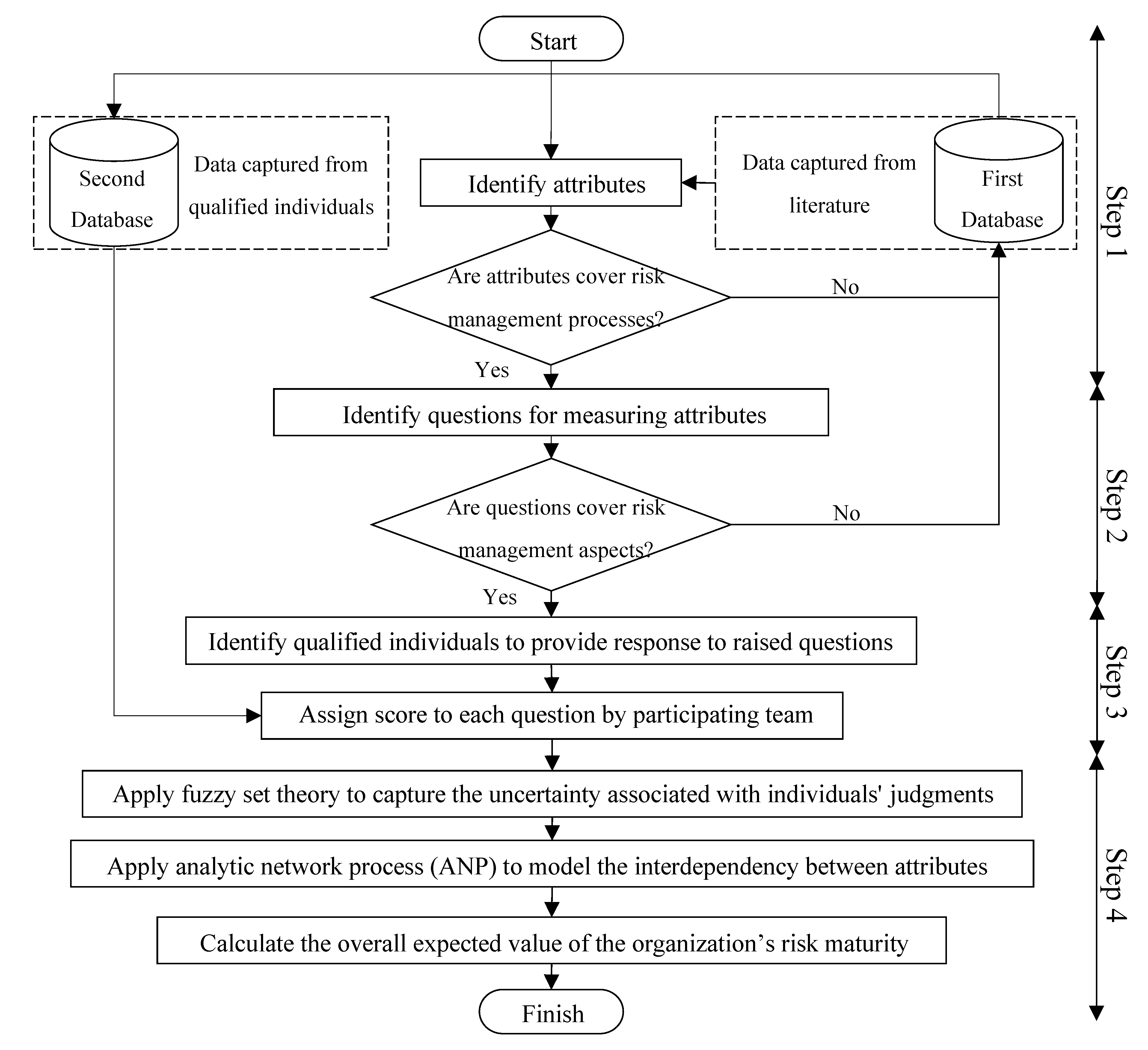
3. Research Methodology
3.1. Identify Attributes
3.2. Identify Questions
3.3. Identify Qualified Individuals
3.4. Data Analysis and Evaluation
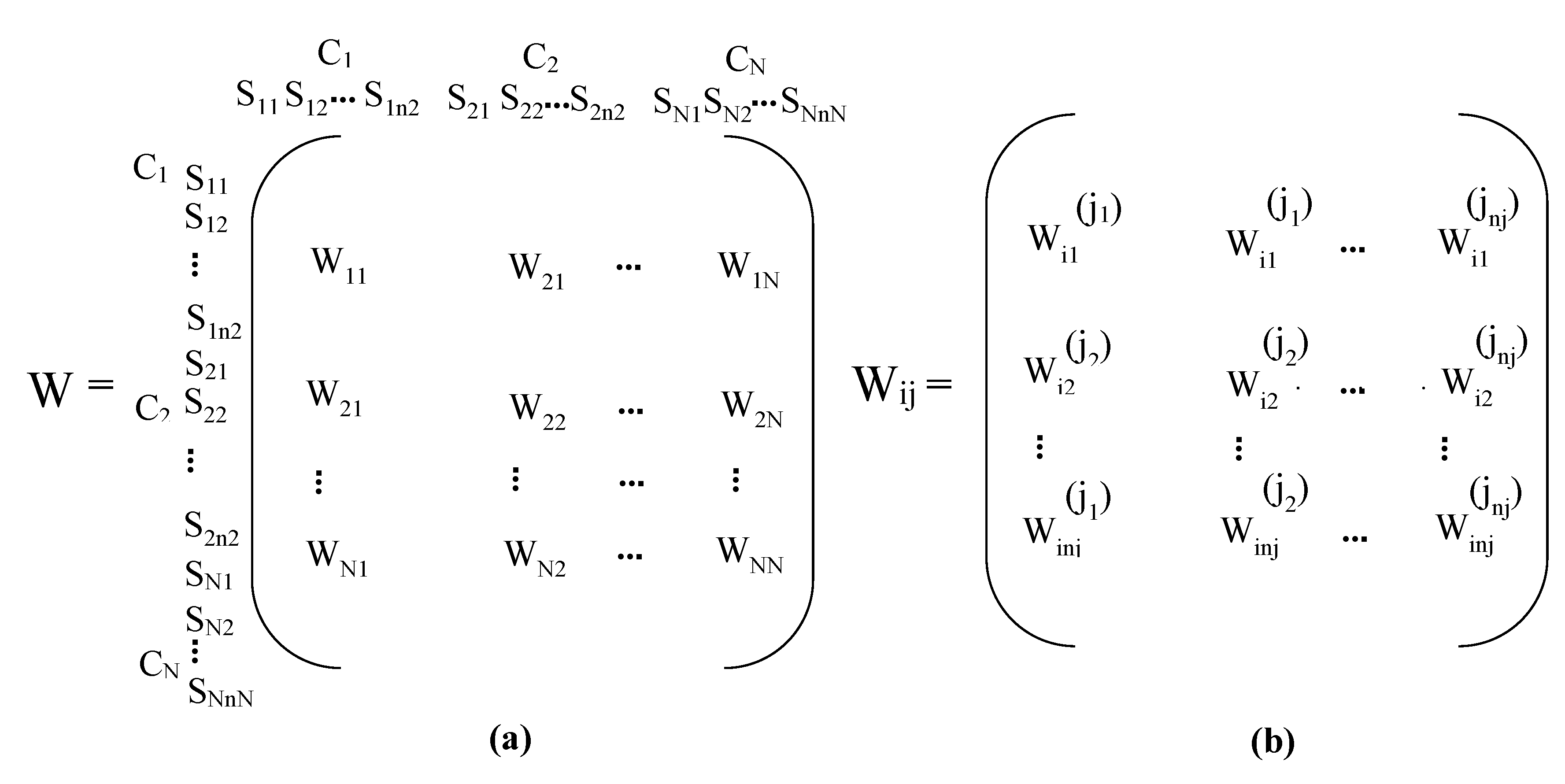
3.4.1. Analytic Network Process (ANP)
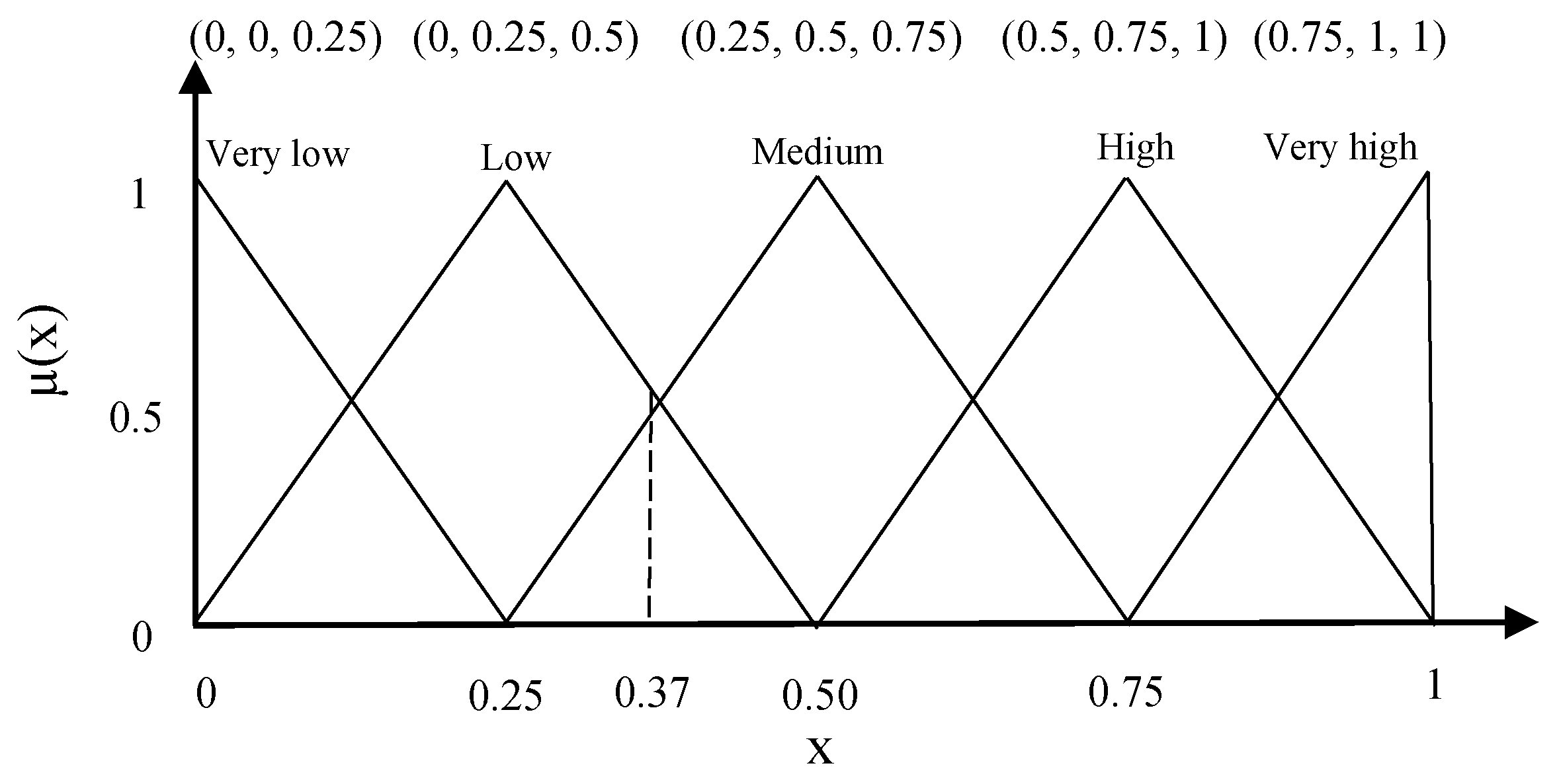
3.4.2. Fuzzy Set Theory
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Salah, A. Fuzzy Set-Based Risk Management for Construction Projects. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2015. [Google Scholar]
- PMI. A Guide to the Project Management Body of Knowledge (PMBOK Guide), 6th ed.; Project Management Institute: Newtown Square, PA, USA, 2017. [Google Scholar]
- PMI. Practice Standard for Project Risk Management; Project Management Institute: Newtown Square, PA, USA, 2009. [Google Scholar]
- ISO 31000. Risk Management–Guidelines; International Organization for Standardization: Geneva, Switzerland, 2018. [Google Scholar]
- AACE International. Required Skills and Knowledge of Decision and Risk Management; Association for the Advancement of Cost Engineering: Morgantown, WV, USA, 2013. [Google Scholar]
- IRM. A Risk Management Standard; The Institute of Risk Management: London, UK; The Association of Insurance and Risk Managers (AIRMIC): London, UK; ALARM The National Forum for Risk Management in the Public Sector: Devon, UK, 2002. [Google Scholar]
- Jia, G.; Ni, X.; Chen, Z.; Hong, B.; Chen, Y.; Yang, F.; Lin, C. Measuring the maturity of risk management in large-scale construction projects. Autom. Constr. 2013, 34, 56–66. [Google Scholar] [CrossRef]
- Hoseini, E.; Hertogh, M.; Bosch-Rekveldt, M. Developing a generic risk maturity model (GRMM) for evaluating risk management in construction projects. J. Risk Res. 2019, 1–20. [Google Scholar] [CrossRef]
- Zou, P.X.; Chen, Y.; Chan, T.Y. Understanding and improving your risk management capability: Assessment model for construction organizations. J. Constr. Eng. Manag. 2010, 136, 854–863. [Google Scholar] [CrossRef]
- Zhao, X.; Hwang, B.G.; Low, S.P. Developing fuzzy enterprise risk management maturity model for construction firms. J. Constr. Eng. Manag. 2013, 139, 1179–1189. [Google Scholar] [CrossRef]
- Zhao, X.; Hwang, B.G.; Low, S.P. Investigating enterprise risk management maturity in construction firms. J. Constr. Eng. Manag. 2014, 140, 05014006. [Google Scholar] [CrossRef]
- Alashwal, A.M.; Abdul-Rahman, H.; Asef, A. Influence of organizational learning and firm size on risk management maturity. J. Constr. Eng. Manag. 2017, 33, 04017034. [Google Scholar] [CrossRef]
- PMI. Organizational Project Management Maturity Model (OPM3); Project Management Institute: Newtown Square, PA, USA, 2008. [Google Scholar]
- Wibowo, A.; Taufik, J. Developing a self-assessment model of risk management maturity for client organizations of public construction projects: Indonesian context. Procedia Eng. 2017, 171, 274–281. [Google Scholar] [CrossRef]
- Jugdev, K.; Thomas, J. From operational process to strategic asset: The evolution of project management’s value in organizations. In Proceedings of the Project Management Institute 33rd Annual Symposium and Conference, San Antonio, TX, USA, 7–8 October 2002. [Google Scholar]
- Popic, Z.; Moselhi, O. Project Delivery Systems Selection for Capital Projects Using the Analytical Hierarchy Process and the Analytical Network Process. In Proceedings of the Construction Research Congress 2014: Construction in a Global Network, Atlanta, GA, USA, 19–21 May 2014; pp. 1339–1348. [Google Scholar]
- Super Decisions Tutorials. Tutorial 04: Changing from AHP to ANP. Super Decisions. Available online: https://superdecisions.com/tutorials/index.php?section=v28_tut04 (accessed on 20 March 2020).
- Saaty, T.L. Decision making—The analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Saaty, T.L.; Özdemir, M.S.; Saaty, T.L. The Encyclicon: A Dictionary of Decisions with Dependence and Feedback Based on the Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 2005; Volume 292. [Google Scholar]
- Islam, M.S.; Nepal, M.P.; Skitmore, M.; Attarzadeh, M. Current research trends and application areas of fuzzy and hybrid methods to the risk assessment of construction projects. Adv. Eng. Inf. 2017, 33, 112–131. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Tamošaitienė, J. An integrated fuzzy DEMATEL-fuzzy ANP model for evaluating construction projects by considering interrelationships among risk factors. J. Civil Eng. Manag. 2019, 25, 114–131. [Google Scholar] [CrossRef]
- Moselhi, O.; Roghabadi, M.A. Risk quantification using fuzzy-based Monte Carlo simulation. J. Inf. Technol. Constr. 2020, 25, 87–98. [Google Scholar] [CrossRef]
- Xia, B.; Chan, A.P.; Yeung, J.F. Developing a fuzzy multicriteria decision-making model for selecting design-build operational variations. J. Constr. Eng. Manag. 2011, 137, 1176–1184. [Google Scholar] [CrossRef]
- Cox, E. The Fuzzy Systems Handbook; AP Professional: Boston, MA, USA, 1998. [Google Scholar]
- Amaya, A.J.R.; Lengerke, O.; Cosenza, C.A.N.; Dutra, M.S.; Tavera, M.J. Comparison of defuzzification methods: Automatic control of temperature and flow in heat exchanger. In Automation Control Theory and Practice; Rodic, A.D., Ed.; Books on Demand: Norderstedt, Germany, 2009; pp. 77–88. [Google Scholar]
- Salah, A. Fuzzy Set-Based Contingency Estimating and Management. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2012. [Google Scholar]


| Risk Management Processes | Professional Organization | |||
|---|---|---|---|---|
| [2] | [4] | [5] | [6] | |
| Communication and consultation | - | ✓ | - | - |
| Scope, context and criteria | - | ✓ | - | - |
| Plan risk management | ✓ | - | ✓ | - |
| Organization’s strategic objectives | - | - | - | ✓ |
| Risk assessment (identification, analysis, evaluation) | - | ✓ | ✓ | ✓ |
| Identify risks | ✓ | - | - | - |
| Perform qualitative risk analysis | ✓ | - | - | - |
| Perform quantitative risk analysis | ✓ | - | - | - |
| Risk Reporting | - | - | - | ✓ |
| Decision | - | - | - | ✓ |
| Risk treatment | - | ✓ | ✓ | ✓ |
| Plan risk responses | ✓ | - | - | - |
| Implement risk responses | ✓ | - | - | - |
| Recording and reporting | - | ✓ | - | - |
| Residual risk reporting | - | - | - | ✓ |
| Monitor risks | ✓ | - | ✓ | ✓ |
| Monitoring and review | - | ✓ | - | - |
| Source | Aspects | ||
|---|---|---|---|
| Modeling Interdependency | Capturing Uncertainty | Considering Individuals’ Weight | |
| [7] | ✓ | - | - |
| [8,9] | - | - | - |
| [10,11] | - | ✓ | - |
| [12,14] | - | - | - |
| Aspects | Attributes |
|---|---|
| Standardization | Development and application of standardized risk management process, Objective setting, Risk management planning. |
| Measurement | Risk identification, Risk analysis, Risk response. |
| Control | Risk management ownership, Iterative and dynamic enterprise risk management (ERM) process steps, Formalized key risk indicators, Integration of risk management into business processes, Risk monitoring, Risk review, Management capability in relation to risk, Risk management report, Project set risk management. |
| Continuous improvement | Risk management planning, Policy and strategy, Organization structure support, Commitment of the board and senior management, Risk appetite and tolerance, Risk-aware culture, Risk communication, Common risk language, Leveraging risks as opportunities, improvement of ERM framework, Organizational risk culture, Training programs, Top-management commitment, Personnel knowledge, Sufficient resources, Stakeholder management. |
| Attributes | Aspects | Questions |
|---|---|---|
| Ability to plan risk (APR) | Standardization | Q1: Does the organization describe the concept of risk maturity and its benefits? Q2: Does the organization define risk in terms of opportunities and threats? Q3: Does the organization describe the concepts of risk breakdown structure and the use of it in risk planning? Q4: Does the organization have a dedicated group for risk management with defined roles, responsibilities? Q5: Does the organization use standard documented procedures (i.e., A Guide to the Project Management Body of Knowledge (PMBOK Guide), International Organization for Standardization (ISO) 31000) for risk management processes? |
| Continuous improvement | Q6: Does the organization consider external risks from outside the company and internal risks from within the company? Q7: Do the organization teams use company-wide procedures, guidelines and methods for project risk planning? Q8: Does the organization regularly review the risk management guidelines and methods to ensure their effectiveness? Q9: Does the organization have a risk-aware culture communicated to staff at all levels in the organization? Q10: Are resources continuously invested in improving the risk management tools, techniques, and professional skills of the organization? | |
| Ability to identify risk (AIR) | Measurement | Q1: Does the organization use the practices of brainstorming, checklists, root cause analysis, for risk identification? Q2: Does the organization apply the concepts of risk register? Q3: Does the organization compare actual risks experienced against those initially identified and update its risk identification method? Q4: Does the organization define generic factors that give rise to risk? Q5: Does the organization define risk factors that depend on the project delivery method and its type of contract? |
| Ability to analyse risk (AAR) | Measurement | Q1: Does the organization apply the recommended practices (e.g., PMBOK, ISO standards) for risk analysis? Q2: Does the organization apply a Monte Carlo simulation for contingency estimation? Q3: Does the organization model the uncertainty and subjectivity of input data which is used in risk analysis? Q4: Does the organization use qualitative and/or quantitative risk analysis tools? Q5: Does the organization consider correlation among cost items in contingency estimation? |
| Ability to plan risk responses (ARR) | Measurement | Q1: Does the organization evaluate and select the best alternative from several risk response strategies using data analysis techniques? Q2: Does organization describe and prioritize risk treatment strategies for threats and for opportunities? Q3: Does the organization devise a set of company-based and a set of project-based risk response strategies? Q4: Does the organization update risk response strategies on a regular basis? Q5: Does the organization evaluate the effectiveness of the selected risk response strategies? |
| Ability to implement risk responses (AIRR) | Control | Q1: Does the organization assess residual risks? Q2: Do organization team members take risk ownerships during project implementation? Q3: Are responsibilities for managing risks distributed and carried out by all team members? Q4: Do risk owners have sufficient authority to oversee risk-related action? Q5: Do the organization staff fully understand the authority and responsibility of risk owners at all levels of the company? |
| Ability to monitor risk (AMR) | Control | Q1: Does the organization have standard project risk monitoring procedures and methods? Q2: Does the organization have standard procedures and methods for forecasting the performance of implemented risk responses? Q3: Does the organization check actual progress against risk treatment plan and do the necessary updating during the execution phase? Q4: Does the organization regularly update the standard monitoring methods? Q5: Does the organization use automated tools to track a risk performance index? |
| Source | Individuals’ Profiles | ||||||
|---|---|---|---|---|---|---|---|
| Risk Manager | Cost Manager | Contract/Bid Manager | Construction Manager | Developer Manager | Project Manager | Project Director | |
| [8] | ✓ | ✓ | ✓ | - | - | ✓ | ✓ |
| [9] | ✓ | ✓ | - | ✓ | ✓ | ✓ | ✓ |
| [10] | ✓ | - | ✓ | ✓ | - | ✓ | - |
| [11] | - | - | - | - | - | ✓ | ✓ |
| [12] | ✓ | - | - | - | - | ✓ | ✓ |
| [14] | - | - | - | - | - | - | - |
| Domain | Individuals | Attributes | |||||
|---|---|---|---|---|---|---|---|
| APR | AIR | AAR | ARR | AIRR | AMR | ||
| Portfolio | Development manager | ✓ | ✓ | - | ✓ | - | - |
| Program | Project director | ✓ | ✓ | ✓ | ✓ | - | ✓ |
| Risk manager | ✓ | ✓ | ✓ | ✓ | - | ✓ | |
| Tender manager | ✓ | ✓ | - | - | - | - | |
| Cost manager | ✓ | ✓ | ✓ | - | - | - | |
| Project | Project manager | - | ✓ | ✓ | - | ✓ | ✓ |
| Construction manager | - | ✓ | ✓ | - | ✓ | ✓ | |
| Source | Authority Level | Profile | Individual Involvement Level per Attribute | |||||
|---|---|---|---|---|---|---|---|---|
| APR | AIR | AAR | ARR | AIRR | AMR | |||
| Industrial partner | Portfolio | Executive vice president | ✓ | ✓ | - | ✓ | - | - |
| Vice president | ✓ | ✓ | - | ✓ | - | ✓ | ||
| Stakeholders | ✓ | ✓ | - | ✓ | - | - | ||
| Program | Construction project director | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Pre-construction project director | ✓ | ✓ | ✓ | ✓ | - | - | ||
| Bid manager | ✓ | ✓ | - | - | - | - | ||
| Insurance manager | - | ✓ | ✓ | - | - | ✓ | ||
| Real estate manager | - | ✓ | - | - | - | - | ||
| Financial risk analyzer | - | ✓ | ✓ | - | - | ✓ | ||
| Project planer | - | ✓ | - | - | - | ✓ | ||
| Project | Project manager | - | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Project coordinator | - | ✓ | - | - | - | - | ||
| Super intendant manager | - | ✓ | - | ✓ | - | ✓ | ||
| Pre-construction manager | - | ✓ | ✓ | - | - | - | ||
| ID | Profile | Years of Experience |
|---|---|---|
| VP | Vice president alternative (projects and infrastructure) | 32 |
| PD1 | Project director | 10 |
| PD2 | Regional director | 13 |
| PD3 | Director - preconstruction and methods | 17 |
| PD4 | Director - project support | 16 |
| PD5 | Project director | 15 |
| PM1 | Project manager | 05 |
| PM2 | Senior project manager | 14 |
| PM3 | Senior project manager | 13 |
| PPM1 | Pre-construction manager | 15 |
| PPM2 | Pre-construction manager | 13 |
| PPM3 | Pre-construction manager | 15 |
| BC | Bid coordinator | 10 |
| RA | Risk analyst—financial risk analyzer | 09 |
| Factors | VP | PD1 | PD2 | PD3 | PD4 | PD5 | PM1 | PM2 | PM3 | PPM1 | PPM2 | PPM3 | BC | RA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VP | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PD1 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PD2 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PD3 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PD4 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PD5 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| PM1 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| PM2 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| PM3 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| PPM1 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| PPM2 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| PPM3 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1/6 | 1 |
| BC | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 1 | 6 |
| RA | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Factors | APR | AIR | AAR | ARR | AIRR | AMR |
|---|---|---|---|---|---|---|
| APR | 1 | 1/2 | 1 | 1/2 | 1/2 | 1 |
| AIR | 2 | 1 | 2 | 1 | 1 | 2 |
| AAR | 1 | 1/2 | 1 | 1/2 | 1/2 | 1 |
| ARR | 2 | 1 | 2 | 1 | 1 | 2 |
| AIRR | 2 | 1 | 2 | 1 | 1 | 2 |
| AMR | 1 | 1/2 | 1 | 1/2 | 1 | 1 |
| Factors | APR | AIR | AAR | ARR | AIRR | AMR | VP | PD1 | PD2 | PD3 | PD4 | PD5 | PM1 | PM2 | PM3 | PPM1 | PPM2 | PPM3 | BC | RA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APR | 0 | 0 | 0 | 0 | 0 | 0 | 0.111 | 0.096 | 0.111 | 0.363 | 0.307 | 0.154 | 0.153 | 0.166 | 0.200 | 0.166 | 0.166 | 0.210 | 0.166 | 0.143 |
| AIR | 0 | 0 | 0 | 0 | 0 | 0 | 0.222 | 0.096 | 0.222 | 0.182 | 0.154 | 0.154 | 0.307 | 0.166 | 0.200 | 0.166 | 0.166 | 0.0105 | 0.166 | 0.285 |
| AAR | 0 | 0 | 0 | 0 | 0 | 0 | 0.111 | 0.051 | 0.111 | 0.182 | 0.077 | 0.154 | 0.077 | 0.166 | 0.200 | 0.166 | 0.166 | 0.052 | 0.166 | 0.285 |
| ARR | 0 | 0 | 0 | 0 | 0 | 0 | 0.222 | 0.369 | 0.222 | 0.091 | 0.154 | 0.307 | 0.153 | 0.166 | 0.100 | 0.166 | 0.166 | 0.210 | 0.166 | 0.143 |
| AIRR | 0 | 0 | 0 | 0 | 0 | 0 | 0.222 | 0.193 | 0.222 | 0.091 | 0.154 | 0.154 | 0.153 | 0.166 | 0.200 | 0.166 | 0.166 | 0.210 | 0.166 | 0.071 |
| AMR | 0 | 0 | 0 | 0 | 0 | 0 | 0.111 | 0.193 | 0.111 | 0.091 | 0.154 | 0.077 | 0.153 | 0.166 | 0.100 | 0.166 | 0.166 | 0.210 | 0.166 | 0.071 |
| VP | 0.122 | 0.071 | 0.039 | 0.100 | 0.058 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PD1 | 0.122 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PD2 | 0.122 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PD3 | 0.122 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PD4 | 0.122 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PD5 | 0.122 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PM1 | 0.020 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PM2 | 0.020 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PM3 | 0.020 | 0.071 | 0.078 | 0.100 | 0.104 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPM1 | 0.020 | 0.071 | 0.078 | 0.016 | 0.024 | 0.015 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPM2 | 0.020 | 0.071 | 0.078 | 0.016 | 0.024 | 0.015 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPM3 | 0.020 | 0.071 | 0.078 | 0.016 | 0.024 | 0.015 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| BC | 0.122 | 0.071 | 0.019 | 0.027 | 0.020 | 0.025 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| RA | 0.020 | 0.071 | 0.078 | 0.016 | 0.017 | 0.093 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
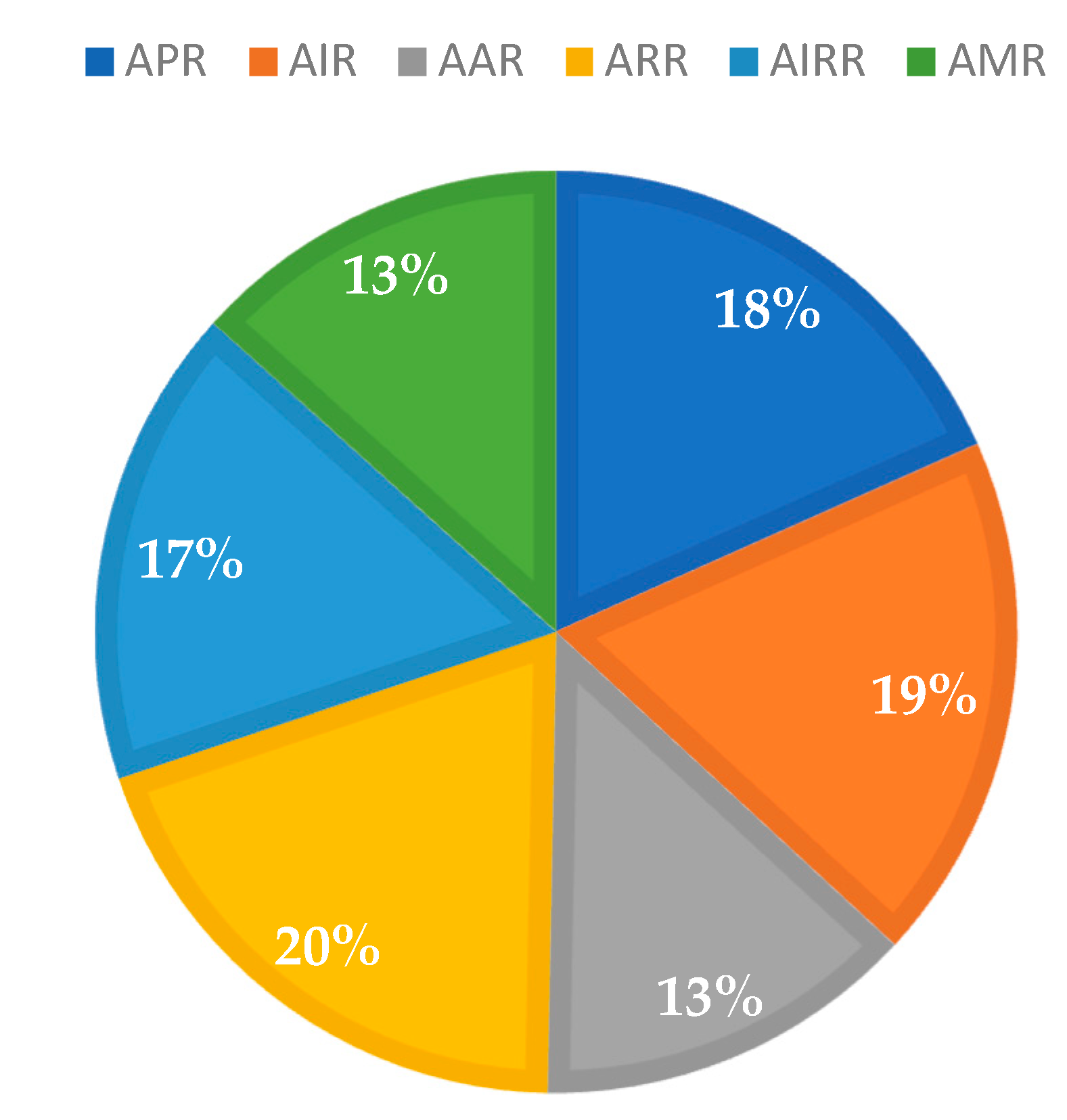
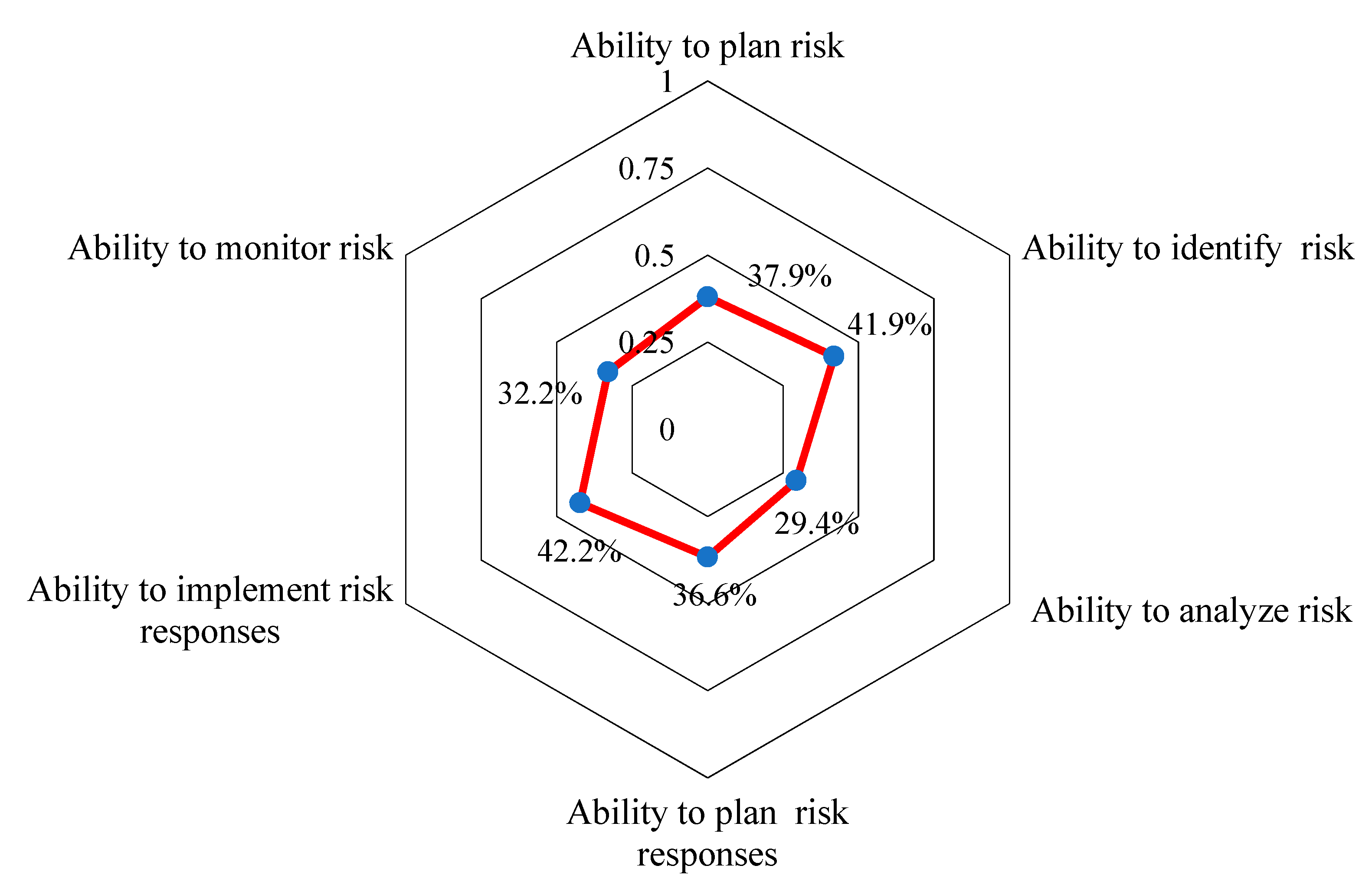
| Attributes | Attributes’ Importance | Degree of Implementation | Attributes’ Maturity Score | ||
|---|---|---|---|---|---|
| Weights (ANP) | Rank | Fuzzy Number | Crisp Number | ||
| APR | 18.33 | 3 | (0.075, 0.408, 0.655) | 0.379 | 6.95 |
| AID | 18.55 | 2 | (0.107, 0.453, 0.696) | 0.419 | 7.77 |
| AAR | 13.42 | 5 | (0.071, 0.282, 0.528) | 0.294 | 3.94 |
| ARR | 19.54 | 1 | (0.064, 0.396, 0.639) | 0.366 | 7.15 |
| AIRR | 16.83 | 4 | (0.092, 0.471, 0.703) | 0.422 | 7.10 |
| AMR | 13.33 | 6 | (0.05, 0.335, 0.582) | 0.322 | 4.29 |
| Industrial partner risk maturity score | 37.2 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roghabadi, M.A.; Moselhi, O. A Fuzzy-Based Decision Support Model for Risk Maturity Evaluation of Construction Organizations. Algorithms 2020, 13, 115. https://doi.org/10.3390/a13050115
Roghabadi MA, Moselhi O. A Fuzzy-Based Decision Support Model for Risk Maturity Evaluation of Construction Organizations. Algorithms. 2020; 13(5):115. https://doi.org/10.3390/a13050115
Chicago/Turabian StyleRoghabadi, Mohammadjavad Arabpour, and Osama Moselhi. 2020. "A Fuzzy-Based Decision Support Model for Risk Maturity Evaluation of Construction Organizations" Algorithms 13, no. 5: 115. https://doi.org/10.3390/a13050115
APA StyleRoghabadi, M. A., & Moselhi, O. (2020). A Fuzzy-Based Decision Support Model for Risk Maturity Evaluation of Construction Organizations. Algorithms, 13(5), 115. https://doi.org/10.3390/a13050115





