Diagnosis in Tennis Serving Technique

Abstract

Tennis is a sport with a very complex technique. Amateur tennis players have trainers and/or coaches, but are not usually accompanied by them to championships. Curiously, in this sport, the result of many matches can be changed by a small hint like ‘hit the ball a little higher when serving’. However, the biomechanical of a tennis stroke is only clear to an expert. We, therefore, developed a prototype of a rule-based expert system (RBES) aimed at an amateur competition player that is not accompanied by his/her coach to a championship and is not serving as usual (the RBES is so far restricted to serving). The player has to answer a set of questions about how he/she is serving that day and his/her usual serving technique and the RBES obtains a diagnosis using logic inference about the possible reasons (according of the logic rules that have been previously given to the RBES). A certain knowledge of the tennis terminology and technique is required from the player, but that is something known at this level. The underlying logic is Boolean and the inference engine is algebraic (it uses Groebner bases).

1. Introduction

The first and third authors of this paper are veteran tennis players, regularly taking part in both veterans and open tennis championship (they were the +55 doubles champions of Extremadura region in 2018). They have a patent ( Fernando María Sánchez Fernández, Eugenio Roanes Lozano: Dispositivo de entrenamiento para determinar la posición óptima en el tenis. Country: Spain. Request number: 201730051. Priority date: 3 de febrero de 2017. Patent holder: Universidad de Extremadura y Universidad Complutense de Madrid.) regarding the recovery position in tennis [1]. The first author has been the +45 champion of Extremadura region several times and is a tennis instructor ranked not so long ago among the top 500 players of Spain).

The second author was their tennis coach. He is an “ITF Level 2 Tennis Coach” with a long experience in teaching tennis and coaching tennis players both in Argentina and Spain.

Finally, the fourth author is an experienced expert systems developer.

Tennis is a sport with a sophisticated technique [2,3,4]. The big distance between the hand and the racket’s sweet spot makes it difficult to play well. The high precision required is normally achieved through the learning of the technique and a hard training. Something similar happens with golf.

It is well known that there are many aspects in tennis teaching that have to be addressed (tactic, technique, physical training, etc.) and a coach is clearly needed for improving the player’s level. For instance, the biomechanical of a stroke is only clear to the expert’s eyes (although there are some personalized computer studies of this aspect for elite athletes like high jumpers).

Most amateur tennis players are not accompanied by a coach when playing championships, except when playing team competitions. In this kind of championship, only the captain of the team can talk to players during the matches. An experience of many tennis players is that a simple hint like “hit the ball at a higher point when you serve” can change the result of a match.

We would like to address here just this aspect of the whole process of tennis coaching: finding out what is going wrong in a certain match with respect to the player’s usual technique. It applies inference to the answers of the player to a set of questions regarding both the problem and the player’s usual technique. It requires a certain knowledge of the technique from the player (let us underline that it is focused to amateur competition players, not to beginners). Therefore, this is neither a system devoted to learn how to play tennis, nor a substitute for a coach. It only tries to correct the mistakes of the stroke going wrong along one match and return the situation to the usual one.

The article is illustrated with the part of the system corresponding to the serve.

While the algebraic model for rule-based expert systems (RBES) is well known (see Section 4), the application to tennis is, as far as we know, entirely novel.

The expert system we have developed tries to model a well-known international standard describing the tennis serving technique. An important issue in an expert system is the knowledge base and the formalism used to represent it. Since propositional Boolean logic is enough to represent this standard, we have adopted this logic to embody the knowledge of our expert system. Artificial Intelligence has proposed many elaborated representation formalisms to model uncertainty or fuzzy knowledge in expert systems, as well as machine learning techniques to acquire this knowledge base. However, we have not required all these techniques for designing our system because of the same purpose of our system: output the recommendations for tennis serving technique, according to a well-known international standard. For our purpose we have only needed to model this standard by means of propositional Boolean logic, resulting in a system with a high performance.

2. Some Introductory Notes about Rule-Based Expert Systems Based on Boolean Propositional Logic

In this section, we will describe some outlines of RBES based on Boolean propositional logic for representing knowledge. It may be skipped by an acquainted reader, but it is included in order to make the article self-contained, as it could have readers from different environments.

Boolean propositional logic uses a finite set of atomic propositions $X_1,\dots ,X_m$ for defining formulae (Definition 1) through the connectives ¬, ∨, ∧, and →.

Definition 1

(Formula). A formula A is recursively defined as:

• $X_i$ where $X_i$ is an atomic proposition
• $\neg B$ where B is a formula
• $B\wedge C$ where $B,C$ are formulae
• $B\vee C$ where $B,C$ are formulae
• $B\to C$ where $B,C$ are formulae.

We define $\mathcal{C}$ as the set of formulae.

Definition 2

(Rule). By its importance, we define rules as the formulae with the form $(A_1\wedge A_2\wedge \dots \wedge A_k)\to (A_{k+1}\vee \dots \vee A_n)$ where each formula $A_1,\dots ,A_n$ is either an atomic proposition (X) or the negation of an atomic proposition ($\neg X$).

Remark 1.

We have chosen the previous definition of rule because we believe it is the most intuitive one. A rule of the form:

$B\to C\vee D$

is equivalent to the rule:

$B\wedge \neg C\to D$

but it is less intuitive as what is a cause and what is an effect is not on different sides of the implication symbol. Similarly, the implications could be substituted by disjunctions, what has the advantage of using fewer symbols, but would make it less readable.

Remark 2.

Sometimes some rules with the same antecedent and different consequents are grouped into a single formula for the sake of brevity and clarity. For example, the information in the three rules:

$B\to C$

$B\to D$

$B\to E$

can be summarized in the formula $B\to C\wedge D\wedge E$. Although it is not formally correct (it doesn’t comply with Definition 2), we shall hereinafter admit these abbreviations as rules too (in order to save space and to clarify the underlying ideas related to tennis hitting technique). The algebraic approach used has no problem to deal with this sort of formulae, and the timings obtained for globally computing which output are obtained are negligible (as will be shown in Section 6).

Definition 3

(IC). An integrity constraint (IC) is a piece of knowledge added by the experts and expressing that some potential facts cannot hold at the same time.

Definition 4

(elements of a RBES). By means of the concept of formula, we can define the elements of which a RBES is composed:

Input:The input of a RBES is concerned with the information related to the environment of the RBES. This information is described by means of a finite number of different atomic propositions.

Output:: The output of a RBES is concerned with the information inferred by the RBES. It is also described by means of a finite number of atomic propositions.

Knowledge-Base:The knowledge-base of the RBES is concerned with the information contained in the system, which is used along with the input of the RBES to infer the output of the system. In a RBES based on propositional Boolean logic, this knowledge-base will be mostly represented by a finite set of rules which may require to define new atomic propositions. Consequently, the knowledge-base of the RBES is described by a finite set of formulae $\{R_1,\dots ,R_{n^{\prime }}\}\subset \mathcal{C}$.

The concept of tautological consequence of propositional logic is used for determining the knowledge which the RBES can infer. As usual, we make use of $\{A_1,\dots ,A_n\}$$\vDash B$ to denote that the formula B is a tautological consequence of the formulae $A_1,\dots ,A_n$ (we say that $\{A_1,\dots ,A_n\}\vDash B$ if and only if, whenever the formulae $A_1$,…,$A_n$ hold, then B also holds). In this way, a RBES with knowledge base $\{R_1,\dots ,R_{n^{\prime }}\}$ and having as input the set of formulae $\{F_1,\dots ,F_n\}$ infers the formula $B\in \mathcal{C}$ if and only if the following holds:

$$\{F_1,\dots ,F_n,R_1,\dots ,R_{n^{\prime }}\}\vDash B$$

Another important issue on propositional Boolean logic is related to the concept of consistency (in an informal way, $\{A_1,\dots ,A_n\}$ is inconsistent if both a formula and its negation can be simultaneously inferred). Obviously, the formulae embodying the knowledge-base of a RBES must be consistent.

3. Organizing the Knowledge of the Tennis Hitting Technique RBES

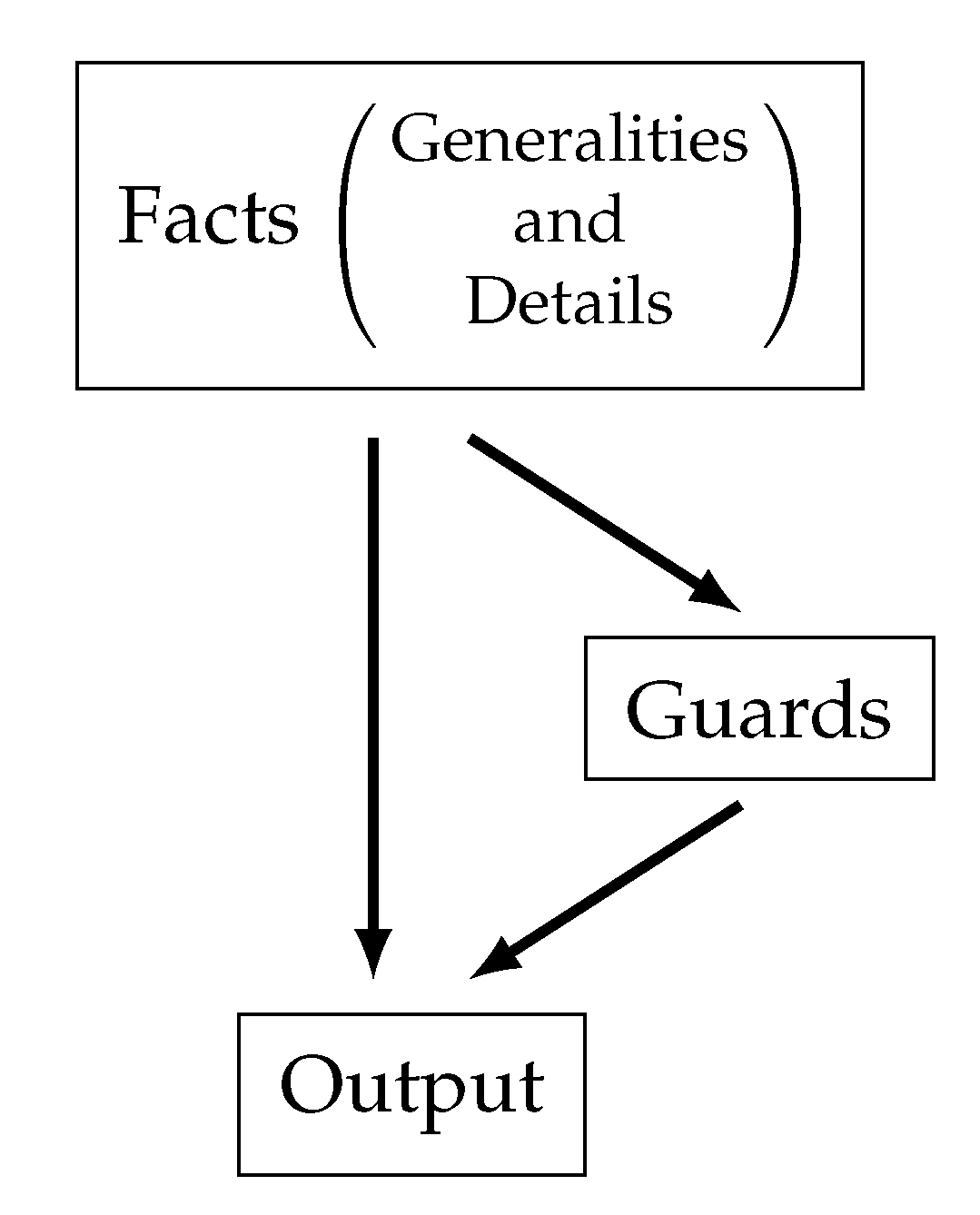
The propositional variables of the RBES have been grouped in four homogeneous blocks:

• Facts – Block I (Generalities): kind of serve the player is executing and player’s level (variables $x_i$, $y_i$, $z_i$ are used in this block).
• Facts – Block II (Details): details of the execution of the serve, kinetic and coordination.
• Guards: intermediate conclusions—not visible for the user (variables $g_i$ are used for the guards).
• Output: conclusions about the way the player is serving (variables $c_i$ are used for the output).

The structure of the RBES is summarized in Figure 1.

3.1. Facts—Block I (Generalities)

In this first block consists just of three questions: the system is informed about the kind of serve the player is executing and two technical details about his/her abilities (see

Table 1. Facts—Block I.

Description	Propositional
	Variable
Kind of serve (choose exactly one):
You are executing a slice serve	$x_1$
You are executing a flat serve	$x_2$
You are executing a topspin serve	$x_3$
You are an expert player and you can serve in any of the
three ways ($x_1$, $x_2$, $x_3$) tossing the ball the same place	$z_0$
You usually jump when executing this kind of serve	$y_1$

). We shall briefly explain these facts for those unaware of tennis technique.

Regarding the spin:

• in a flat serve the ball is not rotating,
• in the slice serve it rotates around a vertical axis (the trajectory is curved and bounces to one side),
• in the topspin serve the ball is rotating around an horizontal axis (the upper part of the ball moves forward and the lower part moves backwards): the aerodynamic effect is that the ball bounces closer and higher.

For the sake of simplicity we consider $x_1$, $x_2$, $x_3$ mutually exclusive. This is not completely accurate, as an advanced player could serve with a mixture of topspin and slice spins.

Each kind of serve normally requires the ball to be tossed at different places (see $l_1$, $l_2$, $l_3$ below) (Let us underline that the encoding chosen use redundant variables, that could be avoided if using 3-valued variables instead. Nevertheless, according to our experience, Boolean computations are much faster, even if more variables are needed.). But this way the opponent is aware of the kind of spin of the serve. It is really difficult although possible to always toss the ball at the same place ($z_0$) (Observe that there is no particular reason for choosing the subscripts of the variables (0, 1, 2, 3, 4, 5, 6, 7) the way they have been chosen.). Roger Federer is a good example of this ability.

If the serve is correctly executed, the player tends to move upwards ($y_1$) and forward (inside the court).

3.2. Facts—Block II (Details)

Tennis is not a precise science in the sense that there isn’t a unique valid truth for everyone. There are different “schools” and ways to teach and even to execute the different strokes.

They also change with time: before Björn Borg nearly no player played two-handed backhand and used topspin. Nowadays the vast majority of professional players play two-handed backhand and use topspin in most strokes from the back of the court. Meanwhile, two-handed forehand wasn’t a success and was only used by a few players like Hans Gildemeister.

There are very successful unorthodox styles, like Jim Courier’s baseball-style forehand or Rafael Nadal’s forehand finishing. A system like the one presented here would be useless in such a case.

There are also great tennis players with an untraditional serve, like John P. McEnroe, and players with a pure traditional service, like Roger Federer.

Therefore we have just considered what could be considered the standard serving technique [2,3,4], and have transcribed the causality underlying what is explained in the tennis books into logical rules to the best of our knowledge.

After many years of development of this sport, we consider that there is a consensus in the clear cause-effect relation in tennis hitting technique. For instance, a clear simplified example is the following: if you serve and the ball is too far away in front of you and too low when you hit it, the racket will be facing the floor when it hits the ball, so the ball will bounce just in front of you, never on the other side of the net. Obviously most situations are more complex, but the consensus in the standard technique and the above mentioned causality is what makes plausible (from our point of view) to use a Boolean logic approach, as we compare what the player is doing with the standard theoretical technique (the latter admitted as a truth). Something due to the authors is how they have translated that consensual knowledge into rules.

As said in Section 3.2 above, we have considered that the different spins are mutually exclusive as simplification.

Table 2. Facts—Block IIa.

Description	Propositional
	Variable
Feet initial position / distance (choose at most one):
Distance between feet too big	$d_1$
Distance between feet too small	$d_2$
Arms initial situation:
Arms initially not relaxed	$v_1$
Shoulders’ initial position (angle w.r.t. baseline)
close to right angle (or your usual position)	$w_1$
Tossing the ball—A (choose exactly one):
Too low toss	$t_1$
Normal height toss	$t_2$
Too high toss	$t_3$
Tossing the ball—B (choose exactly one):
A bit towards the arm holding the racket	$l_1$
On the middle	$l_2$
A bit towards the arm not holding the racket	$l_3$
Hitting the ball (choose at most one):
You are letting the ball drop too low	$a_1$
You are hitting the ball too high (upper part of the racket)	$a_2$
Looking at the ball:
You are keeping your eyes on the ball	$m_1$
Grip:
You are holding the grip firmly	$e_1$
This is your usual grip for this kind of serve	$e_2$

and

Table 3. Facts—Block IIb.

Description	Propositional
	Variable
Kinetic:
You flex slightly your knees before hitting the ball	$k_1$
Your knees are straight when hitting the ball	$k_2$
You balance slightly backward and forward during the
execution of the serve and you move or tend to move forward	$k_3$
You feel your abdominals do work during the execution of the serve	$k_4$
Your racket begins the swing more or less behind your
head at its usual initial position	$k_5$
The swing of your racket finishes too early	$k_6$
You are hitting the ball with your feet on the air	$k_7$
Coordination:
You “feel coordinated” when serving today	$o_1$

(splitted only for the sake of space) collects the most typical items of the execution of the serve to be taken into account (in our personal opinion).

Let us underline the difference between $t_1$ and $a_1$: the toss can be correct or even too high, but the player can let the ball fall too low anyway.

It is clear that we have the following incompatibilities:

• $d_1$ and $d_2$ are incompatible,
• $t_1$, $t_2$ and $t_3$ are mutually incompatible,
• $l_1$, $l_2$ and $l_3$ are mutually incompatible,
• $a_1$ and $a_2$ are incompatible.

3.3. Guards

Some rules will clearly have an immediate consequence in the serve, but others just provoke intermediate consequences that we have denoted “guards” (

Table 4. Guards.

Description	Propositional
	Variable
Lack of balance (equilibrium of the body)	$g_1$
Physical difficulty or impossibility to execute the stroke that way	$g_2$
Acceleration w.r.t. normal rhythm or some parts
of the execution of the serve not on time	$g_3$
Incompatibility with the player’s own technique	$g_4$

). We have decided to introduce these technical intermediate steps in the rule base in order to organize it more clearly, as they somehow give technical reasons for the knowledge expressed in the rules involved. They can be very useful for an expert in tennis and logic revising the RBES.

Initially, we have decided that guards were not visible to the players, as they are technical reasons for reaching an effect in the serve. Nevertheless they could be an explanation for a player that is curious for obtaining a logic explanation of what happens, as they are somehow an intermediate level of diagnosis. If it is considered interesting for the system to include them as visible output, it would be enough to compute some more normal forms (see Section 6.1 and Section 6.2 below).

3.4. Output

Let us detail the main different output of performing a certain serve (

Table 5. Output.

Description	Propositional
	Variable
Imprecision	$c_1$
Stroke too weak (lack of power)	$c_2$
Too low and/or too short	$c_3$
Too long	$c_4$
Little spin	$c_5$

).

No incompatibility should be included among the output. Different technical errors could lead to opposite outputs, what is not contradictory.

3.5. Rules and Incompatibilities (Integrity Constraints)

We shall not detail all the rules but we shall begin by giving an example of two simple concatenated rules.

Rule 5 is:

$$R5:t1\to g1$$

and it means:

R5: Too low toss → Lack of balance (equilibrium of the body)

(the consequent not an output, but a guard—an intermediate technical conclusion, not visible for the end user). This rule expresses that, if the player throws the ball in to the air too low, he/she will hit the ball in a flexed position, what will provoke a lack of balance.

Rule 23 is:

$$R23:g1\to c1\wedge c2$$

and it means:

R23: Lack of balance (equilibrium of the body) → Imprecision ∧ Stroke too weak (lack of power) (the latter are conclusions—output). Therefore, if we have $t1$, we conclude $c1$ and $c3$ This is a very simple example, just to get the flavour of the process. We do not detail all rules in this way for the sake of space.

The rules regarding the facts considered are:

• $R1:d1\to c2$
• $R2:d2\to g1$
• $R3:v1\to c2$
• $R4:\neg w1\to g1$
• $R5:t1\to g1$
• $R6:t3\to c1$
• $R7:l1\wedge \neg z0\wedge \neg x1\to g2\wedge c5$
• $R8:l2\wedge \neg z0\wedge \neg x2\to g2\wedge c5$
• $R9:l3\wedge \neg z0\wedge \neg x3\to g2\wedge c5$
• $R10:a1\to c3xorc4$
• $R11:a2\to g3$
• $R12:\neg m1\to c1$
• $R13:\neg e1\to c1\wedge c2$
• $R14:\neg e2\to g4$
• $R15:\neg k1\to c1\wedge c2$
• $R16:\neg k2\to c1\wedge c2$
• $R17:\neg k3\to c1\wedge c2$
• $R18:\neg k4\to c1\wedge c2$
• $R19:\neg k5\to c1\wedge c2$
• $R20:k6\to c2$
• $R21:\neg k7\wedge y1\to c2\wedge c5$
• $R22:\neg e1\to c1\wedge c2$

and the rules corresponding to the guards are:

• $R23:g1\to c1\wedge c2$
• $R24:g2\to c1\wedge c2$
• $R25:g3\to c1$
• $R26:g4\to c1$

Let us underline that we have grouped some rules for the sake of brevity. For instance

• $R7:l1\wedge \neg z0\wedge \neg x1\to g2\wedge c5$

should be formally written

• $R7a:l1\wedge \neg z0\wedge \neg x1\to g2$
• $R7b:l1\wedge \neg z0\wedge \neg x1\to c5$

(this way it would be in accordance with Definition 4).

Similarly, we have included $xor$ (exclusive or) in $R10$:

$R10:a1\to c3xorc4$

The knowledge behind this rule could have also be written:

• $R10n:a1\to c3\vee c4$
• $IC0:\neg (c3\wedge c4)$

(note that in this case $R10n\wedge IC0\to R10$ but $R10\neg \to R10n\wedge IC0$).

Next, we enumerate integrity constraints related to choose one option over three ones:

• $IC1:\neg (x1\wedge x2)$
• $IC2:\neg (x2\wedge x3)$
• $IC3:\neg (x1\wedge x3)$
• $IC4:x1\vee x2\vee x3$
• $IC5:\neg (t1\wedge t2)$
• $IC6:\neg (t2\wedge t3)$
• $IC7:\neg (t1\wedge t3)$
• $IC8:t1\vee t2\vee t3$
• $IC9:\neg (l1\wedge l2)$
• $IC10:\neg (l2\wedge l3)$
• $IC11:\neg (l1\wedge l3)$
• $IC12:l1\vee l2\vee l3$

and the integrity constraints regarding choosing at most one option out of two are:

• $IC13:\neg (a1\wedge a2)$
• $IC14:\neg (d1\wedge d2)$

4. An Algebraic Model for RBES

In this section, we will see how we can implement an expert system based on Boolean propositional logic in a computer algebra system.

Let us consider an expert system based on Boolean propositional logic with propositions $X_1\dots X_m$. Each formula in $\mathcal{C}$ can be represented as a Boolean polynomial (see Definition 5). This representation makes use of the ideal I in ${\mathbb{Z}}_2[x_1,\dots ,x_m]$:

$$I=\langle x_1^2-x_1,\dots ,x_m^2-x_m\rangle$$

Notation 1

(NF). Let $NF(pol,I)$ denote the ‘normal form’ of polynomial $pol$ modulo ideal I.

Definition 5

(function $\phi$). We define recursively the function $\phi :\mathcal{C}⟶{\mathbb{Z}}_2[x_1,\dots ,x_m]$ as follows:

• If $A\equiv X_i$, then $\phi \left(A\right)=x_i$
• If $A\equiv \neg B$ where $B\in \mathcal{C}$, then $\phi \left(A\right)=NF(1+\phi (B),I)$
• If $A\equiv B\wedge C$ where $B,C\in \mathcal{C}$, then $\phi \left(A\right)=NF\left(\phi \right(B)·\phi (C),I)$
• If $A\equiv B\vee C$ where $B,C\in \mathcal{C}$, then $\phi \left(A\right)=NF\left(\phi \right(B)+\phi (C)+\phi (B)·\phi (C),I)$
• If $A\equiv B\to C$ where $B,C\in \mathcal{C}$, then $\phi \left(A\right)=NF(1+\phi (B)+\phi (B)·\phi (C),I)$.

As may be seen in the previous definition, for any formula A, $\phi \left(A\right)$ is a polynomial in ${\mathbb{Z}}_2[x_1,\dots ,x_m]$ whose variables are never to a power greater than 1 (continuously computing the reduction modulo ideal I is equivalent to work in the residue class ring ${\mathbb{Z}}_2[x_1,\dots ,x_m]/I$). Besides, the total degree of the polynomial may be, at most, equal to the number of variables.

Once described how Boolean formulae are represented by polynomials, we show, by Theorem 1, how the problem of determining if a formula is tautological consequence of others can be translated into an algebraic problem [5]. Previous works not providing a residue class ring as a model for the logic and not considering the extension to RBES are [6,7] (Boolean case) and [8,9] (many-valued case). A detailed survey can be found in [10]. There are recent developments in this line of research such as [11,12].

Theorem 1.

Let $A_1,\dots ,A_n,B\in \mathcal{C}$. The following holds:

(i)

$\{A_1,\dots ,A_n\}\vDash B\iff \phi (\neg B)\in \langle \phi (\neg A_1),\dots ,\phi (\neg A_n)\rangle +I$

(ii)

$\{A_1,\dots ,A_n\}$ is consistent $\iff 1\notin \langle \phi (\neg A_1),\dots ,\phi (\neg A_n)\rangle +I$

Theorem 1 is important since the algebraic problems involved in this theorem may be solved making use of Groebner bases [13,14,15]. On the ground of this, many expert systems have been developed in different fields [16,17,18,19,20,21].

Indeed, the question of determining whether a RBES with knowledge-base $\{R_1,\dots ,R_{n^{\prime }}\}$ infers the formula B when its input is the set of facts $\{F_1,\dots ,F_n\}$ may be solved by checking whether the following holds:

$$NF(\phi (\neg B),I+\langle \phi (\neg F_1),\dots ,\phi (\neg F_n),\phi (\neg R_1),\dots ,\phi (\neg R_n)\rangle )=0$$

We can simplify the previous expression through the definition of the following ideals:

$$J=\langle \phi (\neg F_1),\dots ,\phi (\neg F_n)\rangle$$

$$K=\langle \phi (\neg R_1),\dots ,\phi (\neg R_{n^{\prime }})\rangle$$

In this way, the expression above results into:

$$NF\left(\phi \right(\neg B),I+J+K)=0$$

Similarly, the consistency of such RBES for the set of facts $\{F_1,\dots ,F_n\}$ can be decided using Groebner bases, as it is equivalent to:

$$GB(I+\langle \phi (\neg F_1),\dots ,\phi (\neg F_n),\phi (\neg R_1),\dots ,\phi (\neg R_n)\rangle )\ne \langle 1\rangle$$

what can be written:

$$GB(I+J+K)\ne \langle 1\rangle$$

5. Maple Implementation

The implementation used has been written in the computer algebra system Maple (Maple is a trademark of Waterloo Maple Inc., Waterloo, ON, Canada) and was introduced in 2008 [22]. The complete code is included in order to show how brief the code of the algebraic approach is (just a few lines). Firstly the algebraic packages for computing Groebner bases and normal forms and for declaring the polynomial ring where calculations will take place, are loaded:

• restart;
• with(Groebner):
• with(Ore_algebra):

Afterwards the list of polynomial variables, the polynomial ring, and the ordering (pure lexicographic with the order for variables given by list SV), are declared:

• SV:=x1,x2,x3,z0,y1,d1,d2,v1,w1,t1,t2,t3,l1,l2,l3,a1,a2,m1,e1,e2,
•   k1,k2,k3,k4,k5,k6,k7,o1,g1,g2,g3,g4,c1,c2,c3,c4,c5:
• A:=poly_algebra(SV, characteristic=2):
• Orde:=MonomialOrder(A,’plex’(SV)):

Now the ideal (iI), generated by the square of the polynomial variables minus themselves, is defined using the auxiliary function fu:

• fu:=var->var^2-var:
• iI:=map(fu, [SV]):

Finally, the logical connectives are defined as functions (the binary ones have an “&” in order to be infix operators) and are algebraic expressions reduced modulo the ideal iI in ring A using the ordering OrdeiI:

•  NEG   :=(m::algebraic) -> NormalForm(1+‘m‘,iI, Orde):
• ‘&AND‘ :=(m::algebraic, n::algebraic) ->
                   NormalForm(expand(m*n), iI, Orde):
• ‘&OR‘  :=(m::algebraic, n::algebraic) ->
                   NormalForm(expand(m+n+m*n), iI, Orde):
• ‘&IMP‘ :=(m::algebraic, n::algebraic) ->
                   NormalForm(expand(1+m+m*n), iI, Orde):
• ‘&XOR‘ :=(m::algebraic, n::algebraic) ->
                   (m &OR n) &AND NEG(m &AND n):

The translation of the rules and integrity constraints of the RBES developed in this article in the algebraic approach detailed above is:

• R1:= d1 &IMP c2:
• R2:= d2 &IMP g1:
• R3:= v1 &IMP c2:
• R4:= NEG(w1) &IMP g1:
• R5:= t1 &IMP g1:
• R6:= t3 &IMP c1:
• R7:= (l1 &AND NEG(z0) &AND NEG(x1)) &IMP (g2 &AND c5):
• R8:= (l2 &AND NEG(z0) &AND NEG(x2)) &IMP (g2 &AND c5):
  R9:= (l3 &AND NEG(z0) &AND NEG(x3)) &IMP (g2 &AND c5):
• R10:= a1 &IMP (c3 &XOR c4):
• R11:= a2 &IMP g3:
• R12:= NEG(m1) &IMP c1:
• R13:= NEG(e1) &IMP (c1 &AND c2):
• R14:= NEG(e2) &IMP g4:
• R15:= NEG(k1) &IMP (c1 &AND c2):
• R16:= NEG(k2) &IMP (c1 &AND c2):
• R17:= NEG(k3) &IMP (c1 &AND c2):
• R18:= NEG(k4) &IMP (c1 &AND c2):
• R19:= NEG(k5) &IMP (c1 &AND c2):
• R20:= k6 &IMP c2:
• R21:= (NEG(k7) &AND y1) &IMP (c2 &AND c5):
• R22:= NEG(e1) &IMP (c1 &AND c2):
• R23:= g1 &IMP (c1 &AND c2):
• R24:= g2 &IMP (c1 &AND c2):
• R25:= g3 &IMP c1:
• R26:= g4 &IMP c1:
• IC1:= NEG(x1 &AND x2):
• IC2:= NEG(x2 &AND x3):
• IC3:= NEG(x1 &AND x3):
• IC4:= x1 &OR x2 &OR x3:
• IC5:= NEG(t1 &AND t2):
• IC6:= NEG(t2 &AND t3):
• IC7:= NEG(t1 &AND t3):
• IC8:= t1 &OR t2 &OR t3:
• IC9:= NEG(l1 &AND l2):
• IC10:= NEG(l2 &AND l3):
• IC11:= NEG(l1 &AND l3):
• IC12:= l1 &OR l2 &OR l3:
• IC13:= NEG(a1 &AND a2):
• IC14:= NEG(d1 &AND d2):

And the (polynomial) ideal of rules is, in this case:

• J:=[ NEG(R1),  NEG(R2),  NEG(R3),  NEG(R4), NEG(R5), NEG(R6),
•    NEG(R7),  NEG(R8),  NEG(R9),  NEG(R10),NEG(R11),NEG(R12),
•    NEG(R13), NEG(R14), NEG(R15), NEG(R16),NEG(R17),NEG(R18),
•    NEG(R19), NEG(R20), NEG(R21), NEG(R22),NEG(R23),NEG(R24),
•    NEG(R25), NEG(R26), NEG(IC1), NEG(IC2),NEG(IC3),NEG(IC4),
•    NEG(IC5), NEG(IC6), NEG(IC7), NEG(IC8),NEG(IC9),NEG(IC10),
•    NEG(IC11),NEG(IC12),NEG(IC13),NEG(IC14) ]:

Let us observe that the generators of the ideals are given as lists of polynomials. The Groebner bases of the ideals are automatically computed by Maple command Basis just by introducing the list of generators and the chosen order, as shown in Section 6.

6. Examples

6.1. A Correct Serve

Let us introduce $x3$, $\neg z0$, $y1$, $\neg d1$, $\neg d2$, $\neg v1$, $w1$, $t2$, $l3$, $\neg a1$, $\neg a2$, $m1$, $e1$, $e2$, $k1$, $k2$, $k3$, $k4$, $\neg k6$, $k7$, $o1$ as facts. The ideal K of facts will be:

• K:=[ NEG(x3),NEG(NEG(z0)),NEG(y1),NEG(NEG(d1)),NEG(NEG(d2)),
•    NEG(NEG(v1)),NEG(w1),NEG(t2),NEG(l3),NEG(NEG(a1)),
•    NEG(NEG(a2)),NEG(m1),NEG(e1),NEG(e2),NEG(k1),NEG(k2),
•    NEG(k3),NEG(k4),NEG(NEG(k6)),NEG(k7),NEG(o1) ]:

and the Groebner basis of the ideal generated by the ideal $I+J+K$ (note that I is denoted iI in the Maple implementation) will be:

• time0:=time():
• B:=Basis([op(iI),op(J),op(K)], Orde);
•                [c5^2+c5,...,x2,x1]
• time()-time0;
•                   0.296

(the complete output is omitted for he sake of space). This ideal is not $\langle 1\rangle$, so there is no inconsistency (for these facts).

Let us check if any of $c1$, $c2$, $c3$, $c4$, $c5$ follow from these facts:

• time0:=time():
• NormalForm(NEG(c1), B, Orde);
•              1 + c1
• NormalForm(NEG(c2), B, Orde);
•              1 + c2
• NormalForm(NEG(c3), B, Orde);
•              c3 + 1
• NormalForm(NEG(c4), B, Orde);
•              1 + c4
• NormalForm(NEG(c5), B, Orde);
•              c5 + 1
• time()-time0;
•              0.078

As 0 was never obtained, none of the $c_i$ is obtained by forward firing. It can be seen above how the answers were computed in less than one-tenth of a second (on a standard PC), after the previous computation of the Groebner basis of the ideal $I+J+K$ (what took less than three-tenths of a second).

6.2. An Incorrect Serve

Let us exchange now $l3$ by $l1$. Then the ball is not correctly tossed according to the serve chosen, as the player has affirmed that he/she cannot serve in any of the three ways tossing the ball the same place ($\neg z_0$)

The ideal K of facts will now be:

• K:=[ NEG(x3),NEG(NEG(z0)),NEG(y1),NEG(NEG(d1)),NEG(NEG(d2)),
•    NEG(NEG(v1)),NEG(w1),NEG(t2),NEG(l1),NEG(NEG(a1)),
•    NEG(NEG(a2)),NEG(m1),NEG(e1),NEG(e2),NEG(k1),NEG(k2),
•    NEG(k3),NEG(k4),NEG(NEG(k6)),NEG(k7),NEG(o1) ]:

and the Groebner basis of the ideal generated by $I+J+K$ will be:

• time0:=time():
• B:=Basis([op(iI),op(J),op(K)], Orde):
                 [c5+1,...,x2,x1]
• time()-time0;
                 0.218

(the complete output is again omitted for he sake of space). This ideal is not $\langle 1\rangle$, so there is no inconsistency (for these facts) either.

Let us check if any of $c1$, $c2$, $c3$, $c4$, $c5$ follow from these facts:

• tiempo:=time():
• NormalForm(NEG(c1), B, Orde);
                  0
• NormalForm(NEG(c2), B, Orde);
                  0
• NormalForm(NEG(c3), B, Orde);
                 c3 + 1
• NormalForm(NEG(c4), B, Orde);
                 c4 + 1
• NormalForm(NEG(c5), B, Orde);
                  0
• time()-time0;
                 0.078

Therefore $c_1$, $c_2$ and $c_5$ are obtained by forward firing, that is, we could have:

• imprecision
• stroke too weak (lack of power)
• little spin.

The answers were computed in similar times.

6.3. A Remark about Timings

Although it is well-known that the complexity of Groebner bases computation is double exponential in the worst case in the general case, there are very important simplifications in the algebraic model for RBES knowledge extraction and verification:

• the base field of the polynomial ring is ${\mathbb{Z}}_2$ (it has characteristic 2, instead of 0),
• the degree in each variable is at most 1 for all polynomials,
• the total degree of all polynomials is less or equal to the number of variables

(it is a polynomial Boolean ring, or, if the structure of the RBES is directly translated, a polynomial Boolean algebra [10]).

These features allow to treat problems of a size that would not be treatable, for instance, in real geometry. For example, the RBES of [18] consists of 313 rules (of the type specified in Remark 1) that are simplified to 182 complex rules (in the way mentioned in Remark 2). The problem treated here, with 26 rules and 14 integrity constraints, is tiny in comparison.

The specialized software PolyBoRi [23] is extremely fast due to dealing only with Boolean rings, that is, with this special kind of rings.

7. Conclusions

The main achievement is that there is no comparable RBES devoted to tennis hitting technique (as far as we know).

This is a first step in the exploration of this kind of RBES. Many more things could be done.

As future work, a comfortable GUI should be developed, either stand alone, like in [18], or accessible through Internet, like [19]. If Maple was the chosen tool to implement the RBES, Maplets could be used, although it would be even faster to use a specialized software such as MiniSat [24] or PolyBoRi [23]. Nevertheless, performance is not the key issue here, as we are just exploring the field and the system is (at least so far) simple.

Another important extension is to include backward reasoning in order to automatically determine which single propositional changes could change a certain output. This can be achieved with the same algebraic approach used, as shown in [25], but it development is not trivial and is left for a future work.

Also the possibility to use modal many-valued logics is not yet discarded, as the player can have doubts and perhaps not all variables should be considered Boolean.

Obviously the system could be detailed with more facts (like wind) and more complex possibilities (like mixing slice and topspin effects). Moreover, it could be extended to the other main strokes of tennis.

With the implementation included above, the player can study the effect of changing some of the given facts.