Abstract
In this paper, we consider the problem of improving the reachability of a graph. We approach the problem from a graph augmentation perspective, in which a limited set size of edges is added to the graph to increase the overall number of reachable nodes. We call this new problem the Maximum Connectivity Improvement (MCI) problem. We first show that, for the purpose of solve solving MCI, we can focus on Directed Acyclic Graphs (DAG) only. We show that approximating the MCI problem on DAG to within any constant factor greater than is -hard even if we restrict to graphs with a single source or a single sink, and the problem remains -complete if we further restrict to unitary weights. Finally, this paper presents a dynamic programming algorithm for the MCI problem on trees with a single source that produces optimal solutions in polynomial time. Then, we propose two polynomial-time greedy algorithms that guarantee -approximation ratio on DAGs with a single source, a single sink or two sources.
1. Introduction
The problem of improving the reachability of a graph is an important graph-theoretical question, which finds applications in several areas. There are several recent possible application scenarios for this problem, for example suggesting friends in a social network in order to increase the spreading of information [1,2,3], reducing the convergence time of random walk processes to perform faster network simulations [4,5], improving wireless sensor networks resilience [6] and even control elections in social networks [7,8].
In this paper, we approach the problem from a graph augmentation perspective, which is the problem of adding a set of non-existing edges to a graph to increase the overall number of reachable nodes. In traditional graph theory, this problem was first studied by Eswaran and Tarjan [9]. They considered the problem of adding a minimum-cost set of edges to a graph such that the resulting graph satisfies a given connectivity requirement, e.g., to make a directed graph strongly connected or to make an undirected graph bridge-connected or biconnected. In their seminal paper, Tarjan et al. presented linear time algorithms for many graph augmentation problems and proved that some variants are instead -complete.
More recently, several optimisation problems related to graph augmentation have been addressed. Several papers in the literature deal with the problem of minimising the eccentricity of a graph by adding a limited number of new edges [10,11,12,13].
The problem of minimising the average all-pairs shortest path distance—characteristic path length—of the whole graph was studied by Papagelis [5]. The author considered the problem of adding a small set of edges to minimise the characteristic path length and proves that the problem is -hard. He proposed a path screening technique to select the edges to be added. It is worth noting that the objective function in [5] does not satisfy the submodularity property, and so good approximations cannot be guaranteed via a greedy strategy. The problem of adding a small set of links to maximise the centrality of a given node in a network has been addressed for different centrality measures: page-rank [4,14], average distance [15], harmonic and betweenness centrality [16,17] and some measures related to the number of paths passing through a given node [18]. It is worth noting that many traditional graph problem can also be applied to dynamic graphs. Graph problems close to ours studied in the dynamic setting include connectivity [19], minimum spanning tree [20] and reachability [21,22].
In this work, which is based on and extends previous preliminary research in this direction [23], we study the problem of adding at most B edges to a directed graph in order to maximise the overall weighted number of reachable nodes, which we call the Maximum Connectivity Improvement (MCI) problem. The rest of the paper is organised as follows. We first show that we can focus on Directed Acyclic Graphs (DAG) without loss of generality (Section 2). Then, we focus on the complexity of the problem (Section 3) and we prove that the MCI problem is -hard to approximate to within a factor greater than . This result holds even if the DAG has a single source or a single sink. Moreover, the problem remains -complete if we further restrict to the unweighted case. In Section 4, we give a dynamic programming algorithm for the case in which the graph is a rooted tree, where the root is the only source node. In Section 5, we present a greedy algorithm which guarantees a -approximation factor for the case in which the DAG has a single source or a single sink. As a first step in the direction of extending our approach to general DAGs, i.e., multiple sources and multiple sinks, in Section 6, we tackle the special case of DAGs with two sources providing a constant factor approximation algorithm to solve the problem. We end with some concluding remarks in Section 7. Compared to the conference version, we add the results in Section 6 on DAGs with two sources and we revise the paper in order to improve readability, by adding examples and detailed proofs.
2. Preliminaries
Let be a directed graph. Each node is associated with a non-negative weight and a profit . Given a node , we denote by the set of nodes that are reachable from v in G, that is . Moreover, we denote by the sum of the profits of the nodes reachable from v in G. In the rest of the paper, we also use the form to denote the sum of the profits of the nodes in G that are reachable from v, but not from u. Note that, in the case , it holds . Given a set S of edges not in E, we denote by the graph augmented by adding the edges in S to G, i.e., . Let and be, respectively, the set of nodes that are reachable from v in and the sum of the profits of the nodes in . Note that, augmenting G, the connectivity cannot be worse, and thus: . Let be a weighted measure of the connectivity of G. When weights and profits are unitary, represents the overall number of connected pairs in G.
In this paper, we aim to augment G by adding a set S of edges of at most size B, i.e., and , that maximises the weighted connectivity of . We call this problem the Maximum Connectivity Improvement (MCI) problem because maximising is the same as maximising . Formally,
Definition 1
(Maximum Connectivity Improvement). Given a graph , given for each node a weight and a profit and given a budget , we want to find a set of edges such that
From now on, for simplicity, we omit from the notations the original graph G. Thus, we simply use and to denote and , respectively. Similarly, we simply denote with f and the value of the weighted connectivity in G and in , respectively.
At first, we show how to transform any directed graph G with cycles into a Directed Acyclic Graph (DAG) and how to transform any solution for into a feasible solution for G.
Graph has as many nodes as the number of strongly connected components of G, i.e., there is one vertex in for each strongly connected component of G. Specifically, selects one representative node for each strongly connected component of G and adds one directed edge between two nodes and of if there is a directed edge in G connecting any vertex of the strongly connected component represented by with any vertex of the strongly connected component represented by . Graph is called condensation of G and can be computed in time by using Tarjan’s algorithm which consists in performing a DFS visit [24].
The weight and the profit of a node in is given by the sum of the weights and profits of the nodes of G that belong to the strongly connected component that is represented by , i.e., and . Note that, when the profits are unitary in G, , then is equal to the size of the strongly connected component associated to .
Since the condensation preserves the connectivity of G, the following lemma can be proved:
Lemma 1.
Given a graph G and its condensation , it yields: .
Proof.
First, consider two nodes u and v that belong to the same strongly connected component in . Clearly, .
Moreover, it holds that because contains one node for each different strongly connected component in and thus:
Denoting the strongly connected component represented by , we have:
□
Given a solution for the MCI problem in , we can build a solution S with the same value for the MCI problem in G as follows: For each edge in , we add an edge in S, where u and v are two arbitrary nodes in the connected component corresponding to and , respectively.
This derives from the fact that applying the condensation algorithm to or to we obtain the same condensed graph, say . From Lemma 1, we can conclude that .
Observe that, if we add an edge e within the same strongly connected component in G, we do not add any edge to . Since the condensation of is the same as , we have . Hence, we can assume, without loss of generality, that any solution to MCI in G does not contain any edge within a unique strongly connected component since such edge does not improve the objective function. As a consequence, in the remainder of the paper, we assume that the graph is a DAG.
Given a DAG, we can distinguish between three kinds of nodes: sources, nodes with no incoming edges; sinks, nodes with no outgoing edges; and the rest of the nodes. The next lemma allows us to focus on solutions that contain only edges connecting sink nodes to source nodes. In the remainder of the paper, we use this property to derive algorithms to solve both the simple case with binary trees and the more general case with DAGs (with single or double source and single sink).
Lemma 2.
Let S be a solution to the MCI problem, then there exists a solution such that , , and all edges in connect sink nodes to source nodes.
Proof.
We show how to modify any solution S in order to find a solution that contains only nodes that connect sink nodes to source nodes with the same cardinality and such that . To obtain , we start from S and we repeatedly apply the following modifications to each edge of S such that u is not a sink or v is not a source:
- If u is not a sink, then there exists a path from u to some sink and we swap edge with edge . The objective increases at least by the sum of the weights on a path from u to . Namely, after adding the edge , any node z on the path from u to now reaches v passing through . Note that the objective function does not decrease and, instead, may increase due to the fact that the nodes z now are able to reach the node v.
- If v is not a source, then there exists a path from a source to v and we swap edge with edge . The objective function does not decrease and increases at least by the number of nodes in a path from to v multiplied by .
Note that, in both cases the gain of a node on the path we are extending can be zero if it was already able to reach the source/sink from another edge in the solution. Since we have neither added nor removed any edge, the cardinality of the new solution is equal to the previous solution S. Furthermore, since the objective function can only increase by modifying the edges according to the rules described above, we have that . □
3. Hardness Results
In this section, we first show that the MCI problem is -complete, even in the case in which all the weights and profits are unitary and the graph contains a single sink node or a single source node. Then, we show that it is -hard to approximate MCI to within a factor greater than . This last result holds also in the case of graphs with a single sink node or a single source node, but not in the case of unitary weights.
Theorem 1.
MCI is -complete, even in the case in which all the weights and profits are unitary and the graph contains a single sink node or a single source node.
Proof.
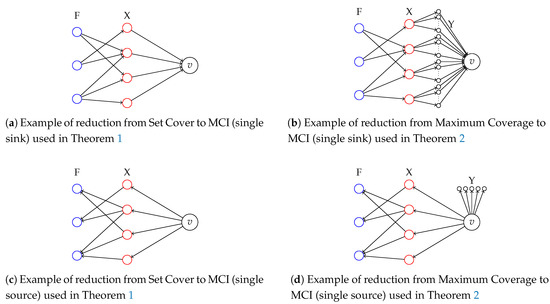
We consider the decision version of MCI in which all the weights and profits are unitary (i.e., ): Given a directed graph and two integers , the goal is to find a set of additional edges such that and . The problem is in since it can be checked in polynomial time if a set of nodes S is such that and . We reduce from the Set Cover (SC) problem which is known to be -complete [25]. Consider an instance of the SC problem defined by a collection of subsets for a ground set of items . The problem is to decide whether there exist k subsets whose union is equal to X. We define a corresponding instance of MCI as follows:
- ;
- , where and ; and
- .
See Figure 1 (left, top) for an example. Note that G is a DAG. By Lemma 2, we can assume that any solution S of MCI contains only edges for some . In fact, v is the only sink node and are the only source nodes. Assume that there exists a set cover ; then, we define a solution S to the MCI instance as . It is easy to show that and . Indeed, all the nodes in G can reach: node v, all the nodes (since is a set cover), and all the nodes such that . Moreover, each node such that can reach itself. Therefore, there are nodes that reach nodes and that reach nodes, that is . On the other hand, assume that there exists a solution for MCI; then, S is in the form and we define a solution for the set cover as . We show that is a set cover. By contradiction, if we assume that is not a set cover and it cover only elements of X, then . Note that, in the above reduction, the graph G has a single sink node. We can prove the -hardness of the case of graphs with a single source node by using the same arguments on an instance of MCI made of the inverse graph of G, , and (see Figure 1 (left, bottom) for an example). □

Figure 1.
Examples of reductions used in Theorems 1 and 2.
Theorem 2.
MCI is -hard to approximate to within a factor , for any , even if graph contains a single sink node or a single source node.
Proof.
We give two approximation factor preserving reductions from the Maximum Coverage problem (MC), which is known to be -hard to approximate to within a factor greater than [26].
The MC problem is defined as follows: given a ground set of items , a collection of subsets of subsets of X, and an integer k, find k sets in that maximise the cardinality of their union.
We first focus on the single sink problem. Given an instance of the MC problem , we define an instance of the (maximisation) MCI problem similar to the one used in Theorem 1, but where we modify the weights and add Y paths of one node between each and v, where Y is an arbitrarily high number (polynomial in ).
In detail, is defined as follows:
- ;
- , where and ;
- and , for each ; and
- for any node .
See Figure 1 (right, top) for an example. We first show that there exists a solution to that covers elements of X if and only if there exists a solution S to such that . Moreover, we can compute from S and vice versa in polynomial time. Indeed, given , we define S as . We can verify that and . Indeed, only node v as a weight different from 0, and then , since v can reach the nodes corresponding to the items covered by , the B nodes it is connected to, and itself. On the other hand, given a solution S to , by Lemma 2, we can assume that it has only edges from v to nodes . Let be the number of nodes in , then and covers elements in X.
If and denote the optimum value for and , respectively, then . Moreover, given the above definition of S and , then for any there exists a value of such that .
Let us assume that there exists a polynomial-time algorithm that guarantees an approximation for , then we can compute a solution S such that . It follows that:
where is the number of nodes covered by the solution to MC obtained from S. Therefore, we obtain an algorithm that approximates the MC problem with a factor (up to lower order terms). Since it is -hard to approximate to within a factor greater than [26], then the statement follows.
Let us now focus on the single source case. Given , we define as follows:
- ;
- , where and ;
- , for each and , for each ; and
- for any node .
Y is an arbitrarily high polynomial value in . See Figure 1 (right, bottom) for an example. We use similar arguments as above. In detail, there exists a solution to that covers elements of X if and only if there exists a solution S to such that , where is the number of sets in F that do not cover any of the elements covered by . Moreover, we can compute from S and vice versa in polynomial time. Given , we define S as and we can verify that and . Given S, if is the number of nodes such that , then and covers elements in X.
As above, we can show that and that there exists a value of such that , for any . Then, the statement follows by using the same arguments as above. □
4. Polynomial-Time Algorithm for Trees
In this section, we focus on the case of directed weighted rooted trees in which the root of the tree is the only source node and all the edges are directed towards the leaves. We give a polynomial-time algorithm based on dynamic programming that focuses on the special case of binary trees and requires time and space. Moreover, exploiting Lemma 2, the algorithm focuses only on edges that connect leaves to the root. We then extend our result and give an algorithm to transform any tree into a binary tree that requires time and space. Using this transformation, each solution for the transformed instance has the same value as the corresponding solution in the original instance.
4.1. Binary Trees
In the following, we introduce our dynamic-programming algorithm to solve the MCI problem in binary trees. Let us consider an instance of the MCI problem with a directed weighted binary tree , where all the edges are directed towards the leaves, the root is the only source node, and . Let us denote by (left child) and (right child) the children of node ; moreover, we denote as the sub-tree rooted at v.
Let us first note that given a node v, and given a solution that connects some leaves of to r. The gain of solution in is simply the increase in weighted reachability of some of the nodes in that can be written as . Note that, given a node , if in the subtree of u is not present one of the edges of , then the value is equal to zero since . On the other hand, if at least one edge is present, then,
The algorithm that we propose computes a solution that connects b leaves of to r and maximises the gain in for each node and for each budget . Formally, we define as the maximum gain in achievable by adding at most b edges from b leaves of to node r. Note that . We then now show how to compute for each node v and for each budget by using a dynamic programming approach. For each leaf and for each , we have that , that is, the sum of profits p of the new nodes that v can reach thanks to the new edge . Moreover for each . Then, the algorithm visits the nodes in T in post order. For each internal node v we compute by using the solutions of its sub-trees, i.e., and .
Let us assume that we have computed and , for each . Recall that, if a solution adds an edge between any leaf of and r, then the gain of node v is since v now reach all the nodes in T. This gain is independent of the number of edges that are added from the leaves of to r. In fact, given as the maximum gain for and budget , the gain in of a solution that connects leaves of to r is equal to . Similarly, the gain in of the solution that connects, for some , leaves of to r is equal to .
Then, once we have decided how many edges to add in and in for , we increase the reachability function of the same quantity, i.e., .
Hence, is given by the combination of and such that the sum is equal to the considered budget, i.e., , that maximises the sum . Precisely:
The optimal value of the problem , where is the value of the objective function on T (i.e., when no edges have been added). The pseudo-code of the algorithm is reported in Algorithm 1.
| Algorithm 1: Dynamic programming algorithm for MCI. |
 |
As a running example, let us consider a binary tree composed by eight nodes, as depicted in Figure 2, with for any node and for any node , finally . If we consider to have budget and to run Algorithm 1, we first have that any leaf in has . Then we start considering the rest of the nodes in post-order, thus we have: , , . Now, note that when considering node c we have that for any , that is, we are considering a solution that had added an edge in the left sub-tree and an edge in the right sub-tree. Finally, .

Figure 2.
Consider the node c with , and . We have: , , and . Therefore .
Theorem 3.
Algorithm 1 finds an optimal solution for MCI if the graph is a binary tree.
Proof.
Let us assume by contradiction that v and b are, respectively, the first node and the first budget for which Algorithm 1 computes a non-maximum gain at Line 9 of Algorithm 1, that is , where is the maximum gain for tree and budget b. Let be an optimal solution that achieves and let , be the edges in that starts from leaves in and , respectively. Let and . Then, the gain of the optimal solution is: .
Since by hypothesis is the first time for which Algorithm 1 does not find the maximum gain and since the cost does not depend on the edges selected in the left and right sub-trees of v, this implies that at Line 9 Algorithm 1 must select
thus contradicting . □
For each node v, the algorithm computes values of function g. Therefore, the variables can be seen for example as a matrix of dimension . For each entry of the matrix, we need to compute the maximum among gains (see Equation (1)) because the number of budgets that we need to try to combine to find the solution is . Thus, it follows that Algorithm 1 takes time. Note that because we limit the new edges to be of the form leaf-root. Moreover, the space complexity is .
4.2. General Trees
In the following, we present an algorithm that requires time and space to transform any generic rooted tree into an equivalent binary tree , following a tree transformation proposed in [27] by adding at most dummy node.
Given a generic rooted tree , let us transform it into a rooted binary tree with weights by adding a set of dummy nodes U as follows:
- Let the root r of T be the root of .
- For each non-leaf node v, let be the children of v:
- (a)
- Add edge to .
- (b)
- If , add to .
- (c)
- If , add dummy nodes .
- (d)
- Add edge and edges to , for each .
- (e)
- Add edge to , for each .
- (f)
- If , add edge to .
- If , then , otherwise and , otherwise .
See Figure 3 for an example of the transformation.
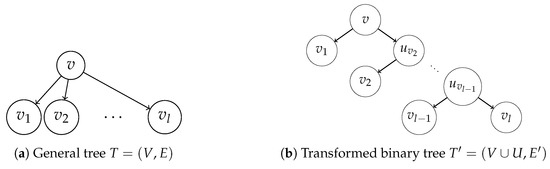
Figure 3.
Example of transformation from general tree to binary tree.
Note that for any node v in T due to the fact that the added dummy nodes have ; moreover, dummy nodes do not increase the objective function because they have the weight set to zero, i.e., any dummy node v will have .
For each node and solution S to MCI in , let . It is easy to see that by applying Algorithm 1 to we obtain an optimal solution with respect to . Moreover, for each solution S to , . Note that a solution S for that connects leaves of to its root is a feasible solution also for T since T and have the same root and leaves.
5. Polynomial-Time Algorithm for DAG with a Single Source or a Single Sink
In this section, we focus on the case of weighted DAGs in which we have a single source node or a single sink node. We first describe our greedy algorithm to approximate MCI on DAGs with a single source. Then, we show how to modify the algorithm for the case of DAGs with a single sink.
In the case of a single source, by using the property of Lemma 2, we restrict our choices to the edges that connect sinks nodes to the source. Let us denote S as the set of edges added to G. With a little abuse of notation, we also use S to denote the set of sinks from which the edges in S start. Note that no information is lost in this way, since we have a DAG with a single source, at most one edge is added for each sink. In fact, if a second edge is added to a sink, this edge would not bring any increase to the objective function.
The Greedy algorithm for MCI on DAGs with a single source (see Algorithm 2), starts with an empty solution and repeatedly adds to S the edge that maximises the function . The edge is chosen from the set of edges , where u is a sink in V, not already inserted in S, and s is the single source in V (see Lines 2 and 4).
To implement the Greedy Algorithm with a single source, some preprocessing is required. First, for each node , we perform a DFS visit on G to compute and . We store in a vector of size . Every time a new edge is added to the solution S, each entry of is updated in constant time because for each node v, is either equal to or , as we explain below. To compute the gain of adding the edge , we need to find all the nodes that reach u in . is computed by performing a DFS visit starting from u on the reverse graph of . Note that the reverse graph of G is initially computed in a preprocessing phase in time, and after every new edge is added to S, is updated in constant time. Finally, to compute for , observe that . After selecting the edge that maximise , we update S and we set for each node in vector because z reaches s traversing the edge and inherits the reachability of .
The Greedy algorithm with a single source requires time. Namely, for each edge , to compute it is required time to compute on , and time to compute . Since there are sinks, the computation of the maximum value at Line 4 costs time. Selected , time is spent to update . Since at most B edges are added, the Greedy algorithm requires .
In the following, we describe the algorithm to compute a solution in the case of DAGs with a single sink. The main differences compared to the previous case mainly concern the preprocessing phase of the algorithm. The greedy algorithm remains the same except that we change the set from which the edges are chosen in the following way: we substitute on Line 2 with the set of edges , where v is a source in V and d is the only sink in V (see Line 2) by Lemma 2.
It is worth noting that, in this case, differently from before, the value of is always equal to V by definition since all the nodes reach the sink, on the other hand, the reachability of a node v does not assume only the values V or . This implies that we it is not required to perform any DFS visit of to compute , in fact, the vicinity of any other node depends on the set of added edges and has to be recomputed each time by performing a DFS visit on the augmented graph. Hence, . Since for computing , we must compute DFS visits, the overall cost of the Greedy algorithm with a single sink increases by a factor of with respect to the case of DAG with a single source, thus becoming . Namely, for each edge , to compute it is required time to compute DFS visits in , one for each node in V, and time to update R and to compute . Since there are sinks, the computation of the maximum value at Line 4 costs time. Then, since at most B edges are added, the Greedy algorithm requires .
Observe that Algorithm 2 that we have just described in the case of a single source can also be used on trees in place of Algorithm 1. However, the complexity of the Greedy algorithm will be that is greater than the complexity of Algorithm 1, which is .
To give a lower bound on the approximation ratio of Algorithm 2, we show that the objective function is monotone and submodular. Recall that, for a ground set N, a function is said to be submodular, if it satisfies the following property of diminishing marginal returns: for any pair of sets and for any element , . This allows us to apply the result by Nemhauser et al. [28]: Given a finite set N, an integer , and a real-valued function z defined on the set of subsets of N, the problem of finding a set such that and is maximum can be approximated by starting with the empty set, and repeatedly adding the element that gives the maximal marginal gain, if z is monotone and submodular.
Recall that and . To prove that is a monotone increasing and submodular function, we just need to show that is monotone increasing and submodular, for each node and solution S. This is due because a non-negative linear combination of monotone submodular functions is also monotone and submodular.
| Algorithm 2: Greedy Algorithm for single source. |
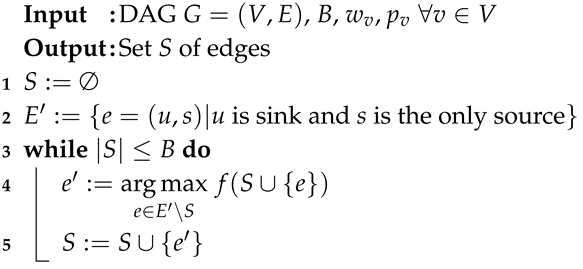 |
Theorem 4.
Function is monotone and submodular with respect to any feasible solution for MCI on DAGs with a single source.
Proof.
To prove that is monotone, we prove that for each , , and , we have .
We first notice that for each node and solution S, if there exists an edge such that , then ; otherwise, . The same holds for .
We analyse the following cases recalling that :
- If there exists an edge such that , then .
- Otherwise:
- −
- If , then and .
- −
- If , then .
It follows that .
To prove that is submodular, we prove that, for any node , any two solutions of MCI such that , and any edge , where is a sink node, it holds:
We analyse the following cases:
- If there exists an edge such that , then, .
- Otherwise,
- −
- If there exists such that , then because .
- −
- If for each , , then and .
In all the cases the inequality in Equation (2) holds. □
Theorem 5.
Function is monotone and submodular with respect to any feasible solution for MCI on DAGs with a single sink.
Proof.
To prove that is monotone, we show that for each , , and , we have . We observe that
Thus, .
To prove that is submodular, we prove that for any node , any two solutions of MCI such that , and any edge , where is a source node:
We first make the following observations based on Equation (3):
- and
Then, and .
The inequality in Equation (4) follows by observing that . □
Corollary 1.
Algorithm 2 provides a -approximation for the MCI problem either on DAG with a single source or with a single sink.
6. Polynomial-Time Algorithm for DAG with Two Sources
In this section, we take a first step in the direction of studying the MCI problem in general DAGs, i.e., multiple sources and multiple sinks, by tackling the special case of weighted DAGs with two source nodes. In the following, we describe an approach that can be easily extended to the case of DAGs with a constant number of sources. However, this approach can be computationally heavy as the number of such sources increases.
We first prove an important property that we exploit to provide a polynomial-time algorithm for this case. The idea is that, if we add an initial edge to the solution, then any other added edge is toward the opposite source node. Using this property, we are able to reduce the number of possible solutions that we have to consider. Furthermore, this allows us to use the greedy algorithm that we proposed in the previous section to solve the problem.
In this section, we improve the notation by defining the two sources and by the sink nodes reachable from source and , respectively. Note that we allow , i.e., the two sources may share sink nodes.
Lemma 3.
Let S be a solution to the MCI problem in a graph with two sources ; then, there exists a solution such that with , and contains at most one edge e directed towards source (, respectively), while all the other edges are directed towards (, respectively).
Proof.
Let us first consider the following case: there exists in S at least one edge connecting a sink in with the source , i.e., edge with . Note that this case is equivalent to connecting a node in to . Now, for any other edge , we prove that we can change such edge to connect to source , i.e., , without decreasing the objective function. In fact, note that, for any node and solution S, we have that can be either equal to , if there exists a path that connect such node to source , or equal to by using edge . Instead, by using edge , we have that any node is able to reach any node in the graph, thus having profit . Therefore, we have that since any node that is able to reach sink in solution actually reaches all the nodes in the graph.
On the other hand, it must be that all edges in S are of the kind with or with , i.e., all the edges from are toward source (, respectively). Let us divide solution S in two subsets: containing all the edges of kind with , and , respectively, with edges of kind with . Then, by changing one edge from in and all the edges in toward we have increased the objective function, since now all the nodes in a path to one of the sources are able to reach any node in the graph. □
The lemma above shows us that we can build a solution for the MCI problem by selecting one initial edge and then we can use the greedy algorithm to choose the rest of the edges. In fact, after we have added the initial edge, we can exploit the algorithm given in Section 5, since the DAG now has only one source node and thus the submodularity holds. The underlying idea for the algorithm is to create different instances by enumerating all possible combination of one initial edge, then, we run the greedy algorithm in each of this instances and we choose the best solution among them. Note that this set of instances is composed by four different kinds of edges: The edges from to (and from to , respectively) and the edges from to (and from to , respectively). In both cases, the algorithm considers (, respectively) as the only source node. Note that, in both cases, we are considering to optimise an MCI instance with only one source node and thus the objective function is monotone and submodular, as proved in Section 5.
Moreover, since our algorithm tries all possible initial edges and then picks the best solution, it must be that the initial edge is also in the optimal solution, otherwise there would another instance with a greater value. Thus, the greedy algorithm gives us the same approximation ratio as before, i.e., , and requires time, in fact note that all the possible instances that the algorithm tries are order of number of nodes, i.e., .
7. Conclusions and Future Works
In this work, we study the problem of improving the reachability of a graph. In particular, we introduce a new problem called the Maximum Connectivity Improvement (MCI) problem: given a directed graph and an integer B, the problem asks to add a set of edges of size at most B in order to maximise the overall weighted number of reachable nodes.
We firstly provide a reduction from the well-known Set Cover problem to prove that the MCI problem is -complete. This result holds even if weights and profits are unitary and the graph contains a single sink node or a single source node. Moreover, via a reduction from the Maximum Coverage problem, we prove that the MCI problem is -hard to approximate to within a factor greater than even in DAGs with a single source or a single sink.
We then propose a dynamic programming algorithm for the MCI problem on trees with a single source that produces optimal solutions in polynomial time. Then, we study the case of DAGs with a single source (or a single sink); in this case, we propose two -approximation algorithms that run in polynomial-time by showing that the objective function is monotone and submodular. Finally, we extend the latter algorithm for DAGs with one source to DAGs with two sources while keeping the same approximation guarantee.
As future works, we plan to extend our approach to general DAGs, i.e., with multiple sources and multiple sinks. Another possible extension is to solve the MCI problem by considering the budgeted version of the problem in which each edge can be added at a different budget cost. The goal is then to find a minimum cost set of pair (sink, source) to which add the edges.
Author Contributions
All authors have equally contributed to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work has been partially supported by the Italian MIUR PRIN 2017 Project ALGADIMAR “Algorithms, Games, and Digital Markets.”
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cordasco, G.; Gargano, L.; Lafond, M.; Narayanan, L.; Rescigno, A.A.; Vaccaro, U.; Wu, K. Whom to befriend to influence people. arXiv 2016, arXiv:1611.08687. [Google Scholar] [CrossRef]
- D’Angelo, G.; Severini, L.; Velaj, Y. Selecting nodes and buying links to maximize the information diffusion in a network. In Proceedings of the 42st International Symposium on Mathematical Foundations of Computer Science, MFCS 2017, Aalborg, Denmark, 21–25 August 2017; Volume 83, pp. 75:1–75:14. [Google Scholar]
- Corò, F.; D’Angelo, G.; Velaj, Y. Recommending Links to Maximize the Influence in Social Networks. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, 10–16 August 2019; pp. 2195–2201. [Google Scholar] [CrossRef]
- Olsen, M.; Viglas, A. On the approximability of the link building problem. Theor. Comput. Sci. 2014, 518, 96–116. [Google Scholar] [CrossRef]
- Papagelis, M. Refining social graph connectivity via shortcut edge addition. ACM Trans. Knowl. Discov. Data (TKDD) 2015, 10, 12. [Google Scholar] [CrossRef]
- Jung, J.; Seo, D.; Lee, J. Counter-Based Broadcast Scheme Considering Reachability, Network Density, and Energy Efficiency for Wireless Sensor Networks. Sensors 2018, 18, 120. [Google Scholar] [CrossRef] [PubMed]
- Corò, F.; D’Angelo, G.; Velaj, Y. Recommending Links to Control Elections via Social Influence. Algorithms 2019, 12, 207. [Google Scholar] [CrossRef]
- Castiglioni, M.; Ferraioli, D.; Gatti, N. Election Control in Social Networks via Edge Addition or Removal. arXiv 2019, arXiv:1911.06198. [Google Scholar]
- Eswaran, K.P.; Tarjan, R.E. Augmentation problems. SIAM J. Comput. 1976, 5, 653–665. [Google Scholar] [CrossRef]
- Demaine, E.D.; Zadimoghaddam, M. Minimizing the Diameter of a Network Using Shortcut Edges. In Proceedings of the 12th Scandinavian Symposium and Workshops on Algorithm Theory (SWAT); Springer: Berlin/Heidelberg, Germany, 2010; Volume 6139, pp. 420–431. [Google Scholar]
- Bilò, D.; Gualà, L.; Proietti, G. Improved approximability and non-approximability results for graph diameter decreasing problems. Theor. Comput. Sci. 2012, 417, 12–22. [Google Scholar] [CrossRef]
- Ianni, M.D.; Gualà, L.; Rossi, G. Reducing the diameter of a unit disk graph via node addition. Inf. Process. Lett. 2015, 115, 845–850. [Google Scholar] [CrossRef]
- Bilò, D. Almost Optimal Algorithms for Diameter-Optimally Augmenting Trees. In Proceedings of the 29th International Symposium on Algorithms and Computation, ISAAC 2018, Jiaoxi, Yilan, Taiwan, 16–19 December 2018; pp. 40:1–40:13. [Google Scholar] [CrossRef]
- Avrachenkov, K.; Litvak, N. The Effect of New Links on Google Pagerank. Stoc. Models 2006, 22, 319–331. [Google Scholar] [CrossRef]
- Meyerson, A.; Tagiku, B. Minimizing Average Shortest Path Distances via Shortcut Edge Addition. In Proceedings of the 13th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX); Springer: Berlin/Heidelberg, Germany, 2009; Volume 5687, pp. 272–285. [Google Scholar]
- Crescenzi, P.; D’Angelo, G.; Severini, L.; Velaj, Y. Greedily improving our own centrality in a network. In Proceedings of the 14th International Symposium on Experimental Algorithms (SEA 2015); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9125, pp. 43–55. [Google Scholar]
- Crescenzi, P.; D’Angelo, G.; Severini, L.; Velaj, Y. Greedily Improving Our Own Closeness Centrality in a Network. TKDD 2016, 11, 9:1–9:32. [Google Scholar] [CrossRef]
- Ishakian, V.; Erdös, D.; Terzi, E.; Bestavros, A. A Framework for the Evaluation and Management of Network Centrality. In Proceedings of the 12th SIAM International Conference on Data Mining (SDM), Anaheim, CA, USA, 26–28 April 2012; pp. 427–438. [Google Scholar]
- Kapron, B.M.; King, V.; Mountjoy, B. Dynamic graph connectivity in polylogarithmic worst case time. In Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2013, New Orleans, LA, USA, 6–8 January 2013; pp. 1131–1142. [Google Scholar] [CrossRef]
- Nanongkai, D.; Saranurak, T.; Wulff-Nilsen, C. Dynamic Minimum Spanning Forest with Subpolynomial Worst-Case Update Time. In Proceedings of the 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, Berkeley, CA, USA, 15–17 October 2017; pp. 950–961. [Google Scholar] [CrossRef]
- Demetrescu, C.; Italiano, G.F. Mantaining Dynamic Matrices for Fully Dynamic Transitive Closure. Algorithmica 2008, 51, 387–427. [Google Scholar] [CrossRef]
- Roditty, L.; Zwick, U. A Fully Dynamic Reachability Algorithm for Directed Graphs with an Almost Linear Update Time. SIAM J. Comput. 2016, 45, 712–733. [Google Scholar] [CrossRef]
- Corò, F.; D’Angelo, G.; Pinotti, C.M. On the Maximum Connectivity Improvement Problem. In Proceedings of the Algorithms for Sensor Systems—14th International Symposium on Algorithms and Experiments for Wireless Sensor Networks, ALGOSENSORS 2018, Helsinki, Finland, 23–24 August 2018; pp. 47–61. [Google Scholar] [CrossRef]
- Tarjan, R. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability, A Guide to the Theory of NP-Completeness; W.H. Freeman and Company: New York, NY, USA, 1979. [Google Scholar]
- Feige, U. A Threshold of Ln N for Approximating Set Cover. J. ACM 1998, 45. [Google Scholar] [CrossRef]
- Tamir, A. An O(pn2). algorithm for the p-median and related problems on tree graphs. Oper. Res. Lett. 1996, 19, 59–64. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Wolsey, L.A.; Fisher, M.L. An analysis of approximations for maximizing submodular set functions—I. Math. Program. 1978, 14, 265–294. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).