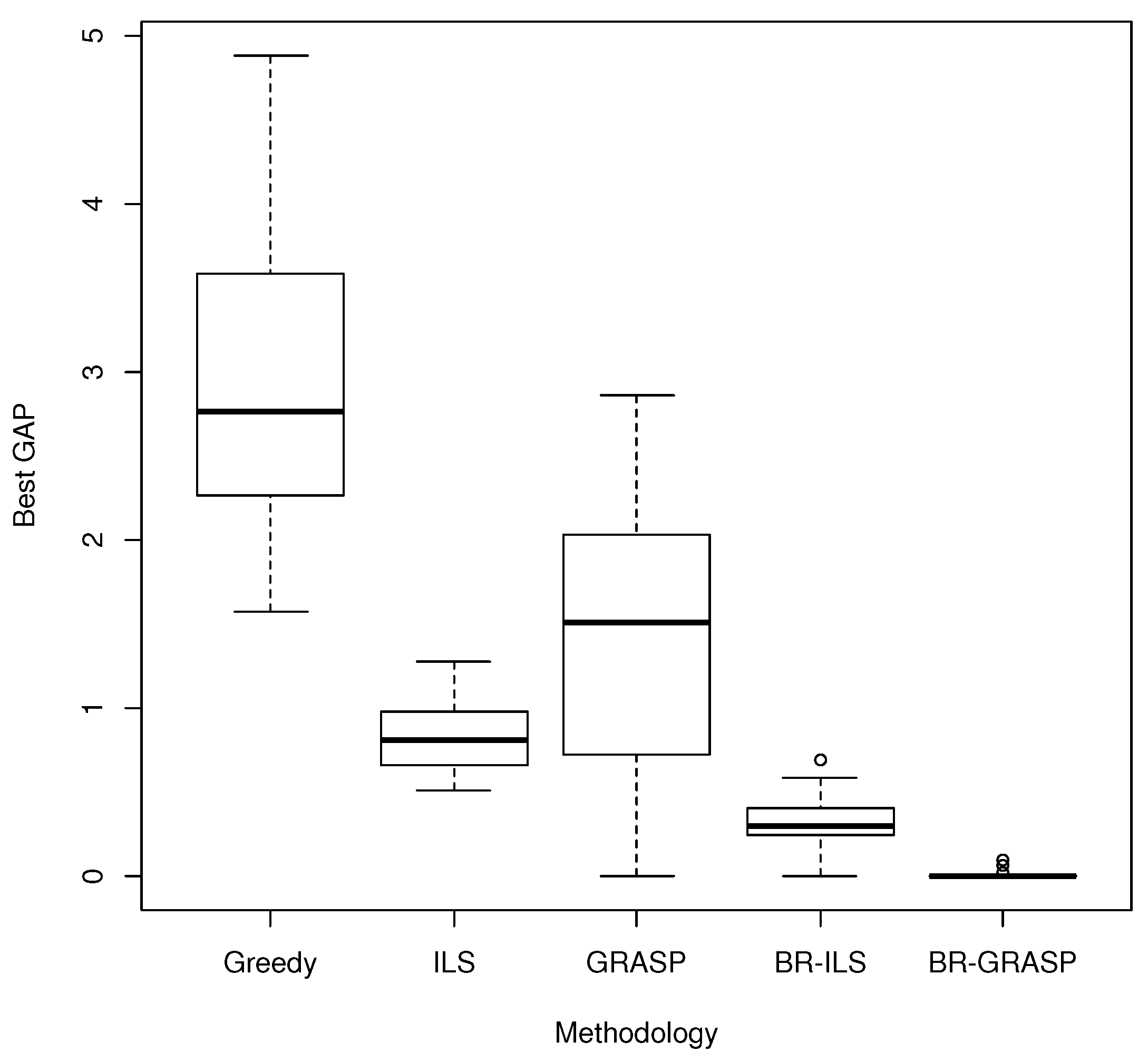1. Introduction
As discussed in Verhoef et al. [
1], customers today are changing the way they decide where, how, and even when to buy. With the rise of Internet-based technologies and mobile devices, different shopping channels have appeared and attracted customers’ attention. Hence, e-commerce not only offers customers the possibility of browsing through different stores in an online environment, but also the ability to get information, opinions, and a vast availability of stock. Omnichannel commerce is a fully-integrated approach to e-commerce that provides customers with a unified experience across different shopping platforms, e.g., a personal computer, a physical retail center, or a mobile device. In an omnichannel environment, retailers at brick-and-mortar stores have to compete with other channels, and especially with the ‘showrooming’ behavior of customers. Showrooming occurs when customers go to a brick-and-mortar store to ‘touch and feel’ the product, but then complete the purchase online. Even when customers are in the position of choosing where and when to buy, most brands still generate a noticeable part of their sales revenue at brick-and-mortar stores, so they play a relevant role in capturing customers’ attention.
One of the strategies used by brick-and-mortar retailers to engage more customers is to offer them a variety of attractive products over a multi-period time horizon, which typically covers several weeks. As pointed out by Galino and Moreno [
2], in order to achieve this goal the retailer needs to decide which combination of products has to be shown at the store, so that the combined attractiveness value is maximized. Some authors define attractiveness as the capacity to cause interest and attract the attention of another party [
3]. According to Ellegaard and Ritter [
4], value creation, interaction process, and emotions define the perceived attractiveness of one actor to another actor. The value creation refers to the potential value, while the interaction process deals with trust and commitment. Finally, emotions are the irrational part of decision making, which is not accessible by rational arguments. In this way, the attractiveness can be seen as an inter-linked concept which combines value, trust, commitment, and satisfaction [
5]. According to Caro and Martínez-de Albéniz [
6], “for many products, consumers tend to make different purchasing decisions over time. For example, most people would usually avoid eating the exact same meal in the exact same restaurant every day. This observed pattern has been called variety-seeking behavior”. The same authors state that “in apparel retailing, part of the success of fast fashion firms such as Zara and H&M relative to the incumbents such as the Gap can be attributed to more frequent assortment rotation, which generates the feeling of novelty among consumers”. Similarly, Caro et al. [
7] studied the concept of product attractiveness in retail stores. In their own words: “carrying a static assortment—one that remains the same over time—becomes ineffective and possibly unprofitable because consumers are quickly bored with the choices within assortment and they divert their purchases to other consumption options. In other words, the customers’ preference for a particular product in the assortment decays over time, as it ages on the shelf”. These authors offer several examples of assortment renewal strategies involving clothing retailers such as H&M and Chico’s. They also discuss similar patterns in industries such as book stores and restaurants, which “frequently change the items on their menu to avoid customer satiation”. A similar concept can be found in Bernstein and Martínez-de Albéniz [
8], who claim that “retailers in industries with short life cycles, such as apparel, have started updating their product offering with significant frequency. In particular, fast-fashion retailers such as Zara or H&M update their assortments periodically to induce frequent visits to their stores”. As exposed in Ferreira and Goh [
9], “assortment rotation… has recently been used by both brick-and-mortar and online retailers as a strategy for gaining competitive advantage. A notable category of retailers who have employed this strategy successfully are fast-fashion retailers such as Zara and H&M, who have differentiated themselves from other retailers by rotating their assortment multiple times throughout the fashion industry standard 6-month selling season”. All in all, the attractiveness value of some products might decay as they are repeatedly displayed. Hence, the retailer must release new products. Similarly, if customers see the same products exposed in a store during several consecutive time periods (days or weeks), their willingness to visit that store will decrease. Accordingly, some popular retailers introduce new products into their stores almost on a daily basis. These dependencies across periods are considered in our work, which constitutes one of the main original contributions of our approach. Schnurr et al. [
10] addresses novelty, placement, and consumers’ opinions as essential factors on the definition of product attractiveness: (i) unfamiliar—or new—products are perceived as more attractive and, consequently, of higher quality when placed in an attractive context; and (ii) the higher the attractiveness score of a product, the higher are the consumers’ intentions to purchase it. In this work, given a product included in a display table, we define its individual attractiveness value as the probability that the product captures the attention (e.g., is selected and analyzed) of a standard customer visiting the shop. Being a probability, it will always be a value between 0 and 1 (or, equivalently, a score between 0 and 100). Attractiveness can also be measured by visual properties, and this is directly related to the existence of correlation between pairs of products (e.g., products that are complementary or substitute). Thus, retailers have to take into account customers’ purchases that occur in channels other than brick-and-mortar stores. Apart from experts’ opinion, a large amount of data can be obtained from customers’ behavior and preferences in an omnichannel environment. These data can provide retailers with vital information, such as which products generate a higher attraction level among customers of a certain retail store. Hence, identifying the best assortment of products to display has to be made considering customers’ preferences [
11]. Selling strategies for retail stores should have the ability to offer customers a set of different surprising experiences. Using display tables to suggest a set of correlated articles in retail stores is one way to achieve the aforementioned goal. In the apparel sector, for example, a yellow sweater may be positively correlated with a white pair of jeans but negatively correlated with orange trousers (since yellow and orange are not colors that match according to certain fashion trends). Likewise, a skirt might be positively correlated with a top and negatively correlated with a pair of jeans, since both cloth pieces are bottom parts. Again, these dependencies across items should be considered. In practice, data gathered in an omnichannel database could be one of the most efficient ways to determine the correlations between pairs of products.
The problem of selecting, over a multi-period horizon, the most attractive configuration of products to be displayed in a limited space (e.g., a physical table at the store, an advertising brochure, or a website front page), is related to well-known problems such as the product recommendation problem [
12], the shelf space allocation problem [
13], and the assortment problem [
14].
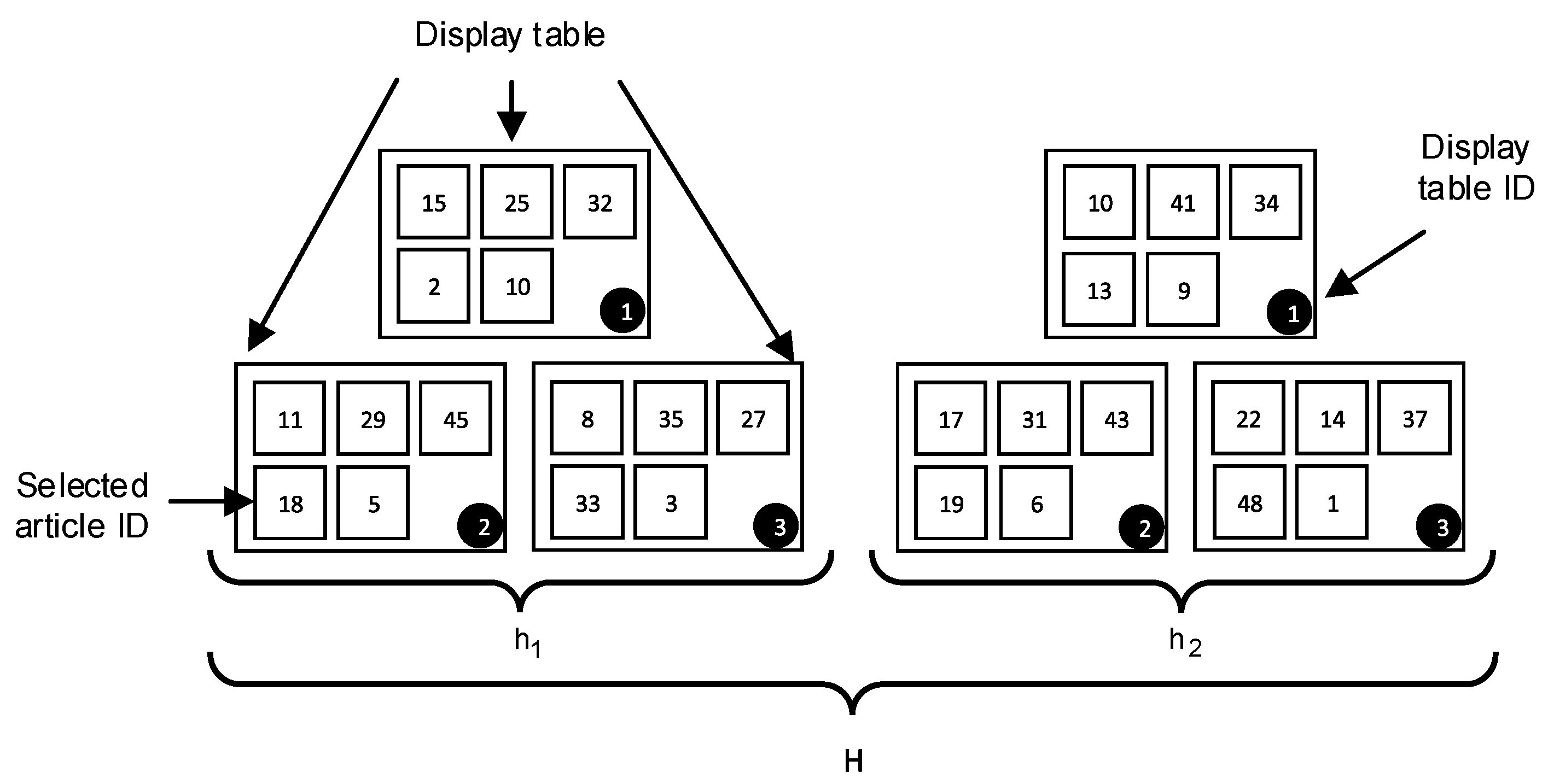
Figure 1 shows a simple example to illustrate the product display problem and its possible solutions. In this case, the solution consists of a 2-period time horizon. In each period, there are 3 display tables with a capacity of 5 items each. Each display table and item is represented by its identifier (ID). Hence, for instance, in period
, display table 2 will be composed of items 11, 29, 45, 18, and 5.
When selecting a set of products to be displayed, one should always consider customer preferences and willingness to buy [
15]. Current online display systems provide a list of products that are either based on the user’s past behavior or on decisions made by similar users. This strategy has been widely applied in e-commerce, where it has generated raised sales as well as customer satisfaction [
16]. Companies such as Amazon use a method called collaborative filtering. Here, ratings and purchases made by similar users are considered to suggest products to online customers [
17]. This product selection problem is also relevant for brick-and-mortar stores, since they might benefit from an optimal selection of products to be displayed over a multi-period time horizon. The main contributions of this paper are described next: (i) a novel mathematical formulation for the multi-period product display problem with dynamic attractiveness levels is proposed in order to clearly define the problem under consideration—while analyzing a case study, the assumptions of this model were discussed with professionals of the retail sector, who were also students in an MBA offered at our business school—(ii) in order to solve this optimization problem in the context of a retail store with several display tables, biased-randomized (BR) versions of the greedy randomized adaptive search procedure (GRASP) and the iterated local search (ILS) are introduced; (iii) a set of novel benchmark instances, considering realistic constraints and different product characteristics, is proposed to test the quality of our approach when compared with non-linear solvers; and (iv) based on the outcomes of our experiments, a series of practical recommendations are provided. A complete introduction to biased-randomization techniques can be found in Grasas et al. [
18]. A review of GRASP algorithms can be found in Festa and Resende [
19], while a description of the ILS metaheuristic framework can be found in Lourenço et al. [
20]. Finally, a recent study on the combination of biased-randomization techniques with GRASP is available in Ferone et al. [
21]. Regarding the constraints considered in this work, they include diversity of fashion collections, selling-price categories, and marginal-profit categories. Likewise, dependencies across both periods and items are considered in our study. The rest of the paper is arranged as follows:
Section 2 presents a literature review of related research;
Section 3 describes the problem in more detail and provides a mathematical formulation for it;
Section 4 introduces the proposed biased-randomized algorithms;
Section 5 includes an explanation of the computational experiments carried out to test the quality of our approach, while
Section 6 contains an analysis of the results; finally,
Section 7 highlights the main conclusions of this work and proposes some lines for future research.
3. A Formal Description of the Multi-Period Product Display Problem
Consider a warehouse holding a set of products or items. It has to supply a retail store for different time periods, which define the planning horizon. Each item belongs to a certain collection (e.g., shirts or jeans in the case of clothes), has a selling price—which might vary with time—and a marginal profit—which is typically given as a percentage of the selling price. Depending on its selling price, an item is classified as ‘expensive’ or not. In any given period the retail store contains a set of tables, each of them displaying a subset of non-repeated items. Each item has an initial attractiveness value, estimated from experts’ opinions and/or historical observations in an omnichannel environment—such as the number of times it has been selected and analyzed in the past, the feedback provided by the customers, etc. The attractiveness value can also depend upon other items currently being displayed in the table, since relations (or dependencies) between pairs of products may need to be considered.
Among all the available products in the warehouse, a subset of different items should be selected to be displayed on the retail display tables. The dependency between each pair of items is registered in a dependency matrix. An inter-period dependency is also considered. The attractiveness value of each item is reduced by a known quantity (typically expressed as a percentage) every time the product is repeatedly shown in two (or more) consecutive periods. In other words, if an item is repeatedly exposed during several consecutive periods of time, its novelty disappears and, as a consequence, its attractiveness value is reduced. On the other hand, whenever an item has not been shown in the previous period, its attractiveness value is increased due to the novelty effect. The goal is then to solve a multi-period product display problem with dynamic attractiveness levels. In this problem, a subset of items has to be selected to be displayed at each table-period combination in order to maximize the aggregated attractiveness level over all periods. In order to make the problem more realistic, a number of additional constraints are also considered in this paper:
Collection constraint: the subset of items assigned to each table should cover at least a minimum number of goods from each collection, .
Price constraint: a minimum number of products at each table, , should belong to the expensive category.
Profit constraint: the profit margin of each table should be greater than a threshold defined by the manager, .
A set of consecutive time periods H is considered, together with a finite set of items, I, which are hosted in a warehouse. Each item is associated with a base price , a marginal benefit (which might be different at each period ), and an initial attractiveness value . The final selling price of each item at period is given by , i.e., . These items belong to a set of collections , where . The subset of expensive items is given by , where is a threshold price value defined by the manager.
At each period
, a subset
items must be exposed using a set of homogeneous tables
T, with each table containing a total of
items. The decision variable
is equal to 1 if item
i is selected for table
t in period
h, and to 0, otherwise. Thus, the set of non-repeated selected items for each table
in period
is given by
, being
. A matrix
provides the existing interaction value,
, between any pair of items
. These intra-period dependencies account for the fact that some items might be positively or negatively correlated with others (i.e., showing them together might generate synergies or, on the contrary, might reduce their aggregated attractiveness). Apart from this intra-period dependencies between pairs of items, inter-period dependencies are also considered to account for the product’s novelty (or the lack of it). Accordingly, the attractiveness value of every item is a dynamic input, i.e., it is reduced or increased by a certain percentage factor depending on whether the item was displayed or not in the previous period. Thus,
, the attractiveness value of item
i in period
h,
, is recursively defined as:
where
are bounds for the attractiveness values and
are decreasing or increasing percentage factors, respectively.
With this notation, the addressed problem can be formulated as follows:
The objective function (
1) maximizes the total attractiveness of the planning horizon by considering the individual attractiveness of the items and the intra-period dependencies between each pair of selected items in each displaying table and period. Equation (
2) ensures that the number of items on each table
does not exceed a pre-defined value
n. Equation (
3) guarantees that each item
i cannot be selected more than once in a given period
. Equation (
4) confirms that, inside each period, each table covers at least
items from each collection
. Equation (
5) guarantees that, inside each period, each table contains at least
expensive items. Equation (
6) ensures, for each period, that the profit margin of each table should be greater than
. Equation (
7) introduces the inter-periods dynamic component in the attractiveness value of the items. Notice that this equation transforms the objective function into a non-smooth one due to the definition of the
values. Equation (
8) states that all decision variables are binary. Finally, Equation (
9) bounds the values that variable
can take. A ‘relaxed’ version of this problem can be obtained when no bounds are imposed on the attractiveness values of each item. In that case, the objective function becomes quadratic since Equation (
10) can be rewritten as:
4. Our BR-GRASP and BR-ILS Solving Approaches
In this paper, biased-randomized versions of the well-known GRASP [
45] and the ILS [
20] metaheuristics are proposed to solve the multi-period product display problem with dynamic attractiveness. Both algorithms consist of some common stages: (i) a construction stage, in which a feasible initial solution is built taking into account the constraints; and (ii) an improvement stage, in which a local search is applied to the initial solution in order to enhance its quality. Apart from these two common stages, the ILS incorporates a perturbation phase and an acceptance criterion phase. As discussed in Resende and Ribeiro [
46] and Grasas et al. [
47], both GRASP and ILS are relatively easy-to-implement and flexible metaheuristic frameworks that have shown their efficiency in solving different optimization problems, including both deterministic and stochastic ones. They typically do not require many parameters or time-consuming fine-tuning processes. The previous properties make them especially suitable for industrial applications. Moreover, they have been successfully combined with biased-randomization techniques in multiple occasions [
21,
48,
49,
50].
In the BR-GRASP approach, a solution is built iteratively, element by element, and then improved via a local search procedure. This two-step process is repeated until a number of iterations (or a maximum running time) is reached. Then, the best-found solution is returned. On the other hand, the BR-ILS starts from a base solution, which is repeatedly perturbed (modified using a destruction-reconstruction process), enhanced via a local search procedure, and finally evaluated by an acceptance criterion until a stop condition is met. In both the BR-GRASP and the BR-ILS, a partial solution is constructed for each new period (taking into account the current configuration of the display tables). Then, this partial solution is improved through a local search procedure. The low-level details of these algorithms are provided next.
4.1. Introducing BR into GRASP and ILS
The use of Monte Carlo sampling techniques to enhance the performance of constructive heuristics was proposed by Faulin and Juan [
51]. In our approach, more advanced biased-randomized techniques—based on the use of a geometric probability distribution—are used every time a new solution is constructed or partially reconstructed after a perturbation phase. BR techniques differ from standard selection strategies, which are usually based on a greedy criterion or on the use of a uniform probability distribution to select the next candidate from a list. Thus, for example, in a classical GRASP framework, a restricted list of candidates (RLC) is considered, and a uniform probability distribution is used to choose a candidate from this RLC. However, in a BR-GRASP, an unrestricted candidate list (UCL) is employed. This UCL is sorted according to some logical criterion, and a geometric distribution is used to select the next element from this sorted UCL [
21]. The geometric distribution uses a single parameter,
, which is proportional to the probability of selecting the first element in the UCL. All elements in the UCL receive a probability of being selected, which is higher the closer the element is to the top of the sorted UCL. The same concept is also employed during the solution–construction processes inside our BR-ILS algorithm.
Pseudocode 1 illustrates this solution-construction process. All items (set
I) are included in the UCL, which is sorted in descending order according to the ‘adjusted’ attractiveness value of each item, i.e., the original attractiveness value in the corresponding period is corrected to consider dependencies with respect to other items already in the display table. Then, the geometric distribution is used to randomly build a solution by selecting one ‘promising’ item at a time. Once selected, the element is removed from the UCL, the adjusted attractiveness values and profit margin of the remaining elements are updated, and the UCL is sorted again.
| Pseudocode 1: Construction stage with biased randomization. |
![Algorithms 13 00034 i001 Algorithms 13 00034 i001]() |
The efficiency of similar BR strategies has been extensively discussed in different studies, such as Dominguez et al. [
52], Dominguez et al. [
53], Juan et al. [
54], and Martin et al. [
55].
4.2. Constructing an Initial Solution for the Current Period
For each period in the planning horizon, an initial solution is built by adding products to the display tables. We assume that these tables are empty at the beginning of the period. Each product is assumed to have an initial attractiveness value at the beginning of the first period. This attractiveness value is based on historical observations and, possibly, expert judgment.
Using the BR strategy previously described, a subset of items is assigned to a given display table. First, a subset is built by selecting n products for table t in period h. At this point, the collection constraint is incorporated into the construction procedure by selecting a minimum number of items from each collection. Next, the price-related constraint and the profit-margin constraint are checked for the subset. If both constraints are satisfied, the next table is considered. Otherwise, the solution is repaired. During the repair process, an item is randomly selected from and replaced by another item not in . In the case of the price constraint, for instance, this swapping process is based on the replacement of items from one price category (e.g., non-expensive) by products belonging to another one (e.g., expensive). In the case of the profit-margin constraint, the swapping process is based on the replacement of items with a low-profit margin by products with a high-profit margin. This process is repeated until a feasible configuration of tables is eventually achieved for the current period. After obtaining a feasible configuration for the current period, an improvement stage is applied as described next.
4.3. Improving the Solution of the Current Period
Pseudocode 2 illustrates the improvement procedure applied to each table in the current period. It starts from the first table
t in the given period
h. An item
i is randomly selected from
t and removed. Then it is replaced by another randomly-selected item
among those that can be inserted without violating any constraint. As a result, a new table
is generated. The adjusted attractiveness value of
is updated taking into account the dependencies between pairs of items. If the adjusted attractiveness value of
is greater than that of
t, the latter table is updated and the counter is reset. Otherwise, another item is randomly chosen until a maximum number of iterations is achieved without any improvement. The same process is applied to the remaining tables in the current period
h. At each iteration of the constructive procedure, the articles’ attractiveness and profit margins are conveniently updated for the next periods of the planning horizon.
| Pseudocode 2: Improving the configuration of tables in period h. |
![Algorithms 13 00034 i002 Algorithms 13 00034 i002]() |
4.4. Perturbation Stage in the BR-ILS
Both the construction of an initial solution and the improvement process are employed in the BR-GRASP and the BR-ILS. However, the BR-ILS also makes use of a base solution which is modified via a perturbation stage. In our case, the perturbation is characterized by a destruction-reconstruction process as described in Pseudocode 3. After selecting a starting period, , all posterior periods are destroyed and then re-built, using the previously described constructive and improvement stages.
The starting period is chosen according to a varying percentage of destruction,
. Hence, for example, if
then the last
of the periods are destroyed and reconstructed (due to the dependencies across periods, if a period is rebuilt all posterior periods need to be recomputed).
| Pseudocode 3: Perturbation stage |
![Algorithms 13 00034 i003 Algorithms 13 00034 i003]() |
4.5. Acceptance Criterion Stage in the BR-ILS
Finally, the ILS metaheuristic also incorporates an acceptance criterion to reduce the probability of getting trapped in a local minimum (Pseudocode 4). In our case, we use the demon-based acceptance criterion described in Juan et al. [
56]. In this criterion, newly generated solutions are compared with the base solution, and the former is updated in two cases: (i) when the new solution is better than the base solution; or (ii) when the new solution is worse than the base solution, but the difference in value is lower than the improvement (credit) obtained in the last update of the base solution.
| Pseudocode 4: Credit-based acceptance criterion. |
![Algorithms 13 00034 i004 Algorithms 13 00034 i004]() |
5. Computational Experiments
This section describes the experimental setup designed to evaluate the performance of our BR-GRASP and BR-ILS algorithms. To the best of our knowledge, this is the first work solving a rich and realistic version of the multi-period product display problem with dynamic attractiveness. Hence, we had to generate a complete set of benchmarks with different characteristics to comprehensively evaluate and test the proposed algorithms. These characteristics are: number of articles (), number of display tables (), number of collections (), and number of items per display table (n).
For small-sized instances (aimed at being solved using non-linear exact methods), we set
,
,
,
, and
. Each of these instances was named according to these specifications. Thus, for example, instance 75i-5c-4p-4t-6it consists of 75 items, 5 collections, 4 periods, 4 tables per period, and 6 items per table. Similarly, for the large-sized instances we set
,
,
,
, and
. Each of these instances was named according to these specifications. Thus, for example, instance a500m5i1 consists of 500 products and 5 tables. The last index represents different instances using the same combination of items and tables. For the purpose of numerical experimentation, most of the specific inputs in these instances (e.g., initial attractiveness values, dependencies between pairs of products, item prices, and associated collection) have been randomly generated. In order to facilitate reproducibility of the experiments, all these instances and inputs are publicly available at
https://www.researchgate.net/publication/330675091_instancesMPPDPDA.
Although all input data is available in the previous link, an overview of these inputs is provided next for the case of the large-sized instances. The final selling price of each product is generated according to a uniform distribution in the range (monetary units). The profit-margin percentage for each product follows a uniform distribution in the range . The price and profit margin are considered to generate the absolute profit, which is used to check whether the respective constraints are satisfied. The initial attractiveness value for each item and the between-items dependencies are generated according to a uniform distribution in the range and , respectively. Regarding the considered constraints, the subset of selected products at each table should cover at least of each collection. Regarding prices, the items are categorized into two different categories: those with a cost inferior to 60 monetary units are considered as non-expensive items. The rest are considered expensive. In our experiments, we required that the selected subset at each table should include at least of expensive products. Finally, for each table, the profit margin per table is set at 100 monetary units or more. To account for the ‘novelty factor’, when a product is displayed on a table during a given period, its attractiveness value is decreased by for the next period (always considering that the minimum attractiveness value that a product can reach is bounded by the modeling parameter ). Conversely, if a product is not displayed at a given period, its attractiveness value increases by for the next period (up to a maximum value given by the modeling parameter ).
After some initial tests, a geometric probability distribution with a parameter randomly chosen in the interval was used for the biased-randomization process during the solution-construction stage. The stopping criterion for the BR-GRASP and BR-ILS is defined by a maximum computing time, , defined as: . In practice, this represents approximately 15 seconds of execution for instances composed of 500 articles, 5 tables, and a planning horizon of 12 days, for example. Regarding the improvement stage, the stopping criterion is set to iterations without observing any improvement. Our algorithms were coded in Java and run on a standard PC with an Intel Core i5 CPU at 2.7 GHz and 8 GB RAM.
Table 2 and
Table 3 summarize the experimental setup and parameters for the computational experiments. Note that a new parameter,
r, is introduced. This parameter refers to the percentage of profit margin (and price) reduction in specific sales periods.
7. Conclusions
Increasing levels of competitiveness among brands as well as among channels of the same brand make it difficult for retailers in brick-and-mortar stores to engage customers while in the shop. One of the ways to attract them to the stores is to offer a different experience and a factor of surprise. Displaying a set of correlated and attractive products on retail display tables that vary often is a promising way to engage customers with a pleasant experience. From a managerial perspective, being able to know the selection of products that maximizes the attractiveness level enables a rationalization of the stock available in the store. Moreover, reducing the time required to make these decisions might significantly increase the productivity of the managers in charge of them.
In this paper, we propose a rich and realistic multi-period product display problem, as well as biased-randomized algorithms that allow us to solve it in an efficient way. In the considered problem, a set of correlated products has to be selected over multiple periods of time in order to maximize the total attractiveness level of the display tables in a retail store. A number of realistic characteristics and constraints have been incorporated in the problem to increase the potential applications of our work. Some of these are: (i) the inclusion of both expensive and non-expensive products on each display table and horizon; (ii) the achievement of a minimum profit margin per table and horizon; (iii) the consideration of dynamic (novelty-based) and correlated (combination-based) attractiveness levels; and (iv) the consideration of dynamic selling prices.
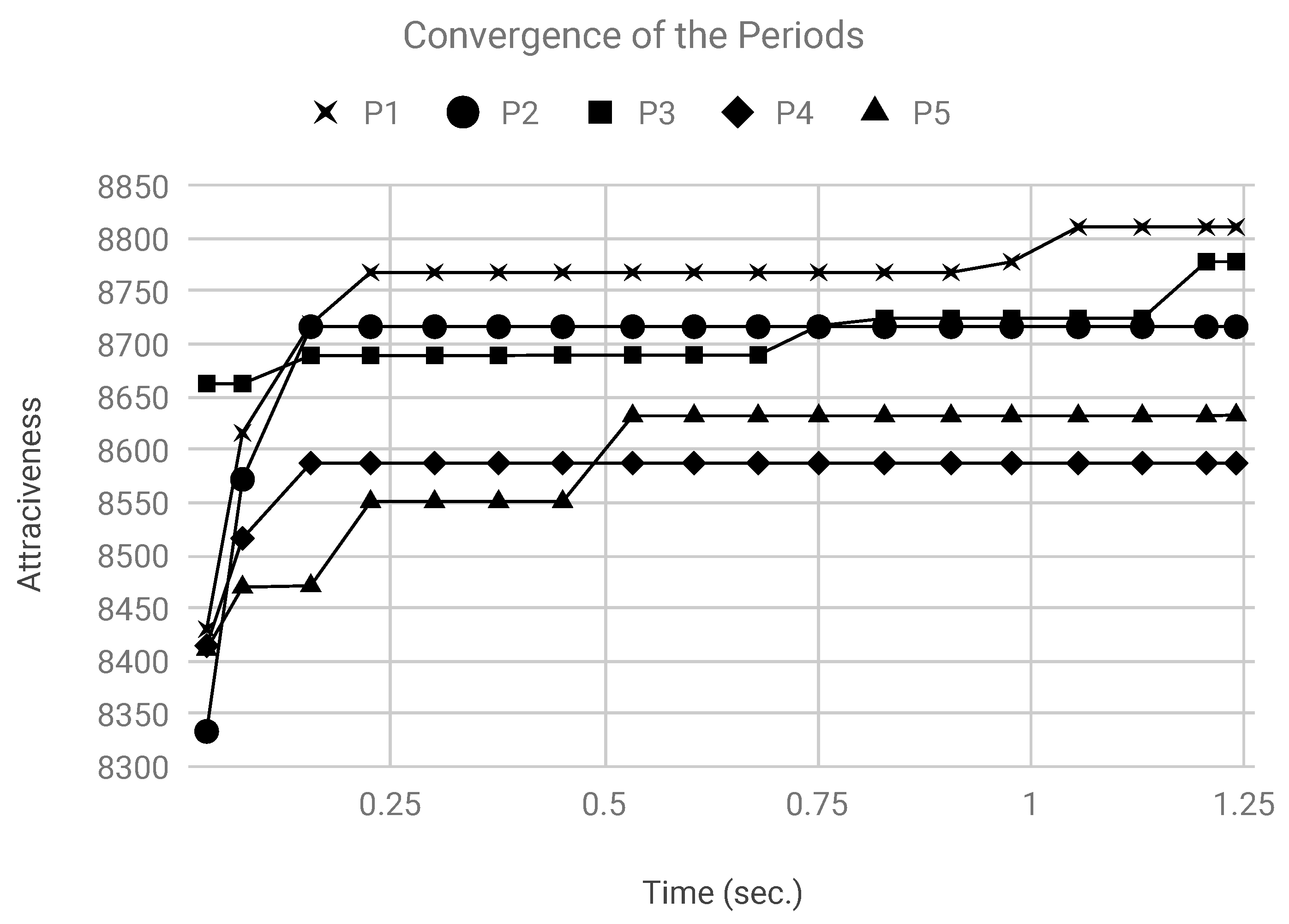
As solution approaches, a biased-randomized GRASP and a biased-randomized ILS have been proposed. To test these methodologies, a complete set of instances was generated by considering realistic assumptions and different design factors. In our approach, it is assumed that the attractiveness value of each product can be estimated using historical data obtained from an omnichannel environment. The experimental results show that both biased-randomized methodologies are able to provide, in short computing times, solutions that clearly outperform the human-behavior and other more standard methodologies. Additionally, a numerical study has shown that our biased-randomized algorithms are very competitive when compared with non-linear solver engines, obtaining better or similar solutions in much shorter computing times.
By increasing the attractiveness level of retail display tables in a short time horizon, managers can reduce customer attrition and, as a consequence, increase sales revenue in their stores. Using biased-randomized algorithms to maximize the attractiveness of products assigned to display tables in the considered scenario represents a clear enhancement over current practice, which might typically require many hours of a dedicated expert to generate even a feasible solution.