Sine Cosine Algorithm Assisted FOPID Controller Design for Interval Systems Using Reduced-Order Modeling Ensuring Stability
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Order Calculus
2.2. Fractional-Order PID (FOPID) Controller
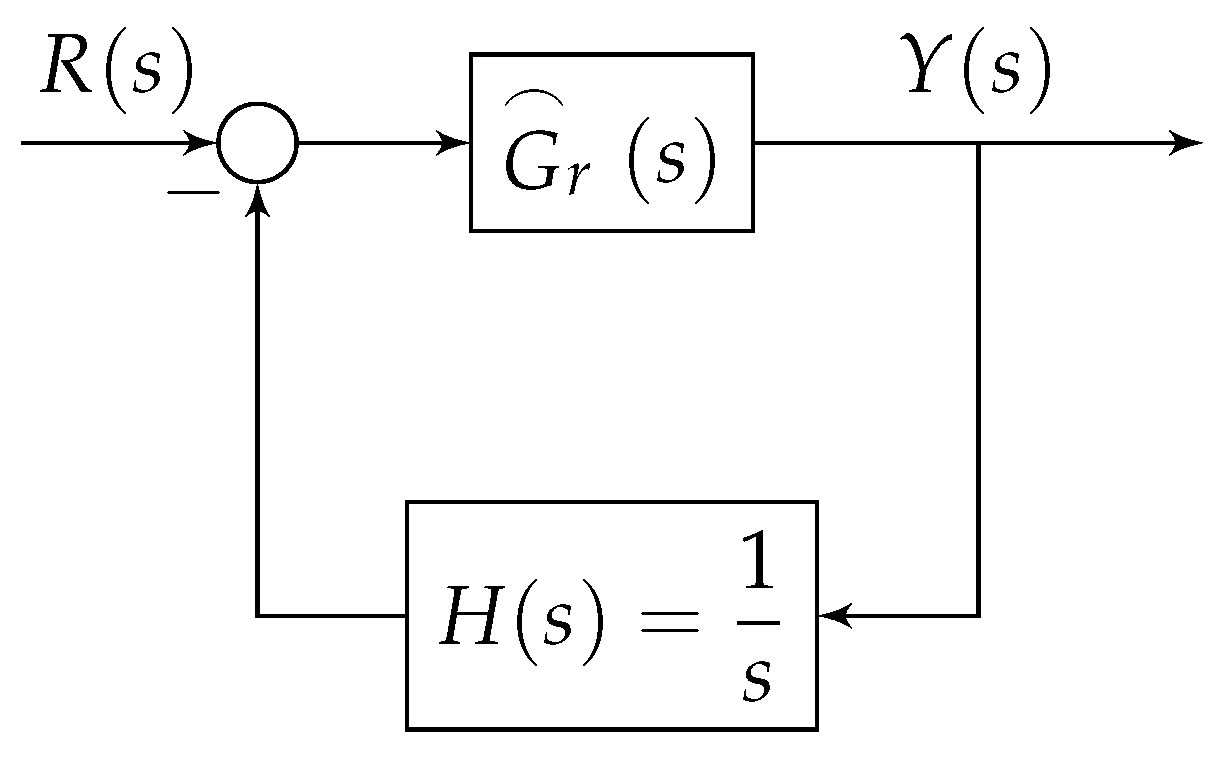
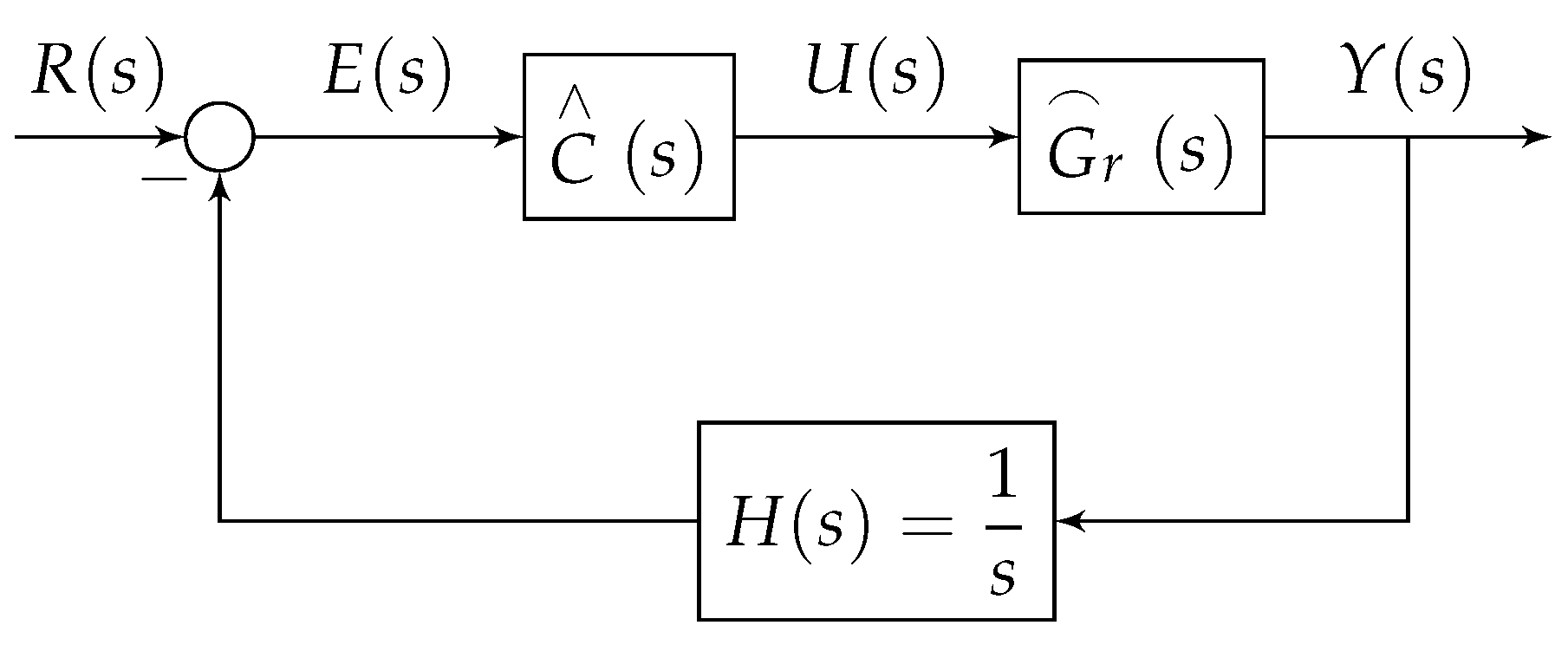
3. Problem Formulation
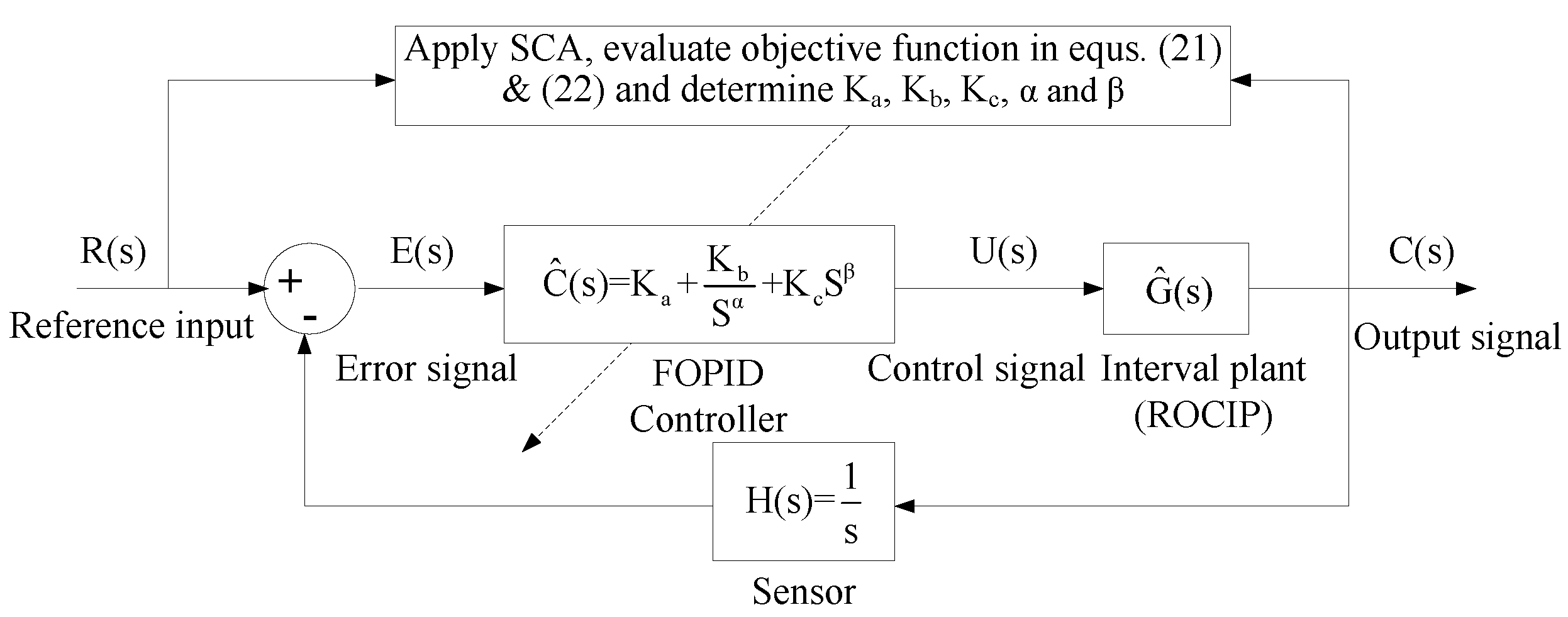
4. Design of FOPID Controller
4.1. Description of Fractional Order Controller Based on Bode Envelope
5. Brief Description of Reduction Method for HOCIP
5.1. Procedure for Denominator
5.2. Procedure for Numerator
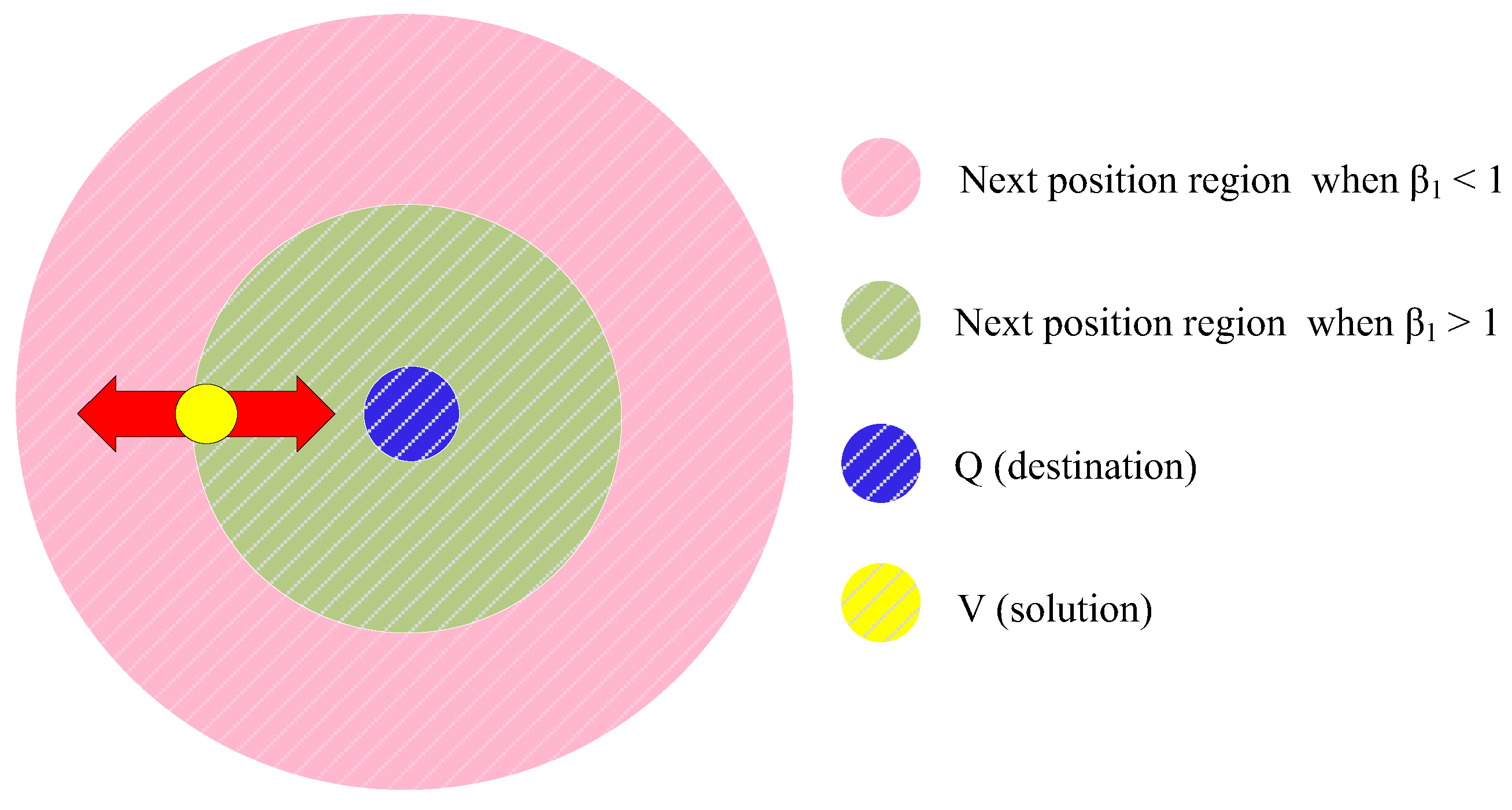
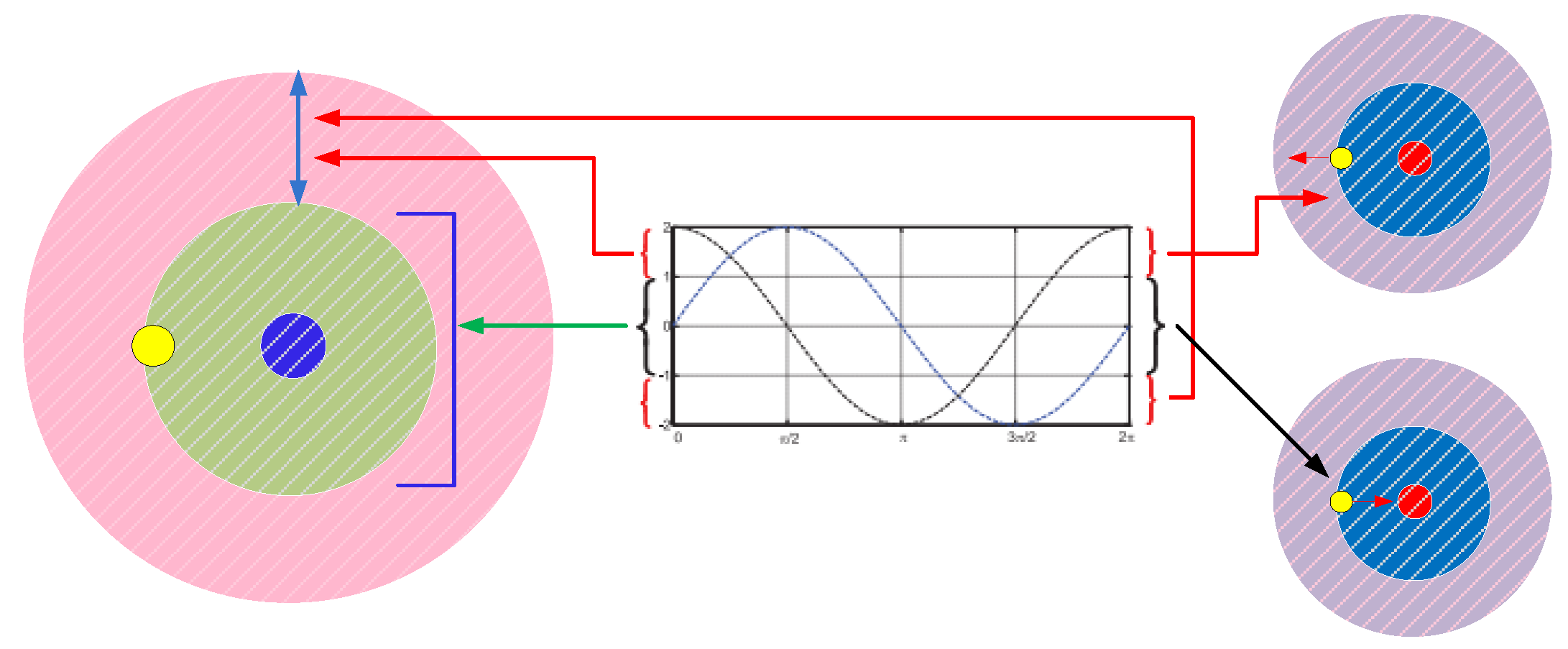
6. Sine-Cosine Algorithm (SCA)
7. Test System
7.1. Improved Routh–Pade Approximation Method
7.1.1. Calculation of Denominator
7.1.2. Calculation of Numerator
7.2. Design of FOPID Controller
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOPID | fractional-order proportional-integral-derivative |
| PM | phase margin |
| MPs | Markov parameters |
| TMs | time moments |
| ROCIP | reduced-order continuous interval plant |
| HOCIP | high-order continuous interval plant |
| SCA | sine-cosine algorithm |
| SISO | single-input-single-output |
| MIMO | multi-input-multi-output |
| PID | proportional-integral-derivative |
| IOPID | integer-order proportional-integral-derivative |
| AVR | automatic voltage regulator |
| MOR | model order reduction |
| ISE | integral-square-error |
| PSO | particle swarm optimization |
| RL | Riemann–Liouville |
| GL | Grunwald–Letnikov |
References
- Cruz-Zavala, E.; Moreno, J.A. Homogeneous high order sliding mode design: A Lyapunov approach. Automatica 2017, 80, 232–238. [Google Scholar] [CrossRef]
- Almabrok, A.; Psarakis, M.; Dounis, A. Fast Tuning of the PID Controller in An HVAC System Using the Big Bang–Big Crunch Algorithm and FPGA Technology. Algorithms 2018, 11, 146. [Google Scholar] [CrossRef]
- Yang, G.; Yi, H.; Chai, C.; Huang, B.; Zhang, Y.; Chen, Z. Predictive current control of boost three-level and T-type inverters cascaded in wind power generation systems. Algorithms 2018, 11, 92. [Google Scholar] [CrossRef]
- Singh, S.; Singh, V.; Singh, V. Analytic hierarchy process based approximation of high-order continuous systems using TLBO algorithm. Int. J. Dyn. Control. 2019, 7, 53–60. [Google Scholar] [CrossRef]
- Nguyen, V.G.; Guo, X.; Zhang, C.; Tran, X.K. Parameter Estimation, Robust Controller Design and Performance Analysis for an Electric Power Steering System. Algorithms 2019, 12, 57. [Google Scholar] [CrossRef]
- Caponetto, R.; Machado, J.T.; Murgano, E.; Xibilia, M.G. Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy 2019, 21, 876. [Google Scholar] [CrossRef]
- Singh, V.P.; Chandra, D. Model reduction of discrete interval system using dominant poles retention and direct series expansion method. In Proceedings of the 2011 5th International Power Engineering and Optimization Conference, Shah Alam, Selangor, 6–7 June 2011; pp. 27–30. [Google Scholar]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, Q. Stability analysis of fractional-order Hopfield neural networks with discontinuous activation functions. Neurocomputing 2016, 171, 1075–1084. [Google Scholar] [CrossRef]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y. Tuning and auto-tuning of fractional order controllers for industry applications. Control. Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y. Continuous fractional-order zero phase error tracking control. ISA Trans. 2018, 75, 226–235. [Google Scholar] [CrossRef]
- Magin, R.; Ovadia, M. Modeling the cardiac tissue electrode interface using fractional calculus. J. Vib. Control. 2008, 14, 1431–1442. [Google Scholar] [CrossRef]
- Lassoued, A.; Boubaker, O. Dynamic analysis and circuit design of a novel hyperchaotic system with fractional-order terms. Complexity 2017, 2017. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. Comparison of PID and FOPID controllers tuned by PSO and ABC algorithms for unstable and integrating systems with time delay. Optim. Control. Appl. Methods 2018, 39, 1431–1450. [Google Scholar] [CrossRef]
- Pitolli, F. A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems. Algorithms 2019, 12, 156. [Google Scholar] [CrossRef]
- Saleem, O.; Awan, F.G.; Mahmood-ul Hasan, K.; Ahmad, M. Self-adaptive fractional-order LQ-PID voltage controller for robust disturbance compensation in DC-DC buck converters. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2718. [Google Scholar] [CrossRef]
- Alamdar Ravari, M.; Yaghoobi, M. Optimum design of fractional order pid controller using chaotic firefly algorithms for a control CSTR system. Asian J. Control. 2019, 21, 2245–2255. [Google Scholar] [CrossRef]
- Debbarma, S.; Saikia, L.C.; Sinha, N. Automatic generation control using two degree of freedom fractional order PID controller. Int. J. Electr. Power Energy Syst. 2014, 58, 120–129. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and fractional-order controllers. Inst. Exp. Phys. Slovak Acad. Sci. Kosice 1994, 12, 1–18. [Google Scholar]
- Aghababa, M.P. Optimal design of fractional-order PID controller for five bar linkage robot using a new particle swarm optimization algorithm. Soft Comput. 2016, 20, 4055–4067. [Google Scholar] [CrossRef]
- Mohsenipour, R.; Fathi Jegarkandi, M. Robust stability analysis of fractional-order interval systems with multiple time delays. Int. J. Robust Nonlinear Control. 2019, 29, 1823–1839. [Google Scholar] [CrossRef]
- Azarmi, R.; Tavakoli-Kakhki, M.; Fatehi, A.; Sedigh, A.K. Robustness analysis and design of fractional order Iλ Dμ controllers using the small gain theorem. Int. J. Control. 2020, 93, 449–461. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S. Robust fractional-order PID controller tuning based on Bode’s optimal loop shaping. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Saidi, B.; Amairi, M.; Najar, S.; Aoun, M. Bode shaping-based design methods of a fractional order PID controller for uncertain systems. Nonlinear Dyn. 2015, 80, 1817–1838. [Google Scholar] [CrossRef]
- Bhookya, J.; Jatoth, R.K. Optimal FOPID/PID controller parameters tuning for the AVR system based on sine–cosine-algorithm. Evol. Intell. 2019, 12, 725–733. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Khezri, R.; Oshnoei, A.; Tarafdar Hagh, M.; Muyeen, S. Coordination of heat pumps, electric vehicles and AGC for efficient LFC in a smart hybrid power system via SCA-based optimized FOPID controllers. Energies 2018, 11, 420. [Google Scholar] [CrossRef]
- Kumar, M.S.; Begum, G. Model order reduction of linear time interval system using stability equation method and a soft computing technique. Adv. Electr. Electron. Eng. 2016, 14, 153–161. [Google Scholar] [CrossRef]
- Singh, V.; Chauhan, D.P.S.; Singh, S.P.; Prakash, T. On time moments and Markov parameters of continuous interval systems. J. Circuits Syst. Comput. 2017, 26, 1750038. [Google Scholar] [CrossRef]
- Choudhary, A.K.; Nagar, S.K. Order reduction techniques via Routh approximation: A critical survey. IETE J. Res. 2019, 65, 365–379. [Google Scholar] [CrossRef]
- Potturu, S.R.; Prasad, R. Qualitative Analysis of Stable Reduced Order Models for Interval Systems Using Mixed Methods. IETE J. Res. 2018, 1–9. [Google Scholar] [CrossRef]
- Vijaya Anand, N.; Siva Kumar, M.; Srinivasa Rao, R. A novel reduced order modeling of interval system using soft computing optimization approach. Proc. Inst. Mech. Eng. Part J. Syst. Control. Eng. 2018, 232, 879–894. [Google Scholar] [CrossRef]
- Potturu, S.R.; Prasad, R. Model Order Reduction of LTI Interval Systems Using Differentiation Method Based on Kharitonov’s Theorem. IETE J. Res. 2019, 1–17. [Google Scholar] [CrossRef]
- Dulf, E.H. Simplified Fractional Order Controller Design Algorithm. Mathematics 2019, 7, 1166. [Google Scholar] [CrossRef]
- Kumar Deveerasetty, K.; Nagar, S. Model order reduction of interval systems using an arithmetic operation. Int. J. Syst. Sci. 2020, 51, 886–902. [Google Scholar] [CrossRef]
- Deveerasetty, K.K.; Zhou, Y.; Kamal, S.; Nagar, S.K. Computation of Impulse-Response Gramian for Interval Systems. IETE J. Res. 2019, 1–15. [Google Scholar] [CrossRef]
- Dewangan, P.; Singh, V.; Sinha, S. Improved Approximation for SISO and MIMO Continuous Interval Systems Ensuring Stability. Circuits Syst. Signal Process. 2020, 1–12. [Google Scholar] [CrossRef]
- Bia, P.; Mescia, L.; Caratelli, D. Fractional calculus-based modeling of electromagnetic field propagation in arbitrary biological tissue. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Shen, X. Applications of Fractional Calculus In Chemical Engineering. Ph.D. Thesis, Université d’Ottawa/University of Ottawa, Ottawa, ON, Canada, 2018. [Google Scholar]
- Ortigueira, M.D.; Tenreiro Machado, J. Fractional calculus applications in signals and systems. Signal Process. 2006, 86, 2503–2504. [Google Scholar] [CrossRef]
- Douglas, J.F. Some applications of fractional calculus to polymer science. Adv. Chem. Phys. 1997, 102, 121–192. [Google Scholar]
- Oldham, K.B. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Bao, C.; Pu, Y.; Zhang, Y. Fractional-order deep backpropagation neural network. Comput. Intell. Neurosci. 2018, 2018, 7361628. [Google Scholar] [CrossRef] [PubMed]
- Kulish, V.V.; Lage, J.L. Application of fractional calculus to fluid mechanics. J. Fluids Eng. 2002, 124, 803–806. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Redding, CA, USA, 2006; Volume 2. [Google Scholar]
- Soriano-Sánchez, A.G.; Rodríguez-Licea, M.A.; Pérez-Pinal, F.J.; Vázquez-López, J.A. Fractional-order approximation and synthesis of a PID controller for a buck converter. Energies 2020, 13, 629. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gu, D.W.; Petkov, P.; Konstantinov, M.M. Robust control design with MATLAB®; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Tarasov, V.E.; Tarasova, S.S. Fractional derivatives and integrals: What are they needed for? Mathematics 2020, 8, 164. [Google Scholar] [CrossRef]
- Tejado, I.; Vinagre, B.M.; Traver, J.E.; Prieto-Arranz, J.; Nuevo-Gallardo, C. Back to basics: Meaning of the parameters of fractional order PID controllers. Mathematics 2019, 7, 530. [Google Scholar] [CrossRef]
- Khubalkar, S.; Chopade, A.; Junghare, A.; Aware, M.; Das, S. Design and realization of stand-alone digital fractional order PID controller for Buck converter fed DC motor. Circuits Syst. Signal Process. 2016, 35, 2189–2211. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y.V. Fractional order controller and its applications: A review. Proc. AsiaMIC 2012. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PI/sup/spl lambda//D/sup/spl mu//-controllers. IEEE Trans. Autom. Control. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Ortigueira, M.D.; Trujillo, J.J.; Martynyuk, V.I.; Coito, F.J. A generalized power series and its application in the inversion of transfer functions. Signal Process. 2015, 107, 238–245. [Google Scholar] [CrossRef]
- Dolgin, Y. Author’s reply [to comments on’On Routh-Pade model reduction of interval systems’]. IEEE Trans. Autom. Control. 2005, 50, 274–275. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Monje, C.A.; Calderón, A.J.; Suárez, J.I. Fractional PID controllers for industry application. A brief introduction. J. Vib. Control. 2007, 13, 1419–1429. [Google Scholar] [CrossRef]
- Monje, C.A.; Calderon, A.J.; Vinagre, B.M.; Chen, Y.; Feliu, V. On fractional PI λ controllers: Some tuning rules for robustness to plant uncertainties. Nonlinear Dyn. 2004, 38, 369–381. [Google Scholar] [CrossRef]
- Yeroglu, C.; Tan, N. Note on fractional-order proportional–integral–differential controller design. IET Control. Theory Appl. 2011, 5, 1978–1989. [Google Scholar] [CrossRef]
- Pal, J. System reduction by a mixed method. IEEE Trans. Autom. Control. 1980, 25, 973–976. [Google Scholar] [CrossRef]
- Singh, V. Sine cosine algorithm based reduction of higher order continuous systems. In Proceedings of the 2017 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 7–8 December 2017; pp. 649–653. [Google Scholar]
- Srivastava, S.; Singh, V.; Singh, S.; Dohare, R.; Kumar, S. Luus-Jaakola based PID controller tuning for double tank system. Int. J. Adv. Technol. Eng. Explor. 2016, 3, 199. [Google Scholar] [CrossRef]
- Singh, V.P.; Chandra, D.; Rastogi, R. Luus jaakola algorithm based order reduction of discrete interval systems. Pratibha Int. J. Sci. Spirit. Bus. Technol. IJSSBT 2012, 1, 1–8. [Google Scholar]
- Prakash, T.; Singh, S.; Singh, V. Analytic hierarchy process-based model reduction of higher order continuous systems using sine cosine algorithm. Int. J. Syst. Control. Commun. 2020, 11, 52–67. [Google Scholar] [CrossRef]
- Mehra, S.; Monga, H.; Singh, V.; Kumar, R. Application of SCA for Level Control of Three-Tank System. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, UAE, 9–10 January 2020; pp. 220–224. [Google Scholar]
- Thakur, A.; Monga, H.; Singh, V.; Kumar, R.; Mathur, A. Sine Cosine Algorithm Assisted Tuning of PID Controller for DC Servo-Motor. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, UAE, 9–10 January 2020; pp. 230–233. [Google Scholar]



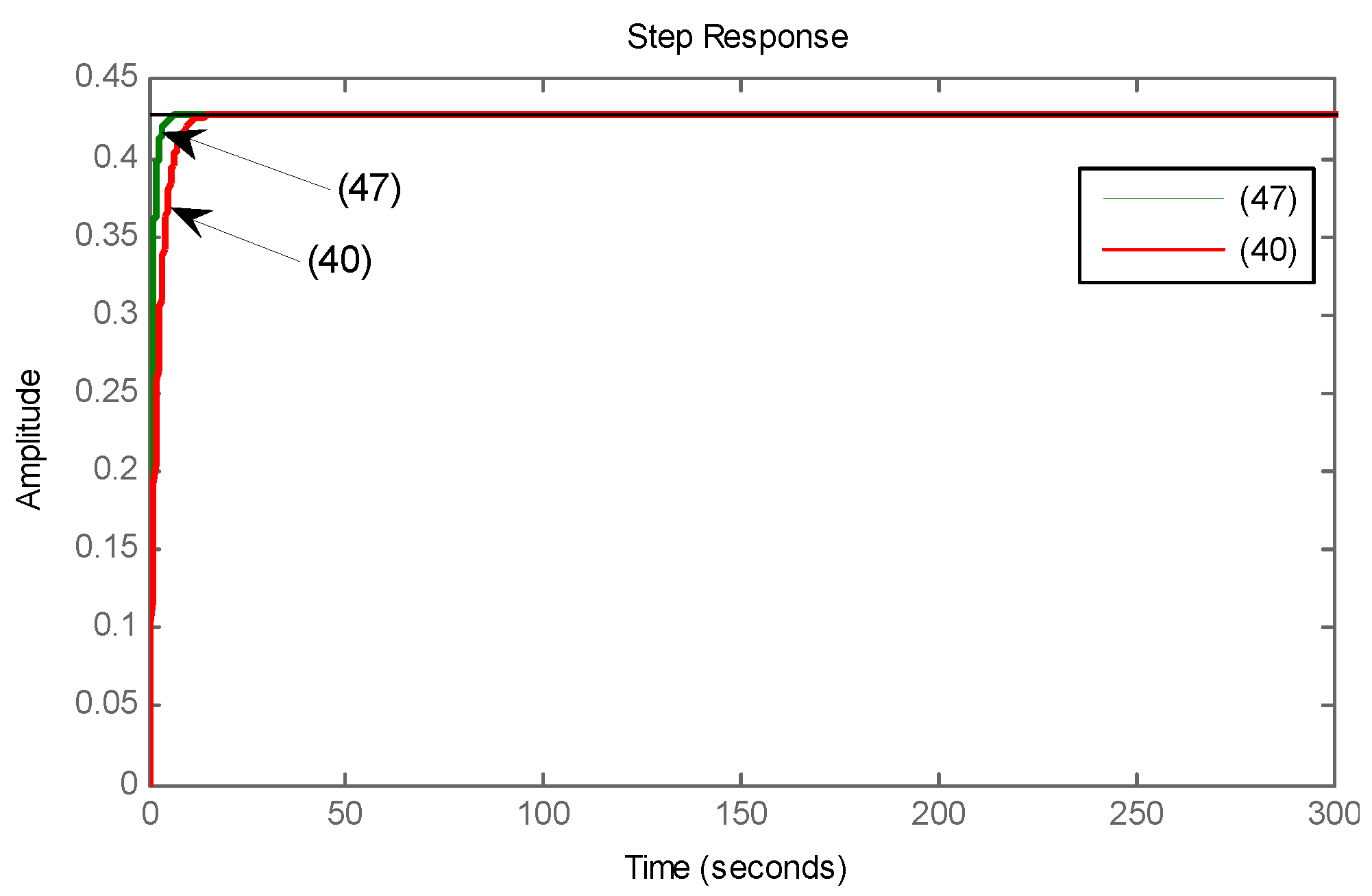
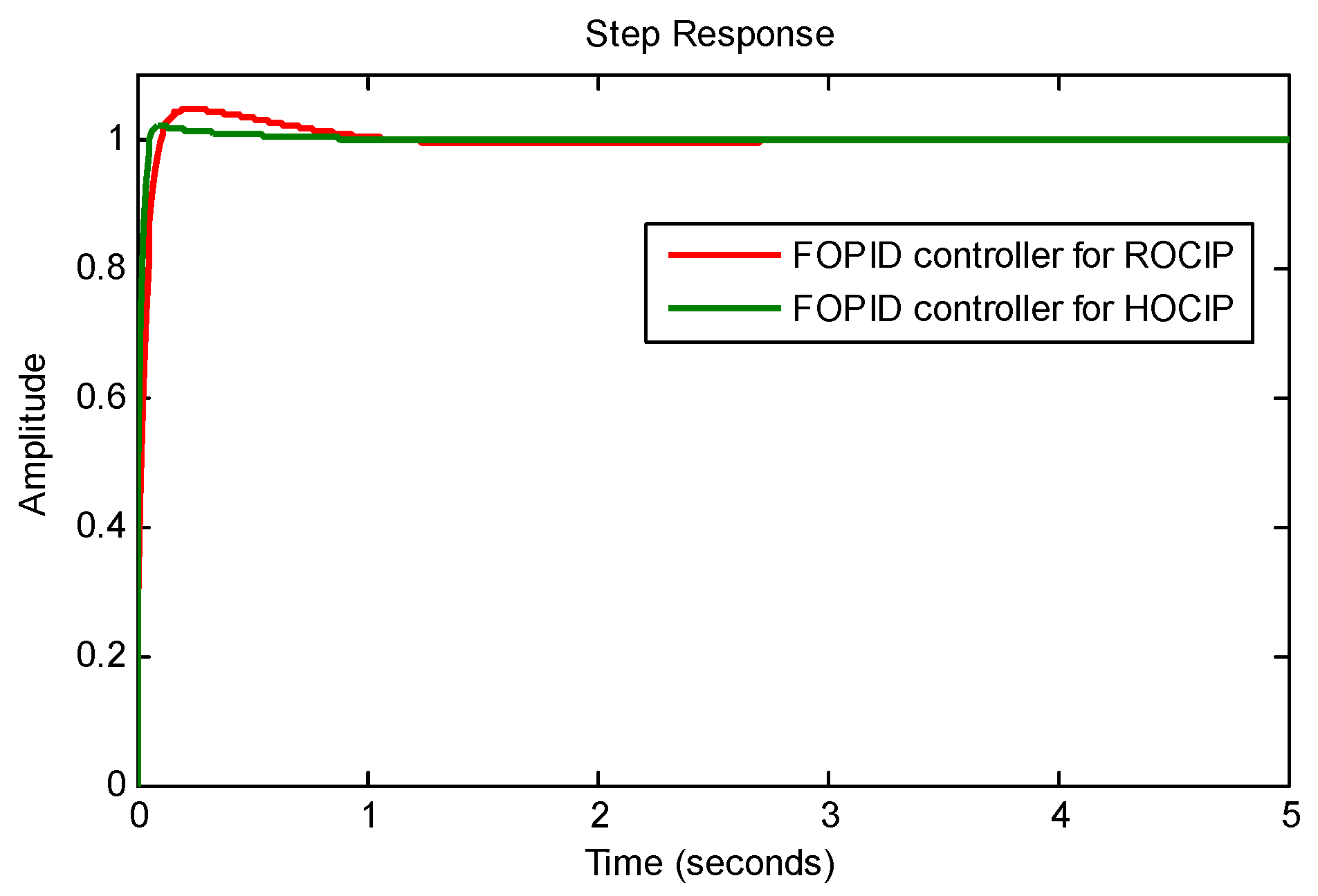
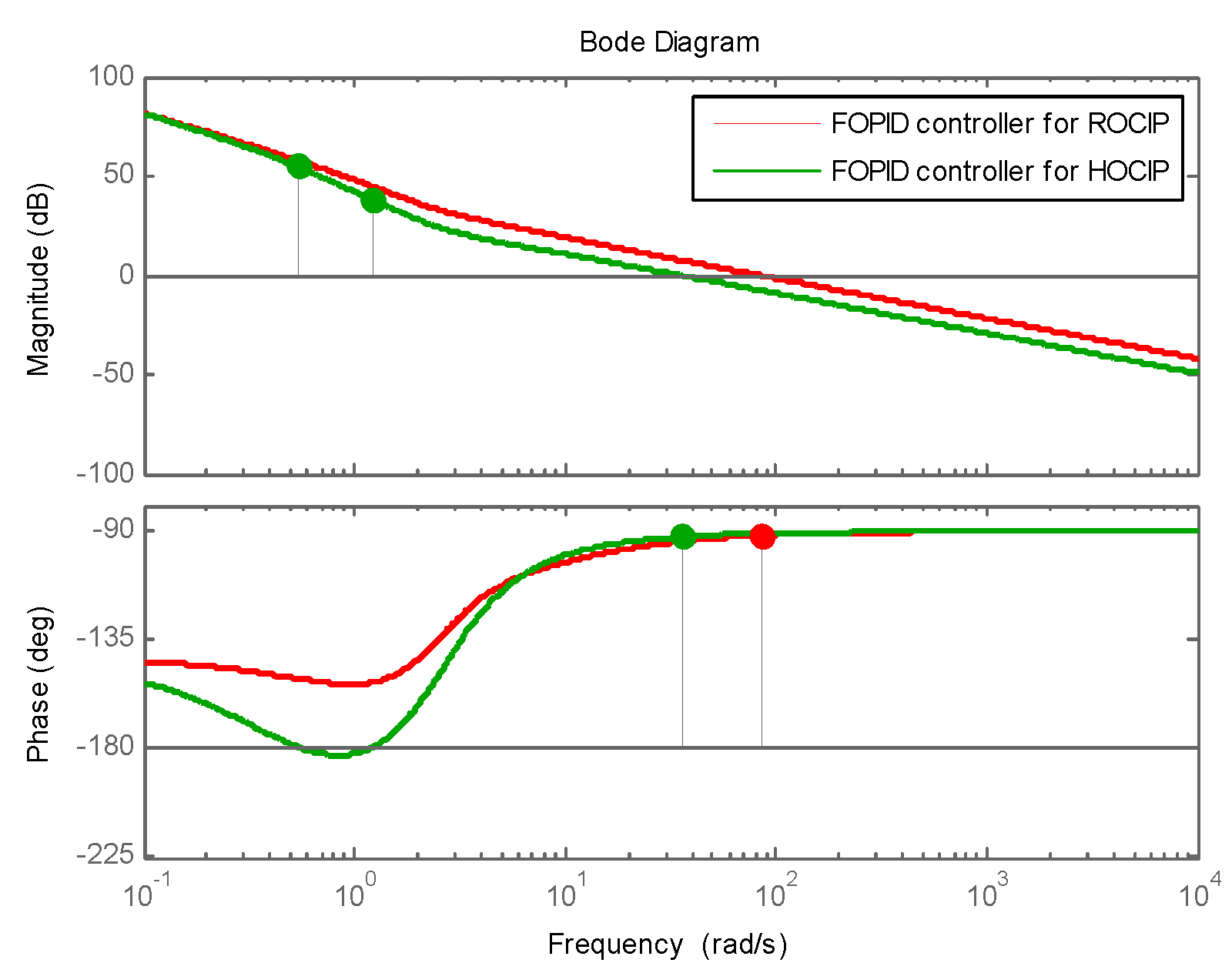

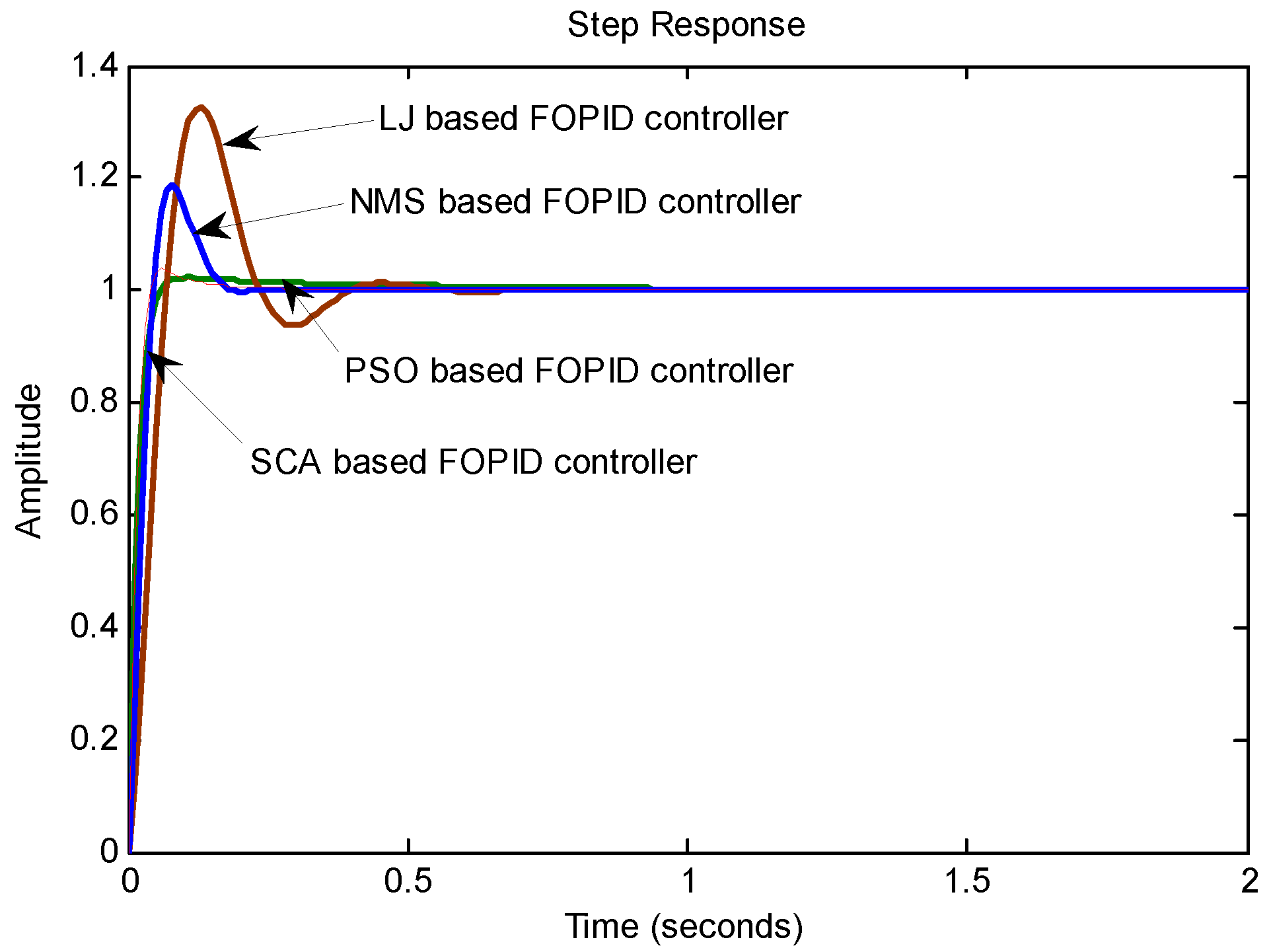
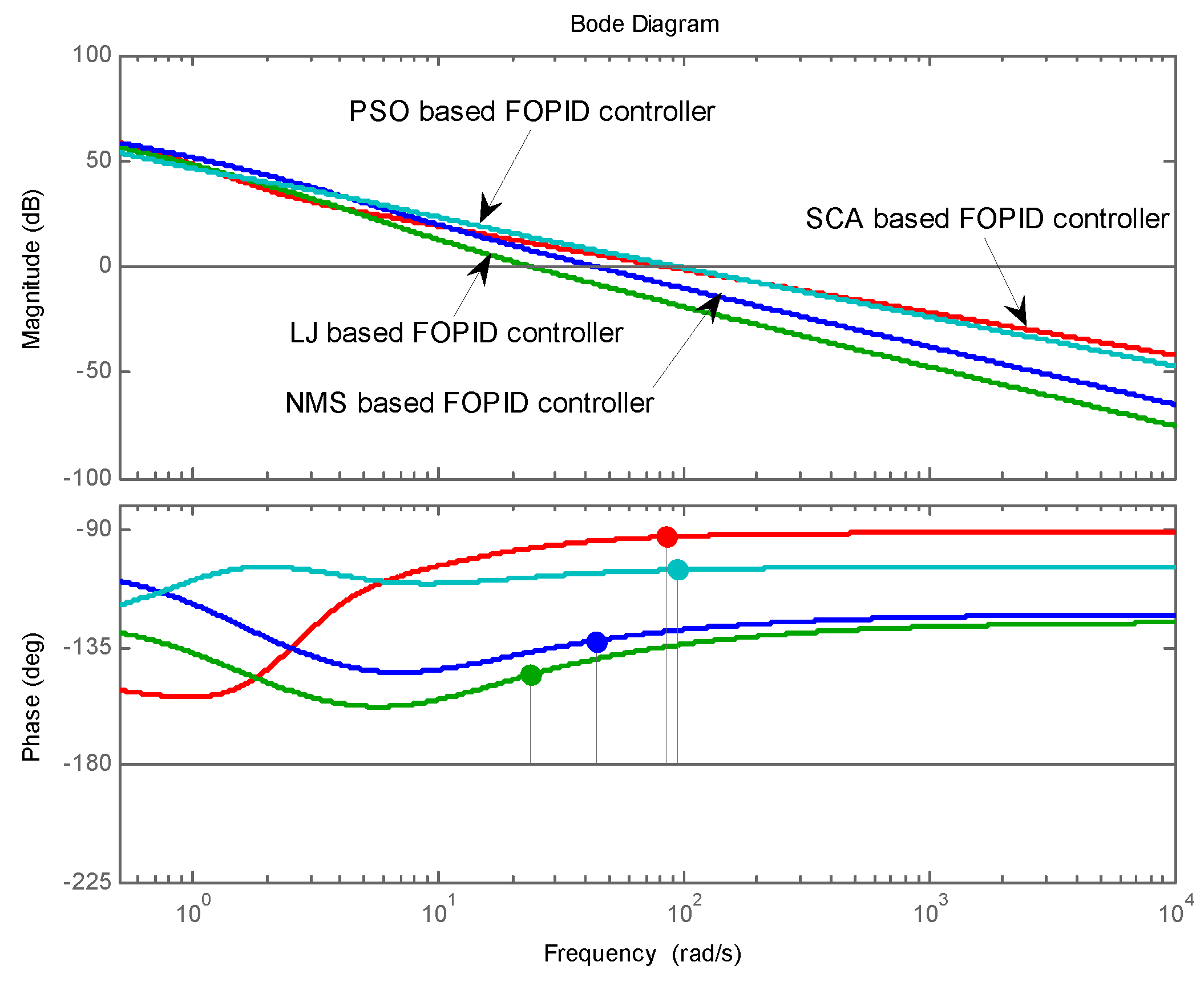
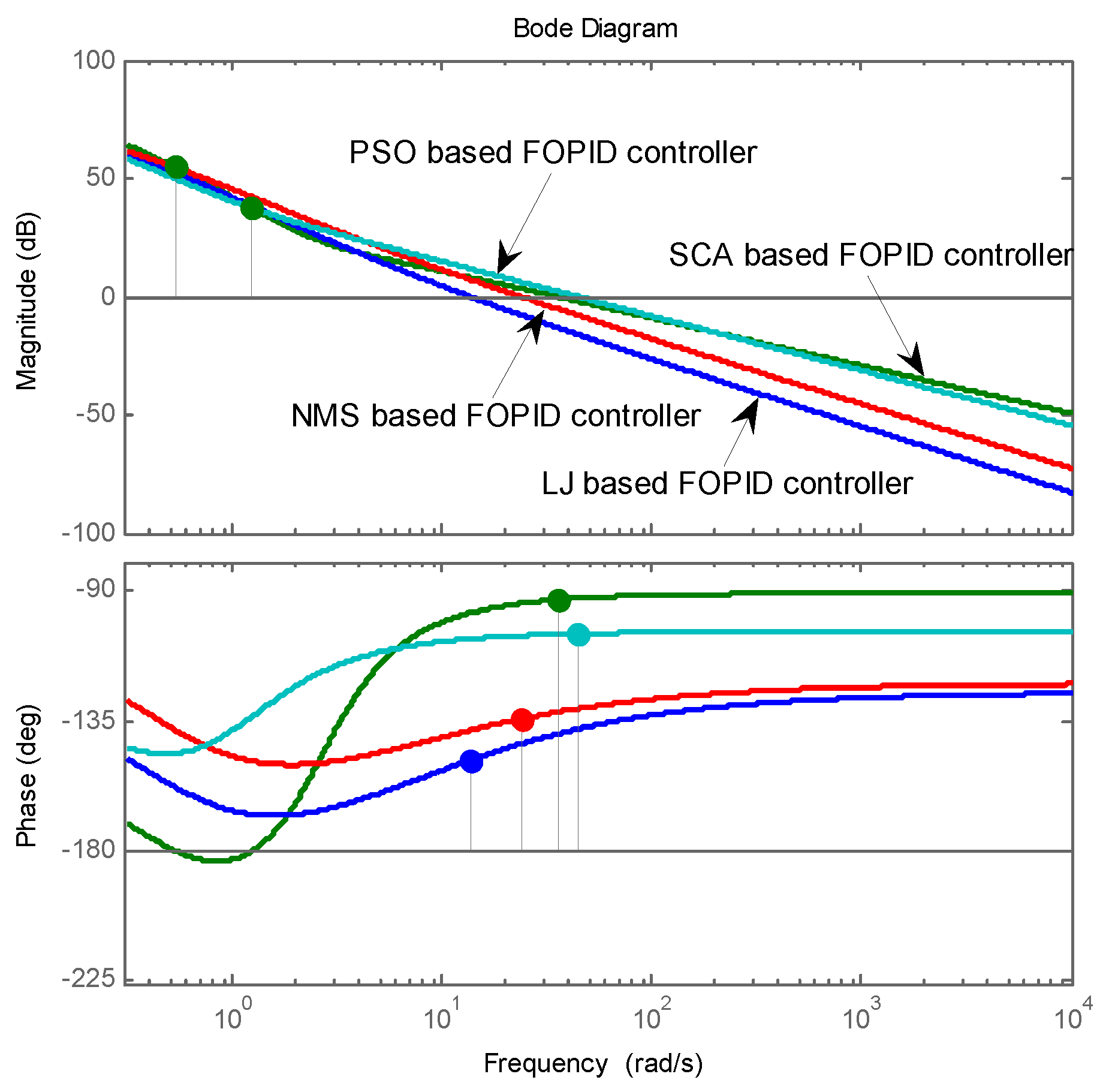
| … | |||
| … | |||
| ⋮ | ⋮ | ⋱ | |
| Algorithms | Parameters | Values |
|---|---|---|
| PSO | Cognitive parameter, Social parameter, Inertia weight, w | 2 2 |
| NMS | Refection coefficient, Contraction coefficient, Expansion coefficient, Shrinking coefficient, | 1 2 |
| LJ | Contraction factor, | |
| SCA | No parameter | − |
| Algorithms | (deg) | (rad/sec) | |||||
|---|---|---|---|---|---|---|---|
| SCA | |||||||
| PSO | |||||||
| NMS | |||||||
| LJ | 478 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bokam, J.K.; Patnana, N.; Varshney, T.; Singh, V.P. Sine Cosine Algorithm Assisted FOPID Controller Design for Interval Systems Using Reduced-Order Modeling Ensuring Stability. Algorithms 2020, 13, 317. https://doi.org/10.3390/a13120317
Bokam JK, Patnana N, Varshney T, Singh VP. Sine Cosine Algorithm Assisted FOPID Controller Design for Interval Systems Using Reduced-Order Modeling Ensuring Stability. Algorithms. 2020; 13(12):317. https://doi.org/10.3390/a13120317
Chicago/Turabian StyleBokam, Jagadish Kumar, Naresh Patnana, Tarun Varshney, and Vinay Pratap Singh. 2020. "Sine Cosine Algorithm Assisted FOPID Controller Design for Interval Systems Using Reduced-Order Modeling Ensuring Stability" Algorithms 13, no. 12: 317. https://doi.org/10.3390/a13120317
APA StyleBokam, J. K., Patnana, N., Varshney, T., & Singh, V. P. (2020). Sine Cosine Algorithm Assisted FOPID Controller Design for Interval Systems Using Reduced-Order Modeling Ensuring Stability. Algorithms, 13(12), 317. https://doi.org/10.3390/a13120317