A Solving Algorithm for Nonlinear Bilevel Programing Problems Based on Human Evolutionary Model
Abstract
1. Introduction
2. The Basic Concepts of Bilevel Programing Problem
- (1)
- Constraint region of the BLPP:
- (2)
- Projection of constraint region onto the upper level decision space:According to the decision variables given by the upper maker, i.e., , the constraint region of the lower level problem is formulated as follows:
- (3)
- For each fixed , the lower level decision-maker’s rational reaction set:
- (4)
- Inducible region of BLPP:
3. Design of the Proposed Algorithm
3.1. Brief Introduction to HEM
3.1.1. The Rational of HEM
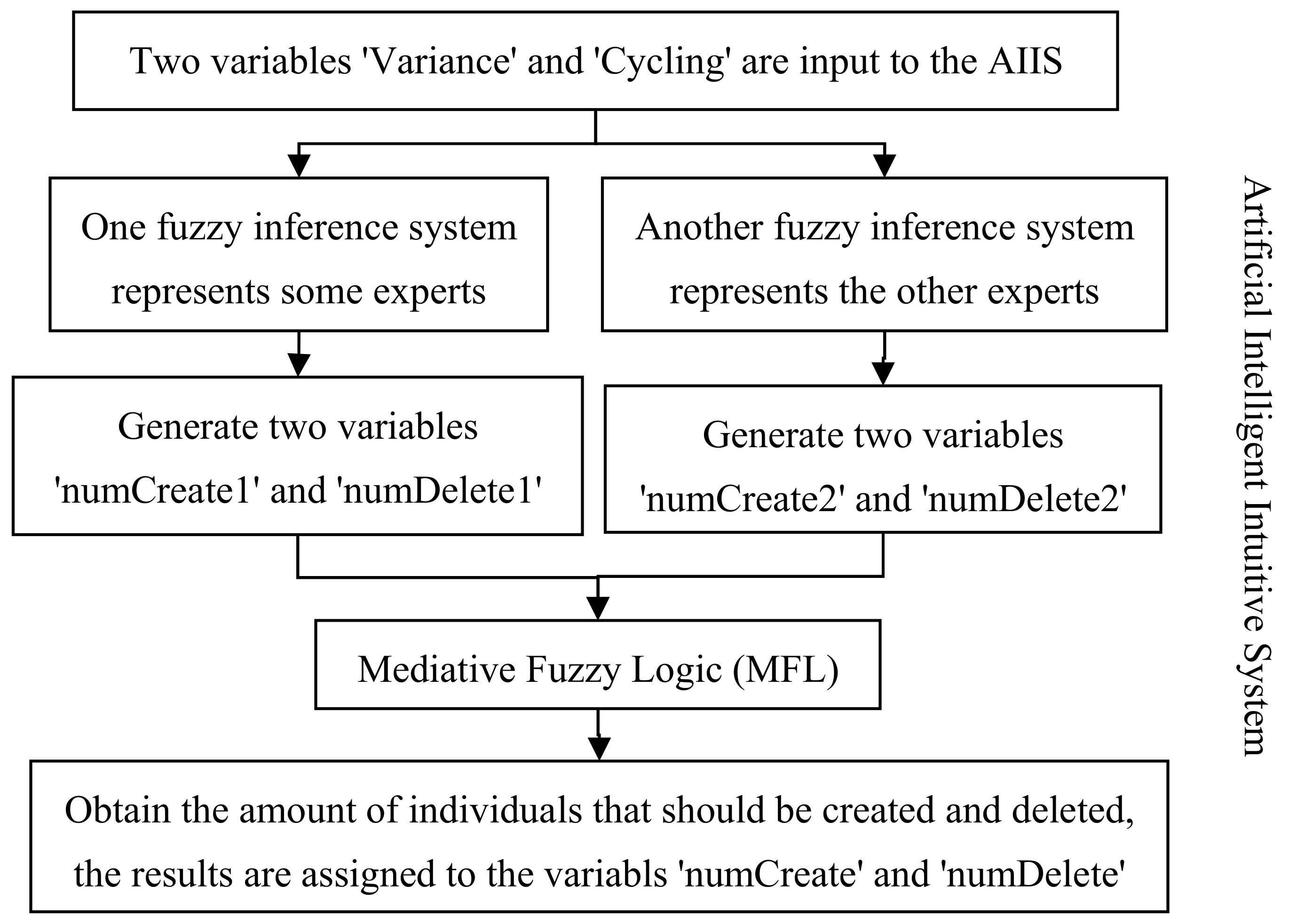
3.1.2. The Artificial Intelligent Intuitive System
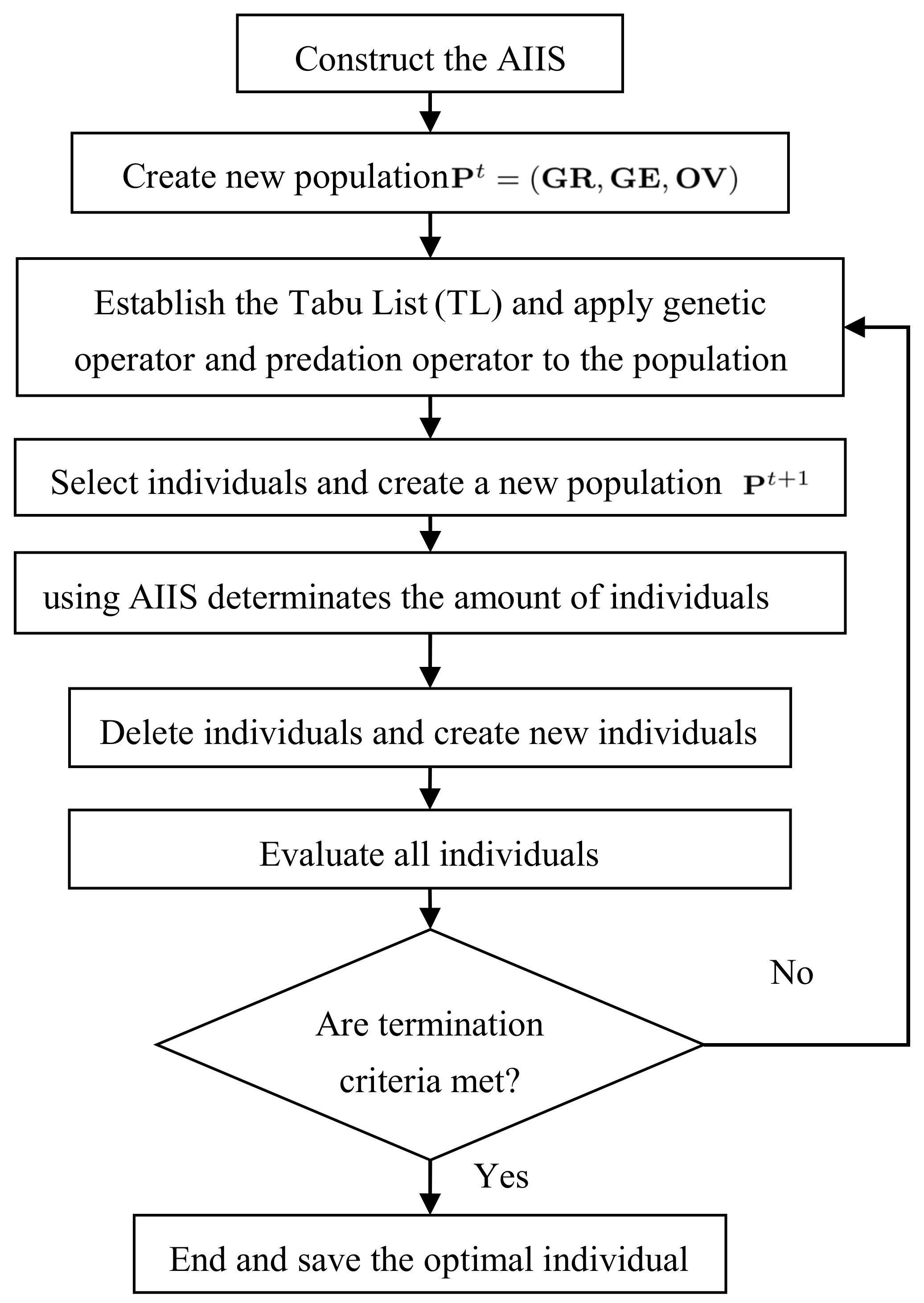
3.2. The Idea of the Proposed Algorithm
- : upper level decision variable,
- : lower level decision variable,
- : upper level objective function,
- : lower level objective function,
- : quantity of new individuals.
4. Computational Experiments
4.1. The Parameters of the Algorithm
4.2. Experimental Results
5. Conclusions
- (1)
- The proposed algorithm is feasible for various bilevel programming problems such as linear, quadratic and nonlinear problems. Our method does not impose any restriction on the problems.
- (2)
- The evolution is basically stable in our method because of the consistent iterations in each run for all examples.
- (3)
- Although in some cases the solutions by our algorithm are not so good as the compared algorithms, within the acceptable precision, the algorithm can converge to the global optima and the solutions are completely acceptable.
- (1)
- We still plan to do more research about the influence of the parameters on the performance so as to control more parameters adaptively using AIIIS and simply the HEM on the basis of the basic HEM.
- (2)
- Many more and larger-scale problems will be solved to demonstrate the efficiency of our proposed algorithm.
- (3)
- Comparison with other algorithms by solving more examples will also be our future work to illustrate the superiority of our algorithm.
Author Contributions
Funding
Conflicts of Interest
References
- Aghajani, S.; Kalantar, M. Operational scheduling of electric vehicles parking lot integrated with renewable generation based on bilevel programming approach. Energy 2017, 139, 422–432. [Google Scholar] [CrossRef]
- Labbe, M.; Violin, A. Bilevel programming and price setting problems. Ann. Oper. Res. 2016, 240, 141–169. [Google Scholar] [CrossRef]
- Bard, F. Practical Bilevel Optimization: Algorithms and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Vicente, L.; Calamai, P.H. Bilevel and multibilevel programming: A bibliography review. Glob. Optim. 1994, 5, 291–306. [Google Scholar] [CrossRef]
- Dempe, S. Foundations of Bilevel Programming; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Dempe, S. Annotated bibliography on bilevel programming and mathematical programs with equilibrium constraints. Optimization 2003, 52, 333–359. [Google Scholar] [CrossRef]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Wang, G.M.; Wang, Z.P.; Wang, X. An overview of two(bi)-level programming review. Adv. Math. 2007, 36, 513–529. [Google Scholar]
- Huang, Z.; Yang, C.; Zhou, X.; Gui, W. A novel cognitively inspired state transition algorithm for solving the linear Bi-level programming problem. Cogn. Comput. 2018, 10, 816–826. [Google Scholar] [CrossRef]
- Jeroslow, R.G. The polynomial hierarchy and a simple model for competitive analysis. Math. Program. 1985, 32, 146–164. [Google Scholar] [CrossRef]
- Ben-Ayed, O.; Blair, C. Computational difficulties of bilevel linear programming. Oper. Res. 2012, 38, 556–560. [Google Scholar] [CrossRef]
- Bard, F. Some properties of the bilevel linear programming problem. J. Optim. Theory Appl. 1991, 68, 146–164. [Google Scholar] [CrossRef]
- Vicente, L.; Savard, G.; Judice, J. Descent approaches for quadratic bilevel programming. J. Optim. Theory Appl. 1994, 81, 379–399. [Google Scholar] [CrossRef]
- Deng, X. Complexity issues in bilevel linear programming. In Multilevel Optimization: Algorithms and Applications; Migdalas, A., Pardalos, P.M., Varbrand, P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; pp. 149–164. [Google Scholar]
- Li, T.; Chen, C.Y.; Su, W.L. Plant growth simulation algorithm for solving bilevel programming. Oper. Res. Manag. Sci. 2012, 21, 123–128. [Google Scholar]
- Watada Roy, A.; Li, R.; Wang, B.; Wang, S. A dual recurrent neural network-based hybrid approach for solving convex quadratic Bi-level programming problem. Neurocomputing 2020, 407, 136–154. [Google Scholar] [CrossRef]
- Yi, Z.K.; Xu, Y.L.; Sun, H.B. Self-adaptive hybrid algorithm based bi-level approach for virtual power plant bidding in multiple retail markets. IET Gener. Transm. Distrib. 2020, 14, 3762–3773. [Google Scholar] [CrossRef]
- Abo-Elnaga, Y.; Nasr, S. Modified evolutionary algorithm and chaotic search for bilevel programming problems. Symmetry 2020, 12, 767. [Google Scholar] [CrossRef]
- Fateh, H.; Bahramara, S.; Safari, A. Modeling operation problem of active distribution networks with retailers and microgrids: A multi-objective bi-level approach. Appl. Soft Comput. 2020, 94, 106484. [Google Scholar] [CrossRef]
- Luo, H.; Liu, L.; Yang, X. Bi-level programming problem in the supply chain and its solution algorithm. Soft Comput. 2020, 24, 2703–2714. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Z.; Chen, W. A cooperative coevolution PSO technique for complex bilevel programming problems and application to watershed water trading decision making problems. J. Nonlinear Sci. Appl. 2017, 10, 2115–2132. [Google Scholar] [CrossRef][Green Version]
- Tang, Q.; Fu, Z.; Qiu, M. A bilevel programming model and algorithm for the static bike repositioning problem. J. Adv. Transp. 2019. [Google Scholar] [CrossRef]
- Abo-Elsayed, Y.; El-Shorbagy, M.A. Multi-sine cosine algorithm for solving nonlinear bilevel programming problems. Int. J. Comput. Intell. Syst. 2020, 13, 421–432. [Google Scholar]
- Zhang, T.; Liu, R.L.; Chen, F. The BP artificial neural network based on elite PSO algorithm for general bilevel programming problems. J. Nonlinear Convex Anal. 2020, 21, 885–898. [Google Scholar]
- Feng, Q.; Qin, S.T.; Shi, F.L.; Zhao, S. A recurrent neural network with finite-time convergence for convex quadratic bilevel programming problems. Neural Comput. Appl. 2018, 30, 3399–3408. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.F. The backpropagation artificial neural network based on elite particle swam optimization algorithm for stochastic linear bilevel programming problem. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Yu, B. A modified homotopy method for solving the principal-agent bilevel programming problem. Comput. Appl. Math. 2018, 37, 541–566. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Deb, K. An improved bilevel evolutionary algorithm based on Quadratic Approximations. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1870–1877. [Google Scholar]
- Lin, D.; Chou, Y.Z.; Li, M.Q. Multi-objective evolutionary algorithm for multi-objective bi-level programming problems. J. Syst. Eng. 2007, 22, 182–186. [Google Scholar]
- Wang, Y.; Li, H.; Dang, C. A new evolutionary algorithm for a class of nonlinear bilevel programming problems and its global convergence. Inf. J. Comput. 2011, 23, 618–629. [Google Scholar] [CrossRef]
- Rodriguez, F.; Lozano, M.; Garcia-Martinez, C.; García-Martínez, J.D. An artificial bee colony algorithm for the maximally diverse grouping problem. Inf. Sci. 2013, 320, 183–196. [Google Scholar] [CrossRef]
- Calvete, H.I.; Gale, C.; Oliveros, M. Bilevel model for production-distribution planning solved by using ant colony optimization. Comput. Oper. Res. 2011, 38, 320–327. [Google Scholar] [CrossRef]
- Wang, G.M.; Ma, L.M. The estimation of particle swarm distribution algorithm with sensitivity analysis for solving nonlinear bilevel programming problems. IEEE Access 2020, 8, 137133–137149. [Google Scholar] [CrossRef]
- Montiel, O.; Castillo, O.; Rodríguez, A.; Melin, P.; Sepúlveda, R. Human evolutionary model: A new approach to optimization. Inf. Sci. 2007, 177, 2075–2098. [Google Scholar] [CrossRef]
- Candler, W.; Norton, R. Multilevel Programming; Technical Report 20; World Bank Development Research Center: Washington, DC, USA, 1977. [Google Scholar]
- Candler, W.; Townsley, R. A linear two-level programming problem. Comput. Oper. Res. 1982, 9, 59–76. [Google Scholar] [CrossRef]
- Bialas, W.F.; Karwan, M.H. On two-level optimization. IEEE Trans. Autom. Control 1982, 7, 211–214. [Google Scholar] [CrossRef]
- Bialas, W.F.; Karwan, M.H. Two-level linear programming. Manag. Sci. 1984, 30, 1004–1020. [Google Scholar] [CrossRef]
- Bard, F. Geometric and algorithmic developments for a hierarchical planning problem. Eur. J. Oper. Res. 1985, 19, 372–383. [Google Scholar] [CrossRef]
- Montiel, O.; Castillo, O. Mediative fuzzy logic: A novel approach for handling contradictory knowledge. In Hybrid Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 75–91. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Sepulveda, R. Mediative fuzzy logic: A new approach for contradictory knowledge management. In Forging New Frontiers: Fuzzy Pioneers II; Springer: Berlin/Heidelberg, Germany, 2008; pp. 135–149. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets: Past, present and future. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003; pp. 12–19. [Google Scholar]
- Li, D.F. Intuitionistic Fuzzy Set Theories Decision and Game Theory in Management with Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–12. [Google Scholar]
- Montiel Ross, O.H.; Castillo, O.; Melin, P.; Sepúlveda, R. Mediative fuzzy logic: A novel approach for handling contradictory knowledge. In Proceedings of the International Conference on Fuzzy Systems, Neural Networks and Genetic Algorithms (FNG 2005), Tijuana, Mexico, 13–14 October 2005. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Sepúlveda, R. Improving the human evolutionary model: An intelligent optimization method. Int. Math. Forum 2007, 2, 21–44. [Google Scholar] [CrossRef][Green Version]
- Montiel, O.; Castillo, O.; Melin, P.; Sepúlveda, R. Reducing the cycling problem in evolutionary algorithm. In Proceedings of the 2005 International Conference on Artificial Intelligence, Las Vegas, NV, USA, 27–30 June 2005; pp. 426–432. [Google Scholar]
- Castillo, O.; Melin, P. A new method for fuzzy inference in intuitionistic fuzzy systems. In Proceedings of the International Conference NAFIPS 2003, Chicago, IL, USA, 24–26 July 2003; IEEE Press: Chicago, IL, USA, 2003; pp. 20–25. [Google Scholar]
- Oduguwa, V.; Roy, R. Bi-level optimisation using genetic algorithm. In Proceedings of the 2002 IEEE International Conference on Artificial Intelligence Systems (ICAIS 2002), Divnomorskoe, Russia, 5–10 September 2002; pp. 322–327. [Google Scholar]
- Wang, Y.; Iao, Y.; Li, H. An evolutionary algorithm for solving nonlinear bilevel programming based on a new constraint-handling scheme. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2005, 35, 221–232. [Google Scholar] [CrossRef]
- Wan, Z.P.; Mao, L.; Wang, G.M. Estimation of distribution algorithm for a class of nonlinear bilevel programming problems. Inf. Sci. 2014, 256, 184–196. [Google Scholar] [CrossRef]
| No. | Type | Scale | Functions |
|---|---|---|---|
| Example 1 | Linear | Convex and differentiable | |
| Example 2 | quadratic | Convex and differentiable | |
| Example 3 | nonlinear | Non-convex and non-differentiable | |
| Example 4 | nonlinear | Non-convex and non-differentiable |
| Recombination | Mutation | Max Age | Population Size | Iteration | |||||
|---|---|---|---|---|---|---|---|---|---|
| K | λ | Initial | Min | Max | Max | Min | |||
| Example 1 | 0.25 | 16 | 0.1 | 10 | 50 | 20 | 150 | 100 | 30 |
| Example 2 | 0.1 | 20 | 50 | 30 | 200 | 150 | 50 | ||
| Example 3 | 0.5 | 5 | 80 | 50 | 150 | 100 | 30 | ||
| Example 4 | 0.5 | 8 | 80 | 50 | 200 | 200 | 50 | ||
| Example 1 | Example 2 | Example 3 | Example 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | Iterations | Time (s) | Iterations | Time (s) | |
| Min(best) | 51 | 11.289 | 50 | 300.404 | 20 | 173.885 | 200 | 38,024.21 |
| Max | 60 | 32.534 | 64 | 2058.331 | 41 | 8082.929 | 200 | 39,149.43 |
| Average | 54.5 | 19.889 | 54.4 | 1125.779 | 27.9 | 1054.349 | 200 | 38,586.82 |
| Our Proposed Algorithm | Reference: Wan et al. | Reference | ||
|---|---|---|---|---|
| Example 1 | −29.199879 | −29.200009 | −29.2 | |
| 3.199977 | 3.200009 | 3.2 | ||
| (0,0.899997) | (2 × 10−6,0.899997) | (0,0.9) | ||
| (1.92 × 10−12,0.599998,0.399992) | (4 × 10−6,0.6,0.400005) | (0,0.6,0.4) | ||
| Example 2 | 100 | 100.01 | 100.58 | |
| 5.72 × 10−16 | 2.5 × 10−7 | 0.01 | ||
| 10 | 10.0005 | 10.03 | ||
| 10 | 9.9995 | 9.969 | ||
| Example 3 | 5.85 × 10−7 | 0 | 0 | |
| 100 | 100 | 100 | ||
| (0,29.999999) | (0,30) | (0,30) | ||
| (−9.999999,9.999999) | (−10,10) | (−10,10) | ||
| Example 4 | 3.26 × 10−3 | 0 | 6.21 × 10−4 | |
| 1 | 1 | 1 | ||
| (1.000087,1.000387, 1.000230,1.000338, 1.000190,0.999098, 1.000254,0.999878, 1.000146,1.000592) | (1, 1, 1, 1, 1, 1, 1, 1, 1, 1) | (0.99999998, 0.99999999, 1.00000006,0.99999999, 1.00000000,1.00000001, 0.99999999,0.99999992, 0.99999998, 1.00000001) | ||
| (3.56 × 10−6,−2.11 × 10−7,7.38 × 10−7, 5.02 × 10−7,−5.38 × 10−7,−1.26 × 10−6, −9.99 × 10−7,−2.30 × 10−6,−9.08 × 10−8, 1.71 × 10−6) | (0, 0, 0, 0, 0, 0, 0, 0, 0, 0) | 1.0 × 10−3 (−0.04845,−0.03471, 0.11674,0.09264,0.2121, 0.09969,0.07125,0.05798,0.04344,0.03512) | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Wang, G. A Solving Algorithm for Nonlinear Bilevel Programing Problems Based on Human Evolutionary Model. Algorithms 2020, 13, 260. https://doi.org/10.3390/a13100260
Ma L, Wang G. A Solving Algorithm for Nonlinear Bilevel Programing Problems Based on Human Evolutionary Model. Algorithms. 2020; 13(10):260. https://doi.org/10.3390/a13100260
Chicago/Turabian StyleMa, Linmao, and Guangmin Wang. 2020. "A Solving Algorithm for Nonlinear Bilevel Programing Problems Based on Human Evolutionary Model" Algorithms 13, no. 10: 260. https://doi.org/10.3390/a13100260
APA StyleMa, L., & Wang, G. (2020). A Solving Algorithm for Nonlinear Bilevel Programing Problems Based on Human Evolutionary Model. Algorithms, 13(10), 260. https://doi.org/10.3390/a13100260




