1. Introduction
Optimization models are used in many practical situations to represent decision-making challenges in areas such as computational finance, transportation and logistics, telecommunication networks, smart cities, etc. [
1]. Many of these challenges can be transformed into optimization problems (OPs) that can be then solved using a plethora of methods of both exact and approximate nature. Typically, solving an OP implies exploring a vast solution space while searching for one solution that minimizes or maximizes a given objective function. In addition, the solution has to satisfy a series of constraints in order to be a feasible one [
2]. It is frequent to model these OPs by using linear programming (LP), integer programming (IP), or mixed integer linear programming (MILP) methods. Unfortunately, in many real-life situations, these OPs are also
NP-hard, which implies that the computing time requested to find an optimal solution grows extraordinarily fast as the size of the problem increases [
3]. Hence, one has to make use of heuristic-based algorithms if reasonably good solutions are needed in short computing times for large-scale
NP-hard OPs [
4]. Moreover, the effective use of exact methods might be also limited whenever the mathematical model does not comply with desirable properties such as convexity or smoothness. In particular, the existence of non-convex and non-smooth objective functions might limit the efficiency of gradient-based optimization methods.
Bagirov and Yearwood [
5] discuss a non-smooth OP called the minimum sum-of-squares clustering problem. According to the authors, previously employed approaches such as dynamic programming, branch-and-bound, or the
k-means algorithm are efficient only for small instances of this problem. The authors also support the idea that the use of heuristic-based approaches becomes necessary for large-size instances. Similarly, Bagirov et al. [
6] analyze another non-smooth OP related to the facility location problem in a wireless sensor network. Roy et al. [
7] study non-smooth power-flow problems, while Lu et al. [
8] propose an adaptive hybrid differential evolution algorithm to cope with a non-smooth version of the dynamic economic dispatch problem. To the best of our knowledge, however, there is a lack of publications considering realistic non-smooth cost functions in many OPs. Nevertheless, OPs with soft constraints might frequently appear in real-life applications. As discussed in Hashimoto et al. [
9], “in real-world simulations, time windows and capacity constraints can be often violated to some extent”. Hence, for example, in cost minimization, problems violating these soft constraints might generate penalty costs that might be taken into account in the objective function. These penalty costs will typically come in the form of a piecewise cost function, which can transform the objective function into a non-smooth one.
This paper reviews different examples of OPs with non-smooth objective functions and then analyzes how biased-randomized algorithms (BRAs) can constitute an effective methodology to generate reasonably good solutions in very short computing times. As described in Ferone et al. [
10], BRAs make use of skewed probability distributions to integrate a “biased” (nonuniform) random behavior into a heuristic. This allows one to quickly generate a large set of alternative good solutions by simply changing the seed of the pseudo-random number generator [
11,
12]. Hence, each execution of the BRA can be seen as an individual “agent” searching the solution space following the logic behind the heuristic but starting from a different point and using a different searching (
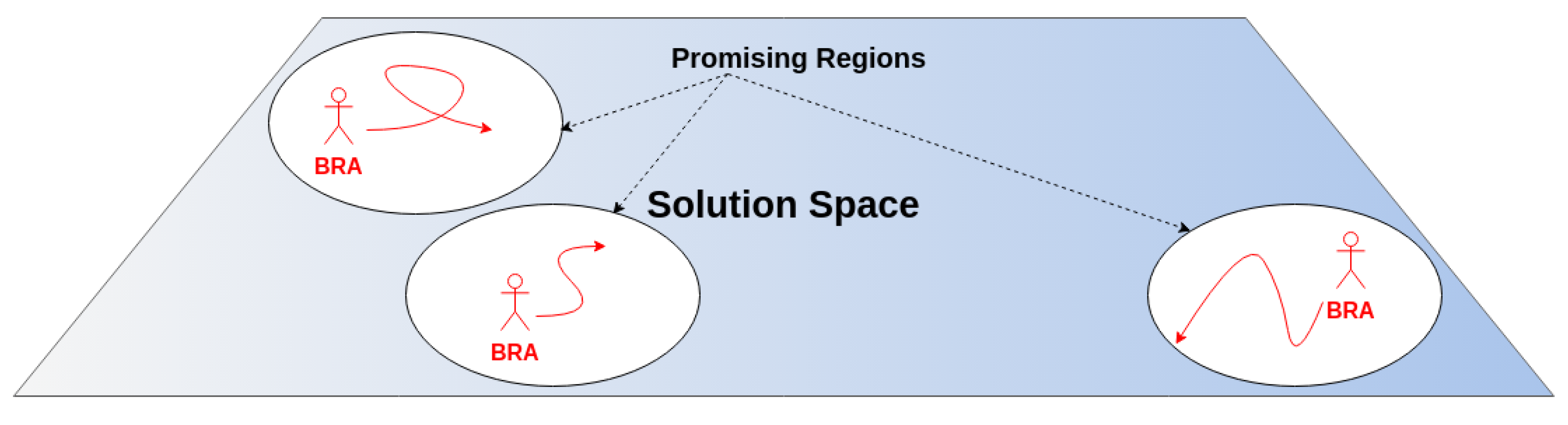
Figure 1). Moreover, the execution of these BRA agents can be performed in parallel, thus consuming virtually the same time as the original heuristic (i.e., milliseconds in most cases).
According to our previous experience with using BRAs to solve OPs in different application fields, these algorithms can be especially useful in cases where the solution space is highly irregular (non-convex and/or non-smooth) and requires an extensive exploration stage, thus reducing the effectiveness of traditional optimization methods. Actually, BRAs have been already proposed to solve non-smooth OPs in different application areas. For instance, they have been used to solve different rich and realistic variants of the well-known vehicle routing problem (VRP), including the two-dimensional VRP [
13], VRP variants with horizontal cooperation [
14], multi-agent versions of the VRP [
15], the location routing problem [
16], the fleet mixed VRP with backhauls [
17,
18], the multi-period VRP [
19], and even other versions of the multi-depot VRP [
20]. BRAs have also been employed in solving other OPs, such as the single-round divisible load scheduling [
21], the stochastic flow-shop scheduling [
22], scheduling heterogeneous multi-round systems [
23], the minimization of open stacks problem [
24], the dynamic home service routing [
25], waste collection management [
26], or the maximum quasi-clique problem [
27].
Accordingly, the main contributions of this paper are as follows: (i) a discussion on the importance of considering non-smooth objective functions in realistic combinatorial OPs, mainly due to the existence of soft constraints which might be violated to some extent by incurring non-smooth penalty costs, and (ii) a discussion on how BRAs can be employed in different applications to solve these non-smooth OPs in short computing times. The remainder of the paper is structured as follows:
Section 2 reviews some basic concepts related to non-smooth OPs.
Section 3 presents a review of recent works on BRAs.
Section 4,
Section 5 and
Section 6 review applications of BRAs to non-smooth OPs in logistics, transportation, and scheduling, respectively.
Section 7 provides an overview on current trends and open research lines. Finally,
Section 8 concludes by highlighting the main contributions of this work.
2. Non-Smooth Optimization Problems
OPs can be broadly classified as convex or non-convex. Convex OPs are usually characterized by a convex objective function and a set of constraints that form a convex region. Each constraint restricts the solution space to a convex region, and the intersection of these regions, which form the feasible solutions, is also convex. The main feature that makes convex OPs easy to work with is that any local optimum is also a global optimum. This significantly reduces the computational time yielding exact solutions in reasonable times. Therefore, if doable, it is of interest to convert any optimization problem into a convex OP. Despite the specific structure needed for a convex OP, we find several applications of it in real-life problems. For example, those problems that can be modeled as a linear programming model are convex problems because all linear functions are by definition convex [
28]. Nevertheless, there are some other problems that cannot be modeled as a convex OP. Non-convex problems have either non-convex objective functions or non-convex feasible regions (or both). This brings in several challenges to solve these problems. The main challenge is that the solution methods employed for convex OPs cannot be directly applied for non-convex ones because of the availability of many disjoint regions in the solution space, each of which usually has its own local optimum. Therefore, it is easy for the algorithm to get trapped into one of these local optima, which may indeed be far away from the global optimum. Also, it is usually time-consuming—or even impossible—to demonstrate that the algorithm reached the global optimum or whether a feasible solution can be obtained.
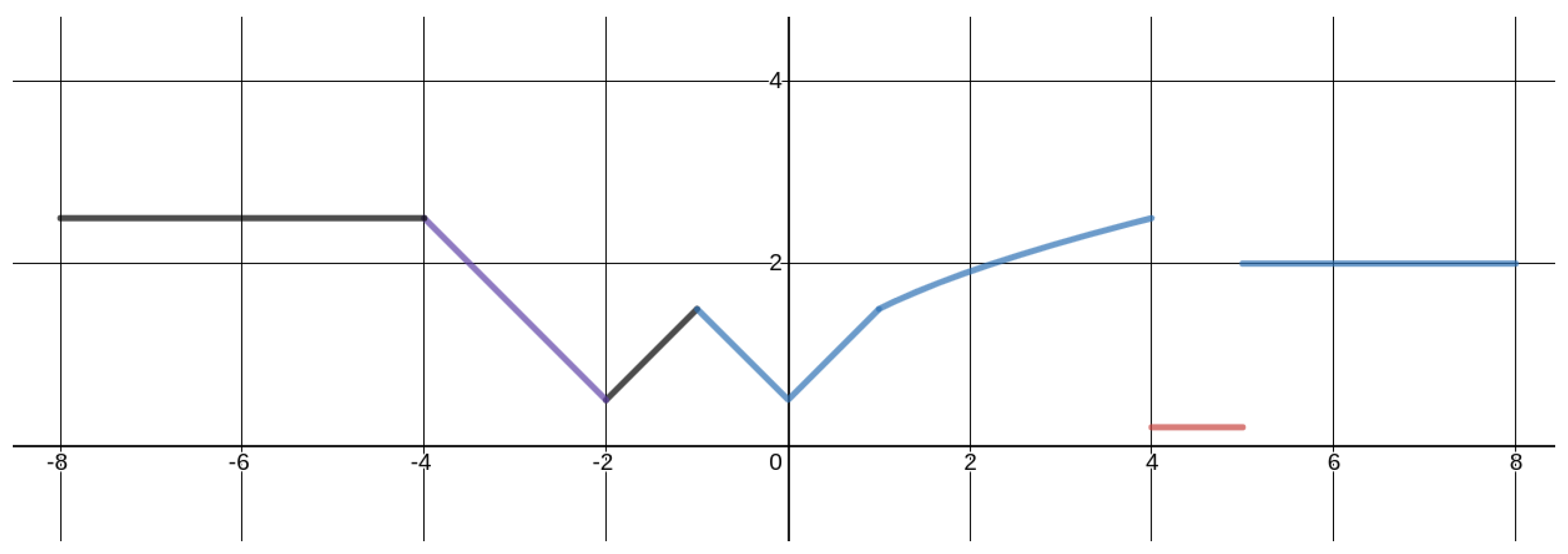
Another way of classifying an OP is by whether it is a smooth or a non-smooth one. Smooth optimization problems have smooth objective functions and constraints. A smooth function has derivatives of all orders and is differentiable. On the contrary, a non-smooth one has an objective function—or at least one constraint—that does not possess at least one of the properties of a smooth function.
Figure 2 shows an example of a one-dimensional function which is neither smooth nor convex.
From a combinatorial point of view, non-smooth OPs possess similar properties as non-convex OPs because they are time consuming to solve. The lack of derivative information makes it almost impossible to determine the direction in which the function is increasing or decreasing. Likewise, the solution space may also have several disjoint regions, each of which has its own local optimum. Unfortunately, non-convex and non-smooth OPs arise in several application domains, including telecommunication networks, economic load dispatch, portfolio optimization, vehicle routing, regression, or clustering problems. For instance, the minimum sum-of-squares clustering problem is solved by Bagirov et al. [
29] and by Karmitsa et al. [
30]. Both papers formulate the clustering problem as a non-smooth and non-convex optimization problem and make use of incremental algorithms. However, the former is based on the difference of convex functions and the latter is based on the limited memory bundle method. Real world data sets are used to test both approaches, demonstrating numerically their efficiency compared to other incremental algorithms. Difference of convex functions are also used by Bagirov et al. [
31] to solve the nonparametric regression estimation problem. These authors propose an algorithm to minimize a non-convex and non-smooth empirical
-risk function. Synthetic and real-world data sets are used to test it. Compared to other algorithms, this approach is proved to be a good alternative in terms of computational time and several prediction indicators.
Several studies have investigated the applicability of well-known metaheuristic approaches—such as tabu search, artificial bee colony optimization, or particle swarm optimization—to solve non-smooth and non-convex OPs [
32]. For example, tabu search has been used in Al-Sultan [
33] for the clustering problem and in Oonsivilai et al. [
34] for a telecommunication network problem. Ant colony optimization has been used to solve the non-smooth economic load dispatch problem in Hemamalini and Simon [
35], while particle swarm optimization has been investigated for the same problem in Niknam et al. [
36] and Basu [
37]. Both ant colony optimization and particle swarm optimization have been utilized for the non-smooth portfolio selection problem in Schlüter et al. [
38] and Corazza et al. [
39], respectively. The remainder of this paper discusses the use of BRAs in solving non-smooth optimization problems in logistics, transportation, and scheduling.
3. Basic Concepts on Biased-Randomized Algorithms
Pure greedy constructive heuristics are algorithms that iteratively build a solution by selecting the next movement from a list of candidates. Such candidates have been sorted previously according to some criteria, such as costs, savings, profits, etc. These heuristics typically select the “most promising” (in the short run) candidate from the list. Since they follow a constructive logic, a good final solution is expected by the end of the procedure. Nevertheless, these algorithms are deterministic, i.e., the solution is always the same every time the heuristic is executed. This means that the exploration process is poor, which prevents the algorithm from finding better solutions unless more complex searching structures—i.e., local searches and perturbation movements—are considered by investing more computing time. Examples of such heuristics are the well-known savings heuristic for the VRP [
40], the nearest neighbor criterion for the traveling salesman problem [
41], or the shortest processing time dispatching rule for some scheduling problems [
42].
As described in Juan et al. [
43], using a skewed (nonuniform) probability distribution to introduce a biased-randomization behavior into the process that selects the candidates from the sorted list is an efficient way of generating better solutions. The idea is to assign a weighted probability to each candidate in the list, in such a way that the more promising candidates—those at the top of the list—receive a higher probability of being selected than those below them. This randomization process leads to the generation of slightly different solutions every time the algorithm is executed. Hence, multiple executions of a BRA—either completed in a sequential or in a parallel mode—will yield a set of alternative solutions, all of them based on the logic behind the heuristic. Since we are executing many biased-random variations of the constructive procedure defined by the heuristic, chances are that some of these “near-greedy” heuristics lead to solutions that outperform the one generated by the greedy heuristic [
10]. Algorithm 1 shows a pseudo-code description of a basic BRA that performs in a sequential way.
| Algorithm 1: Biased-Randomized Algorithm (BRA; basic sequential version). |
![Algorithms 13 00008 i001 Algorithms 13 00008 i001]() |
Notice that, by using this approach, a broad exploration of the solution space is carried out, which might be specially beneficial in the case of highly irregular objective functions as the ones characterizing non-smooth OPs. The proposed methodology can be seen as a natural extension of the basic greedy randomized adaptive search procedure (GRASP) [
44], as analyzed in Ferone et al. [
10]. Instead of employing empirical probability distributions—which require time-consuming parameter fine tuning and thus might slow down computations—a theoretical probability distribution such as the geometric distribution or the decreasing triangular distribution can be used. Random variates from these theoretical distributions can be quickly generated by employing analytical expressions. Moreover, they tend to have less parameters and these are typically easy to set. Application fields such as food logistics [
45], flow-shop scheduling [
46], or mobile cloud computing [
47] have successfully utilized geometric distributions to introduce biased-randomized processes during the selection of the candidates that are employed to construct a feasible solution.
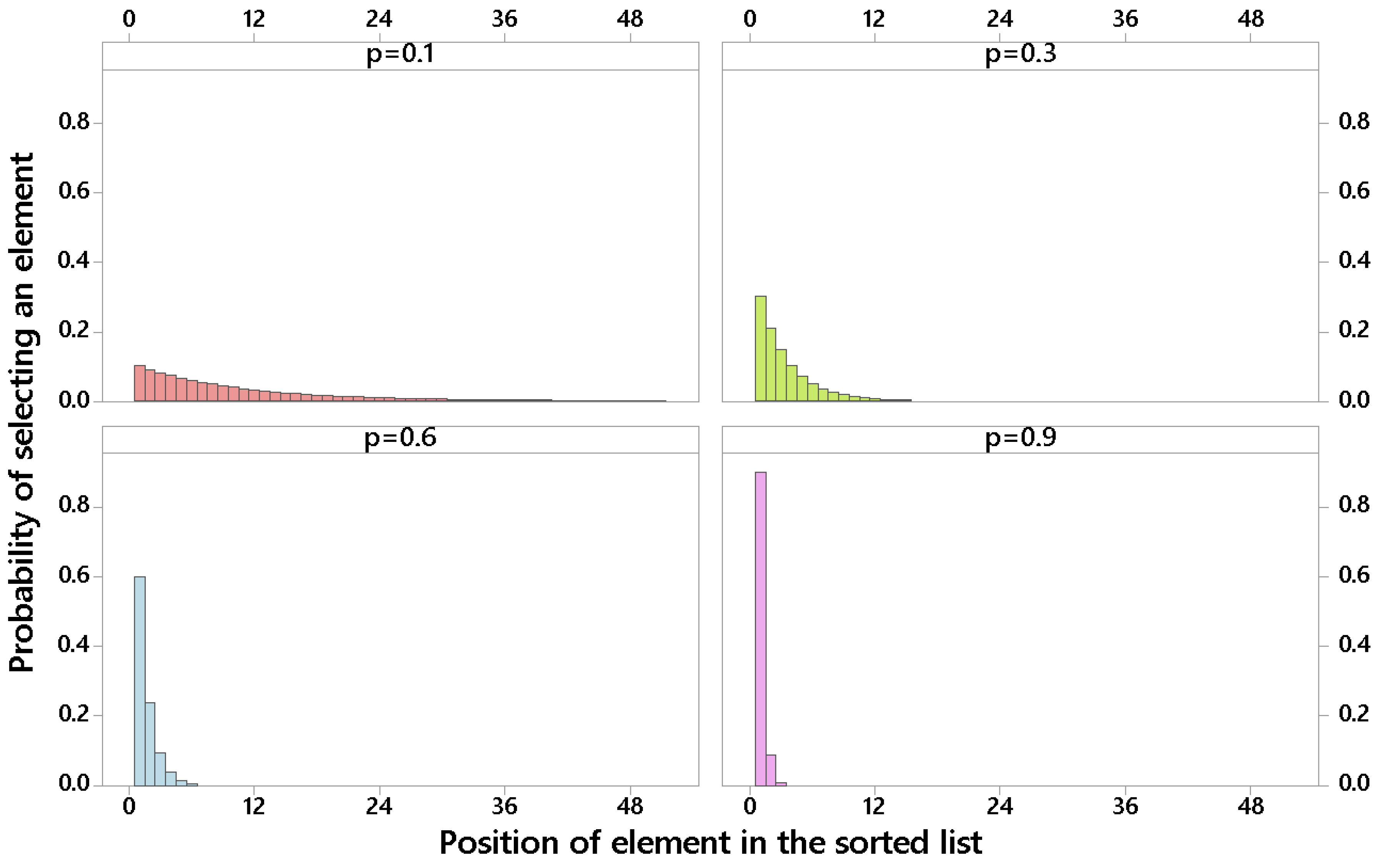
Figure 3 illustrates how geometric probability distributions with four different parameter values (
) will have a different behavior while assigning probabilities of being selected to the elements of the sorted list during the iterative construction of a biased-randomized solution.
Thus, while for the distribution is closer to a uniform one (i.e., the probabilities are distributed among a relatively large number of top positions in the sorted list), for , the behavior is closer to the greedy one that characterizes a classical heuristic, with the top element in the sorted list accumulating most of the chances of being the next selected element. Both extremes ( and ) represent diversification and greediness, respectively. Usually, parameter values in the middle of both extremes are able to provide a better trade-off between these two cases, thus promoting some degree of diversification without losing the rational (domain-specific) criterion employed to sort the list.
4. Applications in Logistics
The field of logistics encompasses several problems, including supply chain design, facility location, warehouse management, etc. All of these problems have been studied extensively in the literature, mostly with the consideration of hard constraints and smooth objective functions. Nevertheless, as previously discussed, real-world problems in the field of logistics may allow some constraints to be violated by incurring a penalty cost, which needs to be incorporated into the objective function. This typically leads to the emergence of non-smooth objective functions. Therefore, traditional exact methods cannot always be efficiently employed to solve these problems and heuristic-based algorithms are required. This section focuses on the use of BRAs in solving the facility location problem (FLP) [
48] and its variants. This problem consists of locating a set of facilities—e.g., production plants, distribution centers, warehouses, etc.—from which a set of customers must be served. Basic decisions are as follows: (i) which potential facilities must be open (or remain open) and which ones must be closed (or not open) and (ii) how to allocate customers to open facilities. This problem is
NP-hard [
49]. Moreover, facilities can be considered capacitated or uncapacitated. The former refers to the case in which each facility has a limited capacity that cannot be exceeded by the total demand served from there. In the latter, the facilities’ total capacity is virtually infinite or at least much greater than the cumulative demand of all customers.
BRAs have been applied successfully to solve both capacitated and uncapacitated FLPs. The latter has been tackled mainly considering hard constraints [
50]. In Correia and Melo [
51], the authors considered a multi-period FLP in which customers are sensitive to delivery lead times (i.e., some flexibility is allowed regarding the delivery dates). Using similar concepts, Estrada-Moreno et al. [
52] consider soft constraints and a non-smooth and non-convex objective function for the single-source capacitated FLP. In this context, “single-source” refers to an additional constraint stating that each customer must be served from just one facility. The capacity of each facility may be exceeded by the consideration soft constraints. In real world, decision-makers manage this by using strategies such as storing safety stocks, performing emergency deliveries, and outsourcing part of the customers’ service. These strategies tend to generate additional costs that need to be considered as well during the optimization process. The aforementioned authors propose the following model to represent the single-source FLP with soft capacity constraints:
In this model,
is a binary variable that takes the value of 1 if customer
i is serviced by facility
j (0 otherwise). Similarly,
is another binary variable that takes the value 1 if facility
j is open;
is the service cost of assigning customer
i to facility
j; and
is a piecewise function representing the cost of opening a facility
j:
where
is the demand of customer
i;
is the nominal capacity of facility
j;
is defined for any
; and
is a non-smooth function which will be applied whenever the total demand assigned to facility
j exceeds its maximum capacity
.
A BRA is integrated within an iterated local search metaheuristic to solve the OP above. The algorithm contains the following components: (i) an initial solution generation, based on a BRA; (ii) a local search procedure composed of functions that open or close facilities; (iii) a perturbation procedure that destroys the current solution by opening a number of closed facilities and reallocating all customers to the newly open facilities; and (iv) an acceptance criterion based on the concept of “credit”, in which a solution with a worse cost is accepted if this credit is not exceeded. The objective is to explore other regions of the solution space to escape from local optima. A total of 60 small-, medium-, and large-scale instances are used to test this approach. Different levels of penalties are also tested. Authors demonstrate the advantages of using soft constraints, obtaining costs that are lower than the optimal ones found in the literature for hard constraints. Authors show that, if penalty costs are low or moderate, hard constraints’ violation is worth because some facilities do not need to be open and a more efficient allocation of customers can be made. Finally, a comparison between their BRA-inspired metaheuristic and the solution provided by the commercial tool LocalSolver is drawn. Both approaches obtain similar solutions for small- and medium-scale instances, but the BRA-based algorithm proves to be superior for large-scale instances.
5. Applications in Transportation
Transportation and distribution are two fields belonging to the operational level of decisions in logistics. The vehicle routing problem [
53,
54] and the arc-routing problem (ARP) [
55,
56] are two well-known optimization problems in the area of transportation and freight distribution. A traditional VRP consists of a graph formed by a set of nodes and a set of arcs. One of the nodes represents a depot and the rest represent customers, which are connected to each other by the set of arcs. A network of routes must be designed to visit each customer in order to meet a known demand. A single vehicle departing and returning to the depot is assigned to each route. The objective is to minimize the total cost of traversing the arcs. The traditional ARP is similar to the VRP, but the former assigns a demand to each arc and not to each node. Moreover, in the ARP, the underlying graph is not usually a complete one. These problems are
NP-hard, i.e., as the number of customers grows, the quantity of alternative solutions increases almost exponentially. Therefore, heuristic and metaheuristic algorithms have been employed extensively to solve these OPs. The problems become even more difficult to solve in the presence of non-smooth and non-convex objective functions, as when soft constraints are considered. In this context, soft constraints would include time window constraints or capacity constraints that are allowed to be violated to some extent [
9]. These soft constraints also allow decision-makers to consider more realistic models that take into account different management strategies and policies. For instance, customers would accept a delayed delivery if the supplier offers a discount. Likewise, a percentage of the deliveries can be outsourced if in-house capacity is exceeded.
In the VRP case, Juan et al. [
43] consider a capacitated version of the problem with a non-smooth and non-convex objective function and soft constraints. These authors propose a BRA-based approach called
MIRHA.This is a multi-start procedure consisting of two phases: a first phase in which a biased-randomized version of a constructive heuristic is designed according to a geometric probability distribution and a second (improvement) phase in which an adaptive local search procedure is implemented. Several instances from the literature are used to test the proposed algorithm and to compare it with a traditional GRASP. In general, the new algorithm outperforms the existing ones in terms of solution quality (efficiency), both in the presence of hard and soft constraints. In the case of the ARP, De Armas et al. [
57] propose a BRA to solve the capacitated version of the problem with a non-smooth and non-convex objective function. The base heuristic considered is
SHARP [
58]. Firstly, they propose the following model:
where
represents a route in a set of routes
;
represents a complete set of routes (i.e., a solution);
is the total cost of using route
;
is the demand of arc
; and
is a binary variable that takes the value 1 if and only if the arc
is covered by a vehicle
k in the set of vehicles
T. The cost function associated with any route
is defined as a piecewise function as follows:
In the former expression, is a non-smooth function which will be applied whenever the actual route cost exceeds the threshold value allowed for any route, C. In this work, the associated penalty factor is linearized to obtain a truncated version of the problem. Then, the authors propose a BRA combined with an iterated local search metaheuristic. This hybrid algorithm is divided into four main phases: (i) an initial solution generation using a biased-randomized version of the SHARP heuristic; (ii) a perturbation procedure based on destruction-reconstruction strategies; (iii) a local search phase using cache memory; and (iv) the use of an acceptance criterion based on a simulated annealing procedure. A total of 87 artificial and real-world instances are used to test this approach. The mathematical model is solved using the CPLEX commercial tool and is used to obtain lower bounds for optimal costs. Thus, the performance of the metaheuristic is assessed, obtaining important average gap reductions regarding previous methods.
The results obtained in the previous studies demonstrate clear advantages of considering soft constraints over hard ones. Moreover, the associated models are better representation of the real-world problems. For example, budget limits established per route can be violated in the model as it is done in real life. The soft constraints are not free, but they enhance profitability. For instance, penalization costs must be incurred for violating budget limits. However, this violation leads to better route design, which generates savings for the company. In the end, it might be worthy to explore if the value of the savings compensates the penalties incurred. Finally, the consideration of soft constraints implies the construction of a more generic model, which includes a combination of soft and hard constraints. A more generic model yields more alternative solutions, and therefore, decision makers have more options to design a routing or distribution plan that better fits their utility function.
6. Applications in Scheduling
In the operations research field, scheduling OPs are among the most studied topics. According to Pinedo [
59], “scheduling is a decision-making process [...] that deals with the allocation of resources to tasks over given time periods and its goal is to optimize one or more objectives.” A typical example considers that the resources are machines, that the tasks are operations carried out by these machines, and that the objective is the minimization of the
makespan—i.e., the completion time of the last task. This apparently simple definition actually includes a huge family of problems that are
NP-hard as well.
BRAs have been proved to be useful also for scheduling problems. For instance, Martin et al. [
15] used them in a multi-agent based framework to solve both routing and scheduling problems. Usually, hard constraints are considered in the literature. However, Ferrer et al. [
60] solved the permutation flow-shop problem (PFSP) with a non-smooth objective function. This problem consists of a set of jobs that must be processed by a set of machines. Each job is composed of a set of operations in which the quantity is equal to the number of machines. Moreover, all operations in each job must be executed in the same sequence by the set of machines. The processing time of each operation in each machine is known, although it is different for each job. The idea is to determine the sequence in which jobs must be executed in order to minimize the makespan. One of the contributions of the aforementioned authors is the consideration of the failure-risk term in the objective function. This term is incorporated into the traditional makespan target. The failure-risk cost is incurred when a machine operates continuously without a break, which is highly usual when minimizing the makespan. This cost is equivalent to a penalty cost in logistics and transportation problems, and therefore, the failure-risk cost introduces a non-smooth component into the objective function. A mathematical model is proposed to tackle this problem. Then, a BRA is combined with an iterated local search to develop the solving approach. Its basic steps are as follows: (i) generation of an initial solution through a biased-randomized version of a classical heuristic; (ii) perturbation and local search procedures are implemented to improve the solution quality; and (iii) the consideration of an acceptance criterion, based on simulated annealing, which may accept worst solutions with the purpose of exploring the solution space and escape from local minima. A total of 120 benchmark instances are used to test this approach. Results show that explicit consideration of the reduction in failure-risk cost leads to a reduction of the total cost for all sets of instances (negative gaps are shown). The makespan cost increases, but the reduction in failure-risk costs compensate this rise. A comparison with other metaheuristic approaches shows that the performance of the new method is similar or even better. This novel approach proves to be useful for decision makers since they have more solution alternatives to select, given the particular goals of each company, i.e., for some decision-makers, the makespan may show a higher relevance, but for others, failure-risk cost may be a more important indicator.
7. General Insights from Previous Numerical Experiments
Based on the data provided by Juan et al. [
43] for the non-smooth VRP, De Armas et al. [
57] for the non-smooth ARP, Ferrer et al. [
60] for the non-smooth permutation FSP, and Estrada-Moreno et al. [
52] for the non-smooth FLP,
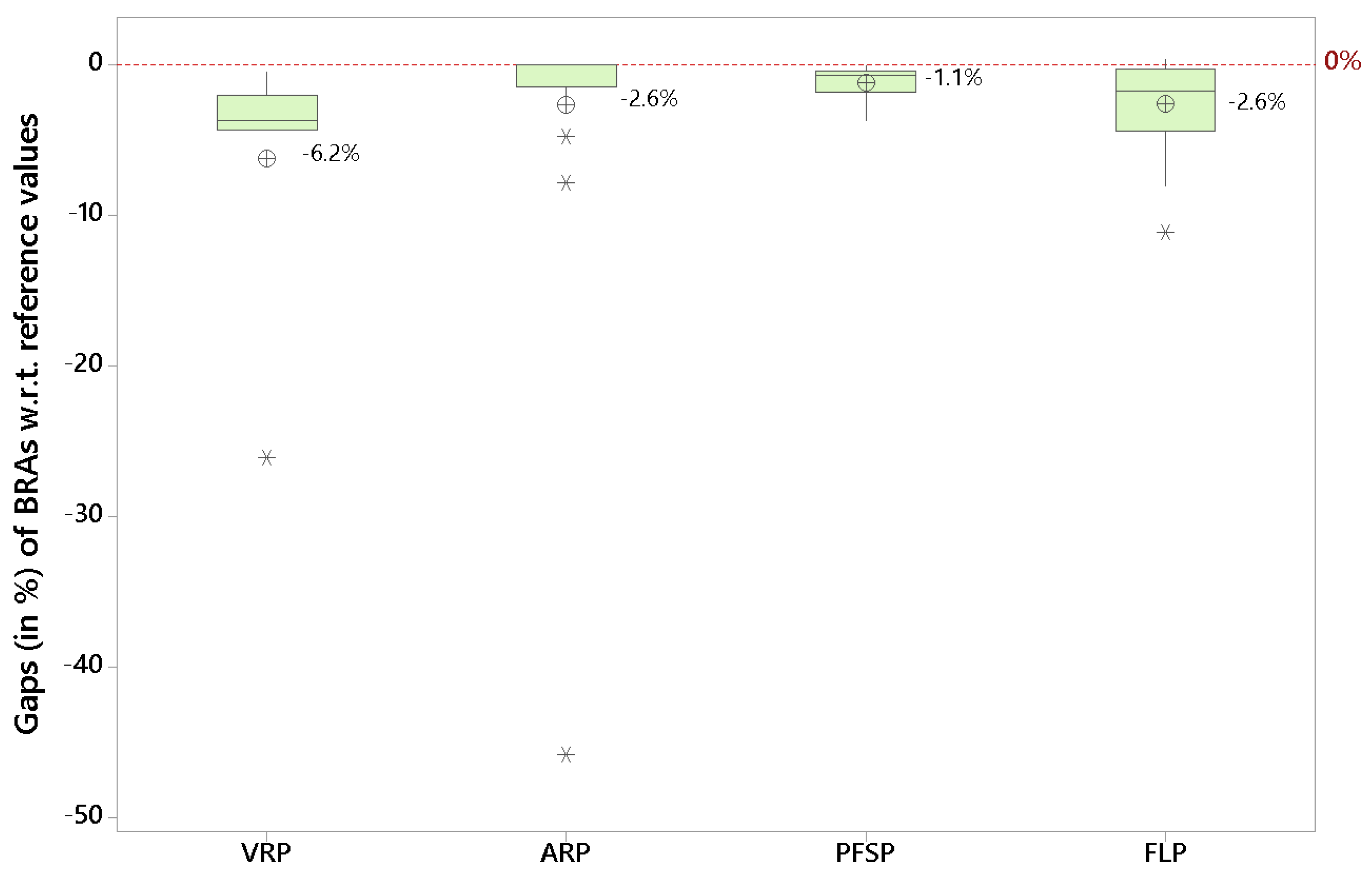
Figure 4 shows percentage gaps between the corresponding BRA and the reference value employed in the corresponding work.
Precaution has to be used while interpreting this figure, since these gaps depend on the particular OP being considered, the specific instances, the selected reference value, etc. However, some insights can be obtained: (i) in all four OPs, BRAs have been able to obtain negative gaps with respect the reference values, which in several cases represent the best-known solutions for the hard-constrained version of the problem; (ii) whenever soft constraints can be considered in a real-life scenario, it might pay off to design solutions that violate these constraints to some extent, since the associated benefits might overcome the corresponding penalties; (iii) since they combine good diversification (exploration) and heuristic-based rational searching of the solution space, BRAs constitute an effective tool to cope with non-smooth OPs with highly irregular objective functions; and (iv) in some particular cases, considering soft constraints instead of hard ones might generate noticable improvements in the quality of the solution; hence, modeling and solving experts should always consider how really hard is a constraint in practice. Finally, it should be also noticed that, in all the four studies and regardless of the specific OP being solved and the application field, the authors illustrated with numerical examples the limitations of exact methods when solving non-smooth OPs. Despite this generalized conclusion, they also recommended to investigate combinations between exact methods (from global optimization and mathematical programming) and heuristic-based algorithms. The latter can play a more exploratory role and can identify promising areas, while the former can intensify the searching process inside these selected areas.
8. Conclusions
Many real-world problems can be more accurately modeled using soft constraints rather than hard ones. Soft constraints can be violated to some extent, and whenever this occurs, a penalty cost—which is usually defined via a piecewise function depending on the magnitude of the violation—has to be taken into account. Hence, non-smooth and non-convex optimization models are highly relevant in many practical applications. In general, decision makers may consider some constraints to be soft, specifically when the associated capacity limitations can be outsourced or certain delays in the service can be managed with the customer. This paper has reviewed several works in this area. These works refer to the consideration of non-smooth objective functions in popular OPs such as the vehicle routing problem, the arc routing problem, the facility location problem, and the permutation flow-shop problem. In all these cases, the use of BRAs has shown to be an effective tool to generate a myriad of high-quality solutions in short computing times, even for large-size instances of these NP-hard OPs. Also, these BRAs have outperformed other classical optimization methods from the areas of mathematical programming, global optimization, and even metaheuristics.
The reviewed papers demonstrate that using BRAs enhances the exploration of the solution space by generating iteratively. The execution of these algorithms might be easily parallelized by simply changing the seed of the pseudo-random number generator, which means that, in many cases, high-quality solutions—close to near-optimal ones—can be frequently obtained in real-time (less than a second). Part of the effectiveness of these algorithms lies in the fact that they preserve the logic of a good constructive heuristics while, at the same time, they offer a much larger exploration capability of the solution space. The paper has also discussed how these BRAs can be hybridized with classical metaheuristic frameworks—e.g., iterated local search, simulated annealing, etc.—in order to increase the searching process if more computing time is allowed.
Several research lines can be explored for future work: (i) the hybridization of the BRAs with the
ECAM global optimization algorithm [
61], so that the former can provide different starting points (exploration) that the latter can use to intensify the search in promising regions; (ii) other optimization problems can be considered as well, especially in application fields such as smart cities, e-commerce, computational finance, or bioinformatics; and (iii) considering even more realistic versions of the optimization problems by adding stochastic and dynamic conditions into them, for which hybridization of BRAs with simulation and machine learning techniques might be necessary.