Markov Chain Monte Carlo Based Energy Use Behaviors Prediction of Office Occupants
Abstract
1. Introduction
2. Methodology
2.1. Markov Chain
2.2. Metropolis–Hastings Algorithm
- The MH algorithm takes random values in the parameter space as the starting parameter . The random parameter is generated from the distribution function of parameters, and the probability density of the current parameter is calculated.
- First, a random number is extracted from the uniform distribution of , and then, we determine whether to keep the current parameter according to whether the probability density ratio between the current parameter and the starting parameter is greater than . If the reception probability of the current parameter is greater than , , the state is accepted, and it needs to be updated , otherwise [36]. The acceptance probability of MH can be described as:
3. Proposed Method
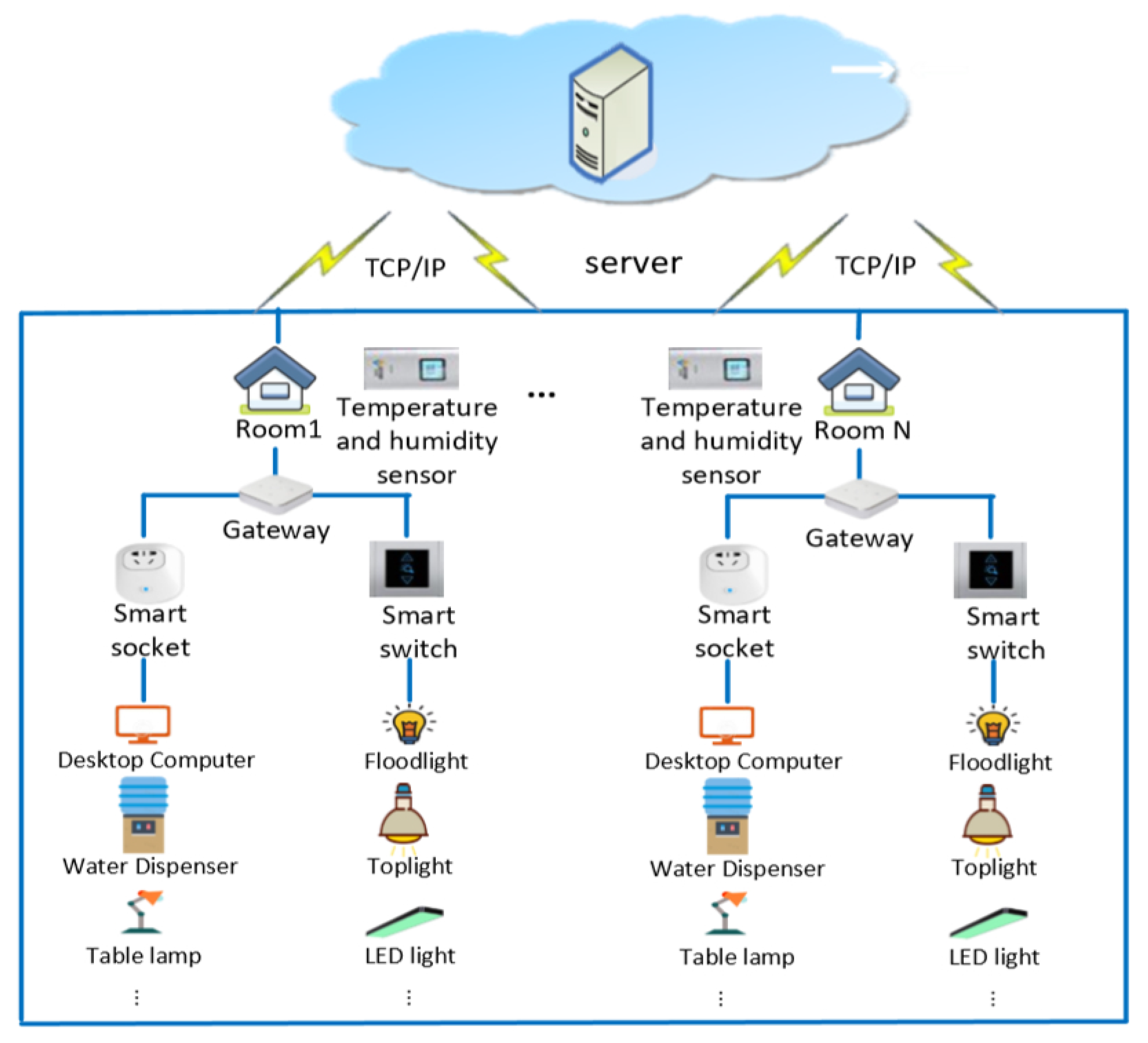
3.1. Data Acquisition
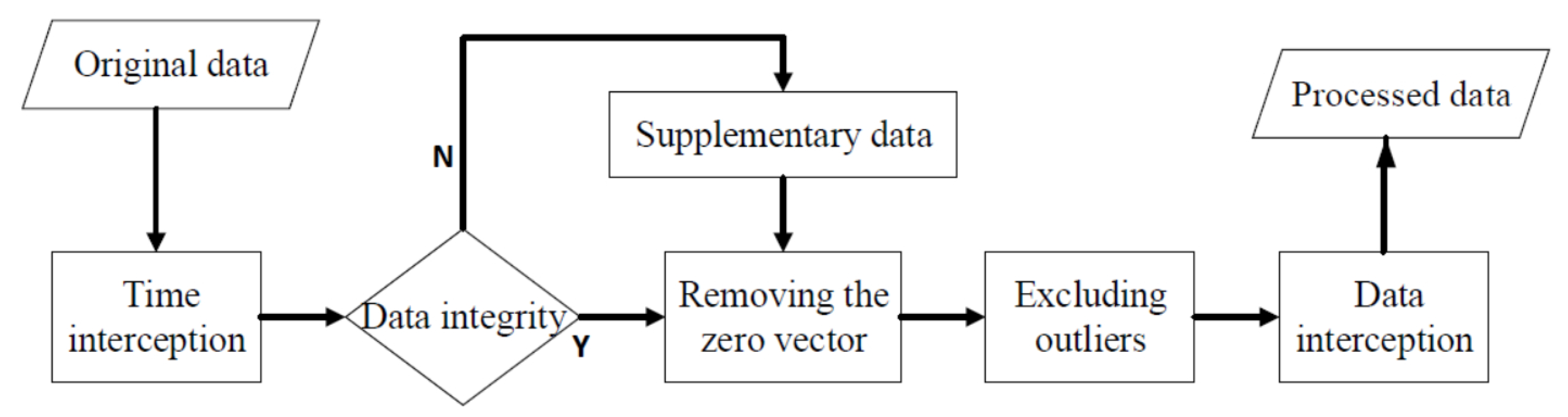
3.2. Data Preprocessing
- (1)
- Time interception: The data should strictly require daily data starting from 00:00, with one minute as the sampling period and yyyy/m/d h:mm as the time format for date processing. One-thousand-four-hundred-forty records could be obtained in one day. It was necessary to determine whether the data were complete. If there was a missing value, we assigned the previous state.
- (2)
- Removing the zero vector: Removing the state data of the powered device that was not working for a whole day.
- (3)
- Excluding outliers: For data outliers that occasionally occurred in the original data, outliers were detected and removed by the Laida algorithm [38].
- (4)
- Data interception: By analyzing the time period of the equipment action daily, the state data during the device on and off time periods were respectively intercepted.
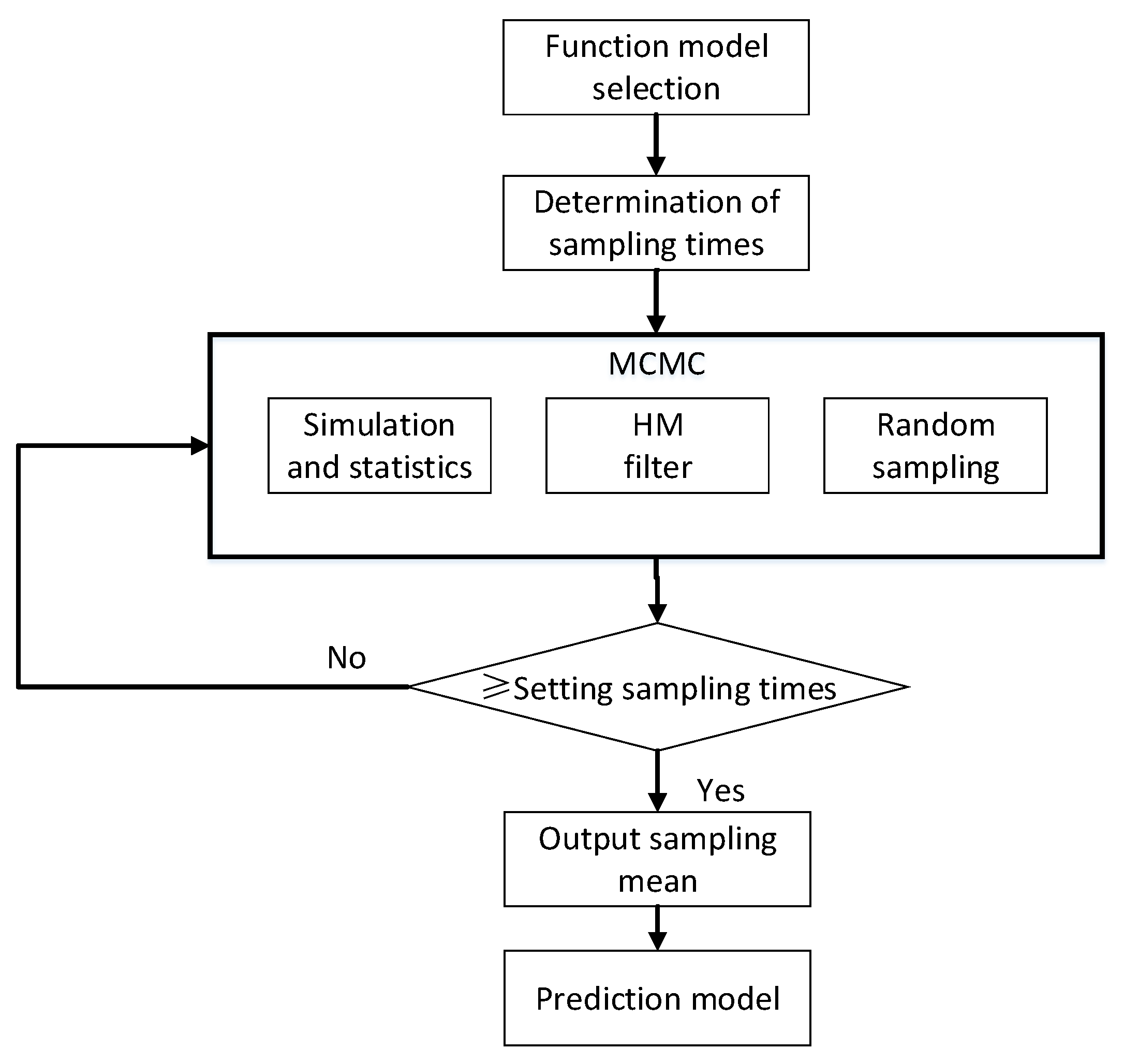
3.3. Model Training
3.3.1. Action Model
3.3.2. Working Hours Model
3.3.3. Air-Conditioner Energy Use Behavior Model
4. Experimental Evaluation
4.1. Evaluation Indices
4.2. Comparison between MCMC Estimation and MLE
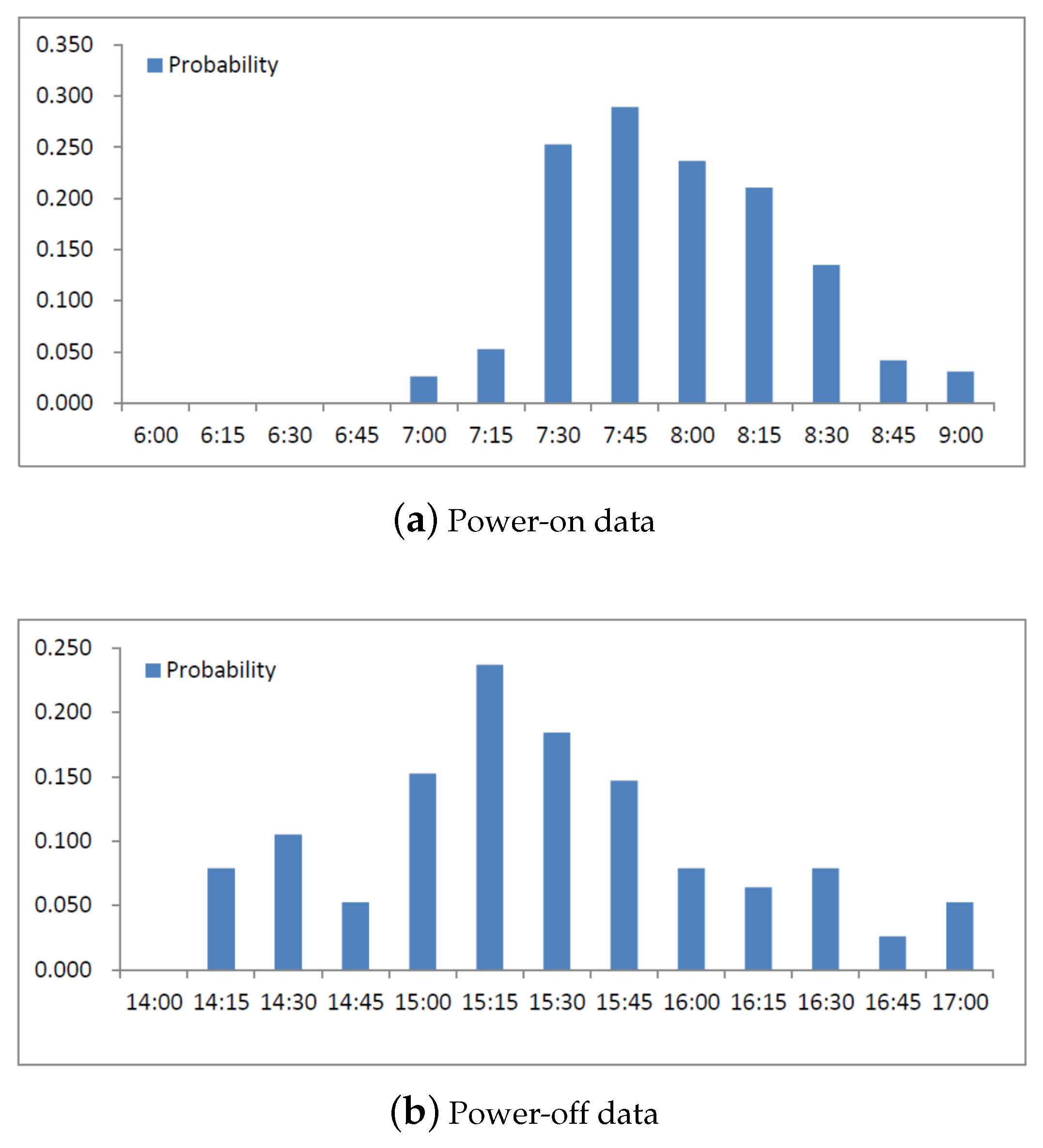
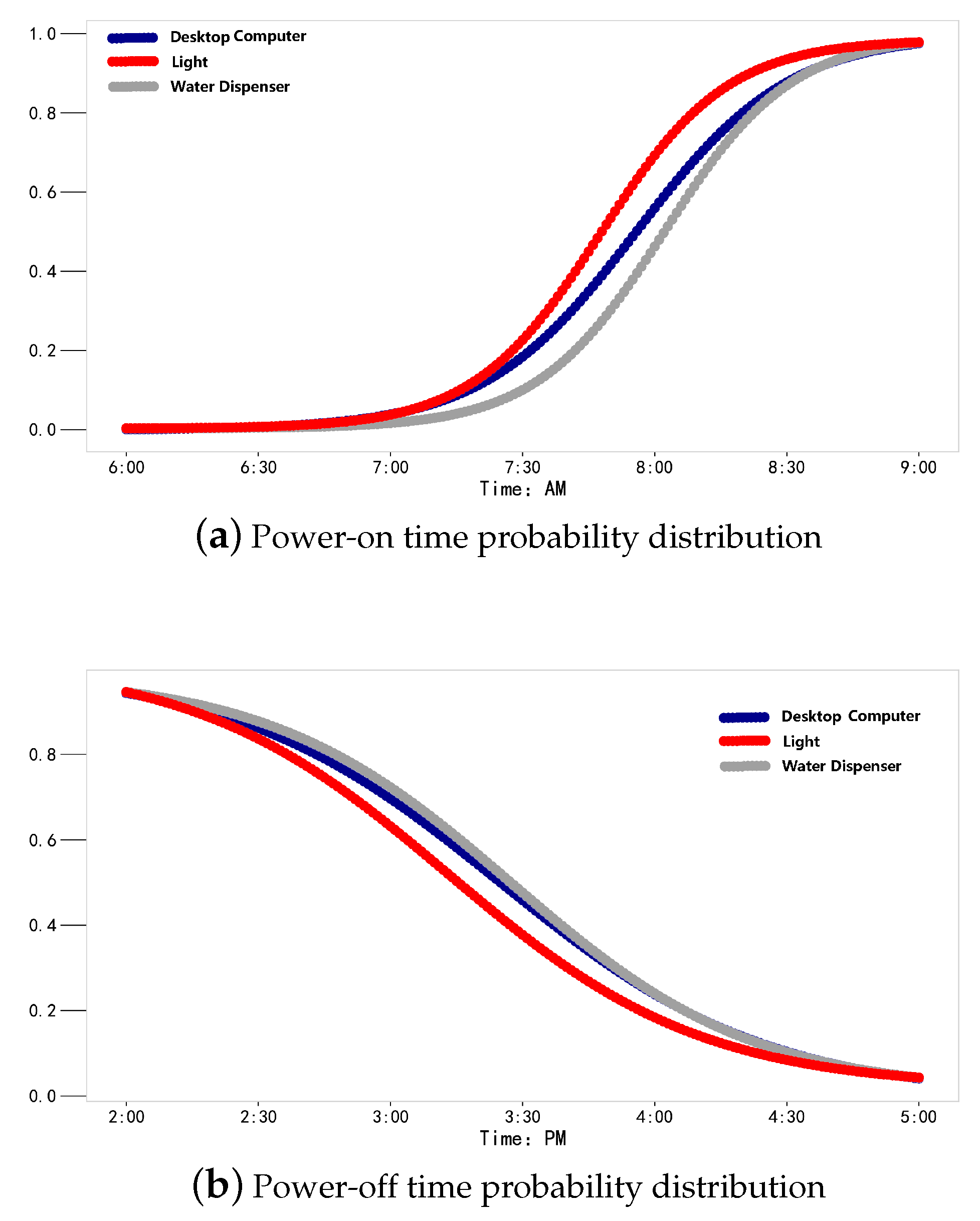
4.3. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tian, C.; Li, C.; Zhang, G.; Lv, Y. Data driven parallel prediction of building energy consumption using generative adversarial nets. Energy Build. 2019, 186, 230–243. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Weckman, G.R.; Young, W.A. An overview of energy demand forecasting methods published in 2005-2015. Energy Syst. 2017, 8, 411–447. [Google Scholar] [CrossRef]
- Ren, X.; Yan, D.; Wang, C. Air-conditioning usage conditional probability model for residential buildings. Build. Environ. 2014, 81, 172–182. [Google Scholar] [CrossRef]
- Rafsanjani, H.N.; Ahn, C.R.; Alahmad, M. A review of approaches for sensing, understanding, and improving occupancy-related energy-use behaviors in commercial buildings. Energies 2015, 8, 10996–11029. [Google Scholar] [CrossRef]
- Muncaster, J.; Ma, Y. Activity recognition using dynamic Bayesian networks with automatic state selection. In Proceedings of the 2007 IEEE Workshop on Motion and Video Computing (WMVC’07), Austin, TX, USA, 23–24 February 2007; p. 30. [Google Scholar]
- Shin, J.H.; Lee, B.; Park, K.S. Detection of abnormal living patterns for elderly living alone using support vector data description. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 438–448. [Google Scholar] [CrossRef]
- Nam, Y.; Park, J.W. Child activity recognition based on cooperative fusion model of a triaxial accelerometer and a barometric pressure sensor. IEEE J. Biomed. Health Inform. 2013, 17, 420–426. [Google Scholar]
- Melián-Gutiérrez, L.; Zazo, S.; Blanco-Murillo, J.L.; Pérez-Álvarez, I.; García-Rodríguez, A.; Pérez-Díaz, B. Hf spectrum activity prediction model based on hmm for cognitive radio applications. Phys. Commun. 2013, 9, 199–211. [Google Scholar] [CrossRef]
- Singh, D.; Merdivan, E.; Hanke, S.; Kropf, J.; Geist, M.; Holzinger, A. Convolutional and recurrent neural networks for activity recognition in smart environment. In Towards Integrative Machine Learning and Knowledge Extraction; Springer: Cham, Switzerland, 2017; pp. 194–205. [Google Scholar]
- Withanage, K.I.; Lee, I.; Brinkworth, R.; Mackintosh, S.; Thewlis, D. Fall recovery subactivity recognition with rgb-d cameras. IEEE Trans. Ind. Inform. 2016, 12, 2312–2320. [Google Scholar] [CrossRef]
- Zou, H.; Chen, Z.; Jiang, H.; Xie, L.; Spanos, C. Accurate indoor localization and tracking using mobile phone inertial sensors, wifi and ibeacon. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; pp. 1–4. [Google Scholar]
- Huang, B.; Qi, G.; Yang, X.; Zhao, L.; Zou, H. Exploiting cyclic features of walking for pedestrian dead reckoning with unconstrained smartphones. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 374–385. [Google Scholar]
- van Kasteren, T.; Noulas, A.; Englebienne, G.; Kröse, B. Accurate activity recognition in a home setting. In Proceedings of the 10th International Conference On Ubiquitous Computing, Seoul, Korea, 21–24 September 2008; pp. 1–9. [Google Scholar]
- Singla, G.; Cook, D.J.; Schmitter-Edgecombe, M. Recognizing independent and joint activities among multiple residents in smart environments. J. Ambient. Intell. Humaniz. Comput. 2010, 1, 57–63. [Google Scholar] [CrossRef]
- van Kasteren, T.L.; Englebienne, G.; Krose, B.J. Hierarchical activity recognition using automatically clustered actions. In Proceedings of the International Joint Conference on Ambient Intelligence, Amsterdam, The Netherlands, 16–18 November 2011; pp. 82–91. [Google Scholar]
- Vail, D.L.; Veloso, M.M.; Lafferty, J.D. Conditional random fields for activity recognition. In Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems, Honolulu, HI, USA, 14–18 May 2007; p. 235. [Google Scholar]
- Wu, T.-Y.; Lian, C.-C.; Hsu, J.Y.-J. Joint recognition of multiple concurrent activities using factorial conditional random fields. In Proceedings of the 22nd Conference on Artificial Intelligence (AAAI-2007), Vancouver, BC, Canada, 22–26 July 2007. [Google Scholar]
- Chen, R.; Tong, Y. A two-stage method for solving multi-resident activity recognition in smart environments. Entropy 2014, 16, 2184–2203. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, D.; Hong, T.; Ren, X. Data analysis and stochastic modeling of lighting energy use in large office buildings in china. Energy Build. 2015, 86, 275–287. [Google Scholar] [CrossRef]
- Indraganti, M. Behavioural adaptation and the use of environmental controls in summer for thermal comfort in apartments in india. Energy Build. 2010, 42, 1019–1025. [Google Scholar] [CrossRef]
- Indraganti, M. Thermal comfort in apartments in india: Adaptive use of environmental controls and hindrances. Renew. Energy 2011, 36, 1182–1189. [Google Scholar] [CrossRef]
- Wang, C.; Yan, D.; Ren, X. Modeling individual’s light switching behavior to understand lighting energy use of office building. Energy Procedia 2016, 88, 781–787. [Google Scholar] [CrossRef]
- Kumagai, S.; Kishima, S. Building air conditioning model using the room-specific thermal inertia and its implementation as a controller. IEEJ Trans. Electron. Inf. Syst. 2014, 134, 620–633. [Google Scholar]
- Glicksman, L.R.; Taub, S. Thermal and behavioral modeling of occupant-controlled heating, ventilating and air conditioning systems. Energy Build. 1997, 25, 243–249. [Google Scholar] [CrossRef]
- Hadfield, J.D. Mcmc methods for multi-response generalized linear mixed models: the mcmcglmm r package. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G.; Casella, G. Introducing Monte Carlo Methods with R; Springer: New York, NY, USA, 2010; Volume 18. [Google Scholar]
- Li, C.-Y.; Ji, H.-B. A new particle filter with ga-mcmc resampling. In Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007; Volume 1, pp. 146–150. [Google Scholar]
- Mingas, G.; Rahman, F.; Bouganis, C.-S. On optimizing the arithmetic precision of mcmc algorithms. In Proceedings of the 2013 IEEE 21st Annual International Symposium on Field-Programmable Custom Computing Machines, Seattle, WA, USA, 28–30 April 2013; pp. 181–188. [Google Scholar]
- Andrieu, C.; de Freitas, N.; Doucet, A.; Jordan, M.I. An introduction to mcmc for machine learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef]
- Jernigan, R.W.; Baran, R.H. Testing lumpability in Markov chains. Stat. Probab. Lett. 2003, 64, 17–23. [Google Scholar] [CrossRef]
- Ng, W.; Reilly, J.P.; Kirubarajan, T.; Larocque, J.-R. Wideband array signal processing using mcmc methods. IEEE Trans. Signal Process. 2005, 53, 411–426. [Google Scholar] [CrossRef]
- Dwivedi, R.; Chen, Y.; Wainwright, M.J.; Yu, B. Log-concave sampling: Metropolis-hastings algorithms are fast! arXiv 2018, arXiv:1801.02309. [Google Scholar]
- Roberts, G.O.; Stramer, O. On inference for partially observed nonlinear diffusion models using the metropolis–hastings algorithm. Biometrika 2001, 88, 603–621. [Google Scholar] [CrossRef]
- Chen, P.; Xu, R.-X. Metropolis-hastings adaptive algorithm and its application. Syst. Eng. Theory Pract. 2008, 1, 100–108. [Google Scholar]
- Chen, M.; Wei, F.; Chao, Y.; Li, X. Bayesian statistics and mcmc method-matlab programming for metropolis-hastings (mh) algorithm. J. East China Jiaotong Univ. 2018, 1, 1–8. [Google Scholar]
- Fries, M.; Baum, A.; Wittmann, M.; Lienkamp, M. Derivation of a real-life driving cycle from fleet testing data with the Markov-chain-monte-carlo method. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2550–2555. [Google Scholar]
- Peng, W.; Li, C.; Zhang, G.; Yi, J. Interval type-2 fuzzy logic based transmission power allocation strategy for lifetime maximization of wsns. Eng. Appl. Artif. Intell. 2020, 87, 103269. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, P.; Jiang, J.; Yang, K.; Lv, Z. A Bayesian approach for sleep and wake classification based on dynamic time warping method. Multimed. Tools Appl. 2017, 76, 17765–17784. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of euler–bernoulli beams using eringen’s integral formulation: a paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Mizuseki, K.; Buzsáki, G. Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep. 2013, 4, 1010–1021. [Google Scholar] [CrossRef]
- Schneck, A.; Kalle, S.; Pryss, R.; Schlee, W.; Probst, T.; Langguth, B.; Landgrebe, M.; Reichert, M.; Spiliopoulou, M. Studying the potential of multi-target classification to characterize combinations of classes with skewed distribution. In Proceedings of the 2017 IEEE 30th International Symposium on Computer-Based Medical Systems (CBMS), Thessaloniki, Greece, 22–24 June 2017; pp. 630–635. [Google Scholar]
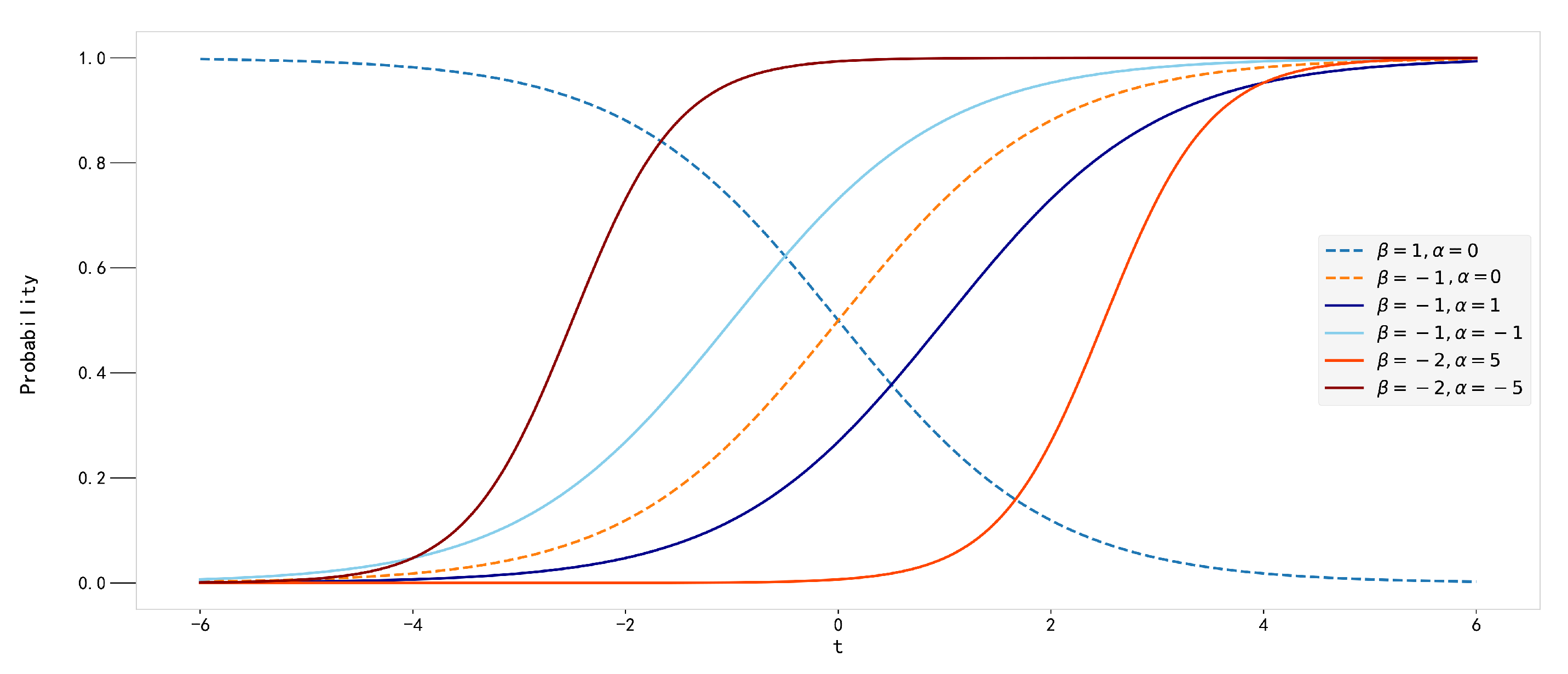
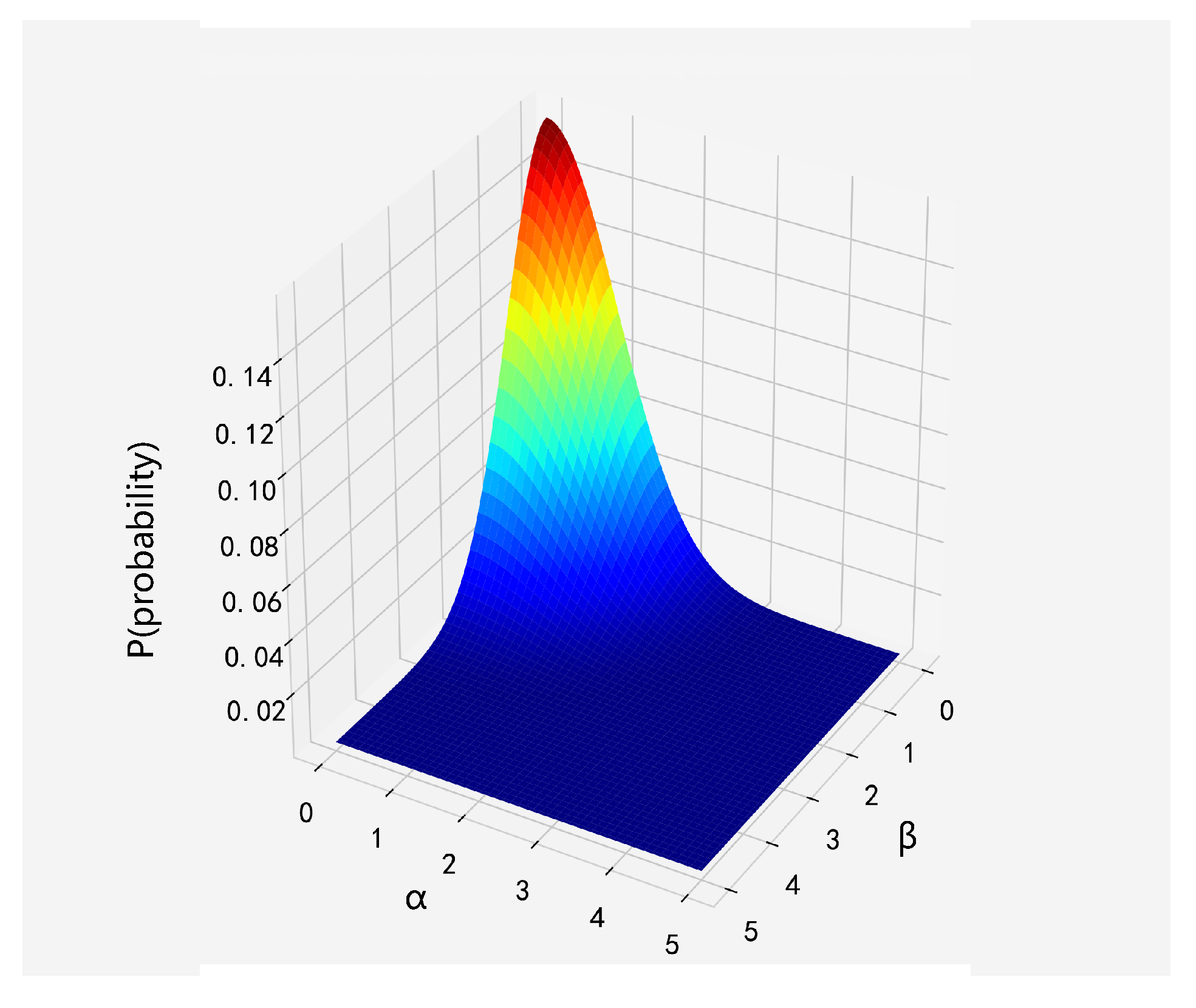
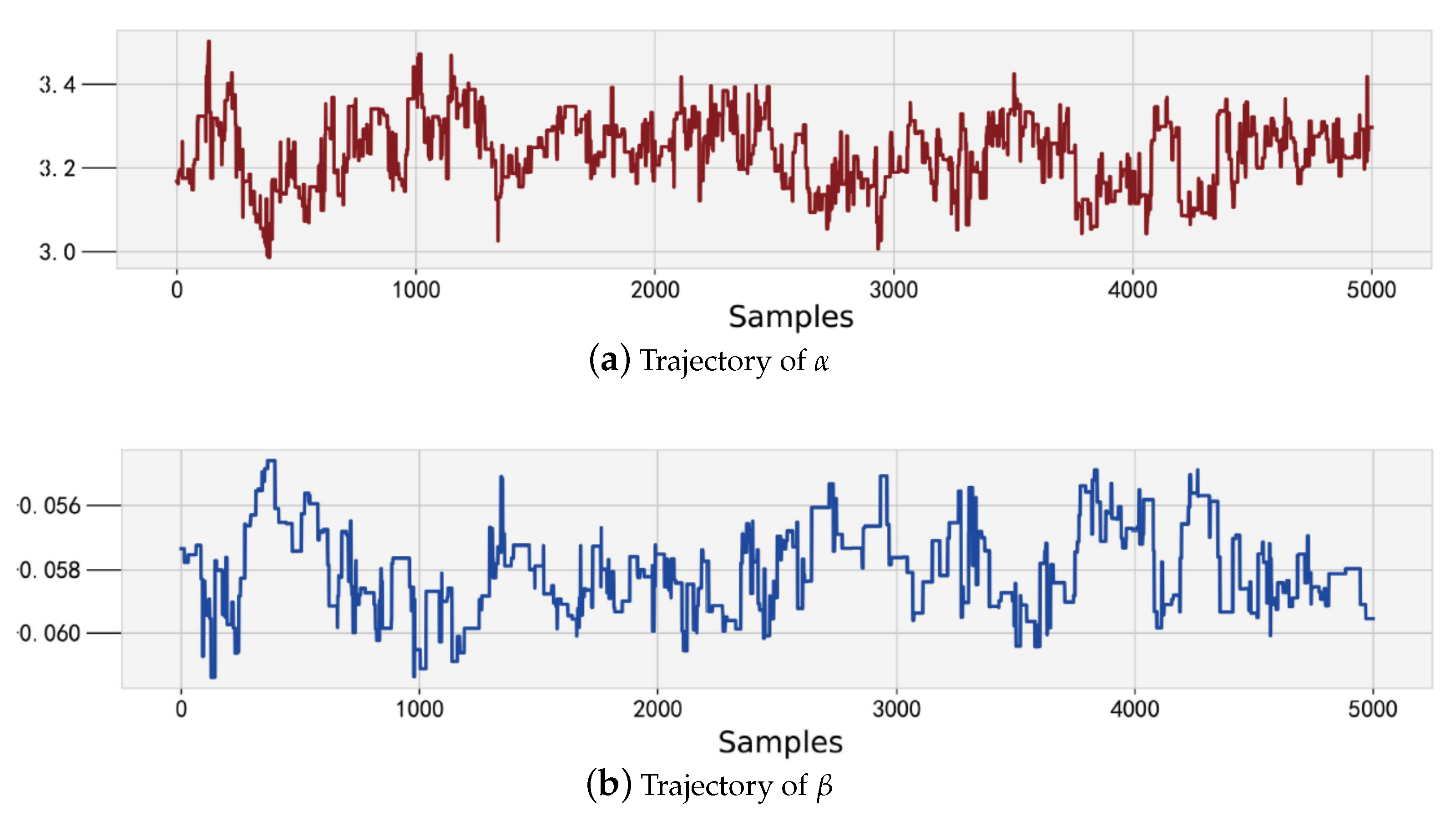
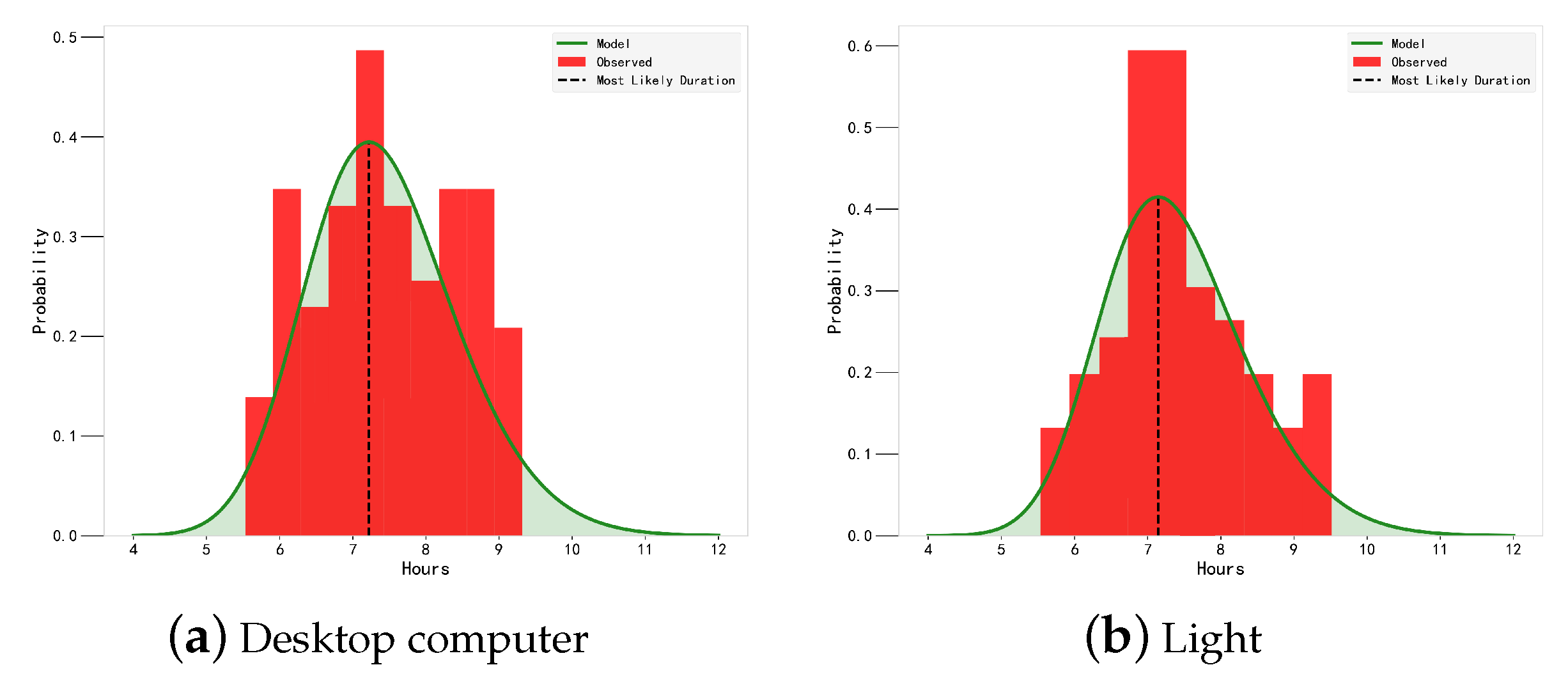
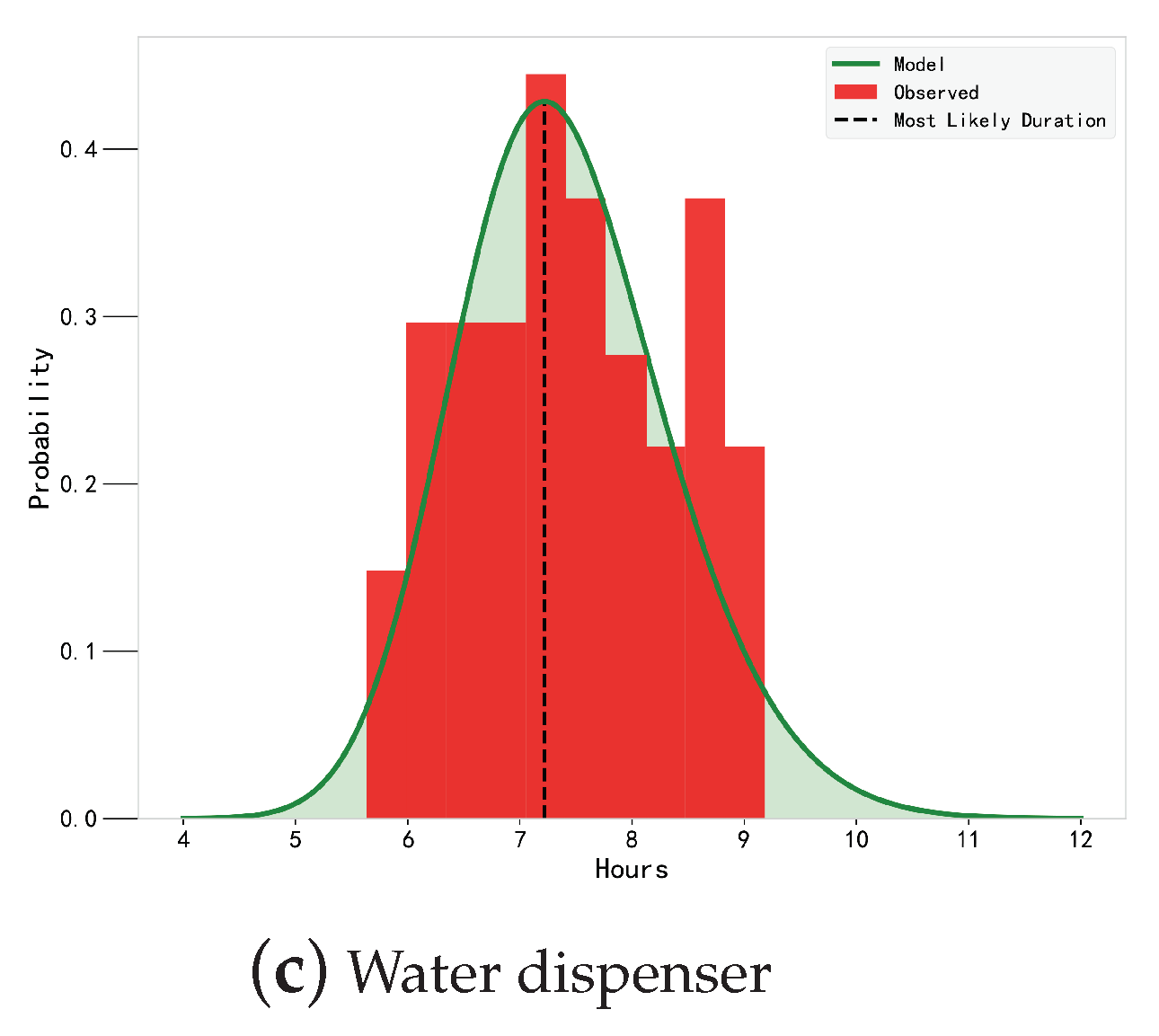
| Equipment Action Model | Optimal Parameter | Evaluation Index | ||
|---|---|---|---|---|
| RMSE | MAE | |||
| Desktop computer Power-on | 3.2269 | −0.0578 | 0.0823 | 0.0517 |
| Desktop computer Power-off | −0.8263 | 0.0331 | 0.0732 | 0.0415 |
| Light Power-on | 3.3025 | −0.0693 | 0.0536 | 0.0346 |
| Light Power-off | −0.4510 | 0.0345 | 0.0634 | 0.0238 |
| Water dispenser Power-on | 4.3892 | −0.0705 | 0.0815 | 0.0591 |
| Water dispenser Power-off | −1.0008 | 0.0362 | 0.0924 | 0.0612 |
| Air-conditioner heating-on | 2.8954 | −0.0873 | 0.0687 | 0.0491 |
| Air-conditioner heating-off | 3.7358 | −0.0492 | 0.0824 | 0.0574 |
| Air-conditioner cooling-on | 5.1029 | −0.0617 | 0.0635 | 0.0329 |
| Air-conditioner cooling-off | 4.8796 | −0.0584 | 0.0744 | 0.0482 |
| Energy Use Model | MLE | MCMC | ||||
|---|---|---|---|---|---|---|
| Desktop computer power-on | 33.2179 | [32.4142,34.0216] | 1.6074 | 33.2637 | [32.7747,33.7527] | 0.9780 |
| Desktop computer power-off | 25.7983 | [24.6318,26.9648] | 2.3330 | 25.4528 | [24.6492,26.2564] | 1.6072 |
| Light power-on | 28.3459 | [26.8734,29.8184] | 2.9450 | 27.1368 | [25.9037,28.3366] | 2.4329 |
| Light power-on | 23.4086 | [22.5467,24.2705] | 1.7238 | 23.8457 | [23.6375,24.0539] | 0.4164 |
| Water dispenser power-on | 40.4608 | [39.0547,41.8669] | 2.8122 | 39.7638 | [38.9513,40.5763] | 1.6250 |
| Water dispenser power-on | 26.0109 | [25.1376,26.8847] | 1.7466 | 26.5534 | [25.7375,27.3693] | 1.6318 |
| Air-conditioner heating-on | 17.9635 | [17.0346,18.8924] | 1.8578 | 18.2389 | [17.8934,18.5844] | 0.6910 |
| Air-conditioner heating-off | 26.0184 | [24.7342,27.3076] | 2.5684 | 25.7267 | [24.8763,26.5771] | 1.7008 |
| Air-conditioner cooling-on | 27.8423 | [26.3756,29.3090] | 2.9334 | 27.5361 | [26.9108,28.1614] | 1.2506 |
| Air-conditioner cooling-off | 23.4861 | [22.0785,24.8937] | 2.8152 | 23.3462 | [22.7658,23.9216] | 1.1608 |
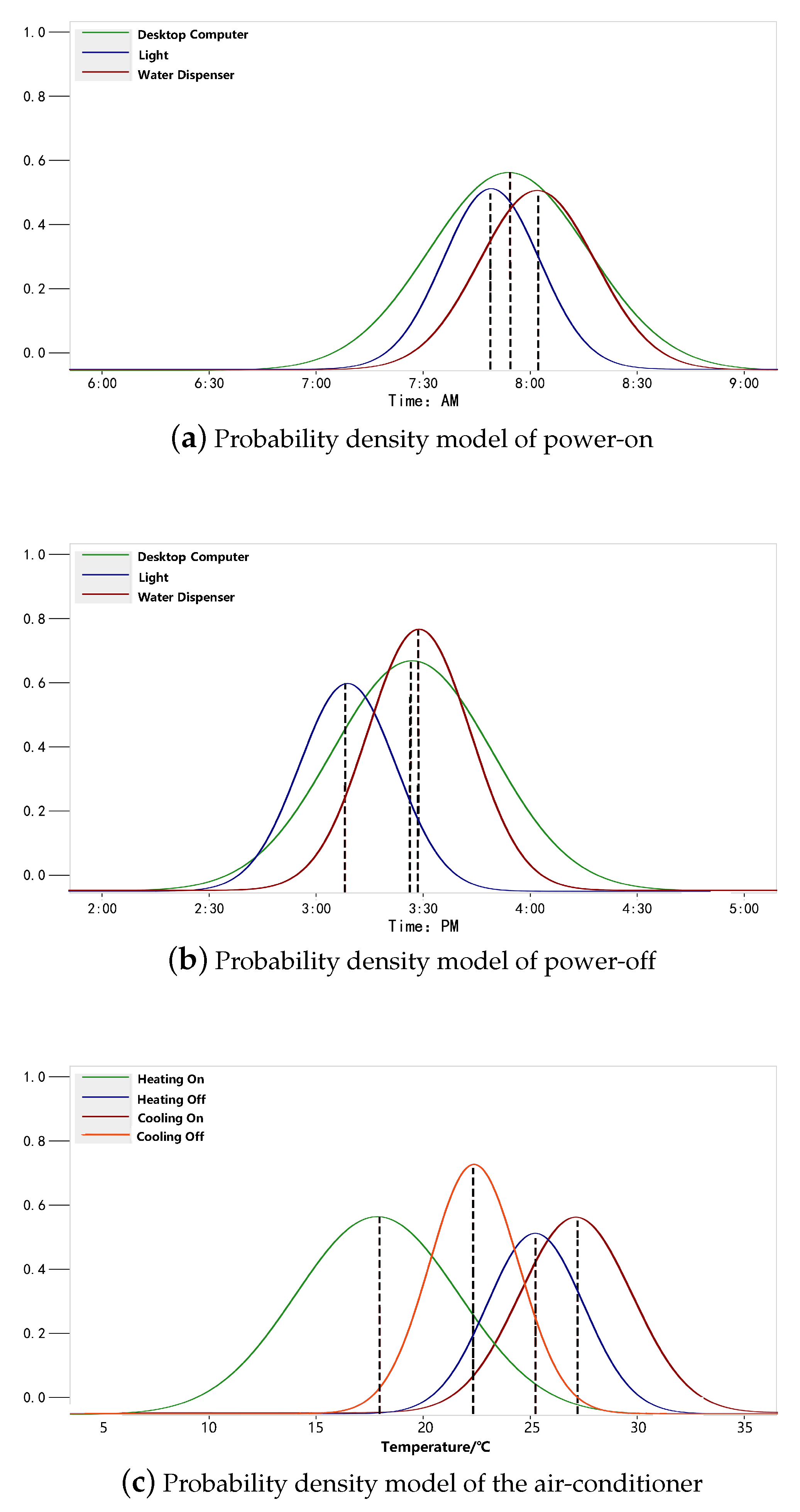
| Prediction | On Period | Off Period | On Time | Off Time | Working Hours (h) | |
|---|---|---|---|---|---|---|
| Device | ||||||
| Desktop computer | 7:50–8:00 | 15:20–15:30 | 7:55 | 15:25 | 7.18 | |
| Light | 7:40–7:50 | 15:10–15:20 | 7:47 | 15:13 | 7.16 | |
| Water dispenser | 8:00–8:10 | 15:20–15:30 | 8:02 | 15:27 | 7.20 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Liu, X.; Deng, X.; Peng, W.; Zhang, G. Markov Chain Monte Carlo Based Energy Use Behaviors Prediction of Office Occupants. Algorithms 2020, 13, 21. https://doi.org/10.3390/a13010021
Yan Q, Liu X, Deng X, Peng W, Zhang G. Markov Chain Monte Carlo Based Energy Use Behaviors Prediction of Office Occupants. Algorithms. 2020; 13(1):21. https://doi.org/10.3390/a13010021
Chicago/Turabian StyleYan, Qiao, Xiaoqian Liu, Xiaoping Deng, Wei Peng, and Guiqing Zhang. 2020. "Markov Chain Monte Carlo Based Energy Use Behaviors Prediction of Office Occupants" Algorithms 13, no. 1: 21. https://doi.org/10.3390/a13010021
APA StyleYan, Q., Liu, X., Deng, X., Peng, W., & Zhang, G. (2020). Markov Chain Monte Carlo Based Energy Use Behaviors Prediction of Office Occupants. Algorithms, 13(1), 21. https://doi.org/10.3390/a13010021






