A Comparative Study of Four Metaheuristic Algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for Evacuation Planning
Abstract
1. Introduction
2. An Overview of Metaheuristic Algorithms
2.1. Archive Multi-Objective Simulated Annealing Algorithm
- The current solution dominates the new solution and k points from the archive dominate the new solution. In this situation, a new solution can be accepted as the current solution with a given probability.
- The current solution and the new solution are non-dominating with respect to each other. Here, the domination status of a new solution and members of the archive are checked through three situations: when a new solution is dominated by k points in the archive, the new solution is non-dominating with respect to the points in the archive, and when new solution dominates k points of the archive.
- The new solution dominates k points of the archive. Here the new solution is selected as the current solution and also added to the archive, while all the k dominated points in the archive are removed. The process in the main loop is repeated through the number of iterations for each temperature, which is reduced to at each iteration using the cooling rate alpha until the minimum temperature is reached. Thereafter, the process stops and the resulting archive contains the final non-dominated solutions.
2.2. Multi-Objective Artificial Bee Colony Algorithm
2.3. Multi-Objective Standard Particle Swarm Optimization Algorithm
2.4. Non-Dominated Sorting Genetic Algorithm-II
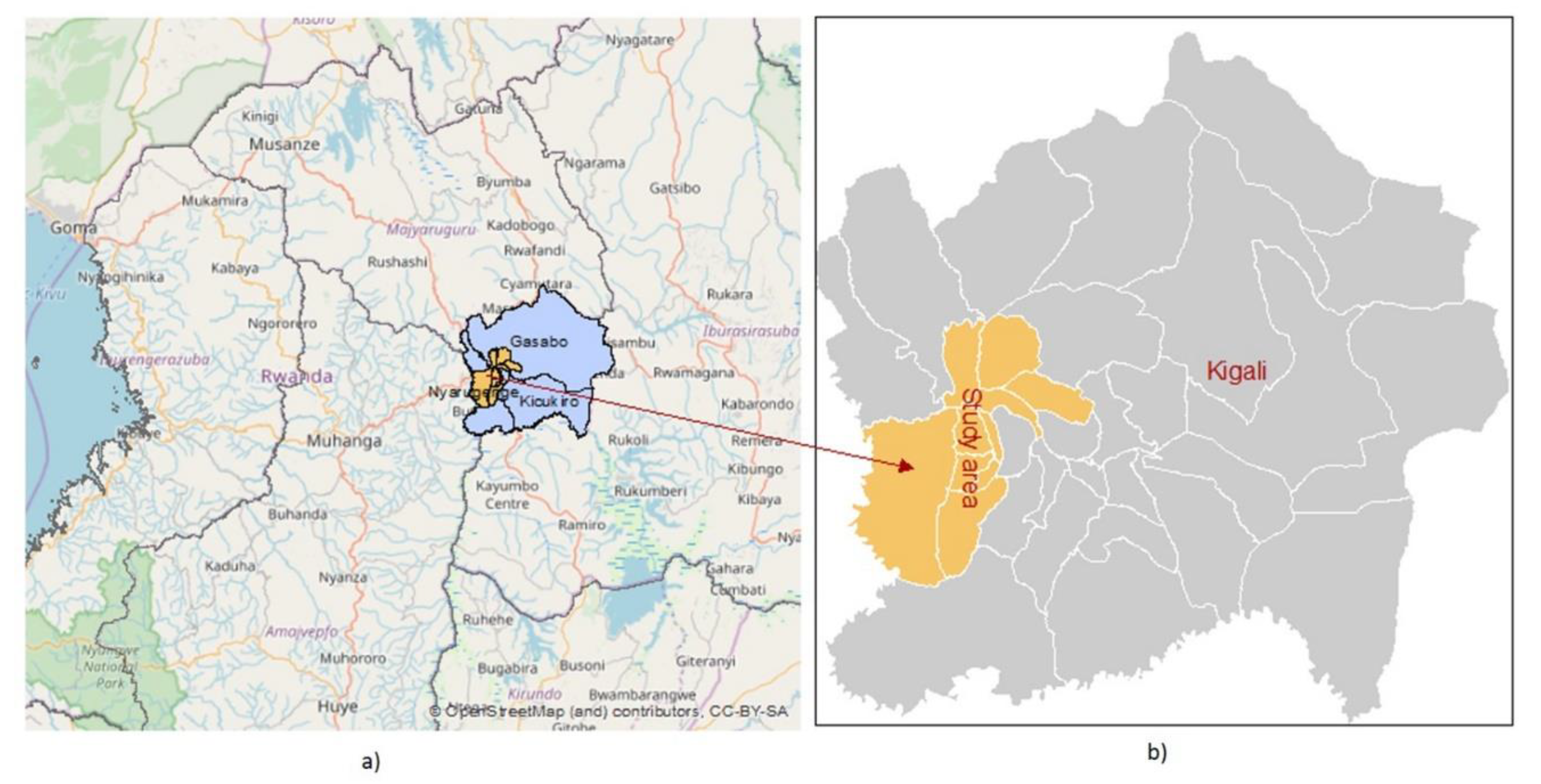
3. Study Area and Data Description
3.1. Study Area
3.2. Data Description
4. Methodology
4.1. Objective Functions for Evacuation Model
- Function to minimize accumulated distance: This objective function aims at allocating each building block to the nearest shelter.
- Function to minimize capacity overload: This objective function aims at distributing the overload of the evacuee population among all shelters.where represents the number of building blocks; is the number of safe areas, is the distance between the building block and the safe area; is the population in the building block being evacuated to the safe area; and is the capacity of the safe area for receiving people.
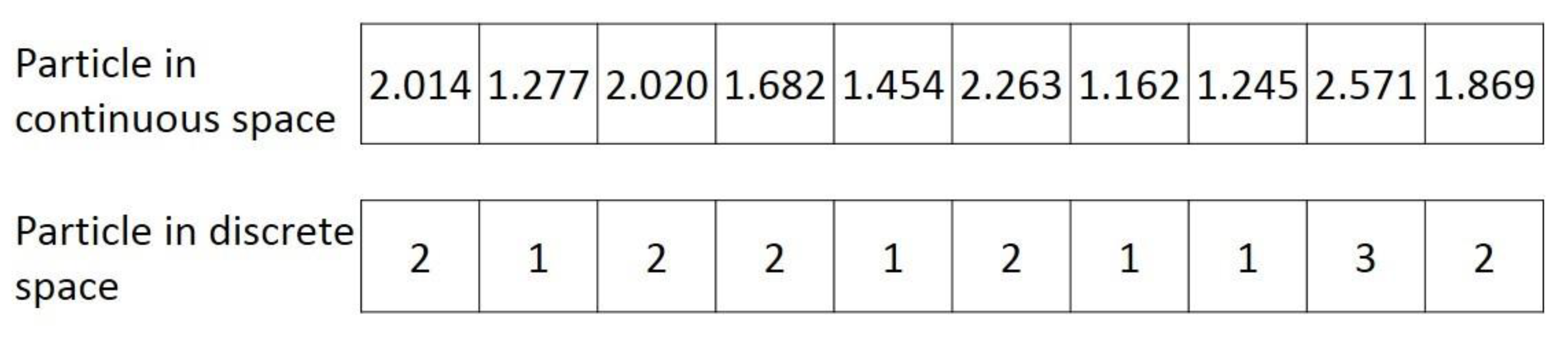
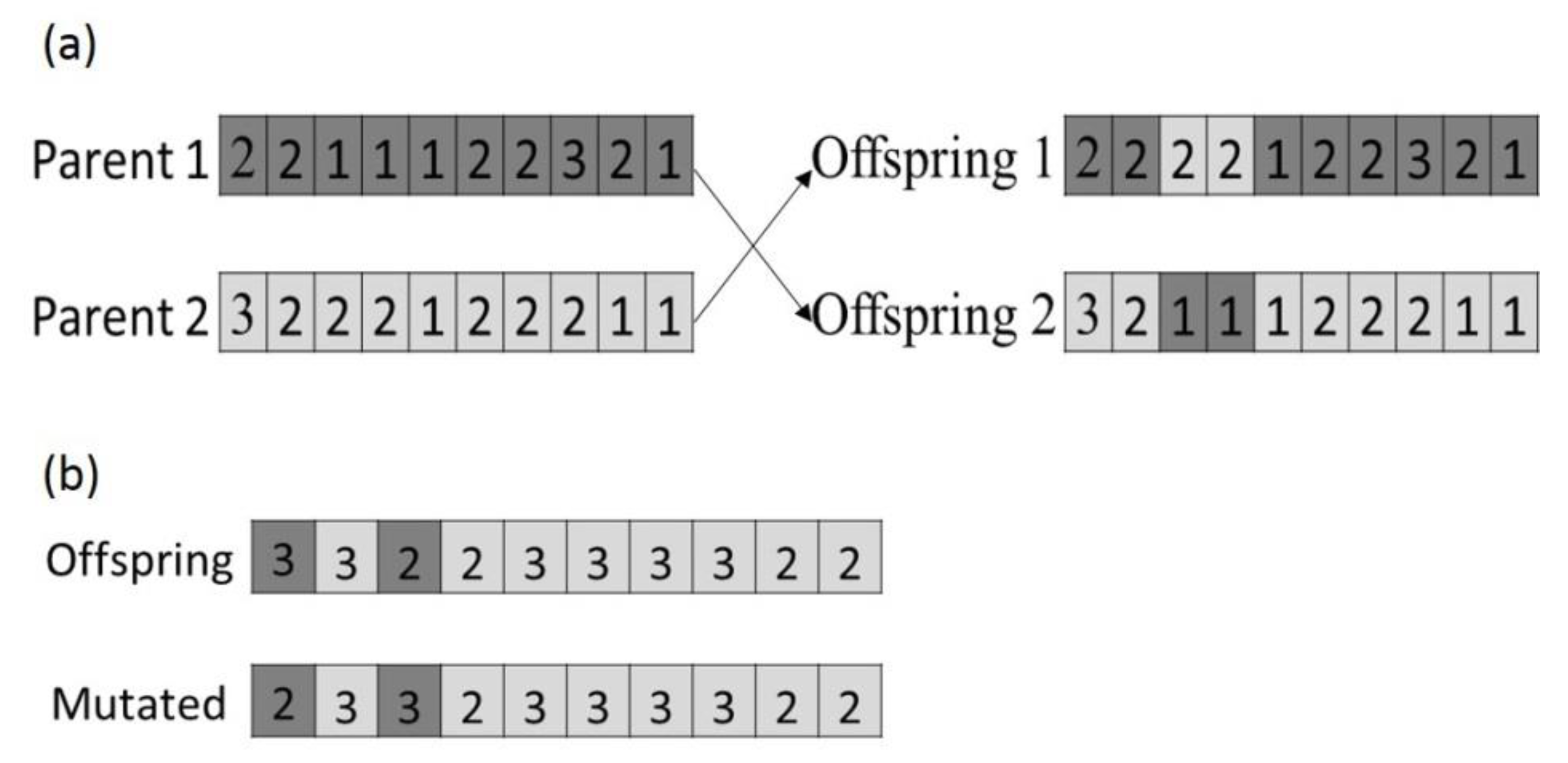
4.2. Modeling Metaheuristic Algorithms for Evacuation Planning
4.2.1. Modeling AMOSA
4.2.2. Modeling MOABC
4.2.3. Modeling MSPSO
4.2.4. Modeling NSGA-II
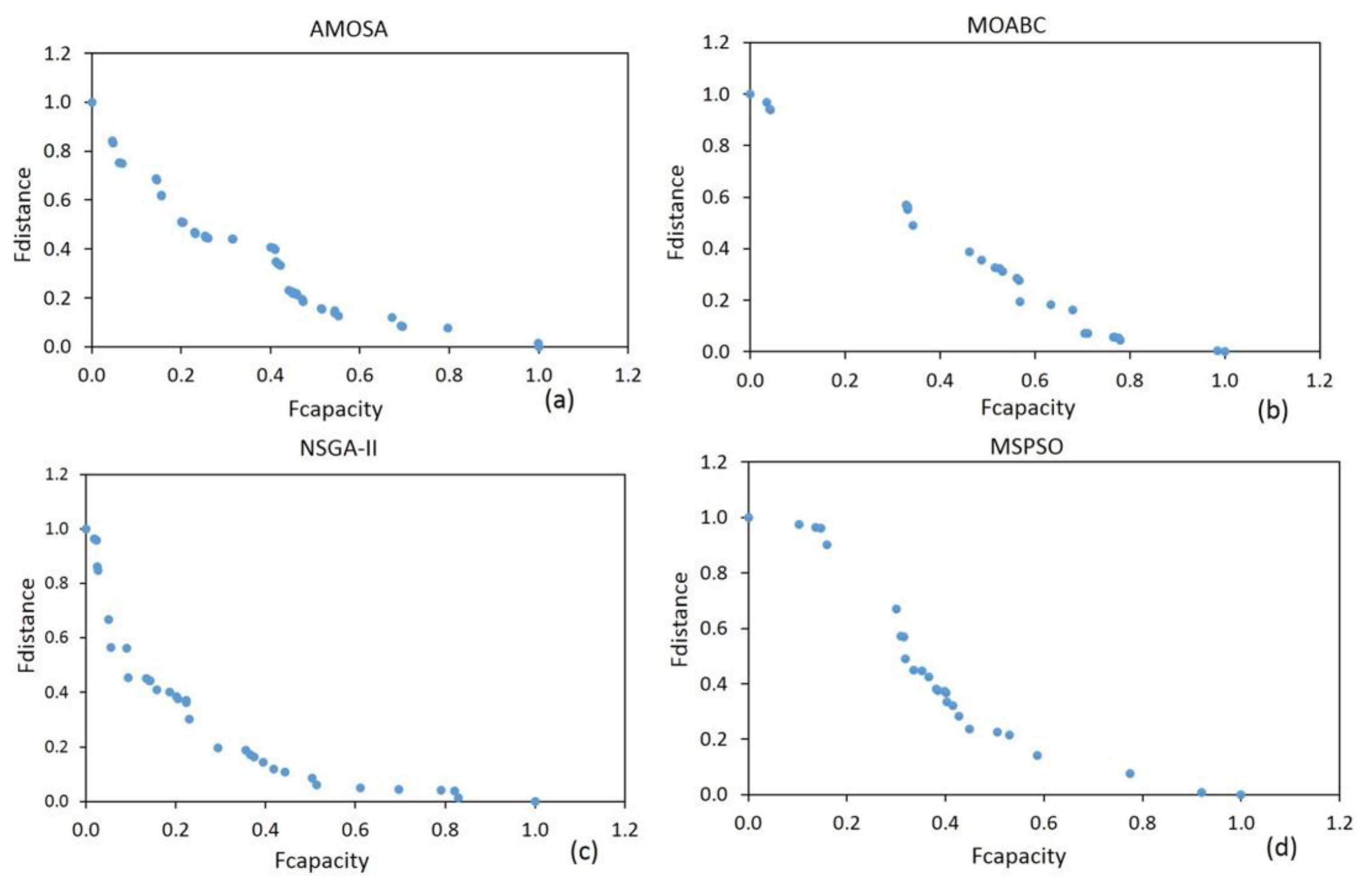
4.3. Comparing and Evaluating the Performances of Algorithms
5. Results of Comparing Algorithms
5.1. Parameter Configuration
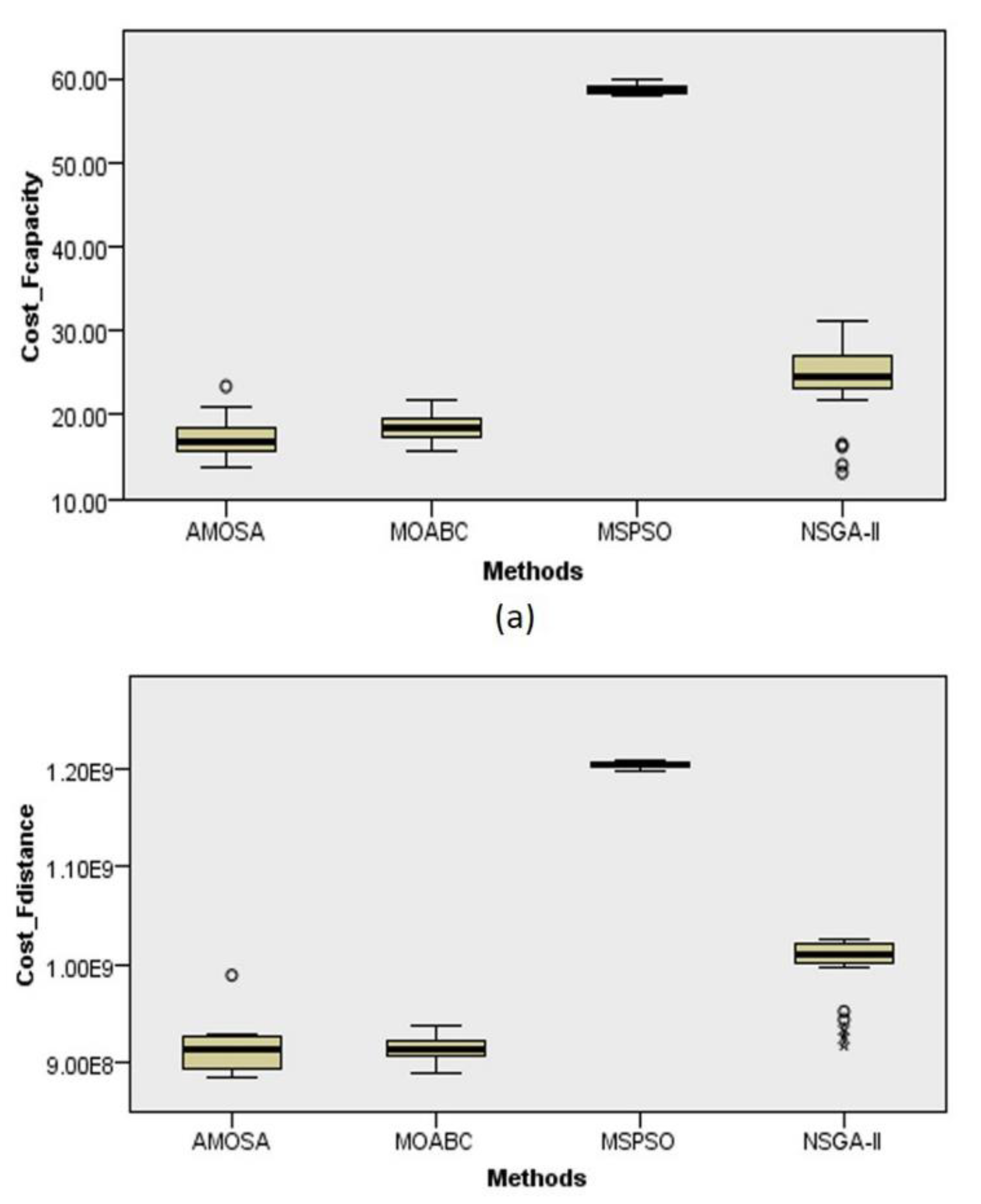
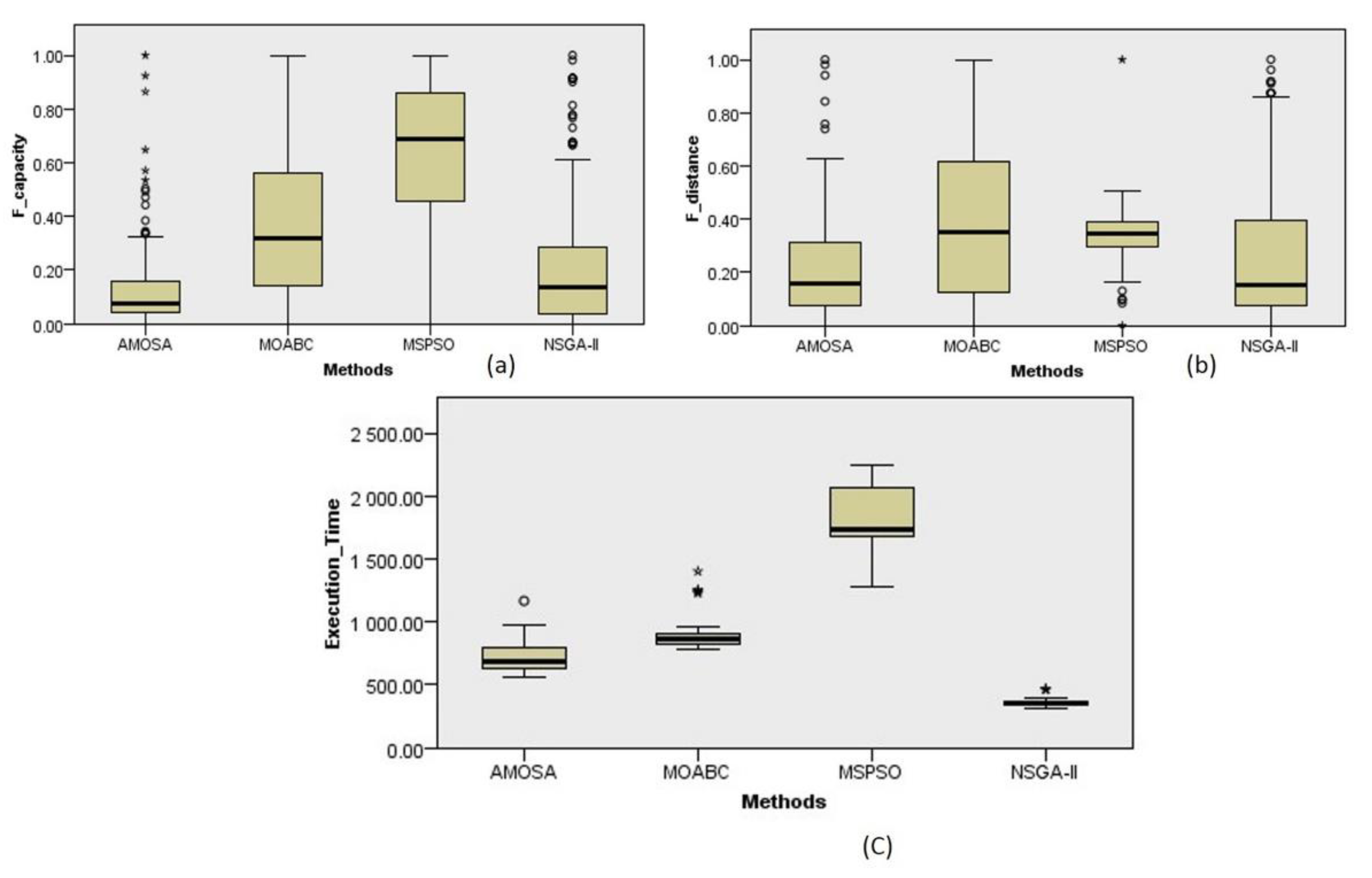
5.2. Effectiveness Comparison
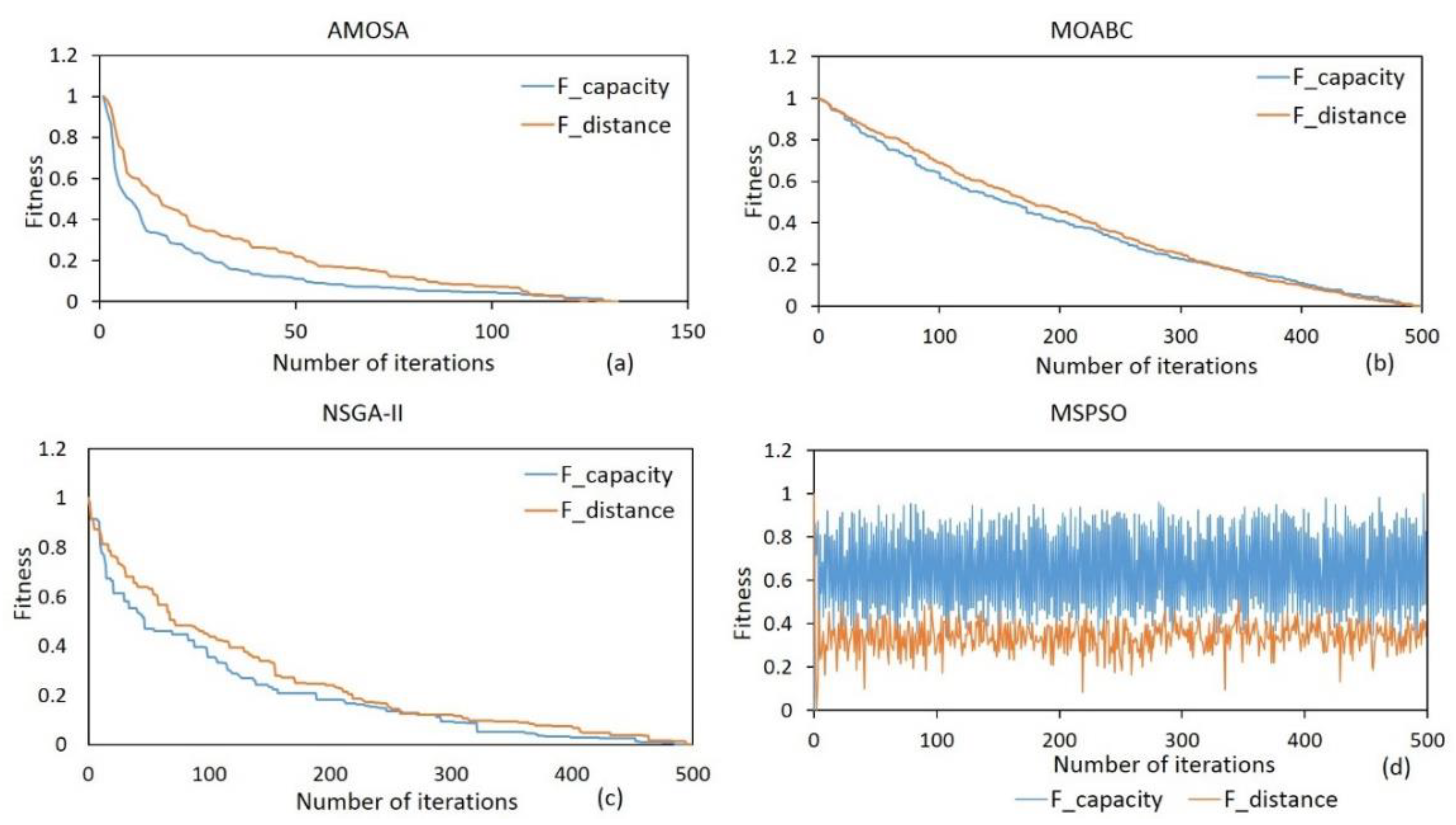
5.3. Efficiency Comparison
5.4. Repeatability Test and Evaluation
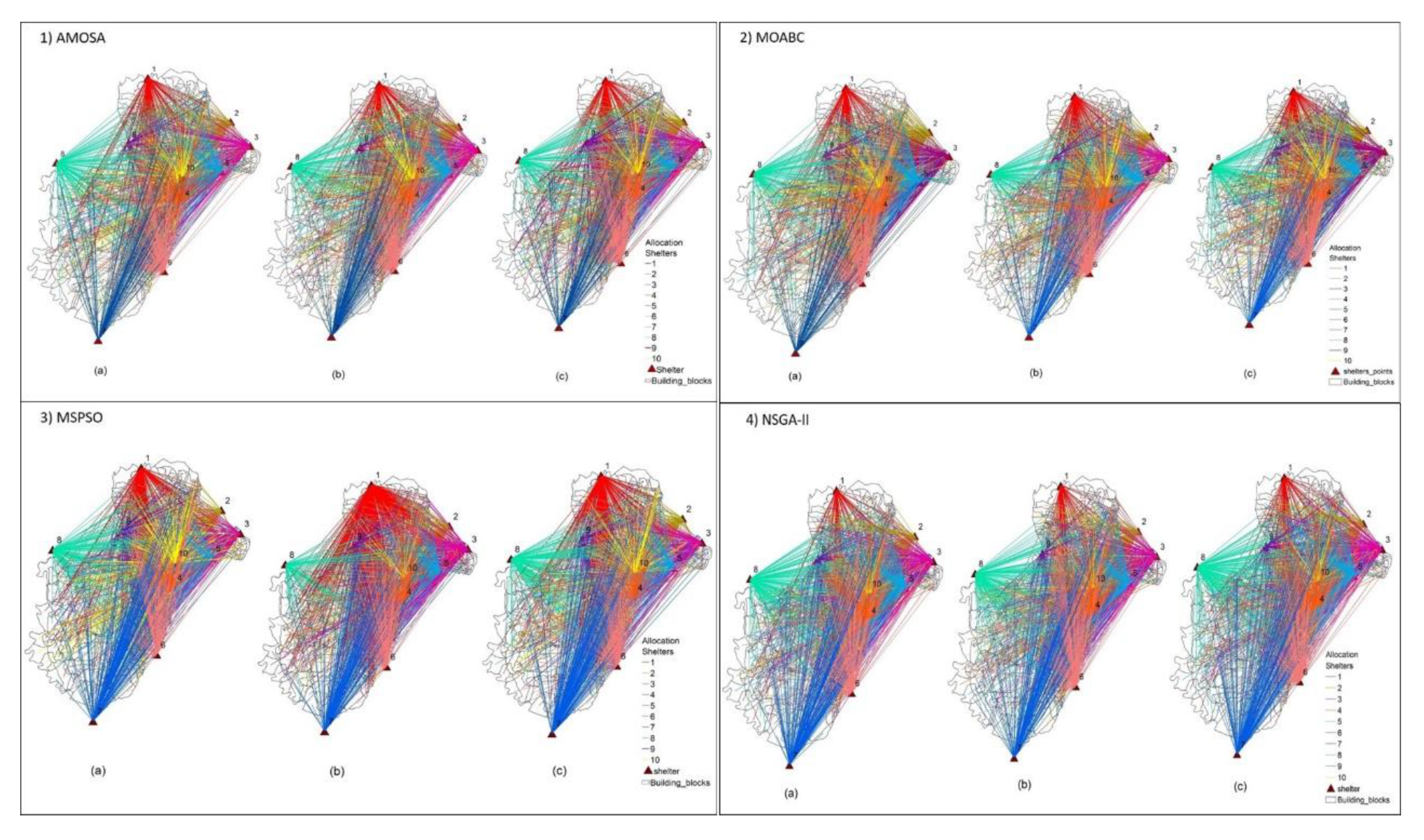
5.5. Allocation Maps
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Runs | Average Minimum Fcapacity | Average Minimum Fdistance | AMOSA Algorithm Worst Fcapacity | Worst Fdistance | Time(s) | Average Minimum Fcapacity | Average Minimum Fdistance | MOABC Algorithm Worst Fcapacity | Worst Fdistance | Time(s) | Average Minimum Fcapacity | Average Minimum Fdistance | MSPSO Algorithm Worst Fcapacity | Worst Fdistance | Time(s) | Average Minimum Fcapacity | Average Minimum Fdistance | NSGA-II Algorithm Worst Fcapacity | Worst Fdistance | Time(s) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 16.13 | 9.19 × 108 | 27.00 | 9.39 × 108 | 564 | 17.97 | 9.28 × 108 | 20.65 | 9.85 × 108 | 1248 | 58.43 | 1.20 × 109 | 70.66 | 1.27 × 109 | 2097 | 16.49 | 9.52 × 108 | 26.53 | 1.02 × 109 | 468 |
| 2 | 17.39 | 9.29 × 108 | 23.07 | 9.71 × 108 | 677 | 19.76 | 9.22 × 108 | 22.91 | 9.56 × 108 | 1255 | 58.56 | 1.21 × 109 | 69.06 | 1.27 × 109 | 2076 | 14.06 | 9.35 × 108 | 18.91 | 9.99 × 108 | 462 |
| 3 | 18.42 | 9.14 × 108 | 25.38 | 9.66 × 108 | 680 | 19.32 | 9.35 × 108 | 22.56 | 9.79 × 108 | 1402 | 58.88 | 1.20 × 109 | 68.60 | 1.26 × 109 | 2077 | 21.66 | 9.44 × 108 | 34.24 | 1.03 × 109 | 465 |
| 4 | 16.47 | 9.24 × 108 | 24.60 | 9.77 × 108 | 580 | 17.22 | 9.27 × 108 | 18.16 | 9.74 × 108 | 1241 | 58.90 | 1.21 × 109 | 70.56 | 1.26 × 109 | 2069 | 16.26 | 9.27 × 108 | 21.96 | 1.04 × 109 | 332 |
| 5 | 16.51 | 8.95 × 108 | 21.82 | 9.36 × 108 | 604 | 16.97 | 9.14 × 108 | 18.10 | 9.34 × 108 | 1228 | 58.69 | 1.21 × 109 | 70.58 | 1.25 × 109 | 2070 | 13.15 | 9.18 × 108 | 21.68 | 9.71 × 108 | 329 |
| 6 | 23.40 | 9.89 × 108 | 25.94 | 1.00 × 109 | 630 | 20.06 | 9.16 × 108 | 23.23 | 9.60 × 108 | 886 | 58.72 | 1.20 × 109 | 73.44 | 1.25 × 109 | 1620 | 26.87 | 1.02 × 109 | 42.01 | 1.12 × 109 | 367 |
| 7 | 15.56 | 8.91 × 108 | 19.77 | 9.33 × 108 | 1167 | 19.51 | 9.10 × 108 | 22.59 | 9.77 × 108 | 797 | 58.42 | 1.20 × 109 | 71.45 | 1.25 × 109 | 1629 | 26.61 | 1.02 × 109 | 51.04 | 1.12 × 109 | 363 |
| 8 | 18.38 | 8.88 × 108 | 27.85 | 9.32 × 108 | 615 | 19.98 | 9.02 × 108 | 21.87 | 9.31 × 108 | 835 | 59.49 | 1.21 × 109 | 68.94 | 1.26 × 109 | 1296 | 26.37 | 1.01 × 109 | 40.29 | 1.15 × 109 | 353 |
| 9 | 18.70 | 8.99 × 108 | 29.47 | 9.39 × 108 | 682 | 16.49 | 9.11 × 108 | 17.67 | 9.22 × 108 | 841 | 58.35 | 1.21 × 109 | 71.81 | 1.27 × 109 | 1278 | 24.46 | 1.02 × 109 | 34.93 | 1.13 × 109 | 346 |
| 10 | 15.07 | 9.30 × 108 | 24.34 | 9.85 × 108 | 689 | 19.20 | 9.10 × 108 | 20.79 | 9.39 × 108 | 823 | 58.40 | 1.20 × 109 | 66.92 | 1.26 × 109 | 1698 | 27.00 | 1.01 × 109 | 38.93 | 1.08 × 109 | 359 |
| 11 | 19.95 | 8.88 × 108 | 32.15 | 9.19 × 108 | 610 | 20.85 | 9.06 × 108 | 24.34 | 9.39 × 108 | 784 | 59.15 | 1.21 × 109 | 70.25 | 1.29 × 109 | 1554 | 25.20 | 1.01 × 109 | 39.10 | 1.08 × 109 | 364 |
| 12 | 21.05 | 9.28 × 108 | 36.64 | 9.93 × 108 | 718 | 18.27 | 9.06 × 108 | 20.69 | 9.28 × 108 | 783 | 59.00 | 1.21 × 109 | 69.64 | 1.27 × 109 | 1781 | 26.70 | 1.03 × 109 | 43.89 | 1.11 × 109 | 314 |
| 13 | 15.30 | 9.22 × 108 | 25.25 | 9.69 × 108 | 743 | 17.46 | 9.03 × 108 | 19.43 | 9.18 × 108 | 812 | 58.96 | 1.21 × 109 | 70.71 | 1.25 × 109 | 1762 | 31.24 | 1.00 × 109 | 56.20 | 1.09 × 109 | 351 |
| 14 | 16.87 | 9.25 × 108 | 30.32 | 9.84 × 108 | 705 | 18.57 | 9.10 × 108 | 21.88 | 9.33 × 108 | 782 | 59.76 | 1.20 × 109 | 71.31 | 1.27 × 109 | 1721 | 24.31 | 1.01 × 109 | 34.61 | 1.13 × 109 | 330 |
| 15 | 16.78 | 9.17 × 108 | 26.60 | 9.70 × 108 | 819 | 17.06 | 9.14 × 108 | 20.01 | 9.53 × 108 | 806 | 58.79 | 1.20 × 109 | 71.52 | 1.29 × 109 | 1703 | 23.38 | 1.00 × 109 | 47.36 | 1.06 × 109 | 356 |
| 16 | 18.56 | 8.87 × 108 | 28.10 | 9.37 × 108 | 683 | 17.66 | 9.24 × 108 | 21.01 | 9.72 × 108 | 958 | 58.78 | 1.21 × 109 | 70.76 | 1.25 × 109 | 1767 | 23.45 | 1.03 × 109 | 40.94 | 1.11 × 109 | 346 |
| 17 | 18.25 | 9.09 × 108 | 26.59 | 9.86 × 108 | 963 | 17.16 | 9.37 × 108 | 19.12 | 9.70 × 108 | 790 | 58.26 | 1.20 × 109 | 71.09 | 1.26 × 109 | 1588 | 25.75 | 1.03 × 109 | 46.97 | 1.14 × 109 | 322 |
| 18 | 15.76 | 9.12 × 108 | 24.80 | 9.84 × 108 | 697 | 19.50 | 9.23 × 108 | 24.16 | 9.68 × 108 | 870 | 58.07 | 1.20 × 109 | 68.30 | 1.24 × 109 | 1680 | 24.52 | 1.03 × 109 | 33.03 | 1.12 × 109 | 348 |
| 19 | 16.79 | 9.18 × 108 | 25.02 | 9.71 × 108 | 956 | 19.91 | 9.12 × 108 | 22.62 | 9.32 × 108 | 915 | 58.13 | 1.21 × 109 | 69.77 | 1.28 × 109 | 1769 | 29.32 | 1.00 × 109 | 46.32 | 1.08 × 109 | 341 |
| 20 | 13.77 | 8.94 × 108 | 18.25 | 9.31 × 108 | 689 | 15.58 | 8.88 × 108 | 16.48 | 8.94 × 108 | 880 | 58.27 | 1.21 × 109 | 69.30 | 1.26 × 109 | 1700 | 22.86 | 1.01 × 109 | 42.98 | 1.09 × 109 | 361 |
| 21 | 14.72 | 9.11 × 108 | 21.05 | 9.42 × 108 | 693 | 18.18 | 9.14 × 108 | 21.00 | 9.68 × 108 | 860 | 58.26 | 1.20 × 109 | 68.44 | 1.26 × 109 | 1846 | 29.70 | 9.97 × 108 | 54.15 | 1.07 × 109 | 341 |
| 22 | 15.79 | 8.85 × 108 | 23.41 | 9.40 × 108 | 948 | 18.64 | 9.24 × 108 | 21.49 | 9.56 × 108 | 861 | 58.05 | 1.21 × 109 | 67.60 | 1.25 × 109 | 1738 | 26.20 | 1.02 × 109 | 40.99 | 1.13 × 109 | 328 |
| 23 | 17.46 | 9.26 × 108 | 26.86 | 9.78 × 108 | 679 | 18.77 | 9.07 × 108 | 23.48 | 9.37 × 108 | 868 | 58.61 | 1.21 × 109 | 74.47 | 1.28 × 109 | 1722 | 23.21 | 1.02 × 109 | 32.06 | 1.11 × 109 | 352 |
| 24 | 18.17 | 9.09 × 108 | 27.70 | 9.65 × 108 | 611 | 17.44 | 9.04 × 108 | 19.57 | 9.41 × 108 | 890 | 59.00 | 1.20 × 109 | 68.60 | 1.25 × 109 | 2222 | 21.94 | 1.03 × 109 | 36.48 | 1.13 × 109 | 360 |
| 25 | 13.67 | 9.16 × 108 | 19.35 | 9.51 × 108 | 972 | 20.21 | 9.17 × 108 | 23.92 | 9.48 × 108 | 893 | 58.58 | 1.21 × 109 | 68.09 | 1.26 × 109 | 1744 | 24.17 | 1.02 × 109 | 32.15 | 1.19 × 109 | 379 |
| 26 | 15.64 | 8.90 × 108 | 22.68 | 9.19 × 108 | 733 | 19.54 | 8.91 × 108 | 21.53 | 8.96 × 108 | 863 | 59.01 | 1.20 × 109 | 73.62 | 1.26 × 109 | 2240 | 29.23 | 1.02 × 109 | 53.30 | 1.12 × 109 | 401 |
| 27 | 18.58 | 9.28 × 108 | 27.06 | 9.95 × 108 | 788 | 18.75 | 9.16 × 108 | 22.95 | 9.33 × 108 | 856 | 58.40 | 1.21 × 109 | 68.96 | 1.26 × 109 | 1753 | 24.29 | 1.00 × 109 | 49.58 | 1.08 × 109 | 357 |
| 28 | 18.74 | 8.92 × 108 | 25.21 | 9.35 × 108 | 685 | 17.00 | 9.17 × 108 | 17.77 | 9.47 × 108 | 895 | 57.83 | 1.20 × 109 | 67.63 | 1.26 × 109 | 2062 | 27.50 | 1.01 × 109 | 40.21 | 1.09 × 109 | 335 |
| 29 | 15.76 | 8.94 × 108 | 22.53 | 9.28 × 108 | 957 | 18.40 | 9.09 × 108 | 20.54 | 9.35 × 108 | 907 | 59.01 | 1.20 × 109 | 73.87 | 1.28 × 109 | 1675 | 27.34 | 1.01 × 109 | 41.97 | 1.09 × 109 | 385 |
| 30 | 18.42 | 9.28 × 108 | 33.86 | 9.70 × 108 | 563 | 21.83 | 9.01 × 108 | 25.67 | 9.31 × 108 | 833 | 58.33 | 1.20 × 109 | 68.49 | 1.24 × 109 | 1670 | 24.75 | 1.01 × 109 | 37.93 | 1.08 × 109 | 376 |
References
- Banholzer, S.; Kossin, J.; Donner, S. The Impact of Climate Change on Natural Disasters. In Reducing Disaster: Early Warning Systems for Climate Change; Singh, A., Zommers, Z., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 21–49. [Google Scholar]
- Perry, R.W.; Lindell, M.K. Preparedness for Emergency Response: Guidelines for the Emergency Planning Process. Disasters 2003, 27, 336–350. [Google Scholar] [CrossRef] [PubMed]
- Galindo, G.; Batta, R. Review of recent developments in OR/MS research in disaster operations management. Eur. J. Oper. Res. 2013, 230, 201–211. [Google Scholar] [CrossRef]
- Özdamar, L.; Ertem, M.A. Models, solutions and enabling technologies in humanitarian logistics. Eur. J. Oper. Res. 2015, 244, 55–65. [Google Scholar] [CrossRef]
- Coutinho-Rodrigues, J.; Tralhão, L.; Alçada-Almeida, L. Solving a location-routing problem with a multiobjective approach: The design of urban evacuation plans. J. Transp. Geogr. 2012, 22, 206–218. [Google Scholar] [CrossRef]
- Wu, W.-X.; Huang, H.-J. A combined, adaptive strategy for managing evacuation routes. Transp. Res. Part B Methodol. 2019, 123, 182–198. [Google Scholar] [CrossRef]
- Stepanov, A.; Smith, J.M. Multi-objective evacuation routing in transportation networks. Eur. J. Oper. Res. 2009, 198, 435–446. [Google Scholar] [CrossRef]
- Murray-Tuite, P.; Wolshon, B. Evacuation transportation modeling: An overview of research, development, and practice. Transp. Res. Part C Emerg. Technol. 2013, 27, 25–45. [Google Scholar] [CrossRef]
- Sherali, H.D.; Carter, T.B.; Hobeika, A.G. A location-allocation model and algorithm for evacuation planning under hurricane/flood conditions. Transp. Res. Part B Methodol. 1991, 25, 439–452. [Google Scholar] [CrossRef]
- Kongsomsaksakul, S.; Yang, C.; Chen, A. Shelter location-allocation model for flood evacuation planning. J. East. Asia Soc. Transp. Stud. 2005, 6, 4237–4252. [Google Scholar]
- Saadatseresht, M.; Mansourian, A.; Taleai, M. Evacuation planning using multiobjective evolutionary optimization approach. Eur. J. Oper. Res. 2009, 198, 305–314. [Google Scholar] [CrossRef]
- Cohon, J.L. Multiobjective Programming and Planning; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Xie, C. Evacuation Network Optimization: Models, Solution Methods and Applications. Available online: https://ecommons.cornell.edu/handle/1813/10869 (accessed on 29 December 2019).
- Cova, T.J.; Johnson, J.P. A network flow model for lane-based evacuation routing. Transp. Res. Part Policy Pract. 2003, 37, 579–604. [Google Scholar] [CrossRef]
- Zheng, Y.-J.; Chen, S.-Y.; Ling, H.-F. Evolutionary optimization for disaster relief operations: A survey. Appl. Soft Comput. 2015, 27, 553–566. [Google Scholar] [CrossRef]
- Urena Serulle, N.; Cirillo, C. The optimal time to evacuate: A behavioral dynamic model on Louisiana resident data. Transp. Res. Part B Methodol. 2017, 106, 447–463. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bujok, P.; Tvrdík, J.; Poláková, R. Comparison of nature-inspired population-based algorithms on continuous optimisation problems. Swarm Evol. Comput. 2019, 50, 100490. [Google Scholar] [CrossRef]
- Saeidian, B.; Mesgari, M.S.; Ghodousi, M. Evaluation and comparison of Genetic Algorithm and Bees Algorithm for location–allocation of earthquake relief centers. Int. J. Disaster Risk Reduct. 2016, 15, 94–107. [Google Scholar] [CrossRef]
- Saeidian, B.; Mesgari, M.S.; Pradhan, B.; Ghodousi, M. Optimized Location-Allocation of Earthquake Relief Centers Using PSO and ACO, Complemented by GIS, Clustering, and TOPSIS. ISPRS Int. J. Geo-Inf. 2018, 7, 292. [Google Scholar] [CrossRef]
- Xu, W.; Ma, Y.; Zhao, X.; Li, Y.; Qin, L.; Du, J. A comparison of scenario-based hybrid bilevel and multi-objective location-allocation models for earthquake emergency shelters: A case study in the central area of Beijing, China. Int. J. Geogr. Inf. Sci. 2018, 32, 236–256. [Google Scholar] [CrossRef]
- Caunhye, A.M.; Nie, X.; Pokharel, S. Optimization models in emergency logistics: A literature review. Socio-Econ. Plan. Sci. 2012, 46, 4–13. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Fister, I., Jr.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. arXiv 2013, arXiv:1307.4186. [Google Scholar]
- Jahangiri, A.; Afandizadeh, S.; Kalantari, N. The optimization of traffic signal timing for emergency evacuation using the simulated annealing algorithm. Transport 2011, 26, 133–140. [Google Scholar] [CrossRef]
- Yadollahnejad, V.; Bozorgi-Amiri, A.; Jabalameli, M. Allocation and Vehicle Routing for Evacuation Operations: A Model and a Simulated Annealing Heuristic. J. Urban Plan. Dev. 2017, 143, 04017018. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Saha, S.; Maulik, U.; Deb, K. A Simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA. IEEE Trans. Evol. Comput. 2008, 12, 269–283. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Acharya, S.; Saha, S.; Thadisina, Y. Multiobjective Simulated Annealing-Based Clustering of Tissue Samples for Cancer Diagnosis. IEEE J. Biomed. Health Inform. 2016, 20, 691–698. [Google Scholar] [CrossRef]
- Alok, A.K.; Saha, S.; Ekbal, A. Multi-objective semi-supervised clustering for automatic pixel classification from remote sensing imagery. Soft Comput. 2016, 20, 4733–4751. [Google Scholar] [CrossRef]
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hassanizadeh, B. A multi-objective artificial bee colony algorithm. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea baSed on Honey Bee Swarm for Numerical Optimization; Erciyes University, Engineering Faculty, Computer Engineering Departement: Kayseri, Turkey, 2005. [Google Scholar]
- Fang, Z.; Li, L.; Li, B.; Zhu, J.; Li, Q.; Xiong, S. An artificial bee colony-based multi-objective route planning algorithm for use in pedestrian navigation at night. Int. J. Geogr. Inf. Sci. 2017, 31, 2020–2044. [Google Scholar] [CrossRef]
- Liu, H.; Xu, B.; Lu, D.; Zhang, G. A path planning approach for crowd evacuation in buildings based on improved artificial bee colony algorithm. Appl. Soft Comput. 2018, 68, 360–376. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Engelbrecht, A.P. Fundamentals of Computational Swarm Intelligence, 1st ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Hu, F.; Xu, W.; Li, X. A modified particle swarm optimization algorithm for optimal allocation of earthquake emergency shelters. Int. J. Geogr. Inf. Sci. 2012, 26, 1643–1666. [Google Scholar] [CrossRef]
- Izquierdo, J.; Montalvo, I.; Pérez, R.; Fuertes, V.S. Forecasting pedestrian evacuation times by using swarm intelligence. Phys. Stat. Mech. Its Appl. 2009, 388, 1213–1220. [Google Scholar] [CrossRef]
- Lin, J.; Lucas, T.A. A Particle Swarm Optimization Model of Emergency Airplane Evacuations with Emotion. Netw. Heterog. Media 2015, 10, 631–646. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Li, H.; Wu, Q.; Zhang, L. A Novel Swarm Intelligence Algorithm for the Evacuation Routing Optimization Problem. Int. Arab J. Inf. Technol. 2017, 14, 880–889. [Google Scholar]
- Zambrano-Bigiarini, M.; Clerc, M.; Rojas-Mujica, R. Standard Particle Swarm Optimisation 2011 at CEC-2013: A baseline for future PSO improvements. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2337–2344. [Google Scholar]
- Ren, G.; Huang, Z.; Cheng, Y.; Zhao, X.; Zhang, Y. An integrated model for evacuation routing and traffic signal optimization with background demand uncertainty. J. Adv. Transp. 2013, 47, 4–27. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J.D.; Zhang, Y.; Gan, X. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems. Transp. Res. Part E-Logist. Transp. Rev. 2017, 99, 77–95. [Google Scholar] [CrossRef]
- Pouraliakbarimamaghani, M.; Mohammadi, M.; Mirzazadeh, A. A multi-objective location-allocation model in mass casualty events response. J. Model. Manag. 2018, 13, 236–275. [Google Scholar] [CrossRef]
- NISR Population and Housing Census of Rwanda, 2012-Rwanda Data Portal. Available online: http://rwanda.opendataforafrica.org//pkzmyhf/population-and-housing-census-of-rwanda-2012 (accessed on 22 November 2018).
- MIDIMAR. The National Risk Atlas of Rwanda. Available online: http://minema.gov.rw/uploads/tx_download/National_Risk_Atlas_of_Rwanda_electronic_version.pdf (accessed on 29 November 2019).
- The Sphere Project. Humanitarian Charter and Minimum Standards in Humanitarian Response: The Sphere Handbook; The Sphere Project: Rugby, UK, 2011. [Google Scholar]
- Friberg, M.; Hjelm, M. Mass Evacuation-Human Behavior and Crowd Dynamics. Available online: https://lup.lub.lu.se/student-papers/search/publication/7766859 (accessed on 29 November 2019).
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction; Wiley: Chichester, UK, 2001. [Google Scholar]
- Datta, D.; Malczewski, J.; Figueira, J.R. Spatial Aggregation and Compactness of Census Areas with a Multiobjective Genetic Algorithm: A Case Study in Canada. Environ. Plan. B Plan. Des. 2012, 39, 376–392. [Google Scholar] [CrossRef]
- Xiao, N. A Unified Conceptual Framework for Geographical Optimization Using Evolutionary Algorithms. Ann. Assoc. Am. Geogr. 2008, 98, 795–817. [Google Scholar] [CrossRef]
- Porta, J.; Parapar, J.; Doallo, R.; Rivera, F.F.; Santé, I.; Crecente, R. High performance genetic algorithm for land use planning. Comput. Environ. Urban Syst. 2013, 37, 45–58. [Google Scholar] [CrossRef]
- McDonald, J.H. Handbook of Biological Statistics, 2nd ed.; Sparky House Publishing: Baltimore, MD, USA, 2009. [Google Scholar]
- Berry, K.J.; Johnston, J.E.; Mielke, P.W., Jr. A Chronicle of Permutation Statistical Methods: 1920–2000, and Beyond; Springer International Publishing: Berlin, Germany, 2014. [Google Scholar]
- Dinno, A. Dunn’s Test of Multiple Comparisons Using Rank Sums. CRAN, 1.3.5. 2017, pp. 1–7. Available online: https://cran.r-project.org/web/packages/dunn.test/dunn.test.pdf (accessed on 30 December 2019).
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an Adaptive Large Neighborhood Search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Advances in Geographic Information Science. In Multicriteria Decision Analysis in Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| AMOSA | |
| Number of population | 100 |
| Number of iterations | 500 |
| Tmax | 100 |
| Tmin | 10 × 10−3 |
| Alpha (α) | 0.9 |
| MOABC | |
| Colony size | 100 |
| Number of iterations | 500 |
| Inertia Weight (w1) | 0.7 |
| Inertia Weight (w2) | 0.8 |
| MSPSO | |
| Number of particles | 100 |
| Number of iterations | 500 |
| Acceleration constant (c1 = c2) | 1.49 |
| Inertia Weight (w) | 0.72 |
| NSGA-II | |
| Number of chromosomes | 100 |
| Number of iterations | 500 |
| cross-mutate rate | 0.9 |
| mutation rate | 0.01 |
| KW Test | Effectiveness | Efficiency (Fitness Variation) | Efficiency (Execution Time) | ||
|---|---|---|---|---|---|
| Cost of Fcapacity | Cost of Fdistance | Cost of Fcapacity | Cost of Fdistance | ||
| Chi-Square | 88.809 | 98.016 | 674.13 | 162.42 | 105.028 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Index | Fcapacity | Fdistance | ||
|---|---|---|---|---|
| t-Statistic | p-Value | t-Statistic | p-Value | |
| AMOSA-MOABC | −3.223 | 0.001 * | −0.393 | 0.852 |
| AMOSA-MSPSO | −17.183 | 0.000 * | −19.693 | 0.000 * |
| MOABC-MSPSO | −13.960 | 0.000 * | −19.300 | 0.000 * |
| AMOSA-NSGA-II | −9.043 | 0.000 * | −11.549 | 0.000 * |
| MOABC-NSGA-II | −5.820 | 0.000 * | −11.156 | 0.000 * |
| MSPSO-NSGA-II | 8.141 | 0.000 * | 8.144 | 0.000 * |
| Index | Fcapacity | Fdistance | ||
|---|---|---|---|---|
| t-Statistic | p-Value | t-Statistic | p-Value | |
| AMOSA-MOABC | −11.272 | 0.000 * | −7.710 | 0.000 * |
| AMOSA-MSPSO | −23.040 | 0.000 * | −8.554 | 0.000 * |
| MOABC-MSPSO | −18.221 | 0.000 * | −1.309 | 0.467 |
| AMOSA-NSGA-II | −3.055 | 0.006 * | −1.575 | 0.340 |
| MOABC-NSGA-II | 12.716 | 0.000 * | 9.495 | 0.000 * |
| MSPSO-NSGA-II | 30.921 | 0.000 * | 10.799 | 0.000 * |
| Algorithm | Average Execution Time in Seconds | The Variance of the Average-Normalized Fitness Values of Capacity Function | The Variance of the Average-Normalized Fitness Values of the Distance Function |
|---|---|---|---|
| AMOSA | 736.67 | 0.045 | 0.040 |
| MOABC | 922.07 | 0.050 | 0.052 |
| MSPSO | 1786.90 | 0.049 | 0.053 |
| NSGA-II | 363.03 | 0.056 | 0.081 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niyomubyeyi, O.; Sicuaio, T.E.; Díaz González, J.I.; Pilesjö, P.; Mansourian, A. A Comparative Study of Four Metaheuristic Algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for Evacuation Planning. Algorithms 2020, 13, 16. https://doi.org/10.3390/a13010016
Niyomubyeyi O, Sicuaio TE, Díaz González JI, Pilesjö P, Mansourian A. A Comparative Study of Four Metaheuristic Algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for Evacuation Planning. Algorithms. 2020; 13(1):16. https://doi.org/10.3390/a13010016
Chicago/Turabian StyleNiyomubyeyi, Olive, Tome Eduardo Sicuaio, José Ignacio Díaz González, Petter Pilesjö, and Ali Mansourian. 2020. "A Comparative Study of Four Metaheuristic Algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for Evacuation Planning" Algorithms 13, no. 1: 16. https://doi.org/10.3390/a13010016
APA StyleNiyomubyeyi, O., Sicuaio, T. E., Díaz González, J. I., Pilesjö, P., & Mansourian, A. (2020). A Comparative Study of Four Metaheuristic Algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for Evacuation Planning. Algorithms, 13(1), 16. https://doi.org/10.3390/a13010016







