Optimal Prefix Free Codes with Partial Sorting †
Abstract
1. Introduction
1.1. Background
- When the weights are given in sorted order, van Leeuwen [14] showed in 1976 that an optimal code can be computed using within algebraic operations.
- When the weights consist of distinct values and are given in a sorted, compressed form, Moffat and Turpin [15] showed in 1998 how to compute an optimal binary prefix free code using within algebraic operations, which is sublinear in n when .
1.2. Question
1.3. Contributions
2. Solution
2.1. General Intuition
 such that the first internal node created has larger weight than the largest weight in the original array (i.e., ). On such an instance, van Leeuwen’s algorithm [14] starts by performing comparisons in the equivalent of a sequential search in W for : a binary search would perform comparisons instead, and a doubling search [22] no more than comparisons.
such that the first internal node created has larger weight than the largest weight in the original array (i.e., ). On such an instance, van Leeuwen’s algorithm [14] starts by performing comparisons in the equivalent of a sequential search in W for : a binary search would perform comparisons instead, and a doubling search [22] no more than comparisons.- 1.
- The number of occurrences of E in the signature is ;
- 2.
- The number of occurrences of I in the signature is ;
- 3.
- The length of the signature is their sum, ;
- 4.
- The signature starts with two E;
- 5.
- The signature finishes with one I;
- 6.
- The number of consecutive occurrences of in the signature is one more than the number of occurrences of in it, ;
- 7.
- The number of consecutive occurrences of in the signature is at least 1 and at most , .
 . It corresponds to an instance of size , of EI signature of length 15, which starts with , finishes with I, and contains only occurrences of (underlined), corresponding to a decomposition into maximal blocks of consecutive s (in bold), out of a maximal potential number of 7 for the alphabet size .
. It corresponds to an instance of size , of EI signature of length 15, which starts with , finishes with I, and contains only occurrences of (underlined), corresponding to a decomposition into maximal blocks of consecutive s (in bold), out of a maximal potential number of 7 for the alphabet size .2.2. Partial Sum Deferred Data Structure
- rank, the number of elements which are strictly smaller than x in W;
- select, the value of the r-th smallest value (counted with multiplicity) in W;
- partialSum, the sum of the r smallest elements (counted with multiplicity) in W.
 ,
,- the number of elements strictly smaller than 5 is rank,
- the sixth smallest value is select (counting with redundancies), and
- the sum of the two smallest elements is partialSum.
2.3. Algorithm “Group–Dock–Mix” (GDM) for the Binary Case
- In the initialization phase, initialize the partial sum deferred data structure with the input, and the first internal node by pairing the two smallest weights of the input.
- In the grouping phase, detect and group the weights smaller than the smallest internal node: this corresponds to a run of consecutive E in the EI signature of the instance.
- In the docking phase, pair the consecutive positions of those weights (as opposed to the weights themselves, which can be reordered by future operations) into internal nodes, and pair those internal nodes until the weight of at least one such internal node becomes equal or larger than the smallest remaining weight: this corresponds to a run of consecutive I in the EI signature of the instance.
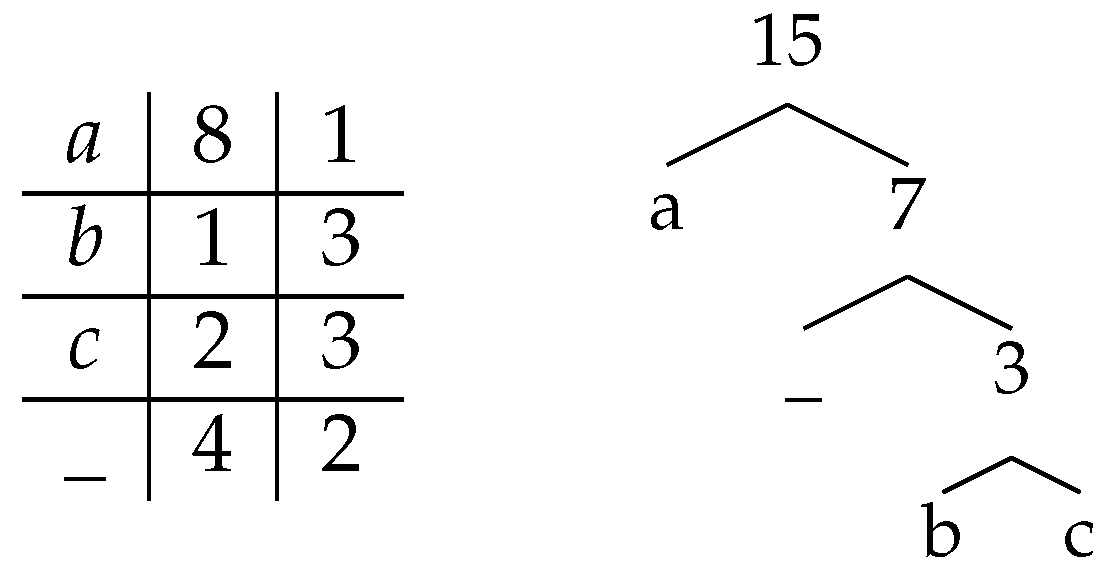
- In the mixing phase, rank the smallest unpaired weight among the weights of the available internal nodes, and pairs the internal node of smaller weight two by two, leaving the largest one unpaired: this corresponds to an occurrence of in the EI signature of the instance. This is the most complicated (and most costly) phase of the algorithm.
- In the conclusion phase, with i internal nodes left to process (and no external node left), assign codelength to the largest ones and codelength to the smallest ones: this corresponds to the last run of consecutive I in the EI signature of the instance.
- Initialization: there is only one internal node at the end of this phase, hence the conditions for the property to stand are created.
- Grouping: no internal node is created, hence the property is preserved.
- Docking: pairing until at least one internal node has weight equal or larger than the smallest weight of a remaining weight (future external node) insures the property.
- Mixing: as this phase pairs all internal nodes except possibly the one of largest weight, the property is preserved.
- Conclusion: A single node is left at the end of the phase, hence the property.
- Initialization: Initialize the deferred data structure partial sum with the input; compute the weight currentMinInternal of the first internal node through the operation partialSum (the sum of the two smallest weights); create this internal node, of weight currentMinInternal and children 1 and 2 (the positions of the first and second weights, in any order); compute the weight currentMinExternal of the first unpaired weight (i.e., the first available external node) by the operation select; setup the variables nbInternals and nbExternalProcessed .
- Grouping: Compute the position r of the first unpaired weight larger than the smallest unpaired internal node, through the operation rank(currentMinInternal); pair the (() modulo 2) indices to form pure internal nodes; compute the parity of the number of unpaired weights smaller than the first unpaired internal node; if it is odd, select the r-th weight through the operation , compute the weight of the first unpaired internal node, compare it with the next unpaired weight, to form one mixed node by combining the minimal of the two with the extraneous weight.
- Docking: Pair all internal nodes by batches (by Property 1, their weights are all within a factor of two, so all internal nodes of a generation are processed before any internal node of the next generation); after each batch, compare the weight of the largest such internal node (compute it through on its range if it is a pure node, otherwise it is already computed) with the first unpaired weight: if smaller, pair another batch, and if larger, the phase is finished.
- Mixing: Rank the smallest unpaired weight among the weights of the available internal nodes, by a doubling search starting from the beginning of the list of internal nodes. For each comparison, if the internal node’s weight is not already known, compute it through a partialSum operation on the corresponding range (if it is a mixed node, it is already known). If the number r of internal nodes of weight smaller than the unpaired weight is odd, pair all but one, compute the weight of the last one and pair it with the unpaired weight. If r is even, pair all of the r internal nodes of weight smaller than the unpaired weight, compare the weight of the next unpaired internal node with the weight of the next unpaired external node, and pair the minimum of the two with the first unpaired weight. If there are some unpaired weights left, go back to the Grouping phase, otherwise continue to the Conclusion phase.
- Conclusion: There are only internal nodes left, and their weights are all within a factor of two from each other. Pair the nodes two by two in batch as in the docking phase, computing the weight of an internal node only when the number of internal nodes of a batch is odd.
3. Analysis
3.1. Parameter Alternation
3.2. Running Time Upper Bound
- The initialization corresponds to a constant number of data structure operations: a select operation to find the third smallest weight (and separate it from the two smallest ones), and a simple partialSum operation to sum the two smallest weights of the input.
- Each grouping phase corresponds to a constant number of data structure operations: a partialSum operation to compute the weight of the smallest internal node if needed, and a rank operation to identify the unpaired weights which are smaller or equal to that of this node.
- The number of operations performed by each docking and mixing phase is better analyzed together: if there are i “I” in the I-block corresponding to this phase in the EI signature, and if the internal nodes are grouped on h levels before generating an internal node of weight larger than the smallest unpaired weight, the docking phase corresponds to at most h partialSum operations, whereas the mixing phase corresponds to at most partialSum operations, which develops to , for a total of data structure operations.
- The conclusion phase corresponds to a number of data structure operations logarithmic in the size of the last block of Is in the EI signature of the instance: in the worst case, the weight of one pure internal node is computed for each batch, through one single partialSum operation each time.
3.3. Lower Bound
- a linear time reduction from multiset sorting to the computation of optimal prefix free codes; and
- the lower bound within (tight in the comparison model) suggested by information theory for the computational complexity of multiset sorting in the worst case over multisets of size n with at most distinct elements.
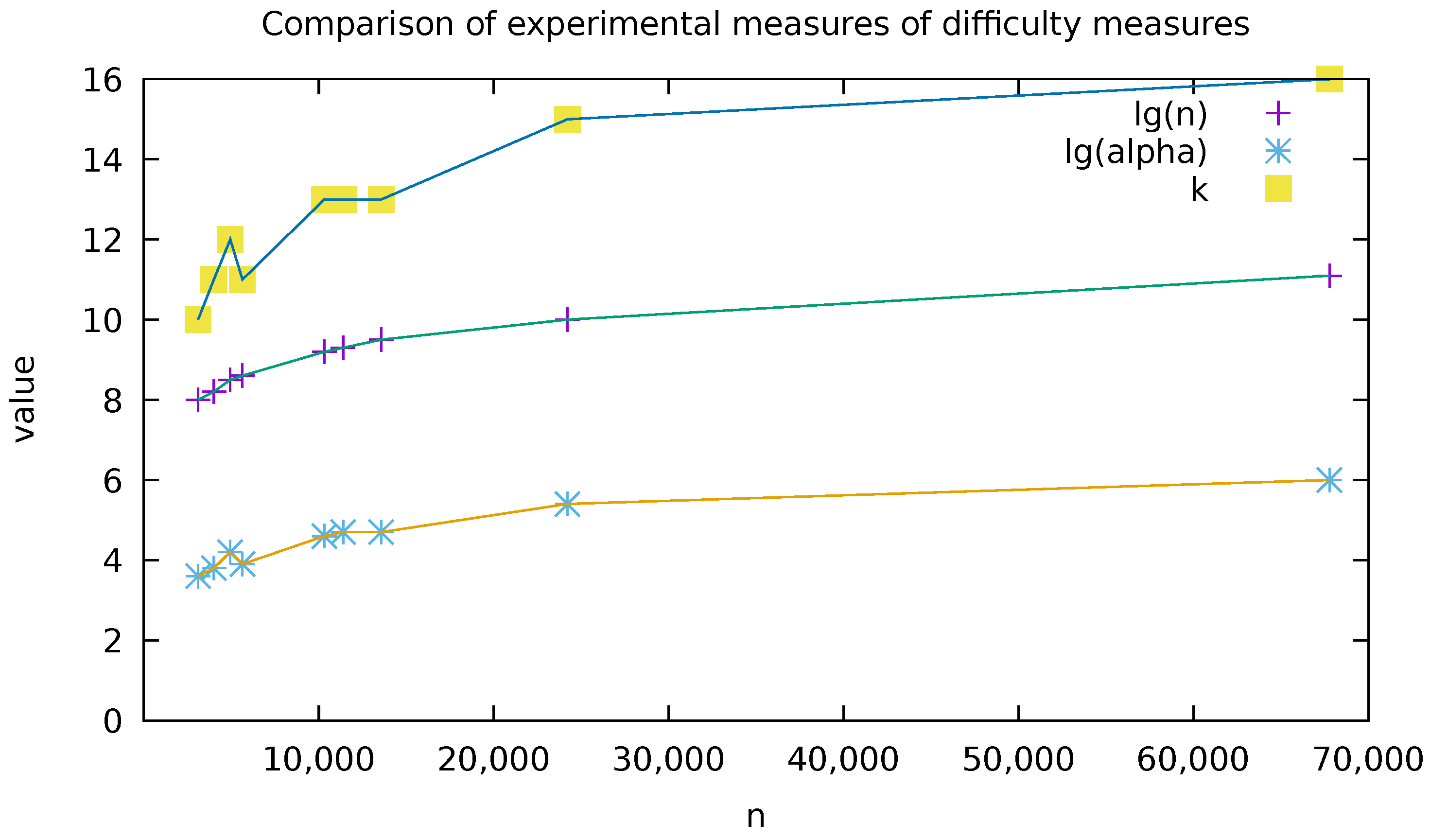
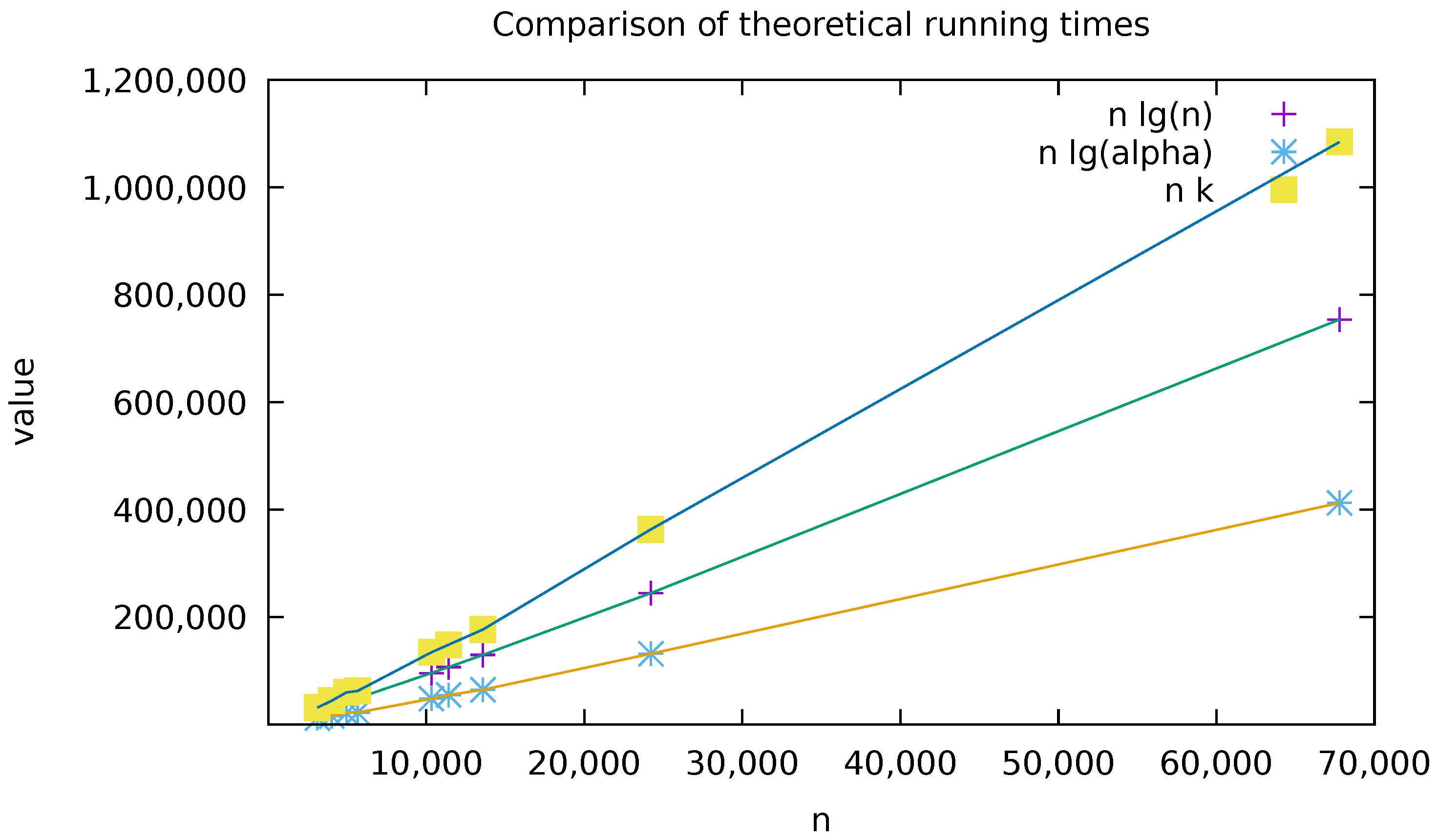
4. Preliminary Experimentations
5. Discussion
5.1. Relation to Previous Work
5.1.1. Previous Work on Optimal Prefix Free Codes
5.1.2. Applicability of Dynamic Results on Deferred Data Structures
5.1.3. Applicability of Refined Results on Deferred Data Structures
5.1.4. Instance Optimality
5.2. Potential (Lack of) Practical Impact
5.2.1. In Classical Computational Models and Applications
5.2.2. Generalisation to Non Binary Output Alphabets
5.2.3. External Memory
5.3. Variants of the Optimal Prefix Free Code Problem
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Huffman, D.A. A Method for the Construction of Minimum-Redundancy Codes. Proc. Inst. Radio Eng. (IRE) 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Chen, C.; Pai, Y.; Ruan, S. Low power Huffman coding for high performance data transmission. In Proceedings of the International Conference on Hybrid Information Technology ICHIT, Cheju Island, Korea, 9–11 November 2006; Volume 1, pp. 71–77. [Google Scholar]
- Moffat, A. Huffman Coding. ACM Comput. Surv. 2019, 52, 85:1–85:35. [Google Scholar] [CrossRef]
- Chandrasekaran, M.N. Discrete Mathematics; PHI Learning Pvt. Ltd.: Delhi, India, 2010. [Google Scholar]
- Moffat, A.; Turpin, A. On the implementation of minimum redundancy prefix codes. ACM Trans. Commun. TCOM 1997, 45, 1200–1207. [Google Scholar] [CrossRef]
- Wikipedia. bzip2. Available online: https://en.wikipedia.org/wiki/Bzip2 (accessed on 20 December 2019).
- Wikipedia. JPEG. Available online: https://en.wikipedia.org/wiki/JPEG#Entropy_coding (accessed on 20 December 2019).
- Takaoka, T.; Nakagawa, Y. Entropy as Computational Complexity. J. Inf. Process. JIP 2010, 18, 227–241. [Google Scholar] [CrossRef][Green Version]
- Takaoka, T. Partial Solution and Entropy. In Proceedings of the 34th International Symposium on Mathematical Foundations of Computer Science 2009 (MFCS 2009), Novy Smokovec, High Tatras, Slovakia, 24–28 August 2009; Královič, R., Niwiński, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 700–711. [Google Scholar]
- Takaoka, T. Minimal Mergesort. Technical Report, University of Canterbury. 1997. Available online: http://ir.canterbury.ac.nz/handle/10092/9676 (accessed on 23 August 2016).
- Barbay, J.; Navarro, G. On Compressing Permutations and Adaptive Sorting. Theor. Comput. Sci. TCS 2013, 513, 109–123. [Google Scholar] [CrossRef]
- Even, S.; Even, G. Graph Algorithms, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; pp. 1–189. [Google Scholar]
- Aho, A.V.; Hopcroft, J.E.; Ullman, J. Data Structures and Algorithms; Addison-Wesley Longman Publishing Company: Massachusetts, MA, USA, 1983. [Google Scholar]
- Van Leeuwen, J. On the construction of Huffman trees. In Proceedings of the International Colloquium on Automata, Languages and Programming ICALP, Edinburgh, UK, 20–23 July 1976; pp. 382–410. [Google Scholar]
- Moffat, A.; Turpin, A. Efficient Construction of Minimum-Redundancy Codes for Large Alphabets. IEEE Trans. Inf. Theory TIT 1998, 44, 1650–1657. [Google Scholar] [CrossRef]
- Belal, A.A.; Elmasry, A. Distribution-Sensitive Construction of Minimum-Redundancy Prefix Codes. In Proceedings of the International Symposium on Theoretical Aspects of Computer Science STACS, Marseille, France, 23–25 February 2006; Lecture Notes in Computer Science. Durand, B., Thomas, W., Eds.; Springer: Berlin, Germany, 2006; Volume 3884, pp. 92–103. [Google Scholar]
- Belal, A.A.; Elmasry, A. Distribution-Sensitive Construction of Minimum-Redundancy Prefix Codes. arXiv 2010, arXiv:cs/0509015v4. Available online: https://arxiv.org/pdf/cs/0509015.pdf (accessed on 29 June 2012).
- Moffat, A.; Katajainen, J. In-Place Calculation of Minimum-Redundancy Codes. In Proceedings of the International Workshop on Algorithms and Data Structures WADS, Kingston, ON, Canada, 16–18 August 1995; Lecture Notes in Computer Science. Springer: London, UK, 1995; Volume 955, pp. 393–402. [Google Scholar]
- Milidiú, R.L.; Pessoa, A.A.; Laber, E.S. Three space-economical algorithms for calculating minimum-redundancy prefix codes. IEEE Trans. Inf. Theory TIT 2001, 47, 2185–2198. [Google Scholar] [CrossRef]
- Kirkpatrick, D. Hyperbolic dovetailing. In Proceedings of the Annual European Symposium on Algorithms ESA, Copenhagen, Denmark, 7–9 September 2009; pp. 516–527. [Google Scholar]
- Barbay, J. Optimal Prefix Free Codes with Partial Sorting. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching CPM, Tel Aviv, Israel, 27–29 June 2016; LIPIcs. Grossi, R., Lewenstein, M., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2016; Volume 54, pp. 29:1–29:13. [Google Scholar]
- Bentley, J.L.; Yao, A.C.C. An almost optimal algorithm for unbounded searching. Inf. Process. Lett. IPL 1976, 5, 82–87. [Google Scholar] [CrossRef]
- Karp, R.; Motwani, R.; Raghavan, P. Deferred Data Structuring. SIAM J. Comput. SJC 1988, 17, 883–902. [Google Scholar] [CrossRef]
- Barbay, J.; Gupta, A.; Jo, S.; Rao, S.S.; Sorenson, J. Theory and Implementation of Online Multiselection Algorithms. In Proceedings of the Annual European Symposium on Algorithms ESA, Sophia Antipolis, France, 2–4 September 2013. [Google Scholar]
- Munro, J.I.; Spira, P.M. Sorting and Searching in Multisets. SIAM J. Comput. SICOMP 1976, 5, 1–8. [Google Scholar] [CrossRef]
- Stix, G. Profile: David A. Huffman. Sci. Am. SA 1991, 54–58. Available online: http://www.huffmancoding.com/my-uncle/scientific-american (accessed on 29 June 2012). [CrossRef]
- Website TCS Stack Exchange. What Are the Real-World Applications of Huffman Coding? 2010. Available online: http://stackoverflow.com/questions/2199383/what-are-the-real-world-applications-of-huffman-coding (accessed on 25 October 2012).
- Wikipedia. Huffman Coding. Available online: https://en.wikipedia.org/wiki/Huffman_coding (accessed on 26 December 2019).
- Moura, E.; Navarro, G.; Ziviani, N.; Baeza-Yates, R. Fast and Flexible Word Searching on Compressed Text. ACM Trans. Inf. Syst. TOIS 2000, 18, 113–139. [Google Scholar] [CrossRef]
- Hart, M. Gutenberg Project. Available online: https://www.gutenberg.org/ (accessed on 27 May 2018).
- Moffat, A.; Petersson, O. An Overview of Adaptive Sorting. Aust. Comput J ACJ 1992, 24, 70–77. [Google Scholar]
- Estivill-Castro, V.; Wood, D. A Survey of Adaptive Sorting Algorithms. ACM Comput. Surv. ACMCS 1992, 24, 441–476. [Google Scholar] [CrossRef]
- Milidiú, R.L.; Pessoa, A.A.; Laber, E.S. A Space-Economical Algorithm for Minimum-Redundancy Coding; Technical Report; Departamento de Informática, PUC-RJ: Rio de Janeiro, Brazil, 1998. [Google Scholar]
- Ching, Y.T.; Mehlhorn, K.; Smid, M.H. Dynamic deferred data structuring. Inf. Process. Lett. IPL 1990, 35, 37–40. [Google Scholar] [CrossRef][Green Version]
- Kaligosi, K.; Mehlhorn, K.; Munro, J.I.; Sanders, P. Towards Optimal Multiple Selection. In Proceedings of the International Colloquium on Automata, Languages and Programming ICALP, Lisbon, Portugal, 11–15 July 2005; pp. 103–114. [Google Scholar]
- Kirkpatrick, D.G.; Seidel, R. The Ultimate Planar Convex Hull Algorithm? SIAM J. Comput. SJC 1986, 15, 287–299. [Google Scholar] [CrossRef]
- Afshani, P.; Barbay, J.; Chan, T.M. Instance-Optimal Geometric Algorithms. J. ACM 2017, 64, 3:1–3:38. [Google Scholar] [CrossRef]
- Barbay, J.; Ochoa, C.; Satti, S.R. Synergistic Solutions on MultiSets. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching CPM, Warsaw, Poland, 4–6 July 2017; Leibniz International Proceedings in Informatics (LIPIcs). Kärkkäinen, J., Radoszewski, J., Rytter, W., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017; Volume 78, pp. 31:1–31:14. [Google Scholar]
- Ferragina, P.; Giancarlo, R.; Manzini, G.; Sciortino, M. Boosting textual compression in optimal linear time. J. ACM 2005, 52, 688–713. [Google Scholar] [CrossRef]
- Han, Y. Deterministic sorting in O(n log log n) time and linear space. J. Algorithms JALG 2004, 50, 96–105. [Google Scholar] [CrossRef]
- Sibeyn, J.F. External selection. J. Algorithms JALG 2006, 58, 104–117. [Google Scholar] [CrossRef]
- Barbay, J.; Gupta, A.; Rao, S.S.; Sorenson, J. Dynamic Online Multiselection in Internal and External Memory. In Proceedings of the International Workshop on Algorithms and Computation WALCOM, Chennai, India, 13–15 February 2014. [Google Scholar]
- Milidiú, R.L.; Pessoa, A.A.; Laber, E.S. Efficient Implementation of the WARM-UP Algorithm for the Construction of Length-Restricted Prefix Codes. In Proceedings of the Workshop on Algorithm Engineering and Experiments ALENEX, Baltimore, MD, USA, 15–16 January 1999; Lecture Notes in Computer Science. Goodrich, M.T., McGeoch, C.C., Eds.; Springer: Berlin, Germany, 1999; Volume 1619, pp. 1–17. [Google Scholar]
- Milidiú, R.L.; Pessoa, A.A.; Laber, E.S. In-Place Length-Restricted Prefix Coding. In Proceedings of the 11th Symposium on String Processing and Information Retrieval SPIRE, Santa Cruz de la Sierra, Bolivia, 9–11 September 1998; pp. 50–59. [Google Scholar]
- Milidiú, R.L.; Laber, E.S. The WARM-UP Algorithm: A Lagrangean Construction of Length Restricted Huffman Codes; Technical Report; Departamento de Informática, PUC-RJ: Rio de Janeiro, Brazil, 1996. [Google Scholar]
- Knuth, D.E. Art of Computer Programming, Volume 3: Sorting and Searching, 2nd ed.; Addison-Wesley Professional: Massachusetts, MA, USA, 1998. [Google Scholar]
- Hu, T.; Tucker, P. Optimal alphabetic trees for binary search. Inf. Process. Lett. IPL 1998, 67, 137–140. [Google Scholar] [CrossRef]
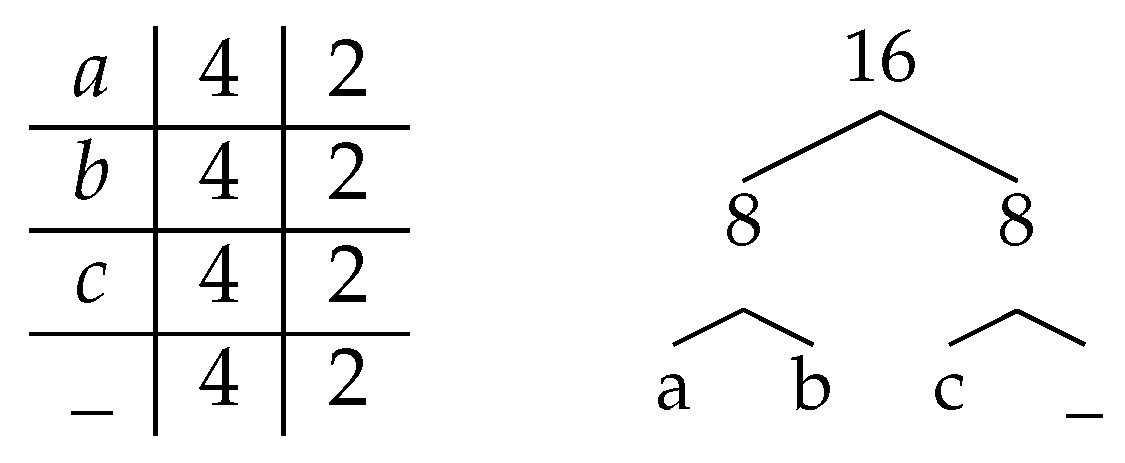
| Year | Name | Time | Space | Ref. | Note |
|---|---|---|---|---|---|
| 1952 | Huffman | [1] | original | ||
| 1976 | van Leeuwen | [14] | sorted input | ||
| 1995 | Moffat and Katajainen | [18] | sorted input | ||
| 1998 | Moffat and Turpin | “efficient” | [15] | compressed input and Output | |
| 2001 | Milidiu et al. | [19] | sorted input | ||
| 2006 | Belal and Elmasry | [16] | k distinct code lengths and sorted input | ||
| 2006 | Belal and Elmasry | potentially | [16] | k distinct code lengths | |
| 2005 | Belal and Elmasry | [17] | k distinct code lengths | ||
| 2016 | Group-Dock-Mix | [here] |
| File Name | Description |
|---|---|
| 14529-0.txt | The Old English Physiologus, EBook #14529 |
| 32575-0.txt | The Head Girl at the Gables, EBook #32575 |
| pg12944.txt | Punch, Or The London Charivari, EBook #12944 |
| pg24742.txt | Mary, Mary, EBook #24742 |
| pg25373.txt | Woodward’s Graperies and Horticultural Buildings, EBook #25373 |
| pg31471.txt | The Girl in the Mirror, EBook #31471 |
| pg4545.txt | An American Papyrus: 25 Poems, EBook #4545 |
| pg7925.txt | Expositions of Holy Scripture, EBook #7925 |
| shakespeare.txt | The Complete Works of William Shakespeare, EBook #100 |
| Filename | n | k | ||
|---|---|---|---|---|
| 14529-0.txt | 7944 | 3099 | 40 | 10 |
| pg4545.txt | 11,887 | 4011 | 49 | 11 |
| pg25373.txt | 24,075 | 4944 | 72 | 12 |
| pg12944.txt | 13,930 | 5639 | 51 | 11 |
| pg24742.txt | 48,039 | 10,323 | 103 | 13 |
| pg31471.txt | 64,959 | 11,398 | 121 | 13 |
| 32575-0.txt | 68,849 | 13,575 | 115 | 13 |
| pg7925.txt | 247,215 | 24,208 | 228 | 15 |
| shakespeare.txt | 904,061 | 67,780 | 440 | 16 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbay, J. Optimal Prefix Free Codes with Partial Sorting. Algorithms 2020, 13, 12. https://doi.org/10.3390/a13010012
Barbay J. Optimal Prefix Free Codes with Partial Sorting. Algorithms. 2020; 13(1):12. https://doi.org/10.3390/a13010012
Chicago/Turabian StyleBarbay, Jérémy. 2020. "Optimal Prefix Free Codes with Partial Sorting" Algorithms 13, no. 1: 12. https://doi.org/10.3390/a13010012
APA StyleBarbay, J. (2020). Optimal Prefix Free Codes with Partial Sorting. Algorithms, 13(1), 12. https://doi.org/10.3390/a13010012





