2.1. K-Medoids Algorithms
A well-known choice of a medoid-based algorithm is the PAM algorithm [
2]. The PAM algorithm consists of three steps: initial medoid selection, medoid swapping, and object labeling. The initial medoids are chosen randomly. Then, medoids are swapped with randomly-selected
possible medoids, where
n is the number of objects and
k is the number of clusters.
Besides PAM, the k-medoids (KM) [
15] and simple and fast k-medoids (SFKM) [
16] algorithms have been developed. Both algorithms have restricted the medoid swapping step. It works within clusters only, i.e., similar to the centroid updating in k-means. However, they both differ in the initial medoid selection where the KM algorithm uses randomly-selected initial medoids. Meanwhile, SFKM selects the initial medoids using a set of ordered
. The value of
is defined as a standardized row sum or standardized column sum of the distance matrix that is calculated by:
where
is the distance between object
i and object
j. When the pre-determined number of clusters is
k, the first
k smallest set is selected from the ordered
as the initial medoids.
Due to the similarity to the k-means centroid updating, the KM and SFKM algorithms suffer from possible local optima [
17] and empty cluster [
18] problems. The result of the partition in the k-means greatly depends on the initialization step. The work in [
17] listed and compared 12 initialization strategies in order to obtain a suitable final partition. For general practice, the procedure of multiple random initial centroids produces a very good partition compared to more complicated methods. In addition, when two or more initial centroids are equal, an empty cluster occurs. It can be solved by preserving the label of one of the initial centroids [
18].
For the k-medoids algorithm, on the other hand, a ranked k-medoids [
19] has been introduced as a way out for the local optima. Instead of using the original distance between objects, it applies a new asymmetric distance based on ranks. The asymmetric rank distance can be calculated by either a row or column direction. Despite its way out of the local optima problem, this algorithm transforms the original distance into an asymmetric rank distance such that a tie rank of two objects having an equal distance can arise. However, it does not discuss how a tie rank is treated, whereas it can be a source of an empty cluster. Thus, we propose a simple k-medoids algorithm.
2.2. Proposed K-Medoids Algorithm
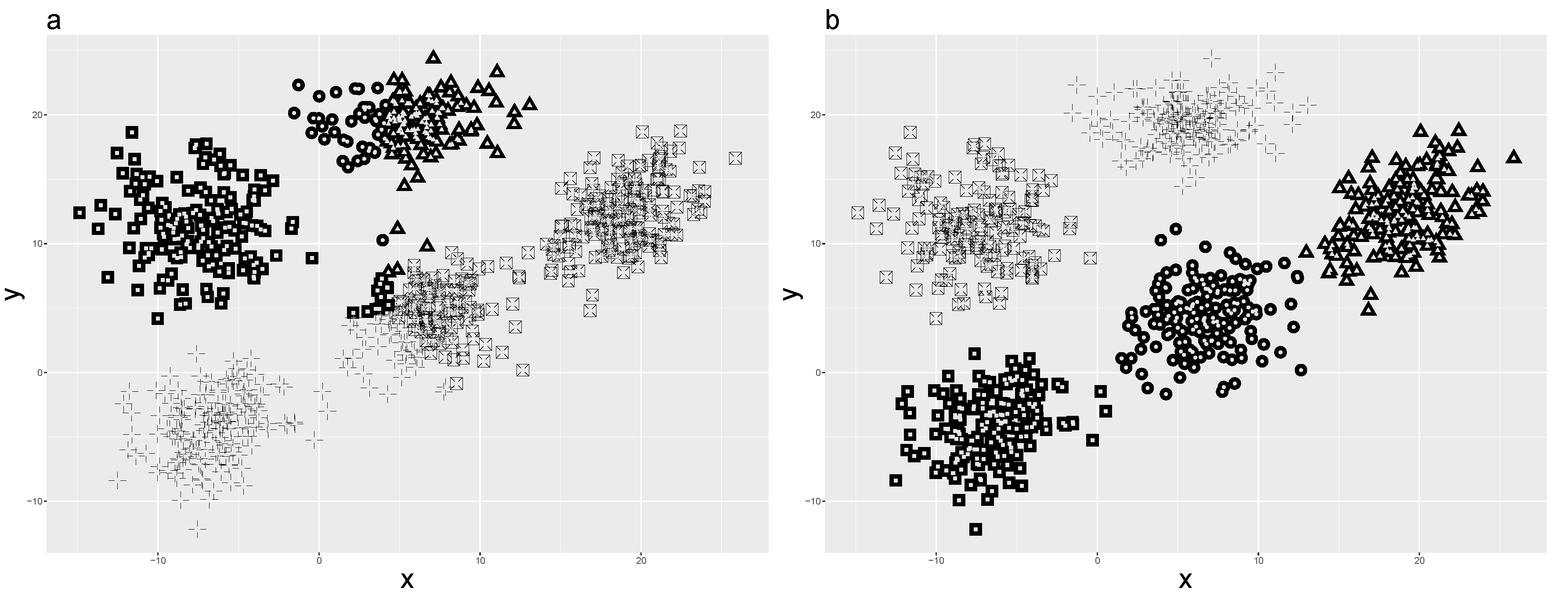
Even though SFKM can adopt any distances, this algorithm was originally simulated in pure numerical and categorical datasets. It performs well in a balanced orientation of a simulated numerical dataset. Unfortunately, when it comes to an unbalanced orientation dataset, the result is poor (
Figure 1a). The dataset in
Figure 1a has 800 objects with two variables [
20]. The objects are assigned into five clusters, and the clusters have a spatially-unbalanced orientation in a two-dimensional space.
Thus, we develop a simple k-medoids (SKM) algorithm, which also applies medoid updating within its clusters in k-medoids setting. The term “simple” is borrowed from the SFKM algorithm for the initial medoids selection. What distinguishes the SFKM and SKM algorithms is that SKM considers the local optima and empty clusters. To minimize the local optima problem, several initializations have been used [
21].
The SKM algorithm is as follows:
Select a set of initial medoids , i.e., selecting k objects from , randomly.
The random initialization is preferred because the random initialization repeated several times is the best approach [
21]. However, a restriction is applied to a single point of the
set. One of the
sets, which is randomly selected, is replaced by the most centrally-located object. It is argued that an optimal medoid is when
is the centrally-located object that minimizes the sum distance to the other objects. Then, the most centrally-located object can be selected based on the row/column sum of the distance matrix. It is given as:
where
is the sum distance of the object
i to the other objects. If vector
is ordered, the first
is selected by the smallest
, which is the most centrally-located object. Note that one/more medoids from the medoids set
can be non-unique objects, for example, two medoids have equal values in all their variables.
Assign the label/membership of each object , , to the closest medoid .
When the medoid set of
is non-unique objects, an empty cluster can occur because the non-unique medoids and their closest objects will have the same membership label. To avoid an empty cluster, the non-unique medoids are restricted to preserve their label. While the closest objects to the non-unique centroids can be labeled as any cluster membership in the k-means case [
18], we regulate that the closest objects to the non-unique medoids are assigned/labeled as only one of the medoids, i.e., a single cluster membership. Hence, this guarantees a faster medoid updating step provided that the non-unique medoid set is not the most centrally-located object.
Update the new set of medoids
, maintaining the clusters label
fixed.
A medoid, , is defined as an object that minimizes the sum distance of this object to the other objects within its cluster.
Calculate the sum of each cluster sum distance (
E), i.e., the sum distance between objects and their medoids.
Repeat Steps 2–4 until E is equal to the previous E, or the set of medoids does not change, or a pre-determined number of iterations is attained.
Repeat Steps 1–5 s times to attain multiple random seeding of the initial medoids.
Note that the centrally-located object always becomes one of the initial medoids. Among the cluster medoids from the multiple random seeding s, the cluster medoid set that has a minimum value of E is selected as the final cluster medoids.
Assign the membership of each object to the final medoids.
The SKM algorithm can be applied in the aforementioned dataset, which yields a better result than the SFKM algorithm (
Figure 1b).
2.3. Proposed Distance Method
As a distance-based algorithm, the SKM algorithm input requires a distance function. Compared to distance measures in either numerical or categorical variables, there are limited alternatives for mixed variable distance. Although the most common distance measure for mixed variable data is the Gower distance [
9], a generalized distance function (GDF) to increase the variation of the mixed variable choices is developed.
The GDF consists of combinations of weights and distances. It sets particular weights in a linear combination of numerical, binary, and categorical distances. The distance between two objects in the GDF form can be computed by:
where
is the weight for the whole function,
,
, and
are the weights for the numerical, binary, and categorical variables, respectively,
is the number of numerical variables,
is the number of binary variables,
is the number of categorical variables,
,
, and
are the numerical, binary, and categorical distances, respectively, and
is the numerical distance between object
i and object
j in the variable
r.
,
, and
are constants implying that each type of all inclusion variables has its own contribution, and each individual variable in the same type equally contributes to the distance computation. When the relative influences of individual variables differ, which can be based on the user domain knowledge or intuition, the constants can be transformed into a vector. This transformation, however, results in a subspace clustering domain [
10], which is out of the scope of this article.
By using the GDF, we can reformulate the Gower distance, which is a special case of the GDF. The Gower similarity [
9] between object
i and object
j is normally calculated as:
where
is the
weight of object
i in the variable
l,
is the value of the object
i on the
(numerical) variable,
is the range of the
(numerical) variable, and
if the objects
i and
j are similar in the
(binary or categorical) variable and zero otherwise. The Gower distance is then obtained by subtracting one from Equation (
2), i.e.,
.
in the Gower distance regulates the contribution of each variable.
is equal to zero if there is a missing value [
22]. When some specific variables are more relevant than others to cluster the objects,
is unequal [
10]. This occurs in the domain of subspace clustering. For a conventional clustering method, on the other hand, equal variable weights (
) for all of the variables are applicable. Thus, the Gower distance for a non-missing value dataset and all variables being equally contributed can be formulated in a GDF form into:
where
is the range of variable
r,
if object
i and object
j are similar and one otherwise, i.e., simple matching distance. With equally-contributing variables and without any missing value, Equations (
2) and (
3) are equal (see
Appendix A). Equation (
3) implies that the distance for the numerical variable is the Manhattan range weighted, while the distance for the binary and categorical variables is the simple matching.
The other available distances for mixed variable data, which are less popular than the Gower distance, can be transformed into a GDF form in a similar way. They are the Wishart [
23], Podani [
22], Huang [
5], and Harikumar-PV [
7] distances. The Wishart and Podani distances have similar properties to the Gower such that the same assumption applies. The Huang and Harikumar-PV distances, on the other hand, do not admit a missing value and have equally-contributing variables by definition.
Table 1 shows the GDF formulation of these distances with respect to their distance combinations and weights. Then, other combinations of distances and weights are possible.