Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity
Abstract
1. Introduction
2. Methodology
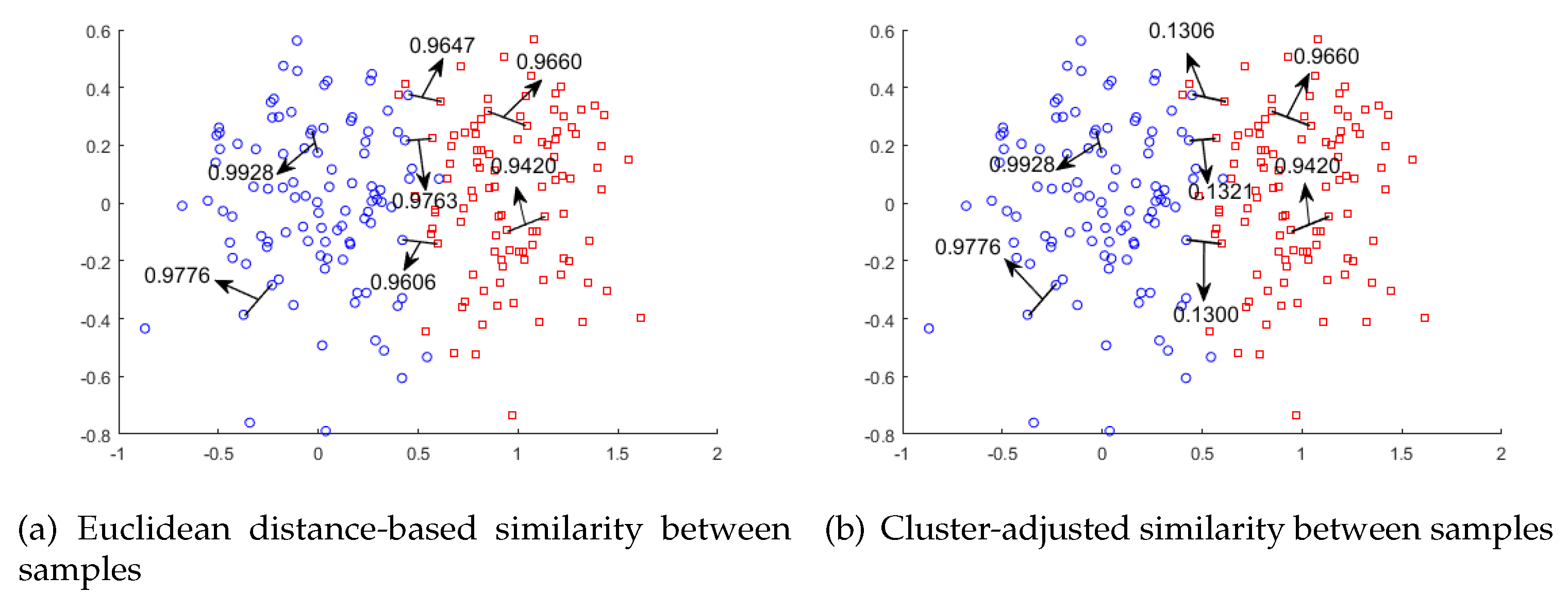
2.1. Clustering-Adjusted Similarity
2.2. Laplacian Eigenmap-Based Clustering-Adjusted Similarity
- Carry out kernel k-means clustering on the original dataset , the original data is clustered into classes. During the clustering, we first use an nonlinear mapping function to map the instances from the original space to a higher-dimensional space F, and then clustering in this space.The instances of the original space becomesOn this basis, kernel clustering is to minimize the following criterion function, is the class-mean of i-th cluster.After clustering, we get the following groups:
- Construct a graph with the edge weight between and specified as Equation (1) (, are instances in ). Set up edges between each point and its nearest points via kNN method, is a preset value. This graph will continue to be used in the following steps.
- To determine the weight between points, which is different from typical LE method, the adjusted weight matrix calculated according to Equation (11) before is selected as the final weight matrix of the previous graph. is Gaussian heat kernel width, , represents the cluster centroids of the cluster which and belongs to. , are indicative vectors.
- Construct graph Laplace matrix , is a diagonal matrix with its (i, i)-element equal to the sum of the i th row of
- The objective function of Laplace feature mapping optimization is as follows:and are the representation of instance i, j in the target c-dimensional subspace . The objective function after transform is as follows:Where the constraint function guarantees the optimization problem has solutions.
- Do feature mapping, and calculate the eigenvectors and eigenvalues of . The column vectors of Y that minimize the formula are the eigenvectors corresponding to c minimum non-zero eigenvalues (including multiple roots) of the generalized eigenvalue problem. The smallest c eigenvectors which are correspond to the non-zero eigenvalues are used as the output after dimensionality reduction.
3. Experiment Setup
3.1. Datasets
3.2. Comparing Methods
3.3. Evaluation Metrics
4. Results
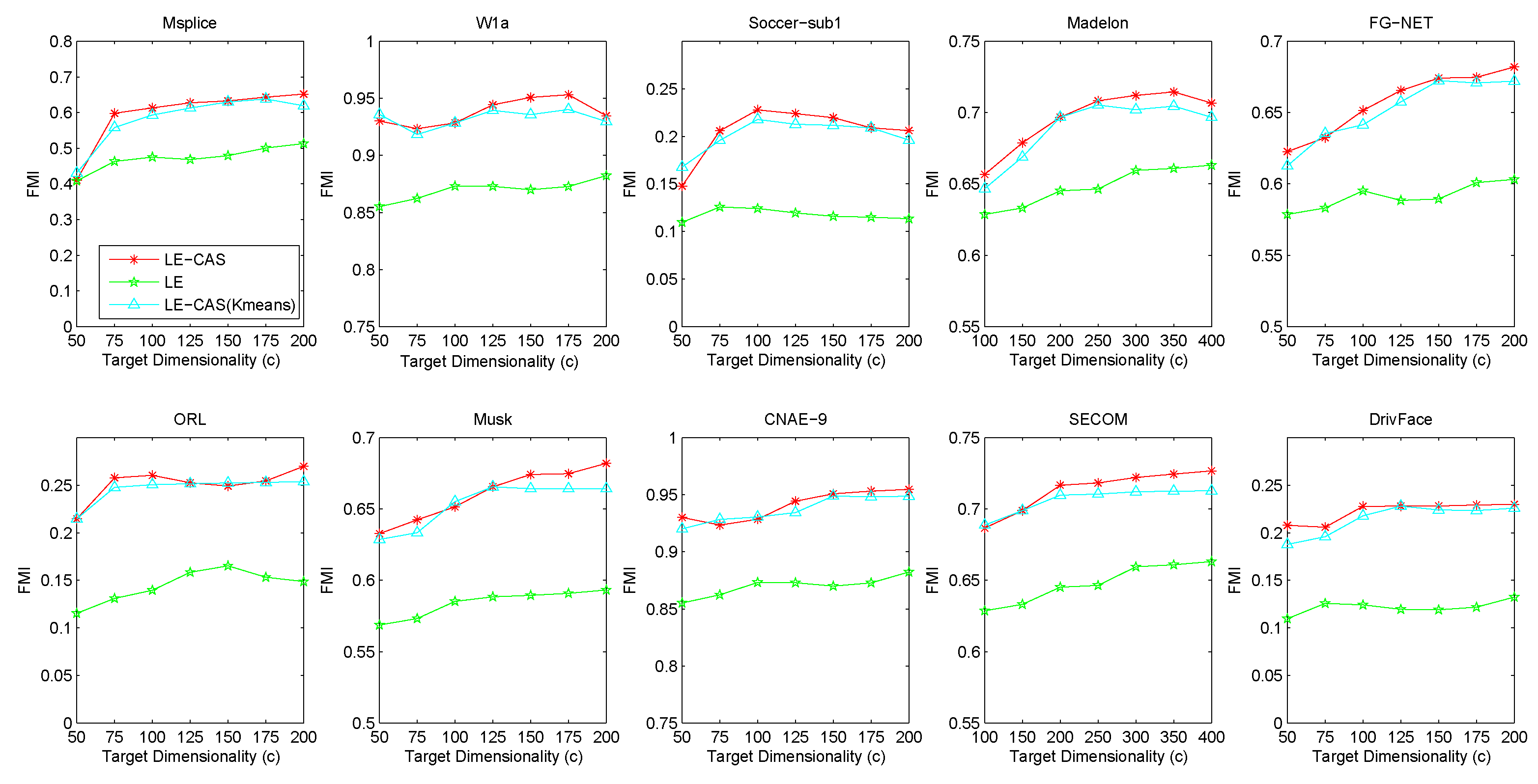
4.1. Results on Different Datasets
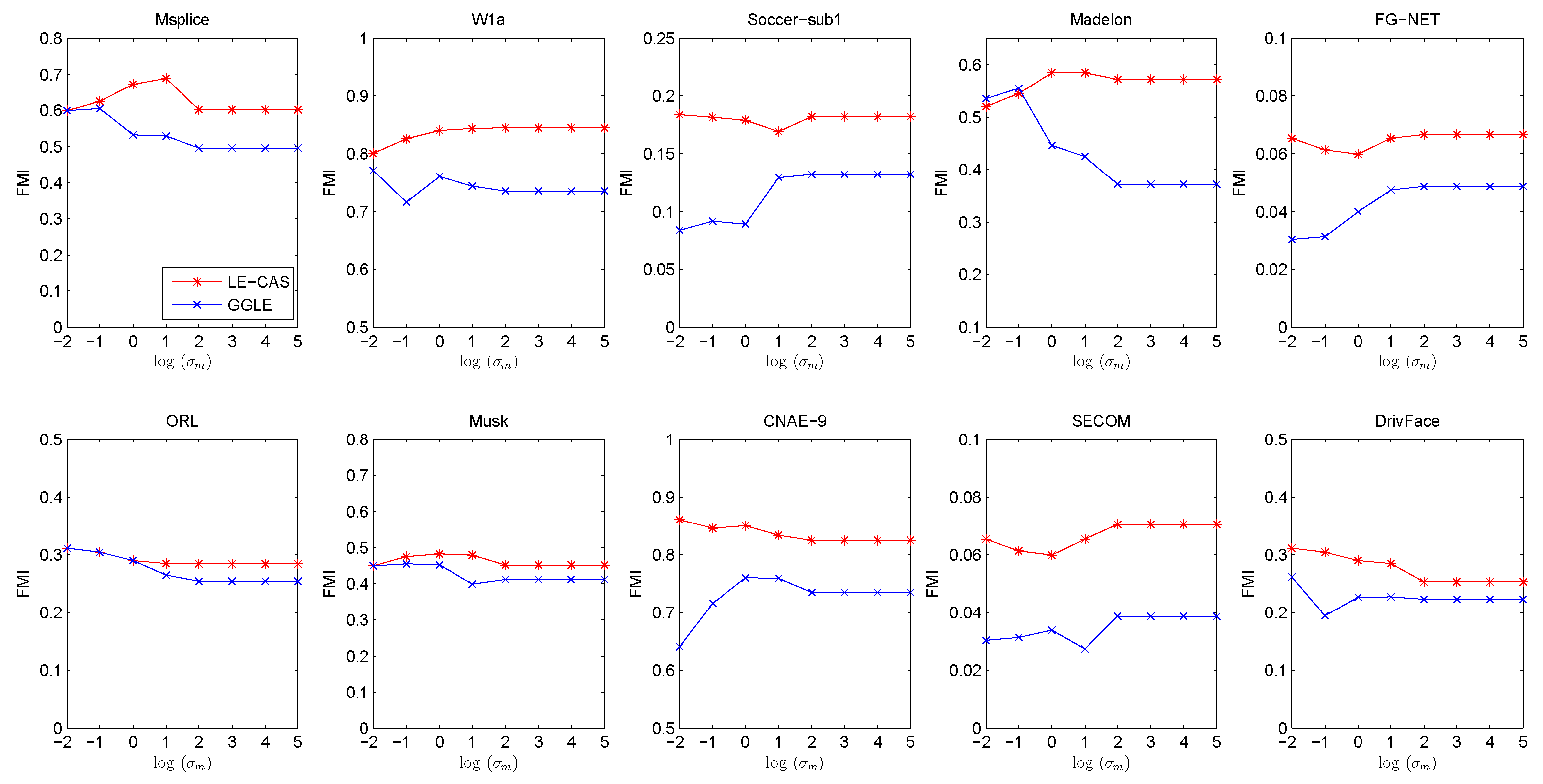
4.2. Parameter Sensitivity Analysis
4.3. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Song, M.; Yang, H.; Siadat, S.H.; Pechenizkiy, M. A comparative study of dimensionality reduction techniques to enhance trace clustering performances. Expert Syst. Appl. 2013, 40, 3722–3737. [Google Scholar] [CrossRef]
- Fan, M.; Gu, N.; Hong, Q.; Bo, Z. Dimensionality reduction: An interpretation from manifold regularization perspective. Inf. Sci. 2014, 277, 694–714. [Google Scholar] [CrossRef]
- Vlachos, M.; Domeniconi, C.; Gunopulos, D.; Kollios, G.; Koudas, N. Non-linear dimensionality reduction techniques for classification and visualization. In Proceedings of the eighth ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 645–651. [Google Scholar]
- Tao, M.; Yuan, X. Recovering Low-Rank and Sparse Components of Matrices from Incomplete and Noisy Observations. SIAM J. Optim. 2011, 21, 57–81. [Google Scholar] [CrossRef]
- Shi, L.; He, P.; Liu, E. An incremental nonlinear dimensionality reduction algorithm based on ISOMAP. In Proceedings of the Australian Joint Conference on Advances in Artificial Intelligence, Sydney, Australia, 5–9 December 2005; pp. 892–895. [Google Scholar]
- Massini, G.; Terzi, S. A new method of Multi Dimensional Scaling. Fuzzy Information Processing Society; IEEE: Toronto, ON, Canada, 2010; ISBN 978-1-4244-7859-0. [Google Scholar]
- Vel, O.D.; Li, S.; Coomans, D. Non-Linear Dimensionality Reduction: A Comparative Performance Analysis. In Learning from Data; Springer: Berlin, Germany, 1996; pp. 323–331. [Google Scholar]
- Leinonen, T. Principal Component Analysis and Factor Analysis, 2nd ed.; Springer: New York, NY, USA, 2004; ISBN 978-0-387-95442-4. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. [Google Scholar]
- Dornaika, F.; Assoum, A. Enhanced and parameterless Locality Preserving Projections for face recognition. Neurocomputing 2013, 99, 448–457. [Google Scholar] [CrossRef]
- Qiang, Y.; Rong, W.; Bing, N.L.; Yang, X.; Yao, M. Robust Locality Preserving Projections With Cosine-Based Dissimilarity for Linear Dimensionality Reduction. IEEE Access 2017, 5, 2676–2684. [Google Scholar]
- He, X. Locality Preserving Projections. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, 2005. [Google Scholar]
- Yu, G.; Hong, P.; Jia, W.; Ma, Q. Enhanced locality preserving projections using robust path based similarity. Neurocomputing 2011, 74, 598–605. [Google Scholar] [CrossRef]
- Deng, C.; He, X.; Han, J. Semi-supervised Discriminant Analysis. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Bunte, K.; Schneider, P.; Hammer, B.; Schleif, F.M.; Villmann, T.; Biehl, M. Limited Rank Matrix Learning, discriminative dimension reduction and visualization. Neural Netw. 2012, 26, 159–173. [Google Scholar] [CrossRef]
- Song, Y.; Nie, F.; Zhang, C.; Xiang, S. A unified framework for semi-supervised dimensionality reduction. Pattern Recognit. 2008, 41, 2789–2799. [Google Scholar] [CrossRef]
- Yu, G.X.; Peng, H.; Wei, J.; Ma, Q.L. Mixture graph based semi-supervised dimensionality reduction. Pattern Recognit. Image Anal. 2010, 20, 536–541. [Google Scholar] [CrossRef]
- Yan, S.; Xu, D.; Zhang, B.; Zhang, H.J.; Yang, Q.; Lin, S. Graph embedding and extensions: A general framework for dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Effrosyni, K.; Yousef, S. Orthogonal neighborhood preserving projections: A projection-based dimensionality reduction technique. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2143–2156. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Trad, M.R.; Joly, A.; Boujemaa, N. Large Scale KNN-Graph Approximation. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining Workshops, Brussels, Belgium, 10 December 2012; pp. 439–448. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Saul, L.K. An introduction to nonlinear dimensionality reduction by maximum variance unfolding. AAAI 2006, 6, 1683–1686. [Google Scholar]
- Weinberger, K.Q.; Saul, L.K. Unsupervised learning of image manifolds by semidefinite programming. Int. J. Comput. Vis. 2006, 70, 77–90. [Google Scholar] [CrossRef]
- Parsons, L.; Haque, E.; Liu, H. Subspace clustering for high dimensional data: A review. ACM Sigkdd Explor. Newsl. 2004, 6, 90–105. [Google Scholar] [CrossRef]
- Zeng, X.; Luo, S.; Wang, J.; Zhao, J. Geodesic distance-based generalized Gaussian Laplacian Eigenmap. J. Softw. 2009, 20, 815–824. [Google Scholar]
- Raducanu, B.; Dornaika, F. A supervised non-linear dimensionality reduction approach for manifold learning. Pattern Recognit. 2012, 45, 2432–2444. [Google Scholar] [CrossRef]
- Ning, W.; Liu, J.; Deng, T. A supervised class-preserving Laplacian eigenmaps for dimensionality reduction. In Proceedings of the International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Changsha, China, 13–15 August 2016; pp. 383–389. [Google Scholar]
- Dhillon, I.S.; Guan, Y.; Kulis, B. Kernel k-means, Spectral Clustering and Normalized Cuts. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 551–556. [Google Scholar]
- Chen, X.; Lu, C.; Tan, Q.; Yu, G. Semi-supervised classification based on clustering adjusted similarity. Int. J. Comput. Appl. 2017, 39, 210–219. [Google Scholar] [CrossRef]
- Nemec, A.F.L.; Brinkhurst, R.O.B. The Fowlkes Mallows statistic and the comparison of two independently determined dendrograms. Can. J. Fish. Aquat. Sci. 1988, 45, 971–975. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, M.; Jiang, F. Regularized F-measure maximization for feature selection and classification. BioMed Res. Int. 2009, 2009, 617946. [Google Scholar] [CrossRef] [PubMed]
- Aliguliyev, R.M. Performance evaluation of density-based clustering methods. Inf. Sci. 2009, 179, 3583–3602. [Google Scholar] [CrossRef]




| Datasets | Instance | Dimensions |
|---|---|---|
| Msplice | 3175 | 240 |
| W1a | 2477 | 300 |
| Soccer-sub1 | 1735 | 279 |
| Madelon | 2600 | 500 |
| FG-NET | 1002 | 262 |
| ORL | 400 | 1024 |
| Musk | 6598 | 223 |
| CNAE-9 | 1080 | 857 |
| SECOM | 1567 | 591 |
| DrivFace | 1606 | 525 |
| FMI | F-measure | PU | |
|---|---|---|---|
| Msplice | |||
| LE-CAS | 0.6133 ± 0.0124 | 0.5425 ± 0.0302 | 0.7284 ± 0.0638 |
| LE | 0.3247 ± 0.0233 | 0.1871 ± 0.0292 | 0.4914 ± 0.0647 |
| S-LE | 0.5552 ± 0.0296 | 0.2956 ± 0.0239 | 0.5324 ± 0.0734 |
| GGLE | 0.4925 ± 0.0334 | 0.4025 ± 0.0108 | 0.6354 ± 0.0619 |
| SCPLE | 0.5852 ± 0.0190 | 0.3928 ± 0.0099 | 0.6203 ± 0.0594 |
| W1a | |||
| LE-CAS | 0.9285 ± 0.0514 | 0.4691 ± 0.0375 | 0.9608 ± 0.0461 |
| LE | 0.6429 ± 0.0285 | 0.2488 ± 0.0215 | 0.6541 ± 0.0427 |
| S-LE | 0.7042 ± 0.0342 | 0.3158 ± 0.0261 | 0.7028 ± 0.0395 |
| GGLE | 0.8731 ± 0.0427 | 0.4021 ± 0.0125 | 0.7936 ± 0.0409 |
| SCPLE | 0.8392 ± 0.0307 | 0.4210 ± 0.0325 | 0.8333 ± 0.0326 |
| Soccer-sub1 | |||
| LE-CAS | 0.4268 ± 0.0014 | 0.3172 ± 0.0025 | 0.4774 ± 0.0259 |
| LE | 0.1242 ± 0.0062 | 0.1573 ± 0.0029 | 0.2358 ± 0.0291 |
| S-LE | 0.1995 ± 0.0051 | 0.2319 ± 0.0015 | 0.2936 ± 0.0245 |
| GGLE | 0.2452 ± 0.0024 | 0.2906 ± 0.0015 | 0.3534 ± 0.0208 |
| SCPLE | 0.3052 ± 0.0099 | 0.3173 ± 0.0024 | 0.3726 ± 0.0213 |
| Medelon | |||
| LE-CAS | 0.6967 ± 0.0416 | 0.3024 ± 0.0252 | 0.7804 ± 0.1860 |
| LE | 0.5852 ± 0.0437 | 0.1921 ± 0.0207 | 0.5046 ± 0.1643 |
| S-LE | 0.6082 ± 0.0367 | 0.2235 ± 0.0200 | 0.5478 ± 0.1302 |
| GGLE | 0.6552 ± 0.0345 | 0.3023 ± 0.0132 | 0.6532 ± 0.1033 |
| SCPLE | 0.6923 ± 0.0570 | 0.3008 ± 0.0219 | 0.6378 ± 0.1126 |
| FG-NET | |||
| LE-CAS | 0.6515 ± 0.0200 | 0. 5042 ± 0.0016 | 0.7520 ± 0.0619 |
| LE | 0.4952 ± 0.0138 | 0.3895 ± 0.0021 | 0.5923 ± 0.0573 |
| S-LE | 0.4652 ± 0.0207 | 0.4014 ± 0.0015 | 0.6752 ± 0.0592 |
| GGLE | 0.5558 ± 0.0169 | 0.4977 ± 0.0020 | 0.6936 ± 0.0499 |
| SCPLE | 0.5874 ± 0.0245 | 0.5044 ± 0.0021 | 0.7233 ± 0.0601 |
| ORL | |||
| LE-CAS | 0.5635 ± 0.0452 | 0.3388 ± 0.0092 | 0.6710 ± 0.0229 |
| LE | 0.1398 ± 0.0226 | 0.1247 ± 0.0084 | 0.4215 ± 0.0198 |
| S-LE | 0.2635 ± 0.0356 | 0.1964 ± 0.0078 | 0.5024 ± 0.0099 |
| GGLE | 0.4545 ± 0.0279 | 0.2311 ± 0.0065 | 0.5924 ± 0.0187 |
| SCPLE | 0.4933 ± 0.0281 | 0.2295 ± 0.0081 | 0.6011 ± 0.0125 |
| Musk | |||
| LE-CAS | 0.6832 ± 0.0216 | 0.4724 ± 0.0222 | 0.8804 ± 0.1846 |
| LE | 0.4956 ± 0.0375 | 0.2121 ± 0.0247 | 0.5376 ± 0.1643 |
| S-LE | 0.5982 ± 0.0299 | 0.3055 ± 0.0200 | 0.5895 ± 0.1302 |
| GGLE | 0.6458 ± 0.0321 | 0.3623 ± 0.0132 | 0.6989 ± 0.1033 |
| SCPLE | 0.6823 ± 0.0370 | 0.4078 ± 0.0219 | 0.7277 ± 0.1023 |
| CNAE-9 | |||
| LE-CAS | 0.9285 ± 0.0514 | 0.7051 ± 0.0193 | 0.9409 ± 0.1860 |
| LE | 0.6541 ± 0.0427 | 0.4621 ± 0.0237 | 0.6746 ± 0.1283 |
| S-LE | 0.7028 ± 0.0365 | 0.5738 ± 0.0224 | 0.5478 ± 0.2302 |
| GGLE | 0.8731 ± 0.0417 | 0.7023 ± 0.0122 | 0.8032 ± 0.1053 |
| SCPLE | 0.8392 ± 0.0347 | 0.6708 ± 0.0238 | 0.7978 ± 0.1926 |
| SECOM | |||
| LE-CAS | 0.6967 ± 0.0416 | 0.5930 ± 0.0192 | 0.7931 ± 0.1427 |
| LE | 0.5852 ± 0.0437 | 0.3247 ± 0.0233 | 0.4388 ± 0.1904 |
| S-LE | 0.6082 ± 0.0367 | 0.5552 ± 0.0296 | 0.5478 ± 0.1309 |
| GGLE | 0.6552 ± 0.0345 | 0.4925 ± 0.0334 | 0.6546 ± 0.1071 |
| SCPLE | 0.6923 ± 0.0570 | 0.5892 ± 0.0270 | 0.6339 ± 0.1286 |
| DrivFace | |||
| LE-CAS | 0.6738 ± 0.0227 | 0.5771 ± 0.0280 | 0.7563 ± 0.0470 |
| LE | 0.3691 ± 0.0322 | 0.1917 ± 0.0267 | 0.4614 ± 0.0234 |
| S-LE | 0.4452 ± 0.0237 | 0.3156 ± 0.0193 | 0.5324 ± 0.0193 |
| GGLE | 0.5892 ± 0.0334 | 0.4622 ± 0.0138 | 0.6474 ± 0.0291 |
| SCPLE | 0.6037 ± 0.0190 | 0.5112 ± 0.0142 | 0.6890 ± 0.0391 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, J. Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity. Algorithms 2019, 12, 210. https://doi.org/10.3390/a12100210
Zhou H, Wang J. Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity. Algorithms. 2019; 12(10):210. https://doi.org/10.3390/a12100210
Chicago/Turabian StyleZhou, Honghu, and Jun Wang. 2019. "Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity" Algorithms 12, no. 10: 210. https://doi.org/10.3390/a12100210
APA StyleZhou, H., & Wang, J. (2019). Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity. Algorithms, 12(10), 210. https://doi.org/10.3390/a12100210





