Abstract
We present two modifications of Duval’s algorithm for computing the Lyndon factorization of a string. One of the algorithms has been designed for strings containing runs of the smallest character. It works best for small alphabets and it is able to skip a significant number of characters of the string. Moreover, it can be engineered to have linear time complexity in the worst case. When there is a run-length encoded string R of length , the other algorithm computes the Lyndon factorization of R in time and in constant space. It is shown by experimental results that the new variations are faster than Duval’s original algorithm in many scenarios.
1. Introduction
A string w is a rotation of another string if and , for some strings u and v. A string is a Lyndon word if it is lexicographically smaller than all its proper rotations. Chen, Fox and Lyndon [1] introduced the unique factorization of a string in Lyndon words such that the sequence of factors is nonincreasing according to the lexicographical order. The Lyndon factorization is a key structure in a method for sorting the suffixes of a text [2], which is applied in the construction of the Burrows-Wheeler transform and the suffix array, as well as in the bijective variant of the Burrows-Wheeler transform [3,4]. The Burrows-Wheeler transform is an invertible transformation of a string, based on sorting of its rotations, while the suffix array is a lexicographically sorted array of the suffixes of a string. They are the groundwork for many indexing and data compression methods.
Duval’s algorithm [5] computes the Lyndon factorization in linear time and in constant space. Various other solutions for computing the Lyndon factorization have been proposed in the past. A parallel algorithm [6] was presented by Apostolico and Crochemore, while Roh et al. described an external memory algorithm [7]. Recently, I et al. and Furuya et al. introduced algorithms to compute the Lyndon factorization of a string given in the grammar-compressed form and in the LZ78 encoding [8,9].
In this paper, we present two new variations of Duval’s algorithm. The paper is an extended version of the conference paper [10]. The first algorithm has been designed for strings containing runs of the smallest character. It works best for small alphabets like the DNA alphabet {a, c, g, t} and it is able to skip a significant portion of the string. The second variation works for strings compressed with run-length encoding. In run-length encoding, maximal sequences in which the same data value occurs in many consecutive data elements (called runs) are stored as a pair of a single data value and a count. When there is a run-length encoded string R of length , our algorithm computes the Lyndon factorization of R in time and in constant space. This variation is thus preferable to Duval’s algorithm when the strings are stored or maintained with run-length encoding. In our experiments, the new algorithms are considerably faster than the original one in the case of small alphabets, for both real and simulated data.
The rest of the paper is organized as follows. Section 2 defines background concepts Section 3 presents Duval’s algorithm, Section 4 and Section 5 introduce our variations of Duval’s algorithm, Section 6 shows the results of our practical experiments, and the discussion of Section 7 concludes the article.
2. Basic Definitions
Let be a finite ordered alphabet of symbols and let be the set of words (strings) over ordered by lexicographic order. In this paper, we use the terms string, sequence, and word interchangeably. The empty word is a word of length 0. Let be equal to . Given a word w, we denote with the length of w and with the i-th symbol of w, for . The concatenation of two words u and v is denoted by . Given two words u and v, v is a substring of u if there are indices such that . If () then v is a prefix (suffix) of u. The substring of u is denoted by , and for . We denote by the concatenation of ku’s, for and . The longest border of a word w, denoted with , is the longest proper prefix of w which is also a suffix of w. Let denote the length of the longest common prefix of words w and . We write if either , i.e., if w is a proper prefix of , or if . For any , is a rotation of w. A Lyndon word is a word w such that , for . Given a Lyndon word w, the following properties hold:
- ;
- either or .
Both properties imply that no word , for , , is a Lyndon word. The following result is due to Chen, Fox and Lyndon [11]:
Theorem 1.
Any word w admits a unique factorization , such that is a Lyndon word, for , and .
The interval of positions in w of the factor in is , where , , for . We assume the following property:
Property 1.
The output of an algorithm that, given a word w, computes the factorization is the sequence of intervals of positions of the factors in .
The run-length encoding (RLE) of a word w, denoted by , is a sequence of pairs (runs) such that , , for , and . The interval of positions in w of the run is where , .
3. Duval’s Algorithm
In this section we briefly describe Duval’s algorithm for the computation of the Lyndon factorization of a word. Let L be the set of Lyndon words and let
be the set of nonempty prefixes of Lyndon words. Let also , where c is the maximum symbol in . Duval’s algorithm is based on the following Lemmas, proved in [5]:
Lemma 1.
Let and be the longest prefix of which is in L. We have .
Lemma 2.
.
Lemma 3.
Let , with , , and . The following propositions hold:
- 1.
- For and , ;
- 2.
- For and , ;
- 3.
- For , .
Lemma 1 states that the computation of the Lyndon factorization of a word w can be carried out by computing the longest prefix of which is a Lyndon word and then recursively restarting the process from . Lemma 2 states that the nonempty prefixes of Lyndon words are all of the form , where . By the first property of Lyndon words, the longest prefix of which is in L is . Hence, if we know that , but , then by Lemma 1 and by induction we have , where . For example, if , we have , since while .
Suppose that we have a procedure LF-next which computes, given a word w and an integer k, the pair where s is the largest integer such that and q is the largest integer such that , for . The factorization of w can then be computed by iteratively calling LF-next starting from position 0. When a given call to LF-next returns, the factorization algorithm outputs the intervals , for , and restarts the factorization at position . Duval’s algorithm implements LF-next using Lemma 3, which explains how to compute, given a word and a symbol , whether , and thus makes it possible to compute the factorization using a left to right parsing. Note that, given a word with , we have and with and . For example, if , we have , , , and . The code of Duval’s algorithm is shown in Figure 1. The algorithm has -time and -space complexity.

Figure 1.
Duval’s algorithm to compute the Lyndon factorization of a string.
The following is an alternative formulation of Duval’s algorithm by I et al. [8]:
Lemma 4.
Let be any position of a string w such that for any and . Then, also holds for any .
Lemma 5.
Let w be a string with . It holds that and , where .
For example, if , we have , , and . Based on these Lemmas, the procedure LF-next can be implemented by initializing and executing the following steps: (1) compute . (2) if and set and repeat step 1; otherwise return the pair . It is not hard to verify that, if the values are computed using symbol comparisons, then this procedure corresponds to the one used by Duval’s original algorithm.
4. Improved Algorithm for Small Alphabets
Let w be a word over an alphabet with and let be the smallest symbol in . Suppose that there exists such that is a prefix of . If the last symbol of w is not , then by Theorem 1 and by the properties of Lyndon words, is a prefix of each of . This property can be exploited to devise an algorithm for Lyndon factorization that can potentially skip symbols. Note that we assume Property 1, i.e., the output of the algorithm is the sequence of intervals of the factors in , as otherwise we have to read all the symbols of w to output . Our algorithm is based on the alternative formulation of Duval’s algorithm by I et al. [8]. Given a set of strings , let be the set of all (starting) positions in w corresponding to occurrences of the strings in . We start with the following Lemmas:
Lemma 6.
Let w be a word and let . Then, we have .
Proof.
If or the Lemma plainly holds. Otherwise, Let be the factor in such that s belongs to , the interval of . To prove the claim we have to show that . Suppose by contradiction that , which implies . Then, , which contradicts the second property of Lyndon words. □
For example, if , we have .
Lemma 7.
Let w be a word such that occurs in it and let . Then, we have .
Proof.
Let be the factor in such that s belongs to , the interval of . To prove the claim we have to show that . Suppose by contradiction that , which implies . If then , which contradicts the second property of Lyndon words. Otherwise, since is a Lyndon word it must hold that . This implies at least that , which contradicts the hypothesis that s is the smallest element in . □
For example, if , we have .
Lemma 8.
Let w be a word such that and . Let r be the smallest position in w such that . Let also . Then we have
where is the ending position of factor .
Proof.
By Lemma 5 we have that . Since and , for any string v such that we must have that either , if , or otherwise. Since , the only position s that satisfies is , corresponding to the empty word. Hence,
□
For example, if , we have , and . Based on these Lemmas, we can devise a faster factorization algorithm for words containing runs of . The key idea is that, using Lemma 8, it is possible to skip symbols in the computation of , if a suitable string matching algorithm is used to compute . W.l.o.g. we assume that the last symbol of w is different from . In the general case, by Lemma 6, we can reduce the factorization of w to the one of its longest prefix with last symbol different from , as the remaining suffix is a concatenation of symbols, whose factorization is a sequence of factors equal to . Suppose that occurs in w. By Lemma 7 we can split the factorization of w in and where and . The factorization of can be computed using Duval’s original algorithm.
Concerning v, let . By definition and , and we can apply Lemma 8 on v to find the ending position s of the first factor in , i.e., , where . To this end, we iteratively compute until either a position i is found that satisfies or we reach the end of the string. Let , for a given . Observe that and, if , then, by Lemma 4, we do not need to verify the positions such that . The computation of can be performed by using either an algorithm for multiple string matching for the set of patterns or an algorithm for single string matching for the pattern , since . Note that the same algorithm can also be used to compute in the first phase.
Given that all the patterns in differ in the last symbol only, we can express more succinctly using a character class for the last symbol and match this pattern using a string matching algorithm that supports character classes, such as the algorithms based on bit-parallelism. In this respect, SBNDM2 [12], a variation of the BNDM algorithm [13] is an ideal choice, as it is sublinear on average. However, this method is preferable only if is less than or equal to the machine word size in bits.
Let and . Based on Lemma 5, the algorithm then outputs the intervals of the factors , for , and iteratively applies the above method on . It is not hard to verify that, if , then , and , and so Lemma 8 can be used on . The code of the algorithm, named LF-skip, is shown in Figure 2. The computation of the value for takes advantage of the fact that , so as to avoid useless comparisons.

Figure 2.
The algorithm to compute the Lyndon factorization that can potentially skip symbols.
If the total time spent for the iteration over the sets is , the worst case time complexity of LF-skip is linear. To see why, it is enough to observe that the positions i for which LF-skip verifies if are a subset of the positions verified by the original algorithm. Indeed, given a string w satisfying the conditions of Lemma 8, for any position there is no such that . Hence, the only way Duval’s algorithm can skip a position using Lemma 4 is by means of a smaller position belonging to , which implies that the algorithms skip or verify the same positions in .
5. Computing the Lyndon Factorization of a Run-Length Encoded String
In this section we present an algorithm to compute the Lyndon factorization of a string given in RLE form. The algorithm is based on Duval’s original algorithm and on a combinatorial property between the Lyndon factorization of a string and its RLE, and has -time and -space complexity, where is the length of the RLE. We start with the following Lemma:
Lemma 9.
Let w be a word over Σ and let be its Lyndon factorization. For any , let , , such that and . Then, either or .
Proof.
Suppose by contradiction that and either or . By definition of , we have . Moreover, since both and overlap with , we also have . If , then, by definition of , we have . Instead, if and , we have that is a prefix of . Hence, in both cases we obtain , which is a contradiction. □
The consequence of this Lemma is that a run of length l in the RLE is either contained in one factor of the Lyndon factorization, or it corresponds to l unit-length factors. Formally:
Corollary 1.
Let w be a word over Σ and let be its Lyndon factorization. Then, for any , either there exists such that is contained in or there exist factors such that and , for .
This property can be exploited to obtain an algorithm for the Lyndon factorization that runs in time. First, we introduce the following definition:
Definition 1.
A word w is a LR word if it is either a Lyndon word or it is equal to , for some , . The LR factorization of a word w is the factorization in LR words obtained from the Lyndon factorization of w by merging in a single factor the maximal sequences of unit-length factors with the same symbol.
For example, the LR factorization of is . Observe that this factorization is a (reversible) encoding of the Lyndon factorization. Moreover, in this encoding it holds that each run in the RLE is contained in one factor and thus the size of the LR factorization is . Let be the set of LR words. Suppose that we have a procedure which computes, given an RLE sequence R and an integer k, the pair where s is the largest integer such that and q is the largest integer such that , for . Observe that, by Lemma 9, is the longest prefix of which is in , since otherwise the run would span two factors in the factorization of . This implies that the pair returned by satisfies
Based on Lemma 1, the factorization of R can then be computed by iteratively calling LF-rle-next starting from position 0. When a given call to LF-rle-next returns, the factorization algorithm outputs the intervals in R, for , and restarts the factorization at position .
We now present the algorithm. Analogously to Duval’s algorithm, it reads the RLE sequence from left to right maintaining two integers, j and ℓ, which satisfy the following invariant:
The integer j, initialized to , is the index of the next run to read and is incremented at each iteration until either or . The integer ℓ, initialized to 0, is the length in runs of the longest border of , if spans at least two runs, and equal to 0 otherwise. For example, in the case of the word we have and . Let . In general, if , we have
Note that the longest border may not fully cover the last (first) run of the corresponding prefix (suffix). Such the case is for example for the word . However, since it must hold that , i.e., the first run of the suffix is fully covered. Let
Informally, the integer z is equal to 1 if the longest border of does not fully cover the run . By 1 we have that can be written as , where
For example, in the case of the word , for , we have . The algorithm is based on the following Lemma:
Lemma 10.
Let be such that invariant 1 holds and let . Then, we have the following cases:
- 1.
- If then ;
- 2.
- If then and 1 holds for , ;
Moreover, if , we also have:
Proof.
The idea is the following: we apply Lemma 3 with the word as defined above and symbol . Observe that is compared with symbol , which is equal to if and to otherwise.
First note that, if , , since otherwise we would have . In the first three cases, we obtain the first, second and third proposition of Lemma 3, respectively, for the word . Independently of the derived proposition, it is easy to verify that the same proposition also holds for , . Consider now the fourth case. By a similar reasoning, we have that the third proposition of Lemma 3 holds for . If we then apply Lemma 3 to and , is compared to and we must have as otherwise . Hence, either the first (if ) or the second (if ) proposition of Lemma 3 must hold for the word . □
We prove by induction that invariant 1 is maintained. At the beginning, the variables j and ℓ are initialized to and 0, respectively, so the base case trivially holds. Suppose that the invariant holds for . Then, by Lemma 10, either or it follows that the invariant also holds for , where is equal to , if , and , and to 0 otherwise. When the algorithm returns the pair , i.e., the length of and the corresponding exponent.
The code of the algorithm is shown in Figure 3. We now prove that the algorithm runs in time. First, observe that, by definition of LR factorization, the for loop at line 4 is executed times. Suppose that the number of iterations of the while loop at line 2 is n and let be the corresponding values of k, with and . We now show that the s-th call to performs less than iterations, which will yield number of iterations in total. This analysis is analogous to the one used by Duval. Suppose that , and are the values of i, j and z at the end of the s-th call to . The number of iterations performed during this call is equal to . We have , where , which implies , since, for any positive integers , holds.

Figure 3.
The algorithm to compute the Lyndon factorization of a run-length encoded string.
6. Experimental Results
We tested extensively the algorithms LF-Duval, LF-skip, and LF-rle. In addition, we also tested variations of LF-Duval and LF-skip, denoted as LF-Duval2 and LF-skip2. LF-Duval2 performs an if-test
which is always true in line 9 of LF-next. This form, which is advantageous for compiler optimization, can be justified by the formulation of the original algorithm [5] where there is a three branch test of and . LF-skip2, after finding the first , searches for until is found, whereas LF-skip searches for where x is a character class.
The experiments were run on Intel Core i7-4578U with 3 GHz clock speed and 16 GB RAM. The algorithms were written in the C programming language and compiled with gcc 5.4.0 using the O3 optimization level.
Testing LF-skip. At first we tested the variations of LF-skip against the variations of LF-Duval. The texts were random sequences of 5 MB symbols. For each alphabet size we generated 100 sequences with a uniform distribution, and each run with each sequence was repeated 500 times. The average run times are given in Table 1 which is shown in a graphical form in Figure 4.

Table 1.
Run times in milliseconds on random sequences (5 MB) with a uniform distribution of a varying alphabet size.
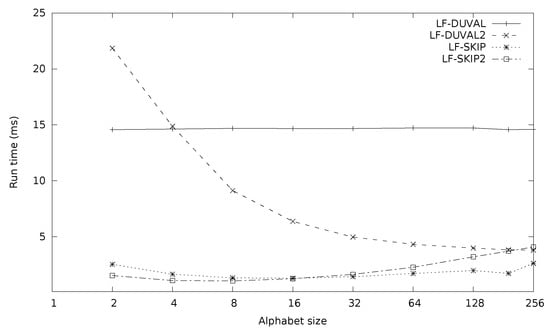
Figure 4.
Comparison of the algorithms on random sequences (5 MB) with a uniform distribution of a varying alphabet size.
LF-skip was faster than the best variation of LF-Duval for all tested values of . The speed-up was significant for small alphabets. LF-skip2 was faster than LF-skip for and slower for .
The speed of LF-Duval did not depend on . LF-Duval2 became faster when the size of the alphabet grew. For large alphabets LF-Duval2 was faster than LF-Duval and for small alphabets the other way round. In additional refined experiments, was the threshold value. When we compiled LF-Duval and LF-Duval2 without optimization, both of the variations behaved in a similar way. So the better performance of LF-Duval2 for large alphabets is due to compiler optimization, possibly by cause of branch prediction.
We tested the variations of LF-skip also with longer random sequences of four characters up to 500 MB. The average speed did not essentially change when the sequence became longer.
In addition, we tested LF-skip and LF-skip2 with real texts. At first we did experiments with texts of natural language. Because runs are very short in a natural language and newline or some other control character is the smallest character, the benefit of LF-skip or LF-skip2 was marginal. If it were acceptable to relax the lexicographic order of the characters, some gain could be obtained. For example, LF-skip achieved the speed-up of 2 over LF-Duval2 in the case of the KJV Bible when ‘l’ is the smallest character.
For the DNA sequence of fruitfly (15 MB), LF-skip2 was 20.3 times faster than LF-Duval. For the protein sequence of the saccharomyces cerevisiae (2.9 MB), LF-skip2 was 8.7 times faster than LF-Duval2. The run times on these biological sequences are shown in Table 2.

Table 2.
Run times in milliseconds on two biological sequences.
Testing LF-rle. To assess the performance of the LF-rle algorithm, we tested it together with LF-Duval, LF-Duval2 and LF-skip2 for random binary sequences of 5 MB with different probability distributions, so as to vary the number of runs in the sequence. The running time of LF-rle does not include the time needed to compute the RLE of the sequence, i.e., we assumed that the sequence is given in the RLE form, since otherwise other algorithms are preferable. For each test we generated 100 sequences, and each run with each sequence was repeated 500 times. The average run times are given in Table 3 which is shown in a graphical form in Figure 5.

Table 3.
Run times in milliseconds on random binary sequences (5 MB) with a skew distribution.
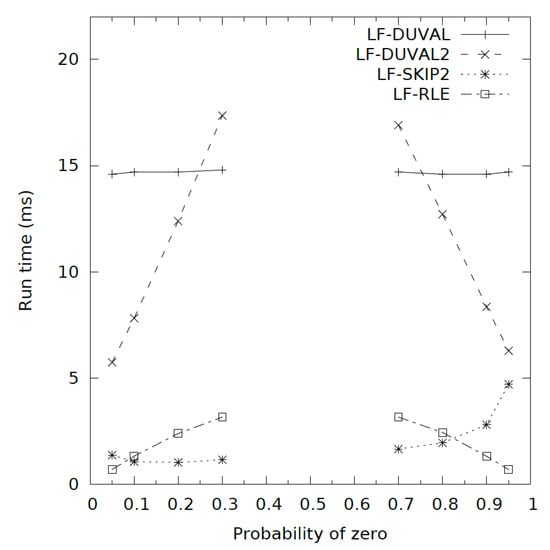
Figure 5.
Comparison of the algorithms on random binary sequences (5 MB) with a skew distribution.
Table 3 shows that LF-rle was the fastest for distributions 0.05, 0.9, and 0.95. Table 3 also reveals that LF-rle and LF-Duval2 worked symmetrically for distributions of zero and one, but LF-skip2 worked unsymmetrically which is due to the fact that LF-skip2 searches for the runs of the smallest character which was zero in this case.
In our tests the run time of LF-Duval was about 14.7 ms for all sequences of 5 MB. Thus LF-Duval is a better choice than LF-Duval2 for cases 0.3 and 0.7.
7. Conclusions
We presented new variations of Duval’s algorithm for computing the Lyndon factorization of a string. The first algorithm LF-skip was designed for strings containing runs of the smallest character in the alphabet and it is able to skip a significant portion of the characters of the string. The second algorithm LF-rle is for strings compressed with run-length encoding and computes the Lyndon factorization of a run-length encoded string of length in time and constant space. Our experimental results show that these algorithms can offer a significant speed-up over Duval’s original algorithm. Especially LF-skip is efficient in the case of biological sequences.
Author Contributions
Formal analysis, E.G.; Investigation, S.S.G.; Methodology, J.T.; Software, E.G. and J.T.; Supervision, J.T.; Writing—original draft, S.S.G. and E.G.; Writing—review & editing, J.T.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, K.T.; Fox, R.H.; Lyndon, R.C. Free differential calculus. IV. The quotient groups of the lower central series. Ann. Math. 1958, 68, 81–95. [Google Scholar] [CrossRef]
- Mantaci, S.; Restivo, A.; Rosone, G.; Sciortino, M. Sorting suffixes of a text via its Lyndon factorization. In Proceedings of the Prague Stringology Conference 2013, Prague, Czech Republic, 2–4 September 2013; pp. 119–127. [Google Scholar]
- Gil, J.Y.; Scott, D.A. A bijective string sorting transform. arXiv 2012, arXiv:1201.3077. [Google Scholar]
- Kufleitner, M. On bijective variants of the Burrows-Wheeler transform. In Proceedings of the Prague Stringology Conference 2009, Prague, Czech Republic, 31 August–2 September 2009; pp. 65–79. [Google Scholar]
- Duval, J.P. Factorizing words over an ordered alphabet. J. Algorithms 1983, 4, 363–381. [Google Scholar] [CrossRef]
- Apostolico, A.; Crochemore, M. Fast parallel Lyndon factorization with applications. Math. Syst. Theory 1995, 28, 89–108. [Google Scholar] [CrossRef]
- Roh, K.; Crochemore, M.; Iliopoulos, C.S.; Park, K. External memory algorithms for string problems. Fundam. Inform. 2008, 84, 17–32. [Google Scholar]
- Tomohiro, I.; Nakashima, Y.; Inenaga, S.; Bannai, H.; Takeda, M. Faster Lyndon factorization algorithms for SLP and LZ78 compressed text. Theor. Comput. Sci. 2016, 656, 215–224. [Google Scholar] [CrossRef]
- Furuya, I.; Nakashima, Y.; Tomohiro, I.; Inenaga, S.; Bannai, H.; Takeda, M. Lyndon Factorization of Grammar Compressed Texts Revisited. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching (CPM 2018), Qingdao, China, 2–4 July 2018. [Google Scholar] [CrossRef]
- Ghuman, S.S.; Giaquinta, E.; Tarhio, J. Alternative algorithms for Lyndon factorization. In Proceedings of the Prague Stringology Conference 2014, Prague, Czech Republic, 1–3 September 2014; pp. 169–178. [Google Scholar]
- Lothaire, M. Combinatorics on Words; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Durian, B.; Holub, J.; Peltola, H.; Tarhio, J. Improving practical exact string matching. Inf. Process. Lett. 2010, 110, 148–152. [Google Scholar] [CrossRef]
- Navarro, G.; Raffinot, M. Fast and flexible string matching by combining bit-parallelism and suffix automata. ACM J. Exp. Algorithm 2000, 5, 4. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).