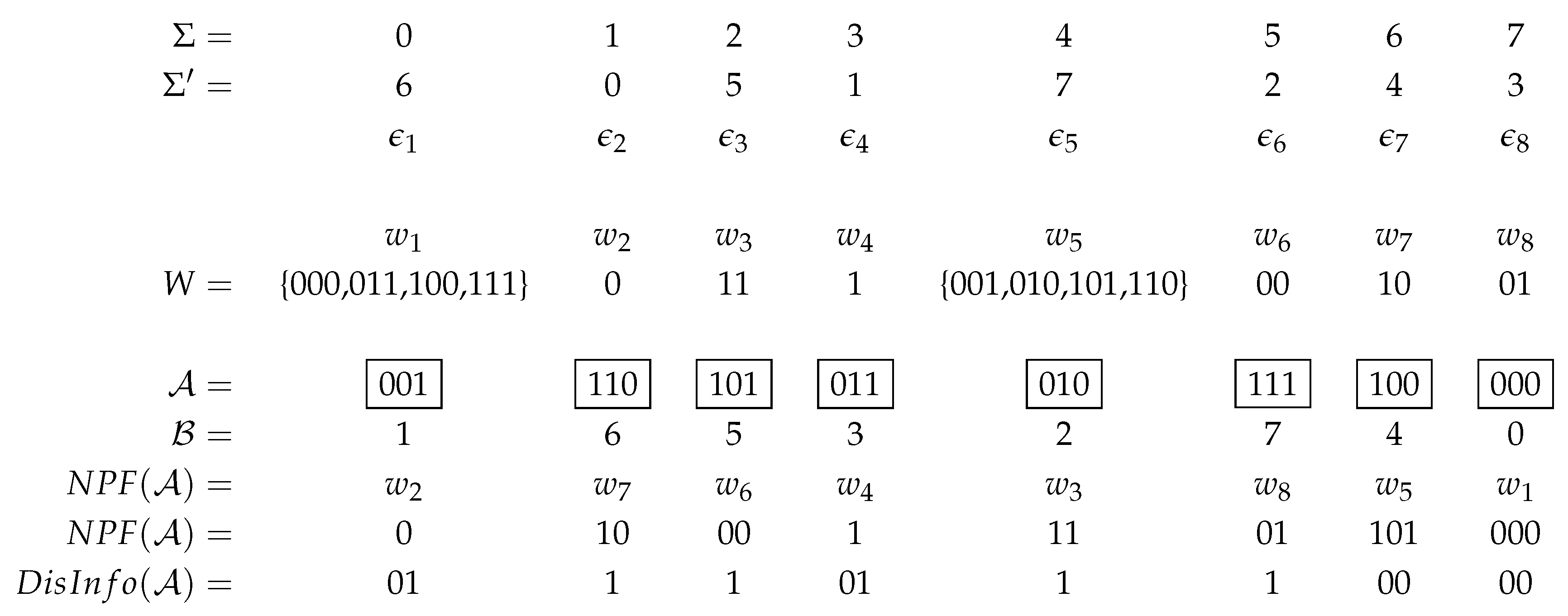Applications of Non-Uniquely Decodable Codes to Privacy-Preserving High-Entropy Data Representation ^†

Abstract

Non-uniquely-decodable (non-UD) codes can be defined as the codes that cannot be uniquely decoded without additional disambiguation information. These are mainly the class of non–prefix–free codes, where a code-word can be a prefix of other(s), and thus, the code-word boundary information is essential for correct decoding. Due to their inherent unique decodability problem, such non-UD codes have not received much attention except a few studies, in which using compressed data structures to represent the disambiguation information efficiently had been previously proposed. It had been shown before that the compression ratio can get quite close to Huffman/Arithmetic codes with an additional capability of providing direct access in compressed data, which is a missing feature in the regular Huffman codes. In this study we investigate non-UD codes in another dimension addressing the privacy of the high-entropy data. We particularly focus on such massive volumes, where typical examples are encoded video or similar multimedia files. Representation of such a volume with non–UD coding creates two elements as the disambiguation information and the payload, where decoding the original data from these elements becomes hard when one of them is missing. We make use of this observation for privacy concerns. and study the space consumption as well as the hardness of that decoding. We conclude that non-uniquely-decodable codes can be an alternative to selective encryption schemes that aim to secure only part of the data when data is huge. We provide a freely available software implementation of the proposed scheme as well.

1. Introduction

A coding scheme basically replaces the symbols of an input sequence with their corresponding code-words. Such a scheme can be referred as ambiguous if it is not possible to uniquely decode the code-words back into the original data without using a disambiguation information. In this study, we study non–prefix–free (NPF) codes, where a code-word can be a prefix of other(s), and the ambiguity arises since the code-word boundaries cannot be determined on the code-word stream without explicit knowledge of the individual code-word lengths. Due to the lack of that unique decodability feature, NPF codes has received limited attention [1,2,3,4,5] in the related literature.

The basic approach in dealing with the decodability problem of NPF schemes is to find an efficient way of representing the code-word boundaries. That had been studied in [5] by maintaining an additional compressed bit array supporting rank and select queries [6] to mark the code-word boundaries on the code-word stream. Similar approaches were also independently mentioned in [7,8]. Yet another way is to create a wavelet tree [9] over the code-word lengths, which was studied in [5] as an alternative to maintaining a bit array. Empirical observations in [5] showed that actually NPF codes can provide compression ratios quite close to and sometimes better than the Huffman codes, while providing random access, which is a missing feature in ordinary Huffman codes, in constant or logarithmic time.

Despite efforts to solve unique decodability of ambigious codes, in this study we focus on the privacy and security opportunities provided by the NPF codes. Achieving the security of massive data volumes with less encryption makes sense on platforms where the cost of encryption becomes hefty according to some metrics, e.g., time, memory, energy, or bandwidth. For example, in battery-constrained environments such as mobile devices [10], sensor networks [11], or unmanned aerial vehicles [12], performing less encryption may help to increase the battery life. It had been shown that symmetric security algorithms roughly doubles the energy consumption of normal operation in those environments, and asymmetric security algorithms increase the energy usage per bit in order of magnitudes (around 5 fold) [13]. Previously, selective encryption schemes [14] have been proposed to reduce the encryption load, particularly on transmission of video/image files [15,16,17]. In selective encryption, segments of the data, which are assumed to include important information, e.g., the I-frames in a video stream, are encrypted, while rest of the data is kept plain. We introduce an alternative approach to reduce the amount of encryption required to secure a source data. As opposed to the partial security provided by the selective encryption schemes, we observe that the intrinsic ambiguity of non-prefix-free (NPF) codes gives us an interesting opportunity for the privacy of the whole data.

The main idea of the proposed technique here is to process the n bit long input bit sequence, which is assumed to be independently and identically distributed, in blocks of d bits according to a predetermined d parameter that is typically between 6 and 20. We create $2^d$ non-prefix code-words by using a permutation of the numbers $[1\dots 2^d]$, and then replace every d-bits long symbol in the input with its corresponding NPF code-word of varying bit-length in between 1 to d. We call the resulting bit stream the payload since it includes the actual content of the source. This sequence can not be decoded properly without the code-word boundaries due to the inherent ambiguity of the NPF codes. Therefore, we need to maintain an efficient representation of the code-word boundaries on the payload. We refer to that second bit stream as the disambiguation information throughout the study. In the proposed scheme, the total space consumed by the payload and the disambiguation information introduces an overhead of $2(d-1)/d·2^d\approx \frac{1}{2^{d-1}}$ bits per each original bit, which becomes negligible as d increases, i.e., it is less than 7 bits per a thousand bit when $d=8$. We prove that the payload occupies $\approx \frac{(d-2)}{d}$, and the disambiguation information takes $\approx \frac{2}{d}$ of the final representation, and the two partitions consume in total almost the same space with the input data.

Following the space consumption analysis, we investigate how much information can be inferred from disambiguation data for the payload and vice versa, which leads us to the conclusion that encrypting one of the partitions and leaving the other one in plain can be considered for the privacy of the data. Since disambiguation information consumes less space, it would be ideal to encrypt it while leaving the payload in plain. However, the other way, encrypting the payload and leaving the the disambiguation information plain can still reduce the to-be-encrypted amount. Yet, nested application of the coding schemes on either partitions can also be considered a good strategy for privacy.

It might have captured the attention of the reader that the analysis assumes the input bit stream is i.i.d., which seems a bit restrictive at a first glance. However, the target data types of the introduced method are mainly the sources that have been previously entropy encoded with some data compression scheme, where each symbol is represented by minimum number of bits close to its entropy according to Shannon’s theorem [18]. Such typical sources are video files in mpeg4 format, sound files in mp3 format, images in JPEG format and similar others. The output of the compression tools squeezing data down to its entropy is actually a quite nice input for our proposal. We support this observation by the experiments performed on various compressed file types on which the results are observed to be very close to the theoretical bounds computed by the uniformly i.i.d. assumption. In that sense, the proposed scheme can also be seen as a method of providing privacy of the compressed data as well.

The outline of the paper is as follows. In Section 2 we introduce the proposed non-UD coding method based on the non–prefix–free codes, and analyze its basic properties mostly focusing on the space consumption of the partitions. We provide verification of the theoretical claims based on uniformly i.i.d. assumption on some files that are already entropy-encoded and investigate the hardness of decoding in absence of the partitions in this section for privacy issues. The implementation of the proposed technique is introduced here and currently available speed is presented as well. Section 3 summarizes the results obtained. We discuss possible practical usage scenarios in Section 4 and then conclude with addressing further research avenues.

2. Materials and Methods

We start with defining the proposed non-UD coding scheme and analyze the space occupied by the disambiguation information, the payload, and the overhead with respect to the original input, which we will assume to be a uniformly and independently distributed bit sequence of length n. We focus next on the complexities of inferring the disambiguation information or the payload in absence of the other.

2.1. Non-Uniquely-Decodable Data Coding

Let $\mathcal{A}=a_1{a}_2\dots a_n$ denotes an independently and identically distributed bit sequence, and $d>1$ is a predetermined block length. Without loss of generality we assume n is divisible by d. Otherwise, it is padded with random bits. $\mathcal{A}$ can be represented as $\mathcal{B}=b_1{b}_2\dots b_r$, for $r=\frac{n}{d}$ such that each d–bits long $b_i$ in $\mathcal{B}$ is from the alphabet $\Sigma =\{0,1,2,\dots 2^d-1\}$. We will first define the minimum binary representation of an integer, and then use this definition to state our encoding scheme.

Definition 1.

The minimum binary representation (MBR) of an integer $i\ge 2$ is its binary representation without the leftmost 1 bit. As an example, $MBR\left(21\right)=0101$ by omitting the leftmost set bit in its binary representation as $21={\left(\mathbf{1}0101\right)}_2$.

Definition 2.

Let ${\Sigma }^{\prime }=\{{ϵ}_1,{ϵ}_2,\dots {ϵ}_{2^d}\}$ be a permutation of the given alphabet $\Sigma =\{0,1,2,\dots ,2^d-1\}$, and $W=\{w_1,w_2,\dots ,w_{2^d}\}$ is a code-word set such that

$$w_i=\left\{\begin{array}{cc}MBR(2+{ϵ}_i)\hfill & ,\mathit{if}{ϵ}_i<2^d-2\hfill \\ \{MBR(2^d+\zeta ):\forall \zeta \in \{0,1,\dots ,2^d-1\},\mathit{where}\zeta =\{0,3\}mod4\}\hfill & ,\mathit{if}{ϵ}_i=2^d-2\hfill \\ \{MBR(2^d+\zeta ):\forall \zeta \in \{0,1,\dots ,2^d-1\},\mathit{where}\zeta =\{1,2\}mod4\}\hfill & ,\mathit{if}{ϵ}_i=2^d-1\hfill \end{array}\right.$$

The representation of the input $\mathcal{A}=\mathcal{B}=b_1{b}_2\dots b_r$ with the non–prefix–free code-word set W is shown by $NPF\left(\mathcal{A}\right)=c_1{c}_2\dots c_r$ such that $c_i=w_{1+b_i}$. When a code-word $c_i$ has multiple options, a randomly selected one among the possibilities is used.

The NPF coding of a sample sequence according to the Definitions 1 and 2 with the parameter $d=3$ is shown in Figure 1. The code-words $w_1$ and $w_5$ are sets as their corresponding ${ϵ}_1=6$ and ${ϵ}_5=7$ values are greater than or equal to $6=2^3-2$. Thus, when $c_i=w_1$ or $c_i=w_5$, a randomly selected code-word respectively from sets $w_1$ or $w_5$, is inserted.

Proposition 1.

In a code-word set W that is generated for a block length $d>1$ according to Definition 2, the lengths of the code-words in bits range from 1 to d, where the number of ℓ–bits long code-words for each $\ell \in \{1,2,\dots ,d-1\}$ is $2^{\ell }$, and for $\ell =d$ there exist 2 sets of code-words each of which includes $2^{d-1}$ elements.

Proof. 

According to Definition 2, the entities in W are minimum binary representations of numbers $\{2,3,\dots ,2^{d+1}-1\}$. Since the MBR bit-lengths of those numbers range from 1 to d, there are d distinct code-word lengths in W. Each code-word length $\ell \in \{1,2,\dots ,d-1\}$ defines $2^{\ell }$ distinct code-words, and thus, total number of code-words defined by all possible $\ell <d$ values becomes ${\sum }_{i=1}^{d-1}{2}^i=2^d-2$. The remaining 2 code-words out of the $\left|W\right|=2^d$ items require d–bits long bit sequences. For example, when $d=3$, the W includes $2(=2^1)$ code-words of 1-bit long, $4(=2^2)$ code-words of length 2, and $2(=2^3-6)$ code-word sets of length 3-bits as shown in Figure 1. □

Lemma 1.

The non-UD encoding $NPF\left(\mathcal{A}\right)$ of an i.i.d. bit sequence $\mathcal{A}$ of length $n=r·d$ is expected to occupy $r·(d-2+\frac{d+1}{2^{d-1}})$ = $n·(1-\frac{2}{d}+\frac{2(d+1)}{d·2^d})$ bits space.

Proof. 

The total bit length of the NPF code-words is simply ${\sum }_{\ell =1}^d{C}_{\ell }·\ell$, where $C_{\ell }$ denotes the number of occurrences of the $b_i$ values represented by ℓ–bits long code-words in $\mathcal{B}$. Assuming the uniform distribution of $\mathcal{B}$, each $b_i\in \{0,1,2,\dots ,2^d-1\}$ appears $\frac{r}{2^d}$ times. The number of distinct $b_i$ values represented by a code-word of length ℓ is $2^{\ell }$ for $1\le \ell <d$, and two of the $b_i$ values require $\ell =d$ bit long code-words as stated in Proposition 1. Thus, $C_{\ell }=\frac{r}{2^d}·2^{\ell }$ for $1\le \ell <d$, and $C_d=\frac{r}{2^d}·2$. The length of the $NPF\left(\mathcal{B}\right)$ bit-stream can then be computed by

$$\begin{array}{cc}\hfill \left|NPF\right(\mathcal{A}\left)\right|& =\frac{r}{2^d}·(1·2+2·2^2+\dots +(d-1)·2^{d-1}+d·2)\hfill \end{array}$$

(1)

$$\begin{array}{c}=\frac{r}{2^d}·(2d+\sum _{i=1}^{d-1}i·2^i)=\frac{r}{2^d}·\left(2d+2^d·(d-2)+2\right)\hfill \end{array}$$

(2)

$$\begin{array}{c}=\frac{r}{2^d}·\left(2^d(d-2)+2(d+1)\right)\hfill \end{array}$$

(3)

$$\begin{array}{c}=r·d-r·(2-\frac{d+1}{2^{d-1}})\hfill \end{array}$$

(4)

$$\begin{array}{c}=r·(d-2+\frac{d+1}{2^{d-1}})\hfill \end{array}$$

(5)

$$\begin{array}{c}=\frac{n}{d}·(d-2+\frac{d+1}{2^{d-1}})\hfill \end{array}$$

(6)

$$\begin{array}{c}=n·(1-\frac{2}{d}+\frac{2(d+1)}{d·2^d})\hfill \end{array}$$

(7)

While computing the summation term in Equation (2), we use the formula from basic algebra that ${\sum }_{i=1}^{p}i·2^i=2^{p+1}(p-1)+2$, and substitute $p=d-1$. □

The NPF coding represents the n bits long input sequence $\mathcal{A}$ with $n·(\frac{2}{d}-\frac{2(d+1)}{2^d})$ bits. However, since non-prefix-free codes are not uniquely decodable, $NPF\left(\mathcal{A}\right)$ cannot be decoded back correctly in absence of the code-word boundaries. Therefore, we need to represent these boundary positions on $NPF\left(\mathcal{A}\right)$ as well. Lemma 2 states an efficient method to achieve this task.

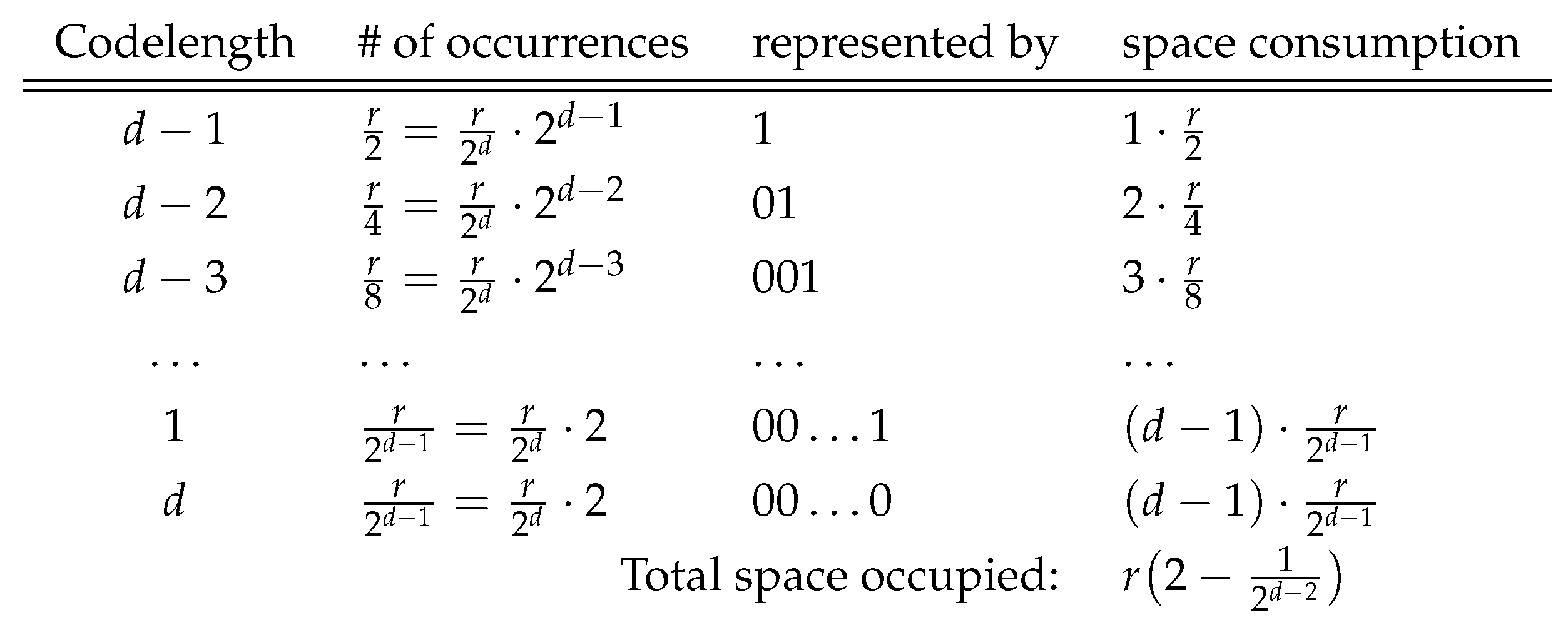
Lemma 2.

The expected number of bits to specify the code-word boundaries in the $NPF\left(\mathcal{A}\right)$ is $n·(\frac{2}{d}-\frac{4}{d·2^d})$, where $\left|\mathcal{A}\right|=n=r·d$.

Proof. 

Due to Proposition 1 there are $2^{\ell }$ distinct code-words with length ℓ for $\ell \in \{1,2,\dots ,d-1\}$ and 2 code-words (sets) are generated for $\ell =d$. Since each d-bits block has equal probability of appearance on $\mathcal{A}$, the number of occurrences of code-words having length $\ell \in \{1,2,\dots ,d-1\}$ is $\frac{r}{2^d}·2^{\ell }$. The most frequent code-word length is $(d-1)$, which appears at half of the r code-words as $\frac{r}{2^d}·2^{d-1}=\frac{r}{2}$. It is followed by the code-word length $(d-2)$ that is observed $\frac{r}{4}$ times. When we examine the number of code-words with length $\ell \in \{1,2,\dots ,d-1\}$, we see that this distribution is geometric, as depicted in Figure 2. The optimal prefix-free codes for the code-word lengths are then $\{1,01,001,\dots ,0^{d-2}1,0^{d-1}\}$, which correspond to code-word lengths $\{d-1,d-2,d-3,\dots ,1,d\}$ respectively. Thus, code-word length $\ell =(d-i)\in \{1,2,\dots ,d-1\}$, which appears $\frac{r}{2^d}·2^{d-i}$ times on $\mathcal{A}$, can be shown by i bits. We use $(d-1)$ consecutive zeros to represent the code-word length $\ell =2$ as the number of occurrences of d–bits long code-words is equal to the number of 1 bit long code-words on $\mathcal{A}$. Notice that the representation of the code-word lengths are prefix-free that can be uniquely decoded. Total number of bits required to represent the individual lengths of the code-words can be computed by

$$\begin{array}{cc}\hfill \frac{r}{2^d}(2(d-1)+\sum _{i=1}^{d-1}i·2^{d-i})& =r·(\frac{2(d-1)}{2^d}+\sum _{i=1}^{d-1}i·2^{-i})\hfill \end{array}$$

(8)

$$\begin{array}{c}=r(\frac{d-1}{2^{d-1}}+\frac{2^d-d-1}{2^{d-1}})\hfill \end{array}$$

(9)

$$\begin{array}{c}=r(2-\frac{1}{2^{d-2}})\hfill \end{array}$$

(10)

$$\begin{array}{c}=\frac{n}{d}·(2-\frac{1}{2^{d-2}})\hfill \end{array}$$

(11)

$$\begin{array}{c}=n(\frac{2}{d}-\frac{4}{d·2^d})\hfill \end{array}$$

(12)

 □

Theorem 1.

The non-UD encoding of n bit long i.i.d. input $\mathcal{A}$ sequence can be achieved with $\frac{2(d-1)}{d·2^d}$ bits overhead per each original bit.

Proof. 

Total overhead can be computed by subtracting the original length n from the sum of the space consumption described in Lemmas 1 and 2. Dividing this value by the n returns the overhead per bit as shown below.

$$\begin{array}{cc}\hfill \frac{1}{n}·\left[n·(1-\frac{2}{d}+\frac{2(d+1)}{d·2^d})+n·(\frac{2}{d}-\frac{4}{d·2^d})-n\right]& =\frac{d-1}{d·2^{d-1}}=\frac{2(d-1)}{d·2^d}\hfill \end{array}$$

(13)

 □

Table 1. The payload, disambiguation information, and overhead bits per each original bit introduced by the proposed non-UD coding for some selected d values.

$\mathit{d}=$	4	6	8	10	12	14	16	20
Overhead per bit
$\frac{d-1}{d·2^{d-1}}\approx$	0.094	0.026	0.007	0.002	$1.1\times {10}^{-4}$	$4.4\times {10}^{-4}$	$2.8\times {10}^{-5}$	$1.8\times {10}^{-6}$
Payload per bit
$1-\frac{2}{d}+\frac{2(d+1)}{d·2^d}\approx$	0.656	0.703	0.759	0.802	0.834	0.857	0.875	0.900
Dis.Info. per bit
$\frac{2}{d}-\frac{4}{d·2^d}\approx$	0.438	0.323	0.248	0.200	0.167	0.143	0.125	0.100

summarizes the amount of extra bits introduced by the proposed encoding per each original bit in $\mathcal{A}$. A large overhead, which seems significant for small d, e.g., $d<8$, may inhibit the usage of the method. However, thanks to the to the exponentially increasing denominator ($2^d$) in the overhead amount that the extra space consumption quickly becomes very small, and even negligible. For instance, when $d=8$, the method produces only $6.8$ extra bits per a thousand bit. Similarly, the overhead becomes less than 3 bits per $100K$ bits, and less than 2 bits per a million bits for the values of $d=16$ and $d=20$, respectively. Thus, for $d\ge 8$, an input uniformly i.i.d. bit sequence can be represented with a negligible space overhead by the proposed non-UD encoding scheme.

Experimental Verification of the Space Usage Results

During the calculations of the payload and disambiguation information sizes as well as the overhead, the input data has been assumed to be independently and identically distributed. In practice, the input to the proposed method is supposed to be the output of an entropy coder, where the distribution of d–bits long items in such a file may deviate from the perfect assumptions. We would like to evaluate whether such entropy-encoded files still provide enough good uniformity close to the theoretical claims based on uniformly i.i.d. assumption. Therefore, we have conducted experiments on different compressed files to observe how much these theoretical values are caught in practice.

We have selected 16 publicly available files.The first ten files are available from http://corpus.canterbury.ac.nz and http://people.unipmn.it/manzini/lightweight/corpus/. The multimedia files are from https://github.com/johndyer/mediaelement-files, where the first ten are gzip compressed data from different sources and the remaining six are multimedia files of mp3, mp4, jpg, webm, ogv, and flv formats. The first $d·2^d$ bits of each file is inspected for distinct values of $d=\{8,12,16,20\}$, and the corresponding observed payload and disambiguation information sizes are computed as well as the overhead bits in each case.

Table 2. Verification of the theoretical claims on selected files for $d=\{8,12,16,20\}$.

File Name	Payload Size	Dis.Info. Size	Overhead Bits	Payload Size	Dis.Info. Size	Overhead Bits
chr22	1555	500	7	40,961	8213	22
etext99	1515	533	0	41,103	8060	11
gcc	1491	578	21	40,764	8410	22
howtobwt	1510	538	0	41,058	8127	33
howto	1551	511	14	41,079	8095	22
jdk	1522	540	14	41,074	8122	44
rctail	1535	527	14	41,075	8088	11
rfc	1522	526	0	40,769	8394	11
sprot34	1538	524	14	41,049	8125	22
w3c2	1529	519	0	41,016	8158	22
mp3	1470	585	7	41,021	8131	0
jpg	1426	636	14	40,819	8344	11
mp4	1415	654	21	41,373	7779	0
webm	1496	566	14	40,835	8317	0
ogv	1456	592	0	40,985	8189	22
flv	1571	484	7	40,796	8367	11
Expected	1554	508	14	40,986	8188	22
	$d=8$			$d=12$
chr22	917,579	131,027	30	18,873,040	2,098,575	95
etext99	917,289	131,302	15	18,872,686	2,098,853	19
gcc	917,397	131,209	30	18,879,975	2,091,602	57
howtobwt	917,518	131,088	30	18,875,332	2,096,207	19
howto	917,812	130,794	30	18,875,502	2,096,037	19
jdk	917,412	131,179	15	18,873,190	2,098,406	76
rctail	917,139	131,437	0	18,876,497	2,095,042	19
rfc	917,346	131,275	45	18,873,175	2,098,364	19
sprot34	918,158	130,433	15	18,878,705	2,092,891	76
w3c2	917,707	130,899	30	18,876,613	2,094,945	38
mp3	914,926	133,695	45	18,863,837	2,107,721	38
jpg	915,821	132,770	15	18,878,914	2,092,625	19
mp4	905,887	142,689	0	18,898,789	2,072,826	95
webm	917,075	131,561	60	18,873,348	2,098,210	38
ogv	916,558	132,108	90	18,875,407	2,096,208	95
flv	915,335	133,286	45	18,909,861	2,061,735	76
Expected	917,538	131,068	30	18,874,410	2,097,148	38
	$d=16$			$d=20$

includes the comparisons of the observed and theoretical values on each analyzed dimension. The payload size, which is the total length of the concatenated NPF code-words, and the disambiguation information size, which is the total length of the prefix–free encoded code-word lengths, are both observed to be compatible with the theoretical claims. This is also reflected on the overhead bits as a consequence. Thus, in terms of space consumption, the experimental results on compressed data support the theoretical findings based on perfect uniformly i.i.d. input data assumption.

2.2. Hardness of Decoding Payload in Absence of Disambiguation Information

The non-UD coding process represents the input data with two elements as the payload and the disambiguation information. We have shown in Lemma 2 that the disambiguation information occupies $\approx \frac{2}{d}$ of the input size. Thus, if one encrypts the disambiguation information and leaves the payload plain, the retrieval of the original sequence will require decoding the payload without the disambiguation information. We provide a combinatorial analysis on the hardness of this decoding below by first proving that disambiguation information of a payload is specific per se, and then use this fact to count the number of possible distinct raw sequences that map to a given payload with the same code-word mapping of $\Sigma \to W$.

Lemma 3.

Each distinct disambiguation information on a given NPF stream decodes into distinct input sequence.

Proof. 

Let $S=s_1{s}_2\dots s_r$ and $S^{\prime }=s_1^{\prime }{s}_2^{\prime }\dots s_r^{\prime }$ denote two different disambiguation information, which are actually the code–word length sequences such that ${\sum }_{i=1}^r{s}_i={\sum }_{i=1}^r{s}_i^{\prime }=\left|NPF\left(\mathcal{A}\right)\right|$, where $s_i$ and $s_i^{\prime }$ are the bit lengths of the ith code–word in the corresponding decoding of the $NPF\left(\mathcal{A}\right)$. Since S and $S^{\prime }$ are distinct, for some $1\le j\le r$, $s_j$ and $s_j^{\prime }$ are not equal, which causes the corresponding code–words extracted from the NPF code–stream to be of different length. Although there is a chance that different code–words of length d may map onto the same symbol in W according to Definition 2, it is for sure that when the two code–word lengths are different they cannot map onto the same symbol. Thus, it is not possible to find two distinct S and $S^{\prime }$ that generate equal $\mathcal{A}$ sequences. □

Lemma 4.

A payload that is generated for an input n–bits long $\mathcal{A}$ with the proposed NPF scheme has more than $2^{\alpha ·(2^{d-1}-2)}$ distinct decodings for $\alpha =\lfloor \frac{n}{d·2^d}\rfloor$, where only one of them, which is specified with the disambiguation information, is the original input $\mathcal{A}$. When d is chosen to be $n=d·2^d$, $\mathsf{\Omega }(2^{·(2^{d-1}-2)})$ different payload generations are possible.

Proof. 

We will analyze the input $\mathcal{A}$ in blocks of $2^d$ d–bits long symbols. Each symbol in a block is mapped to a variable–length non–prefix–free code-word according to the $\Sigma \to W$, and when the code–word boundaries are unknown on that code–stream, then many different decoding possibilities appear. We aim to first count how many different decoding would be possible for a block, and then use this information to determine possibilities for the whole code–word stream.

In a block of $2^d$ symbols, the number of ℓ-bits long code–words is $2^{\ell }$ for $\ell \in \{1,2,\dots ,d-1\}$, and 2 for $\ell =d$ according to Proposition 1. Therefore, the number of possible permutations of those items is more than $2^{(2^{d-1}-2)}$ as shown below.

$$\begin{array}{cc}\hfill \frac{2^d!}{2!·2!·4!·\dots ·2^{d-1}!}& =\frac{1·2}{1·2}·\frac{3·4}{1·2}·\frac{5·6·7·8}{1·2·3·4}·\dots ·\frac{(2^{d-2}+2)·\dots 2^{d-1}+1}{1·\dots ·2^{d-2}}·\frac{2^{d-1}!}{2^{d-1}!}\hfill \end{array}$$

(14)

$$\begin{array}{c}>1·2^2·2^4·2^8·\dots ·2^{2^{d-2}}·1=2^{(2^{d-1}-2)}\hfill \end{array}$$

(15)

Let $\alpha =\lfloor \frac{n}{d·2^d}\rfloor$ be the number of blocks in an input n–bits long data stream. Since there are more than $2^{(2^{d-1}-2)}$ different decodings per each block, then $\alpha$ blocks in total will have more than $2^{\alpha ·(2^{d-1}-2)}$ distinct decoding possibilities. □

Given a payload and the used code–word mapping $\Sigma \to W$, the number of distinct original data decodings is shown in

Table 3. When $n=d·2^d$, the payload size, the disambiguation information size, and the corresponding number of possible decodings are shown. Last column depicts the percentage of the volume to be encrypted to provide privacy with the specified level of ambiguity, i.e., when $d=8$, encrypting only around 25% of the input volume (2048 bits) introduces an ambiguity of around $2^{126}$.

	$\mathit{n}=\mathit{d}·2^{\mathit{d}}$	Payload Size	Minimum Number of	Dis. Info. Size	Percentage of Dis.Info
d	in Bits	$\mathit{n}·(1-\frac{2}{\mathit{d}}+\frac{2(\mathit{d}+1)}{\mathit{d}·2^{\mathit{d}}})$	Distinct Parse $\mathsf{\Omega }(2^{·(2^{\mathit{d}-1}-2)})$	$\mathit{n}·(\frac{2}{\mathit{d}}-\frac{2(\mathit{d}+1)}{2^{\mathit{d}}})$	$100·\frac{\mathit{Dis}.\mathit{Info}.\mathit{Size}}{\mathit{n}}$
8	2048	1554	$2^{126}$	508	% 24.80
12	48 K	40,986	$2^{2046}$	8188	% 16.65
16	1 M	917,538	$2^{32,766}$	131,068	% 12.49
20	20 M	18,874,410	$2^{524,286}$	2,097,148	% 9.99

. Notice that only one of them is the correct $\mathcal{A}$, and actually generating these possibilities is computationally not feasible. Therefore, decoding the NPF stream without the code–word boundary information is computationally hard for sufficiently large d values, where as a minimum $d=8$ in practice brings a complexity of $2^{125})$ for possibilities. Thus, encrypting only the code–word boundary information, and transmitting the code–word stream in plain can provide privacy of the whole data in practice. The interesting point here is that the disambiguation information occupies much less space when compared to the total size of the originl data as previously analyzed in Lemma 2, which can provide a significant reduction in the encryption volume required for the data security.

2.3. Hardness of Decoding Disambiguation Information in Absence of Payload

For the users, who would like to keep their data top secret by the standard encryption algorithms, applying the NPF coding scheme can still provide an advantage. In case of such a necessity, the payload is encrypted, and the disambiguation information, which simply specifies the code–word boundaries in the variable–length non–prefix–free code–words stream payload, is kept plain. Now extracting the code-word bits from the payload can be achieved since disambiguation information is plain, however, since the payload bits are encrypted, decoding the original data is not possible.

Considering that larger d values create smaller disambiguation information and increase the payload size, in this case using small d will be preferred with the aim to achieve higher reduction in the to-be-encrypted data volume. On the other side, when d gets smaller, the overhead becomes more significant. For example, when $d=4$, there appears 10% inflation in the data volume, where both payload and disambiguation information occupy 50% of the inflated data. With that 10 percent inflation it becomes possible to attain 50% decrease in the encryption. Similarly, by choosing $d=6$, the overhead becomes more acceptable by being around 3 bits per 100 bits, and since the ratio of the payload becomes $2/3$ of the final data, around 33% decrease is achieved in the encryption amount.

We start analyzing how much information is leaked by making the disambiguation information public assuming that the code-word set is also public, and then investigate how much it would help to keep the code-word mapping ($\Sigma \to W$) secret.

Lemma 5.

The number of distinct payloads that can be generated from a given disambiguation information is $2^{n-\frac{2n}{d}+\frac{4n}{d{2}^d}}$ by assuming the code-word set W, parameter d, and message length n are known.

Proof. 

A code-word of length $\ell =d-i$, which is representing $2^{\ell }$ distinct symbols, appears $\frac{r}{2^i}$ times in the disambiguation information for $i=1$ to $d-1$ and $r=\frac{n}{d}$. The d bit long code-words appear $\frac{r}{2^{d-1}}$ times, and represent two distinct symbols. Thus, the total number of distinct sequences that can be generated from a known disambiguation information can be counted by

$$\begin{array}{cc}\hfill 2^{\frac{r(d-1)}{2}}·2^{\frac{r(d-2)}{4}}·\dots ·2^{\frac{r}{2^{d-1}}}·2^{\frac{r}{2^{d-1}}}& =2^{rd{\sum }_{i=1}^{d-1}{2}^{-i}}·2^{r{\sum }_{i=1}^{d-1}i{2}^{-i}}·2^{\frac{r}{2^{d-1}}}\hfill \end{array}$$

(16)

$$\begin{array}{c}=2^{\frac{rd(2^{d-1}-1)-r(2^d-d-1)+1}{2^{d-1}}}\hfill \end{array}$$

(17)

$$\begin{array}{c}=2^{r(d-2+\frac{4}{2^d})}\hfill \end{array}$$

(18)

$$\begin{array}{c}=2^{n-\frac{2n}{d}+\frac{4n}{d{2}^d}}\hfill \end{array}$$

(19)

 □

The result of Lemma 5 is consistent with previous Lemma 2 such that the disambiguation information is not squeezing the possible message space by more than its size. In other words, when the codeword set W is known, plain disambiguation information reduces the possible $2^n$ message space to $2^{n-ϵ}$, where $ϵ=n(\frac{2}{d}-\frac{4}{d·2^d})$.

However, when W is private, and we need to investigate whether that secrecy of W accommodates the leakage due to the plain disambiguation information. Lemma 6 shows that for an attacker using the knowledge revealed by the disambiguation information does not provide an advantage over breaking the encryption on the payload as long as the code-word set W is kept secret.

Lemma 6.

The shrinkage in the possible message space due to public disambiguation information can be accommodated by keeping the code-word set W secret in the non-UD coding of $n\le \tau ·d·2^d$ bit long data for $\tau =\frac{d-1.44}{2}$.

Proof. 

W is a secret permutation of the set $\{0,1,2,\dots ,2^{d-1}\}$ containing $2^d$ numbers. Thus, there are $2^d!$ distinct possibilities, which defines $log{2}^d!$ bits of information. On the other hand, the amount of revealed knowledge about the n bit long input by the disambiguation information is $n(\frac{2}{d}-\frac{4}{d·2^d})$ bits. The advantage gained by keeping W secret should accommodate the loss by making disambiguation information public. This simply yields the following equation.

$$\begin{array}{cc}\hfill log(2^d!)& \ge n·(\frac{2}{d}-\frac{4}{d·2^d})\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \frac{ln(2^d!)}{ln2}\approx \frac{2^d·ln{2}^d-2^d}{ln2}& \ge n·\frac{2}{d}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \frac{2^d·d·ln2-2^d}{ln2}& \ge n·\frac{2}{d}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill 2^d(d-1.44)& \ge n·\frac{2}{d}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill d·2^d·(\frac{d-1.44}{2})& \ge n\hfill \end{array}$$

(24)

 □

Due to Lemma 6, the choice of d creates an upper bound on the size of the input data that will be subject to the proposed non-UD coding scheme. On the other hand, it would be appropriate to select d such that the input size is at least $d·2^d$ bits to confirm with the computations in the size arguments of the payload and the disambiguation information, which assumed all possible $2^d$ symbols are uniformly i.i.d. on the input. The minimum and maximum block sizes defined by the d parameter are listed in

Table 4. The minimum ($d·2^d$) and maximum ($d·2^d·(\frac{d-1.44}{2})$) block sizes that are appropriate according to the proposed non-UD coding scheme for selected d values.

d	Block Size in Bits
	min	max
6	384	875
8	2 K	6.7 K
10	10 K	43 K
12	49 K	256 K
14	230 K	144 K
16	1 M	7 M
18	4.7 M	39 M
20	21 M	194 M

considering these facts.

Therefore, given an input bit string $\mathcal{A}$, if it is preferred to keep payload secret and disambiguation information plain, achieving the non-UD coding in blocks of the any preferred size in between these values is appropriate in practice. The value of d plays a crucial role both in the security and in the to-be-encrypted data size. It is good to choose large d for better security with less (even negligible when $d>8$) overhead. On the other hand, the payload size is inversely proportional with d, and thus, the reduction in the data volume to be encrypted decreases when d increases.

2.4. Implementation of the NPF Encoding

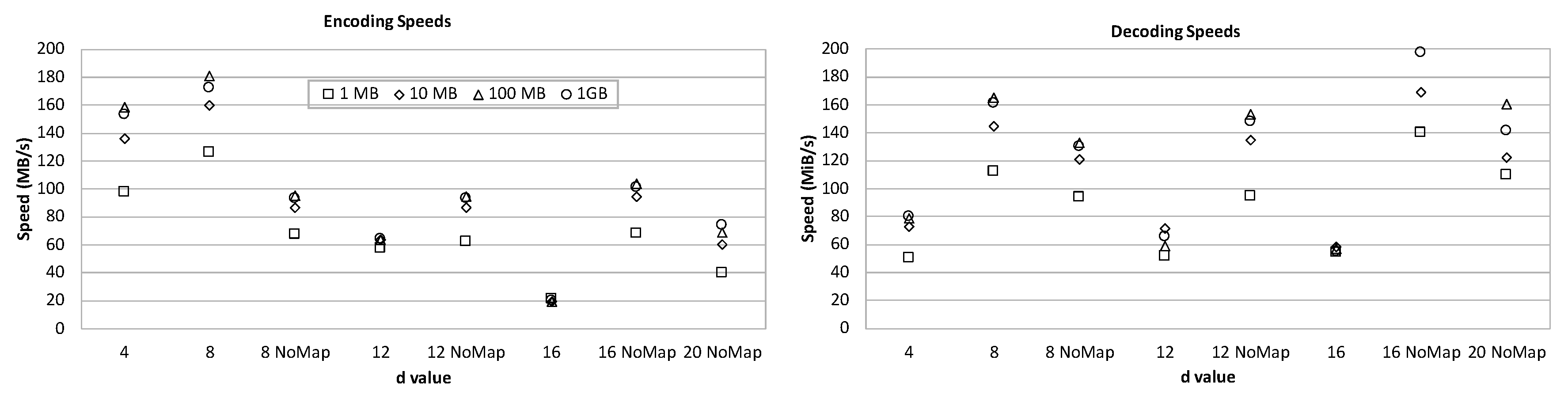
The implementation of the proposed scheme is available at https://github.com/qua11q7/NPFCoding. The Figure 3 presents the speed performance of the implementation on randomly generated files of size 1, 10, 100, and 1000 megabytes respectively. The machine used in the experiments had 16GB memory and Intel i5-6600 CPU with Ubuntu 18.04.2 operating system. For fast processing the implementation follows a similar scheme as in the case of Huffman decoding with lookup tables [19]. Empirical observations showed that this type of look up make sense on small d values, particularly on $d=4$ and $d=8$. However, on larger d values due to the expansion of the number of tables as well as their sizes the performance is not improved. In the regarding tables, the “NoMap” option means look up tables are not used. We observed that the NPF coding maximizes its speed both in coding and decoding process, when d is chosen to be 8, where around 170 megabyte per second is achieved. The performance does not change much with the file size, and seems totally dependent on the d parameter. The payload and disambiguation sizes and overall percentages are also given and observed to be consistent with the theoretical calculations. The decoding speed is about two times of the encoding speed when d is chosen to be 16 or 20, where it reaches 200 MB per second for $d=16$ on 1GB files. More details about the implementation is available on the mentioned code distribution web site.

3. Results

We have shown that the NPF encoding of an input n–bits long high-entropy data creates a payload of size $\approx n·(1-\frac{2}{d})$ which requires $n.\frac{2}{d}$ bits disambiguation information for a chosen d parameter. Larger d, e.g., $d\ge 8$, values decrease the overhead and total space consumption becomes almost equal with the input.

The hardness of decoding an encoded data without the knowledge of the used code-word set had been addressed as early as in 1979 by Rubin [20], and later by others [21,22]. More recently, non-prefix-free codes have also been mentioned [23] in that sense. We observe that in absence of any of the two partitions in the proposed scheme, decoding the original data is hard, which can help to keep data privacy. We proved that a given payload, which has been generated from an input via a known code-word mapping $\Sigma \to W$, has more than $2^{2^{d-1}-2}$ possible decodings in absence of the correct disambiguation information, when d is chosen such that $n=d·2^d$. Since a given payload cannot be decoded properly back into the original input without the correct disambiguation information due to this exponential ambiguity, it can be preferred to encrypt only the disambiguation information, and leave the payload plain. In such a case, the amount of to-be-encrypted volume would be $\frac{2}{d}$ of the original data. For instance, this brings a reduction of around $75\%$ when $d=8$ and $90\%$ when $d=20$. Notice that the ambiguity is computed assuming the $\Sigma \to W$ mapping is public, where keeping the code–word set secret will introduce additional strength in privacy.

We also analyzed the how much information is released by the disambiguation information regarding the payload. It is proved that when $2·2^d\le n\le \tau ·d·2^d$, for $\tau =\frac{d-1.44}{2}$, the contraction of the possible message space $2^n$ due to the public disambiguation information can be accommodated by keeping the code-word set secret. Thus, if one encrypts the payload and keeps the code–word mapping secret, an attacker can not gain an advantage by knowing the disambiguation information. Such a scheme can still provide a reduction in encryption cost, which is expected to be much less when compared with the first scenario above. In this case, the d value needs to be small since the ratio of the payload increases with the larger d values. However, since smaller d values generate an overhead, it seems appropriate to use $d=6$ in practice.

4. Discussions

Applying entropy compression before the transmission is a common daily practice. For instance, the mpeg4 encoded video streams, jpg images, or text resources encoded with arithmetic or Huffman schemes are possible data sources fit well to the proposed architecture with their high entropy. It is noteworthy that the security of the high-entropy data has been previously addressed in [24,25,26]. These studies mainly state that although the perfect security of an input data requires a key length equal to its size (one-time pad), the security of high-entropy data can be provided with much shorter key sequences. However, again the data as a whole should be fed into encryption. On the other hand, high entropy data representation with our proposal creates two elements, where encrypting one of them is adequate since decoding the original data from the plain element is hard in absence of the other encrypted element.

A recursive application of the proposed coding can even reduce the to-be-encrypted volume more. For example, after creating the two elements of the non-UD representation, the disambiguation information or the payload can itself be subject to a one more round of NPF coding. We have shown that when $d=8$, $\approx 25$ percent is the disambiguation information, and with one more round, the disambiguation information will become less then 7 percent of the final volume, where encrypting only that 7% can be considered for privacy. A similar scenario on the payload can be considered as well.

We assumed that the input to the non-UD encoder is uniformly i.i.d. in ideal case, and empirically verified that the compressed volumes ensures the mentioned results. Actually, applying entropy coding before the encryption is a common daily practice, which makes the proposed method to be directly applicable in such a scenario. The mpeg4 video streams, jpg images, compressed text sequences, or mp3 songs are all typical data sources of high-entropy. Digital delivery of such multi-media content has a significant market share in daily practice [27]. Related previous work [24,25] had stated that although the perfect security of an input data requires a key length equal to its size (one-time pad), high-entropy data can be perfectly secured with much shorter keys. This study addressed another dimension and investigated achieving security of such volumes by encrypting less than their original sizes by using the introduced non-UD coding scheme.

Although we target high-entropy data and analyze space consumption and security features based on the assumption of i.i.d input, it might be also interesting to have a look what would happen if we apply the non-UD coding to normal files with biased distributions. On the corpus we studied, we omitted the compression step on the files that have non-uniform symbol distributions, and applied our proposed coding directly with a randomly selected $\Sigma \to W$ mapping. The results are given on

Table 5. The sizes of the payload and disambiguation information when non-UD coding is applied on the files that have non-uniform symbol distribution.

File Name	File Size	Payload Size	Disinfo. Size
etext	100.4	76.4	28.8
howto	37.6	30.1	9.3
rctail96	109.4	84.7	29.9
rfc	111.1	87.4	29.1
w3c2	99.3	77.1	27.2

, where repeating the same experiment with different $\Sigma \to W$ assignments reported similar values. The empirical observation on these results show that the disambiguation information is roughly less than one third of the input volume, when the input sequence is not uniformly distributed. Thus, encrypting only the disambiguation information may make sense still on non i.i.d files as well.

Reducing the amount of data to-be-encrypted can make sense in scenarios where the encryption process defines a bottleneck in terms of some metrics. Non-UD coding becomes particularly efficient on securing large collections over power-limited devices, where the cost of encryption becomes heavy in terms of energy. This reduction also helps to increase the throughput of a security pipeline without a need to expand the relatively expensive security hardware. For instance, let’s assume a case where the data is waiting to be processed by a hardware security unit. When the amount of data exceeds the capacity of this unit, a bottleneck appears, which can be resolved by increasing the number of such security units. However, adding and managing more security units is costly, particularly when the bottleneck is not so frequent, but only appearing at some time. An alternative solution is to use the proposed non-UD coding, where instead of expanding the security units, data can be processed appropriately while waiting in the queue, and the amount to be encrypted can be reduced up to desired level by applying the scheme recursively if needed. Notice that as opposed to previous selective encryption schemes, non-UD coding supports the security of the whole file instead of securing only the selected partitions. Besides massive multimedia files, small public key files around a few kilobytes that are used in asymmetric encryption schemes are also very suitable inputs for the non-UD coding. The exchange of public keys via symmetric ciphers can also benefit from the reduction introduced.

5. Conclusions

We have investigated the non-UD data coding with non-prefix-free codes on high-entropy sources. The proposed scheme represents the input data with two elements as the payload and the disambiguation information, where the later has a smaller footprint depending on the choice of the bit-block length parameter d. Such an encoding can help in privacy protection of the massive volumes with less encryption overhead by keeping one of the partitions secret via encryption, while the other one is kept plain. This encoding model can also help for privacy preserving pattern matching applications without making use of any encryption as well, where an immediate usage can be distributed file storage in cloud environments such that the payload and disambiguation information are stored and maintained by independent vendors, and thus, none can see the data content but still the owner can run efficient search queries. Studying such a scenario for privacy preserving distributed data storage on the cloud can be the next research avenue for non-UD.

6. Patents

Külekci, M.O., Istanbul Teknik Universitesi, 2018. An efficient encryption method to secure data with reduced number of encryption operations. U.S. Patent Application 15/779,853 [28].