Evolutionary Machine Learning for Multi-Objective Class Solutions in Medical Deformable Image Registration
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
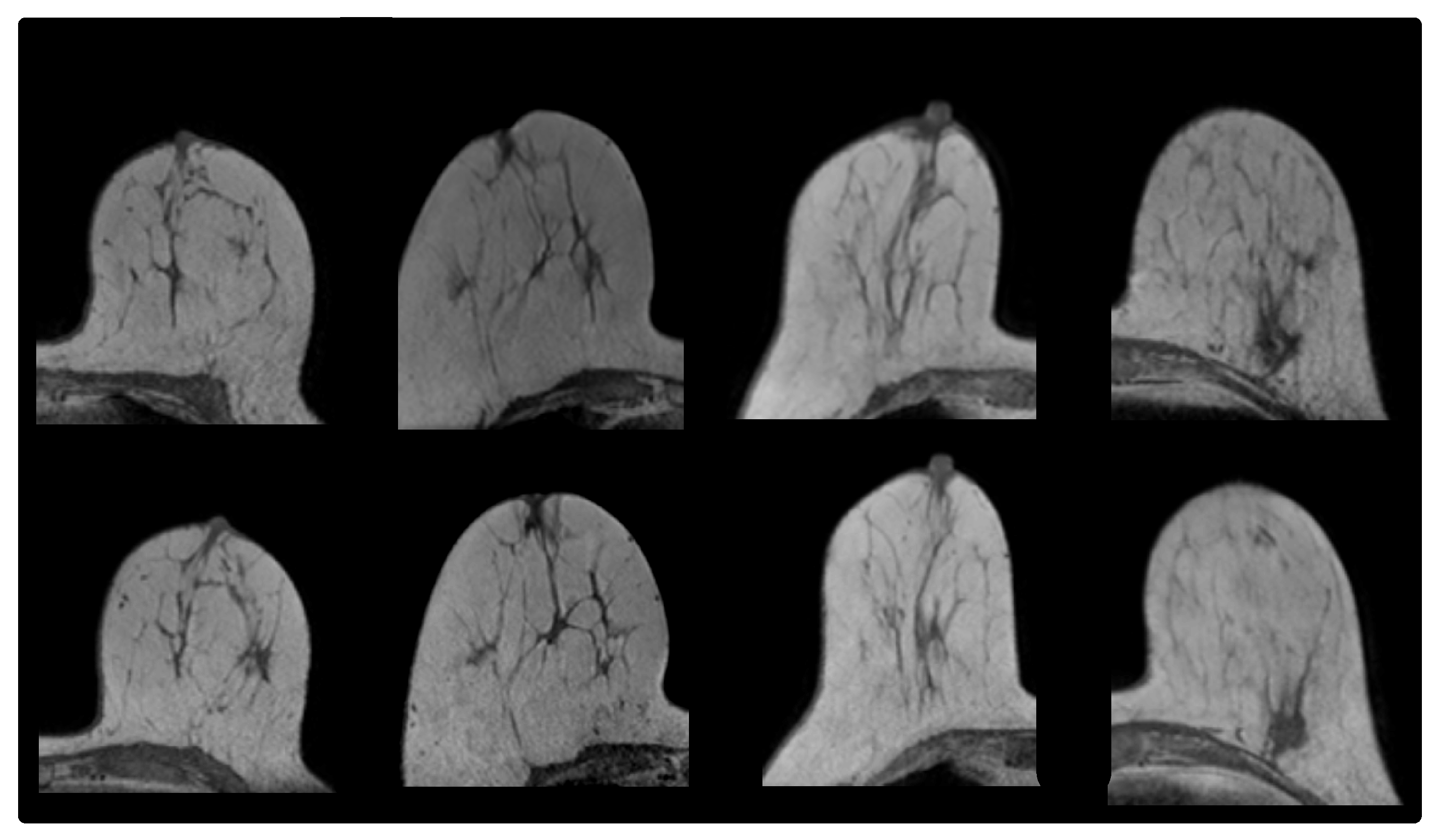
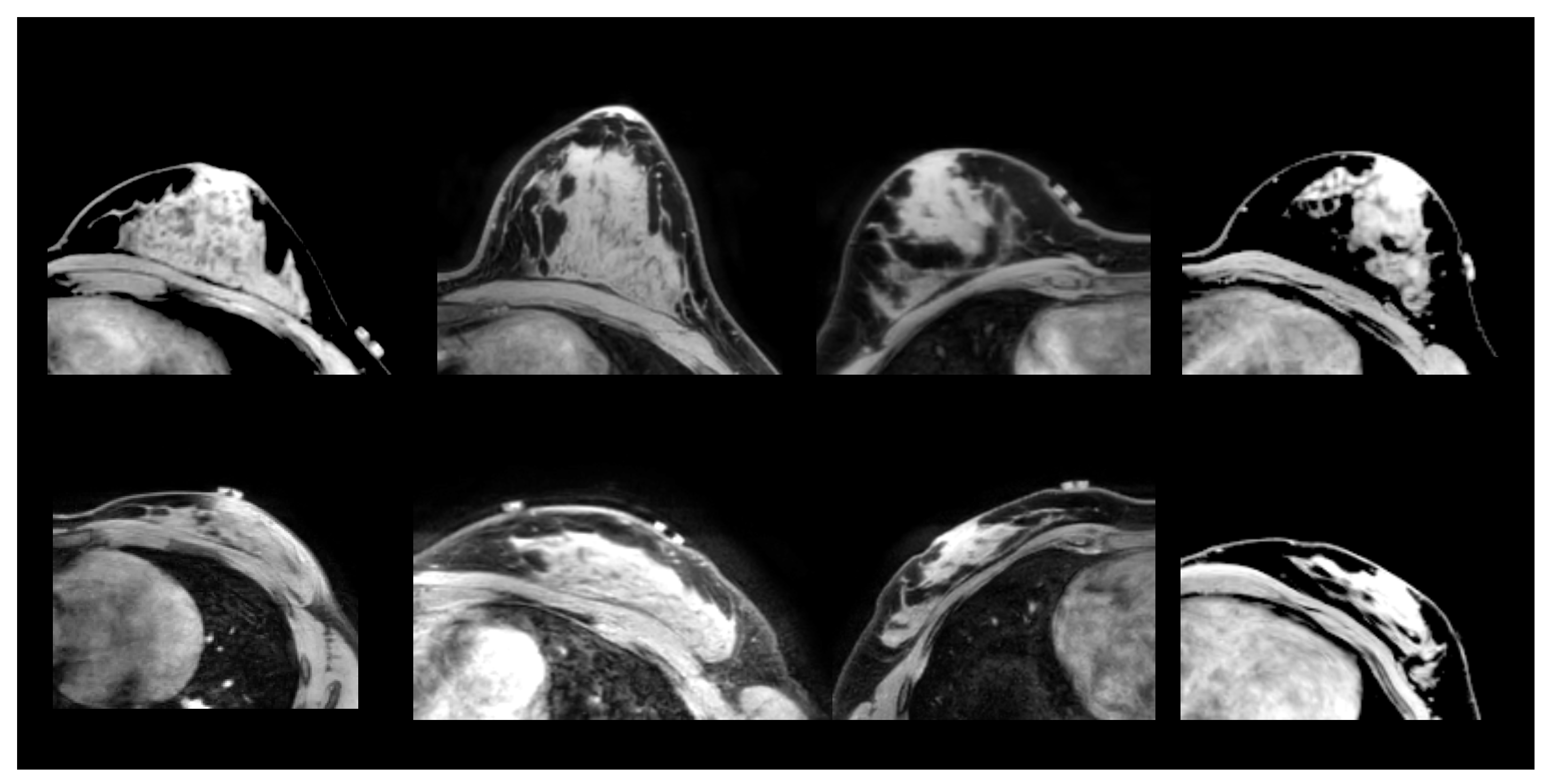
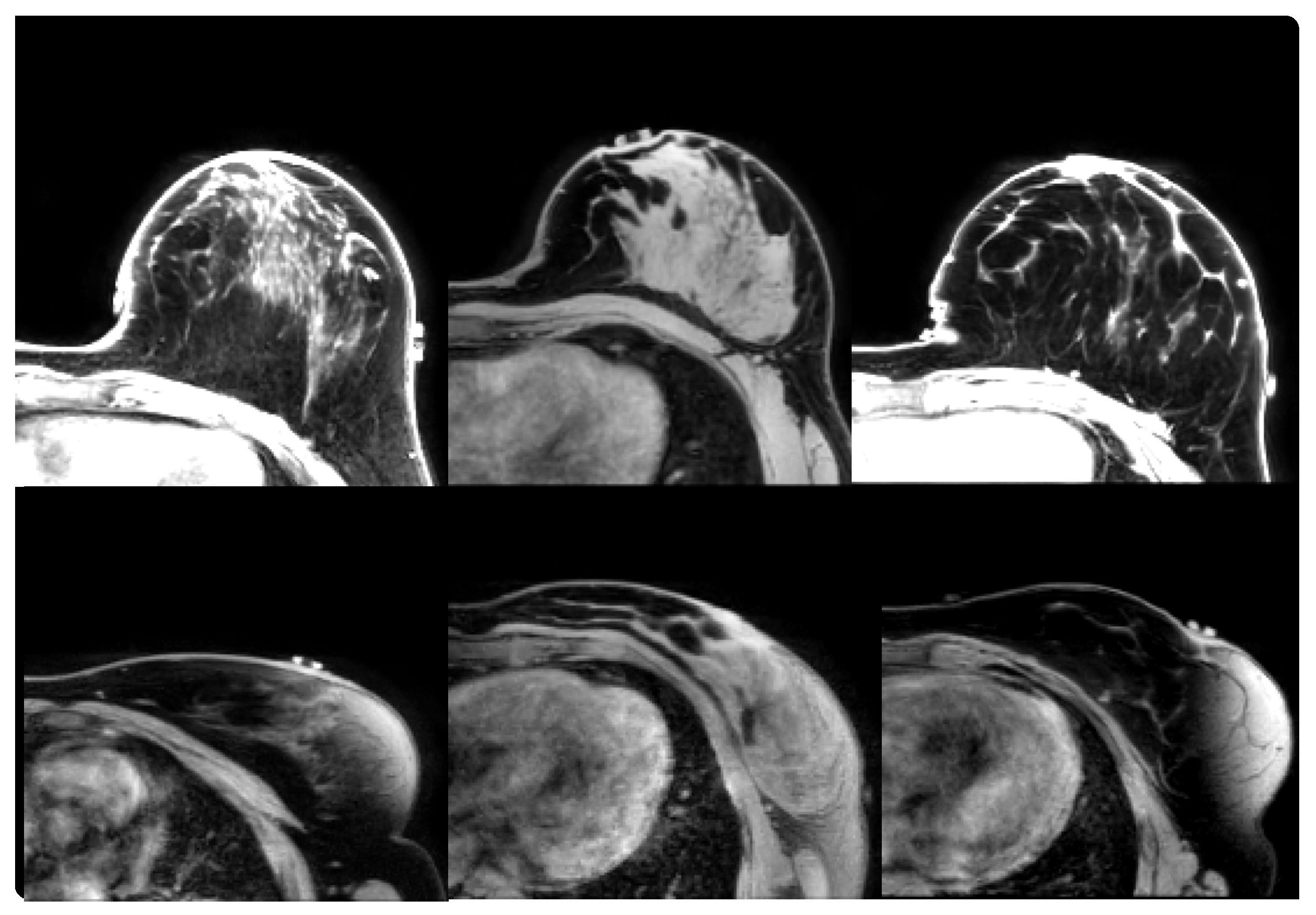
2.1.1. Prone-Prone
2.1.2. Prone-Supine
2.2. Patient-Specific Multi-Objective DIR
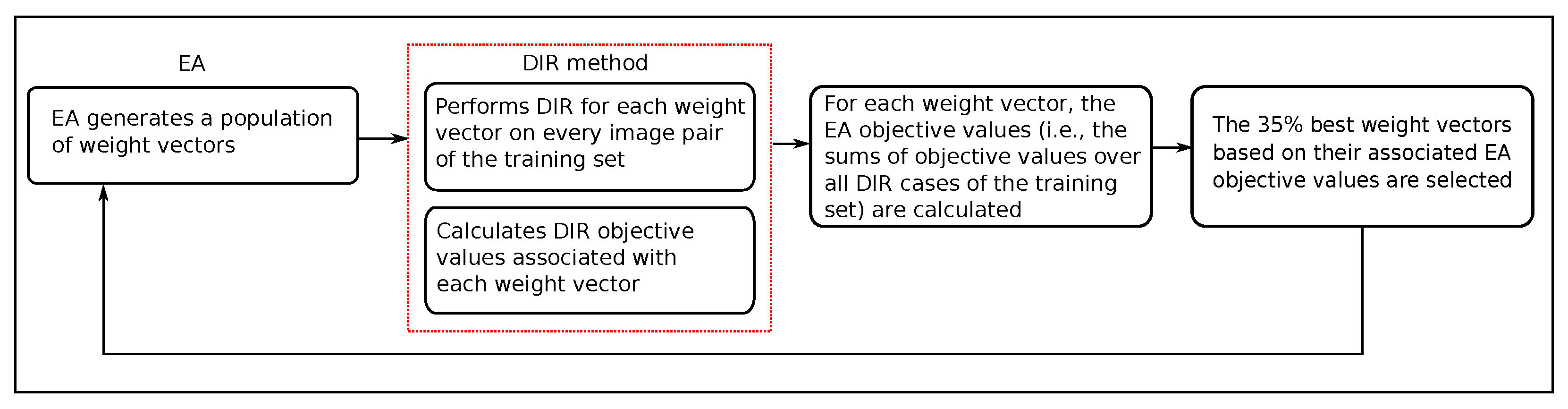
2.3. Evolutionary Multi-Objective Class Solution Learning for DIR
2.3.1. DIR Method
2.3.2. Evolutionary Algorithm
2.4. Evaluation
2.5. Experimental Setup
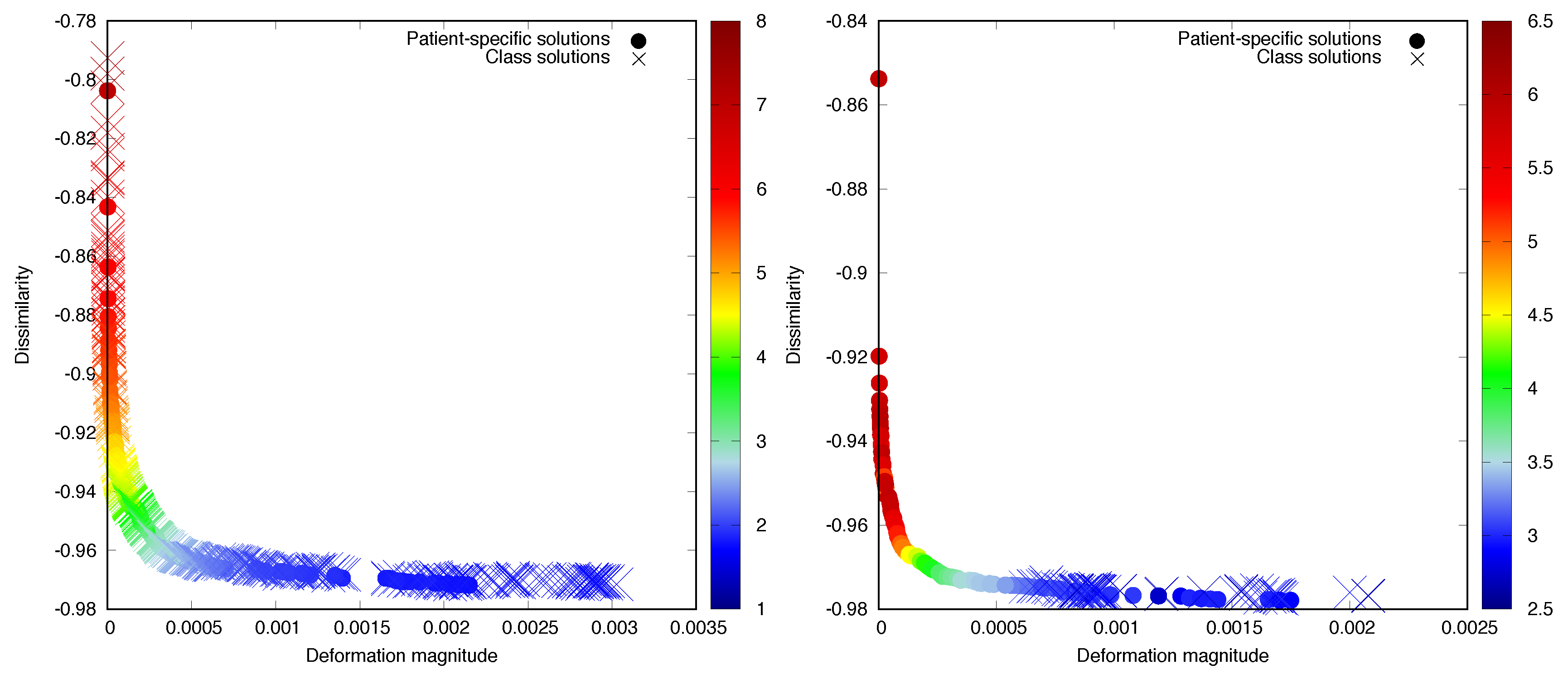
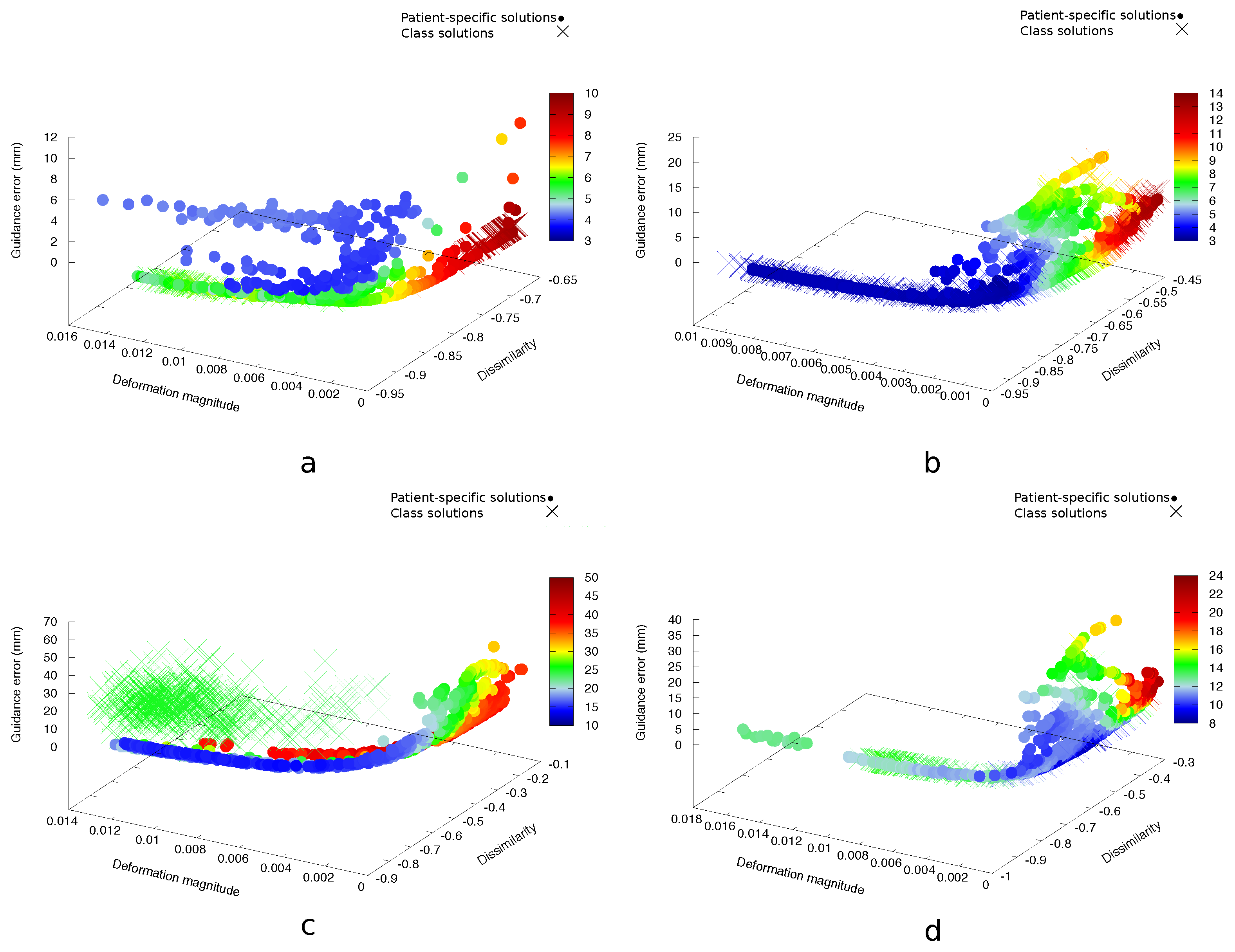
3. Results
3.1. Prone-Prone
3.2. Prone-Supine
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable medical image registration: A survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef]
- Brock, K.K.; Mutic, S.; McNutt, T.R.; Li, H.; Kessler, M.L. Use of image registration and fusion algorithms and techniques in radiotherapy: Report of the AAPM Radiation Therapy Committee Task Group No. 132. Med. Phys. 2017, 44, e43–e76. [Google Scholar] [CrossRef] [PubMed]
- Andersen, E.S.; Muren, L.P.; Sørensen, T.S.; Noe, K.Ø.; Thor, M.; Petersen, J.B.; Høyer, M.; Bentzen, L.; Tanderup, K. Bladder dose accumulation based on a biomechanical deformable image registration algorithm in volumetric modulated arc therapy for prostate cancer. Phys. Med. Biol. 2012, 57, 7089. [Google Scholar] [CrossRef] [PubMed]
- Kraus, K.M.; Jäkel, O.; Niebuhr, N.I.; Pfaffenberger, A. Generation of synthetic CT data using patient specific daily MR image data and image registration. Phys. Med. Biol. 2017, 62, 1358. [Google Scholar] [CrossRef] [PubMed]
- Thor, M.; Petersen, J.B.; Bentzen, L.; Høyer, M.; Muren, L.P. Deformable image registration for contour propagation from CT to cone-beam CT scans in radiotherapy of prostate cancer. Acta Oncol. 2011, 50, 918–925. [Google Scholar] [CrossRef] [PubMed]
- Brock, K.K.; Dawson, L.A.; Sharpe, M.B.; Moseley, D.J.; Jaffray, D.A. Feasibility of a novel deformable image registration technique to facilitate classification, targeting, and monitoring of tumor and normal tissue. Int. J. Radiat. Oncol. Biol. Phys. 2006, 64, 1245–1254. [Google Scholar] [CrossRef] [PubMed]
- Fischer, B.; Modersitzki, J. Ill-posed medicine—An introduction to image registration. Inverse Probl. 2008, 24, 034008. [Google Scholar] [CrossRef]
- Yeo, B.T.T.; Sabuncu, M.R.; Vercauteren, T.; Holt, D.J.; Amunts, K.; Zilles, K.; Golland, P.; Fischl, B. Learning task-optimal registration cost functions for localizing cytoarchitecture and function in the cerebral cortex. IEEE Trans. Med. Imaging 2010, 29, 1424–1441. [Google Scholar] [CrossRef] [PubMed]
- De Groot, M.; Vernooij, M.W.; Klein, S.; Ikram, M.A.; Vos, F.M.; Smith, S.M.; Niessen, W.J.; Andersson, J.L. Improving alignment in Tract-based spatial statistics: Evaluation and optimization of image registration. NeuroImage 2013, 76, 400–411. [Google Scholar] [CrossRef] [PubMed]
- Pirpinia, K.; Bosman, P.A.N.; Loo, C.E.; Winter-Warnars, G.; Janssen, N.N.Y.; Scholten, A.N.; Sonke, J.J.; van Herk, M.; Alderliesten, T. The feasibility of manual parameter tuning for deformable breast MR image registration from a multi-objective optimization perspective. Phys. Med. Biol. 2017, 62, 5723. [Google Scholar] [CrossRef] [PubMed]
- Dou, T.H.; Min, Y.; Neylon, J.; Thomas, D.; Kupelian, P.; Santhanam, A.P. Fast simulated annealing and adaptive Monte Carlo sampling based parameter optimization for dense optical-flow deformable image registration of 4DCT lung anatomy. In Proceedings of SPIE Medical Imaging; Webster, R.J., Yaniv, Z.R., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; p. 97860N. [Google Scholar] [CrossRef]
- Francesca, G.; Pellegrini, P.; Stützle, T.; Birattari, M. Off-line and on-line tuning: a study on operator selection for a memetic algorithm applied to the QAP. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization, Torino, Italy, 27–29 April 2011; Springer: Berlin, Germany, 2011; pp. 203–214. [Google Scholar]
- Pellegrini, P.; Stützle, T.; Birattari, M. Off-line vs. On-line Tuning: A Study on MAX–MIN Ant System for the TSP. In Proceedings of the International Conference on Swarm Intelligence, Beijing, China, 12–15 June 2010; Springer: Berlin, Germany, 2010; pp. 239–250. [Google Scholar]
- Van der Leij, F.; Bosma, S.C.J.; van de Vijver, M.J.; Wesseling, J.; Vreeswijk, S.; Rivera, S.; Bourgier, C.; Garbay, J.R.; Foukakis, T.; Lekberg, T.; et al. First results of the preoperative accelerated partial breast irradiation (PAPBI) trial. Radiother. Oncol. 2015, 114, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Pluim, J. Mutual Information Based Registration of Medical Images. Ph.D. Thesis, Utrecht University of Applied Sciences, Utrecht, The Netherlands, 2001. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Chichester, UK, 2001; p. 497. [Google Scholar]
- Klein, S.; Staring, M.; Murphy, K.; Viergever, M.A.; Pluim, J.P.W. elastix: A toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 2010, 29, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Rueckert, D.; Sonoda, L.I.; Hayes, C.; Hill, D.L.; Leach, M.O.; Hawkes, D.J. Nonrigid registration using free-form deformations: Application to breast MR images. IEEE Trans. Med. Imaging 1999, 18, 712–721. [Google Scholar] [CrossRef] [PubMed]
- Roche, A.; Malandain, G.; Pennec, X.; Ayache, N. The correlation ratio as a new similarity measure for multimodal image registration. In Proceedings of the First International Conference on Medical Image Computing and Computer-Assisted Intervention—MICCAI’98, Cambridge, MA, USA, 11–13 October 1998; Wells, W.M., Colchester, A., Delp, S., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1115–1124. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1990; Volume 59. [Google Scholar]
- Baiker, M.; Staring, M.; Löwik, C.W.; Reiber, J.H.; Lelieveldt, B.P. Automated registration of whole-body follow-up MicroCT data of mice. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Toronto, ON, Canada, 18–22 September 2011; Springer: Berlin, Germany, 2011; pp. 516–523. [Google Scholar]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evolut. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Rodrigues, S.; Bauer, P.; Bosman, P.A.N. A novel population-based multi-objective CMA-ES and the impact of different constraint handling techniques. In Proceedings of the 2014 Conference on Genetic and Evolutionary Computation—GECCO’14, Granada, Spain, 9–11 December 2014; ACM Press: New York, NY, USA, 2014; pp. 991–998. [Google Scholar] [CrossRef]
- Bosman, P.A.N.; Alderliesten, T. Incremental Gaussian model-building in multi-objective EDAs with an application to deformable image registration. In Proceedings of the 2012 International Conference on Genetic and Evolutionary Computation—GECCO 2012, Sydney, Australia, 4–7 December 2012; ACM Press: New York, NY, USA, 2012; pp. 241–248. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Masuda, H.; Tanigaki, Y.; Nojima, Y. Modified distance calculation in generational distance and inverted generational distance. In Evolutionary Multi-Criterion Optimization; Gaspar-Cunha, A., Henggeler Antunes, C., Coello, C.C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 110–125. [Google Scholar]
- Bosman, P.A.N.; Thierens, D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans. Evolut. Comput. 2003, 7, 174–188. [Google Scholar] [CrossRef]
- Pirpinia, K.; Bosman, P.A.N.; Sonke, J.J.; van Herk, M.; Alderliesten, T. Simplex-based navigation tool for a posteriori selection of the preferred deformable image registration outcome from a set of trade-off solutions obtained with multiobjective optimization for the case of breast MRI. J. Med. Imaging 2018, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Shamonin, D.; Bron, E.; Lelieveldt, B.; Smits, M.; Klein, S.; Staring, M. Fast parallel image registration on CPU and GPU for diagnostic classification of alzheimer’s disease. Front. Neuroinform. 2014, 7, 50. [Google Scholar] [CrossRef] [PubMed]
- Allen, D.M. The relationship between variable selection and data augmentation and a method for prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Jin, Y. Multi-Objective Machine Learning; Springer Science & Business Media: Berlin, Germany, 2006; Volume 16. [Google Scholar]
- Alderliesten, T.; Bosman, P.A.N.; Bel, A. Getting the most out of additional guidance information in deformable image registration by leveraging multi-objective optimization. In Proceedings of SPIE Medical Imaging; SPIE: Bellingham, WA, USA, 2015; Volume 9413, pp. 9413–9417. [Google Scholar] [CrossRef]
| Patient | (mm) | (mm) | |
|---|---|---|---|
| 1 | 0.1194 | 0.1018 | 0.1865 |
| 2 | 0.0219 | 0.0077 | 0.0298 |
| 3 | 0.0309 | 0.0058 | 0.0658 |
| 4 | 0.0154 | 0.0053 | 0.0611 |
| 5 | 0.0104 | 0.0075 | 0.0283 |
| 6 | 0.0152 | 0.0069 | 0.0575 |
| 7 | 0.0400 | 0.0021 | 0.2068 |
| 8 | 0.2476 | 1.3751 | 0.0801 |
| 9 | 0.0123 | 0.0077 | 0.0120 |
| 10 | 0.0225 | 0.0348 | 0.0831 |
| Group A | (mm) | (mm) | |
|---|---|---|---|
| A1 | 0.1878 | 0.3072 | 1.2083 |
| A2 | 0.0284 | 0.0076 | 0.0104 |
| A3 | 0.0123 | 0.0180 | 0.0053 |
| A4 | 0.0816 | 0.0280 | 0.0427 |
| Group B | |||
|---|---|---|---|
| B5 | 0.1279 | 0.0215 | 0.0615 |
| B6 | 0.1442 | 8.0500 | 8.7400 |
| B7 | 0.1061 | 1.4100 | 1.5611 |
| B8 | 0.0616 | 0.0872 | 2.4605 |
| B9 | 0.0427 | 0.0774 | 0.2865 |
| B10 | 0.0606 | 0.0629 | 0.0410 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirpinia, K.; Bosman, P.A.N.; Sonke, J.-J.; van Herk, M.; Alderliesten, T. Evolutionary Machine Learning for Multi-Objective Class Solutions in Medical Deformable Image Registration. Algorithms 2019, 12, 99. https://doi.org/10.3390/a12050099
Pirpinia K, Bosman PAN, Sonke J-J, van Herk M, Alderliesten T. Evolutionary Machine Learning for Multi-Objective Class Solutions in Medical Deformable Image Registration. Algorithms. 2019; 12(5):99. https://doi.org/10.3390/a12050099
Chicago/Turabian StylePirpinia, Kleopatra, Peter A. N. Bosman, Jan-Jakob Sonke, Marcel van Herk, and Tanja Alderliesten. 2019. "Evolutionary Machine Learning for Multi-Objective Class Solutions in Medical Deformable Image Registration" Algorithms 12, no. 5: 99. https://doi.org/10.3390/a12050099
APA StylePirpinia, K., Bosman, P. A. N., Sonke, J.-J., van Herk, M., & Alderliesten, T. (2019). Evolutionary Machine Learning for Multi-Objective Class Solutions in Medical Deformable Image Registration. Algorithms, 12(5), 99. https://doi.org/10.3390/a12050099




