Abstract
We describe a simple data structure for storing subsets of , with N a given integer, which has optimal time performance for all the main set operations, whereas previous data structures are non-optimal for at least one such operation. We report on the comparison of a Java implementation of our structure with other structures of the standard Java Collections.
1. Introduction
We describe a data structure for storing and updating a set S of integers whose elements are values taken in the range with N a given integer. Typically, the “superset”, or “universe”, E corresponds to the indices of the N elements of a problem instance, and we are interested in storing, using and updating subsets of the universe.
A set of integers is a very basic mathematical object and it finds use in uncountably many applications of computer programs. Performing the basic set operations (i.e., insertion, deletion, membership test and elements enumeration) in the most effective possible way would benefit all algorithms in which sets of integers play a relevant role (just to mention one example, consider the algorithms operating on graphs, for which the universe is the set of nodes/edges of a graph and the procedure needs to store and update a subset of nodes/edges). The goal of the paper is to provide optimal set primitives such as those mentioned above.
The literature on algorithms and data structures is very rich, and various possible representations and implementations of such sets are discussed in many textbooks, among which there are some classics, such as [1,2,3]. The implementations of the sets fall mainly in two categories: (i) those for which operations such as insertion, deletion and membership test are fast but other operations, such as listing all the elements of the set, performing union and intersection are slow; (ii) those for which operations such as insertion, deletion and membership test are slow but other operations, such as listing all the elements of the set, performing union and intersection are fast. In the first category, we recall the bitmap representation of the set (which uses an array v of N booleans, where iff ) and some forms of hash tables using either optimal hashing or buckets [4]. In the second category, we can represent a set by an array of size N in which only the first entries are filled and contain the elements of the set, a structure called a partially filled array (PFA). Usually the PFA is unsorted (maintaining the elements sorted can speed-up operations such as the membership test, but it slows down insertion and deletion) Another option is to store the elements in a linked list, again unsorted. Finally, one can resort to some tree-like structures, such as the AVL trees, a self-balancing type of binary search trees [5]. For these structures, insertion, deletion and membership tests are reasonably fast (but not optimal), but the trade-off is that some other operations are slowed down by the overhead paid in order to maintain the structure sorted.
Main Results and Paper Organization
In this paper, we propose a new data structure, called FASTSET, that has optimal time performance for all the main set operations. In particular, operations such as insertion and deletion of an element, membership test, and access to an element via an index in are all . From these primitive operations, we derive more complex operations, such as listing all elements at cost , computing the intersection of two sets (i.e., ) at cost and the union of two sets (i.e., ) at cost .
In Table 1 we report a list of operations and their cost both for the various aforementioned types of data structures for set representation and for FASTSET. As far as the memory requirement is concerned, for some of them it is (namely Bitmap, PFAs, and FASTSET), for some it is (namely Linked List and AVL Tree), while it is for the Bucket Hashtable with b buckets.

Table 1.
Comparison of asymptotic worst-case time performance for the main set operations of the most used data structures. We let , and . In the Bucket Hashtable row, b is the number of buckets.
The remainder of the paper is organized as follows. In Section 2 we describe the implementation of the various set operations for a FASTSET. In Section 3 we give two simple examples of algorithms using set data structures. In particular, we describe two popular greedy algorithms, one for Vertex Cover and the other for Max-Cut. Section 4 is devoted to computational experiments, in which FASTSETs are compared to various set implementations from the standard library of the Java distribution [6]. We have chosen Java since it is one of the popular languages and offers state-of-the-art implementations of class data structures for all the structures we want to compare to. Anyway, we remark that the main contribution of this paper is of theoretical nature and thus the results are valid for all implementations (i.e., in whichever language) of the data structures discussed. Some conclusions are drawn in Section 6.
2. Implementation
A FASTSET is implemented by two integer arrays, of size and N, which we call elem[ ] and pos[ ], respectively. The array elem[ ] contains the elements of S, in no particular order, consecutively between the positions 1 and , while elem[0] stores the value of . The array pos[ ] has the function of specifying, for each , if or , and, in the latter case, it tells the position occupied by i within elem[ ]. More specifically,
The main idea in order to achieve optimal time performance is remarkably simple. Our goal is to achieve both the benefits of a PFA, in which listing all elements is optimal (i.e., it is ) but accessing the individual elements, for removal and membership tests is slow (i.e., it is , and of a bitmap implementation where accessing the individual elements is optimal (i.e., it has cost ) but listing all elements is slow (i.e., it is ). To this end, in our implementation we use the array elem[ ] as a PFA, and the array pos[ ] as a bitmap. Moreover, not only pos[ ] is a bitmap, but it provides a way to update the partially filled array elem[ ] after each deletion in time rather than .
We will now describe how the set operations can be implemented with the complexity stated in Table 1. The implementation is quite straightforward. We will use a pseudocode, similar to C. In particular, our functions will have as parameters pointers to FASTSETs, in order to avoid passing the entire data structures.
2.1. Membership
To check for membership of an element v, we just need to look at and see if it is non-zero, at cost .
Boolean Belongs( FASTSET* s, int v ) {
return ( s->pos[v] > 0 )
}
2.2. Cardinality
The cardinality is readily available in at cost .
int Cardinality( FASTSET* s ) {
return s->elem[0]
}
2.3. Insertion
Each insertion happens at the end of the region of consecutive elements stored in elem[ ]. Since we have direct access to the last element through , the cost is .
void Insert( FASTSET* s, int newel ) {
if ( Belongs ( s, newel ) ) return // newel is already present in s
s->elem[0] := s->elem[0] + 1
s->elem[s->elem[0]] := newel
s->pos[newel] := s->elem[0]
}
Please note that there is no need for a test of full-set condition, since there is enough space for the largest subset possible (namely the whole E), and no element can be repeated in this data structure. See Figure 1a–e for examples of insertions in a FASTSET and corresponding updates of the data structure.
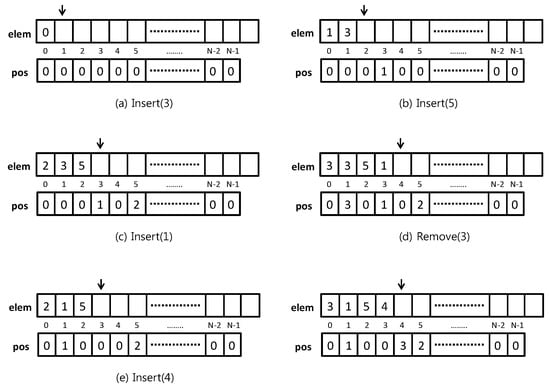
Figure 1.
A sequence of operations on a FASTSET: (a) Insert(3), (b) Insert(5), (c) Insert(1), (d) Remove(3), (e) Insert(4).
2.4. Deletion
Assume we want to delete an element v (which may or may not be in S), so that . When , this is obtained by copying the last element of elem, let it be w, onto v (by using pos, we know where v is) and decreasing (i.e., elem[0]). In doing so, we update pos[w], assigning pos[v] to it, then let pos[v] := 0. The final cost is . See Figure 1d for an example of deletion in a FASTSET and the corresponding update of the data structure.
void Delete( FASTSET* s, int v ) {
if ( NOT Belongs ( s, v ) ) return // v was not in S
int w := s->elem[s->elem[0]]
s->elem[s->pos[v]] := w
s->pos[w] := s->pos[v]
s->pos[v] := 0
s->elem[0] := s->elem[0] - 1
}
2.5. Access to an Element and List All Elements
We can have direct access to each element of S, via an index in , at cost . From this it follows that we can list all elements of S at cost . The corresponding procedures are the following:
int GetElement( FASTSET* s, int k ) {
return s->elem[k]
}
int* GetAll( FASTSET* s ) {
int* list = malloc( s->elem[0] * sizeof(int) )
for ( int k := 1; k <= s->elem[0]; k++ )
list[k-1] = s->elem[k]
return list
}
2.6. Intersection
Assume A and B are sets. We want to compute their intersection and store it in C, initially empty. We go through all the elements of the smaller set, and, if they are also in the other set, we put them in C. The final cost is .
void Intersection( FASTSET* A, FASTSET* B, FASTSET* C ) {
if ( Cardinality(A) < Cardinality(B) )
FASTSET* smaller := A
FASTSET* other := B
else
FASTSET* smaller := B
FASTSET* other := A
for ( int k := 1; k <= Cardinality(smaller); k++ )
if ( Belongs( other, GetElement( smaller, k ) ) )
Insert( C, GetElement( smaller, k ) )
}
2.7. Union
Assume A and B are sets. We want to compute their union and store it in C, initially empty. We go through all the elements of each of the two sets and put them in C. The final cost is .
void Union( FASTSET* A, FASTSET* B, FASTSET* C ) {
for ( int k := 1; k <= Cardinality(A); k++ )
Insert( C, GetElement( A, k ))
for ( int k := 1; k <= Cardinality(B); k++ )
Insert( C, GetElement( B, k ))
}
2.8. Initialization
A FASTSET is initialized by specifying the range for the elements value, and then simply allocating memory for two arrays:
FASTSET* Create( int N ) {
FASTSET* p := calloc( FASTSET, 1 )
p->pos := calloc( int, N )
p->elem := malloc( (N+1) * sizeof(int) )
p->elem[0] := 0 // empty set
return p
}
We assume that calloc allocates a block of memory initialized to 0s, in which case there is nothing else to be done. If, on the other hand, calloc returns a block of memory not initialized to 0, we must perform a for cycle to initialize pos[ ] to 0s (note that there is no need to initialize the other entries of elem[ ], since they will be written before read).
Finally, sometimes the following operation is useful for re-initializing a FASTSET, since, for large N, it can be faster (namely ) than creating an empty FASTSET from scratch (that is because of calloc zeroing):
void Clean( FASTSET* s ) {
for ( int i:=1; i <= s->elem[0]; i++ )
s->pos[s->elem[i]] := 0
s->elem[0] := 0
}
It is clear that both creating and cleaning algorithms for FASTSET, as they are outlined, require time, because of zeroing the pos[ ] array (by calloc or a loop, respectively). It is possible, however, to use a trick originally outlined in [7] (exercise 2.12) to avoid the initialization while leaving “garbage” in pos[ ]:
FASTSET* Create( int N ) { // now O(1)
FASTSET* p := malloc( sizeof(FASTSET) )
p->pos := malloc( N * sizeof(int) ) // unknown data in pos
p->elem := malloc( (N+1) * sizeof(int) )
p->elem[0] := 0 // empty set
return p
}
void Clean( FASTSET* s ) { // now O(1)
s->elem[0] := 0; // no loop needed: garbage left in pos
}
We only need to make a slightly more complex belonging check, that must now handle the garbage possibly present in pos:
Boolean Belongs( FASTSET* s, int v ) { // STILL O(1)
k := s->pos[v]
return ( k > 0 AND k <= s->elem[0] AND s->elem[k] == v )
}
3. Example Algorithms Using Sets
A graph can be represented in memory by an array of sets. Namely, for each , we store the set of its neighbors in V. In this section, we give two simple examples of algorithms for graph problems in which we assume the graph is represented by the array of neighbor sets. The algorithms are two greedy procedures, one for the Vertex Cover problem and the other for Max-Cut. Please note that we are not saying that these are the best possible versions for these algorithms. All we want to do is to give some specific, simple examples in which the implementation of the set data structure can affect the overall time performance of a procedure. The results will be described in detail in Section 4.
3.1. Vertex Cover
Let us consider the greedy algorithm for the Vertex Cover problem. The procedure works by repeatedly selecting the highest-degree vertex, say , among the vertices still in the graph. The edges incident in are then removed from the graph, together with isolated nodes, and the process is repeated until the graph is empty. Besides the sets of neighbors for each vertex, the algorithm uses a set C to store the nodes in the cover, and L to store the vertices with degree still in the graph. The pseudocode for the greedy algorithm, with the main set operations clearly marked, is described in Algorithm 1.
| Algorithm 1Greedy Vertex Cover |
while forto if forto if |
3.2. Max-Cut
Let us consider a greedy local-search procedure for Max-Cut. Assume being given a starting solution, represented by a partition of the nodes into two sets, i.e., shore[0] (the left shore of the cut) and shore[1] (the right shore). The procedure checks if it is profitable to flip the color of any node (i.e., to move the node from one shore to the other). If there exists a node v for which more than half of its neighbors are on the same shore of v, it is profitable to move the node from its shore to the opposite, since the value of the cut will strictly increase. The solution is then updated and the search is repeated, until there are no nodes that can be moved with profit. The pseudocode for this greedy local-search is described in Algorithm 2.
| Algorithm 2Greedy Max-Cut |
| do forton if else forto if cnt++ if while progress |
4. Computational Experiments
In this section, we report on some computational experiments (performed on Intel® Core™ i3 CPU M 350 @ 2.27 GHz with 2.8 GB of RAM) in which we have compared the performance of FASTSETs to that of other set data structures included in the standard library of the Java distribution. In particular, Java provides three classes implementing sets via different data structures, namely (i) BitSet [8] implementing the Bitmap data structure; (ii) TreeSet [9] implementing a set as a self-balancing tree with logarithmic cost for all main operations; (iii) HashSet [10] implementing a set by a hash table. We have coded the class FASTSET in Java and have run a first set of experiments in which we have performed a large number of random operations (such as insertions and removals of random elements) for various values of N. The results are listed in Table 2. From the table it appears that FASTSET and BitSet perform very similarly with respect to single-element operations, and they are both better that the other two data structures. It should be remarked that in actual implementations such as this one, Bitmaps are very effective at these type of operations, since they can exploit the speed of some low-level instructions (such as logical operators) for accessing the individual bits of a word. When we turn to listing all elements, however, FASTSETs outperform the other implementations. In particular, a GetAll after 50,000 random insertion on a FASTSET is from 10 up to 30 times faster than for the other data structures.

Table 2.
Time comparison (in milliseconds) for some set implementations found in the java.util package of the Java standard library vs. FASTSET. The row labels report different values of N. The GetAll column refers to 1000 GetAll operations over a set after 50000 random insertions. Each Insert column is labeled by the total number of random insertions; each Belongs column is labeled by the total number of random searches in the set produced by the previous insertions; each Delete column is labeled by the total number of random deletions from the same previous set.
In a second run of experiments, we have considered the two simple combinatorial algorithms described in Section 3, which make heavy use of sets during their execution. The pseudocode listed in Algorithms 1 and 2 refers to an implementation using FASTSETs. The algorithms were translated in equivalent algorithms using BitSet, TreeSet and HashSet in place of FASTSET. The translation was made so as to be as fair and accurate as possible. This was easy for most operations, since they translate directly into equivalent operations on the other data structures. Other operations, such as using GetElem() in a loop to access all the elements of a FASTSET, were realized by calling the iterator methods that the Java classes provide, and which are optimized to make sequential access to all the elements of each structure.
For both Vertex Cover and Max-Cut the tests were run on random graphs of n vertices and an average of edges, where each edge has probability p of being in the graph. We have used and , so that the largest graphs have 5000 nodes and about edges. For each pair we have generated 5 instances and computed the algorithms average running time. The results are reported in Table 3 for Vertex Cover and Table 4 for Max-Cut. For both problems, the implementation using FASTSETs was the fastest. In particular, on the Vertex Cover problem, the use of FASTSETs yields running times between one half and one quarter with respect to the other data structures. The results for Max-Cut are even better, with the other data structures being, on average, from 3 times to 30 times slower than FASTSETs for this procedure.

Table 3.
Time comparison (in milliseconds) for some set implementation found in the java.util package of the Java standard library vs. FASTSET in solving the vertex cover problem using a greedy algorithm (average time over 5 random graph instances, the same for any set type). The shown percentages are relative to the FASTSET time.

Table 4.
Time comparison (in milliseconds) for some set implementation found in the java.util package of the Java standard library vs. FASTSET in solving the max cut problem using a greedy algorithm (average time over 5 random graph instances, the same for any set type). The shown percentages are relative to the FASTSET time.
5. Space Complexity and Limitations
The data structure we have described may not be appropriate when the universe of all possible values is very large, especially if the amount of available memory is an issue. Indeed, the memory requirement is and this can be prohibitive (e.g., when N is a large power of 2 such as ). In this case, even if the memory is available, it is hard to assume that the allocation of such a chunk of memory is an operation.
The same problem, however, would be true of other data structures which require memory, such as the bitmaps and the optimal hashtables. Clearly, when the size of the set tends to become as large as N, all the possible data structures would incur in the same memory problem (indeed, in this case our structure would be optimal as far as memory consumption, since it would be linear in the size of the set). When, on the other hand then data structures based on dynamic allocation of memory (such as linked lists and AVL trees) are better as far as memory consumption than FASTSETs. We remark, however, that the case of an exponentially large N is a rare situation, since most of the times the integers that we deal with in our sets are indices, identifying the elements of a size-N array representing a problem instance.
6. Conclusions
We have described FASTSET, a new data structure for storing sets of integers in a range. Previous implementations of set data structures were either good at “direct access” to the individual set elements or at “sequential access” to all the set elements, but not at both. Our structure has two main advantages over these implementations, namely (i) it possesses the good qualities of both a “direct access” and a “sequential” structure, and (ii) it is very easy to implement. Some computational experiments have shown that FASTSETs can be profitably added, e.g., to the library of Java implementation of set data structures, to which they compare favorably.
Author Contributions
Conceptualization, G.L.; methodology, G.L. and M.D.; software, G.L. and M.D.; validation, G.L. and M.D. and Z.Z.; formal analysis, G.L.; investigation, G.L. and M.D.; resources, G.L. and M.D.; data curation, M.D.; writing–original draft preparation, G.L. and M.D.; writing–review and editing, G.L. and M.D.; visualization, M.D.; supervision, G.L. and M.D.
Funding
This research received no external funding.
Acknowledgments
We thank John Hopcroft, Ronald Rivest and Thomas Cormen for some useful remarks on an earlier draft, and two anonymous referees for their comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aho, A.V.; Hopcroft, J.E.; Ullman, J.D. Data Structures and Algorithms; Addison-Wesley: Boston, MA, USA, 1983. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Tarjan, R.E. Data Structures and Network Algorithms (CBMS-NSF Regional Conference Series in Applied Mathematics); SIAM press: Philadelphia, PA, USA, 1987. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming. Volume 3: Sorting and Searching; Addison-Wesley: Boston, MA, USA, 1998. [Google Scholar]
- Adel’son-Vel’skh, G.M.; Landis, E.M. An algorithm for the organization of information. Soviet Math. Dokl. 1962, 10, 1259–1262. [Google Scholar]
- Oracle. Available online: http://www.oracle.com/technetwork/java (accessed on 8 April 2019).
- Aho, A.V.; Hopcroft, J.E.; Ullman, J.D. The Design and Analysis of Computer Algorithms; Addison-Wesley: Boston, MA, USA, 1974. [Google Scholar]
- Class BitSet. Available online: http://docs.oracle.com/javase/10/docs/api/java/util/BitSet.html (accessed on 15 April 2019).
- Class TreeSet. Available online: http://docs.oracle.com/javase/10/docs/api/java/util/TreeSet.html (accessed on 10 April 2019).
- Class HashSet. Available online: http://docs.oracle.com/javase/10/docs/api/java/util/HashSet.html (accessed on 18 April 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).