Oriented Coloring on Recursively Defined Digraphs
Abstract
1. Introduction
2. Preliminaries
2.1. Graphs and Digraphs
2.2. Undirected Co-Graphs
- The disjoint union of , denoted by , is the graph with vertex set and edge set .
- The join composition of , denoted by , is defined by their disjoint union plus all possible edges between vertices of and for all , .
2.3. Undirected Graph Coloring
- for every
- 1.
- 2.
2.4. Directed Co-Graphs
- The disjoint union of , denoted by , is the digraph with vertex set and arc set .
- The series composition of , denoted by , is defined by their disjoint union plus all possible arcs between vertices of and for all , .
- The order composition of , denoted by , is defined by their disjoint union plus all possible arcs from vertices of to vertices of for all .
3. Oriented Co-Graphs
- 1.
- Every digraph on a single vertex , denoted by •, is an oriented co-graph.
- 2.
- If are k vertex-disjoint oriented co-graphs, then
- (a)
- and
- (b)
- are oriented co-graphs.
- 1.
- G is an oriented co-graph.
- 2.
- .
- 3.
- and .
- 4.
- and is a co-graph.
- 5.
- G has directed NLC-width 1 and .
- 6.
- G has directed clique-width at most 2 and .
- 7.
- G is transitive and .
4. Graph Coloring on Recursively Defined Digraphs
4.1. Oriented Graph Coloring Problem
- for every
- for every two arcs and with
- Name
- Oriented Chromatic Number (OCN)
- Instance
- An oriented graph and a positive integer .
- Question
- Is there an oriented c-coloring for G?
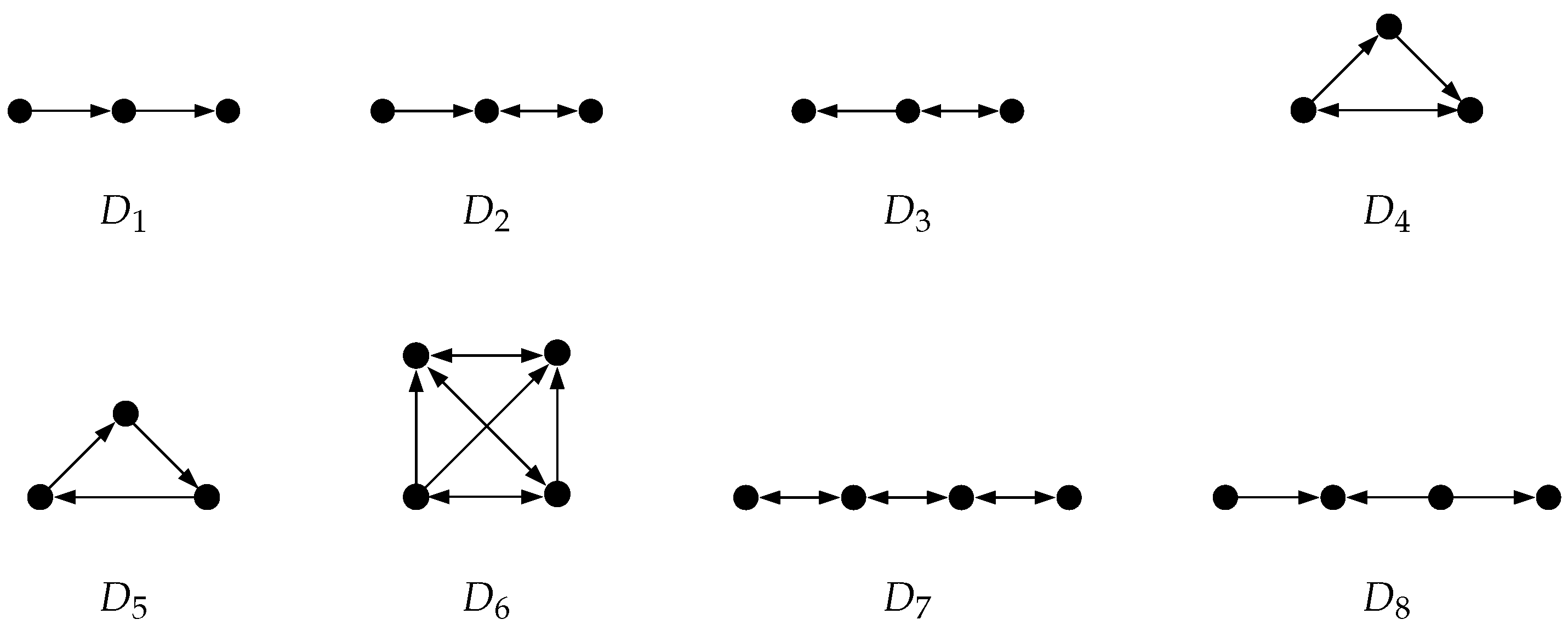
4.2. Oriented Graph Coloring for Oriented Graphs
- 1.
- 2.
- 3.
- Since no new arcs are inserted can keep its colors. The added isolated vertex gets a color of in order to obtain a valid coloring for .This relation holds by Lemma 4, since is an induced subdigraph of .
- Since the digraphs are induced subdigraphs of digraph , all values lead to a lower bound for the number of necessary colors of the combined graph by Lemma 4.
- For let and a coloring for . For we define a mapping as follows.The mapping c satisfies the definition of an oriented coloring, because no two adjacent vertices from , , have the same color by assumption and by definition of c. For a vertex of and a vertex of are always adjacent, but never colored equally by definition of c.Further, the arcs between two color classes of every , , have the same direction by definition of c. For the arcs between a color class of and a color class of have the same direction by definition of the order operation.Since every , , is an induced subdigraph of the combined graph, all values lead to a lower bound for the number of necessary colors of the combined graph by Lemma 4. Further, the order operations implies that for every no vertex in can be colored in the same way as a vertex in . Thus, leads to a lower bound for the number of necessary colors of the combined graph.
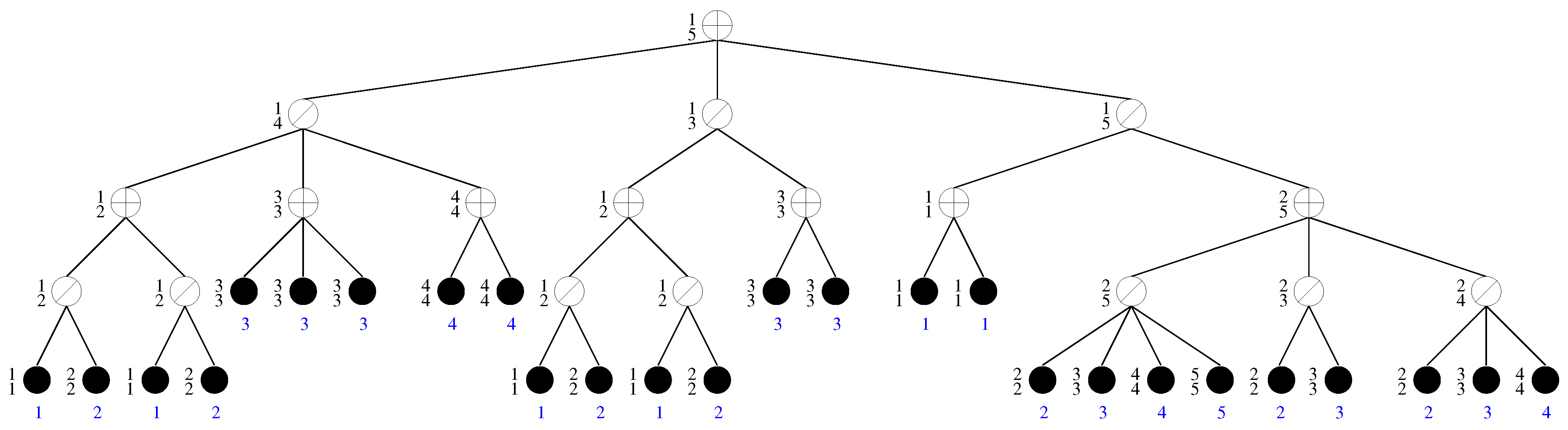
4.3. Oriented Graph Coloring for Oriented Co-Graphs
| Algorithm 1: Computing an oriented coloring for an oriented co-graph. |
| procedure Label if (u is a leaf of T) { ; ; ; } else { ; ; for all children v of u from left to right do { Label; if () ; if (u corresponds to a disjoint union) ; else ▸ u corresponds to an order operation ; } } return ; |
- If u is a leaf of T, then by the algorithm leads to an oriented coloring of .Further, , which obviously corresponds to the oriented chromatic number of .
- Let u be an inner vertex of T which corresponds to an order operation and are the children of u in T.We already know that the oriented colorings of , , are feasible. Further, for , the algorithm’s way of working ensures that a vertex from and a vertex from are never colored equally in . For , the arcs between a color class of and a color class of have the same direction by the definition of the order operation.By the algorithm, value is equal to . By Lemma 5, we conclude that is equal to .
- Let u be an inner vertex of T which corresponds to a disjoint union operation and are the children of u in T.We already know that the oriented colorings of , , are feasible. Since a disjoint union operation does not create any arcs, no two adjacent vertices have the same color in . Further, our method ensures that for every arc in G it holds that . Thus, all arcs between two color classes in have the same direction.By the algorithm, value is equal to . By Lemma 5, we conclude that . The relation holds by the feasibility of our oriented coloring.
- 1.
- G is an oriented clique.
- 2.
- G has a di-co-tree, which does not use any disjoint union operation.
- 3.
- G is a transitive tournament.
5. Longest Oriented Path for Oriented Graphs
- Name
- Oriented Path (OP)
- Instance
- An oriented graph and a positive integer .
- Question
- Is there an oriented path of length at least k in G?
- 1.
- 2.
- If , then it obviously holds .
- If
- If
6. Graph Isomorphism for Oriented Co-Graphs
- Name
- Oriented Co-Graph Isomorphism (OCI)
- Instance
- Two oriented co-graphs and .
- Question
- Are and isomorphic, i.e., is there a bijection such that for all it holds that if and only if ?
| Algorithm 2: Testing graph isomorphism for two oriented co-graphs given by canonical di-co-trees. |
| procedure Test let h be the height of and for downto 0 do for all vertices v on level ℓ in from left to right do if (v is a leaf) else let be the children of v if (v corresponds to a union operation) sort vector ascending let be the sequence of all for all v on level ℓ in for all vertices v on level ℓ in from left to right do if (v is a leaf) else let be the children of v if (v corresponds to a union operation) sort vector ascending let be the sequence of all for all v on level ℓ in sort to obtain and sort to obtain if () return let be the set of all vectors on level ℓ in find a bijection for all vertices v on level ℓ in do ; for all vertices v on level ℓ in do ; } return ; |
7. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Golumbic, M. Algorithmic Graph Theory and Perfect Graphs; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Hoàng, C. Efficient algorithms for minimum weighted coloring of some classes of perfect graphs. Discret. Appl. Math. 1994, 55, 133–143. [Google Scholar] [CrossRef]
- Corneil, D.; Lerchs, H.; Stewart-Burlingham, L. Complement Reducible Graphs. Discret. Appl. Math. 1981, 3, 163–174. [Google Scholar] [CrossRef]
- Courcelle, B. The monadic second-order logic of graphs VI: On several representations of graphs by relational structures. Discret. Appl. Math. 1994, 54, 117–149. [Google Scholar] [CrossRef]
- Culus, J.F.; Demange, M. Oriented Coloring: Complexity and Approximation. In Proceedings of the Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM), Merin, Czech Republic, 21–27 January 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3831, pp. 226–236. [Google Scholar]
- Sopena, É. The chromatic number of oriented graphs. J. Graph Theory 1997, 25, 191–205. [Google Scholar] [CrossRef]
- Marshall, T. Homomorphism bounds for oriented planar graphs of given minimum girth. Graphs Comb. 2013, 29, 1489–1499. [Google Scholar] [CrossRef]
- Dybizbański, J.; Szepietowski, A. The oriented chromatic number of Halin graphs. Inf. Process. Lett. 2014, 114, 45–49. [Google Scholar] [CrossRef]
- Ganian, R. The Parameterized Complexity of Oriented Coloring. In Proceedings of the Doctoral Workshop on Mathematical and Engineering Methods in Computer Science (MEMICS), Znojmo, Czech Republic, 13–15 November 2009; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2009; Volume 13. [Google Scholar]
- Bechet, D.; de Groote, P.; Retoré, C. A complete axiomatisation of the inclusion of series-parallel partial orders. In Rewriting Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1232, pp. 230–240. [Google Scholar]
- Lawler, E. Graphical algorithms and their complexity. Math. Cent. Tracts 1976, 81, 3–32. [Google Scholar]
- Gurski, F.; Wanke, E.; Yilmaz, E. Directed NLC-width. Theor. Comput. Sci. 2016, 616, 1–17. [Google Scholar] [CrossRef]
- Bang-Jensen, J.; Gutin, G. Digraphs. Theory, Algorithms and Applications; Springer: Berlin, Germany, 2009. [Google Scholar]
- Gurski, F. A comparison of two approaches for polynomial time algorithms computing basic graph parameters. arXiv 2008, arXiv:0806.4073. [Google Scholar]
- Fomin, F.; Golovach, P.; Lokshtanov, D.; Saurabh, S. Clique-width: On the price of generality. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms (SODA), New York, NY, USA, 4–6 January 2009; ACM-SIAM: Philadelphia, PA, USA, 2009; pp. 825–834. [Google Scholar]
- Espelage, W.; Gurski, F.; Wanke, E. How to solve NP-hard graph problems on clique-width bounded graphs in polynomial time. In Proceedings of the Graph-Theoretical Concepts in Computer Science (WG), Boltenhagen, Germany, 14–16 June 2001; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2204, pp. 117–128. [Google Scholar]
- Crespelle, C.; Paul, C. Fully dynamic recognition algorithm and certificate for directed cographs. Discret. Appl. Math. 2006, 154, 1722–1741. [Google Scholar] [CrossRef]
- Bang-Jensen, J.; Maddaloni, A. Arc-disjoint paths in decomposable digraphs. J. Graph Theory 2014, 77, 89–110. [Google Scholar] [CrossRef]
- Gurski, F. Dynamic Programming Algorithms on Directed Cographs. Stat. Optim. Inf. Comput. 2017, 5, 35–44. [Google Scholar] [CrossRef][Green Version]
- Retoré, C. Pomset logic as a calculus of directed cographs. In Proceedings of the Fourth Roma Workshop: Dynamic perspectives in Logic and Linguistics, Roma, Italy, 15–17 October 1997; CLUEB: Bologna, Italy, 1998; pp. 221–247. [Google Scholar]
- Gurski, F.; Rehs, C. Directed path-width and directed tree-width of directed co-graphs. In Proceedings of the International Conference on Computing and Combinatorics (COCOON), Qingdao, China, 2–4 July 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10976, pp. 255–267. [Google Scholar]
- Boeckner, D. Oriented Threshold Graphs. Australas. J. Comb. 2018, 71, 43–53. [Google Scholar]
- Gould, R. Graph Theory; Dover Publications Inc.: New York, NY, USA, 2012. [Google Scholar]
- Hell, P.; Nesetril, J. Graphs and Homomorphisms; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Aho, A.; Hopcroft, J.; Ullman, J. The Design and Analysis of Computer Algorithms; Addison-Wesley Publishing Company: Boston, MA, USA, 1974. [Google Scholar]
- Johnson, T.; Robertson, N.; Seymour, P.; Thomas, R. Directed Tree-width. J. Comb. Theory Ser. B 2001, 82, 138–155. [Google Scholar] [CrossRef]
- Wagner, F. Hardness Results for Tournament Isomorphism and Automorphism. In Proceedings of the Mathematical Foundations of Computer Science (MFCS), Cesky Krumlov, Czech Republic, 27–31 August 2007; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4708, pp. 572–583. [Google Scholar]
- Courcelle, B.; Olariu, S. Upper bounds to the clique width of graphs. Discret. Appl. Math. 2000, 101, 77–114. [Google Scholar] [CrossRef]
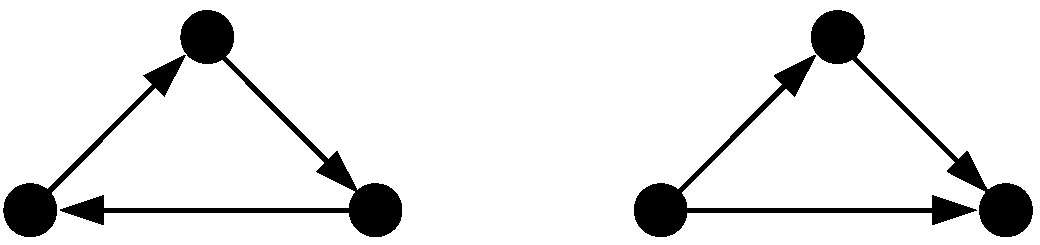
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurski, F.; Komander, D.; Rehs, C. Oriented Coloring on Recursively Defined Digraphs. Algorithms 2019, 12, 87. https://doi.org/10.3390/a12040087
Gurski F, Komander D, Rehs C. Oriented Coloring on Recursively Defined Digraphs. Algorithms. 2019; 12(4):87. https://doi.org/10.3390/a12040087
Chicago/Turabian StyleGurski, Frank, Dominique Komander, and Carolin Rehs. 2019. "Oriented Coloring on Recursively Defined Digraphs" Algorithms 12, no. 4: 87. https://doi.org/10.3390/a12040087
APA StyleGurski, F., Komander, D., & Rehs, C. (2019). Oriented Coloring on Recursively Defined Digraphs. Algorithms, 12(4), 87. https://doi.org/10.3390/a12040087





