Abstract
The horizontal bending angle of scraper conveyor has a great influence on the running resistance, the current consumption, coal winning efficiency of the working surface, etc. Approximately 1–3° is usually the range of horizontal bending angle, but does not indicate the optimum bending angle of the coal mining face. To find the optimal horizontal bending angle, an optimization method is proposed. A mathematical calculation model of the running resistance of the scraper is established based on the direction of the shearer operation. Then, a method of adjusting the step size of the search by inertia weight and expanding fly distance range obeying the t-distribution is proposed based on the basic bat algorithm (BA). Finally, an industrial application was conducted in 21220 Changcun fully mechanized coal mining face, Henan Province. The results show that the current consumption by the scraper conveyor was reduced by 31% when the horizontal bending angle of the S-bending area was 0.66°. Meanwhile, the theoretical current has good consistency with the experimental data, and the average absolute error was 3%.
1. Introduction
The scraper conveyor is one of the key equipment for underground coal mining [1]. It not only transports coal, but also provides the running track of the shearer and the positioning of the hydraulic support. It is the connection point of the fully mechanized mining equipment [2,3]. In the fully mechanized mining face, the middle slot of the scraper conveyor is pushed by the hydraulic support to the coal wall by a step (the length of the step is usually 600–1000 mm), which is pushed to the next cutting plane. At the same time, the adjacent middle grooves will be driven by each other and rotated to form a transition section. To ensure the stable operation of the scraper conveyor, the transition section will form two anti-symmetrical bending lines. This horizontal bending section presents an S shape, hence it is called the S-bending area [4]. The angle between the adjacent middle grooves of the S-bending area of the scraper conveyor is called the horizontal bending angle. The horizontal bending angle of the S-bending area of the scraper conveyor is selected from 1° to 3°, and the horizontal bending angle used under the mine is usually determined empirically.
Previous research on scraper conveyor has mainly focuses on the monitoring [5,6] and calculation [7,8,9] of running load, dynamical problems [10,11,12], friction and wear [13,14,15]. However, studies rarely account for the effect of the horizontal bending angle of the S-bending area on the additional resistance, the running load, the production energy consumption ratio, the mean time between failures (MTBF) of the mining equipment and the shear cutting efficiency has been rarely investigated. In fact, if the horizontal bending angle of the S-bending area is improperly selected, the additional resistance will increase [16], the middle groove and the sprocket assembly will be seriously worn [17], the current fluctuation is large, the energy consumption of the mining equipment is high, the equipment service life is low and the MTBF is small.
Bat Algorithm (BA) was proposed by Yang in 2010 based on swarm intelligence [18,19]. It simulates bat behavior, which avoids obstacles, detects preys and locates the roosting crevices in the dark. Based on the bionic principle, BA simulates the optimization and search process with a population bat individual movement processes and searches for the prey [20,21]. BA has the advantages of simple structure, few parameters, strong robustness, and is easy to understand and implement. Since the BA was proposed, it has been widely applied in construction machinery [22], finances [23], forecasting [24], etc. However, similar to other optimization algorithms, the basic BA also has the disadvantage of falling into local optimum.
Considering the above observations, a method based on improved BA (MBA) for optimizing horizontal bending angle is proposed. The rest of this paper is organized as follows. In Section 2, the basic theory of the mathematical models of the running resistance of scraper conveyor and BA are described. Then, the MBA and the whole flow of proposed horizontal bending angle optimization scheme are illustrated in Section 3. Some simulations and analysis according to the actual working conditions of the fully mechanized mining face are presented in Section 4 to validate the superiority of the proposed method. In Section 5, a mine application is presented to validate the practical effect. In Section 6, some conclusions and outlooks are summarized.
2. Basic Theory
2.1. Analyze the Running Resistance of the Scraper Conveyor
The running resistance of scraper conveyor is related to the amount of coal carried and the running direction of the shearer. Its running resistance is divided into the running resistance of the straight section and the additional resistance of the S-bending section.
Straight line running resistance
Previous calculation of the running resistance did not take into account the actual transport state of scraper conveyor [25,26]. According to the actual working conditions, the middle slot of the scraper conveyor is divided into two parts innovatively, the heavy-duty section and no-load section. Combining with the cutting technology of the shearer, the calculation method of the operating resistance of the scraper conveyor is shown as follows:
where q is the linear density of the heavy-duty part of the scraper conveyor, kg/m; q0 is the load weight per unit length of the scraper chain, kg/m; μss is the resistance coefficient of the load in the chute; μcs is the scraper chain movement resistance coefficient in the chute; L is the total length of the scraper conveyor, m; and θ is the vertical bending angle of the scraper conveyor, °; The length of the heavy-duty section L1 = x0 + vsts, and the no-load length L2 = L − L1, m; vs is the speed of the shearer, m/min; ts is the shearer operating time, s; x0 is the distance from the starting point of the scraper conveyor to the head, m; m = 1 when the shearer and scraper conveyor are running in opposite directions. Otherwise, m = 2; d = 1 indicates the resistance of the upper chain of the middle slot, and d = 2 indicates the resistance of the lower chain of the middle slot.
S-bending section additional resistance
Due to the angle between the adjacent middle slot of the S-bending area, the squeegee chain can be regarded as a flexible body sliding around the fixed circular ring guide when sliding therein [27,28,29,30]. The additional resistance (ΔFm) of the S-bending area includes the additional traction resistance of the chain and the squeezing force of the squeegee striking the middle trough. The expression of ΔFm is expressed as follows:
where K is the total number of horizontal curved chutes; r is the lateral friction coefficient of the squeegee and the middle slot; Fd is the chain tension in the end of the chute before the horizontal bending section, N; α′ is the angle between adjacent middle slots, °; μ is the friction coefficient value of the scraper chain and the chute; the resistance of each middle slot is C1 = l(q + q0)(μsscosθ ± sinθ), C2 = q0(μcscosθ ∓ sinθ); l is the length of a middle slot, m; Fsm is the lateral pressing force [28].
2.2. Bat Algorithm
Bat Algorithm (BA) is a heuristic search algorithm, which was proposed by Yang in 2010. By simulating the bat foraging behavior, local and global optimality can be obtained through appropriate iteration. The bat algorithm search process is as follows:
Step 1.1: Parameter initialization. P is the initial bat population size. The maximum number of iterations is N. The pulse frequency is in the range [fmin, fmax]. ri0 is the pulse rate. A is the maximum pulse sound intensity. The sound intensity attenuation coefficient is α. The frequency increase coefficient is γ. D is the dimension of the search variable.
Step 1.2: Population initialization. Randomly initialize the position of the bat individual xi (i = 1, 2, …, D) within the search range. Find the best bat position x∗ in the current search. Calculate the fitness value f(xi) of each bat, and find out the best location and fitness value of the current bat.
Step 1.3: Movement speed and position update. Let the bats search in the D-dimensional space, the position and velocity of the bat i are xit−1 and vit−1 at (t − 1) time. The current global optimal position is x∗. For bat i at time t, its position xit and speed vit update formula are given by:
where β ∈ [0,1] is a random vector drawn from a uniform distribution.
Step 1.4: Local search. Each bat randomly selects one from the current optimal solution, and its new solution is generated by random walks. The formula is shown as follows:
where ε ∈ [0,1] is the random number, while At = <Ati> is the average loudness of all the bats at this time step.
Step 1.5: Pulse emission loudness and emission frequency update. First, a new random number is generated within [0,1], and then the size relationship between the current bat and the new bat adaptation is compared. New bats are accepted if the following conditions are met. The adjustment formula of the ultrasonic loudness Ai and the pulse rate ri is:
where α and γ are constants.
Step 1.6: Global optimal evaluation. Calculate the fitness of all individuals in the current population, and record the optimal bat position and its fitness value.
Step 1.7: Iteration termination. If the current iteration number t reaches the maximum number of iterations N, the iteration is stopped, otherwise, repeated Steps 1.3–1.6. The iteration process is presented in Figure 1.
Figure 1.
Foraging process of the bat.
3. The Proposed Method
3.1. Improvement of BA
Bat algorithm has the advantages of simple structure, few parameters, strong robustness and easy implementation. However, the bat algorithm has problems such as slow convergence and easily falling into local optimum.
To improve the convergence speed of the bat algorithm, this paper uses the inertia weight (ω(t)) method to adjust the step size of the bat flight. The ω(t) coefficient distribution diagram is shown in Figure 2. The inertia weight function is shown in Equation (7). The speed update formula of the bat search is described in Equation (8).
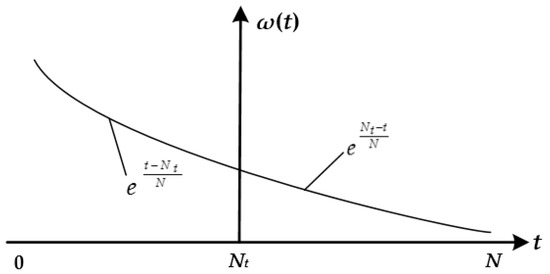
Figure 2.
Distribution of inertia weight coefficient.
To solve the problem of falling into local optimum, this paper expands the range of bat fly distance range (FR) obeying the t-distribution. The shape of the curve of the t-distribution is related to the degree of freedom (df). When df = 1, the t-distribution curve coincides with the Cauchy distribution curve. When df → ∞, the t-distribution is normally distributed. The probability density function curves of Cauchy distribution, t-distribution, and normal distribution are shown in Figure 3. The rules for random migration of bat populations is expressed as:
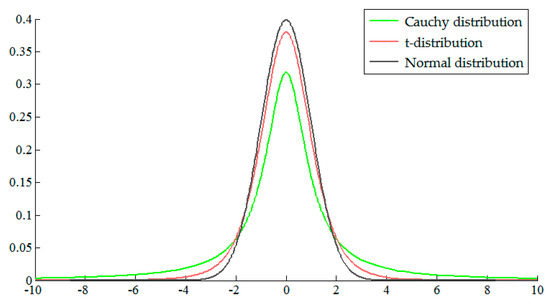
Figure 3.
Probability density function curve of Cauchy distribution, t-distribution and Normal distribution.
The Cauchy distribution has a good global development capability, while the Normal distribution has a stable local search capability. The number of iterations of the bat population is taken as the df of the t-distribution. As the number of iterations increases, the FR varies between the Cauchy distribution and the Normal distribution. At the beginning of the bat population iteration, the t-distribution is close to the Cauchy distribution. At this time, the bat search flight range and population diversity are improved, so that the local optimum is avoided. In the late stage of the bat population iteration, the t-distribution is close to the Normal distribution. In this process, the bat’s local search ability is strong and the convergence speed is fast.
3.2. Design of the Fitness Function
Since the evaluation index value is a dimensional expression, this paper uses linear normalization to transform it into a scalar expression. Considering the three-machine work of the fully mechanized mining face, the running load of the scraper conveyor (pm1), the support requirements of the hydraulic support (pm2) and the efficiency of the shearer chamfering feed (pm3) are used as evaluation indicators (pmj). The calculation formulas for the evaluation indicators pm1, pm2 and pm3 are as follows:
where, Lkp is the length of the S-bending area, m [31]; tcf is the time for the shearer chamfering feed, s; and tcd is the total time used by the shearer to cut a piece of coal, s.
The first and second quadrants of the unit circle are used as the scoring system, which is not only easy to calculate, but also has increasing and decreasing trends. The evaluation score formula is calculated as follows:
where Smj is the score of the j-th index of the known shearer running direction, j is the index number, j = 1, 2, 3; and pmj is the evaluation index of the corresponding Smj. The score of the whole working mode can be obtained from each evaluation score, and the total score function Sscore is shown as follows:
where amj is the weight coefficient, and its size is determined by tomographic analysis [32].
The additional resistance ΔFm of the scraper conveyor, the number of the slot (K) in the S-bending area and the length (Lkp) of the S-bending area are all related to the horizontal bending angle α′. Therefore, the fitness function is created with α′ as the objective of optimization. The higher is the score of the objective function for α′, the better is the working mode of the three-machine collaboration. Sscore is used as the fitness function of the MBA to iteratively optimize.
3.3. Flowchart of Optimization Method for Horizontal Bending Angle
Based on the above analysis, an innovative method based on the improved bat algorithm (MBA) to optimize the horizontal bending angle of the S-bending area of the scraper conveyor is proposed. The flowchart for optimizing horizontal bending angle of S-bending area based on MBA is shown in Figure 4. The optimization steps are summarized as follows:
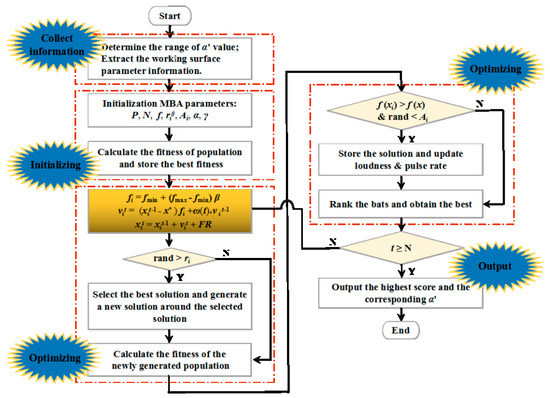
Figure 4.
The flowchart for optimizing horizontal bending angle of S-bending area based on MBA.
Step 2.1: Collect information. Extracting and processing parameter information of fully mechanized mining face.
Step 2.2: Initialize the parameters of the MBA optimization algorithm and set the number of iterations for the population.
Step 2.3: Population initialization. Each position of the bat is considered as a horizontal bending angle value, and the fitness value of each bat is the evaluation value of the working surface.
Step 2.4: Movement speed and position update. The update of the speed and position of each generation of bat population can be obtained according to Equations (8) and (9).
Step 2.5: Termination condition. When the iteration number t reaches the maximum N, the iteration is stopped, and then the highest score and its corresponding optimal α′ value are output; otherwise, Steps 2.2–2.4 are repeated.
4. Simulation and Analysis
To validate the superiority of the proposed method, the established fitness function was substituted into iterative optimization. Then, the original BA (BAO), the bat algorithm based on bacterial algorithm (BCBA) [33] and a globally optimized adaptive BAT memory algorithm (ABAM) [34] and the proposed MBA were compared. Maximum score value (Sscore_max), the mean value of the horizontal bending angle value (Mean) and the standard deviation (SD) were regarded as evaluation criteria for the four optimization algorithms. Finally, compare the optimization effects of the four algorithms were compared. The configuration of the computer used is shown in Table 1.

Table 1.
Computer Configuration.
4.1. Parameter Information Acquisition
All parameter information of working face was acquired from the 21220 fully mechanized mining face of Changcun Mine of Henan Da You Energy Co., Ltd. (Sanmenxia, China). Coal mining face and equipment parameters are shown in Table 2.

Table 2.
Coal mining face and equipment parameters.
4.2. Horizontal Bending Angle Optimization Effect Analysis
In the actual working condition of the mine, the S-bending area of the scraper conveyor, also called transition section, is formed by the hydraulic support pushing the middle groove to the next cutting plane. For the unmined cutting face, shearer cutting coal rock usually starts chamfering in the S-bending area. Therefore, the horizontal bending angle of the S-bending area has an important influence on the production of working face and the chamfering feed of the shearer.
The fitness function was established in combination with the actual working conditions under the mine. The higher was the evaluation score, the higher was the production efficiency of the working face. The parameter information of the working face was inputted into the fitness function. Then, the four algorithms of ABAM, BCBA, BAO and MBA were used to iteratively search for the highest score (Sscore-max) and the corresponding optimal α′. Compare the paths searched by 4 different algorithms 3 times, and the comparison results are shown in Figure 5.
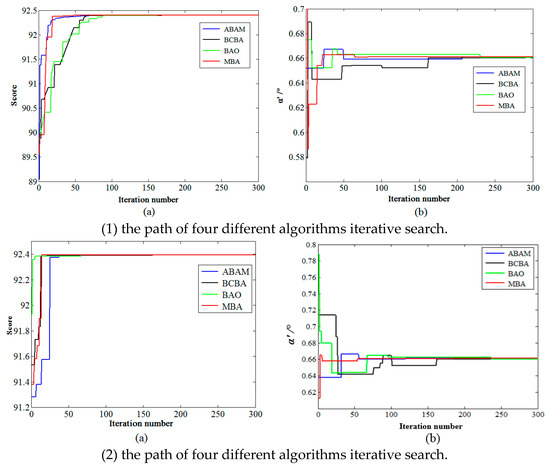
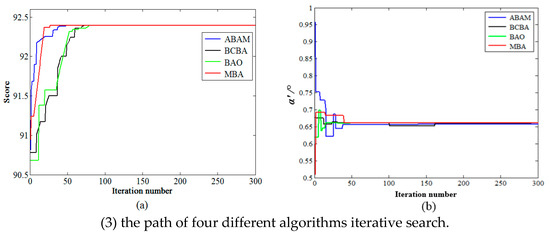
Figure 5.
Comparison of optimization results of four different optimization algorithms.
As shown in Figure 5, the four optimization algorithms were iterated 300 times, and the evaluation score of the search was small, about 92.4 points. In the process of searching, the MBA algorithm reached the optimal value by 40 iterations, while the ABAM and BCBA needed 70 iterations, and the BAO needed 90 iterations, as shown in Figure 5a. when α′ reached the optimum value of 0.66°, the MBA had iterated 40 times, while the BAO 100 times. The ABAM and BCBA algorithm search process oscillated very sharply, and began to stabilize in the 150th generation, as shown in Figure 5b.
To improve the production efficiency of the working face when the shearer bevel cutting, this study combined the running direction of the shearer and optimized the α′ of the S-bending area by using the proposed method and three other algorithms. The optimization results are shown in Figure 6.
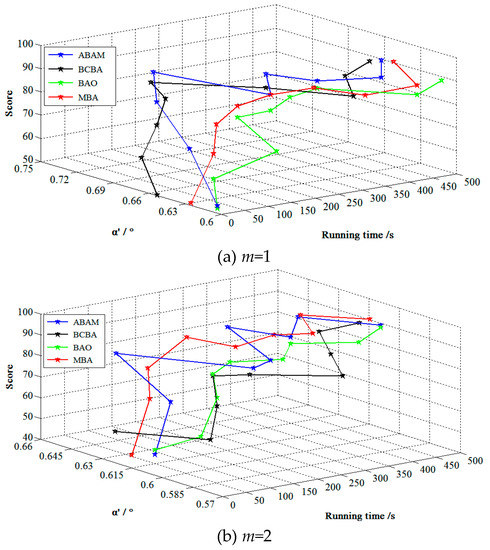
Figure 6.
Optimal horizontal bending angle and corresponding score distribution map.
As shown in Figure 6, in the shearer bevel cutting stage, the horizontal bending angle α′ of the S-bending area was [0.60°, 0.75°], [0.57°, 0.66°]. The optimal horizontal bending angle was not linear with the cutting time. Because the mine environment is complex and variable, the value of the α′ was different when the shearer cuts forward and reverses. In the shearer cutting process, the working surface evaluation score increased from 50 points to 92.4 points.
4.3. Comparison and Discussion
To analyze the superiority of the proposed method, the maximum score (Sscore_max), the mean value (Mean) and the standard deviation (SD) of the four algorithms were compared. The performance comparison results of the four different algorithms are shown in Table 3. As can be seen in the table, the Sscore_max of MBA, ABAM, BCBA and BAO was between 92.394 and 92.396. The mean of the MBA optimized α′ was 0.66°. The mean values of ABAM, BCBA and BAO optimized α′ were 0.659°, 0.656°, 0.655°, respectively. The errors of the means were 0.6%, 0.77%, 1.5%, and 3.4%, respectively. The SDs of MBA, ABAM, BCBA and BAO were 1%, 2.1%, 2.5%, and 2.8%, respectively. Overall, the proposed MBA optimization algorithm converged quickly and with a small deviation.

Table 3.
The performance comparison results of the four different algorithms.
5. Experiment and Application
The horizontal bend angle optimization system for the S-bending area of the scraper conveyor based on the proposed method was experimentally applied to the fully mechanized mining face, as shown in Figure 7. The application was tested at the 21220 working face of Changcun Mine of Henan Da You Energy Co., Ltd. Since the current of the scraper conveyor can intuitively reflect the load [35], combined with the relationship between the α′ and the load analyzed in Section 2.1, the optimal value of the α′ could be verified by collecting the current consumed by scraper conveyor. The current transformer was used to collect the current of the head and tail of the scraper conveyor, and the data were transmitted through the wireless MESH network installed on the hydraulic support. The ground monitoring center was used for remote monitoring and control.
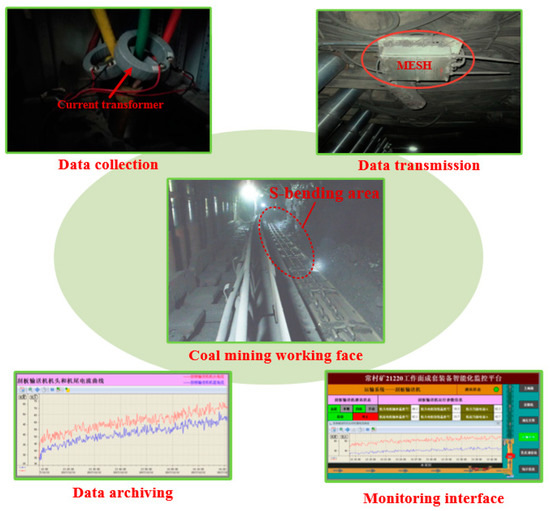
Figure 7.
Industrial application of the proposed method.
Due to the environment under the mine is complicated and dangerous, the three angles of 0.5°, 0.66° and 1.5° were used for comparative experiments, where 1.5° is the horizontal bending angle value commonly used for the working surface. 0.66° is optimal horizontal bending angle obtained by the proposed method, and 0.5° is used to check whether the smaller α′ is, the better the working condition is. To verify the correctness of the proposed method, the current data collected under mine were compared with the theory, and the comparison results are shown in Figure 8 and Figure 9.
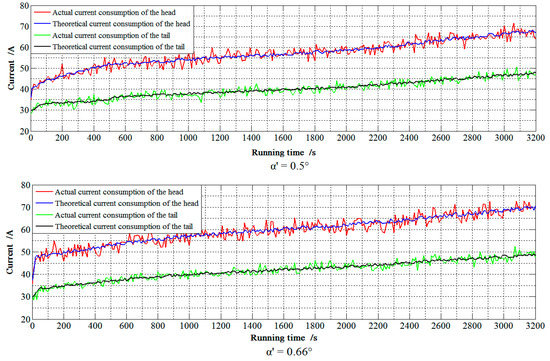
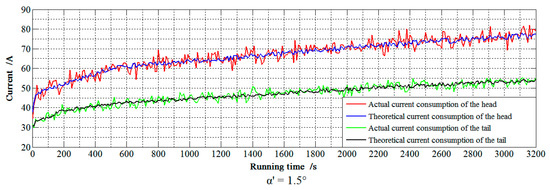
Figure 8.
Comparison between the measured and theoretical current of scraper conveyor when m = 1.
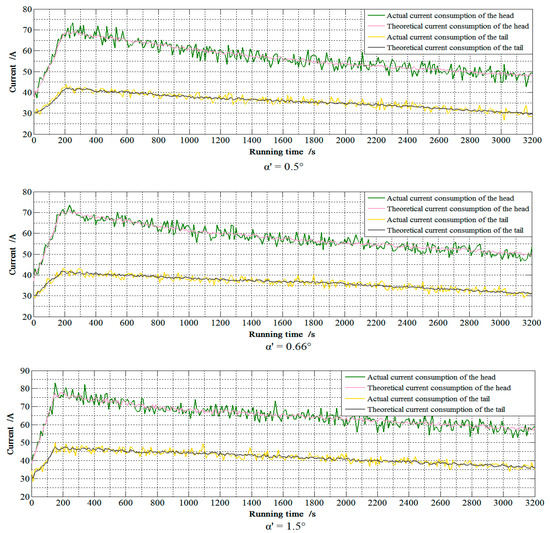
Figure 9.
Comparison between the measured and theoretical current of scraper conveyor when m = 2.
The current required by the scraper conveyor varied with the α′. When α′ = 1.5°, the current consumption of the motor was about 7 A larger than that of α′ = 0.5° and 0.66°. When α′ = 0.66°, the current consumption of the scraper conveyor drive motor was 2 A larger than α′ = 0.5°. To verify the accuracy and practicality of the proposed method, the average absolute error was used. The average absolute error calculation results are shown in Table 4.

Table 4.
Actual vs. theoretical current average absolute error list at different α′.
Under the three different α′, the maximum and minimum average absolute errors of the actual-theoretical current were 3.68% and 2.11%, respectively. The average absolute error of α′ = 0.66° was smaller than that of α′ = 0.5° and 1.5°. The error between the theoretical calculation and experimental data was very small, and the trend of increase and decrease was consistent.
When α′ = 0.5°, the S-bending area was so long that the efficiency of the shearer’s bevel cutting was very low, and the hydraulic support could not be timely supported. Although the scraper conveyor consumed less current when α′ = 0.5°, the time for the shearer to cut a knife coal was increased by 20%, and the MTBF was raised by 15%. Therefore, α′ = 0.5° was unacceptable. In other words, the mining model with smaller α′ was not good.
The horizontal bending angle α′ was changed to 0.66° and used under the mine for one year. The replacement frequency of the sprocket assembly was reduced by 50%, which saved about $284,000. The total electricity consumption of the working face was reduced by 31%, thus $97,000 was saved. Due to the decrease of MTBF, production time increased, and 32,000 more tons of coal were produced than the previous year. The correctness and feasibility of the simulation results were verified.
6. Conclusions and Future Work
To make the working mode of the coal mining face better, a new method based on the running resistance characteristics and the improved BA is proposed in this paper. Under consideration of the direction of the shearer’s running direction, the mathematical model of the running resistance of the scraper conveyor was established. The improved strategy based on adjusting the step size of the search by inertia weight and expanding fly distance range obeying the t-distribution was applied in the optimization process. To verify the feasibility and superiority of MBA, a simulation comparison was made. Finally, the simulation results were applied in the 21220 fully mechanized mining face of Changcun Mine. The conclusions are as follows:
- The current consumption and running resistance of three different α′ cases were compared. The results show that the average absolute error rate of theoretical calculation and measured current value was 3%. The correctness of the mathematical model was verified.
- The improved bat algorithm (MBA) had faster convergence speed and higher accuracy than AMBA, BCBA, and BAO algorithms. MBA was superior in searching for optimal horizontal bending angles.
- When α′ = 0.66° was compared with the usual bending angle, not only the current consumption and the cost per ton of coal were reduced, but the MTBF was reduced by 50%. The correctness and feasibility of the simulation results were verified by industrial application.
In future studies, the authors will focus on improving the proposed approach. This may be done by including unknown factors that affect the operational resistance to be explored and by developing an improved algorithm with higher execution efficiency.
Author Contributions
C.T. and T.L. contributed the new processing method; Z.W. and J.X. designed the simulations and experiments; Y.M. and T.W. performed the experiments; and T.L. wrote the paper.
Acknowledgments
The support of the National Natural Science Foundation of China (No. U1510117), the National Key Basic Research Program of China (No. 2014CB046301) and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions in carrying out this research are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shen, B.H.; Guo, Y.H. Development Status and Tendency of Technology and Equipment for Fully Mechanized Coal Mining in China. Coal Sci. Technol. 2012, 40, 1–3. [Google Scholar]
- Wang, X.W.; Wang, S.P.; Long, R.S.; Yang, Z.J.; Liu, G.P. Rigid-flexible coupled dynamic contact analysis for a chains drive system of a heavy scraper conveyer during loading start-up. J. Vib. Shock 2016, 35, 34–40. [Google Scholar]
- Ordin, A.A.; Metel’Kov, A.A. Analysis of longwall face output in screw-type cutter loader and scraper conveyor system in underground mining of flat-lying coal beds. J. Min. Sci. 2015, 51, 1173–1179. [Google Scholar] [CrossRef]
- Zhang, L. Research on Key Technologies of Autonomous Following Mining Machine for Hydraulic Support. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2017. [Google Scholar]
- Crawford, K.S.; Epperly, R.A.; Murphy, H.G.; Saunders, L.A. Applying Adjustable Frequency Controllers to High-Starting-Torque Loads. In Proceedings of the Petroleum and Chemical Industry Conference, St. Louis, MO, USA, 13–15 September 1993; pp. 89–100. [Google Scholar]
- Murphy, C.J.; Bliss, R.E. Method and Apparatus for Belt Conveyor Load Tracking. U.S. Patent 5,335,777, 9 August 1994. [Google Scholar]
- Dolipski, M.; Remiorz, E.; Sobota, P. Dynamics of Non-Uniformity Loads of AFC Drives. Arch. Min. Sci. 2014, 59, 155–168. [Google Scholar] [CrossRef]
- Wang, K. Research on Shearer Speed Control Technology Based on Scraper Conveyor Load Prediction. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2015. [Google Scholar]
- Morley, L.A.; Kohler, J.L.; Smolnikar, H.M. A model for predicting motor load for an armored face-conveyor drive. IEEE Trans. Ind. Technol. 1988, 24, 649–659. [Google Scholar] [CrossRef]
- Swider, J.; Herbus, K.; Szewerda, K. Dynamic analysis of scraper conveyor operation with external loads. In Proceedings of the 4th International Conference on Computing and Solutions in Manufacturing Engineering 2016—CoSME’16, Braşov, Romania, 3–4 November 2016; pp. 1–6. [Google Scholar]
- Dolipski, M.; Cheluszka, P.; Remiorz, E.; Sobota, P. Follow-Up Chain Tension in an Armoured Face Conveyor/Nadążne Napinanie Łańcucha Zgrzebłowego W Przenośniku Ścianowym. Arch. Min. Sci. 2015, 60, 25–38. [Google Scholar] [CrossRef]
- Sdvyzhkova, O.; Patyńska, R. Effect of increasing mining rate on longwall coal mining—Western donbass case study. Stud. Geotech. Mech. 2016, 38, 91–98. [Google Scholar] [CrossRef]
- Krawczyk, J.; Pawlowski, B. The Analysis of the Tribological Properties of the Armoured Face Conveyor Chain Race. Arch. Min. Sci. 2013, 58, 1251–1262. [Google Scholar]
- Broadfoot, A.R.; Betz, R.E. Power requirement prediction for armoured face conveyors. Min. Technol. 2014, 109, 93–101. [Google Scholar] [CrossRef]
- Shi, Z.; Zhu, Z. Case study: Wear analysis of the middle plate of a heavy-load scraper conveyor chute under a range of operating conditions. Wear 2017, 380, 36–41. [Google Scholar] [CrossRef]
- Liu, K.M. The Mechanical Study of Scraper Conveyor. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2005. [Google Scholar]
- Jiao, H.Z.; Yang, Z.J.; Wang, S.P. Contact dynamics simulation analysis for sprocket transmission system of scraper conveyor. J. China Coal Soc. 2012, 37, 494–498. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Comput. Knowl. Technol. 2010, 284, 65–74. [Google Scholar]
- Yang, X.; Ah, G. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Altringham, J.D.; Mcowat, T.; Hammond, L. Bats: Biology and behaviour. Q. Rev. Biol. 1998, 78, 43–57. [Google Scholar]
- Chen, M.; Feng, J.; Li, Z.; Zhou, J.; Zhao, H.; Zhang, S.; Sheng, L. Echolocation sound waves, morphological features and foraging strategies in Hipposideros pratti. Chin. J. Appl. Ecol. 2002, 13, 1629–1632. [Google Scholar]
- Heraguemi, K.E.; Kamel, N.; Drias, H. Multi-swarm bat algorithm for association rule mining using multiple cooperative strategies. Appl. Intell. 2016, 45, 1–13. [Google Scholar] [CrossRef]
- Hafezi, R.; Shahrabi, J.; Hadavandi, E. A bat-neural network multi-agent system (BNNMAS) for stock price prediction: Case study of DAX stock price. Appl. Soft Comput. J. 2015, 29, 196–210. [Google Scholar] [CrossRef]
- Bento, P.M.R.; Pombo, J.A.N.; Calado, M.R.A.; Mariano, S.J.P.S. A bat optimized neural network and wavelet transform approach for short-term price forecasting. Appl. Energy 2018, 210, 88–97. [Google Scholar] [CrossRef]
- Furmanik, K.; Pracik, M. Method for evaluation of movement resistance in scraper pipe conveyors. Proc. Appl. Math. Mech. 2010, 7, 4130043–4130044. [Google Scholar] [CrossRef]
- Mao, J.; Cao, H.; Xie, M. Load characteristic analysis and simulation of scraper conveyor under stable operation. J. Liaoning Technol. Univ. 2017, 36, 1298–1302. [Google Scholar]
- Nie, R.; He, B.Y.; Yuan, P.; Zhang, L.; Li, G. Novel approach to and implementation of design and analysis of armored face conveyor power train. Sci. China Technol. Sci. 2015, 58, 2153–2168. [Google Scholar] [CrossRef]
- Yu, Y.D. Calculation of additional resistance of curved conveyor chain of scraper conveyor. J. Hunan Univ. Sci. Technol. 1995, 2, 38–42. [Google Scholar]
- Euler, L. Leonhard Euler and the Koenigsberg Bridges. Sci. Am. 1953, 189, 66–70. [Google Scholar] [CrossRef]
- Wang, C.J.; An, J.S.; Wu, X.G.; Liu, D.Y.; Zheng, Y.Z. Research and Application of Tighting Chain Device for 40T Scraper Conveyor. Colliery Mech. Electron. Technol. 2013, 767, 141–147. [Google Scholar]
- Xie, J.C.; Yang, Z.J.; Wang, X.W.; Wang, S.P.; Zhang, Q. Cooperative solving method of chute postures in the bending section of a scraper conveyor. Adv. Mech. Eng. 2018, 10, 1687814018767684. [Google Scholar] [CrossRef]
- Liao, H.Q.; Qiu, Y.; Yang, X. A Study of Weight Coefficient Method Based on AHP. Mech. Eng. 2012, 6, 22–25. [Google Scholar]
- Goyal, S.; Patterh, M.S. Modified Bat Algorithm for Localization of Wireless Sensor Network. Wirel. Pers. Commun. 2016, 86, 657–670. [Google Scholar] [CrossRef]
- Wang, C.F.; Song, W.X.; Liu, L.X. An adaptive bat algorithm with memory for global optimization. IAENG Int. J. Comput. Sci. 2018, 45, 320–327. [Google Scholar]
- Wang, Y.P. Research on Key Technology of Scraper Conveyor and Shearer Coordinated Speed Control. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).