1. Introduction
A horizontal Christmas tree wellhead connector links the Christmas tree body to the subsea wellhead. Its working performance directly affects the stability and reliability of a subsea production system [
1]. Sealing performance is the most important index for evaluating a connector’s working capability, and attempts to improve the connector’s sealing performance are underway. Research is currently focused primarily on improving the seal’s form and optimizing its structural parameters. To address seal form improvement, Peng et al. [
2] designed a double sealing structure comprised of a lens gasket and an O seal ring. When applied in deepwater pipelines, the sealing structure had a certain temperature compensation capability, and the axial pretension force on the collar’s flange was also reduced, indicating an improvement in the sealing performance of the subsea connector. Wang et al. [
3] designed a collect connector that was applied in the end of the subsea pipeline. Testing results showed that the highest sealing strength of the connector is 65 MPa. With respect to sealing structure parameter optimization, to improve the sealing performance of a novel subsea pipeline connector, Wei et al. [
4] established a multiobjective connector optimization model focused on minimum plastic strain and contact pressure variance. In this model, the radial basis function method was used to construct the objective functions. The model optimization significantly improved the connector’s sealing performance. Yun et al. [
5], considering the lens gasket of a collect connector of an object, identified the gasket’s spherical radius and flange taper as two main parameters affecting sealing performance after the relationships between the contact performance and the compacting force were revealed. After establishing the sealing structure of the optimization model, an optimized structure of the connector was obtained, taking the optimization objective as the minimum compacting force. Wang and Wei [
6] analyzed the sealing mechanism of a deepwater pipeline connector. In their study, the authors used the contact pressure and its variance on the primary and secondary sealing surfaces as the optimization objectives to obtain an optimized connector sealing structure after the multiobjective optimization model was established.
Previous research following different approaches has resulted in improved connector sealing performance mainly via improving the seal’s form or optimizing the sealing structure. However, in all approaches, the working load was regarded as a stable value, whereas a connector’s actual working load is a random variable that fluctuates with the well’s production pressure. Studies have shown that it is easier for the sealing structure to fail under a random working load condition [
7], indicating that the obtained optimized sealing structure is not optimum if the randomness of the working load is not considered. Meanwhile, time consumption remains a problem during sealing structure optimization, which affects a subsea connector’s optimization efficiency. A complete sealing structure’s optimization process for a subsea connector requires 500 h, even though multidisciplinary virtual simulation methods are used [
5]. Therefore, optimizing the sealing structure while taking into consideration the randomness of the working load is necessary to further improve the connector’s sealing performance. In this context, new optimization algorithms are required for improving the optimization efficiency of a subsea connector.
Modern intelligent algorithms are becoming popular optimization approaches for their global search abilities and relatively high solution speed. For example, in the field of structural optimization, modern intelligent algorithms are often combined with surrogate models for engineering optimization problems with a high computational cost. Atthaphon et al. [
8,
9] proposed a multiobjective optimization method, combining the efficient global optimization (EGO) and multifidelity hybrid surrogate models, for optimizing helicopter blades. The study showed that both the computation cost and optimization accuracy were improved. More specifically, that the optimization approach based on the Kriging surrogate model and genetic algorithm is suited for complex engineering optimization problems, particularly those with strong nonlinearity. For example, in order to improve the riding quality of a rail vehicle, Yang [
10] and Zeng [
11] applied this approach to optimize rail vehicle suspension parameters, which solved the problem of low optimization efficiency. Furthermore, Han et al. [
12] employed this approach for airfoil structure optimization, aiming to obtain better aerocraft aerodynamic performance, while taking into consideration the strong nonlinearity during aerodynamic analysis. Considering the time consumption and strong nonlinearity performance of an automobile’s collision deformation analysis, this optimization approach has been also used to optimize the front structure for an automobile [
13]. These data indicate that the optimization approach based on the Kriging surrogate model and genetic algorithm is an effective method for complex engineering optimization with a high computational cost and strong nonlinearity, which could also be introduced to VX gasket sealing structure optimization.
In this paper, we intended to present a multiobjective optimization approach for the VX gasket structure based on the Kriging surrogate model-NSGA-II algorithm. We also considered the randomness of the working load, in which the Kriging surrogate models of the sealing performance are constructed to accelerate the optimization efficiency. A random finite element (R-FE) model of the subsea connector was established to account for the randomness of the working load during the responses calculation of the samples for the Kriging surrogate models. In addition, the second generation of the non-dominated sorting genetic algorithm (NSGA-II) was used to determine the optimum solution for the VX gasket structure.
2. Problem Description
The VX gasket is an important part of the wellhead connector, which seals the gap between the Christmas tree body and wellhead. It prevents leakage of the high-pressure medium in the wellhead, and prevents seawater entering the pipeline. The concrete structure of a subsea Christmas tree wellhead connector is presented in
Figure 1.
During setup, the VX gasket and sealing groove formed by the Christmas tree body and wellhead are connected under an interference fit to produce radial deformation, which can enforce the gasket sticks onto the sealing groove, thereby forming an effective seal interface [
7]. During the working process, the high-pressure medium with random pressure value fluctuations acts on the gasket to produce a radial force. The corresponding compacting force exerted onto the sealing surface is further increased, the plastic deformation appears in the gasket, and a type of self-tightening seal structure is ultimately formed [
14].
As shown in
Figure 2, the VX gasket taper α and the interface width
b are two main structure parameters that affect the sealing performance of a VX gasket [
15,
16]. The maximum value and distribution uniformity of contact stress are two important indices for evaluating a gasket’s sealing performance [
17,
18]. We, therefore, selected the sealing surface angle α and the sealing surface width
b as the optimization design variables. To obtain a large enough sample to cover all of the optimal structure parameters, upper and lower bounds were determined for 50% fluctuations above and below the initial value of the design variables. The maximum value of contact stress
σm and the contact stress variance
S2 were used to evaluate sealing performance. The corresponding calculation formulas for
σm and
S2 are presented in Equations (1) and (2).
where
σi is the contact stress value of the
i-th node in the contact area of the gasket,
is the mean value of the sum of all the nodal contact stress values in the contact area, and
n is the number of the nodes in the contact line.
The working process of the VX gasket contains two phases: pre-tightening and working pressure acting. In the pre-tightening phase, a preload acts on the gasket to produce a radial force, and the initial seal is formed. In the working pressure acting phase, the high-pressure medium enforces the gasket sticks on the sealing groove, and the contact force between sealing interfaces increase. Production complexity in the well leads to random fluctuations in the working load, which lead to sealing performance reductions. Ultimately, the designed solution is not optimum if the randomness of the working load is not considered during VX gasket structure optimization [
19]. Therefore, working load randomness should be considered during the VX gasket structure’s design optimization.
Based on the descriptions above, this paper aims to obtain the optimal design variables
α and
b to guarantee that the subsea connector has the best sealing performance, i.e., the maximum value of
σm and the minimum value of
S2. The randomness of the working load should be considered in the optimization process. The problem could be described in Equation (3) as follows:
Optimization efficiency is relatively low due to the high computation cost during sealing performance index simulation using traditional methods, such as the finite element (FE) model. Therefore, improving the optimization speed is another target of the new optimization algorithm presented in this paper.
3. Optimization Based on the Kriging Surrogate Model-NSGA-II Algorithm
The NSGA-II algorithm [
20] is a very popular choice for multiobjective optimization problems, which we used to identify the VX gasket’s optimum structure. In order to improve the gasket structure’s optimization efficiency, we predicted the sealing performance indices using the Kriging surrogate model, as the structure parameters were different. In addition, a random load model based on the Gaussian distribution function was constructed to simulate the randomness of the working load fluctuation. These methods were combined to construct an optimization algorithm based on the Kriging surrogate model [
21] and NSGA-II. The concrete flowchart of the algorithm is illustrated in
Figure 3.
Step 1: Establishing the Random Working Load Model Based on the Gaussian Distribution Function
In order to improve the optimal design solution, we regarded the working load
P as a random variable, obeying the Gaussian distribution function [
14], where the mean value is
μ and the coefficient of variation is
cv [
22]. The corresponding upper and lower bounds were
μ − 3 ×
cv and
μ + 3 ×
cv based on the 3σ-rule [
23]. The random load is shown in Equation (4).
where
P is the random variable: working load; and
p is concrete value of the working load.
Step 2: Constructing a Random Finite Element (R-FE) Model of the VX Gasket
Compared to the simple traditional FE model, the main feature of the R-FE model is that the randomness of the working load is considered during simulation. To reduce computation costs, a two-dimensional axial symmetric model of the gasket was established to simulate the sealing performance, considering the symmetries of the geometric structure and the working load. In order to simulate the plastic deformation behavior of the VX gasket on the sealing surface, the elastic–plastic constitutive equation was applied during the modeling of the R-FE model. During the preload phase, the displacement in the bottom of the wellhead was fixed, and the axial preload
W on the Christmas tree body was calculated using Equation (5) [
24,
25]. In the working load phase, the random load calculated using Equation (4) was applied to the inner walls of the wellhead, the VX gasket, and the Christmas tree’s body. Then, the R-FE model of the VX gasket was established, illustrated in
Figure 4, using the Abaqus software.
where,
bm (mm) represents the effective contact width, which can be simulated using the R-FE model,
q0(MPa) is the contact press in the pre-tightening phase, the minimum value is the sealing pressure [
26],
ρ(°) is the frictional angle between the gasket and the sealing groove, and the value is 8.5° [
27].
Step 3: Construction of Kriging surrogate models of Sealing Performance Indices
(1) Basic form of the Kriging surrogate model
The Kriging surrogate model is a type of interpolation method. The interpolation result is a linear weighted sum of the training samples response value as shown in Equation (6).
where
yi is the
i-th response value of the
i-th training sample, and
x is the variables of the training sample. Therefore, the fitting result of any point in the design space can be calculated after the weighted coefficient is determined. To calculate the weighted coefficient
ω, the Gaussian stationary random process is introduced to fit the response surface function, and the concrete definition is presented in Equation (7).
where
β0 is the trend model, which represents the mathematical expectation of
Y(
x);
Z(·) is a stationary random process, with a mean value of 0; and variance is
σ2. There is a relative correlation of different random variables, which can be calculated using Equation (8).
where
R(
x,
x′) is the correlation model, which is used to describe the correlations between any two points
x and
x′, and it meets the assumption that the value is 1 when the distance of any two points is 0, while the value is 0 when the distance is ∞.
The optimum weighted coefficient ω ensures that the mean square error shown in Equation (9) is minimum, and the unbiased interpolation condition shown in Equation (10) should also be satisfied.
Then, the optimum weighted coefficient
ω can be calculated using the Lagrange multiplier method, and the Kriging model is constructed. The concrete derivation will not be presented in this paper, and the details can be found in the original paper published by Sacks et al. [
28].
(2) Kriging surrogate model of different sealing performance indices
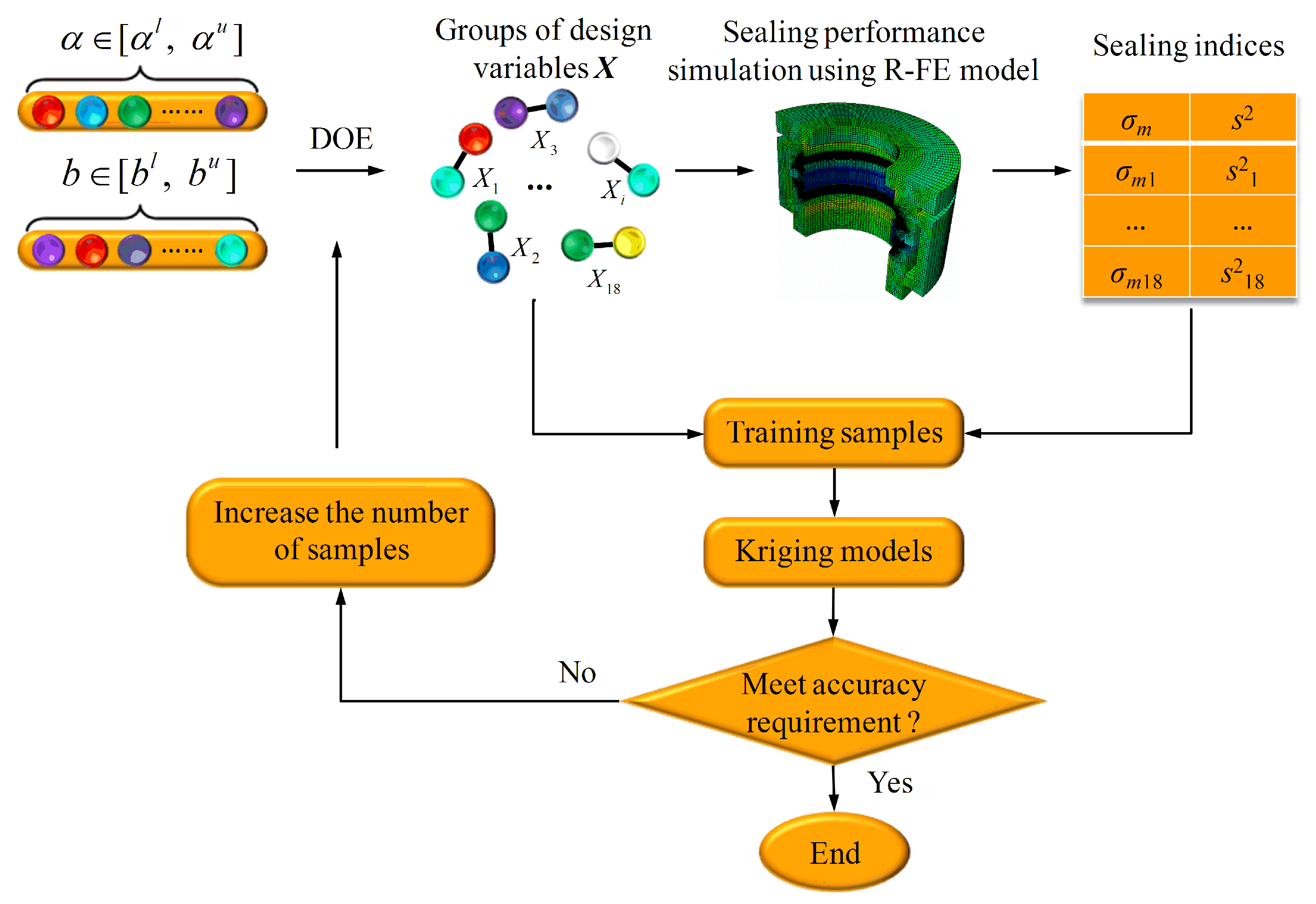
To establish Kriging models of gasket sealing performance, we took the gasket taper
α and interface width
b as design variables to design the experimental method; e.g., the Latin Hypercube sampling method [
29] was selected as the design of experiment (DOE) method to obtain different groups of sealing structure parameters, and the corresponding sealing performance indices
σm and
S2 were simulated using the established R-FE model proposed in Step 2. Then, the Kriging models of sealing performance were established, in which the training samples represented the obtained design variables and the corresponding sealing performance indices. The concrete construction is illustrated in
Figure 5, depicting the method where an increase in the number of samples is the key step to ensure the accuracy of the final constructed Kriging surrogate model. The mean square error based adaptive sampling method [
30] was applied to obtain the new samples, and to improve the accuracy of the Kriging surrogate model, considering the unique capability of error estimation in any unknown point for a Kriging model.
Step 4: Create a Random Initial Population
Individuals within the population represent values of the design variables and sealing performance indices. The initial population of size F0 was randomly designed.
Step 5: Compute the Sealing Performance Indices of Population Pt and Obtain a Progeny Population Qt
Use the constructed Kriging surrogate model to compute the values of the sealing performance index for the current population Pt. Non-dominated sorting and a crowding distance calculation were executed for the current parent population Pt, and the parent population was selected based on the calculated order and the crowding distance. A progeny population Qt was obtained through crossover and mutation operations.
Step 6: Compute the Values of the Sealing Performance Indices for All of the Individuals in a New Population Rt, and Obtain a New Parent Population Pt + 1
In order to guarantee the diversity and homogeneity of the Pareto solution, a new population Rt was obtained by merging Pt and Qt. The sealing performance indices values for all of the individuals in the population Rt were computed using the constructed Kriging surrogate model of sealing performance indices in Step 3. Non-dominated sorting and a crowding distance calculation were executed again to the new population Rt, and the new parent population was selected and regenerated based on the calculated results of the non-dominated sorting and crowding distance. A new progeny population Pt+1 was then obtained through crossover and mutation operations.
Step 7: Judging the Stop Condition
Taking the maximum number of evolutionary generations as the stop condition of the algorithm, a judgment on the stop condition was executed to indicate whether the whole evolutionary process was completed. The generation number was increased to 1 if the whole evolutionary process was not completed, then Steps 5 and 6 were executed again until the actual number of evolutionary generations met the default value. Otherwise, the elitist populations were used as an output representing the final optimal solution.
4. Case Study
In this section, we used a subsea Christmas tree wellhead connector matching the 20'' casing head as an example to validate the presented optimization approach. The concrete initial structure parameters of the VX gasket are shown in
Table 1. The mean value of the oil–gas pressure of the subsea connector was 34.5 MPa, and the random model of the oil–gas pressure was established based on the method presented in Step 1, in which the relative parameters were:
μ = 34.5 and
cv = 0.05. Then, the concrete form was illustrated using Equation (11). Eventually, the random load model was loaded onto the connector’s inner surface, and the stress–strain curve of the VX gasket material illustrated in
Figure 6 was applied to simulate the plastic’s deformation behavior.
As mentioned in Step 3 of
Section 3, groups of design variables required selection using the experimental method design in modeling the Kriging model. The optimal Latin hypercube sampling method [
31] was used in this paper to sample the design variables. According to the determining method of the upper and lower bounds of the design variables in
Section 2, the corresponding parameters were:
αl = 11.5°,
αu = 34.5°,
bl = 15 mm, and
bu = 45 mm, separately. The sampling ranges of the design variables are listed in
Table 2.
In order to guarantee the fitting accuracy of a Kriging model, an appropriate number of training samples should be determined. In general, training samples should be 3 times the number of a quadratic polynomial coefficient
k, where
k = (
n + 1)(
n + 2)/2, and
n is the number of design variables [
32]. As the number of structure parameters in this case is 2, the number of training samples is set to 18. Therefore, 18 groups of structure parameters were selected using the optimal Latin hypercube method, and the corresponding values of the maximum contact stress
σm and contact stress variance
S2 were simulated using the R-FE model proposed in Step 3 of
Section 3. Then, the training sample, provided in
Table 3, was formed by combining 18 groups of maximum contact stress
σm and contact stress variance
S2 with the corresponding design variables.
The sealing performance Kriging models of the VX gasket were established based on the training sample provided in
Table 2, using the construction illustrated in
Figure 5. The contours of the sealing performance Kriging models are shown in
Figure 7.
To test the fitting error of the established sealing performance Kriging models, the
R square coefficient as shown in Equation (10) [
10] was used to evaluate the fitting accuracy of the Kriging models.
where
yi is the obtained sealing performance index value using the R-FE model, and
is the fitting values using the established Kriging models. In order to achieve the aim of unbiased estimation, the
R square value should be kept at a maximum; however, its value should be smaller than 1. Nine groups of sealing performance indices were selected randomly according to the comparison from
Table 2. Then, corresponding sealing performance indices values
were obtained after nine groups of design variables were substituted to the Kriging models of sealing performance. The
R square value of the
σm and the
S2 Kriging models were 0.963 and 0.945, calculated in Equation (10), respectively. These results indicate that the fitting accuracy of the Kriging models is suitably high, and that the models can be used to fit the sealing performance indices of the VX gasket.
A multiobjective optimization model of the VX gasket is proposed in Equation (11), in which the design variables are structure parameters
α and
b, and the objective functions are the established Kriging models of
σm and
S2.
where,
is the
σm Kriging model,
is the
S2 Kriging model, and
αl,
αu,
bl, and
bu are the lower and upper bounds of the design variables shown in
Table 2.
The NSGA-II algorithm parameters are: the amount of initial population size F
0, 44; the number of evolutional generations
N, 50; the mutation ratio, 0.02; and the maximum crossover ratio
υ, 0.9. The Pareto front was finally obtained (
Figure 8). The data show that in the AB section of the Pareto front set, an increase in the maximum contact stress
σm did not cause an obvious rise in the contact stress variance
S2; in the CD section, great changes in
S2 occurred, although the
σm increase was small; therefore, all solutions both in the AB and CD sections were not the optimal results. The optimum solution can be selected in section BC by the designer, considering the values of
σm and
S2. The final selected optimum Pareto solution of the sealing performance indices were
σm = 544.7 MPa and
vσ = 107.02 × 10
2, and the corresponding optimum structure parameters were
α = 25.10° and
b = 29.11 mm, respectively. To check the convergence of the results searched by NSGA-II, the Hypervolume (HV) indicator [
9] was applied to show the convergence of the results every 100 interpolations. A schematic illustration of HV and the concrete tendency of HV values with interpolation increases are illustrated in
Figure 9a,b, separately. The HV value was kept at 0.85 after 1500 interpolations, which meant that the optimization results searched by NSGA-II converged after 1500 interpolations.
To verify the effectiveness of the optimization results above, the sealing performance indices were simulated in the R-FE model, in which the values of the design variables were the obtained optimum structure parameters. Then, the contact stress contours and contact stress values distributed in the contact interface were obtained (
Figure 10 and
Figure 11, respectively).
Table 3 provides a comparison of the sealing performance indices and the structure parameters before and after optimization.
Based on the analysis shown in
Table 4, the value of
σm increased by 16.79% and the value of
S2 declined by 18.75%, indicating that the sealing performance improved significantly compared to the initial version after VX gasket optimization.
To demonstrate the advantages of optimization speed in the presented method compared to traditional FE methods, the time required by these two methods was quantified. The time required to simulate the sealing performance indices once was 1.5 h using the traditional FE method. Thus, the total time required to complete the whole optimization process was 3300 h when the optimization algorithm parameters were similar to those followed in the current study (the initial population size F0 was 44; the number of evolutional generations N was 50). However, the corresponding time consumption was only 30 h, because the Kriging surrogate model was applied to predict the corresponding sealing performance indices, and it only required 18 simulations to construct the Kriging surrogate model using the time-consuming traditional FE method. This means that the optimization speed of the presented method was enhanced by 99% compared to the traditional FE method.
In order to further verify the sealing performance of the optimum structure, the subsea connector engineering prototype was constructed to test the sealing performance of the VX gasket with the optimum structure. The concrete test scheme is illustrated in
Figure 12. The working medium, a 90% ethylene glycol/water (v/v) mixture, was injected into the pipeline of the connector using the intelligent pressure testing system, and guaranteeing that the initial pressure of the working medium in the pipeline was 35 MPa. The working medium pressure was then measured every 0.5 h during the whole test process (5 h) using the automatic pressure data acquisition system. Pressure curves were then obtained using statistical methods. On this basis, the VX gasket’s sealing performances before and after optimization were tested using this test scheme. The change trend of the inner pressure of the connector is presented in
Figure 13.
The analysis in
Figure 13a shows that the inner pressure of the connector continues to decline as the testing time extends until 4.5 h, after which it becomes steady. The final pressure values of the initial and optimal VX gasket were 34.35 MPa and 34.59 MPa, separately. In
Figure 13b, the decrease trends of the initial and optimal VX gaskets were almost consistent until 0.5 h. However, the decreasing rate of the initial VX gasket was higher compared to the optimal condition, which finally stabilized at 1.85% after 5 hours. Otherwise, the final decrease percentage was 1.17% after 5 h. The test results indicate that the connector with the optimal VX gasket has better sealing performance, meaning that the proposed optimization approach is effective.
5. Conclusions
In this paper, we present a VX gasket optimization approach for subsea connectors based on the Kriging surrogate-NSGA-II algorithm, while taking into consideration the load randomness. The effectiveness of this approach is verified by a specific engineering case. The final conclusions are as follows:
(1) To simulate the actual condition of the wellhead connector more accurately, a random working load model of the VX gasket is simulated based on the normal distribution function. An R-FE model of the gasket sealing structure is constructed to simulate and extract the sealing performance indices in different structure parameters considering the randomness of the working load.
(2) An optimization approach of the VX gasket for subsea connectors based on the Kriging surrogate-NSGA-II algorithm is presented, in which sealing performance Kriging surrogate models are constructed to improve the calculation efficiency of the sealing performance values of the initial populations; and the Pareto solution of structure parameters is determined using the NSGA-II algorithm.
(3) A specific engineering case is used to verify the effectiveness of the proposed approach. The test results indicate that the sealing performance of the connector is improved significantly after optimization, and the optimization speed is enhanced 99% compared to traditional, time-consuming FE methods.