Tensor-Based Algorithms for Image Classification
Abstract
1. Introduction
- Extension of MANDy: We show that the efficacy of the pseudoinverse computation in the tensor train format can be improved by eliminating the need to left- and right-orthonormalize the tensor. Although this is a straightforward modification of the original algorithm, it enables us to consider large data sets. The resulting method is closely related to kernel ridge regression.
- Alternating ridge regression: We introduce a modified TT representation of transformed data tensors for the development of a tensor-based regression technique which computes low-rank representations of coefficient tensors. We show that it is possible to obtain results which are competitive with those computed by MANDy and, at the same time, reduce the computational costs and the memory consumption significantly.
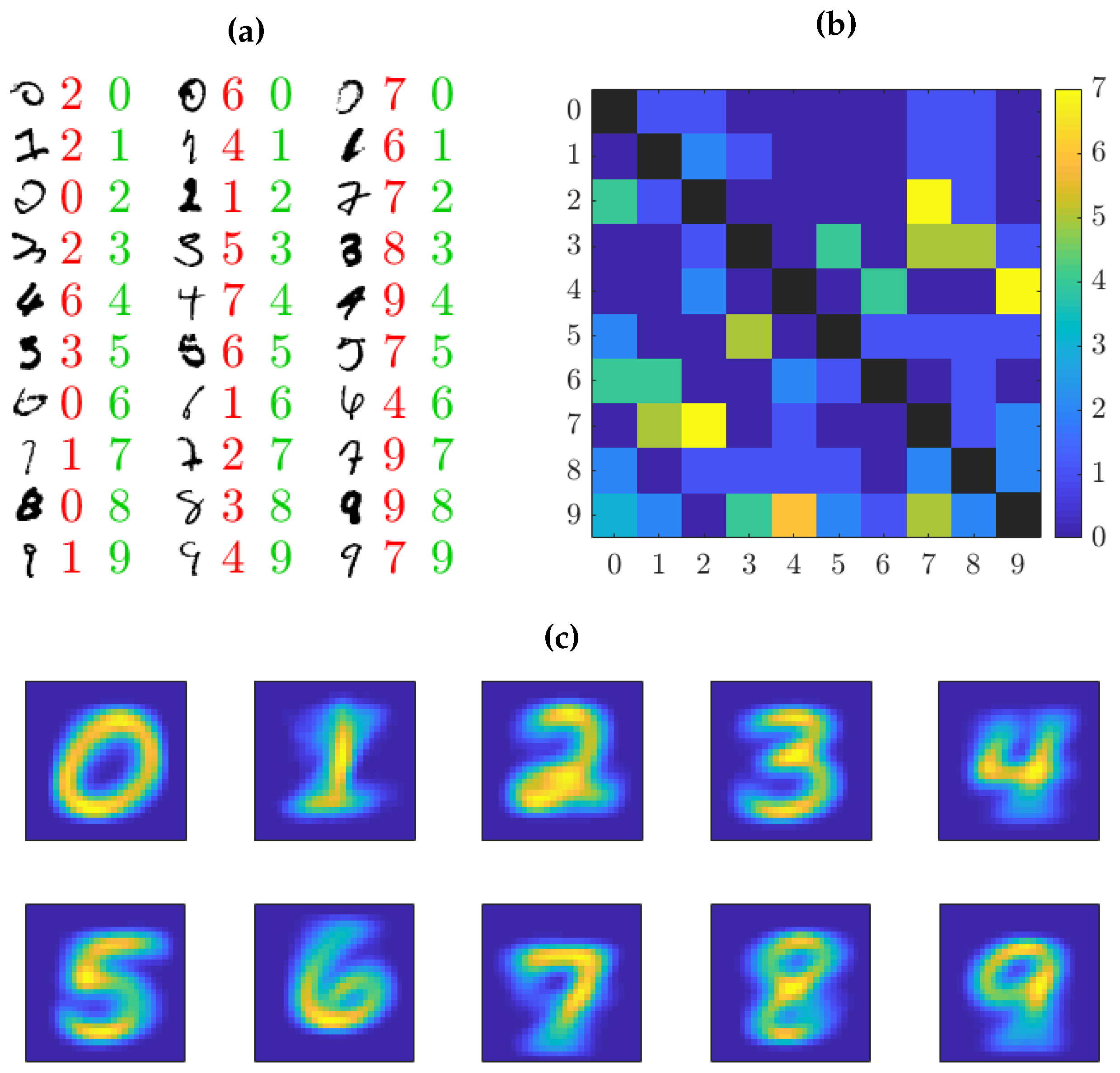
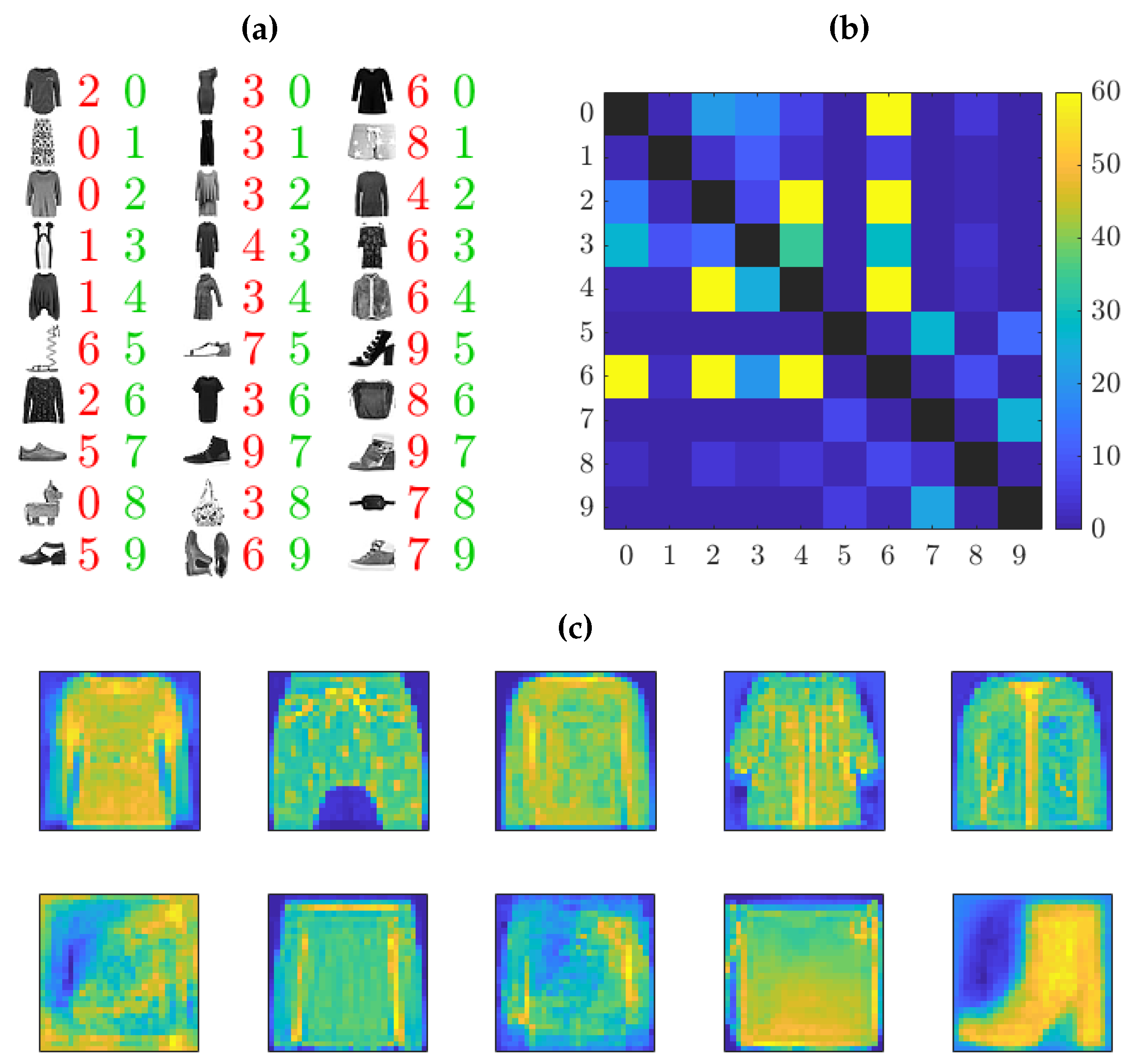
- Classification of image data: Although originally designed for system identification, we apply these methods to classification problems and visualize the learned classifier, which allows us to interpret features detected in the images.
2. Prerequisites
2.1. MNIST and Fashion MNIST
2.2. SINDy
2.3. Tensor-Based Learning
2.3.1. Tensor Decompositions
2.3.2. MANDy
2.3.3. Supervised Learning with Tensor Networks
3. Tensor-Based Classification Algorithms
3.1. Basis Decomposition
3.2. Kernel-Based MANDy
| Algorithm 1 Kernel-based MANDy for classification. |
| Input: Training set X and label matrix Y, test set , basis functions. |
| Output: Label matrix . |
|
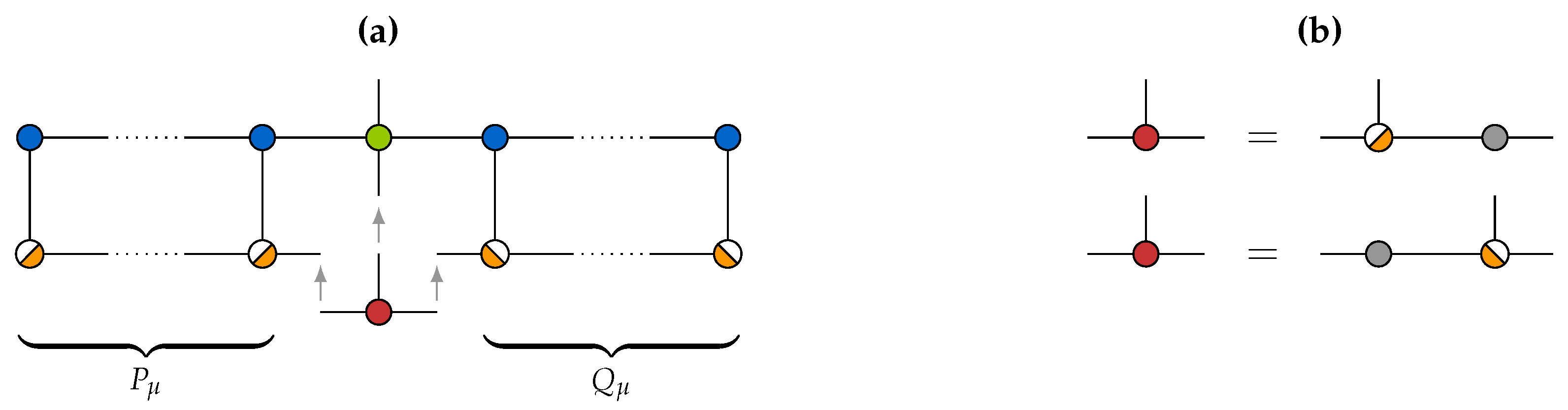
3.3. Alternating Ridge Regression
| Algorithm 2 Alternating ridge regression (ARR) for classification. | |
| Input: Training set X and label matrix Y, test set , basis functions, initial guesses. | |
| Output: Label matrix . | |
| (parallelizable) |
| |
| |
| |
| (first half sweep) |
| |
| |
| |
| |
| (second half sweep) |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
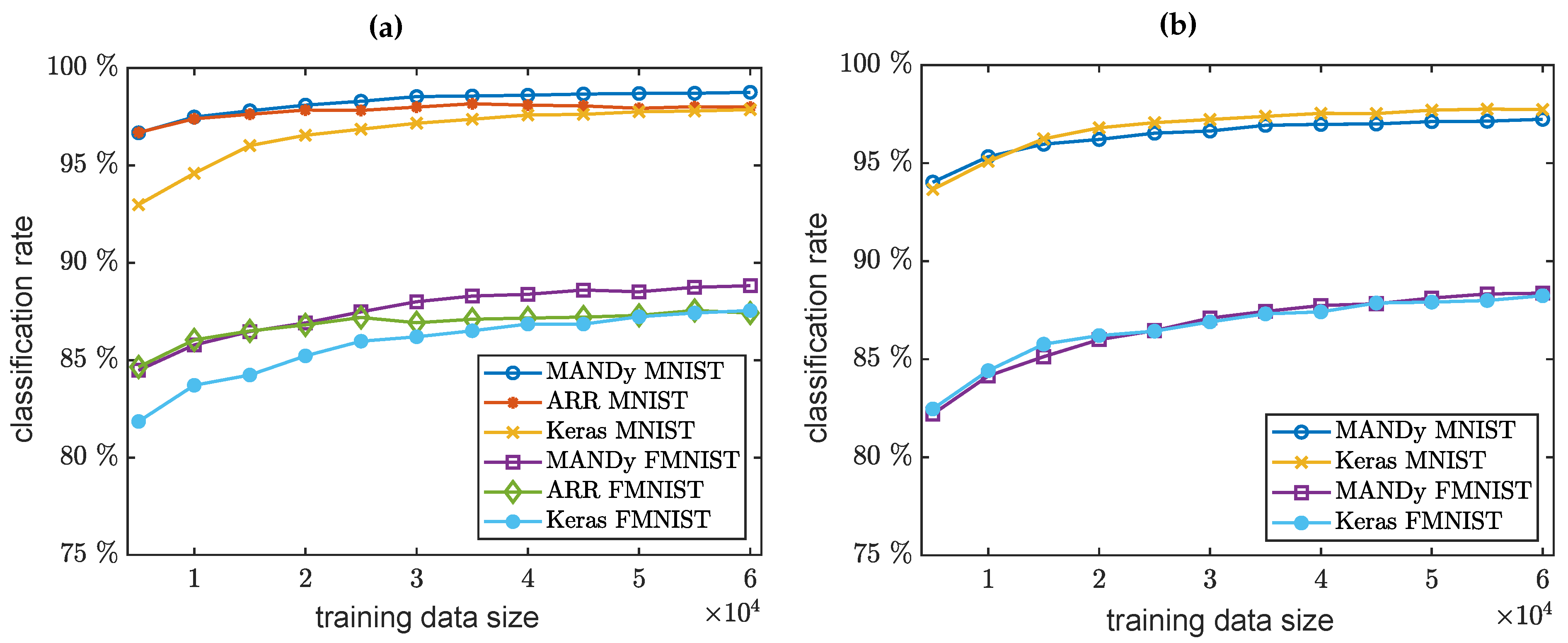
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Representation of Transformed Data Tensors
Appendix B. Interpretation of ARR as ALS Ridge Regression
References
- Beylkin, G.; Garcke, J.; Mohlenkamp, M.J. Multivariate Regression and Machine Learning with Sums of Separable Functions. SIAM J. Sci. Comput. 2009, 31, 1840–1857. [Google Scholar] [CrossRef]
- Novikov, A.; Podoprikhin, D.; Osokin, A.; Vetrov, D. Tensorizing Neural Networks. In Advances in Neural Information Processing Systems 28 (NIPS); Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 442–450. [Google Scholar]
- Cohen, N.; Sharir, O.; Shashua, A. On the expressive power of deep learning: A tensor analysis. In Proceedings of the 29th Annual Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; Feldman, V., Rakhlin, A., Shamir, O., Eds.; Proceedings of Machine Learning Research. Columbia University: New York, NY, USA, 2016; Volume 49, pp. 698–728. [Google Scholar]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- Stoudenmire, E.M.; Schwab, D.J. Supervised learning with tensor networks. In Advances in Neural Information Processing Systems 29 (NIPS); Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 4799–4807. [Google Scholar]
- Stoudenmire, E.M.; Schwab, D.J. Supervised learning with quantum-inspired tensor networks. arXiv 2016, arXiv:1605.05775. [Google Scholar]
- Stoudenmire, E.M. Learning relevant features of data with multi-scale tensor networks. Quantum Sci. Technol. 2018, 3, 034003. [Google Scholar] [CrossRef]
- Huggins, W.; Patil, P.; Mitchell, B.; Whaley, K.B.; Stoudenmire, E.M. Towards quantum machine learning with tensor networks. Quantum Sci. Technol. 2019, 4, 024001. [Google Scholar] [CrossRef]
- Roberts, C.; Milsted, A.; Ganahl, M.; Zalcman, A.; Fontaine, B.; Zou, Y.; Hidary, J.; Vidal, G.; Leichenauer, S. TensorNetwork: A library for physics and machine learning. arXiv 2019, arXiv:1905.01330. [Google Scholar]
- Efthymiou, S.; Hidary, J.; Leichenauer, S. TensorNetwork for Machine Learning. arXiv 2019, arXiv:1906.06329. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Gelß, P.; Klus, S.; Eisert, J.; Schütte, C. Multidimensional Approximation of Nonlinear Dynamical Systems. J. Comput. Nonlinear Dyn. 2019, 14, 061006. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Nüske, F.; Gelß, P.; Klus, S.; Clementi, C. Tensor-based EDMD for the Koopman analysis of high-dimensional systems. arXiv 2019, arXiv:1908.04741. [Google Scholar]
- Hansen, P.C. The truncated SVD as a method for regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 4th ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Oseledets, I.V. A New Tensor Decomposition. Dokl. Math. 2009, 80, 495–496. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-Train Decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Penrose, R. Applications of negative dimensional tensors. In Combinatorial Mathematics and Its Applications; Welsh, D.J.A., Ed.; Academic Press Inc.: Cambridge, MA, USA, 1971; pp. 221–244. [Google Scholar]
- Oseledets, I.V.; Tyrtyshnikov, E.E. Breaking the Curse of Dimensionality, Or How to Use SVD in Many Dimensions. SIAM J. Sci. Comput. 2009, 31, 3744–3759. [Google Scholar] [CrossRef]
- Klus, S.; Gelß, P.; Peitz, S.; Schütte, C. Tensor-based dynamic mode decomposition. Nonlinearity 2018, 31. [Google Scholar] [CrossRef]
- Gelß, P.; Matera, S.; Schütte, C. Solving the Master Equation Without Kinetic Monte Carlo. J. Comput. Phys. 2016, 314, 489–502. [Google Scholar] [CrossRef]
- Gelß, P.; Klus, S.; Matera, S.; Schütte, C. Nearest-neighbor interaction systems in the tensor-train format. J. Comput. Phys. 2017, 341, 140–162. [Google Scholar] [CrossRef]
- Holtz, S.; Rohwedder, T.; Schneider, R. The Alternating Linear Scheme for Tensor Optimization in the Tensor Train Format. SIAM J. Sci. Comput. 2012, 34, A683–A713. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Lewenstein, M.; Ran, S. Entanglement-guided architectures of machine learning by quantum tensor network. arXiv 2018, arXiv:1803.09111. [Google Scholar]
- Groetsch, C.W. Inverse Problems in the Mathematical Sciences; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1993. [Google Scholar] [CrossRef]
- Zhdanov, A.I. The method of augmented regularized normal equations. Comput. Math. Math. Phys. 2012, 52, 194–197. [Google Scholar] [CrossRef]
- Barata, J.C.A.; Hussein, M.S. The Moore–Penrose pseudoinverse: A tutorial review of the theory. Braz. J. Phys. 2012, 42, 146–165. [Google Scholar] [CrossRef]


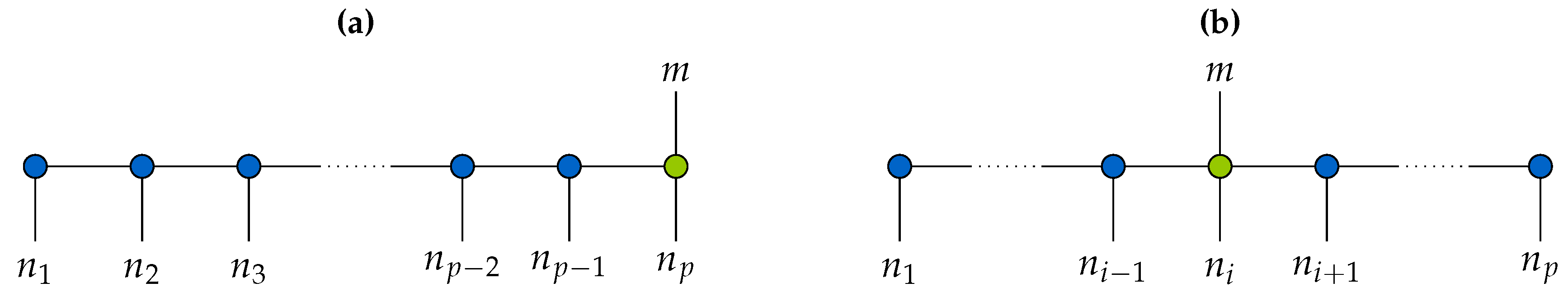
| Symbol | Description |
|---|---|
| data matrix in | |
| label matrix in | |
| mode dimensions of tensors | |
| ranks of tensor trains | |
| basis functions | |
| / | transformed data matrices/tensors |
| / | coefficient matrices/tensors |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klus, S.; Gelß, P. Tensor-Based Algorithms for Image Classification. Algorithms 2019, 12, 240. https://doi.org/10.3390/a12110240
Klus S, Gelß P. Tensor-Based Algorithms for Image Classification. Algorithms. 2019; 12(11):240. https://doi.org/10.3390/a12110240
Chicago/Turabian StyleKlus, Stefan, and Patrick Gelß. 2019. "Tensor-Based Algorithms for Image Classification" Algorithms 12, no. 11: 240. https://doi.org/10.3390/a12110240
APA StyleKlus, S., & Gelß, P. (2019). Tensor-Based Algorithms for Image Classification. Algorithms, 12(11), 240. https://doi.org/10.3390/a12110240




