A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions
Abstract
:1. Introduction
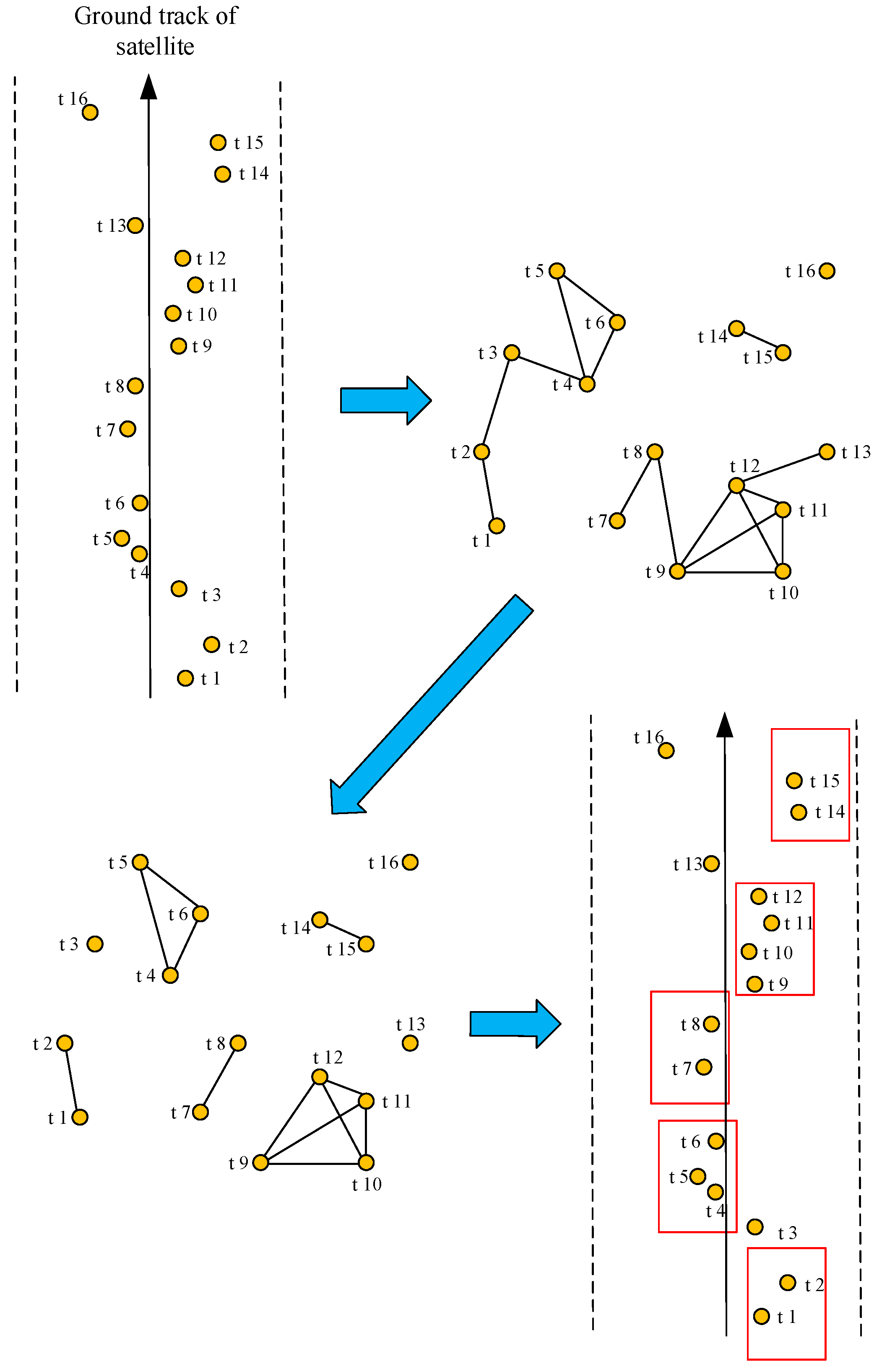
2. Review of the Improved Clustering Algorithm
- In the cluster graph, select the edge with the largest number of common neighbors in the edge set.
- If the edge is not unique, select the edge that needs to delete the least number of edges after merging.
- If the edge is still not unique, select two vertices with higher priority and smaller clustering task slew angle to form the edge.
- Combine the two vertices of the edge into a new virtual vertex and delete the edges associated with the merged vertex to create a new edge. Update the vertex and edge collections.
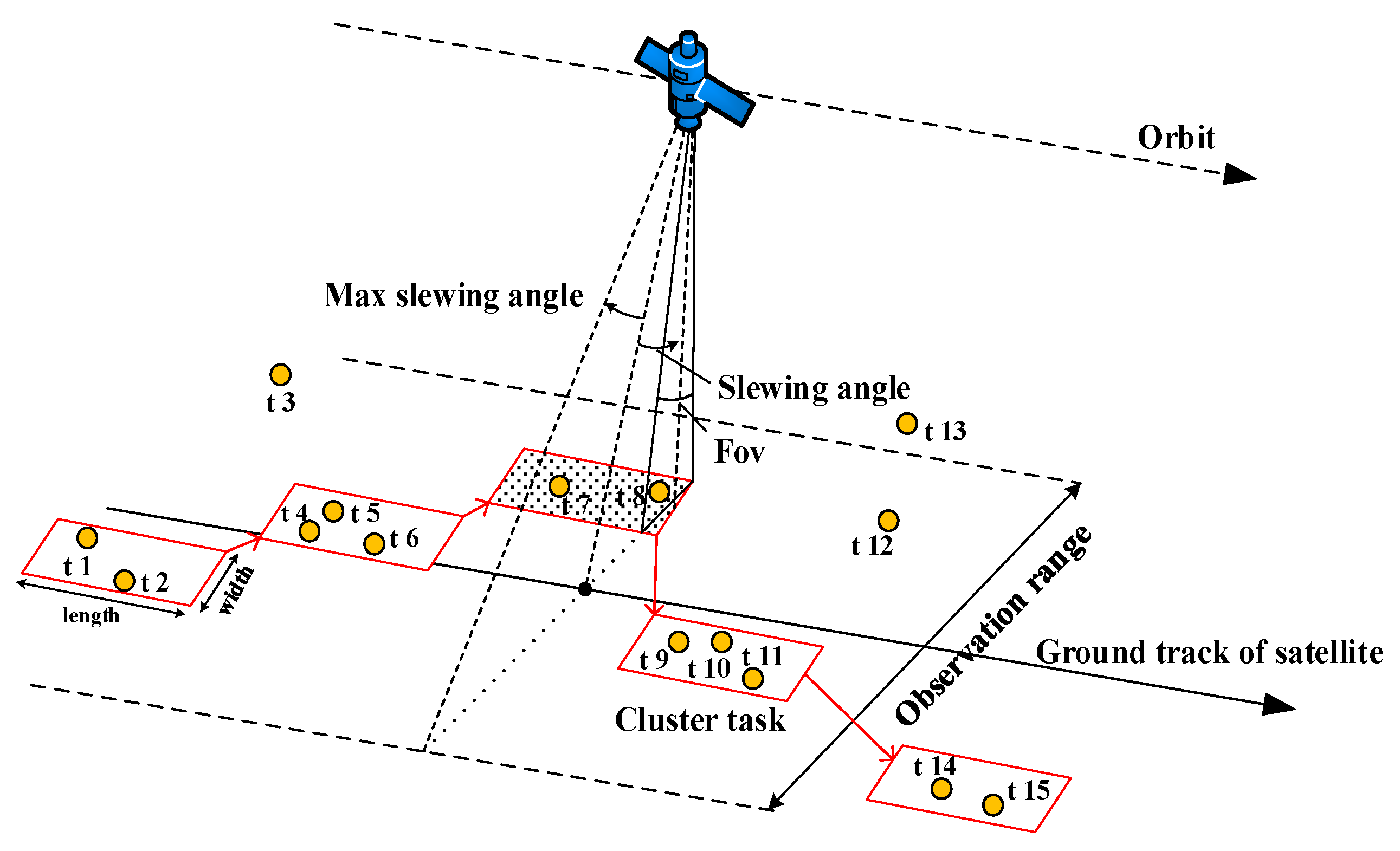
3. Task Planning Model and Solving Algorithm
3.1. Task Planning Model
3.1.1. Main Constraints of the Planning Model
3.1.2. Optimization Objective Function
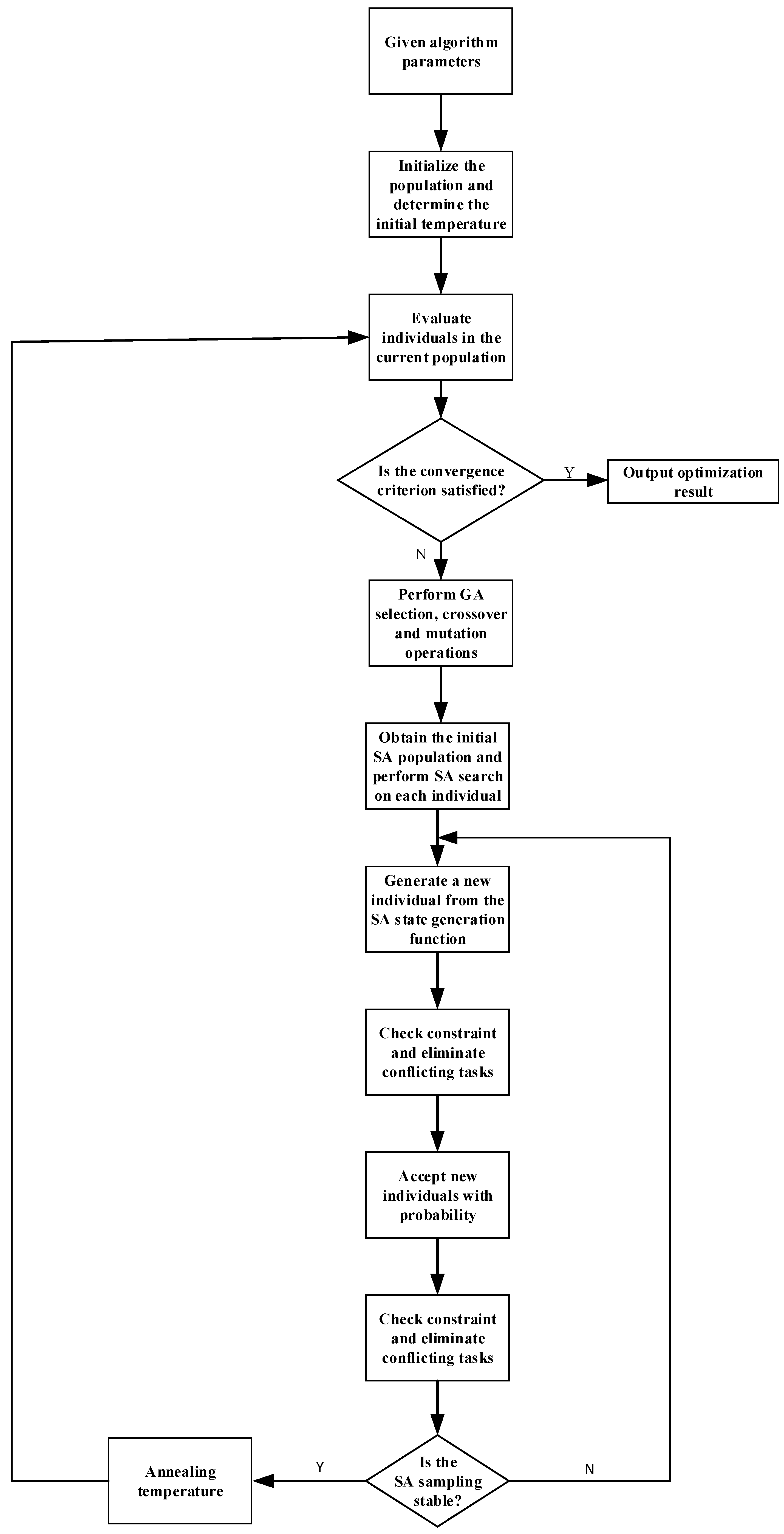
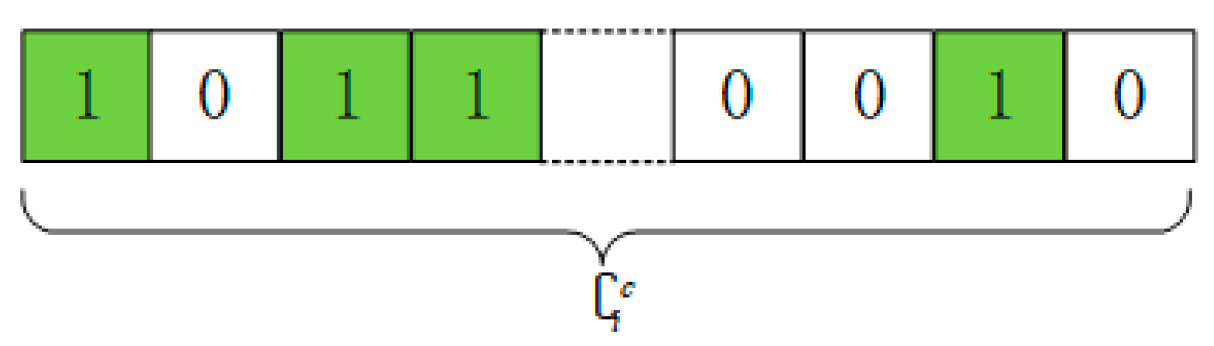
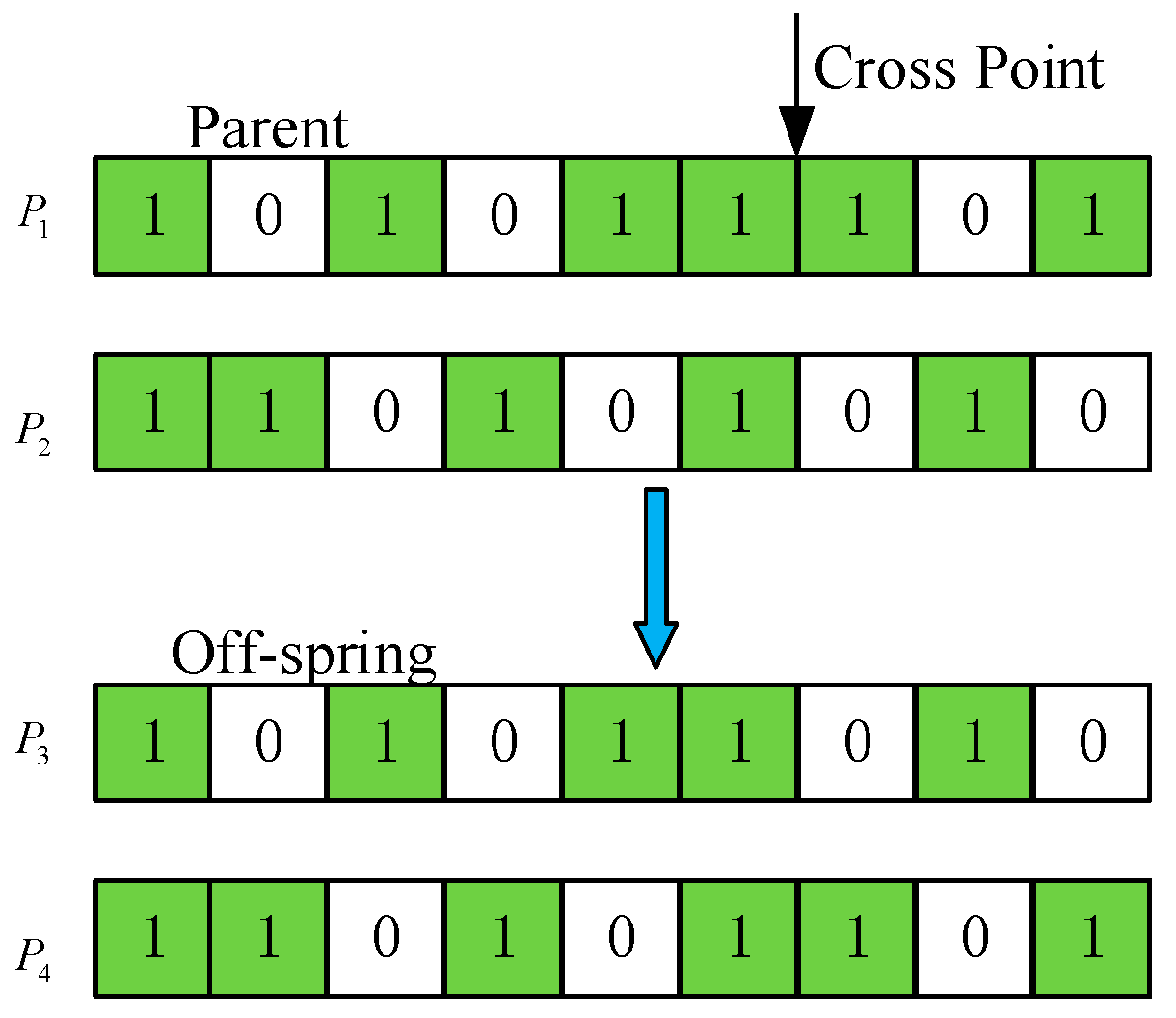
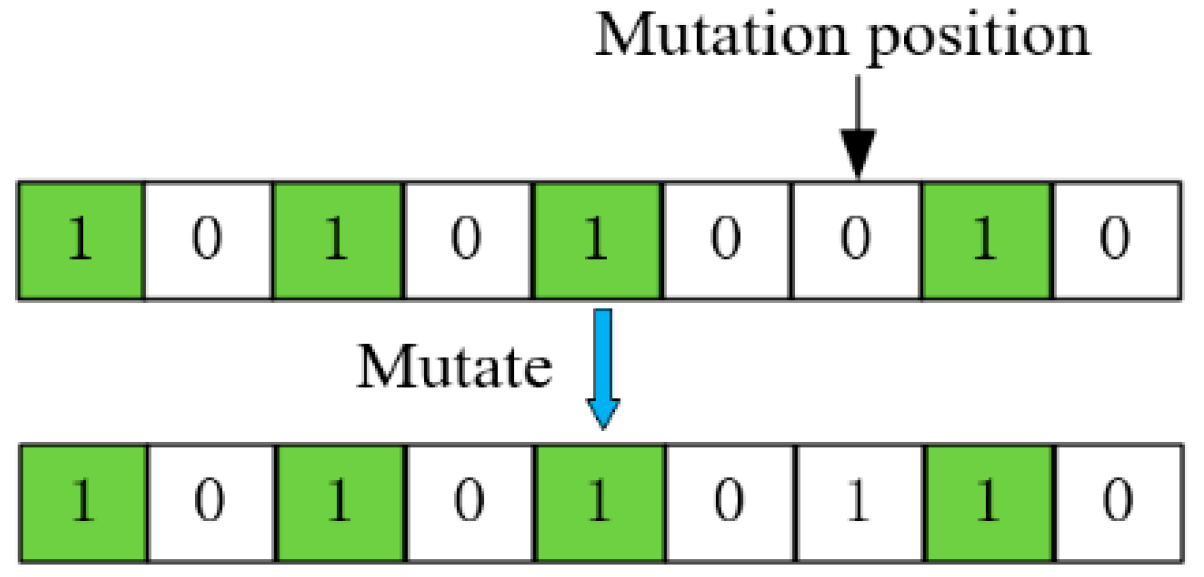
3.2. Optimization Solving Algorithm
4. Experimental Simulation
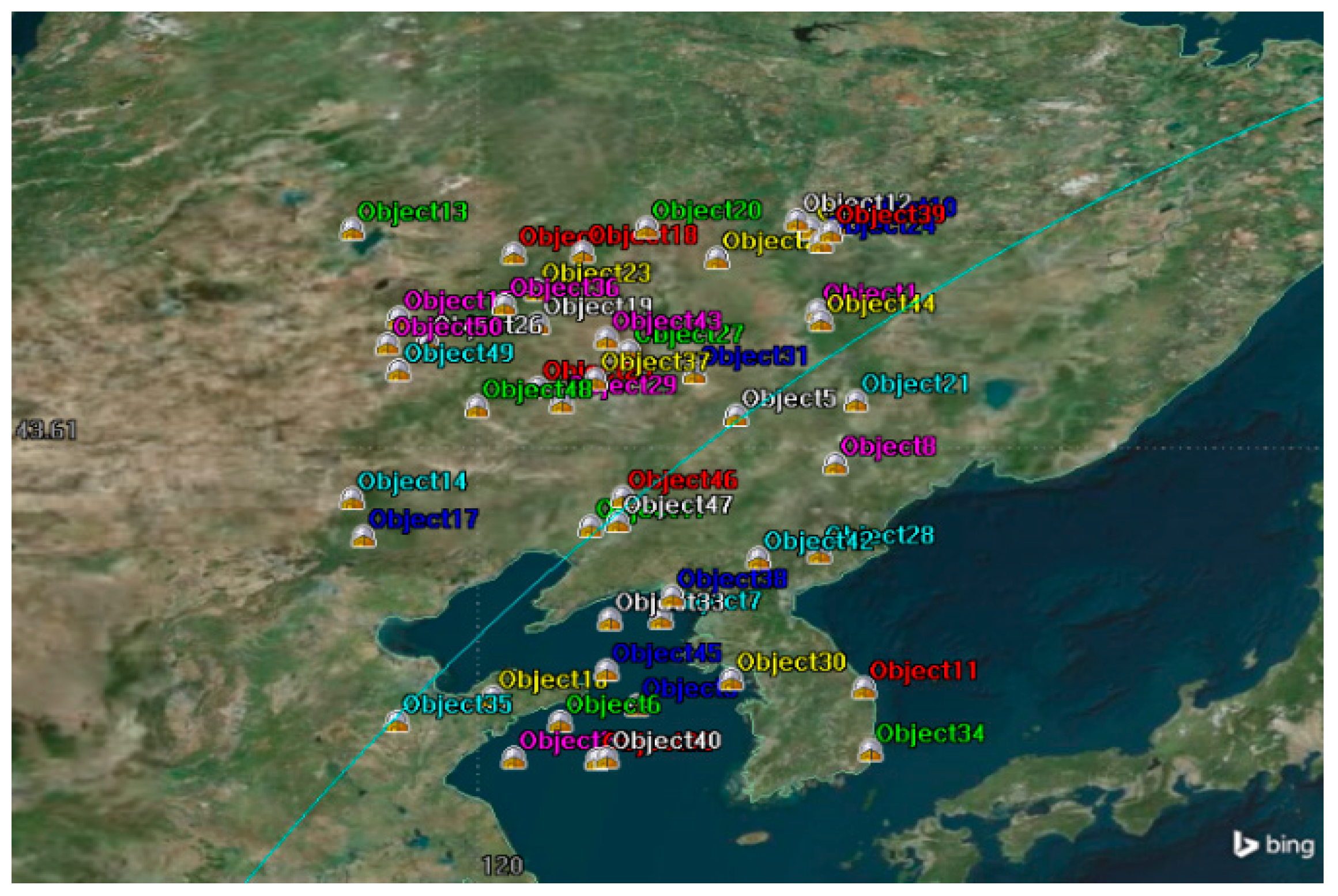
4.1. Simulation Condition
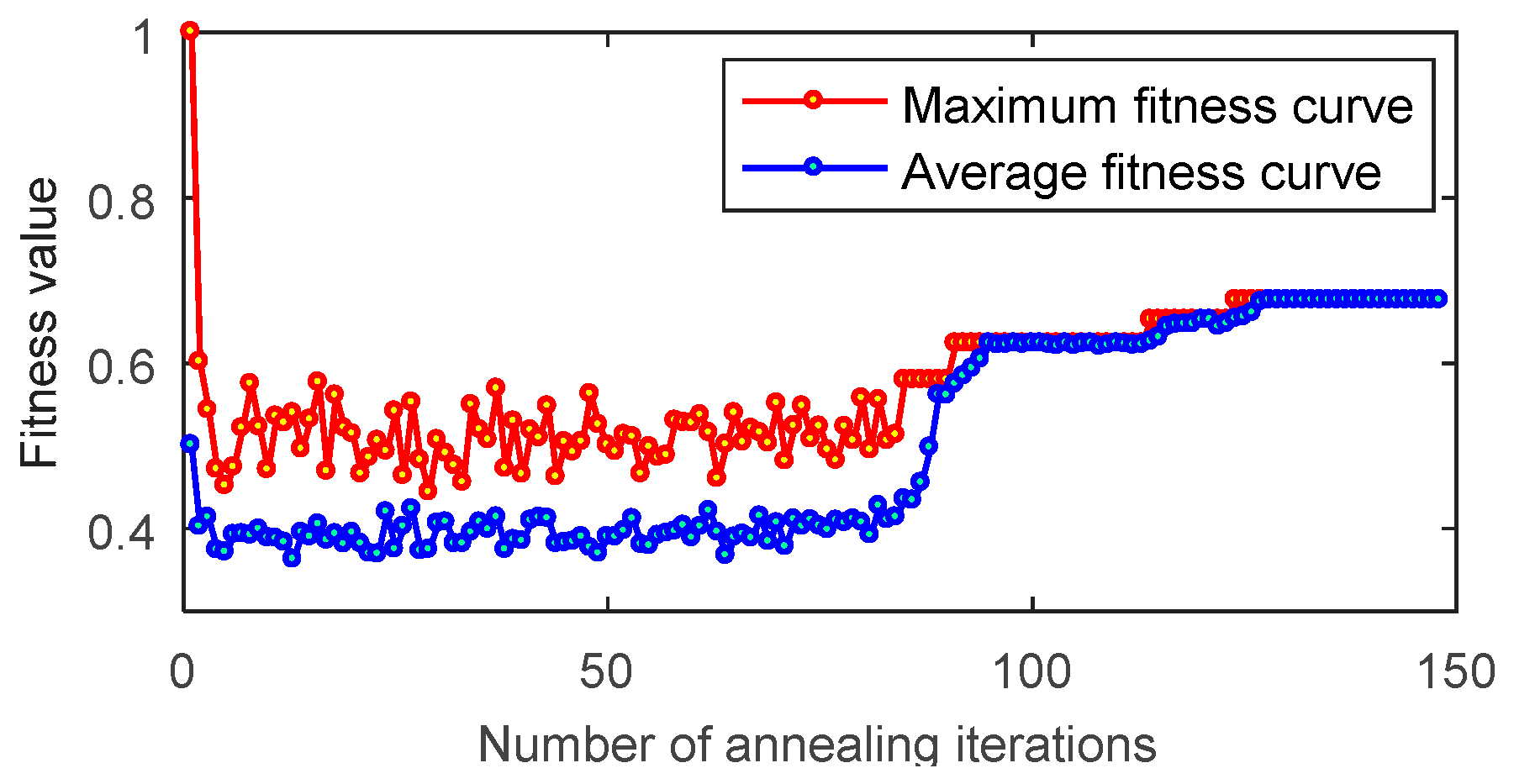
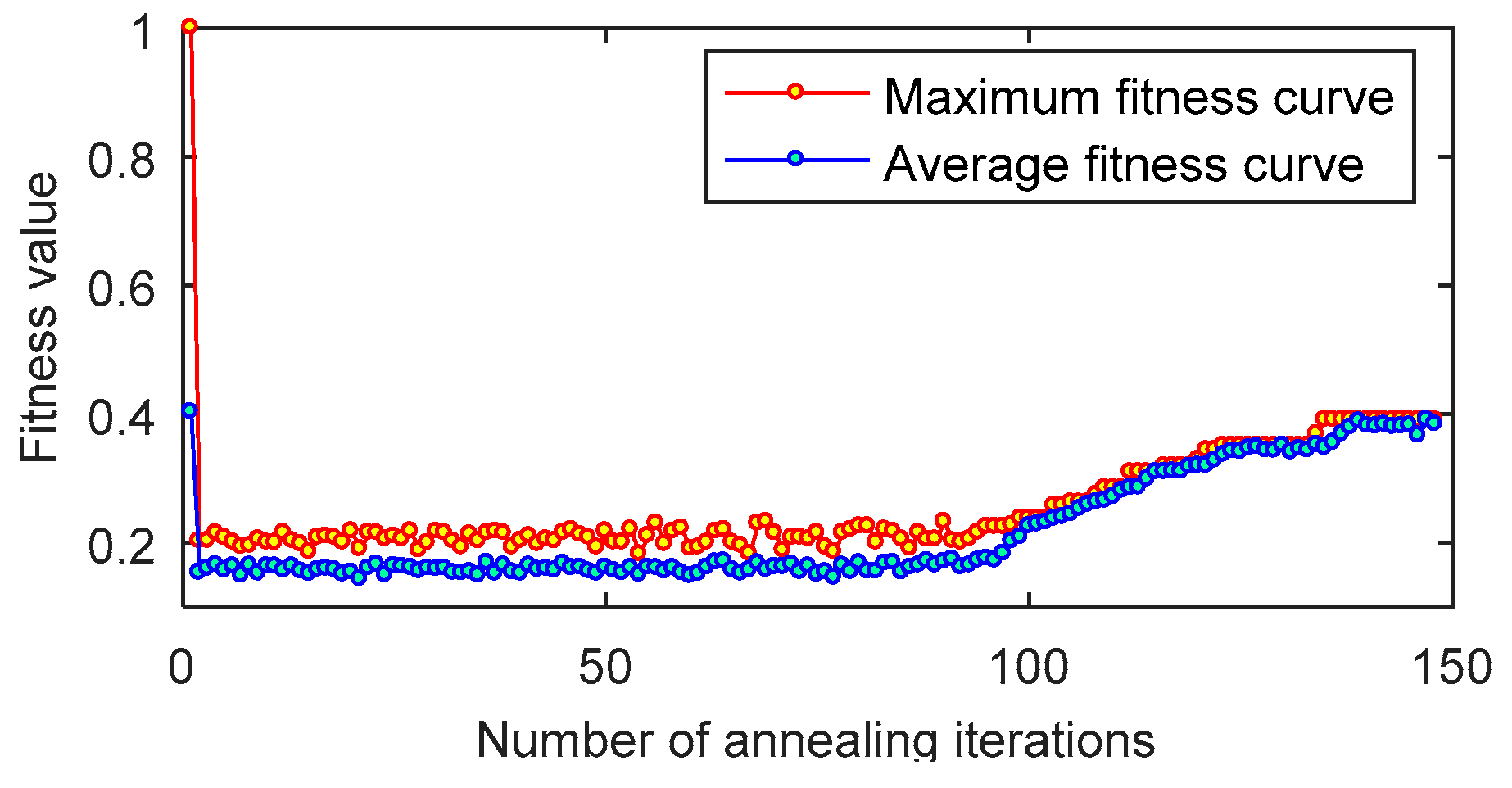
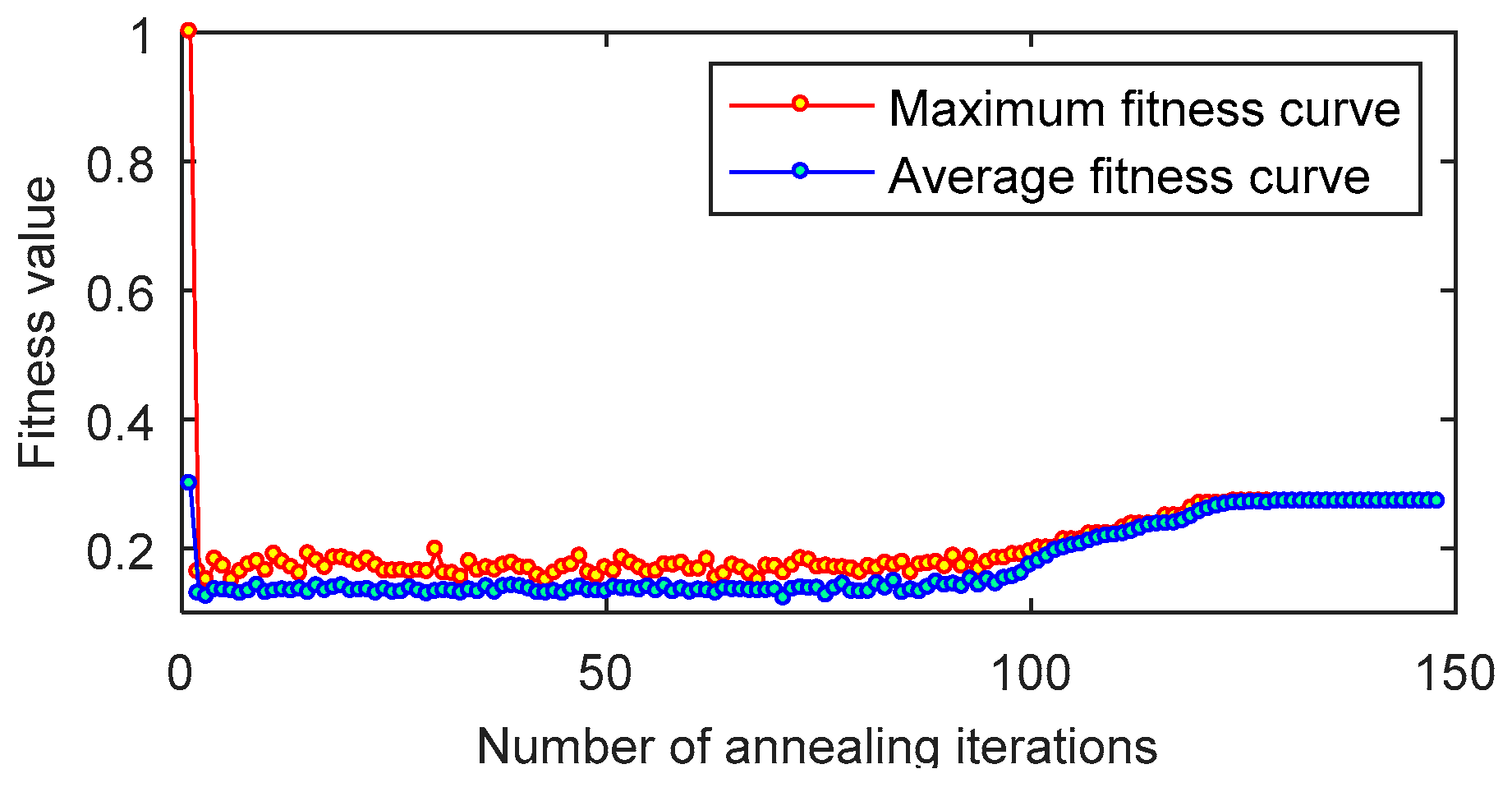
4.2. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Long, X.; Wu, S.; Cui, B.; Mu, Z.; Huang, Y.; Chu, S. Analysis of satellite observation task clustering based on the improved clique partition algorithm. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1314–1321. [Google Scholar]
- Wu, G.; Liu, J.; Ma, M.; Qiu, D. A two-phase scheduling method with the consideration of task clustering for earth observing satellites. Comput. Oper. Res. 2013, 40, 1884–1894. [Google Scholar] [CrossRef]
- Jaehn, F.; Pesch, E. New bounds and constraint propagation techniques for the clique partitioning problem. Discret. Appl. Math. 2013, 161, 2025–2037. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Pedrycz, W.; Li, H.; Wang, L. Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy. Comput. Ind. Eng. 2017, 113, 576–588. [Google Scholar] [CrossRef]
- Xu, Y.L.; Xu, P.D.; Wang, H.L.; Peng, Y.H. Clustering of Imaging Reconnaissance Tasks Based on Clique Partition. Oper. Res. Manag. Sci. 2010, 19, 143–149. [Google Scholar]
- Du, B.; Li, S. A new multi-satellite autonomous mission allocation and planning method. Acta Astronaut. 2018, 163, 287–298. [Google Scholar] [CrossRef]
- Tseng, C.J.; Siewiorek, D.P. Automated synthesis of data paths in digital systems. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1986, 5, 379–395. [Google Scholar] [CrossRef]
- Frank, J.; Jonsson, A.; Morris, R.; Smith, D.E.; Norvig, P. Planning and scheduling for fleets of earth observing satellites. In Proceedings of the Sixth International Symposium on Artificial Intelligence, Robotics, Automation and Space, Montreal, QC, Canada, 18–22 June 2001; p. 307. [Google Scholar]
- Globus, A.; Crawford, J.; Lohn, J.; Pryor, A. A Comparison of Techniques for Scheduling Earth-Observing Satellites. In Proceedings of the Conference on Nineteenth National Conference on Artificial Intelligence, San Jose, CA, USA, 25–29 July 2004. [Google Scholar]
- Li, Z.; Li, X. A multi-objective binary-encoding differential evolution algorithm for proactive scheduling of agile earth observation satellites. Adv. Space Rese. 2019, 63, 3258–3269. [Google Scholar] [CrossRef]
- Kim, H.; Chang, Y.K. Mission scheduling optimization of SAR satellite constellation for minimizing system response time. Aerosp. Sci. Technol. 2015, 40, 17–32. [Google Scholar] [CrossRef]
- Grasset-Bourdel, R.; Verfaillie, G.; Flipo, A. Planning and replanning for a constellation of agile Earth observation satellites. In Proceedings of the ICAPS-11 Workshop on Scheduling and Planning Applications (SPARK-11), Freiburg, Germany, 13 June 2011. [Google Scholar]
- Sarkheyli, A.; Vaghei, B.G.; Bagheri, A. New tabu search heuristic in scheduling earth observation satellites. In Proceedings of the 2010 2nd International Conference on Software Technology and Engineering, San Juan, Puerto Rico, 3–5 October 2010; pp. 199–203. [Google Scholar]
- Liu, S.; Chen, Y.; Xing, L.; Sun, K. Method of agile imaging satellites autonomous task planning. Comput. Integr. Manuf. Syst. 2016, 22, 928–934. [Google Scholar]
- Niu, X.; Tang, H.; Wu, L. Satellite scheduling of large areal tasks for rapid response to natural disaster using a multi-objective genetic algorithm. Int. J. Disaster Risk Reduct. 2018, 28, 813–825. [Google Scholar] [CrossRef]
- He, R.; Gao, P.; Bai, B.; Li, J.F.; Yao, F.; Xing, L.N. Models, algorithms and applications to the mission planning system of imaging satellites. Syst. Eng. Theory Pract. 2010, 31, 411–422. [Google Scholar]
- Xu, R.; Chen, H.; Liang, X.; Wang, H. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization. Expert Syst. Appl. 2016, 51, 195–206. [Google Scholar] [CrossRef]
- Li, W.; Gao, P.; Chen, Y.W.; Li, J.F. A Petri Net Model and Algorithm for Remotely Sensed Data Processing Task Scheduling Problem. J. Univ. Def. Technol. 2011, 33, 138–142. [Google Scholar]
- Jiang, W.; Pang, X. Collaborative Mission Planning for Networked Imaging Satellites; Harbin Institute of Technology Press: Harbin, China, 2016. [Google Scholar]
- Wang, L. Intelligent Optimization Algorithms with Applications; Tsinghua University Press: Beijing, China, 2001. [Google Scholar]
- Yu, H. The Improvement of Genetic Algorithm and It’s Application on Knapsack Problem. Master’s Thesis, Shandong Normal University, Jinan, China, 2009. [Google Scholar]
- Yu, H.; Wang, H.; Xu, X. A genetic algorithm with competitive selection between adjacent two generations and its applications to TSP. Inf. Control 2000, 29, 309–314. [Google Scholar]
- Bao, Z.; Yu, X. Intelligent Optimization Algorithm and Its MATLAB Example; Publishing House of Electronics Industry: Beijing, China, 2016. [Google Scholar]

| a (km) | e | i | Ω | ||
|---|---|---|---|---|---|
| 7000 | 0 | 60 | 285 | 0 | 0 |
| FOV (°) | ||
|---|---|---|
| 10 | 150 | ±40 |
| No. | Time Window Start (s) | Time Window End (s) | Slew Angle (°) | Priority | Observation Duration | No. | Time Window Start (s) | Time Window End (s) | Slew Angle (°) | Priority | Observation Duration |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 2 | 15 | 26 | 755.31 | 921.78 | -30.62 | 10 | 9 |
| 2 | 0 | 0 | 0 | 2 | 8 | 27 | 761.24 | 943.91 | 24.16 | 3 | 14 |
| 3 | 0 | 0 | 0 | 3 | 14 | 28 | 765.82 | 967.39 | 1.37 | 10 | 12 |
| 4 | 0 | 0 | 0 | 4 | 13 | 29 | 773.18 | 870.23 | 42.05 | 4 | 10 |
| 5 | 597.31 | 797.68 | -0.92 | 1 | 7 | 30 | 774.55 | 970.67 | 13.88 | 2 | 13 |
| 6 | 616.36 | 799.20 | -23.48 | 6 | 15 | 31 | 775.45 | 965.48 | -19.60 | 8 | 8 |
| 7 | 626.61 | 823.31 | -11.83 | 4 | 14 | 32 | 776.70 | 958.86 | 24.48 | 3 | 13 |
| 8 | 638.59 | 819.65 | -24.50 | 3 | 7 | 33 | 781.49 | 954.96 | 28.35 | 2 | 12 |
| 9 | 645.73 | 801.74 | -33.28 | 4 | 11 | 34 | 788.95 | 883.36 | 42.28 | 6 | 10 |
| 10 | 650.16 | 802.55 | -34.14 | 5 | 8 | 35 | 789.16 | 933.76 | 36.10 | 8 | 13 |
| 11 | 664.20 | 847.74 | -23.27 | 3 | 13 | 36 | 795.37 | 993.48 | -11.44 | 2 | 10 |
| 12 | 668.63 | 832.54 | -31.21 | 5 | 14 | 37 | 802.47 | 856.06 | 44.54 | 7 | 13 |
| 13 | 673.04 | 842.09 | 29.65 | 7 | 8 | 38 | 803.60 | 920.39 | 40.19 | 6 | 14 |
| 14 | 677.64 | 870.96 | -16.21 | 8 | 11 | 39 | 810.20 | 934.45 | 39.30 | 0 | 10 |
| 15 | 692.36 | 877.29 | -22.59 | 1 | 6 | 40 | 812.67 | 1012.95 | 7.53 | 1 | 10 |
| 16 | 692.96 | 844.41 | 34.53 | 8 | 14 | 41 | 816.26 | 1015.43 | 9.86 | 2 | 10 |
| 17 | 700.43 | 888.42 | -20.69 | 1 | 8 | 42 | 827.59 | 1000.99 | 28.50 | 7 | 11 |
| 18 | 701.47 | 902.48 | 1.82 | 2 | 8 | 43 | 831.90 | 954.35 | 39.56 | 8 | 8 |
| 19 | 707.94 | 909.03 | -1.39 | 5 | 7 | 44 | 843.73 | 1031.98 | 21.17 | 3 | 15 |
| 20 | 710.33 | 846.91 | -37.25 | 7 | 6 | 45 | 844.04 | 980.46 | 37.60 | 4 | 12 |
| 21 | 717.58 | 918.66 | 2.14 | 10 | 8 | 46 | 844.39 | 918.45 | 43.66 | 7 | 9 |
| 22 | 734.11 | 914.19 | -25.33 | 1 | 7 | 47 | 848.81 | 1032.19 | 24.10 | 4 | 13 |
| 23 | 742.31 | 902.24 | 32.57 | 2 | 9 | 48 | 848.82 | 1036.36 | 21.66 | 7 | 12 |
| 24 | 748.16 | 929.55 | 24.77 | 1 | 10 | 49 | 851.04 | 1029.37 | 26.55 | 1 | 11 |
| 25 | 753.34 | 925.03 | 28.94 | 6 | 10 | 50 | 853.69 | 1040.94 | 21.87 | 6 | 9 |
| 1 | 0.5 | 1 | 1200 | 600 | 60 |
| N | T0 | K | eps | |
|---|---|---|---|---|
| 20 | 500 | 20 | 0.85 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, X.; Wu, S.; Wu, X.; Huang, Y.; Mu, Z. A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions. Algorithms 2019, 12, 231. https://doi.org/10.3390/a12110231
Long X, Wu S, Wu X, Huang Y, Mu Z. A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions. Algorithms. 2019; 12(11):231. https://doi.org/10.3390/a12110231
Chicago/Turabian StyleLong, Xiangyu, Shufan Wu, Xiaofeng Wu, Yixin Huang, and Zhongcheng Mu. 2019. "A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions" Algorithms 12, no. 11: 231. https://doi.org/10.3390/a12110231
APA StyleLong, X., Wu, S., Wu, X., Huang, Y., & Mu, Z. (2019). A GA-SA Hybrid Planning Algorithm Combined with Improved Clustering for LEO Observation Satellite Missions. Algorithms, 12(11), 231. https://doi.org/10.3390/a12110231





