Self-Improving Generative Artificial Neural Network for Pseudorehearsal Incremental Class Learning

Abstract

Deep learning models are part of the family of artificial neural networks and, as such, they suffer catastrophic interference when learning sequentially. In addition, the greater number of these models have a rigid architecture which prevents the incremental learning of new classes. To overcome these drawbacks, we propose the Self-Improving Generative Artificial Neural Network (SIGANN), an end-to-end deep neural network system which can ease the catastrophic forgetting problem when learning new classes. In this method, we introduce a novel detection model that automatically detects samples of new classes, and an adversarial autoencoder is used to produce samples of previous classes. This system consists of three main modules: a classifier module implemented using a Deep Convolutional Neural Network, a generator module based on an adversarial autoencoder, and a novelty-detection module implemented using an OpenMax activation function. Using the EMNIST data set, the model was trained incrementally, starting with a small set of classes. The results of the simulation show that SIGANN can retain previous knowledge while incorporating gradual forgetfulness of each learning sequence at a rate of about 7% per training step. Moreover, SIGANN can detect new classes that are hidden in the data with a median accuracy of 43% and, therefore, proceed with incremental class learning.

1. Introduction

Deep Neural Networks (DNN) are one of the most promising and successful models of recent times, due to their performance having become state of the art in many highly complex classification problems. However, there is great concern on the part of the community regarding one of the major limitations of connectionist models: these models catastrophically forget previously learned patterns when they learn new data or classes. This limitation prevents these models from being used in real applications which require continuous learning but gradual forgetting of past information. The problem of incremental learning has been studied in depth by several authors [1,2,3,4,5], but it is still an open issue.

One of the problems that appear with incremental learning is known as Catastrophic Interference, referring to the inability of an Artificial Neural Network (ANN) to retain previous knowledge while trying to learn a new and unknown task [6]. This problem is known as the Stability versus Plasticity Dilemma [7,8] which consists of a concession between the neural network’s capacity of generalization when applied to new samples, and its ability to retain previously learned concepts. Some authors have addressed this by using local representations from data [9], while the authors’ previous works showed how catastrophic interference might be mitigated by giving flexibility to ANNs. This would allow them to adapt their structure to data, improving their capability to both retain information and reduce catastrophic interference [2,10]. Recently, Kemker et al. [11] compare five different mechanisms designed to mitigate catastrophic forgetting in neural networks: regularization, ensembling, rehearsal, dual-memory, and sparse-coding.

Goodfellow et al. [12] have studied the effect of catastrophic interference on deep neural networks, suggesting using the dropout algorithm for balance between learning a new task and remembering a previous task. On the other hand, some recent studies show how generative networks might help with the recognition of unknown classes on multi-class classification tasks [13]. Rebuffi et al. [14] have introduced a new training strategy known as iCaRL to learn classes incrementally. The method starts with training data containing a small number of classes presented at the same time, and new classes are added progressively. Z. Li et al. [15] proposed the SupportNet framework that combines Deep Learning with stored samples that contains the essential information of the old data when learning the new information. Z. Li et al. [16] have proposed the Learning without forgetting (LwF) approach, which uses data samples coming from the new prediction tasks only, without accessing training data for previously learned tasks. Although the authors do not use data from the previous training sets, the new datasets have some representatives from the previously learned classes. Thus, the approach used by the authors is rehearsal, i.e., they have a small set of samples that they help to retain concepts from the classes that were previously learned. Recently, Shin et al. [17] proposed the Deep Generative Replay, an architecture consisting of a deep generative model (generator) and a task solving model (solver). The proposed method can sequentially train deep neural networks without referring to past data. However, there is not much literature on methods that are able to detect the presence of new classes hidden in the data without any supervision [18,19,20].

In this paper, we propose an end-to-end deep neural network system that acts both as a generator and classifier of data that incrementally learns by generating samples from previous information, and which is able to detect if there is new information present and to learn from it when necessary. This system consists of three major modules: the classifier, the generator, and the novelty detector. The classifier was instantiated with a convolutional neural network that, given an input image, assigns it a label from a set of known categories. The generator module was instantiated with an adversarial autoencoder, and its primary task is to generate pseudo-samples to enrich the training set. The classifier was embedded as a detector into the encoder of the adversarial autoencoder. Finally, the novelty detector implements an extreme-value detector allowing the network to identify whenever novel information is presented as a new class. At the end, we measure the impact of incremental training with generated data from previously learned information while learning a new task. Further details can be found at D. Mellado’s Thesis [21] and the preprint [22]

The main contributions of this paper are:

• Designing a neural network model that combines a generative model with a classifier to learn new patterns while reducing the need for storage of training data.
• Introducing a novelty-detection model that can help recognize new tasks for incremental learning tasks.

The rest of the paper is organized as follows: we briefly explain in Section 2 the main methods used to tackle the catastrophic interference problem. In Section 3, we explain the architecture of the proposed model, how it works and learns. Then in Section 4, we show our results from a series of proposed experiments using a small image dataset to measure its performance when trained incrementally. Finally, in Section 5 we discuss how the model improves reduction of catastrophic interference, and we propose future improvements for it in Section 6.

2. Theoretical Framework

ANNs are affected by catastrophic interference. Therefore, they require a mechanism able to remember both short and long-term, and they need to be able to accurately recognize if novel information is present in the data to learn from it. Several training methods have been proposed and used to retain previous knowledge, but some of the most common involve previous data being presented to the network while training a new task.

2.1. Rehearsal and Pseudorehearsal Learning

Rehearsal training in ANNs involves the collection of data from the previous classes and their incorporation into the model when new data are found, and the model needs to be retrained. One way of doing rehearsal training involves adding a set of the most recently trained examples alongside the new sample, known as Recency Rehearsal [23]. This mechanism reinforces what has the network has already learned, and associates this knowledge with the new data. Another conventional method consists of using a random subset of the previous data alongside the new sample [24]. While this achieves better results than the previous method, there is still some loss of knowledge of most connectionist networks when using either method. Mellado et al. [25] shows how performance worsens even though previous samples are reused. Another point to consider is that both methods require the storage of previous training samples. Although it is not an issue in most cases, this becomes a considerable drawback when training vast and increasing databases, as seen in Big Data; where storage of an increasing number of examples can become a problem. The additional storage may not be biologically plausible (the neural network metaphor), because brains are not able to store the exact representation of something learned. Rather, they construct meaning from information, and store it within neural patterns, while ultimately discarding the original information [26].

Pseudorehearsal, in contrast, does not involve the use of previously trained items and instead uses randomly generated elements that act in a way similar to the original training data [24]. These random elements are usually added to the previously trained network to get their outputs, and added to the new item to train the network for the new set. This method allows the training of new data by approximating the previous information whenever needed [27]. One caveat was presented by Ans et al. [28], where they demonstrated that using only random samples can cause problems while generalizing in increasing data due to their noisy origin, effectively destroying what previous knowledge was in the model. A secondary, parallel, network is needed to create pseudo-samples for the primary network to learn from representations. This method, compared to rehearsal learning, is more biologically plausible because it does not require the storage of all previous data directly, and uses stochastic processes to generate them, thus giving the impression of “evoking” the concepts that the neural network has already learned. This evoking allows for approximation of old information, by sampling how the neural network should behave regarding these inputs, allowing the consolidation of information while learning a new task [27].

Previous research by the authors [25] showed that pseudorehearsal has slightly lower performance when training with pseudo-samples in comparison to a rehearsal approach. However, in both methods, the classifier has a peak accuracy of almost 90%, when using as few as 10% of a total of 512 generated samples per trained class, showing that this method can be useful for incremental training of DNNs without having to store or generate a significant amount of data. Atkinson et al. [29] expanded on this idea by using a Generative Adversarial Network to generate data in order to train a model incrementally, whereas Besedin et al. [30] expanded this model and analyzed the impact of image regeneration when training incrementally. Further details about the main challenges for incremental learning and catastrophic forgetting are given in Parisi et al. [31].

2.2. Variational Autoencoders for Image Generation

A variational autoencoder (VAE) is a neural network model capable of encoding and decoding information onto a probabilistic distribution, commonly Gaussian or Bernoulli [32]. These models encode the information from the input data X into a random latent vector z sampled from $P\left(z\right)$ defined over distribution space $\mathcal{Z}$, which is then decoded onto a generated representation $\widehat{X}\in P\left(X\right)$ of the original data Equation (1).

$$P(X)=\int P(X|z;\theta )P(z)dz$$

(1)

where $P\left(X\right|z)$ is a set of functions, parameterized by $\theta$ or the parameters we want to optimize. This allows sampling from $P\left(z\right)$ with a high probability of obtaining a value from X [33].

This latent vector acts as a prior that enables the decoder to map information onto a representation, using the maximum likelihood to the image. Both encoder and decoder network uses a similar structure to recreate an output with features similar to the initial input as an autoencoder structure.

To optimize these networks, the Kullback–Leibler distance between latent vector z and a defined random distribution is minimized Equation (2).

$$\mathcal{KL}\left[Q\left(z\right)\left|\right|P\left(z\right|X)\right]=E_{z\sim Q}\left[logQ\left(z\right)-logP\left(z\right|X)\right]$$

(2)

where $P\left(z\right|X)\sim \mathcal{Z}\left(\mu ,\sigma +ϵ\right)$, $\mu$ and $\sigma$ are obtained as output from the encoder, $ϵ$ is stochastic noise, and $Q\left(z\right)$ is usually similar to a Gaussian distribution $\mathcal{N}\left(0,I\right)$, I being an identity matrix. Moreover, the difference between the input and its reconstruction (usually the Mean Squared Error or the binary cross-entropy between input and output) is reduced, allowing spatial information to be decoded from a reduced, stochastic source with similar characteristics to a real input [33].

These types of networks are widely used for generating small images by encoding image features and enabling the generation of new images with small variations on these features [34,35]. Newer variations try to improve encoding by making the images indistinguishable from real information. Neural Network models such as [36,37] use a discriminator network, similar to Generative Adversarial Network models, to create generated samples that are similar to real examples. Adversarial models allow this through competition between the generator and a discriminator network that identifies whether the input is generated or belongs to a real set, each balancing the other [38].

2.3. Novelty Recognition

Novel pattern recognition is the field that studies how an algorithm or system can recognize if a pattern is unknown to it, compared to a set of previously learned patterns [39]. Some of these techniques are commonly used for outlier detection, due to how these events deviate from what the system usually outputs from a given input. Detection can be probabilistic, distance-based, reconstruction-based, from domain or by measuring information content, among other methods [40].

Novelty recognition has been recently used on deep neural network (DNN) models to improve detection of new information available on inference. Richter et al. [41] for example, developed an autoencoder model for novelty recognition for a reinforcement learning problem. This algorithm can identify if the environment is similar to the training environment, improving navigation in an autonomous system when trying to identify its navigation confidence.

Novelty detection can be used as a tool for recognition of an object from a universe of different unknown objects, considering the “unknown” category as a possibility, known as open-set recognition. Bendale et al. [42] created a DNN for open-set recognition by measuring the activation distance of the output layer from a classifier compared to the maximum response of a specific class and using Extreme-Value Theory to model the probability of the input’s rejection from a perceived class.

Extreme-Value Theory involves the study of extrema, or maximum or minimum values, in probabilistic distributions; commonly used for rejection of outliers. A general representation of the cumulative distribution function of an extreme-value distribution is in Equation (3).

$$P\left[X\le x\right]={\left[1+\xi \left(\frac{x-\mu }{\sigma }\right)\right]}^{\frac{1}{\xi }}$$

(3)

where $1+\xi \left(\frac{x-\mu }{\sigma }\right)>0$, $-\infty <\xi <\infty$ and $\sigma >0$. The value of $\xi$ defines the distribution, if $\xi <0$ becomes a Weibull-type distribution, a value of $\xi >0$ becomes a Fréchet-type distribution and when $\xi \to -\infty$ or ∞, becomes a Gumbel-type distribution [43]. As activation parameters in a neural network are bounded, their distribution reduces to a Weibull distribution [44]. The probability of rejection of an outlier is given by the output of this distribution, in relation to how data is distributed within it.

Novelty-detection algorithms have also been used with Adversarial Autoencoders (AAE) for measurement of the likelihood of images belonging to the training set, allowing for better sample generation [19].

3. Proposal

Our proposed neural network system, “Self-Improving Generative Artificial Neural Network” (SIGANN) (Available at https://github.com/dmelladoc/SIGANN), consists of 3 major sub-structures: A classifier, a generator and a novelty detector working in conjunction in order to learn and identify unknown data from a starting subset of a dataset, and training itself to learn new classes. For both the classifier and generator, we implemented a semi-supervised AAE model, based on the structure presented in [36] for semi-supervised training, and added the novelty detector.

To incrementally train SIGANN, we train the classifier and generator at the same time, as in a standard AAE model; then fit the mean activations for each initial class on our novelty detector by inferring from the training set at the end of the training process. On inference, the novelty detector checks if new information belongs to a new class. If so, it temporarily stores the sample for future training, as the generator starts sampling a set of previous knowledge representations for the next training step. This set is used in conjunction with all newly detected samples, and the categorical output layer from the classifier is expanded to add the new class. Finally, the network is trained for a defined number of epochs, learning new information without loss of previous knowledge.

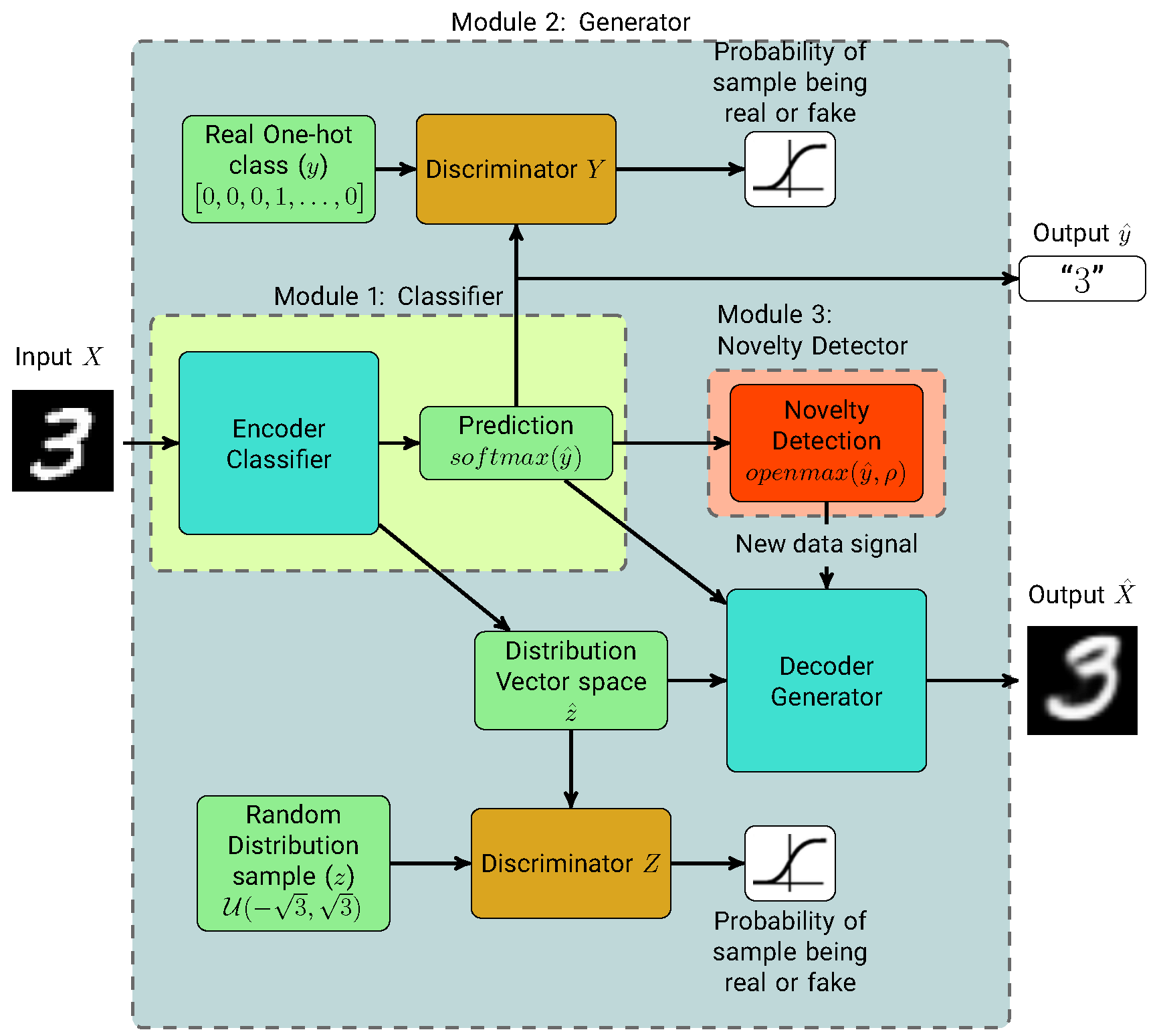
The complete operation of our method is presented in Algorithm 1 and the structure of the semi-supervised AAE model used in conjunction with the novelty detector is shown in Figure 1. In the following subsections we explain each module.

Algorithm 1 SIGANN Model training.
Require: Set of initial data $X_{train}$ and output classes $y_{train}\in \{1,\cdots ,C\}$
1:	Uniform Distribution Generator $Z=\mathcal{U}(-\sqrt{3},\sqrt{3})$ of sample length n
2:	Train Adversarial Autoencoder: $\widehat{X},\widehat{z},\widehat{y}=AAE(X_{train},y_{train},Z)$
3:	for c = 1, …, C do
4:	Get Mean Activation of trained samples ${\mu }_c=mean(\widehat{y}\in c)$
5:	Compute distance of each output of class c: $d_c=|{\widehat{y}}_c-{\mu }_c|$
6:	Fit $d_c$ to Weibull distribution ${\mathcal{W}}_c$ and get parameters ${\rho }_c=({\kappa }_c,{\lambda }_c)$
7:	while Receiving new data $X_{new}$ do
8:	Evaluate samples of data $X_{new}$ on inference: $\widehat{y}=AA{E}_{enc}\left(X_{new}\right)$
9:	Revise OpenMax activation of data: $y^{\star }=\mathrm{OpenMax}(\widehat{y},\rho ,ϵ=0.95)$
10:	if $y^{\star }=C+1$ then
11:	Store input $X^{\star }$ and output $y^{\star }$
12:	Generate samples $X_{gen}$ from classes $y_{gen}\in \{1,\cdots ,C\}$
13:	Evaluate generated samples: ${\widehat{y}}_{gen}=AA{E}_{enc}\left(X_{gen}\right)$
14:	if ${\widehat{y}}_{gen}=y_{gen}$ and $P({\widehat{y}}_{gen}=c|X)>0.9$ then
15:	Store $X_{gen},y_{gen}$
16:	else
17:	Discard $X_{gen},y_{gen}$ and Re-generate
18:	Update Number of classes: $C=C+1$
19:	Re-train Adversarial Autoencoder with new and generated data: $\widehat{X},\widehat{z},\widehat{y}=AAE(X_{gen}+X^{\star },y_{gen}+y^{\star },Z)$
20:	Fit new class and samples to Weibull distribution
21:

3.1. Module 1: Classifier

The classifier module consists of an encoder unit which is shared with the generator module, and the SoftMax function that outputs the predicted class of image X. This module also outputs the encoded style information for the generator module.

We use a set of convolutional layers with kernel size $3\times 3$ and a stride size of 2 to reduce the dimensions of the image; followed by convolutional inception layers with the same number of neurons, ending with two 2-layered dense networks in parallel, which encode style information onto latent vector $\widehat{z}$ and output the SoftMax classification probability $\widehat{y}$ of the input image X. The latent vector $\widehat{z}$ encodes style information from the image, onto a uniform distribution $z\in \mathcal{U}\left(\left[-\sqrt{3},\sqrt{3}\right]\right)$, defined so as to maximize unit variance between samples (Figure 2).

3.2. Module 2: Generator

The generator module is based on an adversarial autoencoder, whose units are the encoder structure from the classifier, the decoder, and the distribution and categorical discriminators. These structures allow SIGANN to learn spatial information and generate real-looking samples for use on future training operations.

Both $\widehat{z}$ and $\widehat{y}$ output from the encoder structure from input image X, are concatenated and used as an input for the decoder structure, which mirrors the encoding network structure using deconvolution filters, outputting a decoded image $\tilde{X}$. The generator can encode information from random noise to generate nearly real samples by training two discriminator networks Z and Y (as shown in Figure 1) which try to differentiate between the true categorical and random uniform priors and the generated inputs from the encoder [36]. These discriminators are built using two sets of 2-layer perceptron networks with a binary output, to identify if the distribution sample Z and categorical sample y comes from real or generated samples. The generator ultimately tries to fool the discriminators, by creating encoding vectors with a distribution similar to the distribution sample Z and categorical output y, to decode them into a real image, similar to the original.

The complete loss function $\mathcal{L}$ used for the training is obtained as the aggregation of the following loss functions: (1) the reconstruction loss ${\mathcal{L}}_{rec}$, obtained from the binary cross-entropy between the original image X and the generated image $\widehat{X}$; (2) the discriminative losses ${\mathcal{L}}_{dis}$ from both the encoding vector $\widehat{z}$ and the class $\widehat{y}$ discriminators; (3) the generative loss ${\mathcal{L}}_{gen}$ from the generator when fooling the discriminators; and (4) the classification loss ${\mathcal{L}}_{cls}$ from the classifier.

3.3. Module 3: Novelty Detector

The novelty detector consists of the joint action of the Meta-Recognition and OpenMax algorithms. After training the AAE for a defined number of classes, we evaluate data to classify it. Generally, if a sample is from a new, unknown class, the classifier should not be able to identify it as such. Therefore, we replace the activation function of the classifier in the inference stage with an OpenMax function [42] for novelty detection. This activation function was initially designed as a replacement for SoftMax activation in open-set recognition networks.

By using the Meta-Recognition algorithm presented by [44] as a basis, this function fits data into a Weibull distribution to obtain the probability of each sample being on a high or low tail of the set, selecting the $\eta$ values from the tail of the distribution. The reason for selecting the Weibull distribution is due to its versatility, where both the shape $\kappa$ and the scale $\lambda$ parameter, affect the shape of the probability-density-function curve, the reliability, and the failure rate. Moreover, the Weibull distribution becomes suitable when the conditions for strict randomness of the exponential distribution are not satisfied. This distribution is widely used in reliability and life data analysis (For more details see [45]).

The fitting of the Weibull distribution is done using the Euclidean distance between each training sample’s output activation logit, or the output from the last layer of a classifier before applying the SoftMax activation function; and the mean activation of all samples from class c, obtaining the scale and shape parameters of the Weibull distribution for class c. By defining ${\rho }_c$ as these parameters, we use the Weibull CDF on the Euclidean distance between the mean activation logits of class ${\mu }_c$ from the training set and the logits obtained on inference. We obtain this value for the top $\alpha$ classes, obtaining weights $\omega \left(x\right)$ for each class of the logit output. The sum difference between the original and corrected logits gives us the “unknown logit” which is then evaluated using the SoftMax Equation (4).

$$P{\left(z\right)}_j=\frac{e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}j=1,\cdots ,K$$

(4)

We then reject the original predicted class and define element X as being from an unknown class if the probability of belonging to a known class is lower than $ϵ<95\%$ or if the maximum probability belongs to the unknown class. This value of $ϵ$ was defined as such, as it allowed for the best performance for detection. This allows the network to measure the probability of a fooling or unknown image to be misclassified, by rejecting the probability that this data is part of a known set, allowing us to recognize if the input data is unknown, in order to store it as new information to further train the network with new data. The Meta-Recognition and OpenMax algorithms are presented in Algorithm 2 and in Algorithm 3, respectively.

Algorithm 2 Meta-Recognition Algorithm.

Require: Logits from the final layer from each class ${\mathbf{v}}_c\left(x\right)=v_1\left(x\right)\cdots v_N\left(x\right)$ from training phase; Number of extreme values to fit $\eta$

1: for $c=1\cdots N$ do

2:    Compute Mean Activation: ${\mu }_c=mean\left({\mathbf{v}}_c\right)$

3:     Fit to Weibull: ${\rho }_c=({\kappa }_c,{\lambda }_c)=\mathrm{FitHigh}\left(\Vert {\mathbf{v}}_c-{\mu }_c\Vert ,\eta \right)$

4: return ${\mu }_c$ and ${\rho }_c$ for each class

Algorithm 3 OpenMax Algorithm.

Require: Logits from the final layer from each class ${\mathbf{v}}_c\left(x\right)=v_1\left(x\right)\cdots v_C\left(x\right)$ from evaluation; $\alpha$ number of top classes to revise.

1: Execute Algorithm 2 of the Meta-Recognition to obtain the Mean ${\mu }_c$ and Weibull parameters ${\rho }_c=({\kappa }_c,{\lambda }_c)$ for each class c

2: for $i=1,\cdots ,\alpha$ do

3:     $s\left(i\right)=argsort\left(v_c\left(x\right)\right)$

4:     ${\omega }_{s\left(i\right)}\left(x\right)=1-\frac{\alpha -i}{\alpha }{e^{-\left(\frac{\Vert v_i\left(x\right)-{\mu }_{s\left(i\right)}\Vert }{{\lambda }_{s\left(i\right)}}\right)}}^{{\kappa }_{s\left(i\right)}}$

5: Revise activations: $\widehat{v}\left(x\right)=\mathbf{v}\left(x\right)\circ \omega \left(x\right)$

6: Define ${\widehat{v}}_{new}\left(x\right)={\sum }_i({\mathbf{v}}_i\left(x\right)-{\widehat{v}}_i\left(x\right))$

7: $\widehat{P}(y=j|x)=\frac{e^{{\widehat{v}}_c\left(x\right)}}{{\sum }_{c=0}^N{e}^{{\widehat{v}}_c\left(x\right)}}$

8: Let $y^{\star }=argma{x}_{i}P(y=i|\mathbf{x})$

9: return New class if $y^{\star }=C+1$ or $P(y=y^{☆}|\mathbf{x})<ϵ$

With all unknown information identified, we then use the generator to create a balanced set of generated samples from the previously learned classes, adding them to the new training set, and start training with the new data. This allows our model to “finetune” its weights for the old data and accommodate new features which might help to activate the corresponding output for the new class.

4. Experiments

To assess SIGANN’s learning capabilities, three experiments were proposed. First, we measure the rate at which the method forgets previously learned classes. Second, we study the ability of the method to detect new unknown classes. And third, we study how long the method could last without catastrophically forgetting the former classes in a continual learning setting.

We used the EMNIST dataset (https://www.nist.gov/node/1298471/emnist-dataset) [46] as a benchmark for our experiments. This is an extension of the original MNIST dataset for handwritten digits, with the inclusion of handwritten characters and numbers from the NIST Special Database 19. The EMNIST Balanced subset, is comprised of 131,600 character images, with 47 different classes from 0–9, A–Z and a set of lowercase a-z characters different from their uppercase counterparts. We have decided to maintain a balanced classes set to isolate this variable in the following experiments. For the initial training task, we trained the model using the number classes, incrementally adding each letter in alphabetical order at each training stage.

For all experiments, our network was trained for 25 epochs for each training step, using Adam Optimizer, with an initial learning rate of 0.001 and with the decay values of ${\beta }_1=0.9$ and ${\beta }_2=0.999$ to control the moving averages of the gradient and the squared gradient, respectively. The dataset was augmented by resizing an image to a target width and height by either centrally cropping the image or padding it evenly with zeros, moreover the brightness of the image is randomly perturbed. For all the experiments, we have divided the dataset for each stage into training and test sets, and we report the average and standard deviation performance of 15 runs in the test set. Our setup was an HP Proliant Workstation with Intel Xeon ES-2620 CPU with 16GB of RAM and an NVIDIA GeForce GTX960 GPU; and implemented with TensorFlow 1.8 for GPU using Python 3.6.

4.1. Experiment 1: Does the Method Gradually Forget?

As a first experiment, our model was trained to learn iteratively on splits of these datasets, in order to study if our network can retain previous information while learning new data, and to see how much information is lost when learning a new task using only what the model remembers of the previous task. The dataset was split into four parts, each with an even number of classes. The network was trained using an initial set. After training each set, we evaluated classification accuracy and generated a set of images from each learned class, to append it to the new learning task. The generated images were selected for training if the predicted class from the classifier matched the input class from the generator. In the steps that followed, we retrained the model with the next batch of new classes, plus a defined number of generated data: around 75% of the amount of the original training samples for each class from the previous set. We decided upon this value due to an unbalancing issue with the previously learned classes when training the new set.

As a base metric, the obtained accuracy for our classifier when evaluating the complete dataset was 87.71% on EMNIST; this result is similar to state of the art on this particular subset (Performance results of different Deep Learning techniques for the MNIST dataset can be found in https://benchmarks.ai/mnist, in [46] the authors reports the performance for the EMNIST dataset). While training the generated set, the accuracy of each training iteration lowered in a constant decay per training step of around 9.27 ± 0.75%. When trained to add a small subset of the original data to the generated samples, the decay rate in each training step is cut almost in half, as shown in

Table 1. Accuracy evaluated in the test sets using EMNIST partition in four splits.

Training Scheme	SIGANN with the Complete Data Set	Pseudorehearsal SIGANN	Rehearsal SIGANN with 10% Real Data
Split 1	$87.71\%$	$97.91\pm 0.24\%$	$97.97\pm 0.17\%$
Split 2	−	$89.25\pm 0.54\%$	$90.34\pm 0.42\%$
Split 3	−	$81.84\pm 0.98\%$	$86.58\pm 0.55\%$
Split 4	−	$70.11\pm 2.21\%$	$81.28\pm 0.71\%$
Decay Rate	−	$9.27\pm 0.75\%$	$5.56\pm 0.21\%$

. This decay can be explained as a gradual interference effect to do with how information is learned within the model, and related to the model’s plasticity when learning new features of the newer classes. As a comparison, we trained the same model with generated samples and an additional 10% of randomly sampled original training data, to test performance in pseudorehearsal training.

This gradual loss of information can be seen in the generated samples from the model in Figure 3. In each training split, the recently learned task starts with a better form style definition, due to how it is encoded on the distribution vector. In following splits, its shape starts to lose form due to the increasing number of classes within the encoding space.

4.2. Experiment 2: Is the Method Able to Detect New Unknown Classes?

Our second experiment consisted of measuring how our classifier can properly identify data from an unknown class, using a novelty-detection activation function, and measuring how similarity to the original set can affect proper detection of novelty. We trained our model using a set of numbers (0–9) and measured what percentage of data from each letter (A–Z) was accurately identified as a new class. In this experiment, we expected that similar-looking characters (such as 0 with O, 5 with S, etc.) would be less likely to be identified as a new class, while distinct data from the original set would be quickly identified as new.

Our novelty detector, when trained with numbers only, detects up to 55% of the unknown data in classes which are further from what is already known. Accuracy while classifying without novelty detection is around 61%, consistent with the number from test data from the original set, since almost all failures come from the unknown class. Using OpenMax, accuracy raises from $60.08\pm 4.04\%$ at its lowest detecting the letter Z, and up to $80.035\pm 4.48\%$ detecting the letter C. On average, the mean accuracy using OpenMax is $71.64\pm 5.75\%$. On average, the detector can identify around $37.065\pm 15.77\%$ of the total samples of new data presented in inference, using a rejection threshold of $ϵ=0.95$. Although in some cases the novelty detector has a relatively low accuracy in the detection of new classes, only a small number of samples are required in order to be recognized as novel to begin the process of expanding the model to learn this new class.

By measuring the Euclidean distance between each activation logit from a new class, and the mean activation from each training class, we can infer how similarity can impact the misclassification of a sample. In Figure 4, we compare the distances between the uppercase A character and each number character from the dataset. This character typically gets misclassified with the number 4, and its distance distribution intersects with a large part of the activation distances from the training set. Still, a large chunk of the set is further than the maximum tail of class 4, and thus, those examples have a higher probability of being rejected and reclassified as a new class.

In

Table 2. Percentage of new class identification for each non-number character images on EMNIST after training with number images.

Char	%	Char	%
A	$49.91\pm 7.66\%$	T	$32.82\pm 9.12\%$
B	$28.76\pm 8.88\%$	U	$44.44\pm 13.44\%$
C	$61.49\pm 10.40\%$	V	$41.43\pm 11.63\%$
D	$45.71\pm 27.46\%$	W	$47.37\pm 8.36\%$
E	$45.42\pm 8.17\%$	X	$47.07\pm 11.92\%$
F	$60.38\pm 7.66\%$	Y	$19.45\pm 5.03\%$
G	$38.38\pm 7.44\%$	Z	$8.27\pm 3.54\%$
H	$14.92\pm 7.78\%$	a	$46.16\pm 9.43\%$
I	$14.11\pm 11.89\%$	b	$19.83\pm 7.69\%$
J	$40.46\pm 6.87\%$	d	$51.22\pm 8.56\%$
K	$45.56\pm 7.56\%$	e	$57.91\pm 6.29\%$
L	$11.38\pm 6.33\%$	f	$60.82\pm 8.16\%$
M	$60.21\pm 8.85\%$	g	$25.36\pm 4.39\%$
N	$42.64\pm 8.00\%$	h	$43.84\pm 8.01\%$
O	$35.84\pm 37.46\%$	n	$54.74\pm 9.65\%$
P	$42.73\pm 7.54\%$	q	$22.27\pm 4.51\%$
Q	$48.37\pm 8.46\%$	r	$55.91\pm 10.83\%$
R	$36.09\pm 6.66\%$	t	$29.99\pm 8.64\%$
S	$15.38\pm 8.06\%$

, we show the mean percentage of the total number of samples from each character detected by the novelty detector. The uppercase O character is the most complex to accurately identify as a new class, due to its similarity to the number 0. This trend is also noticeable with similar number-shaped characters, such as I, H, S, and Z, which are similar to the numbers, 1, 8, 5, and 2, respectively.

While this detection can be improved using lower thresholds, the detector starts to misclassify previous classes more. This $ϵ$ value achieves a balance between good novelty detection and accuracy regarding previous information. This shows that whenever we are using the OpenMax algorithm as a novelty detector, we can safely detect new data if it is sufficiently different from the learned set.

4.3. Experiment 3: How Long Could the Method Last?

As a final experiment, we measured the number of incremental training cycles our network can perform when learning a new set of data identified by the detector. We trained the model with ten classes, representing numbers, and incrementally trained with a new random class containing samples obtained from the detection stage of our model, and measured the accuracy loss in each training step until the number of correctly identified new samples was less than 5% of the total from that class.

When combining both our network and novelty detector, we start to see a slow decline in accuracy in each evaluation step, mostly due to an increase in noise in the network’s generated samples from earlier tasks, this is an effect of using generated samples of already generated data. Figure 5 shows that for at least three training iterations, our model can adequately retain previous information while learning a new task, without any effects caused by generator noise. Afterwards, the network starts to gradually lose information, lowering its accuracy at a rate of 7% per training step.

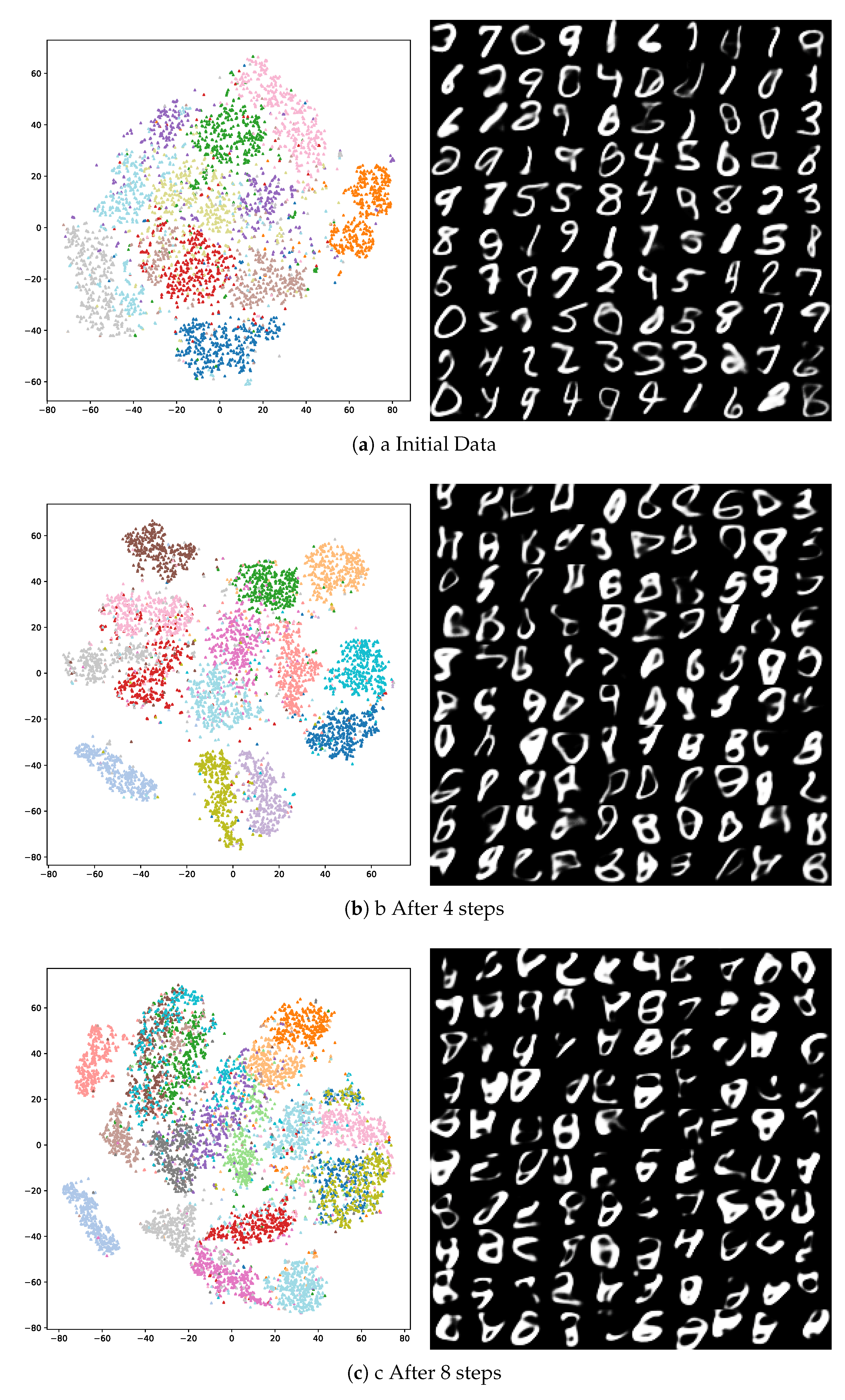
This information loss can be explained by the way information is encoded in a limited space, defined on $\widehat{z}$, as shown in Figure 6.

When trained on the initial classes (Figure 6a), each character clusters within the distribution space, allowing the generation of different characters as the encoding vector $\widehat{z}$ is defined within it. As the number of new classes increases, information regarding shape, style, and class is clustered within a reduced space, thus reducing the variability of the generated samples upon decoding. This effect is shown in Figure 6b,c, where boundaries between clusters are muddled, thus reducing differences between outputs from different classes. In addition to this, as previous information is continuously retrained without the original content, this reduction in variability creates less-defined outputs, impacting how the network can retain long-term information about old data.

4.4. Case of Study with CIFAR10

To test the proposed SIGANN model to a different and more complex dataset, we have selected the CIFAR10 [47]. The CIFAR-10 dataset (https://www.cs.toronto.edu/~kriz/cifar.html) consists of 60,000 tiny color images of size $32\times 32$ separated in 10 classes, with 6000 images per class. The color RGB images were converted to a grayscale images ($G=0.3R+0.59G+0.11B$). The 10 different classes represent airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. The data set was randomly split into three parts, with several classes of 4, 3, 3. Similar to experiment 1, the network was trained using an initial set and then it was retrained in the following steps with the data of the new segment and samples generated by the model.

Table 3. Accuracy evaluated in the test sets using CIFAR10 partition in three splits.

Training Scheme	SIGANN with the Complete Data Set	Pseudorehearsal SIGANN	Rehearsal SIGANN with 10% Real Data
Split 1	$81.23\%$	$83.76\%$	$83.76\%$
Split 2	−	$77.12\%$	$79.48\%$
Split 3	−	$68.82\%$	$72.29\%$
Decay Rate	−	$9.34\%$	$7.08\%$

shows the performance results with this dataset. The accuracy of the base model using the complete data set was 81.23% on CIFAR10 (Performance results of different Deep Learning techniques for the CIFAR10 dataset can be found in https://benchmarks.ai/cifar-10). When a pseudorehearsal approach was used, we obtained a gradual forgetfulness of an average 9% in decreasing accuracy. On the other hand, when we introduce a small subset of 10% of the original data, the resulting decay rate was approximately 7%.

Once again, the proposed framework favors the gradual forgetting of information avoiding catastrophic interference. On the other hand, having representative data of the class contributes to the lower rate of forgetting.

5. Discussion

Our model can recognize new classes when examining its activation output from the classifier, and generate samples from previously learned information to improve itself and learn new classes, without storing previous information for training. This reduces the impact of catastrophic interference when trained on new information without original data, allowing for several training steps to learn new information while holding onto old data. We showed that new classes could be inferred by measuring the distance from the activation output to a mean activation from each learned class, and that by adjusting by the rejection probability using a Weibull distribution, we can effectively select examples from new information.

Despite being able to learn and retain information for a limited number of training iterations without significant loss, when trained continuously using only a small number of generated samples, a gradual forgetting effect is present. The decay rate presented while training with this effect is significantly lower than expected, considering the risk of catastrophic interference caused by not using original training samples from previous training iterations, and could be mitigated by using a greater amount of data or by improving the novelty detector. This process can be compared to the impact upon memory when learning, as previous knowledge is harder to recall after learning newer information, due to interference while encoding both what is previously known and the new stimulus. With fewer samples to re-order information alongside what is known, the model shows a similar effect to when there is less time to reorganize information in the brain between learning epochs [48].

The difference between Rebuffi et al. [14] and Li’s et al. [16] works with respect to our proposal lies in that our method does not consider a memory module. It can detect whenever a new class appears in the data set. It is important to note that our SIGANN proposal forgets at a higher rate than iCaRL due mainly to the pseudorehearsal approach of our method where the SIGANN model does not use any sample from the classes that were previously learned. However, when we use 10% of new samples from the previous class we can have comparable results (Rehearsal approach). Thus, our approach could be a step towards achieving a self-training neural network, able to perform life-long learning of new information as required.

6. Conclusions

In this work, we proposed a neural network system which combined the capabilities of Adversarial Autoencoders to generate and classify information, and a novelty-detection algorithm for the identification of unknown data, in order to incrementally learn new information in an unsupervised way and reduce the need for storage of previously learned data.

SIGANN achieves its purpose of learning new information incrementally through self-improvement, thanks to its ability to identify new information and learn new emerging patterns from these, without requiring storage of previous samples. This ability can be applied to incremental learning of streaming data in a semi-supervised way, allowing training of new information without having to store information and only when needed.

In future works, we expect to extend our model to more complex image classification datasets such as ImageNet. Future work will improve the long-term retention of prior information to reduce the effects of gradual forgetfulness and information loss when learning new classes; as this is one of the most significant challenges for achieving life-long learning of an increasing number of data classes. Also, giving the system a long-term memory module might improve on the storage of sample variance within the distributional space. Achieving this might improve stability, and allow for the generation of better samples with which to continually self-improve.