1. Introduction
Civil infrastructures such as buildings, roads and bridges will continuously accumulate damage due to material deterioration, natural hazard and harsh environments such as earthquakes, storms, fires, long-term fatigues and corrosions. Some of such anomalies could not be ignored since they may lead to catastrophic, economic loss, or even human life loss. Thus, the demand to monitor sustainable conditions of these infrastructures has increased dramatically, which is generally described as Structural Health Monitoring (SHM) [
1] in the research community.
Vibration-based methods have been widely used for damage detection and identification in SHM research [
2]. The basic idea for vibration-based damage identification is that the structural physical properties (such as stiffness mass and damping matrices) will change once there are some damages occurred in the structure and these changes will lead the modal information (e.g., natural frequencies, mode shapes and other damage sensitive parameters) changes [
3]. Therefore, by analysing these changes in the structural modal information of a given structure, one can detect the potential damages and identify the location as well as the severity of damages. However, it is not practical to collect data under a big amount of different damage scenarios from real civil structures. A finite element model (FEM) of a given structure can be used to simulate different damage scenarios. The FEM updating technique has emerged in the 1990s as a subject of immense importance to the design, construction and maintenance of civil engineering structures [
4]. It provides an efficient way to identify the structural damage and perform the assessment of the structure. This technique has been widely used in SHM applications for decades [
5,
6]. Brownjohn et al. [
7] have utilized the FEM updating method for assessing modal and structural parameters of a highway bridge. Also, a sensitivity-based FEM updating has been carried out for damage detection in [
8].
In the past, one of the most popular non-linear approaches that have been widely adopted in SHM for vibrational damage identification is Artificial Neural Networks (ANNs). It was observed by Yun et al. [
9] that the joint damages occurring at the beam-to-column connections of a steel frame structure can be predicted from modal data via ANN approach. Also, a noise-injection learning method is proposed in which certain level of noise is injected into the training data, which can improve the robustness and accuracy of the damage detection algorithm [
9]. A statistical approach is presented in [
10] to consider the effect of uncertainties in developing an ANN model for structural damage detection. A back-propagation (BP) based neural network, which is one of the most popular algorithms for training ANNs, can perform well in estimating the location and severity of damages in a bridge structure [
11]. It aims to find the minimum of the error function in the weight space by using the gradient descent optimization method [
11]. Generally, the BP neural network works quite well in some particular circumstances [
12,
13] when the initialized weights are quite close to a good solution, a large amount of training data is provided and enough computational resources are available. However, as the number of hidden layers increased, the ‘gradient values’ might be vanished during the process of backpropagation. Hence, it is difficult to optimize the weights in neural networks with a deep architecture. That is also a bottleneck for ANNs with deep architectures.
The concept of Deep Learning Neural Networks (DLNN) was introduced by Hinton and Salakhutdinov [
14] to reduce the dimensionality of data and overcome the above limitations. DLNN can learn the representative and discriminative features in a hierarchical manner from the data [
15]. In contrast to the shallow linear and non-linear methods in ANNs, DLNN can achieve higher accuracy by using a larger number of layers. Since various layers can abstract various structures of the data, it is possible to learn the true underlying structure and the non-reducible nonlinearities of the original data. The typical training process for DLNN consists of unsupervised feature learning that facilitates the process of extracting features implicitly in comparison to other feature learning methods that have explicit formulations. DLNN is a popular technique in machine learning community with applications ranging from computer vision [
16,
17], natural language processing [
18,
19] and audio processing [
20] and so forth. It has recently been applied to the community for SHM via big data analysis [
21,
22]. A vision-based method using a deep architecture of Convolutional Neural Networks (CNN) was proposed in Cha et al. [
22] for detecting concrete cracks without calculating the defect features. Later, they have developed a Faster Region-based Convolutional Neural Networks (Faster R-CNN) [
23] method to detect multiple types of surface damages, which has better computation efficiency in comparison with CNN-based method of Cha et al. [
22]. Moreover, the Faster R-CNN has been used with UAVs for damage detection recently in 2018 [
24].
Auto-encoder is one kind of unsupervised learning method that has usually been used to produce a lower-dimensional representation for data, which preserves the information that is useful for the ultimate task. By stacking multiple hidden layers of auto-encoders, a Deep Auto-encoder (DAE) model can be established to learn high-level features with an unsupervised learning algorithm. Particularly, DAE can be utilised for performing non-linear regression task [
25,
26] with a supervised learning algorithm. Recent progress in Reference [
3] shows a promising future for deep auto-encoder model (named AutoDNet) in comparison with traditional ANNs with applications in SHM. They have demonstrated that AutoDNet can achieve good performance for structural damage detection/identification via two stages: effective dimensionality reduction and accurate relationship learning [
3]. A layer-wise pre-training scheme is performed in both two stages. After pre-training, the obtained weightings should be close to a global optimal solution. Then, the entire network is fine-tuned with respect to ultimate objective function. Also, the hyperbolic tangent function named ‘tanh’ has been utilized as the activation function in the neural network. However, this leads to learn a latent dense representation of the original input which may not be robust enough under several types of noise environment [
3]. For such problems, Glorot et al. [
27] developed a sparse deep auto-encoder model which can attain better robust features under noise compared to its non-sparse variant. By introducing a sparsity constraint to the reconstruction loss function, a better de-noising performance has been achieved. In fact, sparse representations have drawn much attention in different fields and they have a number of advantages in both theoretical research and practical applications [
28,
29,
30]. Researches on sparse coding have demonstrated that the sparseness plays a key role in learning useful features [
31,
32]. In sparse methods, the code is forced to have only a few non-zero units while most code units are zero most of the time. It has been found out in [
15] that sparse representations learned in the context of auto-encoder variants are very useful in training deep architectures, especially for unsupervised pre-training of neural networks [
33]. In particular, they have good robustness to noise and provide a good tiling of the joint space of location and frequency.
Recently, a sparse auto-encoder based framework (SAF) [
34] is proposed for SHM and shows a better performance in structural detection/identification in comparison with AutoDNet [
3]. In their work, a Rectified Linear Unit (ReLU) activation function is used instead of ‘tanh’ which introduces sparsity effect in the neural networks. Meanwhile, a sparsity penalty term is introduced in the dimensionality reduction component to regularize the reconstruction loss, while improving the performance in final task on top of AutoDNet. However, the proposed AutoDNet model in [
3] and SAF model in [
34] are basically processing the entire input datasets together which include different types of features such as frequencies and mode shapes. This will increase the difficulty in training a robust model due to several problems. (1) As one mode shape is associated with one frequency and different mode shapes are unrelated to each other, it is better to deal with each of them specifically than put them together in dimension reduction; (2) The data for frequencies and mode shapes are in different scale magnitudes, it is improper to put them in the same network, especially in the normalization process.
In this paper, we propose a new parallel auto-encoder framework (Para-AF) and our aim is to achieve parallel dimensionality reduction and feature extraction for the frequency data and mode shape data and put them together in relationship learning for detection/identification of damage in a seven-storey steel frame structure. The proposed framework is also incorporated with sparsity to enhance the performance of parallel dimensionality reduction. The modal information such as natural frequencies and their associated mode shapes will be utilized as input separately in several sparse auto-encoders while the output will be the structural elementary stiffness parameters of the structure after integration of these several models. This is the first time for deep learning networks to deal with multi-scale dataset in SHM and it is also new in machine learning. Furthermore, the measurement noise effect and uncertainties effect are considered in the training dataset motivated by [
10] in ANNs. Both baseline datasets (without noise effect) and noisy datasets (with measurement noises and uncertainties) are utilised to demonstrate the robustness of the proposed approach. The efficiency and accuracy of predictions for the proposed framework are evaluated by extensive experiments in terms of the Mean Squared Error (MSE) and the defined Regression Value (R-value) [
2]. Finally, we conducted experiments by using the sparse auto-encoder method with our proposed parallel structure. The results from the previous SAF is compared with those obtained by our proposed approach, which can show the significant advantages of the proposed parallel structure.
The organization of this paper is as follows:
Section 2 describes the parallel auto-encoder framework (Para-AF) and the sparsity feature in details;
Section 3 evaluates the performances of the proposed framework with numerical studies; Finally,
Section 4 presents our conclusions.
3. Numerical Experiments
Numerical studies including the numerical model, data generation, data pre-processing as well as the evaluation of the proposed framework will be described in this section. With the consideration of the uncertainties in the finite element modelling and measurement noise effect in the data, the accuracy and efficiency of the proposed approach will be examined through the simulation data generated from the numerical finite element model.
3.1. Infrastructure Model and Numerical Model
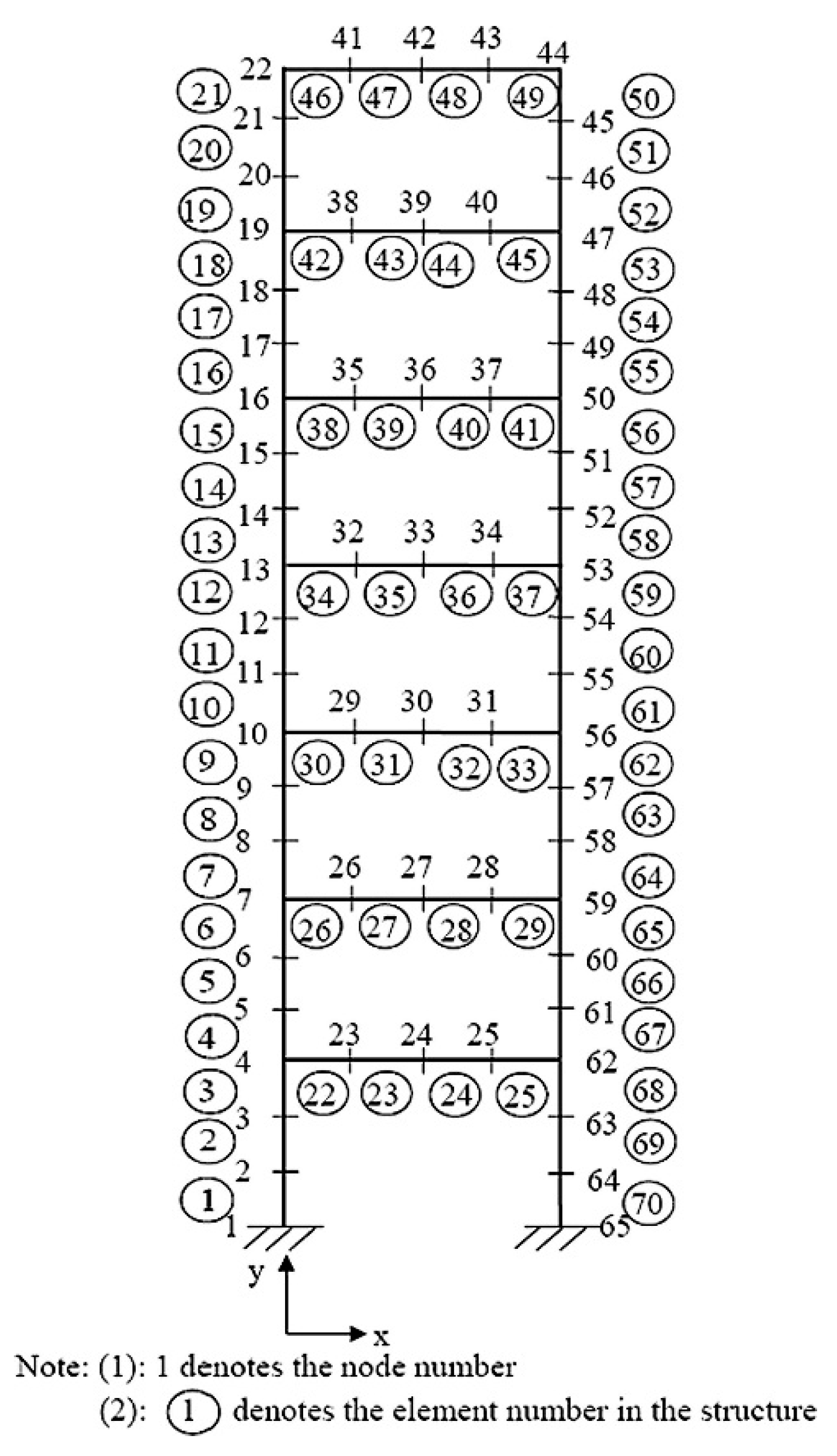
A seven-storey steel frame structure has been built in the laboratory at Curtin University and its frame dimensions are illustrated in
Figure 3. Each storey is 0.3 m in height, composing up to 2.1 m for the total column height of the steel frame whereas the beam length of the steel frame is 0.5 m. The cross-sections of the column and beam elements are shown with dimensions of 49.98 mm × 4.85 mm and 49.89 mm × 8.92 mm respectively, while the corresponding measured mass densities of the column and beam elements are 7850 kg/m
3 and 7734.2 kg/m
3. Initial Young’s modulus of 210 GPa is applied to all members. The column and beam elements are connected continuously by welding at the top and bottom of the beam sections. The two columns at the bottom of the steel frame are welded onto a thick and solid steel plate which is fixed to the ground. In order to simulate the mass from the floor of a building structure, two pairs of mass blocks with each around 4 kg in weight are fixed at the quarter and three-quarter length of the beam in each storey.
The finite element model of the whole frame structure is shown in
Figure 4 which includes 65 nodes and 70 planar frame elements. The weights of steel blocks are loaded as concentrated masses at the corresponding nodes of the finite element model. Each node has three DOFs (two translational displacements x, y and a rotational displacement), contributing total 195 DOFs to the system. The translational (Node 1) and rotational (Node 65) restraints at the supports are expressed initially by the large stiffness of 3 × 109 N/m and 3 × 109 N·m/rad respectively. The initial finite element model updating has been executed to minimize the discrepancies between the analytical finite element model and the experimental model in the laboratory. This updated finite element model is adopted as the baseline model for generating the training, validation and testing data. The detailed model updating process can be referred to [
4].
Notice that the data generated from FEM model could not totally replace the data from real structures. There are thousands of possibilities for the structural damage scenarios in real world. However, it is not practical to collect the data under such huge different damage scenarios from real civil structures. Therefore, the simulated data from FEM model is used in this paper to explore the damage identification problem.
3.2. Data Generation
Modal analysis is conducted using the finite element model above to generate the training dataset for both the input and output. As mentioned before, 7 frequencies and their corresponding mode shape parameters at 14 beam-column joints are measured and defined as the input. Seventy elemental stiffness parameters are generated as the output. The output is normalized to the range between 0 and 1, where 0 represents the totally damaged state whereas 1 represents the intact state of the structure element. For an instance, if a particular stiffness parameter is equivalent to 0.9, it indicates there is 10% stiffness reduction at this element.
Both single damage and multiple damage cases are considered in the 70 elements model. For single damage cases, there are total 2100 data sets generated from the baseline model based on the varying stiffness parameter of each element from 1, 0.99, 0.98… to 0.7 with leaving the other elements undamaged. Hence, for single element damage cases, 30 data sets are generated for each element with introducing a local damage. While 10,300 data sets are generated for multiple damage cases, two or more elements are considered as damage statuses with the stiffness parameter changing from 1, 0.99, 0.98… to 0.7. Meanwhile, the other elements are considered as intact statuses. Overall, 12,400 baseline data sets are generated based on the finite element model for training and validation.
Apart from the clean baseline datasets, noise datasets with measurement noise and uncertainty are also included in our study to further investigate the effectiveness and robustness of our proposed parallel structured model. For the noise datasets, 1% and 5% Gaussian noises are added to first seven frequencies and the associated mode shapes respectively with consideration of structural frequencies measured more accurately as reported in [
21]. Besides, 1% uncertainty is considered in the stiffness parameters to simulate the finite element modelling errors. We expect to make the proposed model trained by these noise data more robust for predicting unknown data with measurement noises and uncertainties. Both baseline datasets and noise datasets will be used in comparison with the state-of-the-art models and the proposed model in the following experiments.
3.3. Data Pre-Processing
Since each mode shape subset belongs to a natural frequency; in addition, the input subsets of frequency features and mode shapes features are measured in different scales. Thus, to avoid the additional complexity in the input dataset, we first divide the entire dataset which including all the frequencies and mode shape parameters into 8 subsets. Each subset is normalized to the range of [0, 1] to serve the active range of ‘ReLU’.
For the output vector, each element lies in the range between 0 and 1, where 0 denotes the fully damaged state while 1 denotes the intact state. Since only a few elements are defined to be in damage situation in each sample and the stiffness parameter does not vary a lot in damage cases. Therefore, the stiffness parameters are normalized to the expanded range of [−1, 1] to serve the operating range of linear activation function at the output.
Then these pre-processed input and output datasets will be utilized to evaluate the proposed approach in the following sections.
4. Performance Evaluation
The above both baseline datasets and noise datasets are utilised to evaluate the performances of the proposed approach against the state-of-the-art model, for example, “Sparse Auto-encoder Framework (SAF)” [
34]. For each of the model training, the pre-processed dataset is randomly split into training, validation and testing subsets according to the percentages 70%, 15% and 15% respectively. Finally, the Mean Squared Error (MSE) value and Regression value (R-value) are used to evaluate the quality of damage predictions of the proposed parallel model with the state-of-the-art models on the testing datasets. In particular, the MSE measures the distance between the estimated output of testing datasets from the proposed model and the labelled output. R-value represents the coefficient of correlation, which is used to measure the correlation between estimated output and labelled output. For our case, the higher R-value the more accurate of the proposed model. The details of proposed model architecture and evaluated performances are presented as follows.
In our experiment, the proposed parallel auto-encoder framework utilizes one hidden layer for each parallel block in dimensionality reduction component, with 9 hidden neurons in the 1st block for frequency data while 13 hidden neurons for the rest of 7 blocks for mode shape data. Since we implement sparse auto-encoders in this component, the number of hidden neurons are chosen carefully to allow the model to have more capacity for learning. To demonstrate the effectiveness of utilising many relationship learning layers, five hidden layers of having 90, 85, 80, 75 and 70 neurons respectively are defined in the relationship learning component. By using the decreasing number of hidden units in the hidden layers, the input vector is gradually compressed and regressed to the target vector. To perform a fair comparison with SAF, a simple proposed parallel model Para-AF-0 with the same number of hidden layers and neurons (90-80-70) as SAF in relationship learning component is also evaluated in this study.
The performances of using the SAF and the proposed approach are compared by investigating the MSE values and R-values on the testing datasets. Both baseline datasets and noise datasets with measurement noise and uncertainty effect are used. The performance evaluation results are shown as below.
As shown in
Table 1, for the baseline dataset, MSE values obtained from SAF, Para-AF-0 and Para-AF are
,
and
, respectively. Para-AF-0 has marginally improved the performance over SAF with a smaller MSE value for baseline dataset. Meanwhile, for noisy datasets, we can observe a 3% increment in R-value of Para-AF-0 versus SAF. They indicate that the proposed parallel dimensionality reduction has achieved the expected effectiveness by extracting features in parallel from multi-scale datasets. In addition, a significant increment (around 8%) in R-value is observed in Para-AF-0 against Para-AF, which shows the effectiveness of applying more relationship learning layers. For both datasets, the performances of these three methods show the same trend. Therefore, the proposed parallel method not only improves the effectiveness but also improves the noise robustness for damage detection/identification.
Since dealing with the noise dataset is much more challenging in the real-world, only this case will be further presented in the following comparisons. To further evaluate the quality of damage identification in terms of both magnitudes and locations, the prediction of a single damage case and a multiple damage case randomly selected from the testing datasets are shown in
Figure 5 and
Figure 6 respectively.
Firstly, for the single damage case, SAF can predict the true location of the single damage but fail to identify the true magnitude of the damage. In contrary, it can be observed clearly that the proposed method performs the best in damage identification with a very close identified stiffness reduction value against the true value. Besides, SAF produces a considerable false identification at the 13th element location of the structure. Therefore, the proposed method gives the higher accuracy in the prediction of damage pattern in terms of both the location and severity.
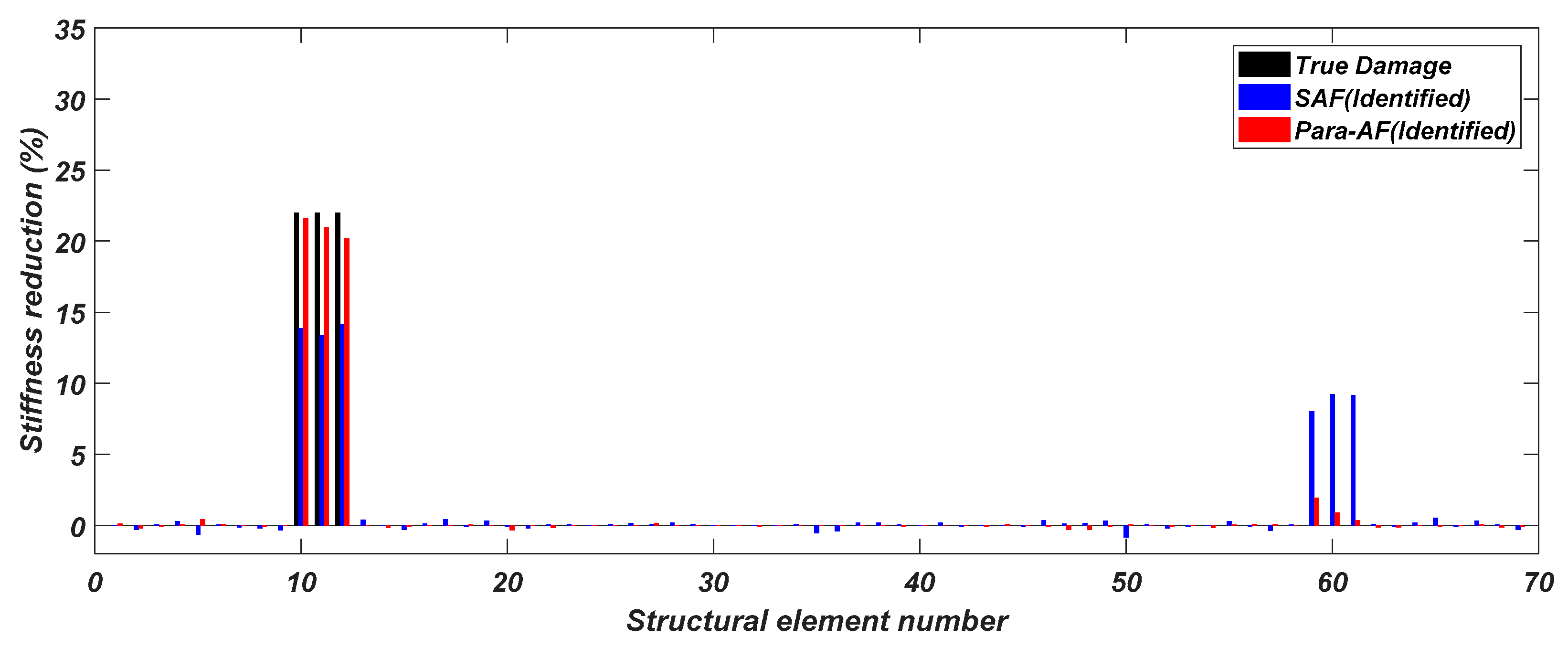
Furthermore, to evaluate the models for multiple structural damage cases, following example is chosen from the testing dataset and the predictions are shown in
Figure 6. In comparison to the single damage case, the multiple damage cases need higher precision in identifying multiple damages’ locations and severities. It can be observed that the proposed approach performs much better in multiple damage cases too, with all the damage locations accurately detected. Furthermore, the identified stiffness reductions are very close to the true values with very small false identifications. In contrast, SAF is not working very well in identifying multiple damages with some significant false identifications appeared at non-damage locations.
As shown in the figures above, the identified stiffness reductions of the proposed method are superior to SAF in terms of both the magnitude and the location and this implies the robustness of using the proposed approach in structural elemental stiffness predictions.
Therefore, it has been demonstrated that our proposed parallel based approach not only improves the effectiveness but also improves the robustness for damage detection/identification in structural health monitoring against the state-of-the-art approach.