Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion
Abstract
:1. Introduction
2. Literature Review
3. Modified Multi-Depot Vehicle Routing Problem
3.1. Modification
3.2. Impact of the Modified Criterion
4. Metaheuristic Solution
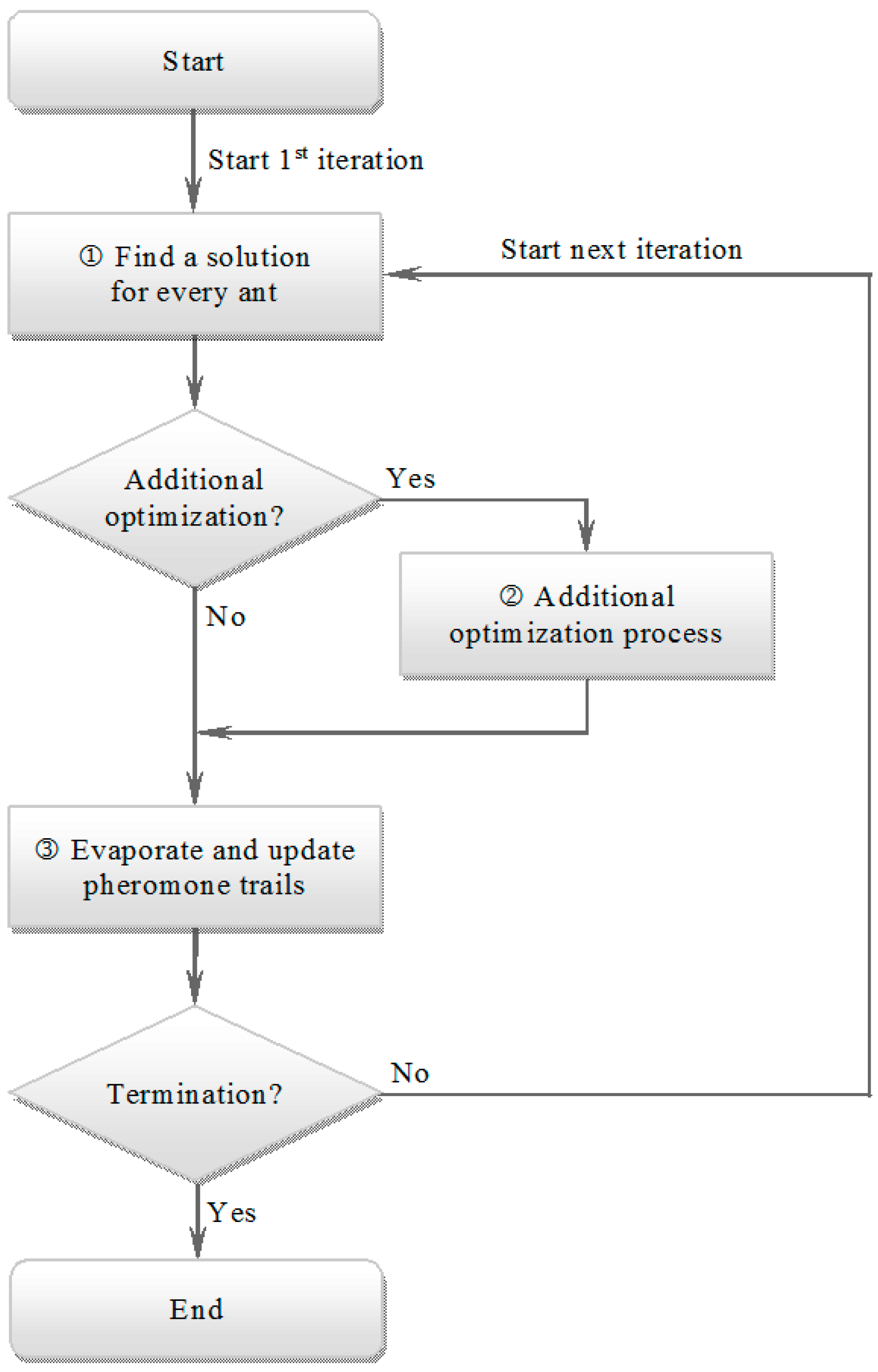
4.1. Original Algorithm
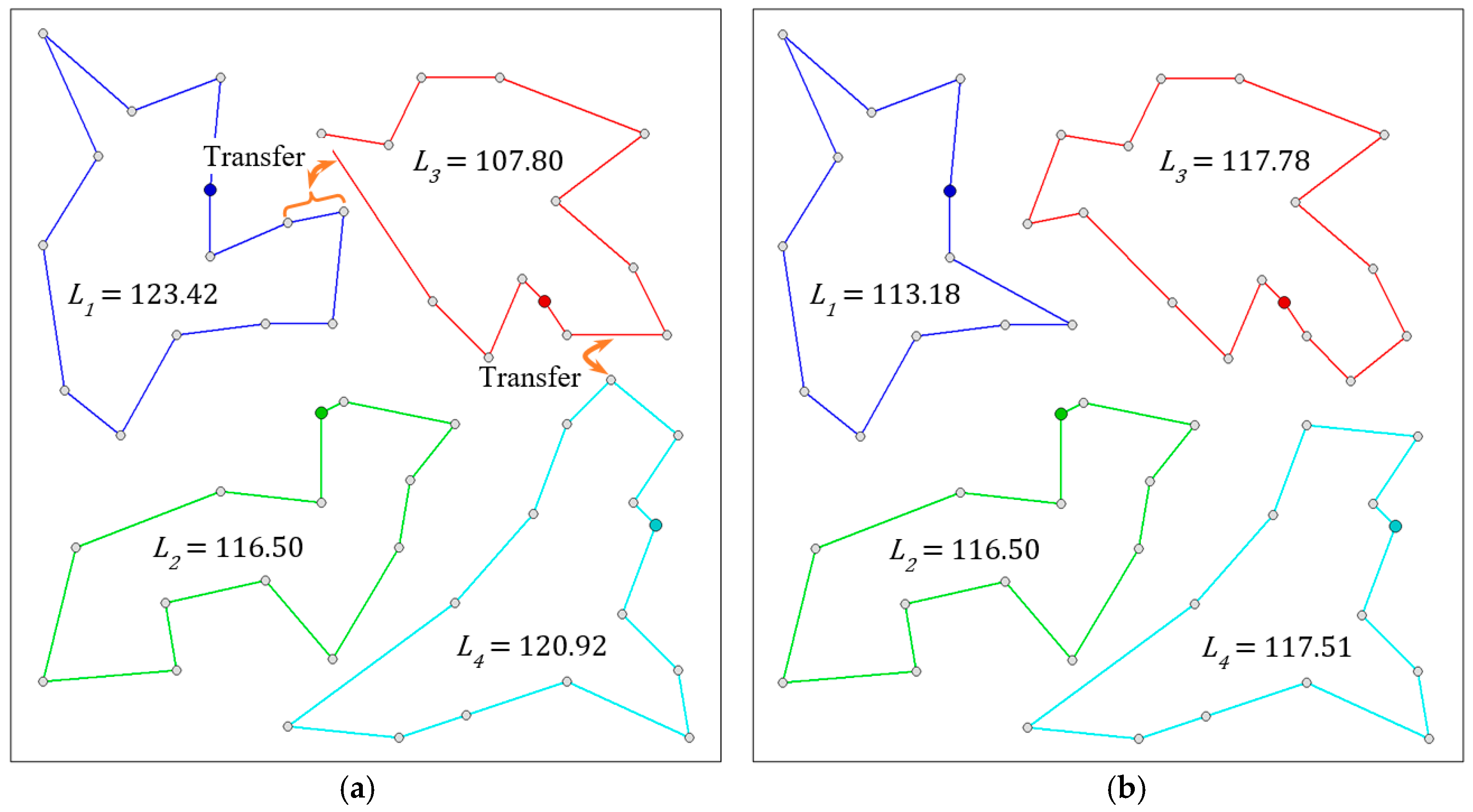
4.2. Additional Optimization Process
- Single route optimization (SRO),
- Mutual routes optimization (MRO).
| Algorithms 1. Single route optimization in pseudocode. |
 |
| Algorithms 2. Mutual routes optimization in pseudocode. |
 |
5. Experiments and Results
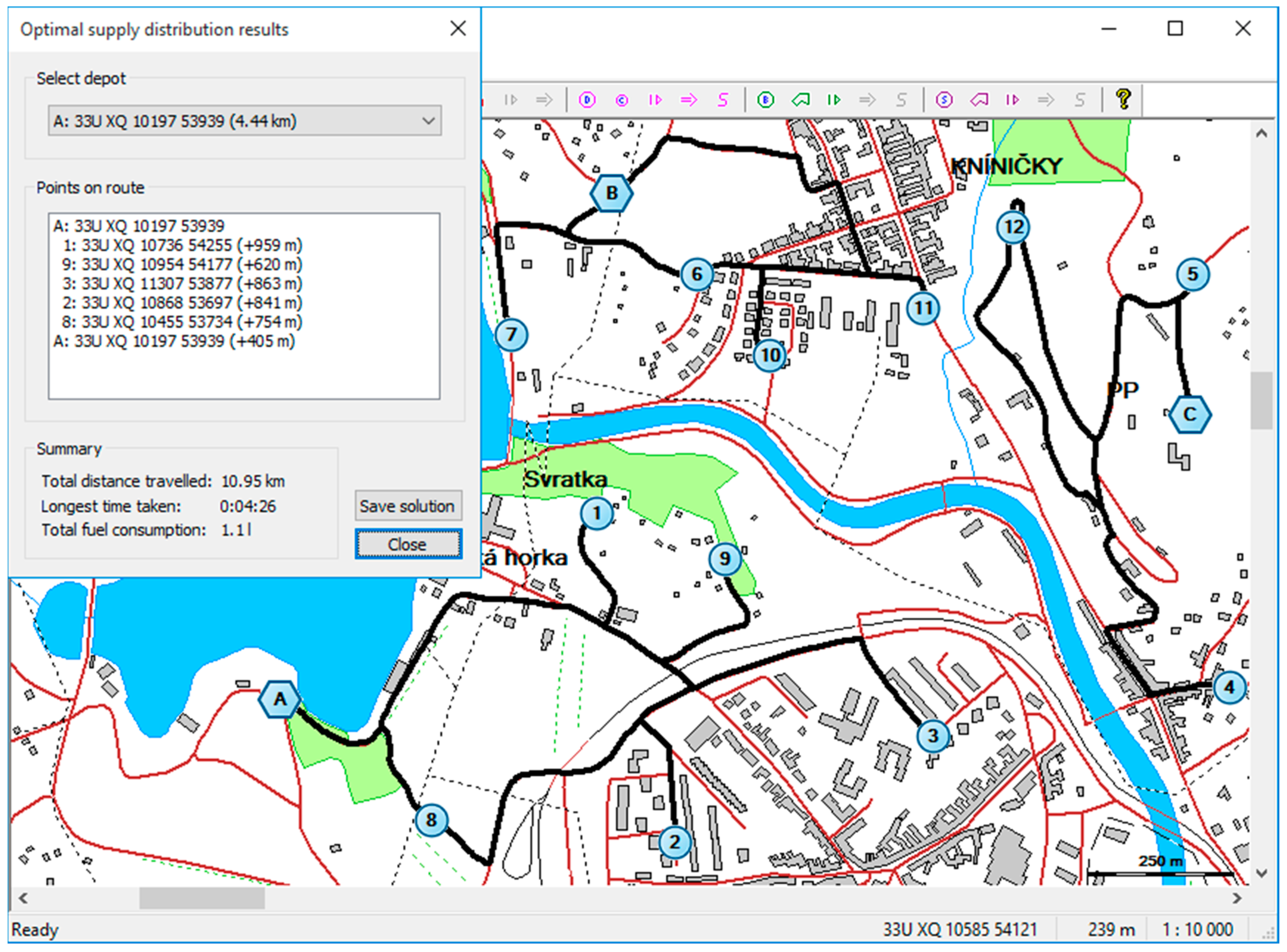
6. Practical Application
7. Conclusions
Funding
Conflicts of Interest
References
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Carlsson, J.; Ge, D.; Subramaniam, A.; Wu, A.; Ye, Y. Solving min-max multi-depot vehicle routing problem. Lect. Glob. Optim. 2009, 55, 31–46. [Google Scholar]
- Narasimha, K.V.; Kivelevitch, E.; Sharma, B.; Kumar, M. An ant colony optimization technique for solving min–max multi-depot vehicle routing problem. Swarm Evolut. Comput. 2013, 13, 63–73. [Google Scholar] [CrossRef]
- Ho, W.; Ho, G.T.S.; Ji, P.; Lau, H.C.W. A hybrid genetic algorithm for the multi-depot vehicle routing problem. Eng. Appl. Artif. Intell. 2008, 21, 548–557. [Google Scholar] [CrossRef]
- Sharma, N.; Monika, M.A. Literature Survey on Multi-Depot Vehicle Routing Problem. Int. J. Res. Dev. 2015, 3, 1752–1757. [Google Scholar]
- Montoya-Torres, J.R.; Franco, J.L.; Isaza, S.N.; Jiménez, H.F.; Herazo-Padilla, N. A literature review of the vehicle routing problem with multiple depots. Comput. Ind. Eng. 2015, 79, 115–129. [Google Scholar] [CrossRef]
- Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
- Gillett, B.E.; Johnson, J.G. Multi-terminal vehicle-dispatch algorithm. Omega 1976, 4, 711–718. [Google Scholar] [CrossRef]
- Chao, M.I.; Golden, B.L.; Wasil, E. A new heuristic for the multi-depot vehicle routing problem that improves upon best-known solutions. Am. J. Math. Manag. Sci. 1993, 13, 371–406. [Google Scholar] [CrossRef]
- Renaud, J.; Laporte, G.; Boctor, F.F. A tabu search heuristic for the multi-depot vehicle routing problem. Comput. Oper. Res. 1996, 23, 229–235. [Google Scholar] [CrossRef]
- Escobar, J.W.; Linfati, R.; Toth, P.; Baldoquin, M.G. A hybrid Granular Tabu Search algorithm for the Multi-Depot Vehicle Routing Problem. J. Heuristics 2014, 20, 483–509. [Google Scholar] [CrossRef]
- Soto, M.; Sevaux, M.; Rossi, A.; Reinholzc, A. Multiple neighborhood search, tabu search and ejection chains for the multi-depot open vehicle routing problem. Comput. Ind. Eng. 2017, 107, 211–222. [Google Scholar] [CrossRef]
- Wu, T.H.; Low, C.; Bai, J.W. Heuristic solutions to multi-depot location routing problems. Comput. Oper. Res. 2002, 29, 1393–1415. [Google Scholar] [CrossRef]
- Lim, A.; Zhu, W. A fast and effective insertion algorithm for multi-depot vehicle routing problem and a new simulated annealing approach. In Advances in Artificial Intelligence, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4031, pp. 282–291. [Google Scholar]
- Ombuki-Berman, B.; Hanshar, F.T. Using Genetic Algorithms for Multi-depot Vehicle Routing. In Bio-Inspired Algorithms for the Vehicle Routing Problem; Springer: Berlin/Heidelberg, Germany, 2009; Volume 161, pp. 77–99. [Google Scholar]
- Seidgar, H.; Abedi, M.; Tadayoni, S.; Rezaeian, J. An efficient hybrid of genetic and simulated annealing algorithms for multi server vehicle routing problem with multi entry. Int. J. Ind. Syst. Eng. 2016, 24, 333–360. [Google Scholar] [CrossRef]
- Karakatic, S.; Podgorelec, V. A survey of genetic algorithms for solving multi-depot vehicle routing problem. Appl. Soft Comput. 2015, 27, 519–532. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.Z.; Xie, J.X. A parallel improved ant colony optimization for multi-depot vehicle routing problem. J. Oper. Res. Soc. 2010, 62, 183–188. [Google Scholar] [CrossRef]
- Yao, B.; Hu, P.; Zhang, M.; Tian, X. Improved Ant Colony Optimization for Seafood Product Delivery Routing Problem. Promet-Traffic Transp. 2014, 26, 1–10. [Google Scholar] [CrossRef]
- Tang, Y. An Improved Ant Colony Optimization for Multi-Depot Vehicle Routing Problem. International. J. Eng. Technol. 2016, 8, 385–388. [Google Scholar]
- Gao, J. Automobile chain maintenance parts delivery problem using an improved ant colony algorithm. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Ma, Y.; Han, J.; Kang, K.; Yan, F. An Improved ACO for the Multi-depot Vehicle Routing Problem with Time Windows. In Proceedings of the Tenth International Conference on Management Science and Engineering Management; Advances in Intelligent Systems and Computing; Springer: Singapore, 2017; Volume 502. [Google Scholar]
- Ting, C.J.; Chen, C.H. Combination of multiple ant colony system and simulated annealing for the multi-depot vehicle routing problem with time windows. Transp. Res. Rec. J. Transp. Res. Board 2008, 2089, 85–92. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Lahrichi, N.; Rei, W. A Hybrid Genetic Algorithm for Multi-Depot and Periodic Vehicle Routing Problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- De Oliveira, F.B.; Enayatifar, R.; Sadaei, H.J.; Guimarães, F.G.; Potvin, J.Y. A cooperative coevolutionary algorithm for the Multi-Depot Vehicle Routing Problem. Expert Syst. Appl. 2016, 43, 117–130. [Google Scholar] [CrossRef]
- Wang, X.; Golden, B.; Wasil, E. The min-max multi-depot vehicle routing problem: Heuristics and computational results. J. Oper. Res. Soc. 2015, 66, 1430–1441. [Google Scholar] [CrossRef]
- Wang, X.; Golden, B.; Wasil, E.; Zhang, R. The min–max split delivery multi-depot vehicle routing problem with minimum service time requirement. Comput. Oper. Res. 2016, 71, 110–126. [Google Scholar] [CrossRef]
- Benning, L. Why Is the Traveling Salesman Problem NP Complete? Quora.com. 2014. Available online: https://www.quora.com/Why-is-the-traveling-salesman-problem-NP-complete (accessed on 10 May 2018).
- Cordeau, J.F.; Gendreau, M.; Laporte, G. A tabu search heuristic for periodic and multi-depot vehicle routing problems. Networks 1997, 30, 105–119. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Maischberger, M. A parallel iterated tabu search heuristic for vehicle routing problems. Comput. Oper. Res. 2012, 39, 2033–2050. [Google Scholar] [CrossRef]
- NEO Web, Networking and Emerging Optimization. University of Malaga, Spain. Available online: http://neo.lcc.uma.es/vrp/vrp-instances/multiple-depot-vrp-instances/ (accessed on 19 February 2018).
- Stodola, P.; Mazal, J. Applying the Ant Colony Optimisation Algorithm to the Capacitated Multi-Depot Vehicle Routing Problem. Int. J. Bio-Inspir. Comput. 2016, 8, 228–233. [Google Scholar]
- Stodola, P.; Mazal, J. Tactical Decision Support System to Aid Commanders in their Decision-Making. In Modelling and Simulation for Autonomous Systems; Springer: Cham, Switzerland, 2016; pp. 396–406. [Google Scholar]
- Blaha, M.; Silinger, K. Application support for topographical-geodetic issues for tactical and technical control of artillery fire. Int. J. Circuits Syst. Signal Proc. 2018, 12, 48–57. [Google Scholar]
- Hodicky, J. Standards to support military autonomous system life cycle. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; Volume 644, pp. 671–678. [Google Scholar]
- Rybansky, M. Trafficability analysis through vegetation. In Proceedings of the International Conference on Military Technologies, Brno, Czech Republic, 31 May–2 June 2017; pp. 207–210. [Google Scholar]
- Drozd, J. Analysis Results of the Military Observer Training System. Econ. Manag. 2016, 2016, 24–31. [Google Scholar]
- Farlik, J.; Casar, J.; Stary, V. Simplification of missile effective coverage zone in air defence simulations. In Proceedings of the International Conference on Military Technologies, Brno, Czech Republic, 31 May–2 June 2017; pp. 733–737. [Google Scholar]
- Hasilova, K.; Vališ, D. Non-parametric estimates of the first hitting time of Li-ion battery. Measurement 2018, 113, 82–91. [Google Scholar] [CrossRef]
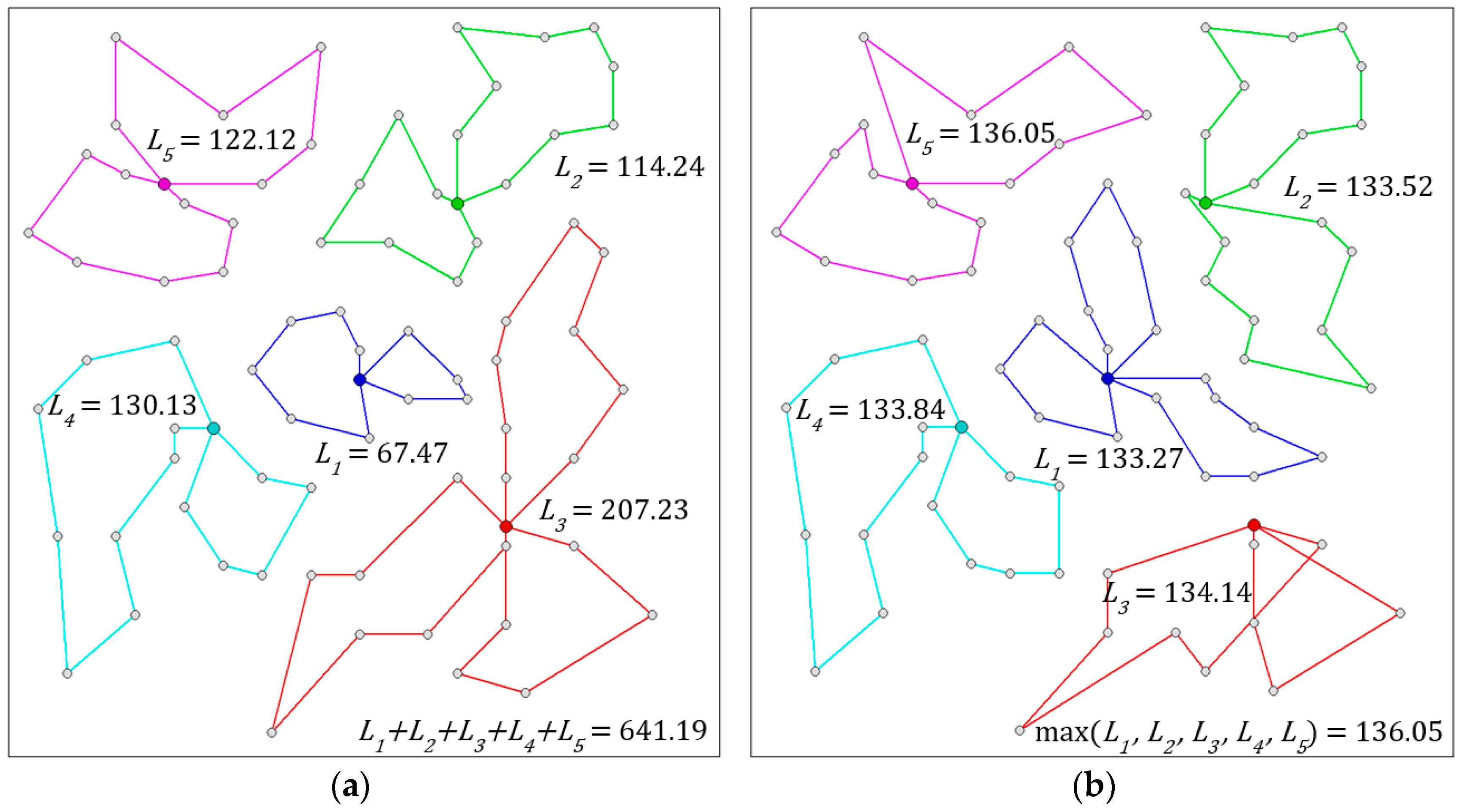

| Problem | BKS | ACO | Gap |
|---|---|---|---|
| MDVRP | (a) 641.19 | (c) 670.82 | (e) 4.62% |
| M-MDVRP | (b) 207.23 | (d) 136.05 | (f) 52.32% |
| Instance | Original ACO | Orig. ACO Runtime | ACO with AOP | ACO AOP Runtime | Solution Gap | Runtime Gap |
|---|---|---|---|---|---|---|
| p01 | 157.31 | 1.5 s | 152.54 | 1.7 s | 3.13% | 11.11% |
| p02 | 129.00 | 1.6 s | 125.82 | 1.8 s | 2.53% | 14.58% |
| p03 | 139.66 | 3.7 s | 136.05 | 4.3 s | 2.65% | 16.22% |
| p04 | 518.37 | 23.1 s | 511.41 | 28.4 s | 1.36% | 22.94% |
| p05 | 381.99 | 20.7 s | 378.17 | 25.6 s | 1.01% | 23.83% |
| p06 | 314.87 | 25.7 s | 301.75 | 31.9 s | 4.35% | 24.25% |
| p07 | 248.07 | 25.2 s | 228.95 | 30.9 s | 8.35% | 22.75% |
| p08 | 2480.46 | 233.1 s | 2224.85 | 361.0 s | 11.49% | 54.85% |
| p09 | 1468.86 | 267.3 s | 1364.70 | 418.3 s | 7.63% | 56.49% |
| p10 | 1055.09 | 301.0 s | 960.76 | 468.5 s | 9.82% | 55.65% |
| p11 | 795.28 | 278.5 s | 749.41 | 422.9 s | 6.12% | 51.85% |
| p12 | 663.04 | 12.8 s | 659.48 | 15.4 s | 0.54% | 20.58% |
| p13 | 659.48 | 13.4 s | 659.48 | 16.0 s | 0.00% | 19.59% |
| p14 | 682.84 | 14.2 s | 682.84 | 16.9 s | 0.00% | 18.86% |
| p15 | 730.20 | 124.6 s | 640.58 | 167.1 s | 13.99% | 34.08% |
| p16 | 788.12 | 138.0 s | 651.55 | 188.1 s | 20.96% | 36.28% |
| p17 | 817.65 | 111.4 s | 677.27 | 147.3 s | 20.73% | 32.26% |
| p18 | 761.92 | 188.9 s | 652.24 | 279.2 s | 16.82% | 47.79% |
| p19 | 870.90 | 175.3 s | 651.55 | 253.1 s | 33.67% | 44.40% |
| p20 | 916.53 | 200.3 s | 681.13 | 292.8 s | 34.56% | 46.18% |
| p21 | 862.00 | 466.0 s | 659.25 | 818.8 s | 30.75% | 75.70% |
| p22 | 962.17 | 506.2 s | 657.90 | 952.4 s | 46.25% | 88.14% |
| p23 | 1010.87 | 488.5 s | 686.69 | 895.2 s | 47.21% | 83.25% |
| Instance (N/M) | Problem | BKS | ACO | Gap |
|---|---|---|---|---|
| p01 (50/4) | MDVRP | 576.87 | 607.66 | 5.34% |
| M-MDVRP | 237.81 | 152.54 | 55.90% | |
| p02 (50/4) | MDVRP | 473.53 | 495.34 | 4.61% |
| M-MDVRP | 169.57 | 125.82 | 34.77% | |
| p03 (75/5) | MDVRP | 641.19 | 670.82 | 4.62% |
| M-MDVRP | 207.23 | 136.05 | 52.32% | |
| p04 (100/2) | MDVRP | 1001.59 | 1021.36 | 1.97% |
| M-MDVRP | 532.24 | 511.41 | 4.07% | |
| p05 (100/2) | MDVRP | 750.03 | 750.72 | 0.09% |
| M-MDVRP | 378.17 | 378.17 | 0.00% | |
| p06 (100/3) | MDVRP | 876.50 | 902.91 | 3.01% |
| M-MDVRP | 432.59 | 301.75 | 43.36% | |
| p07 (100/4) | MDVRP | 885.80 | 907.55 | 2.46% |
| M-MDVRP | 246.21 | 228.95 | 7.54% | |
| p08 (249/2) | MDVRP | 4437.68 | 4449.65 | 0.27% |
| M-MDVRP | 2474.82 | 2224.85 | 11.24% | |
| p09 (249/3) | MDVRP | 3900.22 | 4085.51 | 4.75% |
| M-MDVRP | 1836.00 | 1364.70 | 34.54% | |
| p10 (249/4) | MDVRP | 3663.02 | 3825.73 | 4.44% |
| M-MDVRP | 1049.12 | 960.76 | 9.20% | |
| p11 (249/5) | MDVRP | 3554.18 | 3732.36 | 5.01% |
| M-MDVRP | 808.21 | 749.41 | 7.85% | |
| p12 (80/2) | MDVRP | 1318.95 | 1318.95 | 0.00% |
| M-MDVRP | 659.48 | 659.48 | 0.00% | |
| p13 (80/2) | MDVRP | 1318.95 | 1318.95 | 0.00% |
| M-MDVRP | 659.48 | 659.48 | 0.00% | |
| p14 (80/2) | MDVRP | 1360.12 | 1365.69 | 0.41% |
| M-MDVRP | 686.69 | 682.84 | 0.56% | |
| p15 (160/4) | MDVRP | 2505.42 | 2554.12 | 1.94% |
| M-MDVRP | 646.92 | 640.58 | 0.99% | |
| p16 (160/4) | MDVRP | 2572.23 | 2606.22 | 1.32% |
| M-MDVRP | 694.27 | 651.55 | 6.56% | |
| p17 (160/4) | MDVRP | 2709.09 | 2709.09 | 0.00% |
| M-MDVRP | 690.55 | 677.27 | 1.96% | |
| p18 (240/6) | MDVRP | 3702.85 | 3871.01 | 4.54% |
| M-MDVRP | 895.50 | 652.24 | 37.30% | |
| p19 (240/6) | MDVRP | 3827.06 | 3884.81 | 1.51% |
| M-MDVRP | 694.27 | 651.55 | 6.56% | |
| p20 (240/6) | MDVRP | 4058.07 | 4058.07 | 0.00% |
| M-MDVRP | 690.55 | 681.13 | 1.38% | |
| p21 (360/9) | MDVRP | 5474.84 | 5824.58 | 6.39% |
| M-MDVRP | 936.62 | 659.25 | 42.07% | |
| p22 (360/9) | MDVRP | 5702.16 | 5873.41 | 3.00% |
| M-MDVRP | 719.64 | 657.90 | 9.38% | |
| p23 (360/9) | MDVRP | 6095.46 | 6124.67 | 0.48% |
| M-MDVRP | 690.55 | 686.69 | 0.56% |
| Instance | Routes (Solution in Bold) | AvgDev (%) | StDev (%) |
|---|---|---|---|
| p01 | 152.24|151.86|151.02|152.54 | 0.477 (0.31%) | 0.661 (0.43%) |
| p02 | 125.15|125.47|125.82|118.90 | 2.469 (1.96%) | 3.303 (2.63%) |
| p03 | 133.27|133.52|134.14|133.84|136.05 | 0.754 (0.55%) | 1.104 (0.81%) |
| p04 | 511.41|509.95 | 0.732 (0.14%) | 1.035 (0.20%) |
| p05 | 378.17|372.55 | 2.808 (0.74%) | 3.971 (1.05%) |
| p06 | 301.02|300.14|301.75 | 0.551 (0.18%) | 0.802 (0.27%) |
| p07 | 228.95|224.81|226.79|227.00 | 1.088 (0.48%) | 1.695 (0.74%) |
| p08 | 2224.81|2224.85 | 0.020 (0.00%) | 0.028 (0.00%) |
| p09 | 1364.70|1362.17|1358.63 | 2.134 (0.16%) | 3.047 (0.22%) |
| p10 | 957.14|960.76|949.74|958.09 | 3.347 (0.35%) | 4.720 (0.49%) |
| p11 | 741.42|747.49|749.41|748.34|745.70 | 2.328 (0.31%) | 3.133 (0.42%) |
| p12 | 659.48|659.48 | 0.000 (0.00%) | 0.000 (0.00%) |
| p13 | 659.48|659.48 | 0.000 (0.00%) | 0.000 (0.00%) |
| p14 | 682.84|682.84 | 0.000 (0.00%) | 0.000 (0.00%) |
| p15 | 638.15|640.58|636.12|639.28 | 1.398 (0.22%) | 1.891 (0.30%) |
| p16 | 651.55|651.55|651.55|651.55 | 0.000 (0.00%) | 0.000 (0.00%) |
| p17 | 677.27|677.27|677.27|677.27 | 0.000 (0.00%) | 0.000 (0.00%) |
| p18 | 646.11|641.43|647.94|652.24|650.51|632.78 | 5.375 (0.82%) | 7.135 (1.09%) |
| p19 | 645.53|643.08|650.47|649.13|651.55|645.04 | 2.917 (0.45%) | 3.387 (0.52%) |
| p20 | 667.85|677.27|677.27|681.13|677.27|677.27 | 2.831 (0.42%) | 4.437 (0.65%) |
| p21 | 659.25|638.74|635.47|637.61|644.01|653.75|644.89|655.23|655.63 | 7.814 (1.19%) | 8.948 (1.36%) |
| p22 | 653.49|656.33|655.88|643.55|643.08|657.90|652.34|654.27|656.57 | 4.185 (0.64%) | 5.530 (0.84%) |
| p23 | 675.58|683.13|677.27|679.28|673.42|686.69|681.15|683.13|685.00 | 3.671 (0.53%) | 4.460 (0.65%) |
| Instance | BKS | Original ACO | ACO with AOP |
|---|---|---|---|
| StDev (%) | StDev (%) | StDev (%) | |
| p01 | 75.912 (31.92%) | 3.547 (2.25%) | 0.661 (0.43%) |
| p02 | 35.989 (21.22%) | 3.040 (2.36%) | 3.303 (2.63%) |
| p03 | 50.421 (24.33%) | 0.667 (0.48%) | 1.104 (0.81%) |
| p04 | 44.466 (8.35%) | 0.743 (0.14%) | 1.035 (0.20%) |
| p05 | 4.457 (1.18%) | 0.605 (0.16%) | 3.971 (1.05%) |
| p06 | 122.020 (28.21%) | 2.761 (0.88%) | 0.802 (0.27%) |
| p07 | 21.018 (8.54%) | 9.725 (3.92%) | 1.695 (0.74%) |
| p08 | 9.393 (0.42%) | 3.486 (0.14%) | 0.028 (0.00%) |
| p09 | 480.583 (26.18%) | 8.838 (0.60%) | 3.047 (0.22%) |
| p10 | 114.528 (10.92%) | 3.722 (0.35%) | 4.720 (0.49%) |
| p11 | 96.537 (11.94%) | 24.424 (3.07%) | 3.133 (0.42%) |
| p12 | 0.000 (0.00%) | 0.000 (0.00%) | 0.000 (0.00%) |
| p13 | 0.000 (0.00%) | 0.000 (0.00%) | 0.000 (0.00%) |
| p14 | 9.385 (1.37%) | 0.000 (0.00%) | 0.000 (0.00%) |
| p15 | 23.746 (3.67%) | 20.894 (2.86%) | 1.891 (0.30%) |
| p16 | 59.136 (8.52%) | 5.189 (0.66%) | 0.000 (0.00%) |
| p17 | 10.837 (1.57%) | 24.148 (2.95%) | 0.000 (0.00%) |
| p18 | 209.406 (23.38%) | 31.286 (4.11%) | 7.135 (1.09%) |
| p19 | 46.958 (6.76%) | 22.779 (2.62%) | 3.387 (0.52%) |
| p20 | 11.839 (1.71%) | 35.761 (3.90%) | 4.437 (0.65%) |
| p21 | 199.647 (21.32%) | 41.186 (4.78%) | 8.948 (1.36%) |
| p22 | 69.188 (9.61%) | 60.946 (6.33%) | 5.530 (0.84%) |
| p23 | 9.598 (1.39%) | 80.569 (7.97%) | 4.460 (0.65%) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stodola, P. Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion. Algorithms 2018, 11, 74. https://doi.org/10.3390/a11050074
Stodola P. Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion. Algorithms. 2018; 11(5):74. https://doi.org/10.3390/a11050074
Chicago/Turabian StyleStodola, Petr. 2018. "Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion" Algorithms 11, no. 5: 74. https://doi.org/10.3390/a11050074
APA StyleStodola, P. (2018). Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion. Algorithms, 11(5), 74. https://doi.org/10.3390/a11050074





