The NIRS Brain AnalyzIR Toolbox
Abstract
1. Introduction
2. Architecture of Toolbox
2.1. Data Classes
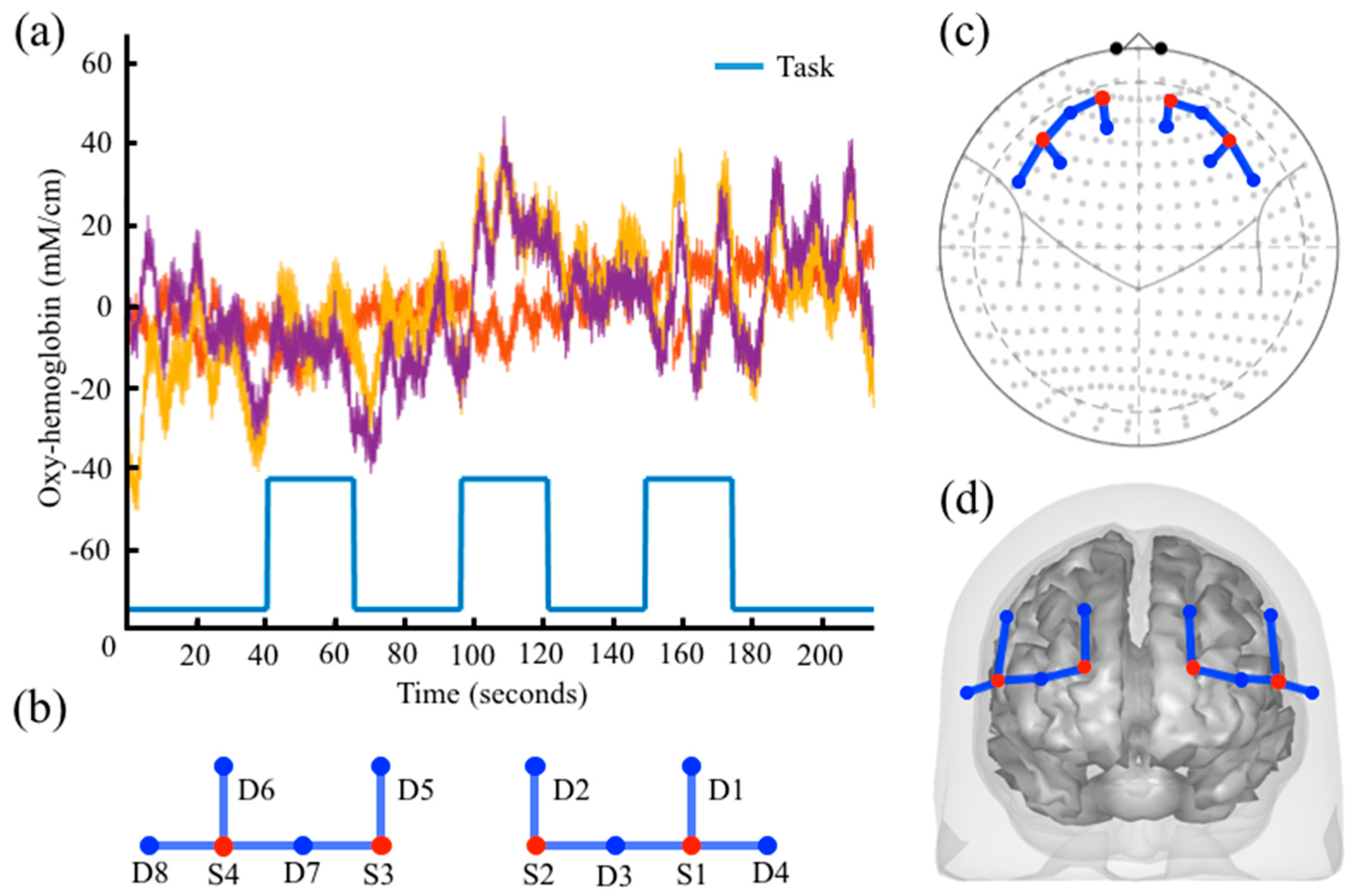
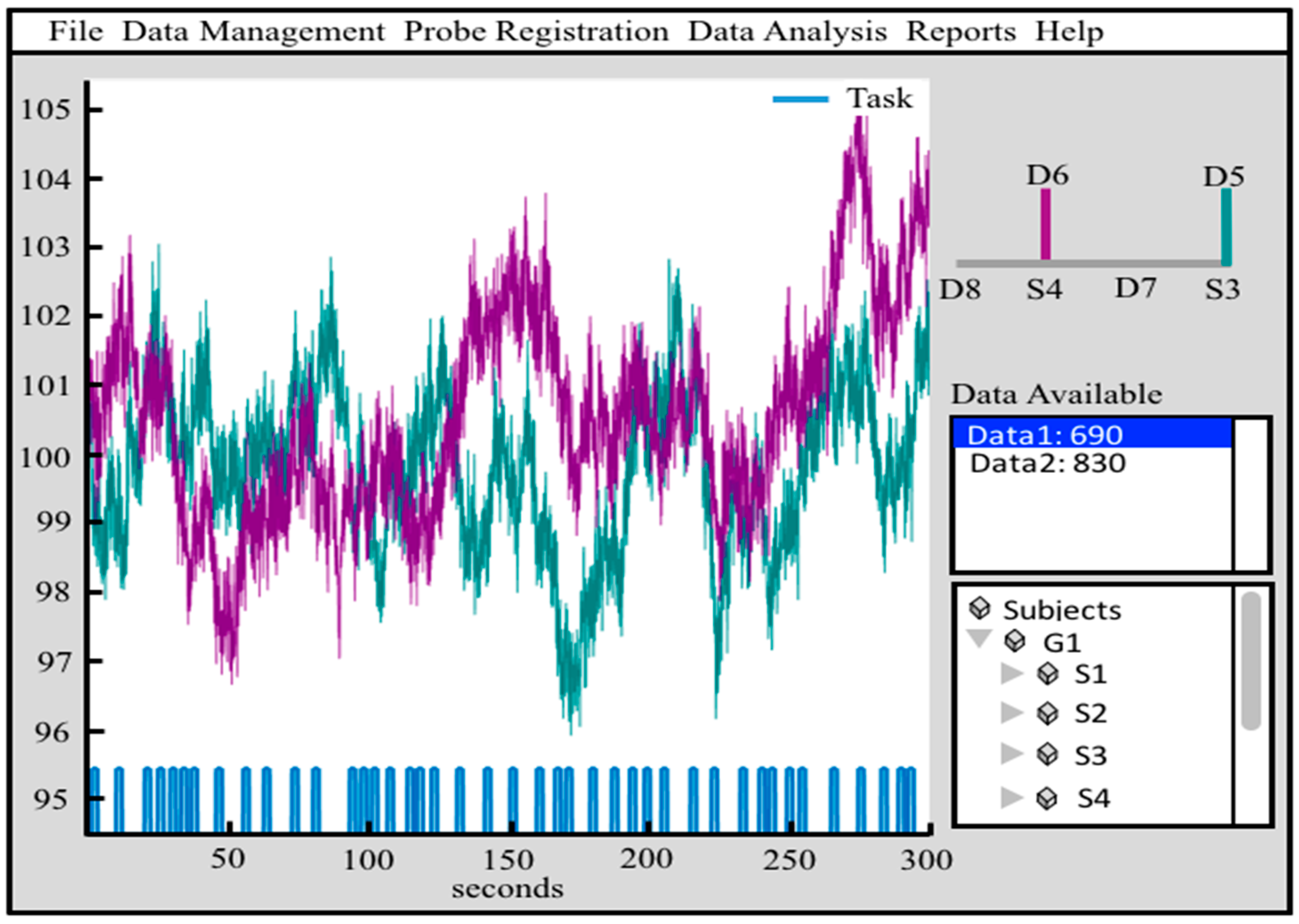
2.1.1. nirs.core.Data
2.1.2. nirs.core.Data
2.1.3. nirs.core.ChannelStats
2.1.4. nirs.core.ImageStats
2.1.5. Multimodal Object Classes
2.2. Processing Modules Classes
2.2.1. Data Management
2.2.2. Pre-Processing
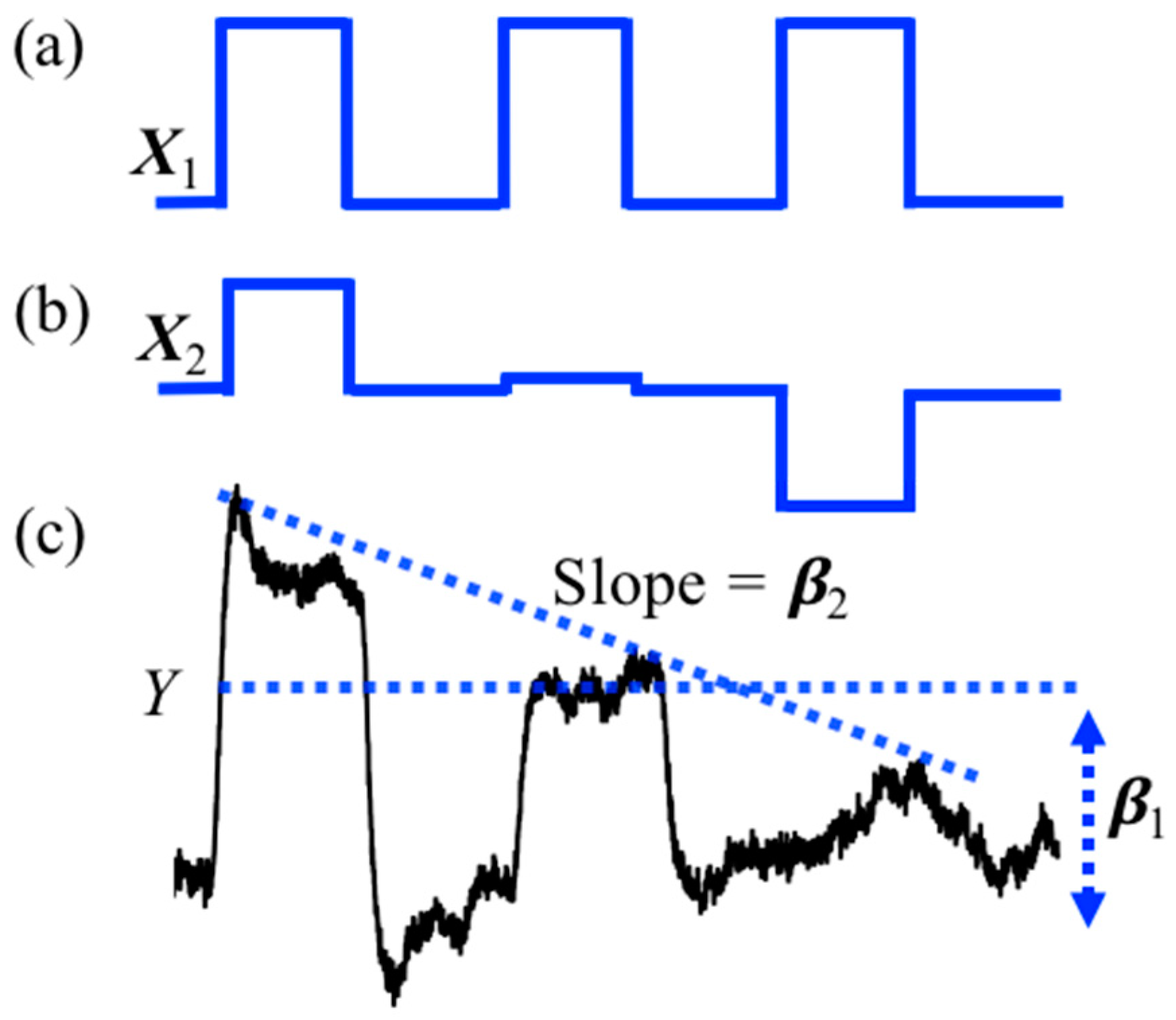
2.2.2.1. Baseline Correction
2.2.2.2. PCAfilter
2.2.3. Calculate CMRO2
2.2.4. HOMER-2 Interface
3. Statistical Modules
3.1. First-Level Statistical Models
3.1.1. OLS
3.1.2. AR-IRLS
3.1.3. NIRS-SPM
3.1.4. Nonlinear GLM
3.2. Canonical and Basis Sets
3.2.1. Canonical HRF
3.2.2. Gamma Function
3.2.3. Boxcar Function
3.2.4. FIR-Deconvolution
3.2.5. FIR-Impulse Response Deconvolution
3.2.6. General Canonical
3.2.7. Vestibular Canonical
3.3. Parametric Models
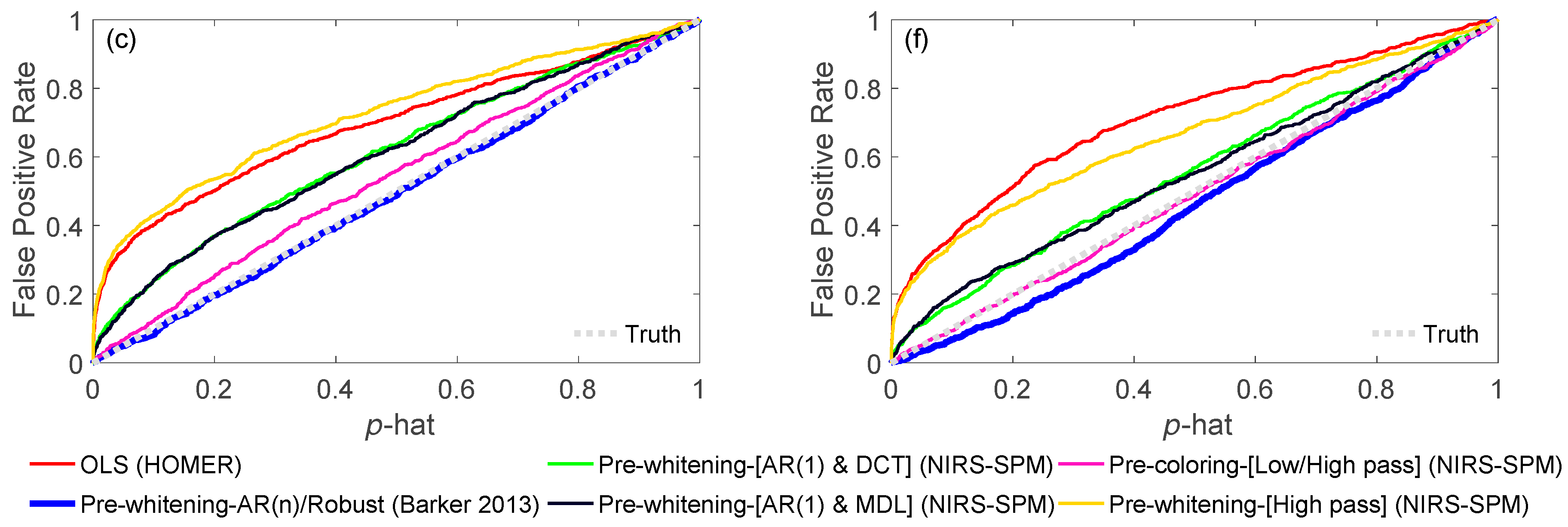
3.4. Comparison of Models
3.5. Second-Level Statistical Models
4. Image Reconstruction Modules
4.1. Optical Forward Model
4.2. Hierarchal Bayesian Inverse Models
4.3. Group-Level Image Reconstruction
4.4. Statistical Testing
5. Connectivity and Hyper-Scanning Modules
5.1. Correlation Models
5.1.1. Pre-Whitening
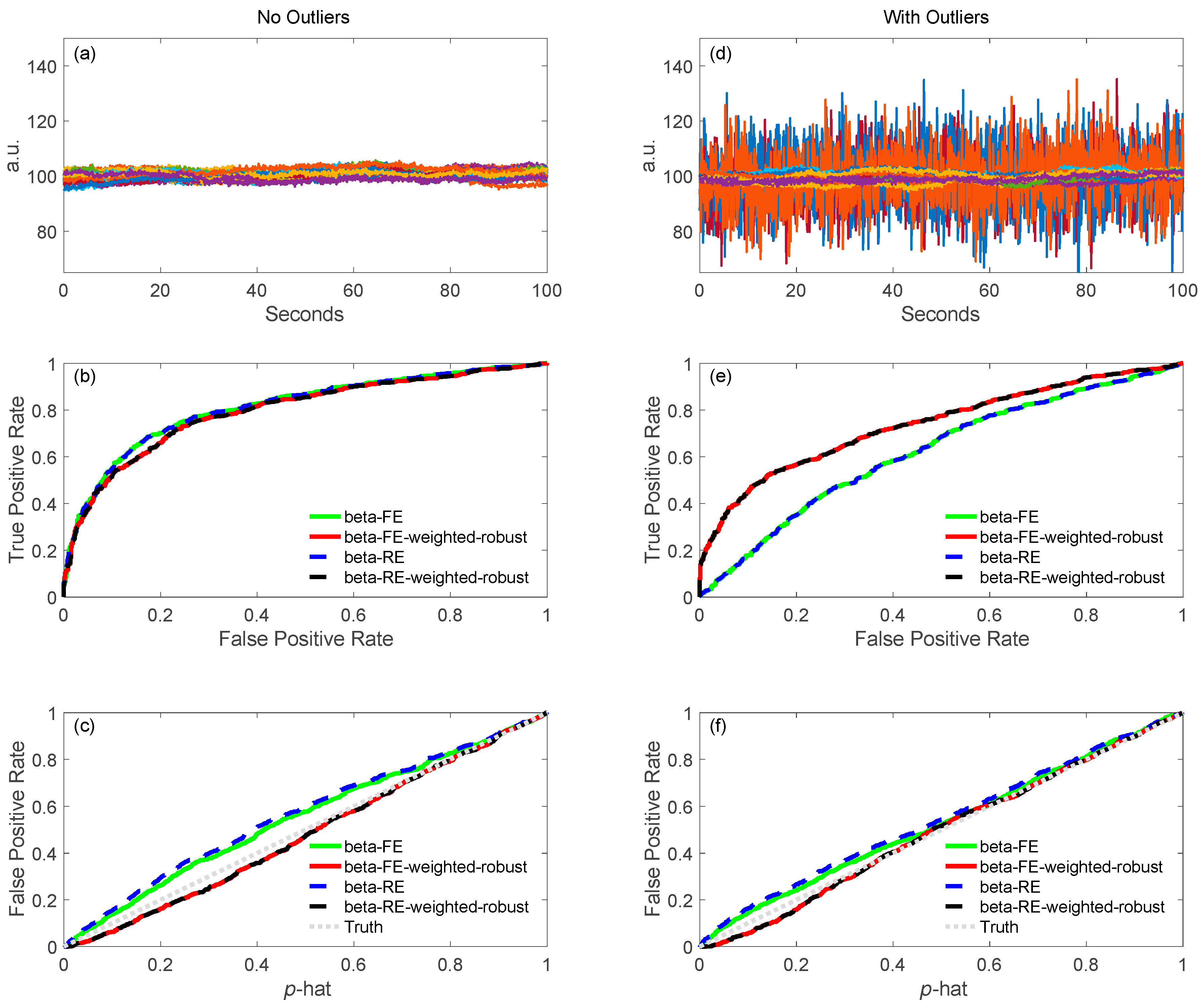
5.1.2. Robust Methods
5.2. Coherence Models
5.3. Hyperscanning
5.4. Group Connectivity Models
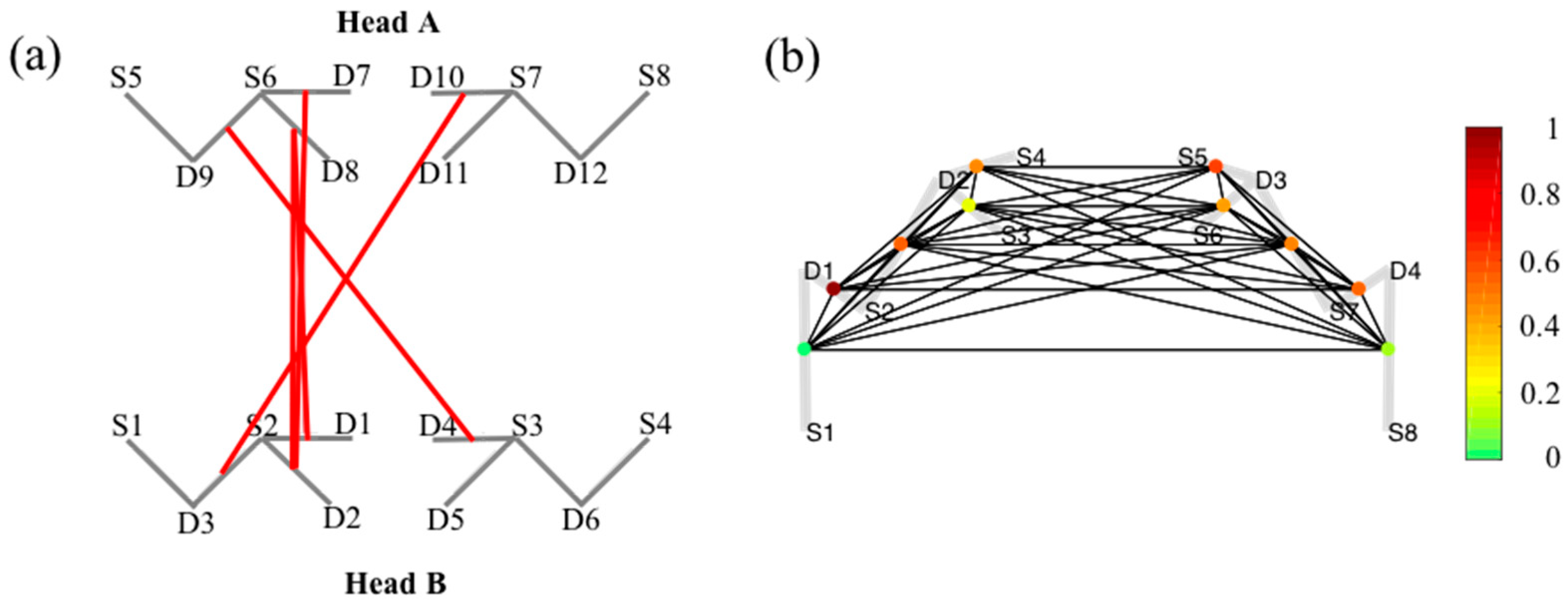
5.5. Graph-Models
6. Toolbox Utilities
6.1. Probe Registration
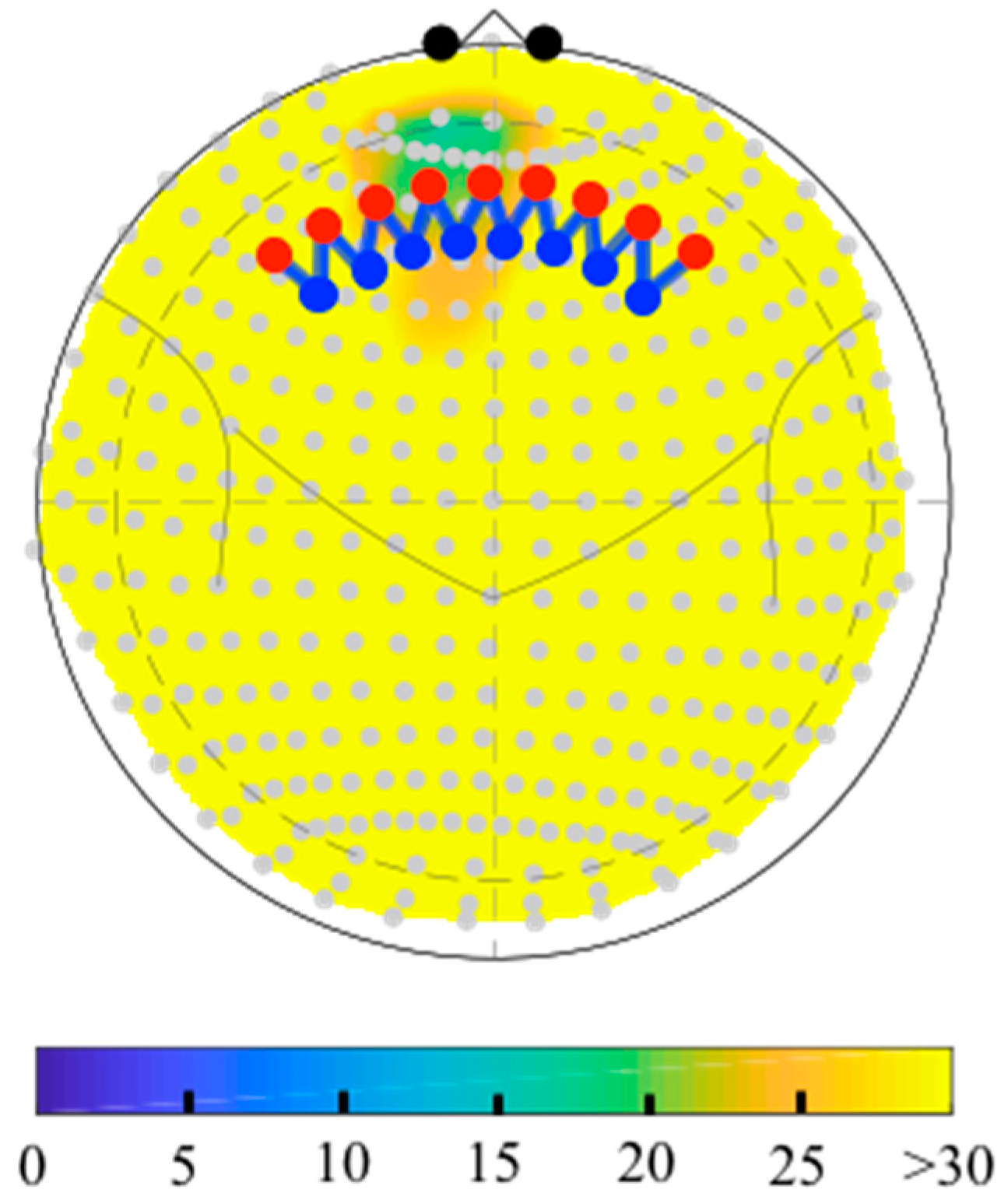
6.2. Depth-Maps
6.3. Region of Interest Analysis
6.4. Regression Testing
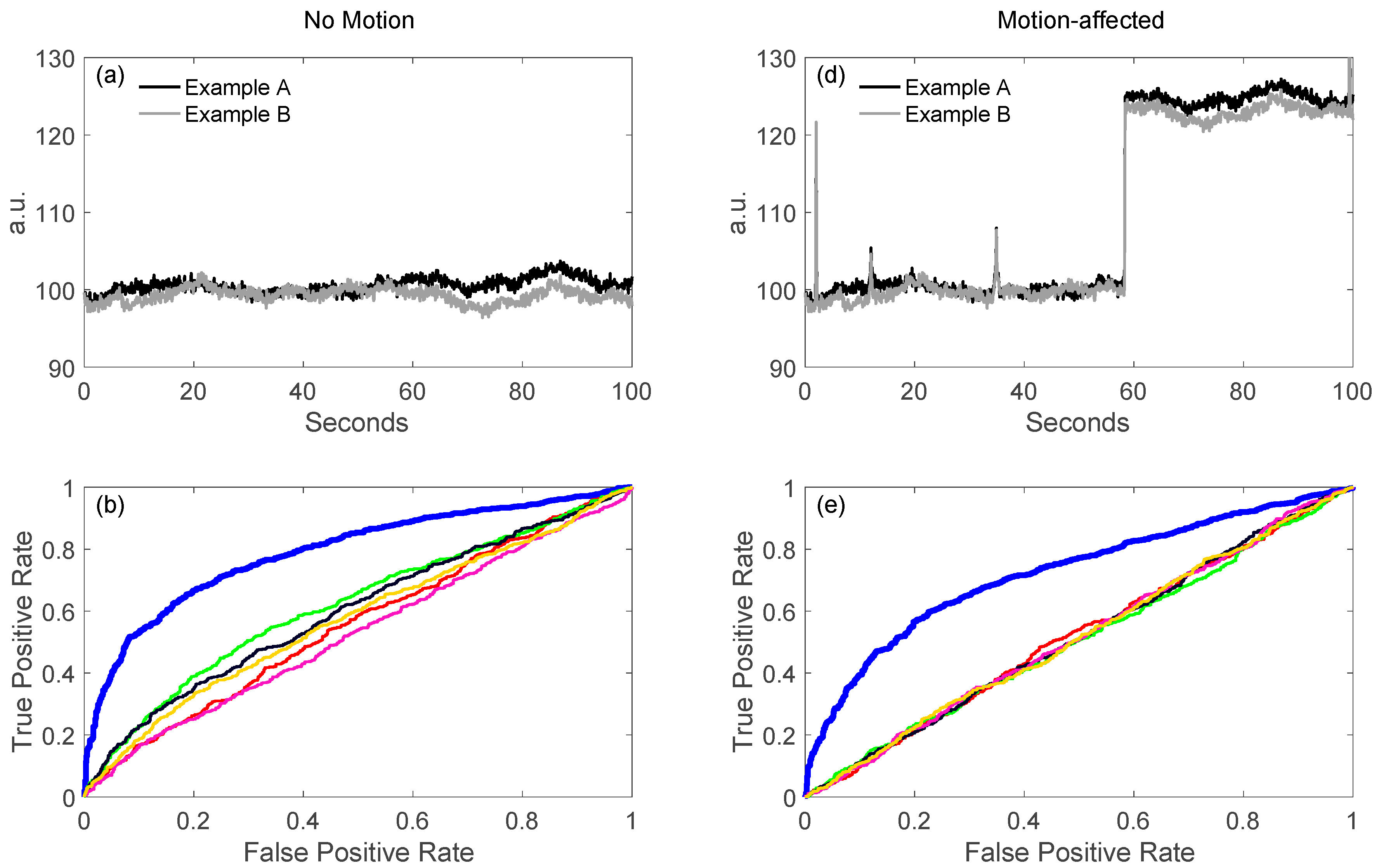
6.4.1. Data Simulation
Noise Generation
Stimulus Generation
6.4.2. ROC Definitions
7. Graphical Interfaces
8. Minimum Processing Recommendations
9. Future Direction
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wolf, M.; Ferrari, M.; Quaresima, V. Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications. J. Biomed. Opt. 2007, 12, 062104. [Google Scholar] [PubMed]
- Ferrari, M.; Quaresima, V. A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 2012, 63, 921–935. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Kleiser, S.; Metz, A.J.; Zimmermann, R.; Pavia, J.M.; Wolf, U.; Wolf, M. A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. Neuroimage 2014, 85, 6–27. [Google Scholar] [CrossRef] [PubMed]
- Boas, D.A.; Dale, A.M.; Franceschini, M.A. Diffuse optical imaging of brain activation: Approaches to optimizing image sensitivity, resolution, and accuracy. Neuroimage 2004, 23, 275S–S288. [Google Scholar] [CrossRef] [PubMed]
- Tachtsidis, I.; Scholkmann, F. False positives and false negatives in functional near-infrared spectroscopy: Issues, challenges, and the way forward. Neurophotonics 2016, 3, 031405. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Takikawa, Y.; Kawagoe, R.; Shibuya, S.; Iwano, T.; Kitazawa, S. Influence of skin blood flow on near-infrared spectroscopy signals measured on the forehead during a verbal fluency task. Neuroimage 2011, 57, 991–1002. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Fox, S.; Blasi, A.; Elwell, C.E. Illuminating the developing brain: The past, present and future of functional near infrared spectroscopy. Neurosci. Biobehav. Rev. 2010, 34, 269–284. [Google Scholar] [CrossRef] [PubMed]
- Obrig, H. NIRS in clinical neurology—A ‘promising’ tool? Neuroimage 2014, 85 Pt 1, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Barker, J.W.; Schmidt, B.; Walls, S.; Ghuman, A. Comparison of group-level, source localized activity for simultaneous functional near-infrared spectroscopy-magnetoencephalography and simultanous fNIRS-fMRI during parametric median nerve stimulation. Neurophotonics 2017, 4, 015001. [Google Scholar] [CrossRef] [PubMed]
- Yucel, M.A.; Selb, J.J.; Huppert, T.J.; Franceschini, M.A.; Boas, D.A. Functional near infrared spectroscopy: Enabling routine functional brain imaging. Curr. Opin. Biomed. Eng. 2017, 4, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Miyai, I.; Tanabe, H.C.; Sase, I.; Eda, H.; Oda, I.; Konishi, I.; Tsunazawa, Y.; Suzuki, T.; Yanagida, T.; Kubota, K. Cortical mapping of gait in humans: A near-infrared spectroscopic topography study. Neuroimage 2001, 14, 1186–1192. [Google Scholar] [CrossRef] [PubMed]
- Quaresima, V.; Ferrari, M. Functional near-infrared spectroscopy (fNIRS) for assessing cerebral cortex function during human behavior in natural/social situations: A concise review. Organ. Res. Methods 2016. [Google Scholar] [CrossRef]
- SPSS. Available online: www.ibm.com/products/spss-statistics (accessed on 28 March 2018).
- SAS. Available online: www.sas.com (accessed on 28 March 2018).
- Huppert, T.J. Commentary on the statistical properties of noise and its implication on general linear models in functional near-infrared spectroscopy. Neurophotonics 2016, 3, 010401. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.W.; Aarabi, A.; Huppert, T.J. Autoregressive model based algorithm for correcting motion and serially correlated errors in fnirs. Biomed. Opt. Express 2013, 4, 1366–1379. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.W.; Rosso, A.L.; Sparto, P.J.; Huppert, T.J. Correction of motion artifacts and serial correlations for real-time functional near-infrared spectroscopy. Neurophotonics 2016, 3, 031410. [Google Scholar] [CrossRef] [PubMed]
- Santosa, H.; Aarabi, A.; Perlman, S.B.; Huppert, T.J. Characterization and correction of the false-discovery rates in resting state connectivity using functional near-infrared spectroscopy. J. Biomed. Opt. 2017, 22, 055002. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Diamond, S.G.; Franceschini, M.A.; Boas, D.A. Homer: A review of time-series analysis methods for near-infrared spectroscopy of the brain. Appl. Opt. 2009, 48, D280–D298. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.C.; Tak, S.; Jang, K.E.; Jung, J.; Jang, J. NIRS-SPM: Statistical parametric mapping for near-infrared spectroscopy. Neuroimage 2009, 44, 428–447. [Google Scholar] [CrossRef] [PubMed]
- Jermyn, M.; Ghadyani, H.; Mastanduno, M.A.; Turner, W.; Davis, S.C.; Dehghani, H.; Pogue, B.W. Fast segmentation and high-quality three-dimensional volume mesh creation from medical images for diffuse optical tomography. J. Biomed. Opt. 2013, 18, 086007. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, H.; Eames, M.E.; Yalavarthy, P.K.; Davis, S.C.; Srinivasan, S.; Carpenter, C.M.; Pogue, B.W.; Paulsen, K.D. Near infrared optical tomography using NIRFAST: Algorithm for numerical model and image reconstruction. Commun. Numer. Methods Eng. 2008, 25, 711–732. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Boas, D. Tetrahedral mesh generation from volumetric binary and gray-scale images. In Proceedings of the IEEE International Symposium on Biomedical Imaging, Boston, MA, USA, 28 June–1 July 2009; pp. 1142–1145. [Google Scholar]
- Fang, Q.; Kaeli, D.R. Accelerating mesh-based Monte Carlo method on modern CPU architectures. Biomed. Opt. Express 2012, 3, 3223–3230. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Fang, Q.; Intes, X. Mesh-based Monte Carlo method in time-domain widefield fluorescence molecular tomography. J. Biomed. Opt. 2012, 17, 106009. [Google Scholar] [CrossRef] [PubMed]
- Boas, D.; Culver, J.; Stott, J.; Dunn, A. Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head. Opt. Express 2002, 10, 159–170. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, E. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methodol. 1995, 57, 289–300. [Google Scholar]
- Harcum, J.B.; Dressing, S.A. Technical Memorandum #3: Minimum Detectable Change and Power Analysis; Agency USEP: Washington, DC, USA, 2015; p. 10. [Google Scholar]
- Hotelling, H. The generalization of student’s ratio. Ann. Math. Stat. 1931, 2, 360–378. [Google Scholar] [CrossRef]
- CIFTI-2 Specification. Available online: https://www.nitrc.org/projects/cifti/ (accessed on 28 March 2018).
- Huppert, T.J.; Diamond, S.G.; Boas, D.A. Direct estimation of evoked hemoglobin changes by multimodality fusion imaging. J. Biomed. Opt. 2008, 13, 054031. [Google Scholar] [CrossRef] [PubMed]
- Yucel, M.A.; Evans, K.C.; Selb, J.; Huppert, T.J.; Boas, D.A.; Gagnon, L. Validation of the hypercapnic calibrated fMRI method using DOT-fMRI fusion imaging. Neuroimage 2014, 102 Pt 2, 729–735. [Google Scholar] [CrossRef] [PubMed]
- Abdelnour, F.; Genovese, C.; Huppert, T. Hierarchical bayesian regularization of reconstructions for diffuse optical tomography using multiple priors. Biomed. Opt. Express 2010, 1, 1084–1103. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef] [PubMed]
- Molavi, B.; Dumont, G.A. Wavelet-based motion artifact removal for functional near-infrared spectroscopy. Physiol. Meas. 2012, 33, 259–270. [Google Scholar] [CrossRef] [PubMed]
- Abdelnour, F.; Huppert, T. A random-effects model for group-level analysis of diffuse optical brain imaging. Biomed. Opt. Express 2010, 2, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Abdelnour, F.; Schmidt, B.; Huppert, T.J. Topographic localization of brain activation in diffuse optical imaging using spherical wavelets. Phys. Med. Biol. 2009, 54, 6383–6413. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Brooks, D.H.; Franceschini, M.A.; Boas, D.A. Eigenvector-based spatial filtering for reduction of physiological interference in diffuse optical imaging. J. Biomed. Opt. 2005, 10, 11014. [Google Scholar] [CrossRef] [PubMed]
- Themelis, G.; D’Arceuil, H.; Diamond, S.G.; Thaker, S.; Huppert, T.J.; Boas, D.A.; Franceschini, M.A. Near-infrared spectroscopy measurement of the pulsatile component of cerebral blood flow and volume from arterial oscillations. J. Biomed. Opt. 2007, 12, 014033. [Google Scholar] [CrossRef] [PubMed]
- Hoge, R.D.; Franceschini, M.A.; Covolan, R.J.; Huppert, T.; Mandeville, J.B.; Boas, D.A. Simultaneous recording of task-induced changes in blood oxygenation, volume, and flow using diffuse optical imaging and arterial spin-labeling MRI. Neuroimage 2005, 25, 701–707. [Google Scholar] [CrossRef] [PubMed]
- Riera, J.J.; Watanabe, J.; Kazuki, I.; Naoki, M.; Aubert, E.; Ozaki, T.; Kawashima, R. A state-space model of the hemodynamic approach: Nonlinear filtering of bold signals. Neuroimage 2004, 21, 547–567. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Allen, M.S.; Diamond, S.G.; Boas, D.A. Estimating cerebral oxygen metabolism from fMRI with a dynamic multicompartment windkessel model. Hum. Brain Mapp. 2009, 30, 1548–1567. [Google Scholar] [CrossRef] [PubMed]
- Boas, D.A.; Jones, S.R.; Devor, A.; Huppert, T.J.; Dale, A.M. A vascular anatomical network model of the spatio-temporal response to brain activation. Neuroimage 2008, 40, 1116–1129. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Allen, M.S.; Benav, H.; Jones, P.B.; Boas, D.A. A multicompartment vascular model for inferring baseline and functional changes in cerebral oxygen metabolism and arterial dilation. J. Cereb. Blood Flow Metab. 2007, 27, 1262–1279. [Google Scholar] [CrossRef] [PubMed]
- Beaton, A.E.; Tukey, J.W. The fitting of power series, meaning polynomials, illustrated on band-spectroscopic data. Technometrics 1974, 16, 147–185. [Google Scholar] [CrossRef]
- Jang, K.E.; Tak, S.; Jung, J.; Jang, J.; Jeong, Y.; Ye, J.C. Wavelet minimum description length detrending for near-infrared spectroscopy. J. Biomed. Opt. 2009, 14, 034004. [Google Scholar] [CrossRef] [PubMed]
- Karim, H.; Fuhrman, S.I.; Sparto, P.; Furman, J.; Huppert, T. Functional brain imaging of multi-sensory vestibular processing during computerized dynamic posturography using near-infrared spectroscopy. Neuroimage 2013, 74, 318–325. [Google Scholar] [CrossRef] [PubMed]
- Karim, H.T.; Fuhrman, S.I.; Furman, J.M.; Huppert, T.J. Neuroimaging to detect cortical projection of vestibular response to caloric stimulation in young and older adults using functional near-infrared spectroscopy (fNIRS). Neuroimage 2013, 76, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Karim, H.T.; Sparto, P.J.; Aizenstein, H.J.; Furman, J.M.; Huppert, T.J.; Erickson, K.I.; Loughlin, P.J. Functional MR imaging of a simulated balance task. Brain Res. 2014, 1555, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, G.N.; Rogers, C.E. Symbolic description of factorial models for analysis of variance. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1973, 22, 3920399. [Google Scholar] [CrossRef]
- Fang, Q. Mesh-based Monte Carlo method using fast ray-tracing in Plucker coordinates. Biomed. Opt. Express 2010, 1, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41. [Google Scholar] [CrossRef]
- Cule, E.; Vineis, P.; De Iorio, M. Significance testing in ridge regression for genetic data. BMC Bioinform. 2011, 12, 372. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Wiener, N. The theory of prediction. In Modern Mathematics for the Engineer; Beckenbach, E.F., Ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Langville, A.; Meyer, C. Google’s PageRank and Beyond: The Science of Search Engine Rankings; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Bonanich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Aasted, C.M.; Yücel, M.A.; Cooper, R.J.; Dubb, J.; Tsuzuki, D.; Becerra, L.; Petkov, M.P.; Borsook, D.; Dan, I.; Boas, D.A. Anatomical guidance for functional near-infrared spectroscopy: AtlasViewer tutorial. Neurophotonics 2015, 2, 020801. [Google Scholar] [CrossRef] [PubMed]
- Holmes, C.J.; Hoge, R.; Collins, L.; Woods, R.; Toga, A.W.; Evans, A.C. Enhancement of mr images using registration for signal averaging. J. Comput. Assist. Tomogr. 1998, 22, 324–333. [Google Scholar] [CrossRef] [PubMed]
- Dale, A.M.; Fischl, B.; Sereno, M.I. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 1999, 9, 179–194. [Google Scholar] [CrossRef] [PubMed]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef] [PubMed]
- Rolls, E.T.; Joliot, M.; Tzourio-Mazoyer, N. Implementation of a new parcellation of the orbitofrontal cortex in the automated anatomical labeling atlas. Neuroimage 2015, 122, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Fischl, B.; van der Kouwe, A.; Destrieux, C.; Halgren, E.; Segonne, F.; Salat, D.H.; Busa, E.; Seidman, L.J.; Goldstein, J.; Kennedy, D.; et al. Automatically parcellating the human cerebral cortex. Cereb. Cortex 2004, 14, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Karim, H.; Lin, C.C.; Alqahtani, B.A.; Greenspan, S.L.; Sparto, P.J. Functional imaging of cognition in an old-old population: A case for portable functional near-infrared spectroscopy. PLoS ONE 2017, 12, e0184918. [Google Scholar] [CrossRef] [PubMed]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
| Class | Purpose | Methods | Description |
|---|---|---|---|
| nirs.core.Data | Holds time-series information including stimulus events | < >.draw([channel index]) | Draws the time-course of a channel of data |
| nirs.core.Probe | Holds information about | < >.draw() | Draws the layout of the probe in 2D or 3D |
| the probe design and | <> .default_draw_function | Sets the default draw behavior on 3D registered probes | |
| registration | < >.link | A table describing the connections of source-detector pairs | |
| < >.optodes | A table describing the source-detector and any additional probe points | ||
| nirs.core.ChannelStats | Holds the statistical maps in | < >.draw(type,range,alpha) | Draws the statistical map according to the probe |
| first and second-level | < >.table | Returns a formatted table of the statistical values | |
| analysis | < >.ttest(conditions) | Performs a student’s t-test to compare two or more contrasts | |
| < >.jointTest() | Returns a FChannelStats variable for the T^2 test using HbO2/Hb | ||
| < >.printAll(*, outfolder, imagetype) | Draws and saves the figures in TIFF or JPEG format | ||
| < >.sorted | Returns sorted stats by columns in variables | ||
| nirs.core.ChannelFStats | Holds F-statistics in channel | < >.draw(range, alpha) | Draws the statistical map according to the probe |
| Space | < >.table | Returns a table of all channel wise stats | |
| < >.getCritF | Returns critical F value | ||
| nirs.core.ImageStats | Holds the statistics for reconstructed images | < >.draw(type, range, alpha, beta, [power]) | Draws the statistical map according to the probe |
| < >.jointTest() | Performs a joint hypothesis test across all channels in each source-detector pair | ||
| nirs.core.sFCStats | Holds connectivity and | < >.draw | Draws the correlation values |
| hyper-scanning statistical | < >.table | Returns a table of all stats | |
| models | < >.graph | Returns a graph object from the connectivity model |
| Modules | Description | Citation |
|---|---|---|
| Pre-processing | ||
| BeerLambertLaw | Converts optical density to hemoglobin | [34] |
| Resample | Nyquist filter and resample the data | Matlab: resample.m function |
| OpticalDensity | Conversion of raw data to optical density | |
| Data management | ||
| AddDemographics | Add subject information from the table | |
| ChangeStimulusInfo | Change stimulus info to data given a table | |
| DiscardStims | Removes specified stimulus conditions from design | |
| FixStims | Modify onset/duration/amplitude of stimulus | |
| KeepStims | Removes all stimuli except those specified | |
| RemoveStimLess | Discard data files with no stimulus information | |
| Filter | ||
| BaselineCorrection | Motion-correction filter to remove DC sifts | See Section 2.2.2.1 |
| PCAFilter | PCA filter for motion or physiology | [19] |
| WaveletFilter | Filter to remove outliers and low-frequency characteristics | [35] |
| Statistical analysis | ||
| ANOVA | Group-level ANOVA model | Matlab: fitlme.m function |
| AR-IRLS | GLM analysis using autoregressive model | [16] |
| Connectivity | Computes all-to-all connectivity model | [18] |
| Hyperscanning | Computes all-to-all connectivity between two files | [18] |
| ImageReconstruction | Subject or group-level image reconstruction model | [33,36,37] |
| MixedEffects | Group-level linear mixed effects model | Matlab: fitlme.m function |
| NIRS-SPM | GLM analysis using NIRS-SPM | [20] |
| OLS | GLM analysis using ordinary least squares | [19] |
| RemoveOutlierSubjects | Flags and removes outlier subjects based on leverage | |
| SubjLevelStats | Subject-level analysis | Matlab: fitlme.m function |
| Additional | ||
| HOMER2 | Interface to HOMER2 code | [10,19] |
| Formula | Interpretation |
|---|---|
| beta ~ −1 + cond + (1|subject) | Effect of condition, controlling for subject |
| beta ~ −1 + group:cond + (1|age) | Effect of condition for each group, controlling for age |
| beta ~ −1 + group + cond + group*cond + (1|IQ) | Main effects of group and condition, and a group x condition interaction, controlling for IQ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santosa, H.; Zhai, X.; Fishburn, F.; Huppert, T. The NIRS Brain AnalyzIR Toolbox. Algorithms 2018, 11, 73. https://doi.org/10.3390/a11050073
Santosa H, Zhai X, Fishburn F, Huppert T. The NIRS Brain AnalyzIR Toolbox. Algorithms. 2018; 11(5):73. https://doi.org/10.3390/a11050073
Chicago/Turabian StyleSantosa, Hendrik, Xuetong Zhai, Frank Fishburn, and Theodore Huppert. 2018. "The NIRS Brain AnalyzIR Toolbox" Algorithms 11, no. 5: 73. https://doi.org/10.3390/a11050073
APA StyleSantosa, H., Zhai, X., Fishburn, F., & Huppert, T. (2018). The NIRS Brain AnalyzIR Toolbox. Algorithms, 11(5), 73. https://doi.org/10.3390/a11050073





