Gray Wolf Optimization Algorithm for Multi-Constraints Second-Order Stochastic Dominance Portfolio Optimization
Abstract
1. Introduction
2. The MCVSK and MVSK Portfolio Optimization Model
2.1. The Measure of Return and Risk
2.2. The Second-Order Stochastic Dominance Constraint
2.3. The Skewness and Kurtosis Constraints
2.4. The MCVSK and MVSK Portfolio Optimization Model
3. The GWO Algorithm for the MCVSK and MVSK Portfolio Optimization Model
3.1. Prey Searching
3.2. Prey Encirclement
3.3. Chasing (Hunting)
| Algorithm 1 the main procedure of GWO algorithm for the MCVSK and MVSK model. |
| Input: problem to solve, problem; number of search agents, SearchAgents no; number of iterations, Max iteration; number of variables, dim; etc |
| Output: the best portfolio and the return of the portfolio |
|
4. Numerical Experiments
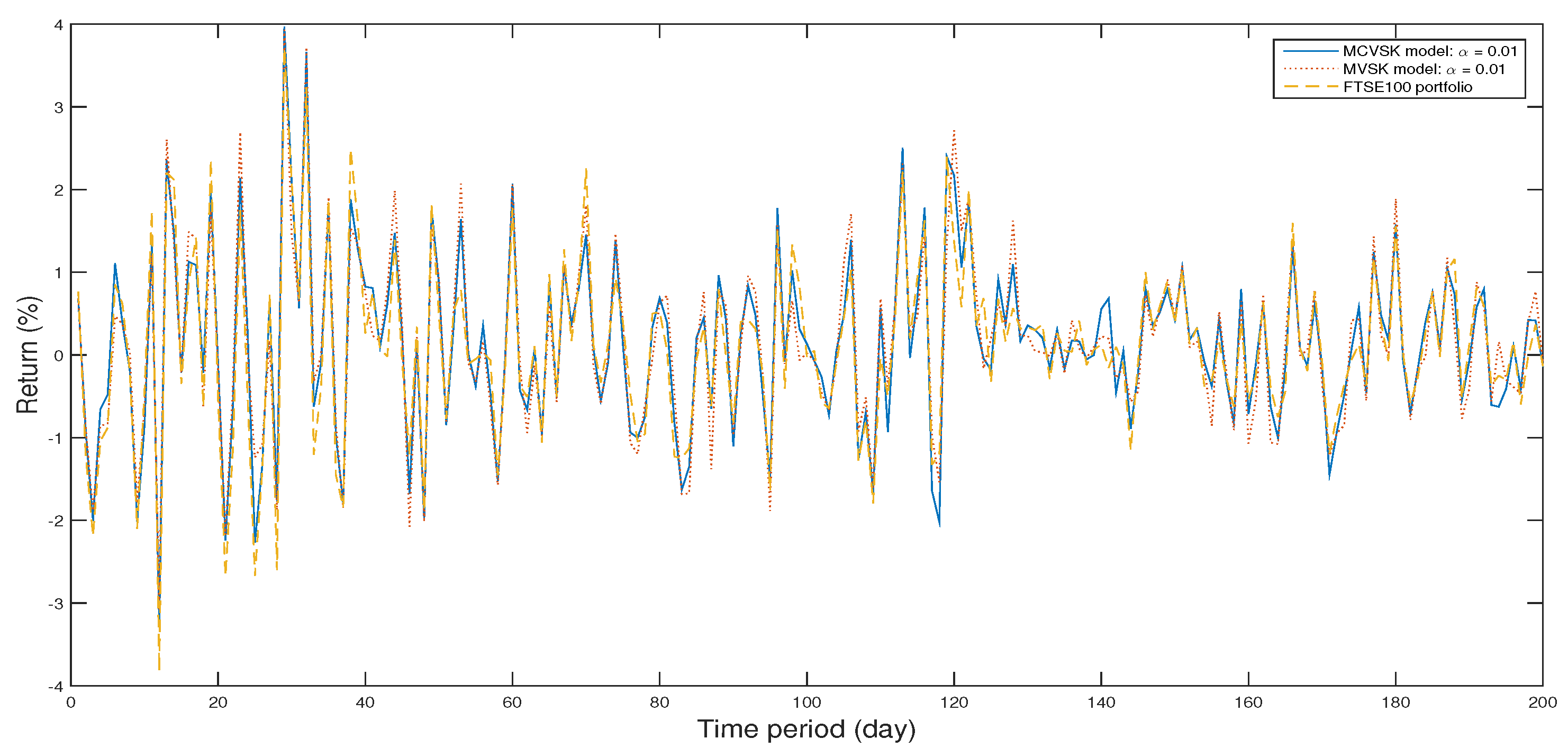
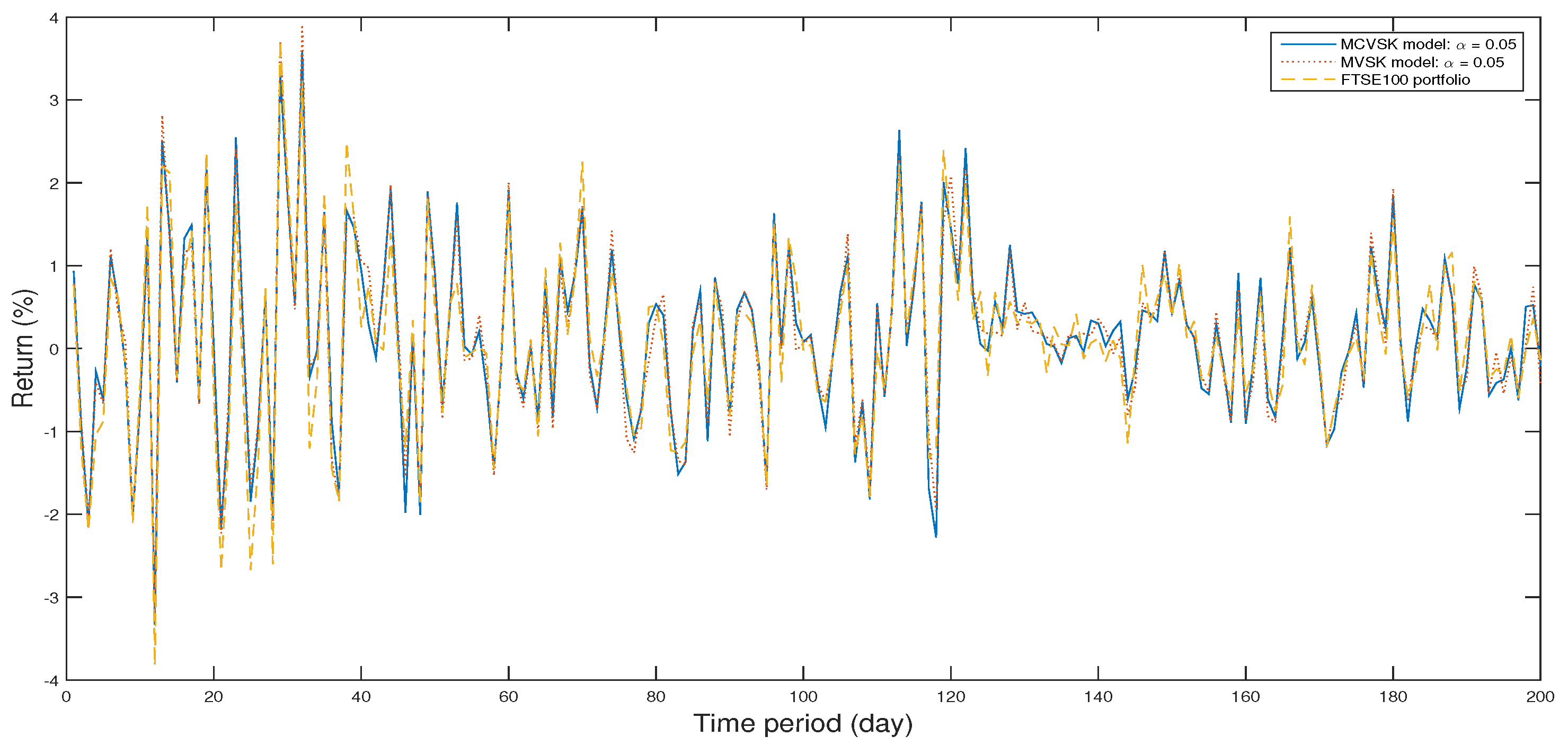
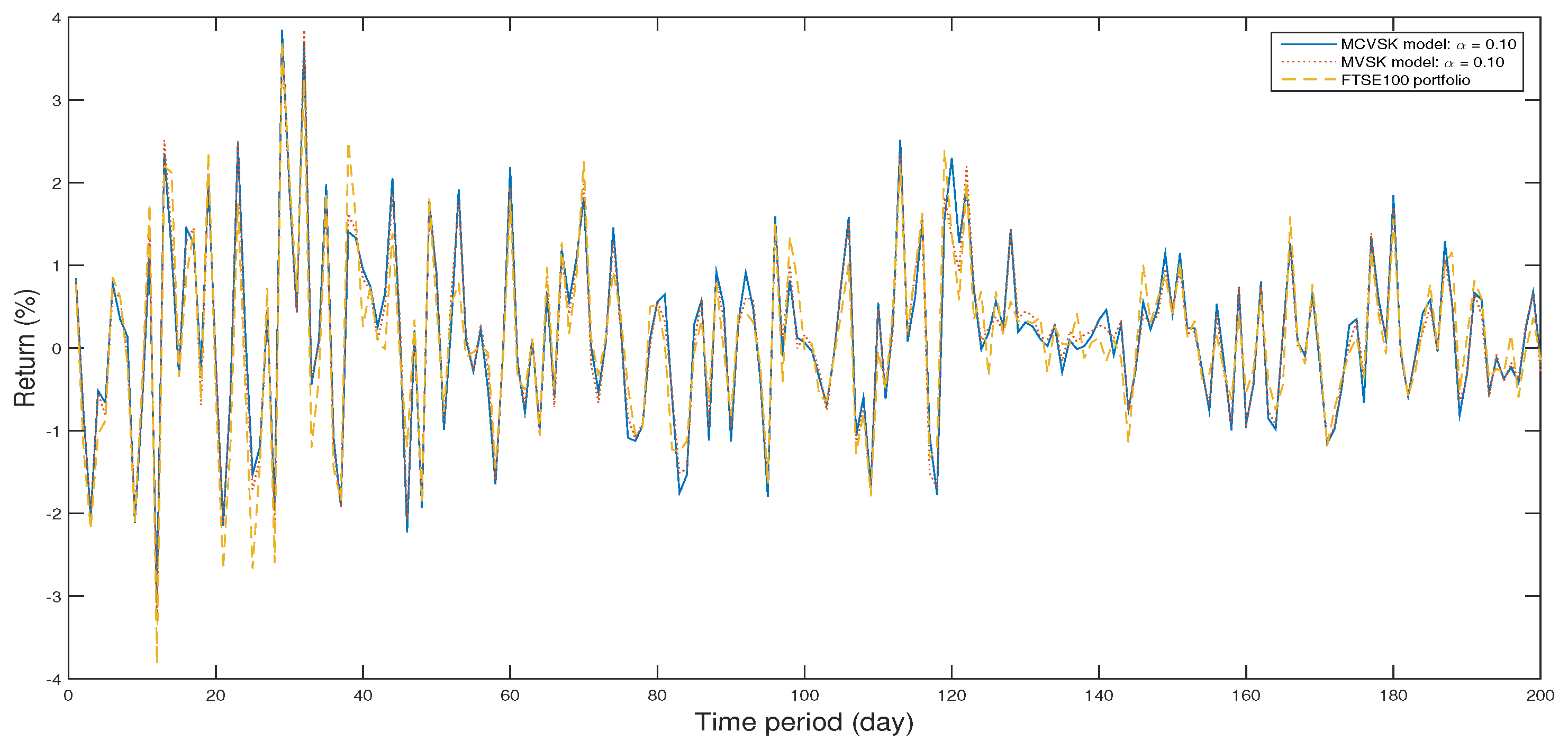
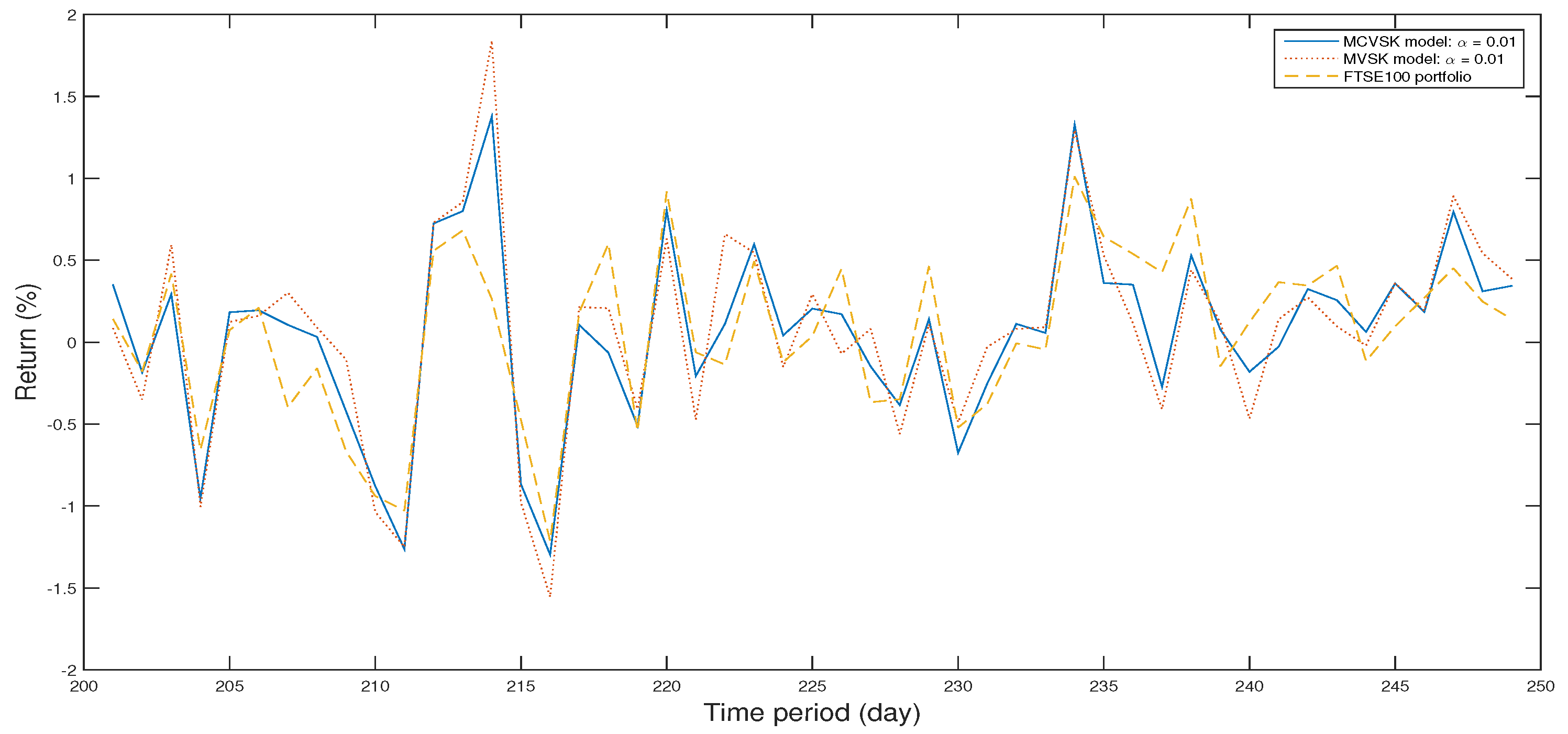
4.1. Backtesting and Out-of-Sample Test
4.2. Numerical Analysis
5. Conclusions and Future Research
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| GWO | Gray Wolf Optimization |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| MV | Mean-Variance |
| MAD | Mean Absolute Deviation |
| VaR | Value at Risk |
| CVaR | Conditional Value at Risk |
| SD | Stochastic Dominance |
| FSD | First-Order Stochastic Dominance |
| SSD | Second-Order Stochastic Dominance |
| ASD | Almost Stochastic Dominance |
| MVS | Mean-Variance-Skewness |
| MOEAs | Multi-Objective Evolutionary Algorithms |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| SPEA-II | Strength Parato Evolutionary Algorithm II |
| MCVSK | Mean-CVaR-skewness-kurtosis |
| MVSK | Mean-VaR-skewness-kurtosis |
| IPSO | Immune Particle Swarm Optimization |
| ACA | Ant Colony Algrothrim |
| BBO | Biogeography-based Optimization |
| CNN | Convolutional Neural Network |
| LSSVM | Least Squares Support Vector Machine |
Appendix A
| Constitution | Index Weight (%) | Constitution | Index Weight (%) |
|---|---|---|---|
| 3i Group | 0.38 | Admiral Group | 0.2 |
| Anglo American | 0.84 | Antofagasta | 0.13 |
| Ashtead Group | 0.44 | Associated British Foods | 0.53 |
| AstraZeneca | 3.1 | Aviva | 1.09 |
| Babcock International Group | 0.27 | BAE Systems | 1.04 |
| Barclays | 2.09 | Barratt Developments | 0.26 |
| BHP Billition | 1.53 | BP | 5.3 |
| British American Tobacco | 4.77 | British Land Co | 0.36 |
| BT Group | 1.7 | Bunzl | 0.39 |
| Burberry Group | 0.37 | Capita | 0.19 |
| Carnival | 0.42 | Centrica | 0.7 |
| Coca-Cola HBC AG | 0.19 | Compass Group | 1.37 |
| ConvaTec Group | 0.08 | CRH | 1.3 |
| Croda International | 0.23 | DCC | 0.3 |
| Diageo | 2.94 | Direct Line Insurance Group | 0.28 |
| Dixons Carphone | 0.2 | Easyjet | 0.14 |
| Experian | 0.84 | Fresnillo | 0.11 |
| GKN | 0.31 | GlaxoSmithKline | 4.21 |
| Glencore | 1.79 | Hammerson | 0.25 |
| Hargreaves Lansdown | 0.16 | Hikma Pharmaceuticals | 0.15 |
| HSBC HIdgs | 7.3 | Imperial Brands | 1.89 |
| Informa | 0.31 | InterContinental Hotels Group | 0.4 |
| International Consolidated Airlines Group | 0.41 | Intertek Group | 0.31 |
| Intu Properties | 0.14 | ITV | 0.43 |
| Johnson Matthey | 0.34 | Kingfisher | 0.44 |
| Land Securities Group | 0.46 | Legal & General Group | 0.81 |
| LIoyds Banking Group | 2.22 | London Stock Exchange Group | 0.51 |
| Marks & Spencer Group | 0.31 | Mediclinic International pIc | 0.17 |
| Merlin Entertainments | 0.18 | Micro Focus International | 0.27 |
| Mondi | 0.34 | Morrison (Wm) Supermarkets | 0.28 |
| National Grid | 1.99 | Next | 0.39 |
| Old Mutual | 0.56 | Paddy Power Betfair | 0.4 |
| Pearson | 0.37 | Persimmon | 0.3 |
| Provident Financial | 0.23 | Prudential | 2.33 |
| Randgold Resources | 0.33 | Reckitt Benckiser Group | 2.4 |
| RELX | 0.88 | Rio Tinto | 2.12 |
| Rolls-Royce Holdings | 0.61 | Royal Bank Of Scotland Group | 0.41 |
| Royal Dutch Shell A | 5.43 | Royal Dutch Shell B | 4.89 |
| Royal Mail | 0.23 | RSA Insurance Group | 0.33 |
| Sage Group | 0.39 | Sainsbury (J) | 0.23 |
| Schroders | 0.19 | Severn Trent | 0.29 |
| Shire | 2.34 | Sky | 0.58 |
| Smith & Nephew | 0.6 | Smiths Group | 0.31 |
| Smurfit Kappa Group | 0.24 | SSE | 0.87 |
| St. James’s Place | 0.29 | Standard Chartered | 0.99 |
| Standard Life | 0.41 | Taylor Wimpey | 0.28 |
| Tesco | 0.93 | TUI AG | 0.3 |
| Unilever | 2.2 | United Utilities Group | 0.34 |
| Vodafone Group | 2.94 | Whitbread | 0.38 |
| Wolseley | 0.69 | Worldpay Group | 0.25 |
| WPP | 1.29 |
References
- Markowitz, H.M. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments; John Wiley and Sons: New York, NY, USA, 1959. [Google Scholar]
- Lwin, K.T.; Qu, R.; MacCarthy, B.L. Mean-VaR portfolio optimization: A nonparametric approach. Eur. J. Oper. Res. 2017, 260, 751–766. [Google Scholar] [CrossRef]
- Chunhachinda, P.; Dandapani, K.; Hamid, S.; Prakash, A.J. Portfolio selection and skewness: Evidence from international stock markets. J. Bank. Financ. 1997, 21, 143–167. [Google Scholar] [CrossRef]
- Markowitz, H.; Todd, P.; Xu, G.; Yamane, Y. Computation of mean-semivariance efficient sets by the critical line algorithm. Ann. Oper. Res. 1993, 45, 307–317. [Google Scholar] [CrossRef]
- Konno, H.; Yamazaki, H. Mean-Absolute Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market. Manag. Sci. 1991, 37, 519–531. [Google Scholar] [CrossRef]
- Speranza, G.M. Linear Programming Models for Portfolio Optimization. Finance 1993, 14, 107–123. [Google Scholar]
- Zhou, K.; Gao, J.; Li, D.; Cui, X. Dynamic mean—VaR portfolio selection in continuous time. Quant. Financ. 2017, 17, 1631–1643. [Google Scholar] [CrossRef]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Coherent measures of risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Fishburn, P.C. Mean-Risk Analysis with Risk Associated with Below-Target Returns. Am. Econ. Rev. 1975, 67, 116–126. [Google Scholar]
- Dentcheva, D.; Ruszczyński, A. Portfolio optimization with stochastic dominance constraints. J. Bank. Financ. 2006, 30, 433–451. [Google Scholar] [CrossRef]
- Leshno, M.; Levy, H. Preferred by “All” and Preferred by “Most” Decision Makers: Almost Stochastic Dominance. Manag. Sci. 2002, 48, 1074–1085. [Google Scholar] [CrossRef]
- Javanmardi, L.; Lawryshyn, Y. A new rank dependent utility approach to model risk averse preferences in portfolio optimization. Ann. Oper. Res. 2016, 237, 161–176. [Google Scholar] [CrossRef]
- Arditti, F.D. Risk and the Required Return on Equity. J. Financ. 1967, 22, 19–36. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. Neural network-based mean–variance–skewness model for portfolio selection. Comput. Oper. Res. 2008, 35, 34–46. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Kar, S.; Majumder, D.D. Fuzzy Mean-Variance-skewness portfolio selection models by interval analysis. Comput. Math. Appl. 2011, 61, 126–137. [Google Scholar] [CrossRef]
- Pouya, A.R.; Solimanpur, M.; Rezaee, M.J. Solving multi-objective portfolio optimization problem using invasive weed optimization. Swarm. Evol. Comput. 2016, 28, 42–57. [Google Scholar] [CrossRef]
- Soleimani, H.; Golmakani, H.R.; Salimi, M.H. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm. Expert. Syst. Appl. 2009, 36, 5058–5063. [Google Scholar] [CrossRef]
- Macedo, L.L.; Godinho, P.; Alves, M.J. Mean-Semivariance Portfolio Optimization with Multiobjective Evolutionary Algorithms and Technical Analysis Rules. Expert. Syst. Appl. 2017, 79, 33–43. [Google Scholar] [CrossRef]
- Lai, T.Y. Portfolio selection with skewness: A multiple-objective approach. Rev. Quant. Financ. Account. 1991, 1, 293–305. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Y.; Zhang, J.; Lu, S. Uncertain portfolio selection with high-order moments. J. Intell. Fuzzy. Syst. 2017, 33, 1–15. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wang, S.; Li, P.; Chen, P.; Phillips, P.; Liu, G.; Du, S.; Zhang, Y. Pathological brain detection via wavelet packet tsallis entropy and real-coded biogeography-based optimization. Fund. Inform. 2017, 151, 275–291. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Zhang, Y.; Lv, Y.D.; Hou, X.X.; Liu, F.Y.; Jia, W.J.; Yang, M.M.; Phillips, P.; Wang, S.H. Alcoholism detection by medical robots based on Hu moment invariants and predator–prey adaptive-inertia chaotic particle swarm optimization. Comput. Electr. Eng. 2017, 63, 126–138. [Google Scholar] [CrossRef]
- Kumaran, N.; Vadivel, A.; Kumar, S.S. Recognition of human actions using CNN-GWO: A novel modeling of CNN for enhancement of classification performance. Mutimed. Tools Appl. 2018, 1, 1–33. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Sulaiman, M.H.; Kahar, M.N.M. Training LSSVM with GWO for price forecasting. Electron. Vis. 2015, 1–6. [Google Scholar] [CrossRef]
- Zhang, H.W.; Yu, H.S.; Pang, L.P.; Wang, J.H. Solution to constrained optimization problem of second order stochastic dominance by gentic algorithm. J. Dalian Univ. Technol. 2016, 56, 299–303. [Google Scholar]
- Pflug, G.C. Some Remarks on the Value-at-Risk and the Conditional Value-at-Risk; Probabilistic Constrained Optimization; Springer: Boston, MA, USA, 2000; pp. 272–281. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk. 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Ye, T.; Yang, Z.; Feng, S. Biogeography-Based Optimization of the Portfolio Optimization Problem with Second Order Stochastic Dominance Constraints. Algorithms 2017, 10, 100. [Google Scholar] [CrossRef]
- Kallio, M.; Hardoroudi, N.D. Second-order Stochastic Dominance Constrained Portfolio Optimization: Theory and Computational Tests. Eur. J. Oper. Res. 2017, 264, 675–685. [Google Scholar] [CrossRef]
- Fábián, C.I.; Mitra, G.; Roman, D. Processing second-order stochastic dominance models using cutting-plane representations. Math. Program. 2011, 130, 33–57. [Google Scholar] [CrossRef]
- Ogryczak, W.; Ruszczyński, A. From stochastic dominance to mean-risk models: Semideviations as risk measures. Eur. J. Oper. Res. 1999, 116, 33–50. [Google Scholar] [CrossRef]
- Noyan, N.; Rudolf, G. Optimization with Multivariate Conditional Value-at-Risk Constraints. Oper. Res. 2013, 61, 990–1013. [Google Scholar] [CrossRef]
- Yoshimoto, A. The mean-variance approach to portfolio optimization subject to transaction costs. J. Oper. Res. Soc. Jpn. 1996, 39, 99–117. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Chatterjee, A.; Kar, S. Uncertainty theory based multiple objective mean-entropy-skewness stock portfolio selection model with transaction costs. J. Uncertain. Anal. Appl. 2013, 1, 16. [Google Scholar] [CrossRef]
- Lobo, M.S.; Fazel, M.; Boyd, S. Portfolio optimization with linear and fixed transaction costs. Ann. Oper. Res. 2007, 152, 341–365. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Grosan, C.; Snasel, V. Large-dimensionality small-instance set feature selection: A hybrid bio-inspired heuristic approach. Swarm. Evol. Comput. 2018. [Google Scholar] [CrossRef]
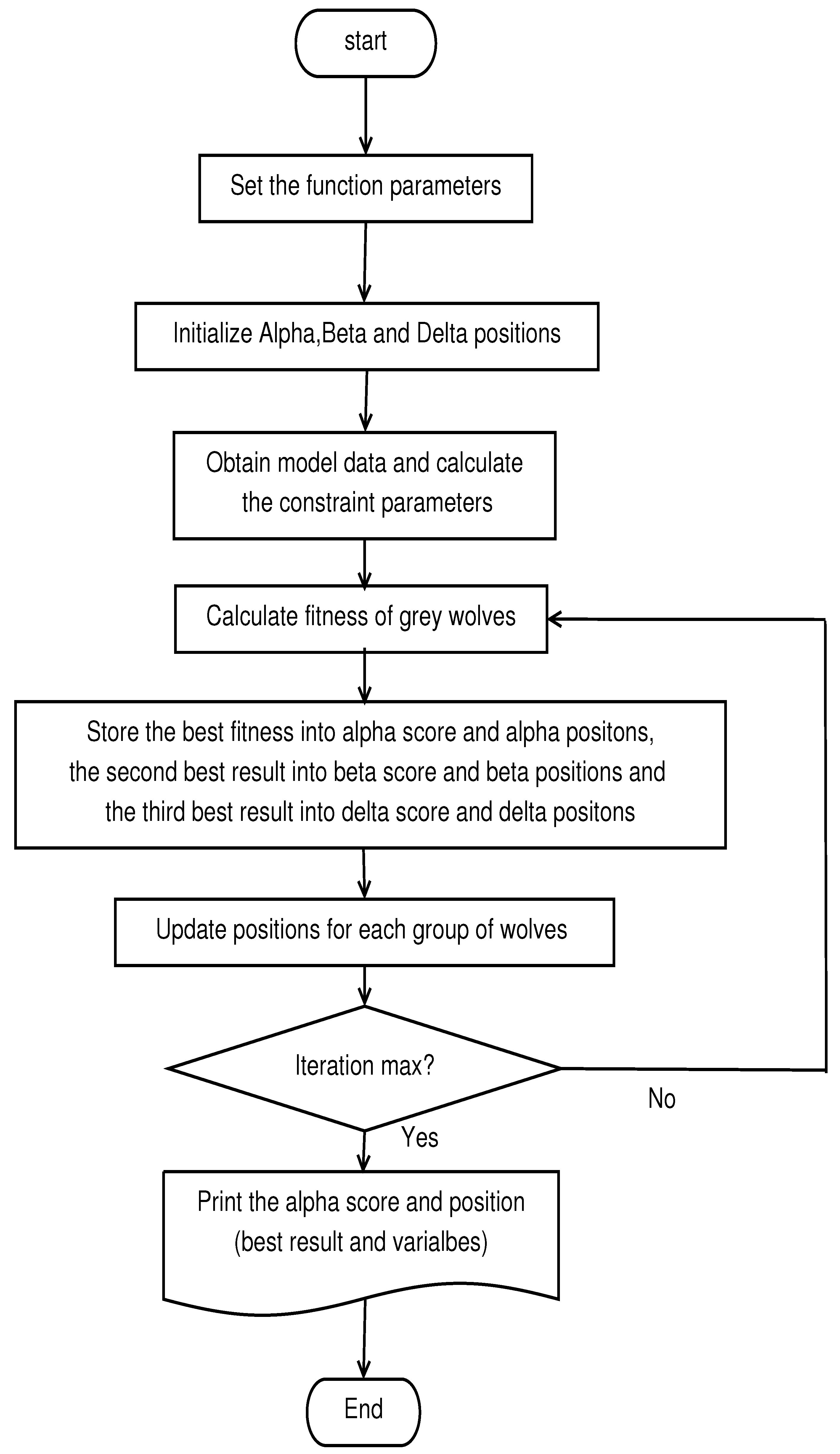
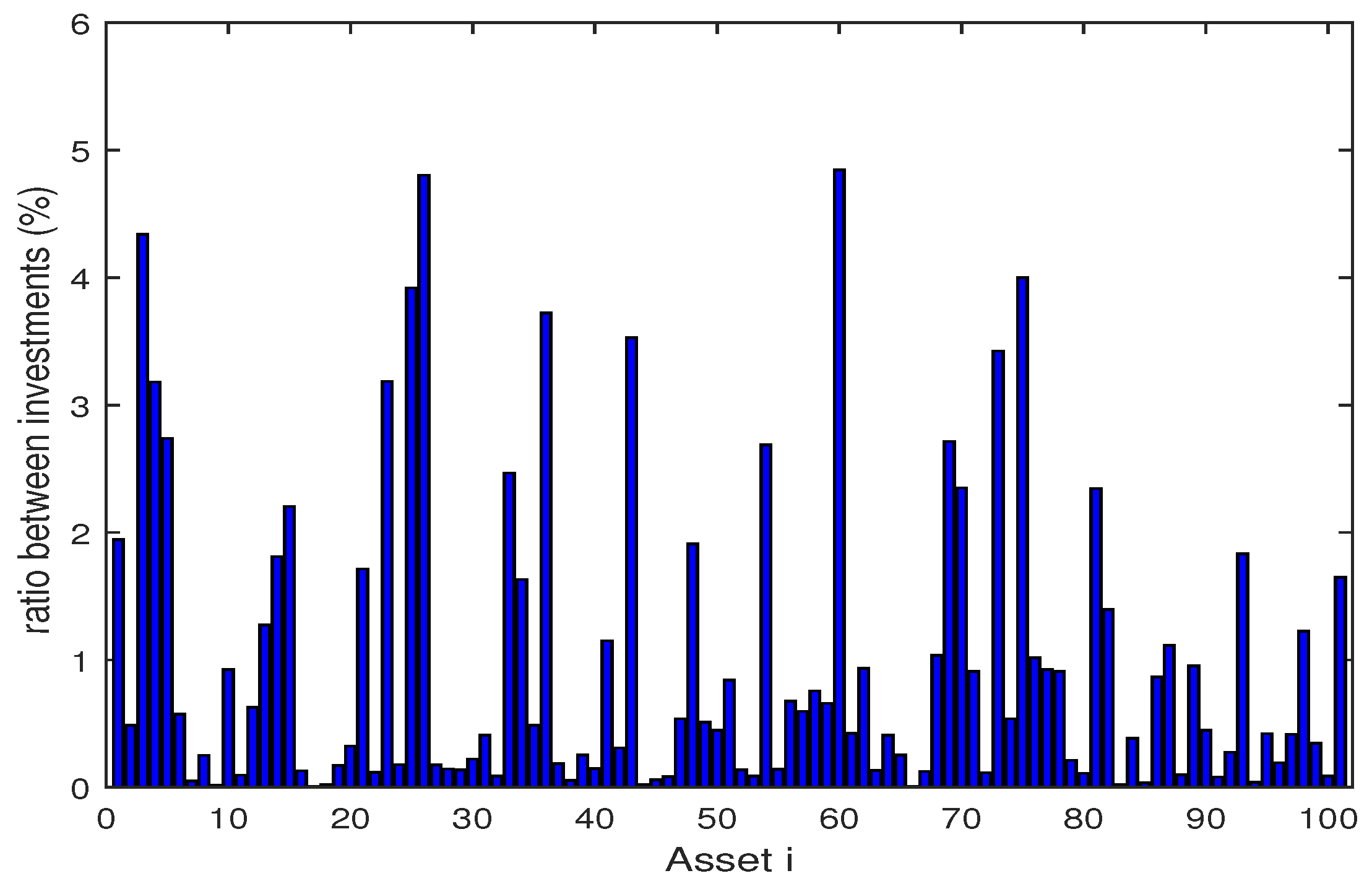
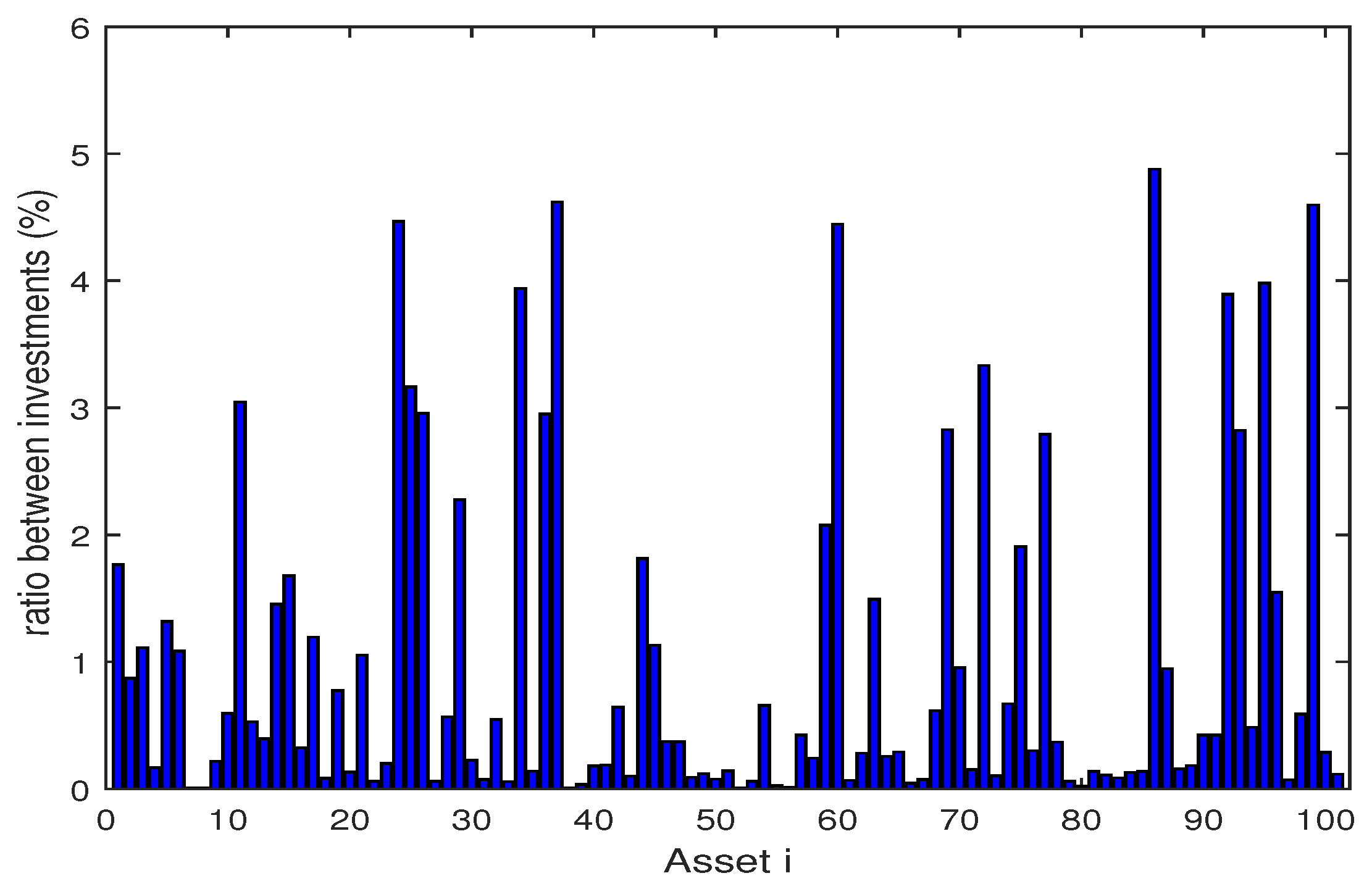
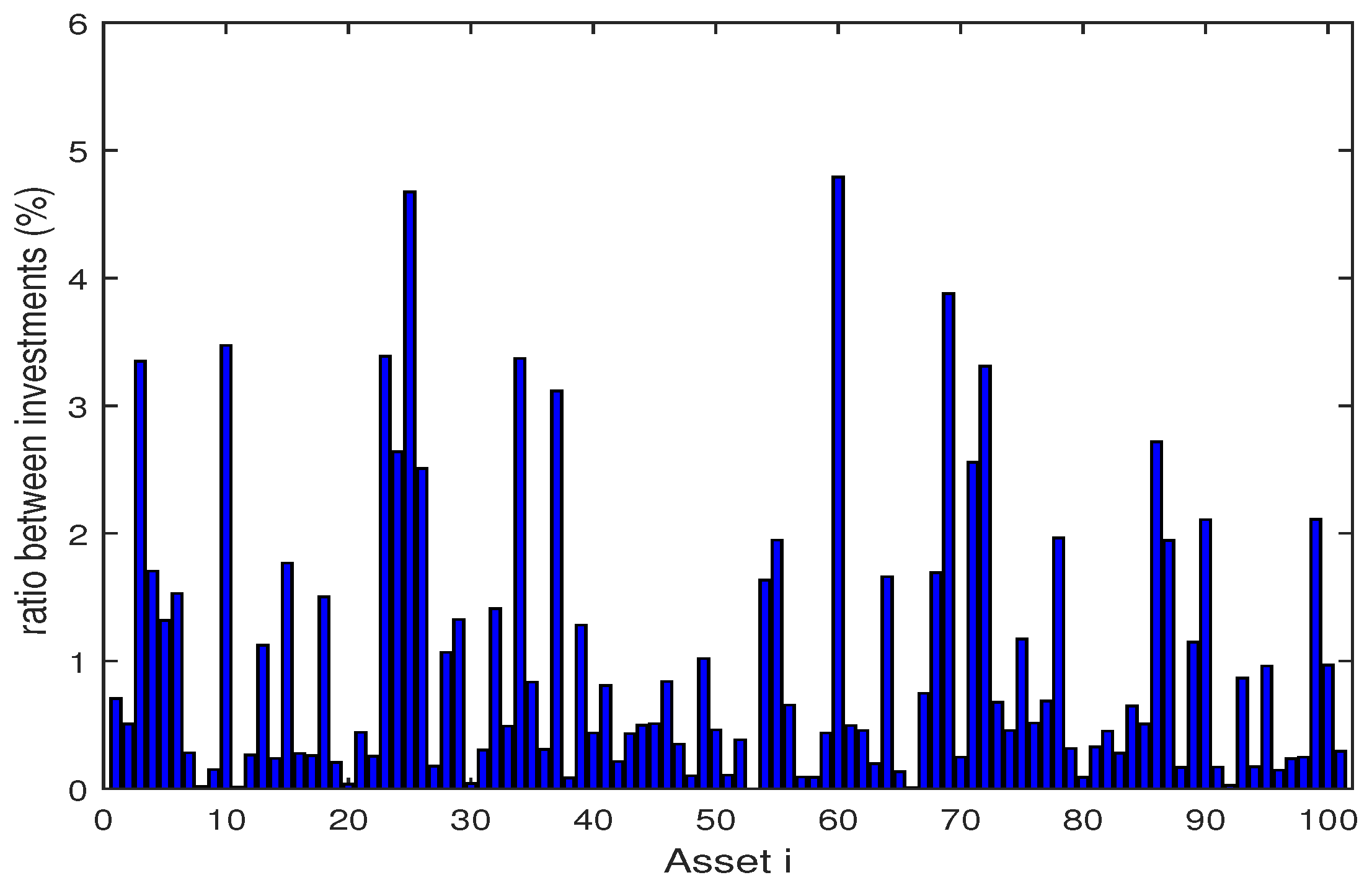
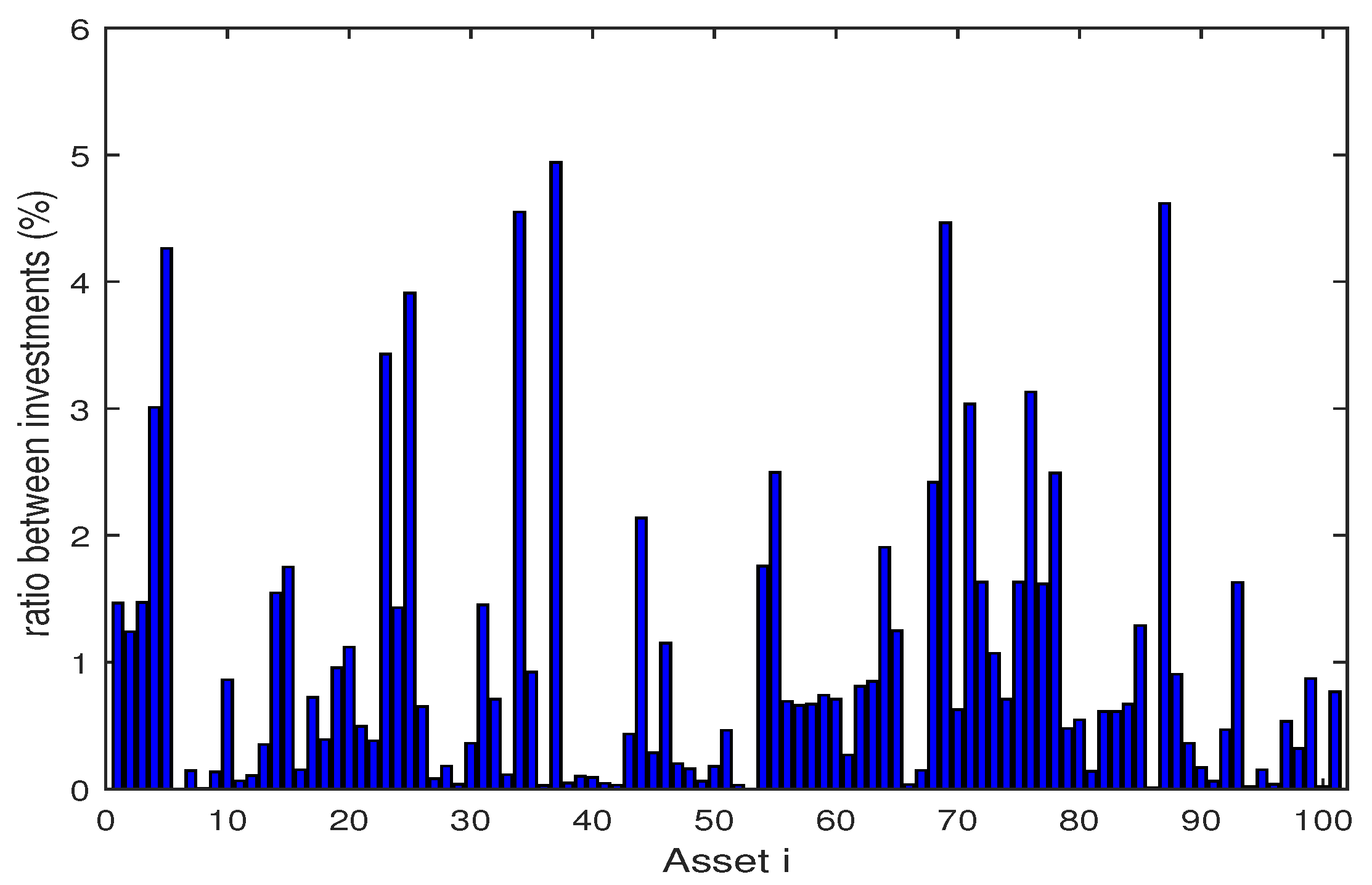
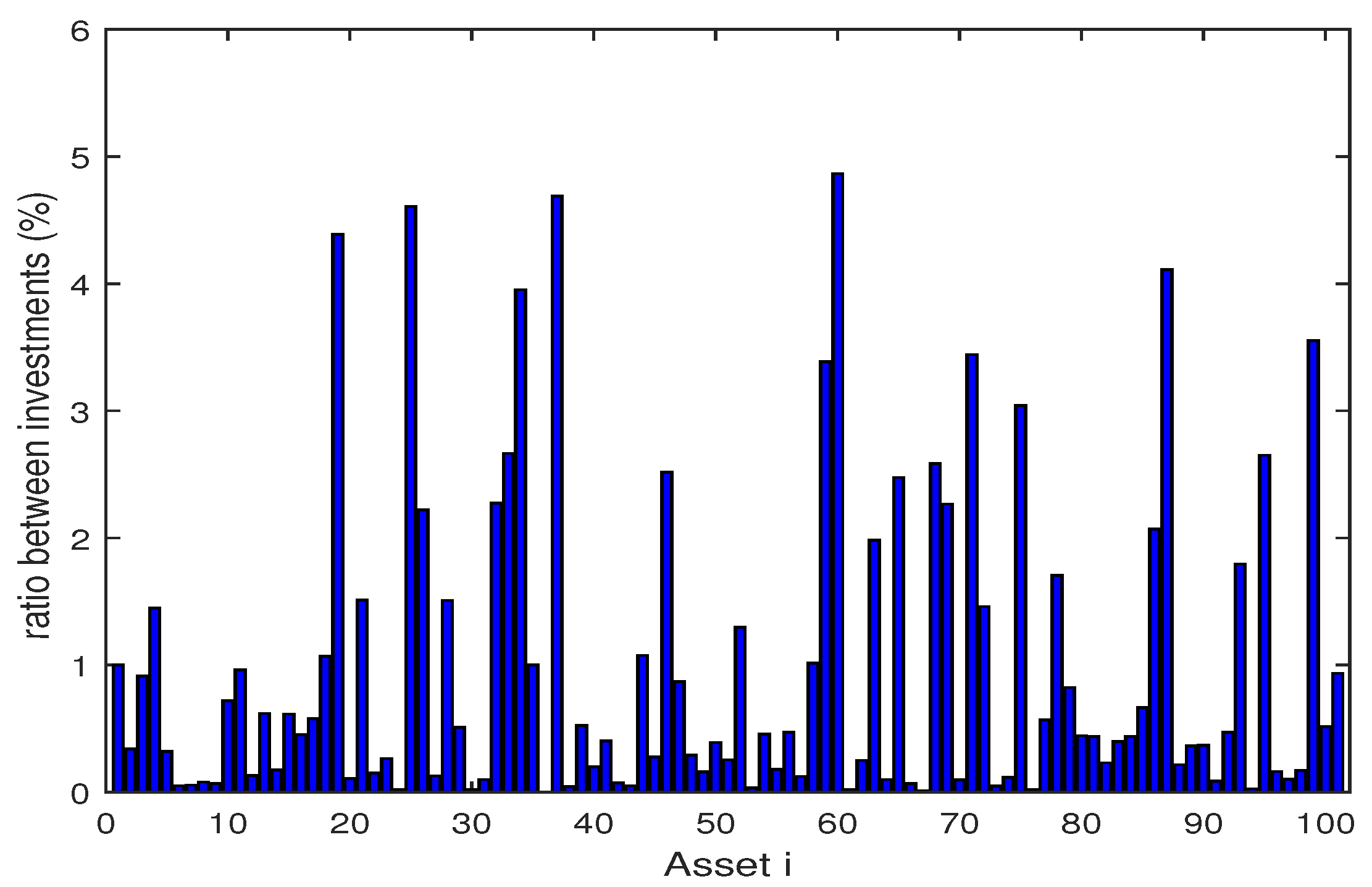
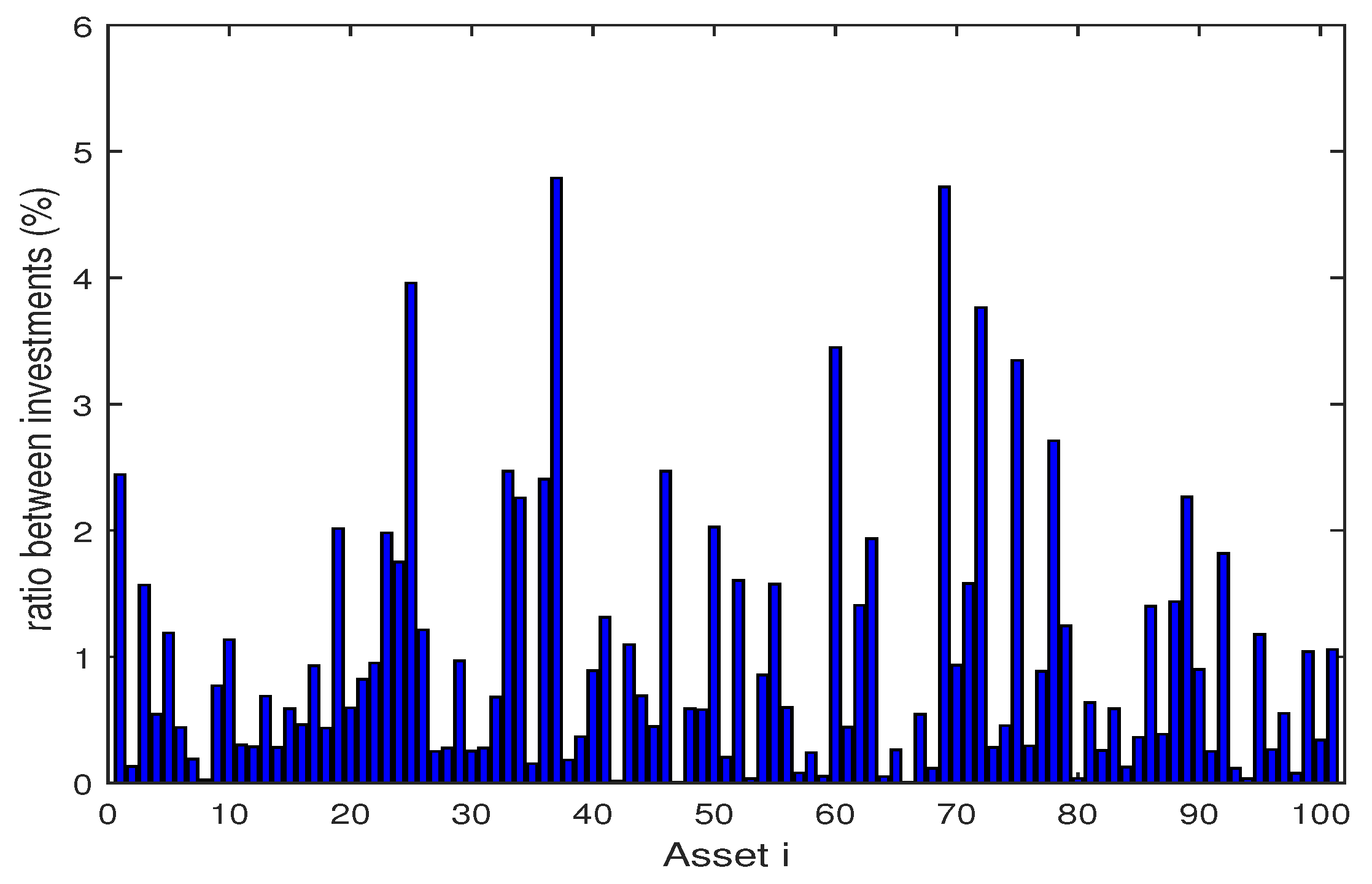
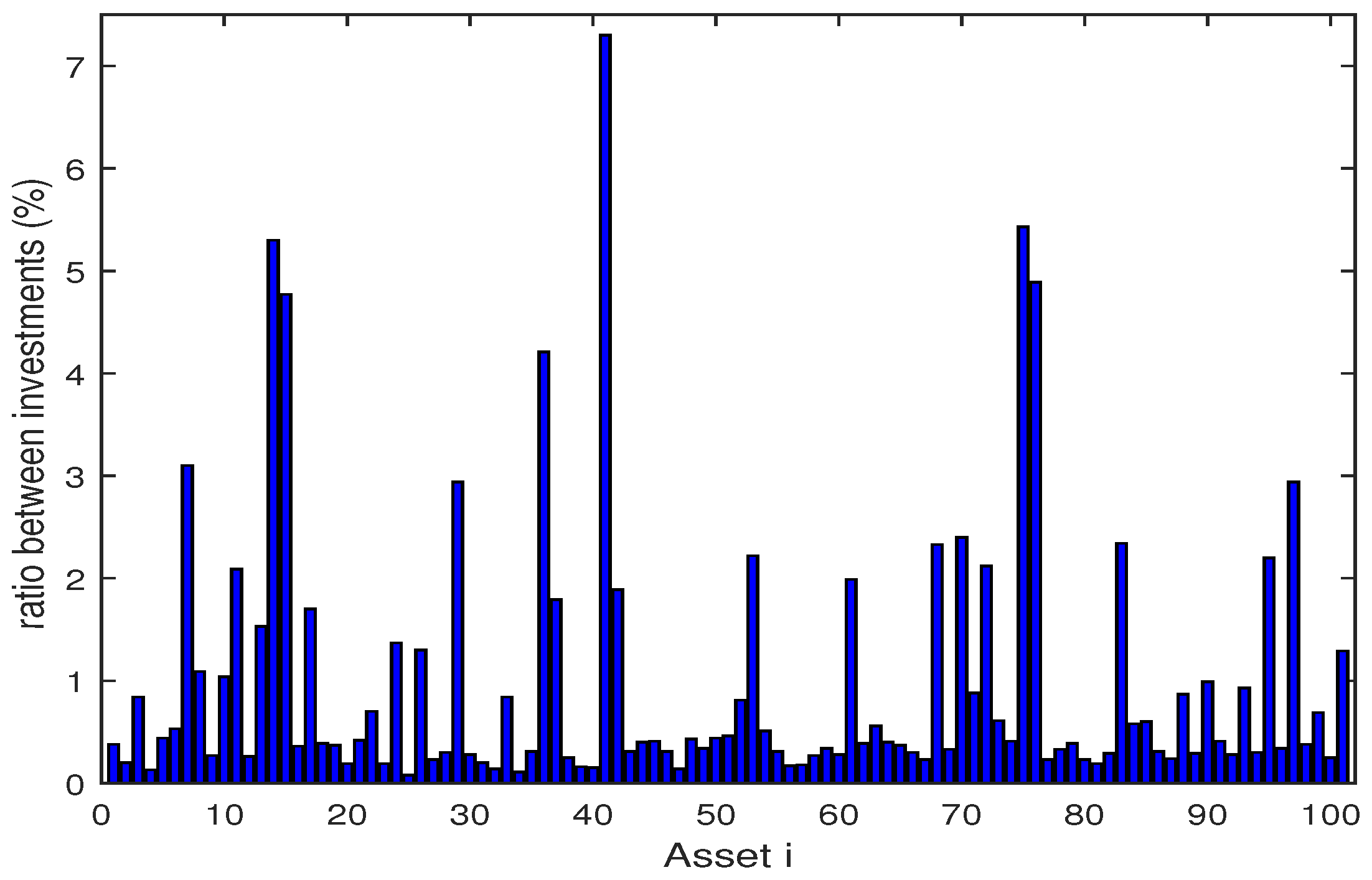
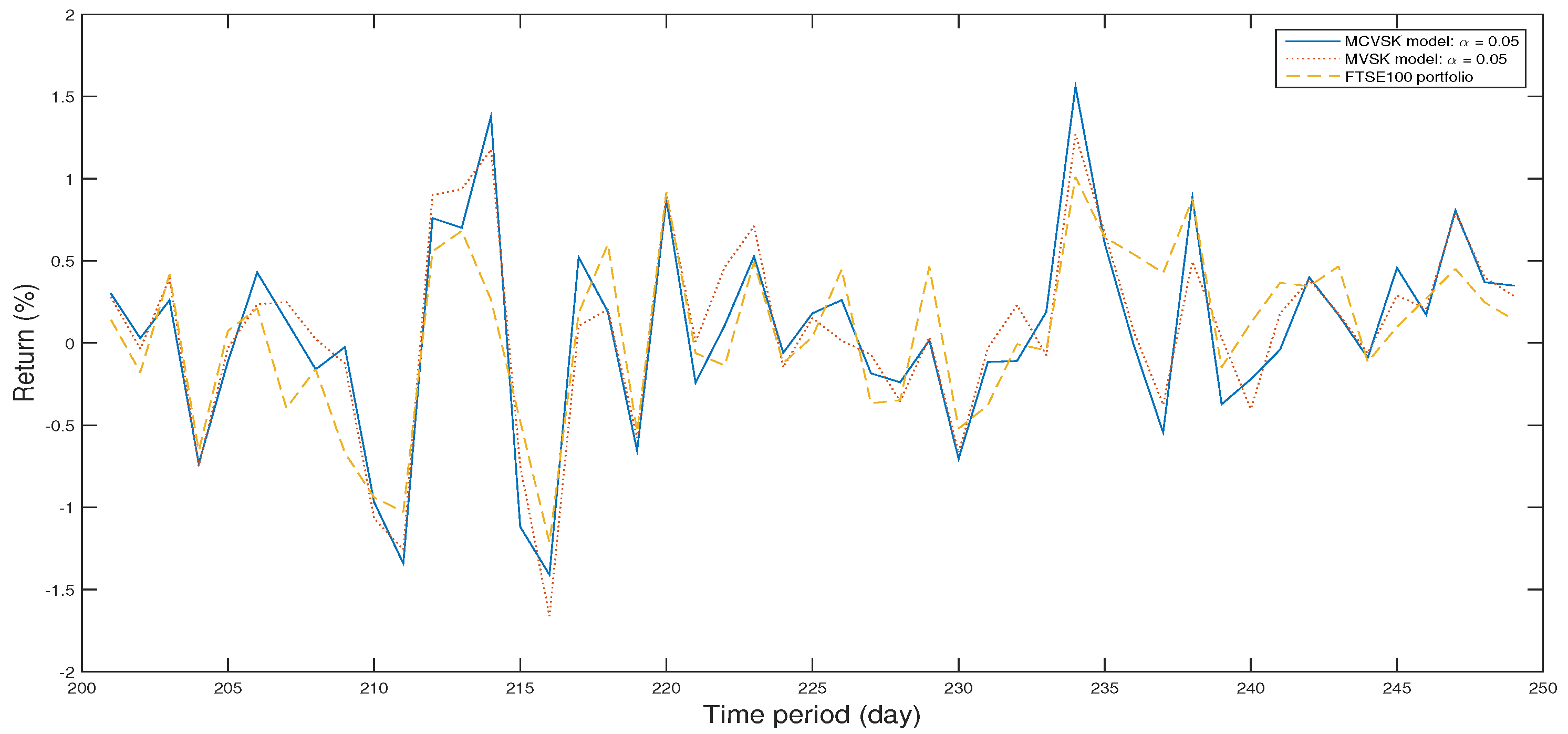
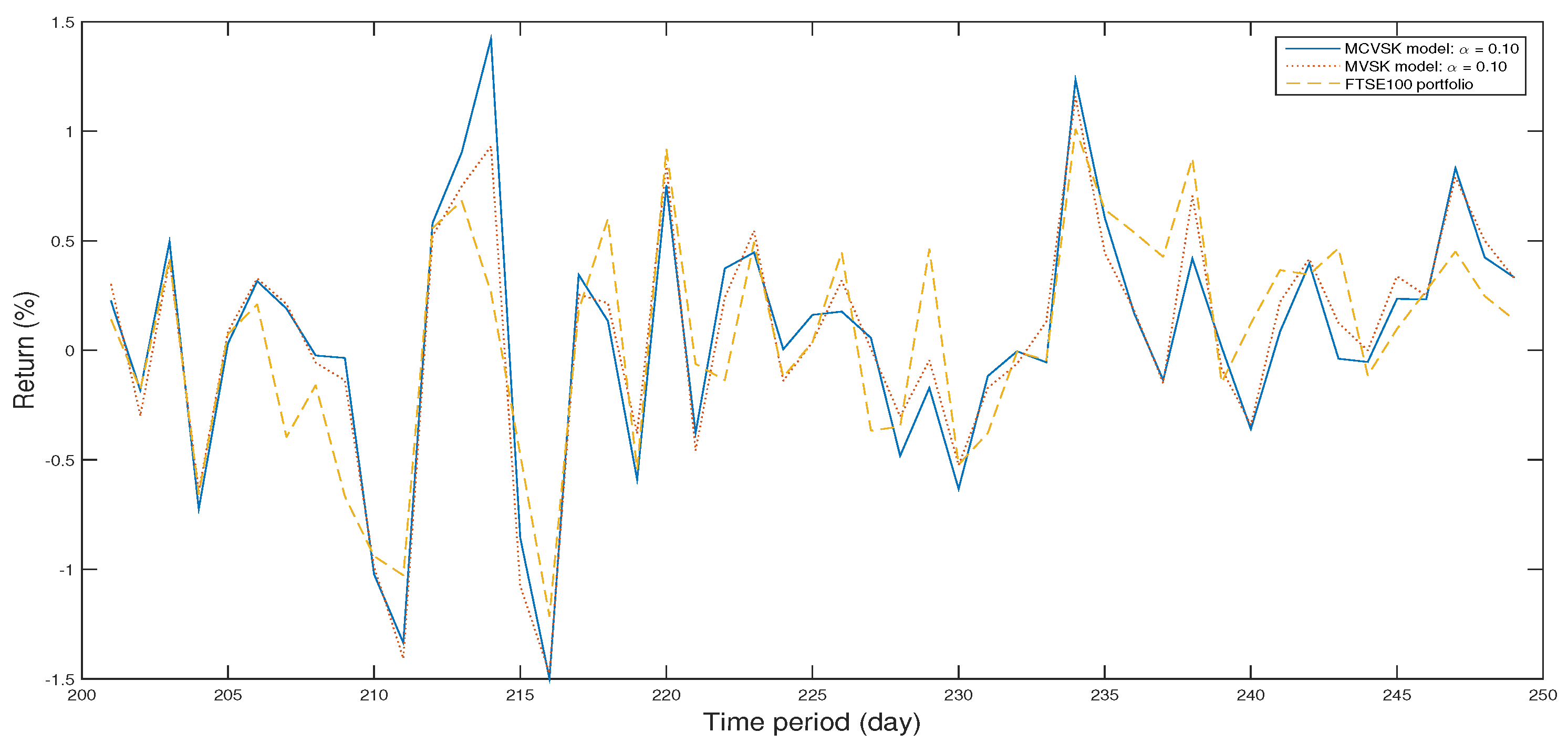
| Algorithm | Skew | Kurt | VaR | CVaR | E [g(x,)] | Max | Time (s) | ||
|---|---|---|---|---|---|---|---|---|---|
| MCVSK | 0.01 | GWO | 0.1726 | 4.0974 | −2.2535 | −2.7743 | 0.1430 | 0.0484 | 30.77 |
| PSO | 0.0878 | 3.9355 | −2.3300 | −2.7368 | 0.1107 | 0.0389 | 27.77 | ||
| GA | 0.1307 | 3.8451 | −2.2777 | −2.7744 | 0.1215 | 0.0378 | 28.59 | ||
| 0.05 | GWO | 0.0734 | 3.8483 | −1.7844 | −2.1648 | 0.1478 | 0.0488 | 24.94 | |
| PSO | 0.0292 | 4.0188 | −1.5916 | −2.2091 | 0.1109 | 0.0369 | 32.45 | ||
| GA | 0.1362 | 4.0364 | −1.7264 | −2.1502 | 0.1282 | 0.0386 | 30.20 | ||
| 0.10 | GWO | 0.2033 | 3.8933 | −1.1009 | −1.7413 | 0.1512 | 0.0479 | 32.12 | |
| PSO | 0.0346 | 3.9227 | −1.0638 | −1.7982 | 0.1110 | 0.0349 | 30.07 | ||
| GA | 0.2087 | 3.9117 | −1.1509 | −1.7554 | 0.1210 | 0.0356 | 27.47 | ||
| MVSK | 0.01 | GWO | 0.3197 | 3.9699 | −2.1251 | −2.6291 | 0.1402 | 0.0494 | 30.12 |
| PSO | 0.0934 | 3.8752 | −2.4055 | −2.8165 | 0.1117 | 0.0353 | 31.21 | ||
| GA | 0.0898 | 3.9745 | −2.2682 | −2.7807 | 0.1228 | 0.0366 | 27.47 | ||
| 0.05 | GWO | 0.2464 | 4.1137 | −1.6823 | −2.0712 | 0.1451 | 0.0487 | 28.60 | |
| PSO | 0.1575 | 3.9913 | −1.7283 | −2.1363 | 0.1347 | 0.0423 | 27.77 | ||
| GA | 0.1324 | 3.9691 | −1.7344 | −2.1379 | 0.1215 | 0.0359 | 23.86 | ||
| 0.10 | GWO | 0.1880 | 4.1003 | −1.1198 | −1.7461 | 0.1393 | 0.0479 | 26.73 | |
| PSO | 0.0440 | 3.9591 | −0.9915 | −1.7541 | 0.1064 | 0.0333 | 26.81 | ||
| GA | 0.1612 | 3.9245 | 1.1932 | 1.7606 | 0.1261 | 0.0341 | 26.02 | ||
| FTSE100 | 0.01 | × | 0.0151 | 4.3361 | −2.6739 | −3.2503 | 0.1017 | 0.0730 | × |
| 0.05 | −1.5442 | −2.3205 | |||||||
| 0.10 | −1.1953 | −1.8086 | |||||||
| y | 0.01 | × | −0.1992 | 4.6663 | −3.1508 | −3.2600 | 0.0612 | 0.0099 | × |
| 0.05 | −1.6022 | −2.4337 | |||||||
| 0.10 | −1.0599 | −1.8505 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Ye, T.; Huang, M.; Feng, S. Gray Wolf Optimization Algorithm for Multi-Constraints Second-Order Stochastic Dominance Portfolio Optimization. Algorithms 2018, 11, 72. https://doi.org/10.3390/a11050072
Ren Y, Ye T, Huang M, Feng S. Gray Wolf Optimization Algorithm for Multi-Constraints Second-Order Stochastic Dominance Portfolio Optimization. Algorithms. 2018; 11(5):72. https://doi.org/10.3390/a11050072
Chicago/Turabian StyleRen, Yixuan, Tao Ye, Mengxing Huang, and Siling Feng. 2018. "Gray Wolf Optimization Algorithm for Multi-Constraints Second-Order Stochastic Dominance Portfolio Optimization" Algorithms 11, no. 5: 72. https://doi.org/10.3390/a11050072
APA StyleRen, Y., Ye, T., Huang, M., & Feng, S. (2018). Gray Wolf Optimization Algorithm for Multi-Constraints Second-Order Stochastic Dominance Portfolio Optimization. Algorithms, 11(5), 72. https://doi.org/10.3390/a11050072





