Utility Distribution Strategy of the Task Agents in Coalition Skill Games
Abstract
:1. Introduction
2. Related Work
3. Definition of the Problem Model
4. The Task Selection Strategies of Service Agents and the Utility Distribution Strategies of Task Agents
4.1. Task Selection Strategy of Service Agent
- (1)
- HiR(τ) = 1 indicates that ri is still in the system and waiting to select a task at time τ. HiR(τ) = 0 indicates that ri is deleted from the system at time τ. HkT(τ) = 1 (HkT(τ) = 0) indicates that tk is still (is not) in the system.
- (2)
- P(i,k,τ) denotes the set of skills that can be provided to tk by ri at time τ, that is:P(i,k,τ): = {sj ∈ S|RSi,j = 1˄STj,k = 1˄¬∃ri’∈R/{ri}(RTSi’,0(τ) = k˄RTSi’,j(τ) = 1)}
- (3)
- complete(i,k,τ) = 1 (complete(i,k,τ) = 0) indicates that tk can (cannot) be completed if ri selects tk at time τ.
- (4)
- Ni(τ) denotes the set of task agents which need the skills possessed by ri ∈ R at time τ:Ni(τ): = {tk ∈ T|HkT(τ) = 1˄P(i,k,τ) ≠ Φ}
- (5)
- Ci(τ): = {tk∈T|HkT(τ) = 1˄complete(i,k,τ) = 1}.
- (6)
- f(i,k,τ) denotes the share of utility ri ∈ R can get if it selected tk ∈ T at time τ without considering whether it can be completed or not:
- (7)
- R1(k,j,τ): = {ri ∈ R|HiR(τ) = 1˄RSi,j = 1˄STj,k = 1˄RTSi,0(τ) = k˄RTSi,j(τ) = 1}.
- (8)
- R2(k,j,τ): = {ri ∈ R|HiR(τ) = 1˄RSi,j = 1˄STj,k = 1˄RTSi,0(τ) ≠ k˄f(i,k,τ) > f(i,RTSi,0(τ),τ)}.
- (9)
- R3(k,j,τ): = {ri ∈ R|HiR(τ) = 1˄RSi,j = 1˄complete(i,k,τ) = 1˄j ∈ P(i,k,τ)}.
- (10)
- R4(k,j,τ): = {ri ∈ R|HiR(τ) = 1˄RSi,j = 1}.
- (11)
- T1(j,τ): = {tk ∈ T|HkT(τ) = 1˄STj,k = 1˄R1(k,j,τ)∪R2(k,j,τ) = Φ}.
| Sub-Procedure 1 Task selection strategy of service agent ri ∈ R |
| 1: IF Ni(τ)∩Ci(τ)≠Φ THEN 2: ; 3: ELSE IF Ni(τ)≠Φ˄Ci(τ) = Φ THEN 4: ; 5: ELSE 6: t(i,τ+1)←0; 7: END IF |
4.2. Utility Distribution Strategy of Task Agent
- (1)
- Among the skills needed by tk ∈ T, whose share of utility needs to be increased? Let Skneed(τ) denote the set of skills of this type:sj ∈ Skneed(τ) must satisfy the following three conditions: (1) STj,k = 1, (2) R1(k,j,τ) = Φ and (3) R2(k,j,τ) = Φ.
- (2)
- For sj ∈ Skneed(τ), what is the minimum increase? It is denoted with fmin(k,j,τ), whose computing method is given in Sub-procedure 2, where , if , otherwise ).
Sub-Procedure 2 Compute the value of fmin(k,j,τ) 1: IF R3(k,j,τ)≠Φ THEN
2: ;
3: ELSE IF R4(k,j,τ)≠Φ THEN
4: ;
5: ELSE
8: fmin(k,j,τ)←-1;
9: END IF - (3)
- From which skills can tk adjust shares of utility to sj ∈ Skneed(τ)? Let Slend(k,j,τ) denote the set of skills of this type:Slend(k,j,τ) ← {sj’ ∈ S|j’ ≠ j˄STj’,k = 1˄(R1(k,j,τ)∪R2(k,j,τ)) ≠ Φ}.
- (4)
- For sj’ ∈ Slend(k,j,τ), what is the maximum decrease? It is denoted with fmax(k,j,j’), whose computing method is shown in Sub-procedure 3. Where ksec denotes the serial number of the task agents which will be selected by ri if tk was out of consideration. The method to compute the values of ξ1 and ξ2 is: if , ξ1 ← 1, otherwise, ξ1 ← 0. If , ξ2 ← 1, otherwise, ξ2 ← 0. If , , .
Sub-Procedure 3 Compute the value of fmax(k,j,j’) 1: IF R1(k,j,τ)≠Φ˄R2(k,j,τ)≠Φ THEN
2: ;
3: ELSE IF R1(k,j’,τ)≠Φ THEN
4: ;
5: ELSE IF R2(k,j’,τ)≠Φ THEN
6: ;
7: ELSE
8: fmax(k,j,j’)←0;
9: END IF
10: fmax(k,j,j’)←min(fmax(k,j,j’),TSk,j’(τ)).
4.3. The Whole Frame of TAAUDA
| Algorithm 1 TAAUDA |
| Inputs: RS, ST, U, DRS, DN, IN; Outputs: the maximal system total revenue and the corresponding RTS. 1: FORdrs∈{1,2,···,DRS} 2: Disturb the order in which the service agents select the most satisfied task agents; 3: Initialize TS(0): the utilities of task agents are distributed averagely.
4: FORdn∈{1,2,···,DN} 5: oldRTS←RTS(τ); 6: WHILE ∃tk∈T(HkT(τ) = 1) 7: in←0; 8: WHILE TS(τ)≠oldTS˄in<IN 9: in++; 10: oldTS←TS(τ); 11: FOR tk∈{tk’∈T|Hk’T(τ) = 1} 12: FOR sj ∈Skneed(τ) 13: Increase TSk,j(τ) through decreasing TSk,j’(τ)(sj’ ∈Slend(k,j,τ)). If the minimum increase fmin(k,j,τ) is reached, success←true, otherwise, success←false; 14: WHILE success 15: For tk’∈T1(j,τ), increase TSk’,j(τ)(sj ∈Sk’need(τ)) through decreasing TSk’,j’(τ)(sj’ ∈Slend(k’,j,τ)). If the minimum increase fmin(k’,j,τ) is satisfied, success←true, otherwise, success←false. 16: END WHILE 17: END FOR 18: END FOR 19: END WHILE 20: Delete the task agents who have all the needed skills and their corresponding service agents. 21: Delete the task agents that cannot be completed. 22: If there is not any task agent is deleted in line 20 and 21, delete . A set of service agents needed by td are chosen with a Greedy Strategy and deleted. 23: END WHILE 24: ri∈{ri’∈R|Hi’R(τ) = 1} selects task agent tei according to oldRTS, where . 25: Record the maximum system total revenue and its corresponding RTS. Disturbing oldRTS: each service agent randomly selects a task that requires its skills. 26: END FOR 27: END FOR |
4.4. Further Analyses of the Example in Section 1
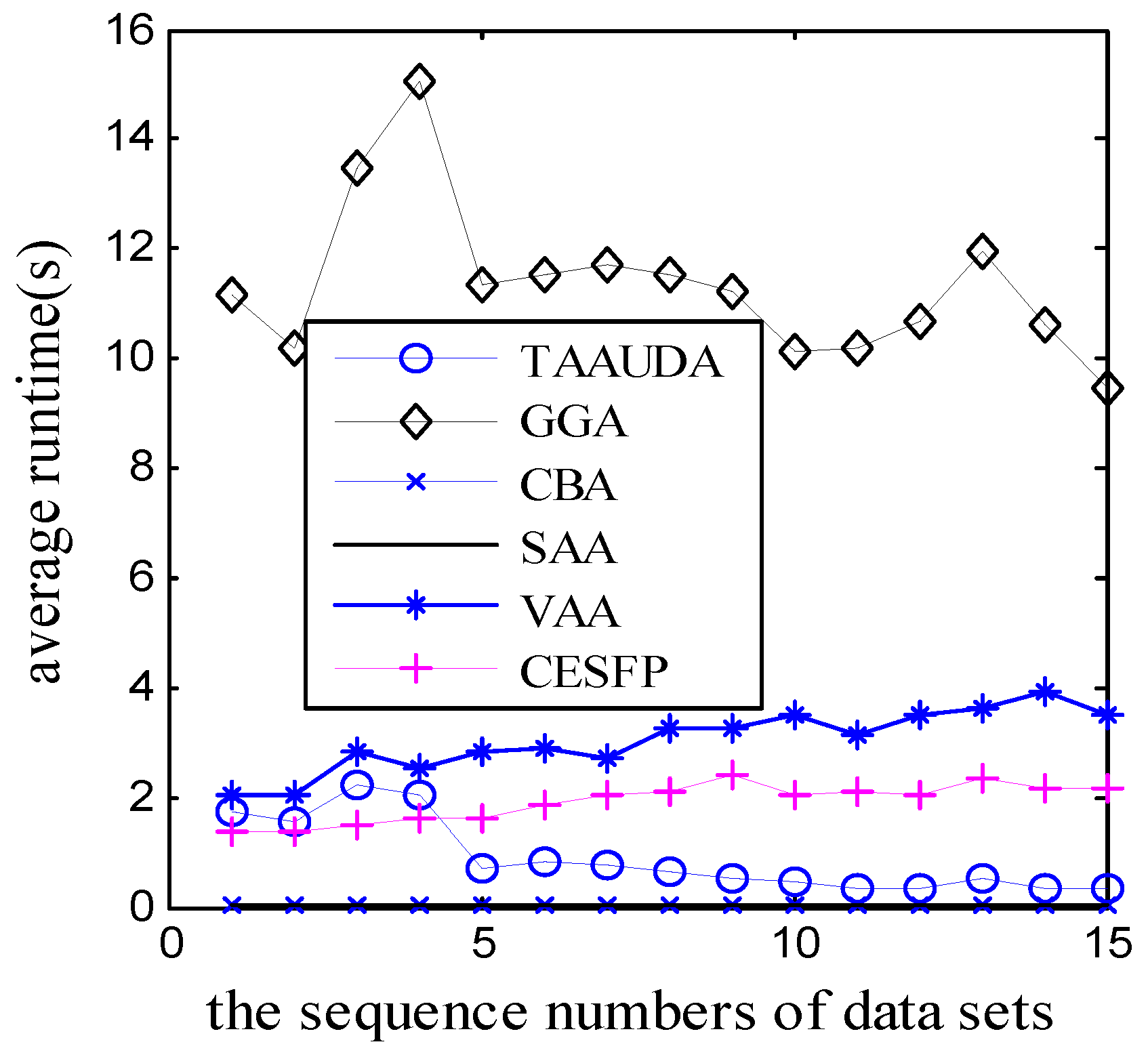
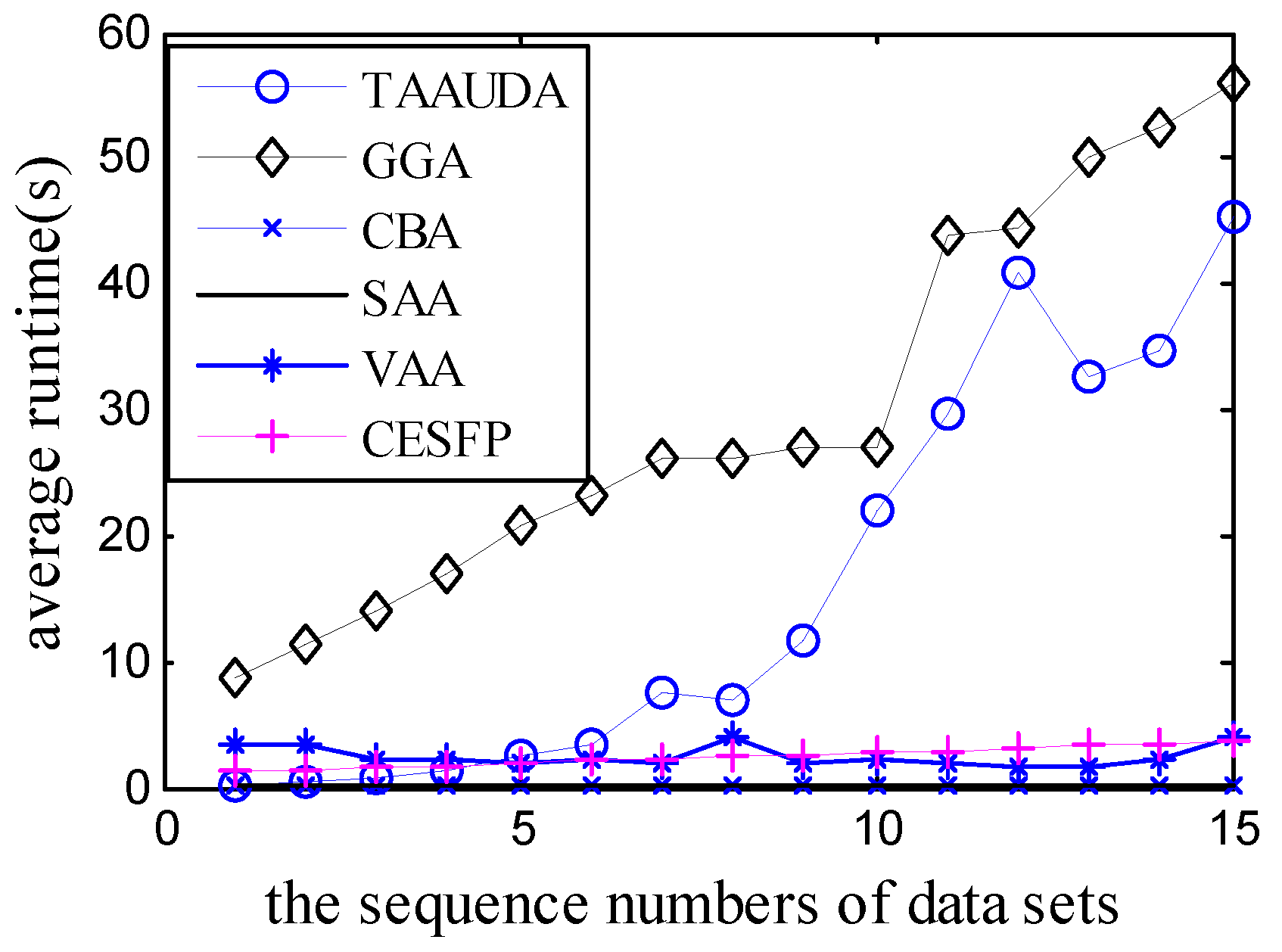
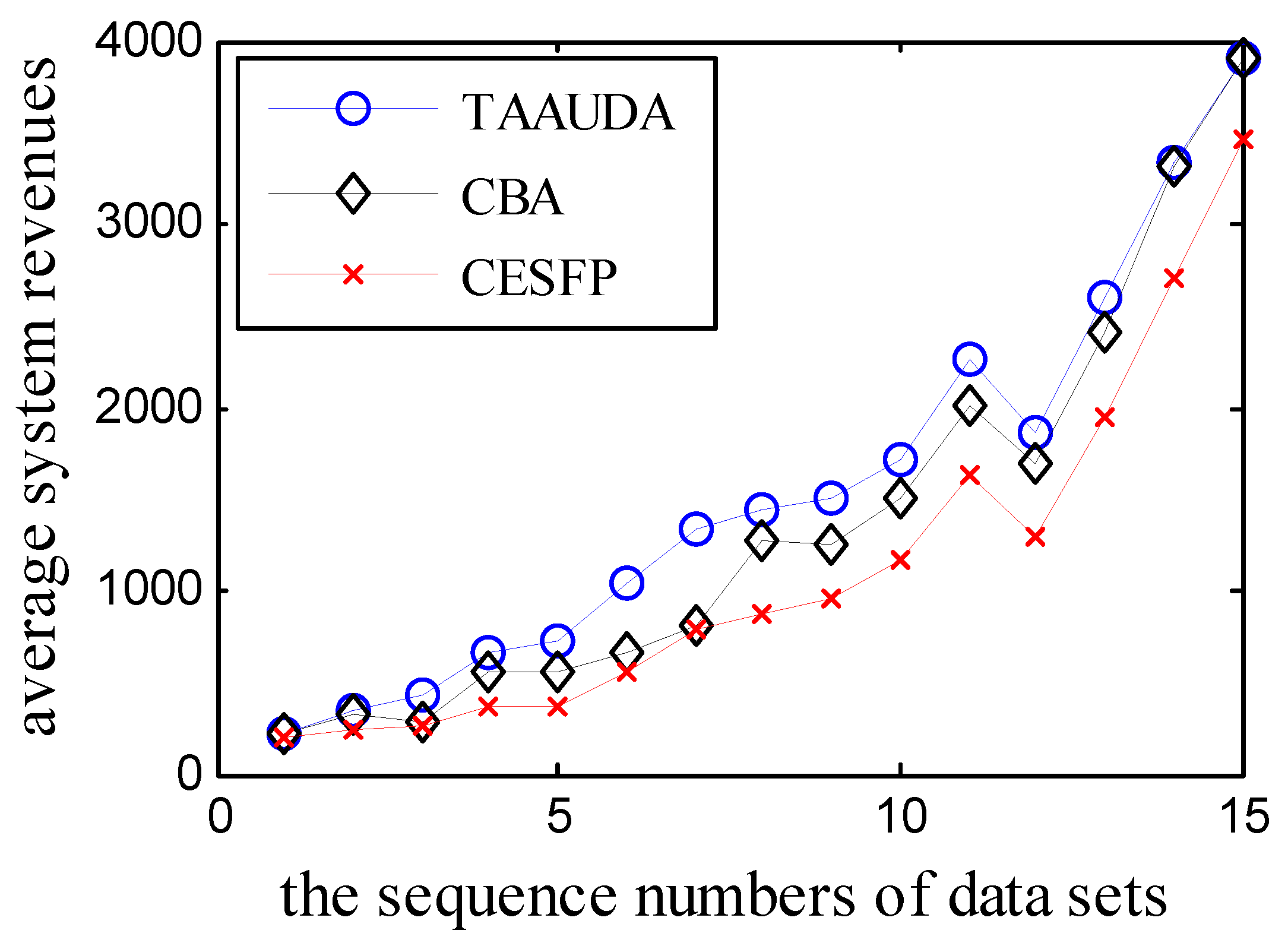
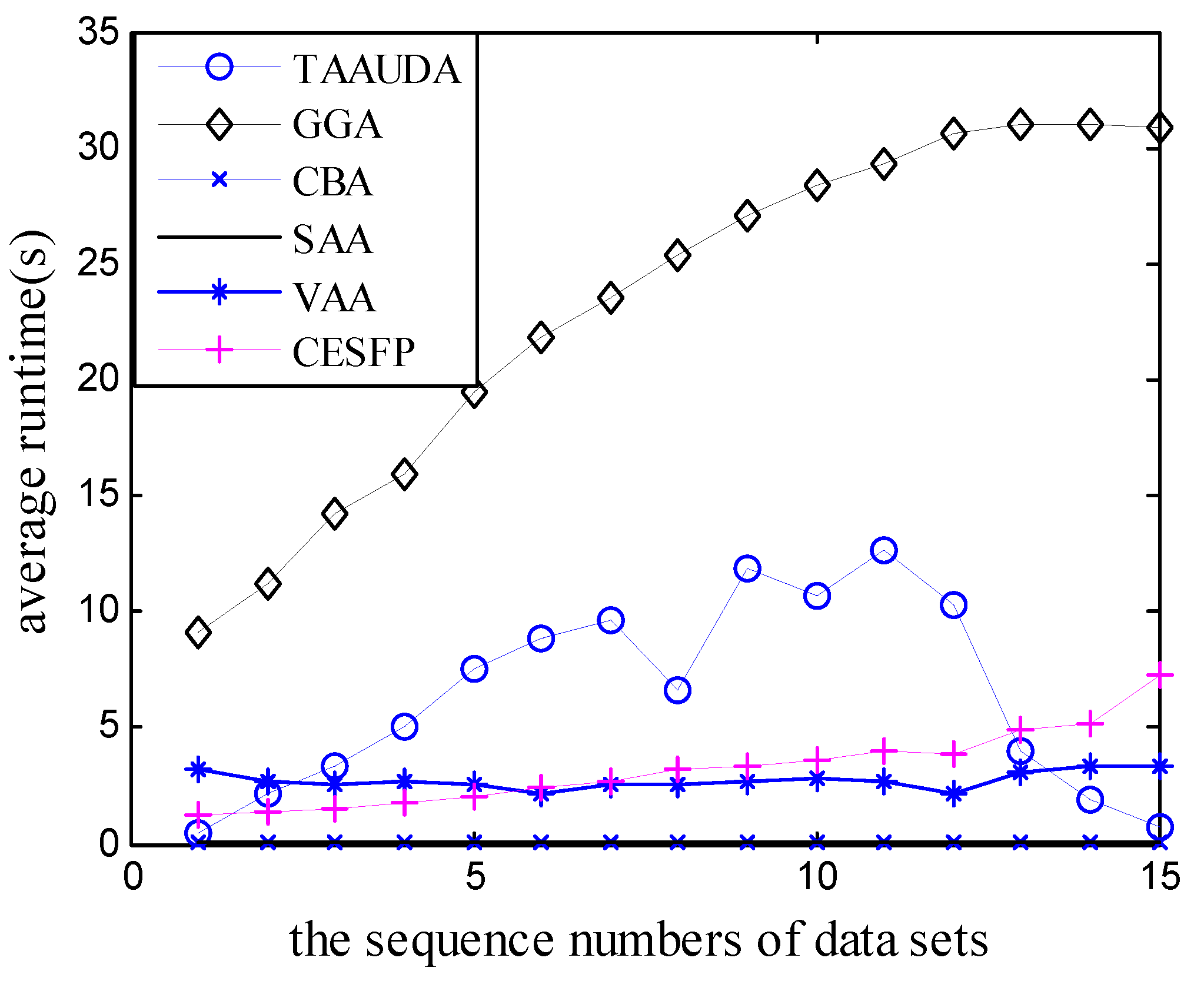
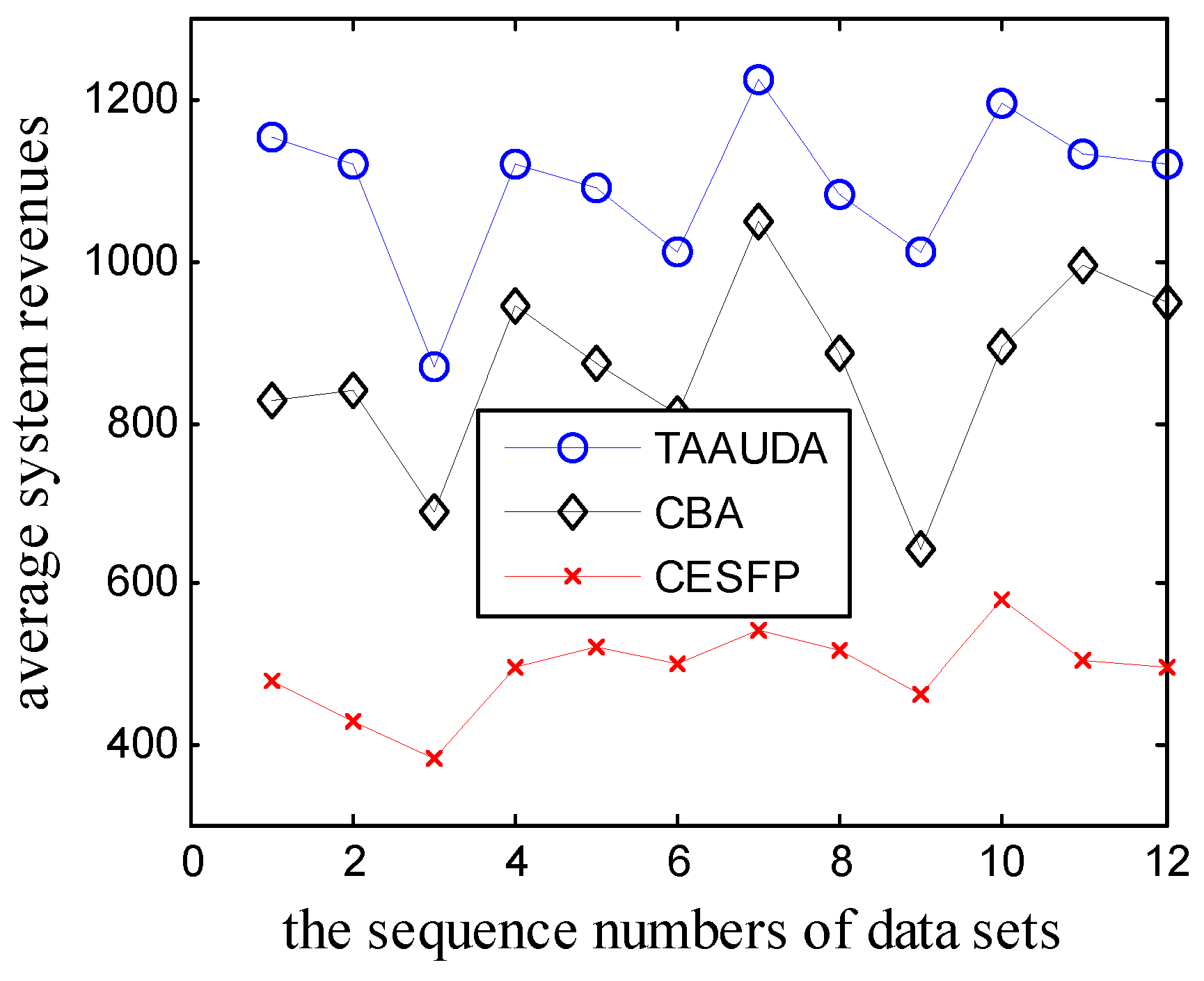
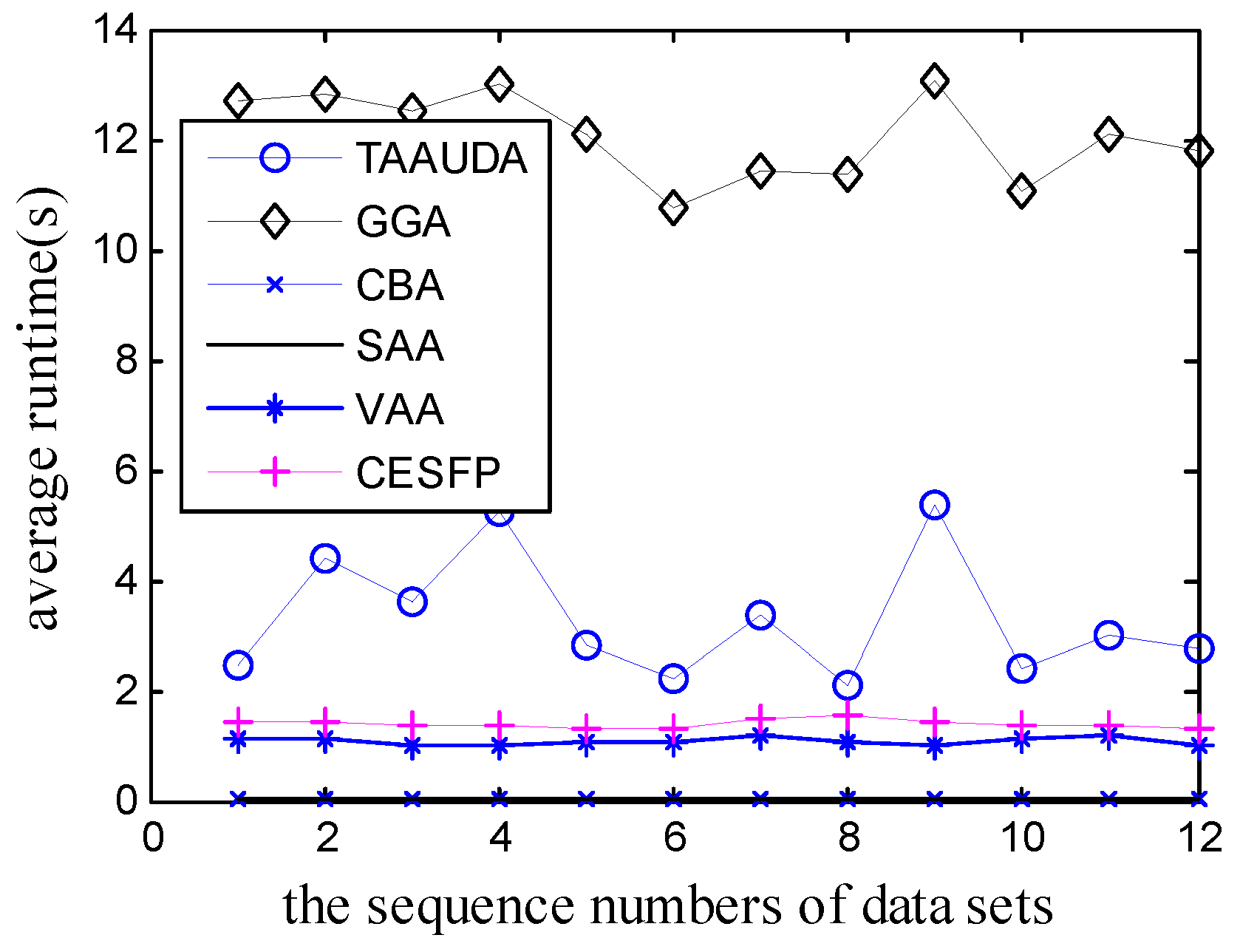
5. Simulation Results
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bachrach, Y.; Rosenschein, J.S. Coalitional skill games. In Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems, Estoril, Portugal, 12–16 May 2008; pp. 1023–1030. [Google Scholar]
- Bachrach, Y.; Parkes, D.C.; Rosenschein, J.S. Computing cooperative solution concepts in coalitional skill games. Artif. Intell. 2013, 204, 1–21. [Google Scholar] [CrossRef]
- Bachrach, Y.; Meir, R.; Jung, K.; Kohli, P. Coalitional Structure Generation in Skill Games. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence (AAAI-10), Atlanta, GA, USA, 11 July 2010; Volume 10, pp. 703–708. [Google Scholar]
- Rahwan, T.; Michalak, T.P.; Wooldridge, M.; Jennings, N.R. Coalition structure generation: A survey. Artif. Intell. 2015, 229, 139–174. [Google Scholar] [CrossRef]
- Vig, L.; Adams, J.A. Coalition formation: From software agents to robots. J. Intell. Robot. Syst. 2007, 50, 85–118. [Google Scholar] [CrossRef]
- Adams, J.A. Coalition formation for task allocation: Theory and algorithms. Auton. Agents Multi Agent Syst. 2011, 22, 225–248. [Google Scholar]
- Cui, R.; Guo, J.; Gao, B. Game theory-based negotiation for multiple robots task allocation. Robotica 2013, 31, 923–934. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Swenson, B.; Kar, S.; Xavier, J. A computationally efficient implementation of fictitious play for large-scale games. arXiv, 2015; arXiv:1506.04320. [Google Scholar]
- Marden, J.R.; Arslan, G.; Shamma, J.S. Cooperative control and potential games. IEEE Trans. Syst. Man Cybern. Part B 2009, 39, 1393–1407. [Google Scholar] [CrossRef] [PubMed]
- Marden, J.R.; Arslan, G.; Shamma, J.S. Regret based dynamics: Convergence in weakly acyclic games. In Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems, Honolulu, Hawaii, 14–18 May 2007; p. 42. [Google Scholar]
- Genin, T.; Aknine, S. Coalition formation strategies for self-interested agents in task oriented domains. In Proceedings of the 2010 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Toronto, ON, Canada, 31 August–3 September 2010; pp. 205–212. [Google Scholar]
- Kong, Y.; Zhang, M.; Ye, D.; Zhu, J.; Choi, J. An intelligent agent-based method for task allocation in competitive cloud environments. Concurr. Comput. Pract. Exp. 2017, 30, e4178. [Google Scholar] [CrossRef]
- Barile, F.; Rossi, A.; Staffa, M.; Napoli, C.D.; Rossi, S.A. Market Mechanism for QoS-aware Multi-Robot Task Allocation. In Proceedings of the 16th Workshop “From Objects to Agents” (WOA15), Naples, Italy, 17–19 June 2015; pp. 129–134. [Google Scholar]
- Kong, Y.; Zhang, M.; Ye, D. An auction-based approach for group task allocation in an open network environment. Comput. J. 2016, 59, 403–422. [Google Scholar] [CrossRef]
- Service, T.C.; Sen, S.D.; Adams, J.A. A simultaneous descending auction for task allocation. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Dieg, CA, USA, 5–8 October 2014; pp. 379–384. [Google Scholar]
- Lin, L.; Zheng, Z. Combinatorial bids based multi-robot task allocation method. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1145–1150. [Google Scholar]
- Liu, Y.; Zhang, G.F.; Su, Z.P.; Yue, F.; Jiang, J.G. Using Computational Intelligence Algorithms to Solve the Coalition Structure Generation Problem in Coalitional Skill Games. J. Comput. Sci. Technol. 2016, 31, 1136–1150. [Google Scholar] [CrossRef]
- Aziz, H.; De Keijzer, B. Complexity of coalition structure generation. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems, TaiPei, Taiwan, 2–6 May 2011; pp. 191–198. [Google Scholar]
- Tran-Thanh, L.; Nguyen, T.D.; Rahwan, T.; Rogers, A.R.; Jennings, N. An efficient vector-based representation for coalitional games. In Proceedings of the IJCAI’13, Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 383–389. [Google Scholar]
- Kolisch, R.; Sprecher, A. PSPLIB—A project scheduling problem library: OR software-ORSEP operations research software exchange program. Eur. J. Op. Res. 1997, 96, 205–216. [Google Scholar] [CrossRef]
- Myszkowski, P.B.; Skowronski, M.E.; Sikora, K. A new benchmark dataset for Multi-Skill Resource-Constrained Project Scheduling Problem. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems (FedCSIS), Lodz, Poland, 13–16 September 2015; pp. 129–138. [Google Scholar]
- Myszkowski, P.B.; Skowroński, M.E.; Olech, Ł.P.; Oślizło, K. Hybrid ant colony optimization in solving multi-skill resource-constrained project scheduling problem. Soft Comput. 2015, 19, 3599–3619. [Google Scholar] [CrossRef]
- Hegazy, T.; Shabeeb, A.K.; Elbeltagi, E.; Cheema, T. Algorithm for scheduling with multiskilled constrained resources. J. Constr. Eng. Manag. 2000, 126, 414–421. [Google Scholar] [CrossRef]
- Santos, M.A.; Tereso, A.P. On the multi-mode, multi-skill resource constrained project scheduling problem—A software application. In Soft Computing in Industrial Applications; Gaspar-Cunha, A., Takahashi, R., Schaefer, G., Costa, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 239–248. [Google Scholar]
- Hooshangi, N.; Alesheikh, A.A. Agent-based task allocation under uncertainties in disaster environments: An approach to interval uncertainty. Int. J. Disaster Risk Reduct. 2017, 24, 150–171. [Google Scholar] [CrossRef]
- Vig, L.; Adams, J.A. Multi-robot coalition formation. IEEE Trans. Robot. 2006, 22, 637–649. [Google Scholar] [CrossRef]
- Elango, M.; Nachiappan, S.; Tiwari, M.K. Balancing task allocation in multi-robot systems using K-means clustering and auction based mechanisms. Expert Syst. Appl. 2011, 38, 6486–6491. [Google Scholar] [CrossRef]
- Kong, Y.; Zhang, M.; Ye, D. A group task allocation strategy in open and dynamic grid environments. In Recent Advances in Agent-based Complex Automated Negotiation. Studies in Computational Intelligence; Fukuta, N., Ito, T., Zhang, M., Fujita, K., Robu, V., Eds.; Springer: Cham, Switzerland, 2016; Volume 638, pp. 121–139. ISBN 978-3-319-30305-5. [Google Scholar]
- Tian, Y.; Sarkar, N. Game-based pursuit evasion for nonholonomic wheeled mobile robots subject to wheel slips. Adv. Robot. 2013, 27, 1087–1097. [Google Scholar] [CrossRef]
- Zadeh, L.A. Stochastic finite-state systems in control theory. Inf. Sci. 2013, 251, 1–9. [Google Scholar] [CrossRef]
- Kawamura, A.; Soejima, M. Simple strategies versus optimal schedules in multi-agent patrolling. In Algorithms and Complexity. CIAC 2015. Lecture Notes in Computer Science; Paschos, V., Widmayer, P., Eds.; Springer: Cham, Switzerland, 2015; Volume 9079, pp. 261–273. [Google Scholar]
- Hernández, E.; Cerro, J.; Barrientos, A. Game theory models for multi-robot patrolling of infrastructures. Int. J. Adv. Robot. Syst. 2013, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
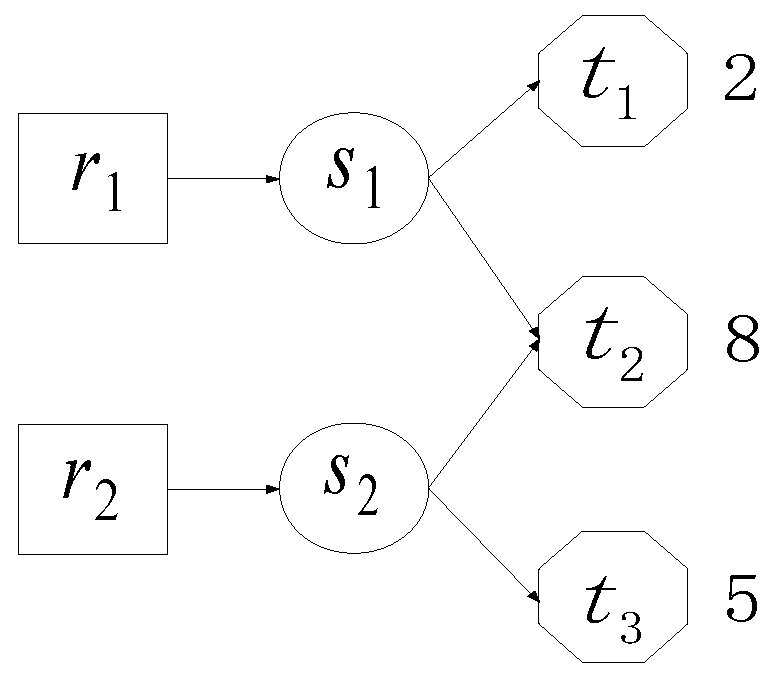
| r2,t1 | r2,t2 | r2,t3 | |
| r1,t1 | (2,0) | (2,0) | (2,5) |
| r1,t2 | (0,0) | (4,4) | (0,5) |
| r1,t3 | (0,0) | (0,0) | (0,5) |
| r2,t1 | r2,t2 | r2,t3 | |
| r1,t1 | (2,0) | (2,0) | (2,5) |
| r1,t2 | (0,0) | (3,5) | (0,5) |
| r1,t3 | (0,0) | (0,0) | (0,5) |
| 0.01 | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.4 | 0.6 | 0.8 | 0.9 | 0.95 | |
| 0.01 | 415.1 | 440.0 | 441.8 | 474.3 | 508.3 | 515.8 | 543.8 | 552.3 | 566.0 | 584.0 | 581.3 |
| 0.05 | 483.3 | 506.5 | 524.0 | 563.5 | 558.5 | 568.8 | 595.8 | 634.5 | 637.8 | 632.3 | 627.3 |
| 0.1 | 513.3 | 551.5 | 566.5 | 553.0 | 598.3 | 628.5 | 606.5 | 668.0 | 656.5 | 645.0 | 642.0 |
| 0.15 | 505.5 | 534.5 | 577.5 | 592.0 | 601.5 | 623.8 | 629.8 | 577.0 | 529.3 | 518.0 | 535.3 |
| 0.2 | 534.3 | 538.8 | 574.0 | 598.0 | 574.5 | 544.8 | 502.5 | 462.5 | 437.3 | 411.0 | 421.8 |
| 0.3 | 433.8 | 424.3 | 428.3 | 415.0 | 405.8 | 382.3 | 361.0 | 348.0 | 347.5 | 340.5 | 335.5 |
| 0.4 | 328.0 | 331.3 | 328.5 | 341.5 | 341.3 | 323.3 | 327.5 | 288.5 | 288.5 | 288.8 | 279.8 |
| 0.6 | 226.3 | 230.0 | 228.3 | 240.0 | 247.3 | 234.8 | 229.0 | 231.0 | 210.8 | 213.3 | 217.3 |
| 0.8 | 201.3 | 201.3 | 202.5 | 179.5 | 199.3 | 183.5 | 203.3 | 186.8 | 191.3 | 185.3 | 177.8 |
| λ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 0.95 |
| average system revenues | 313.3 | 338.5 | 368.3 | 373.7 | 374.9 | 373.5 | 375.1 | 392.9 | 358.2 | 337.2 |
| TAAUDA | GGA | VAA | SAA | |
| 1.1 | 220.52 | 157.43 | 230.0 | 206 |
| 1.2 | 344.51 | 291.10 | 322.0 | 322 |
| 1.3 | 511.19 | 444.12 | 482.0 | 506 |
| 1.4 | 534.55 | 443.08 | 516 | 503 |
| 1.5 | 601.67 | 552.42 | 588 | 599 |
| 1.6 | 613.37 | 593.28 | 612 | 601 |
| 1.7 | 650.32 | 636.84 | 632 | 625 |
| 1.8 | 790.2 | 781.14 | 775 | 747 |
| 1.9 | 826.86 | 820.5 | 818 | 817 |
| 1.10 | 563.54 | 562.92 | 554 | 564 |
| 1.11 | 604.36 | 602.12 | 597 | 601 |
| 1.12 | 699.0 | 697.72 | 699 | 693 |
| 1.13 | 837.85 | 835.32 | 835 | 836 |
| 1.14 | 646.0 | 642.86 | 646 | 646 |
| 1.15 | 880.0 | 875.86 | 880 | 880 |
| TAAUDA | GGA | VAA | SAA | |
| 2.1 | 270.29 | 276.04 | 263.0 | 263.0 |
| 2.2 | 341.9 | 334.0 | 340.0 | 340.0 |
| 2.3 | 468.3 | 432.6 | 399.0 | 429.0 |
| 2.4 | 389.48 | 315.12 | 368.0 | 328.0 |
| 2.5 | 458.5 | 348.9 | 435.0 | 405.0 |
| 2.6 | 504.66 | 316.8 | 504.0 | 384.0 |
| 2.7 | 526.75 | 263.76 | 448.0 | 392.0 |
| 2.8 | 710.88 | 380.36 | 560.0 | 424.0 |
| 2.9 | 661.95 | 333.36 | 477.0 | 594.0 |
| 2.10 | 817.9 | 359.4 | 620.0 | 520.0 |
| 2.11 | 503.47 | 169.77 | 429.0 | 429.0 |
| 2.12 | 538.2 | 227.6 | 348.0 | 348.0 |
| 2.13 | 664.3 | 104.9 | 663.0 | 663.0 |
| 2.14 | 762.16 | 88.2 | 770.0 | 602.0 |
| 15 | 1002.3 | 19.4 | 870.0 | 870.0 |
| TAAUDA | GGA | VAA | SAA | |
| 3.1 | 221.00 | 221.0 | 221.0 | 221.0 |
| 3.2 | 350.08 | 326.2 | 348.0 | 328.0 |
| 3.3 | 435.84 | 392.16 | 384.0 | 372.0 |
| 3.4 | 652.88 | 595.60 | 620.0 | 600.0 |
| 3.5 | 734.3 | 642.1 | 695.0 | 710.0 |
| 3.6 | 1051.62 | 941.04 | 1038.0 | 984.0 |
| 3.7 | 1336.51 | 1210.86 | 1288.0 | 1232.0 |
| 3.8 | 1448.88 | 1347.04 | 1392.0 | 1368.0 |
| 3.9 | 1508.08 | 1423.8 | 1413.0 | 1422.0 |
| 3.10 | 1719.50 | 1657.00 | 1650.0 | 1630.0 |
| 3.11 | 2265.23 | 2208.14 | 2244.0 | 2145.0 |
| 3.12 | 1857.48 | 1819.44 | 1776.0 | 1776.0 |
| 3.13 | 2597.66 | 2542.8 | 2379.0 | 2314.0 |
| 3.14 | 3329.2 | 3277.12 | 3318.0 | 3318.0 |
| 3.15 | 3900.0 | 3885.9 | 3900.0 | 3900.0 |
| TAAUDA | GGA | VAA | SAA | |
| 3.1 | 1157.1 | 890.8 | 1099.0 | 1070.0 |
| 3.2 | 1120.86 | 809.83 | 1092.0 | 1055.0 |
| 3.3 | 867.82 | 595.77 | 866.0 | 888.0 |
| 3.4 | 1121.79 | 831.8 | 1060.0 | 1072.0 |
| 3.5 | 1092.54 | 844.12 | 1033.0 | 1041.0 |
| 3.6 | 1010.29 | 806.23 | 939.0 | 967.0 |
| 3.7 | 1226.82 | 896.08 | 1223.0 | 1123.0 |
| 3.8 | 1082.19 | 880.92 | 1116.0 | 1051.0 |
| 3.9 | 1011.25 | 756.03 | 1056.0 | 1020.0 |
| 3.10 | 1195.9 | 966.22 | 1194.0 | 1133.0 |
| 3.11 | 1132.27 | 836.15 | 1088.0 | 1024.0 |
| 3.12 | 1121.52 | 710.1 | 1114.0 | 1083.0 |
| 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 1.10 | 1.11 | 1.12 | 1.13 | 1.14 | 1.15 | |
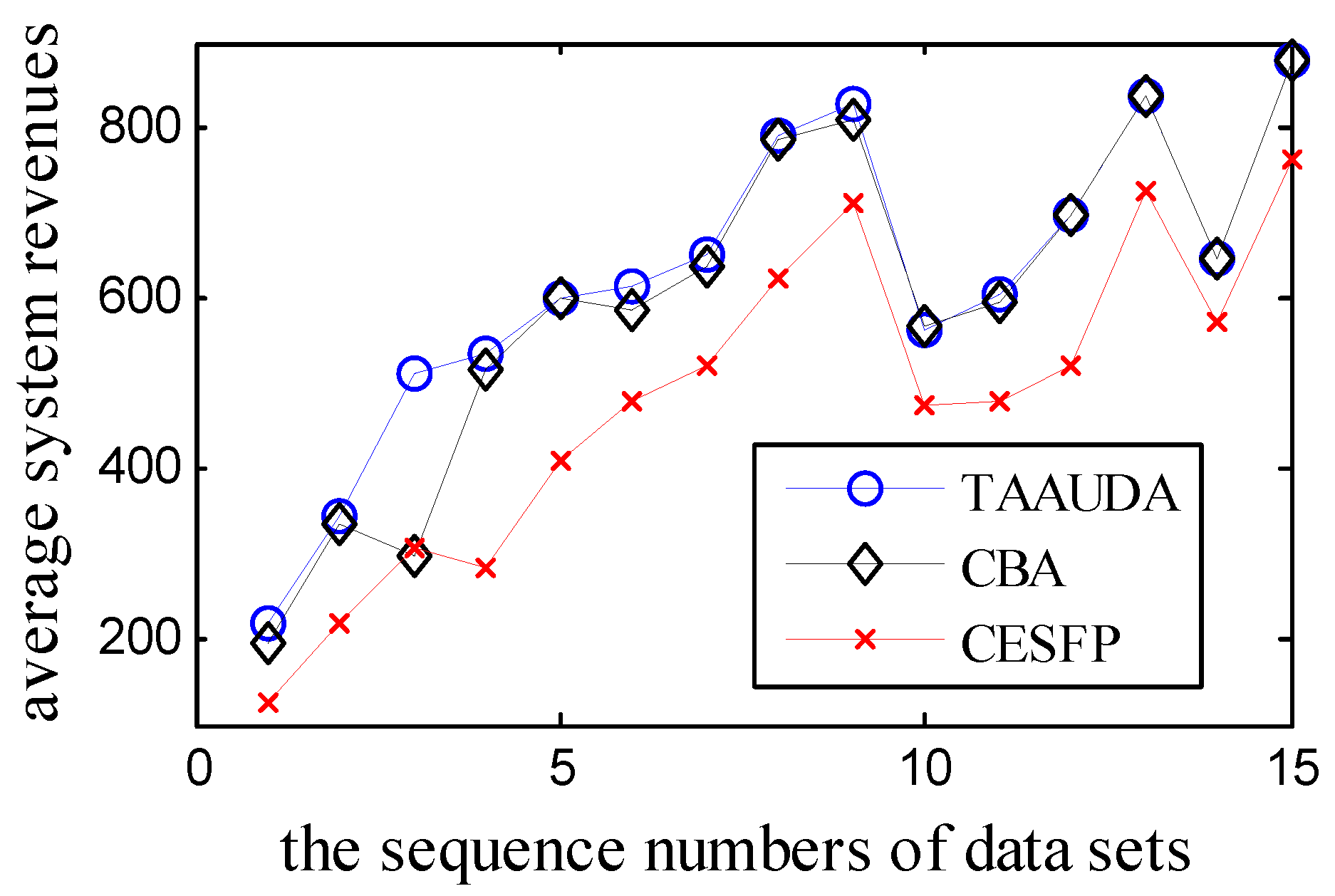
| TAAUDA | 220.5 | 344.5 | 511.2 | 534.5 | 601.7 | 609.5 | 650.3 | 790.2 | 826.9 | 563.6 | 604.4 | 698.3 | 837.9 | 646.0 | 880.0 |
| TADUA | 179.2 | 335.2 | 498.6 | 526.4 | 600.5 | 605.6 | 649.3 | 787.0 | 825.6 | 563.0 | 603.4 | 698.1 | 836.8 | 645.9 | 880.0 |
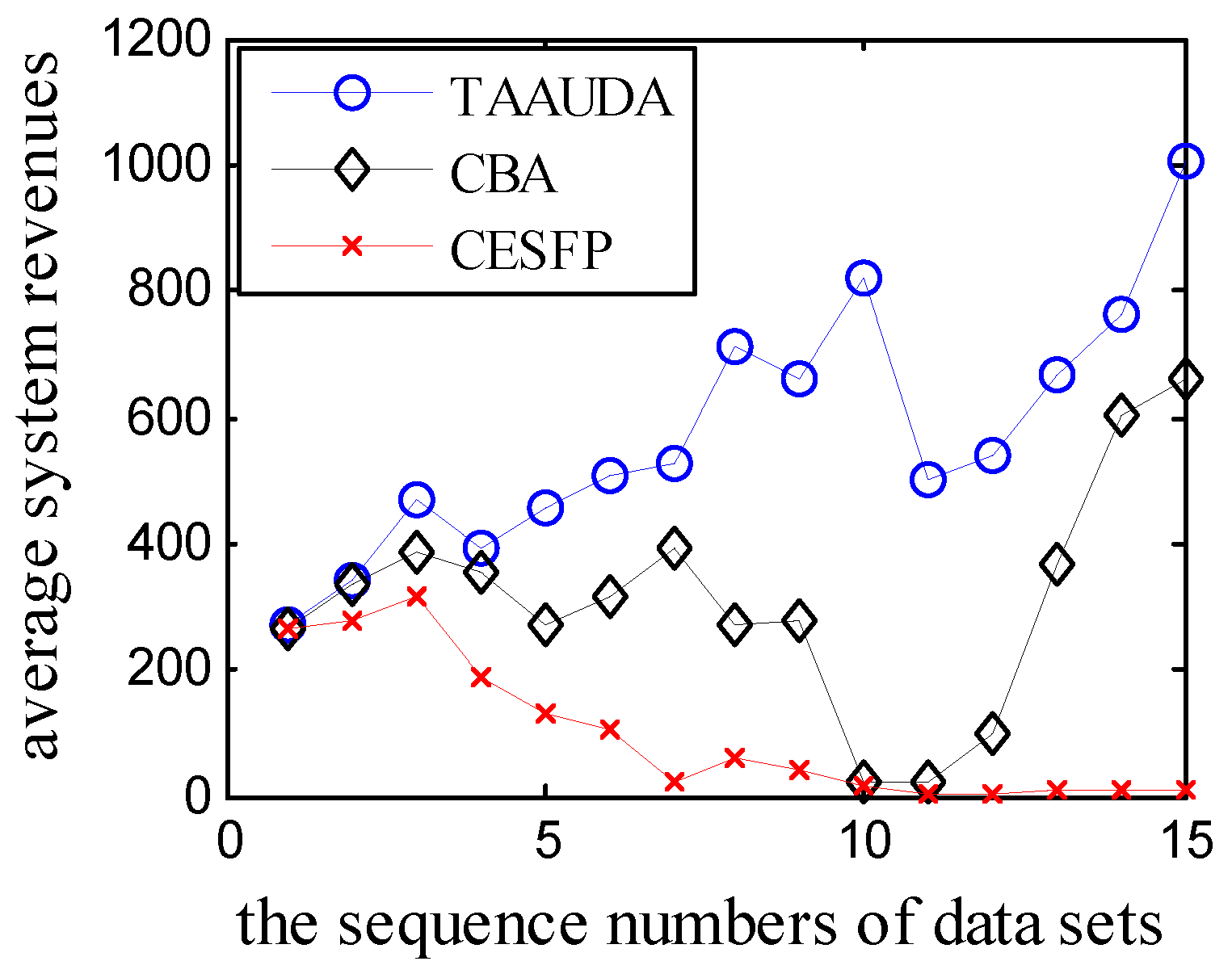
| 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2.10 | 2.11 | 2.12 | 2.13 | 2.14 | 2.15 | |
| TAAUDA | 272.6 | 343.4 | 477.9 | 396.2 | 468.2 | 521.8 | 552.0 | 724.7 | 693.0 | 839.3 | 526.1 | 583.7 | 668.9 | 769.2 | 1056.0 |
| TADUA | 272.8 | 336.3 | 466.9 | 379.4 | 450.2 | 500.1 | 503.3 | 693.2 | 653.3 | 793.7 | 486.2 | 407.3 | 667.3 | 749.8 | 917.7 |
| 3.1 | 3.2 | 3.3 | 3.4 | 3.5 | 3.6 | 3.7 | 3.8 | 3.9 | 3.10 | 3.11 | 3.12 | 3.13 | 3.14 | 3.15 | |
| TAAUDA | 221.0 | 348.3 | 430.8 | 649.6 | 729.4 | 1042.5 | 1328.1 | 1444.9 | 1505.2 | 1717.4 | 2263.5 | 1853.4 | 2589.5 | 3327.4 | 3900 |
| TADUA | 221.0 | 341.3 | 417.7 | 637.6 | 708.3 | 1027.6 | 1309.5 | 1440.9 | 1500.5 | 1715.5 | 2262.8 | 1853.2 | 2583.6 | 3323.6 | 3900 |
| 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 4.10 | 4.11 | 4.12 | |
| TAAUDA | 1149.7 | 1116.07 | 856.46 | 1114.9 | 1078.16 | 1003.1 | 1219.91 | 1075.19 | 1007.04 | 1184.45 | 1126.19 | 1101.03 |
| TADUA | 1142.89 | 1095.52 | 834.09 | 1098.04 | 1078.68 | 991.6 | 1204.39 | 1064.53 | 965.1 | 1151.04 | 1105.65 | 1097.76 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.L.; Wang, H.; Fang, B.F. Utility Distribution Strategy of the Task Agents in Coalition Skill Games. Algorithms 2018, 11, 64. https://doi.org/10.3390/a11050064
Fu ML, Wang H, Fang BF. Utility Distribution Strategy of the Task Agents in Coalition Skill Games. Algorithms. 2018; 11(5):64. https://doi.org/10.3390/a11050064
Chicago/Turabian StyleFu, Ming Lan, Hao Wang, and Bao Fu Fang. 2018. "Utility Distribution Strategy of the Task Agents in Coalition Skill Games" Algorithms 11, no. 5: 64. https://doi.org/10.3390/a11050064
APA StyleFu, M. L., Wang, H., & Fang, B. F. (2018). Utility Distribution Strategy of the Task Agents in Coalition Skill Games. Algorithms, 11(5), 64. https://doi.org/10.3390/a11050064





