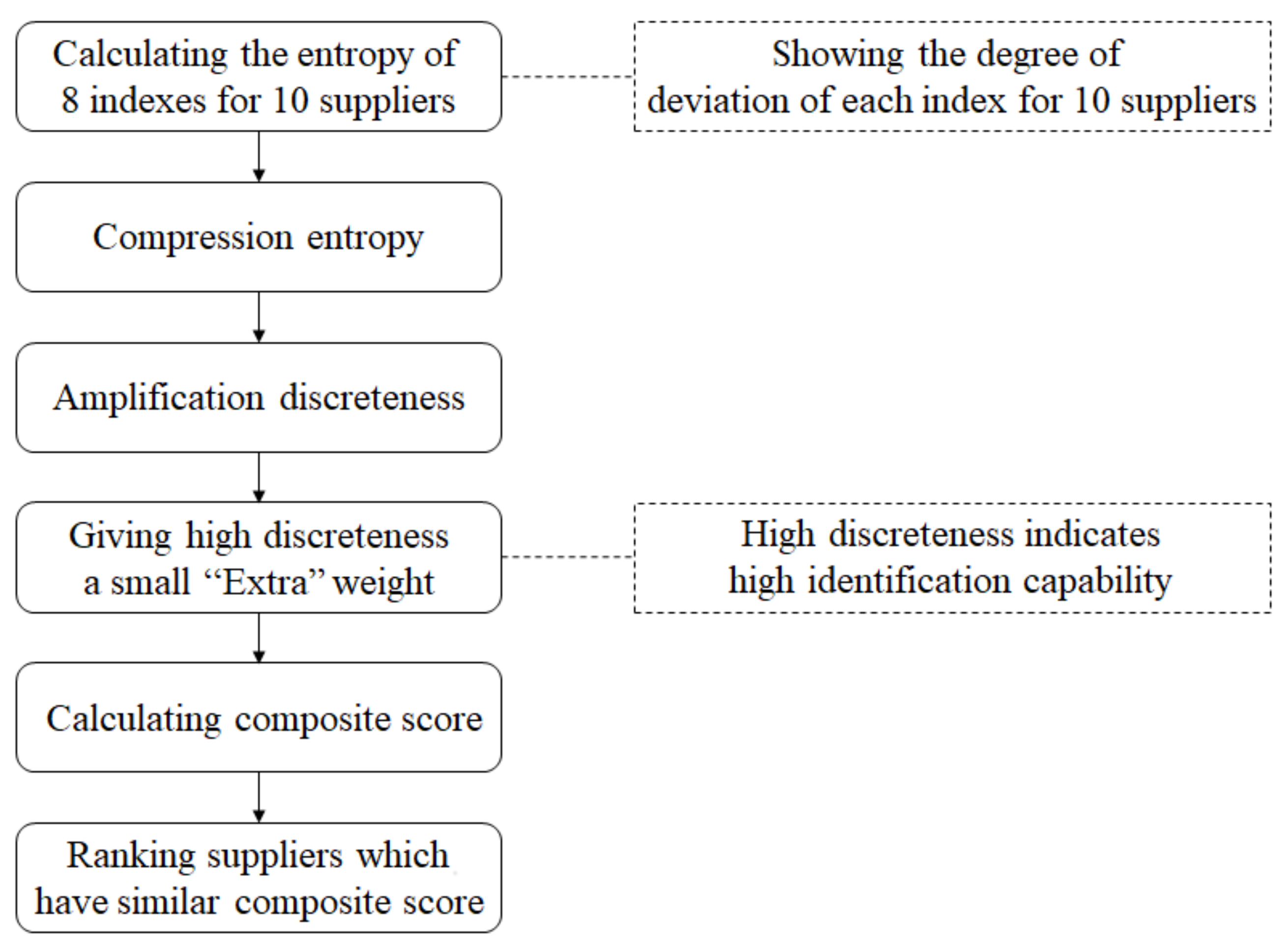
4.1. Correction of Index Weights by Limited Diversity Factors
Weights that were obtained through entropy could objectively reflect the difference degree of each index in the system, namely the influence degree of change of each index on the final evaluation results, providing an objective mathematical methods and theoretical basis for weight determination [
26].
If the diversity factors of entropy are directly applied to the adjustment of weights that were obtained through the analytic hierarchy process, it may lead to over correction because of an excessive adjustment range. Hence, the LDFM was put forward in order to carry out the fine adjustment of index weights on the basis of remaining the relative importance of index.
Steps of adjustment of weights obtained through analytic hierarchy process by diversity factors are: first,
p(
xij), the weight of Index
xij in Index
j, is figured out through Equation (2).
For example, on the basis of eight evaluation indexes in criterion layers, six experts who had served as judges in projects of supplier selection of this ship model, and three of them have experience in operating salvage ships, while three of them are senior engineers in shipbuilding field, were invited to mark indexes of 25 shipyards, which has the ability to building salvage ships, according to the data, such as technical equipment data, historical building data, numbers of senior engineering, and the collecting of historical shipbuilding scheme, which were obtained from these shipyards. If the variance of set of scores, which is made by six experts, is more than 0.6, all of the scores should be re-evaluate by using Delphi method. Finally, for each index, take the average scores of six experts as the final score of the supplier. In order to study the difficulty of distinguishing indexes when the overall scores of different suppliers are similar in the bidding process, 10 shipyards with similar overall scores have been selected out of 25 shipyards, the table of scoring, as shown in
Table 4.
According to Equation (2),
By working out
ej, the entropy of Index
xij, Equation (3) was obtained:
where
k > 0 and
ej ≥ 0. If
k = 1/ln(
n), 0 ≤
ej ≤ 1. So
k = 1/ln(
n) is token in Equation (3).
Hence, the weights of indexes with similar scores should be properly reduced and transferred to indexes with significant differences. The greater the difference between indexes is, the smaller
ej will be, as shown in Equation (4). Thus, the greater the difference is, the smaller
δ will be.
δ can be used to characterize differences of indexes. However, application of δ to adjustment of weights may lead to over correction, where the importance of indexes is ignored. Therefore, this paper proposed ζ, the limited diversity factors, in order to cover the shortage of the DFM.
Scoring for the various indexes of suppliers and the arrays of the index scores, which represent the scores of single index for all suppliers and lie in the interval of (6.5, 10), can be obtained. Generally speaking, the supplier is not capable of satisfying the requirements of bidding when score of single index is too low. The analysis of all the possible arrays of an index scores for 10 supplies, which lie in the interval of (6.5, 10) is conducted. Among all of the arrays, the array of (6.5, 6.5, 6.5, 6.5, 6.5, 10, 10, 10, 10, 10) has the highest discreteness, and its entropy value
ej is 0.9902. The array of (8, 8, 8, 8, 8, 8, 8, 8, 8, 8) has the lowest discreteness, and its entropy value
ej is 1. Therefore, the entropy values of arrays always lie in the interval of (0.9902, 1), regardless of the change of scores in the array within the above mentioned interval, and the entropy values vary only on the second or third decimal place. By using data in
Table 4, the entropy values of eight index scores arrays of 10 suppliers can be calculated, and they are, respectively, 0.9997, 0.9966, 0.9979, 0.9959, 0.9996, 0.9972, 0.9973, and 0.9959.
Due to the linear operation, the change interval of
ζ′ was also changed at the third and fourth significant digit, as shown in Equation (5).
ζ′ retained the discreteness of characterization data of entropy and it plays a similar role in correcting weights. Limited diversity factors
ζ was obtained through the diversity factors of
ζ′, as shown in Equation (6).
with
ζ = (0.8747, 0.8751, 0.8749, 0.8752, 0.8747, 0.8750, 0.8750, and 0.8752). Its change interval was also less than tenths and transformation of entropy into the limited diversity factors was realized through linear operation, ensuring 0.87 as the significant figure of a limited diversity factors, regardless of the index value and realizing fine adjustment of index weight.
The diversity factors and the limited diversity factors were normalized with the results of (0.0145, 0.1695, 0.1041, 0.2052, 0.0206, 0.1412, 0.1367, and 0.2082) and (0.12496, 0.12501, 0.12499, 0.12502, 0.12496, 0.12500, 0.12500, and 0.12503), respectively. It can be seen that the direct application of the diversity factors to adjustment of weights may lead to over correction, which may impair the weight of index with high importance. In other words, the adjustment process cannot take the importance of the index into consideration while conducting correction.
However, the direct application of the limited diversity factors to the adjustment of weights results in a small adjustment range. In order to enhance its adjustment range, as the significant figure of a limited diversity factors, 0.87 was used to reserve the initial weight. Then, significant figures of discreteness of other characterization data were used to reallocate the rest weight, leading to adjustment.
Reserved weight is
wi′ = 0.87 ×
wi,
wi′ = (0.31600, 0.05222, 0.05612, 0.08302, 0.31104, 0.04977, 0.07967, and 0.05216). The rest weight is
The limited diversity factors were used to reallocate the rest weight and the diversity factors of each index wic = (0.015639, 0.015646, 0.015643, 0.015648, 0.015639, 0.015645, 0.015645, and 0.015648).
The final adjusted weight
wif =
wi′ +
wic = (0.31600, 0.05222, 0.05612, 0.08302, 0.31104, 0.04977, 0.07967, and 0.05216). Results of the weight adjustment and the computation process are shown in
Table 5.
In order to further analyze corrected effects, the integrated computation and ranking of final results of ten suppliers were carried out with index weights before and after adjustment. Comparative analysis of their final results before and after adjustment and related ranking were conducted. The final scores are shown in
Table 6.
According to
Table 4 and
Table 6, a comparison of weight changes before and after correction was conducted. After weight adjustment through
ζ, the overall scores of suppliers before correction were very close and many suppliers got the same score and ranking.
After adjustment through the limited diversity factors can be seen from
Table 5, the revised weight of indicators index X
1 and X
5 is reduced due to common scores being similar, while the other which difference of scores is bigger but significant be neglected had be improved, according to a different degree, so the problem that the suppliers have the same score and rank can not identify the optimal supplier. Contrast
Table 4 and
Table 5 we can find the sorting before correction, ranking in the first three suppliers mainly because the X
1 and X
5 index of excellent performance, but as a result of each supplier in the X
1 and X
5 index, difference between small, other indexes with more difference degree should be focused on considering to get a more reasonable supplier sorting, so after correction, due to the rest of the indicators such as X
2 more difference degree and higher score, supplier S
2, S
5, S
9 enter into the top 3. For example, supplier S
5 took a first from the sixth and its scores were (9.00, 9.40, 9.00, 6.70, 8.50, 7.50, 8.70, and 9.40). However, S4 took the fourth place from the first place after the adjustment and its scores were (9.50, 9.40, 8.60, 9.40, 7.80, 7.40, 7.20, and 6.80). Results of highly weighted Indexes X
1 and X
5 of these two suppliers were similar. Proper enhancement of weights of other indexes, such as “Launching pattern” X
6, “Important test” X
7 and “Centralized purchasing of equipment” X
8, enhanced the overall score of S
5, making expected weight adjustment realized. After adjustment, results became more practical.
According to analysis above, the diversity factors of entropy played a proper role in adjusting weights, which is a good solution for declining discrimination of salvage ship supplier selection.
After calculation, the purpose of reordering has been achieved by once correction. But, if there are two conditions that need to be corrected multiple times, the result of LDFM will not apply or will achieve a similar effect by the DFM method:
- (1)
change the order of the original weight after repeated correction; and,
- (2)
the weight correction of an index or some indexes by the LDFM with multiple times is greater than the results of DFM with once correction.