Synthetic Datasets
The definitions of these functions are listed in
Table 2.
Where, is the added Gaussian noise with a mean of zero and a standard deviation of 0.01.
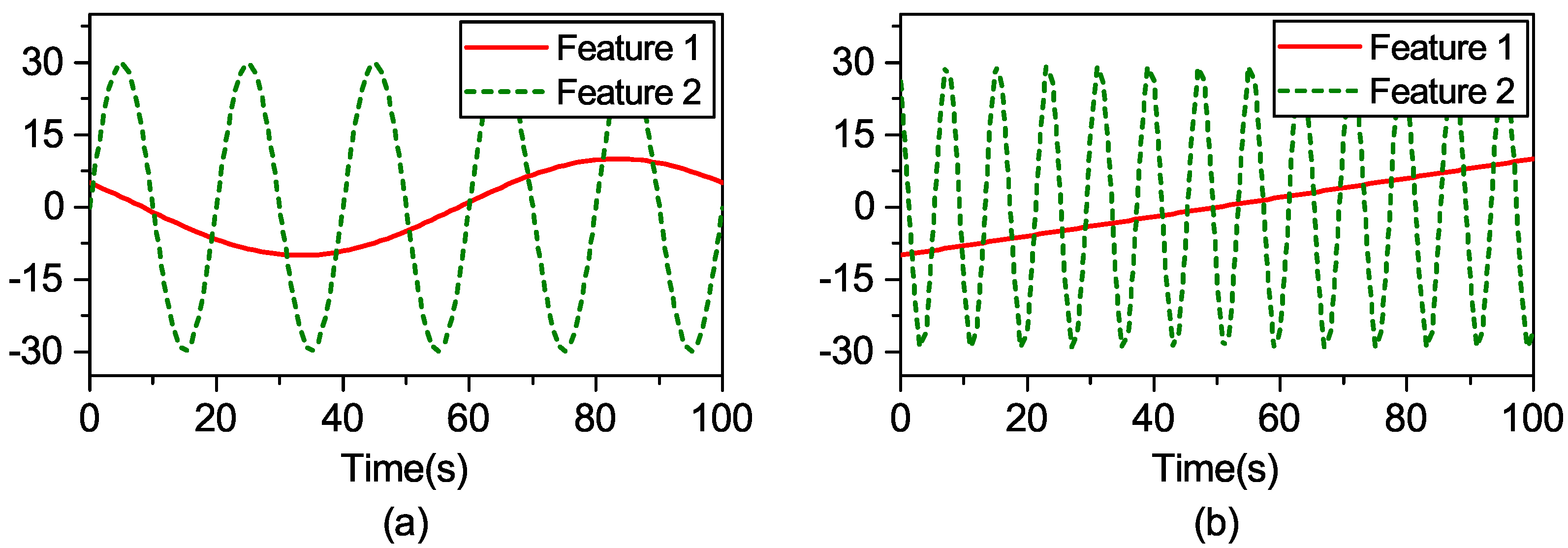
The synthetic dataset “F1” is chosen as an example. Feature 1 (
) and Feature 2 (
) in the training data are taken from the sinusoidal signals of 0.01 Hz and 0.05 Hz, respectively. Their corresponding test data are extracted from linear functions and the sinusoidal signal 0.125 Hz, respectively, as shown in
Figure 1.
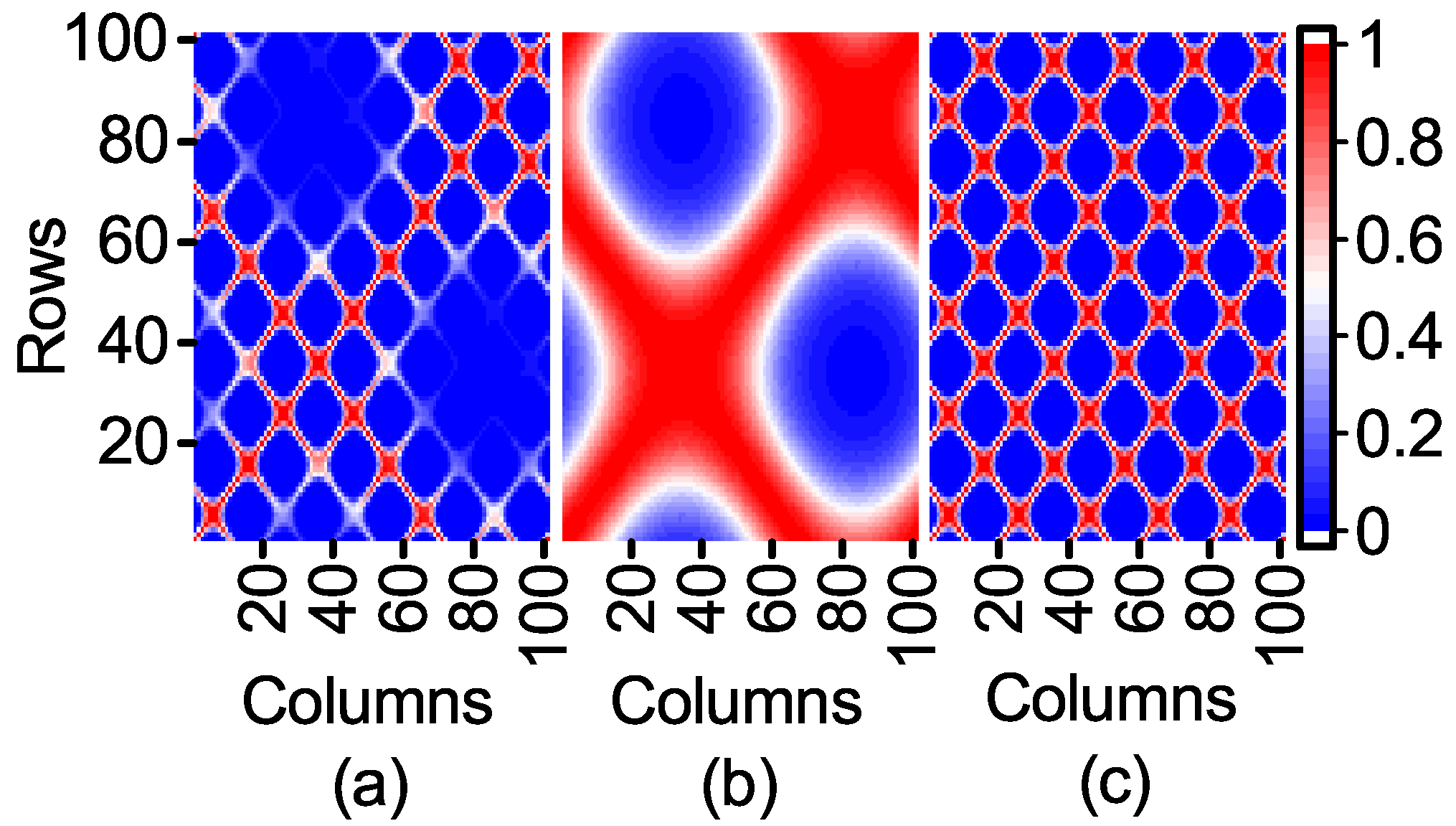
The expression of F1 shows that the range of the first item affected by Feature 1 is [−0.2172, 1] and that of the second item affected by Feature 2 is restricted to [−0.03, 0.03]. It is deduced that Feature 1, which has a great contribution to the output, is an important feature, while Feature 2 is to the contrary. However, the contribution of Feature 2 to the output of the model is neglected when the kernel matrix is calculated. In order to observe the influence of Feature 1 and Feature 2 on the kernel matrix, a kernel width = 0.01 is used to compare the three kernel matrices visualized in 2D heat-maps as follows.
According to Equation (
12), the kernel matrix can fully reflect the similarity between the sample points in kernel space. The similarity of the sample points in
Figure 2c is clearly shown in
Figure 2a, while the influence of Feature 1 with a high contribution to the output is obviously weakened.
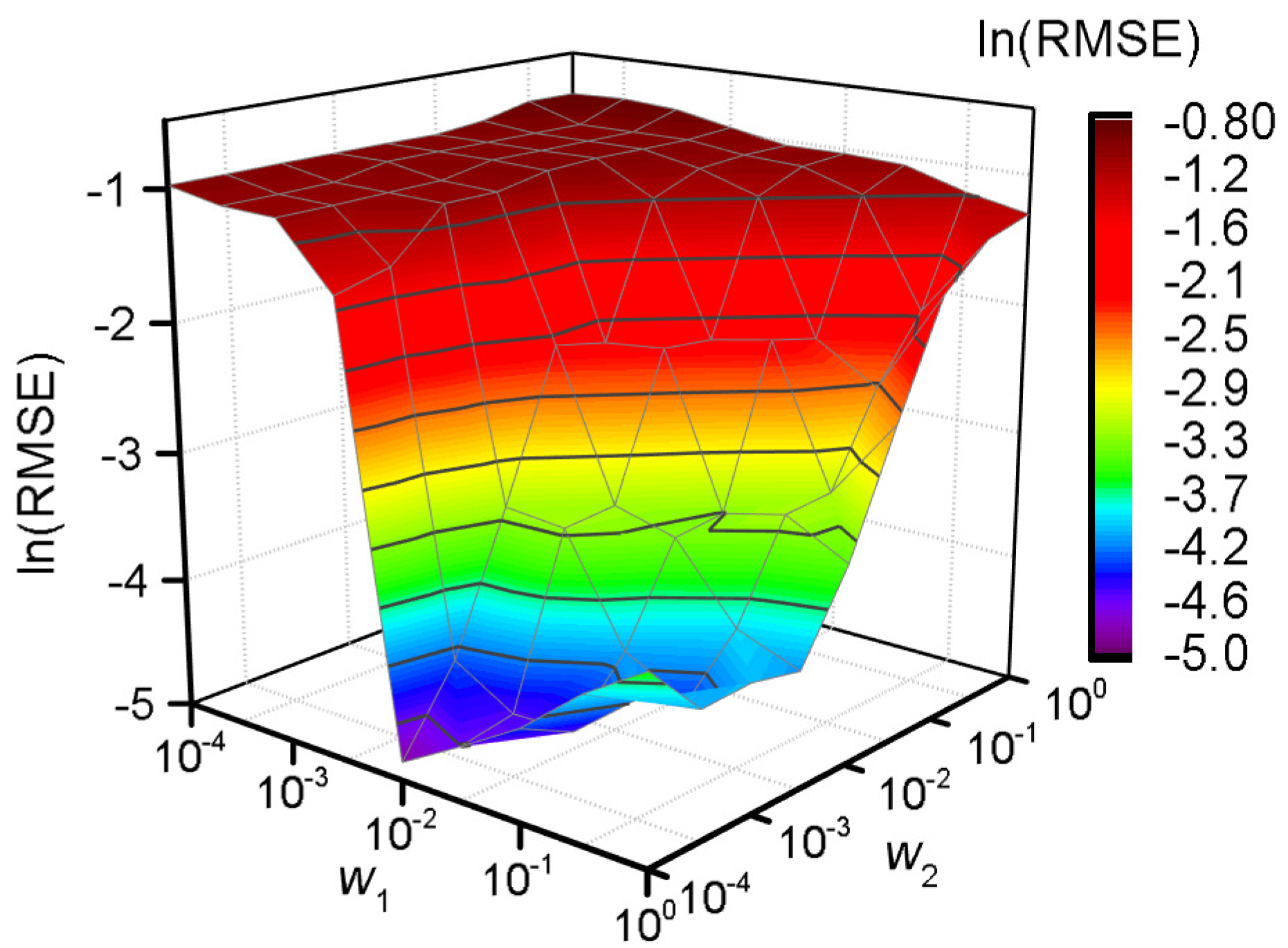
A grid search method is applied to obtain the corresponding RMSE for each possible combination of
to verify the necessity of feature weighting [
34]. The value of
and
is searched from the set
. The model performance is shown as
Figure 3 accordingly.
According to
Figure 3, a better generalization ability occurs when the value of
is around 100, and the best is acquired when
and
. As a whole, a better generalization ability can be obtained when
vs. when
. The FW-SVR is degraded to the classical SVR when
, and the generalization ability of the model is poor.
We compare the feature weighting method with the feature selection and the normalization. In feature weighting, and . In feature selection, Feature 2 is deleted. In the normalization method, the min-max normalization and the Z-normalization are employed.
Min-max normalization converts raw data to [0, 1] by linearization. The
k-th feature of the
i-th sample
is normalized to
:
where
is the maximum and minimum value of the
k-th feature, respectively.
The Z-normalization method normalizes the raw data to a dataset with a mean value of zero and a variance of one.
where
is the mean and standard deviation of the
k-th feature, respectively.
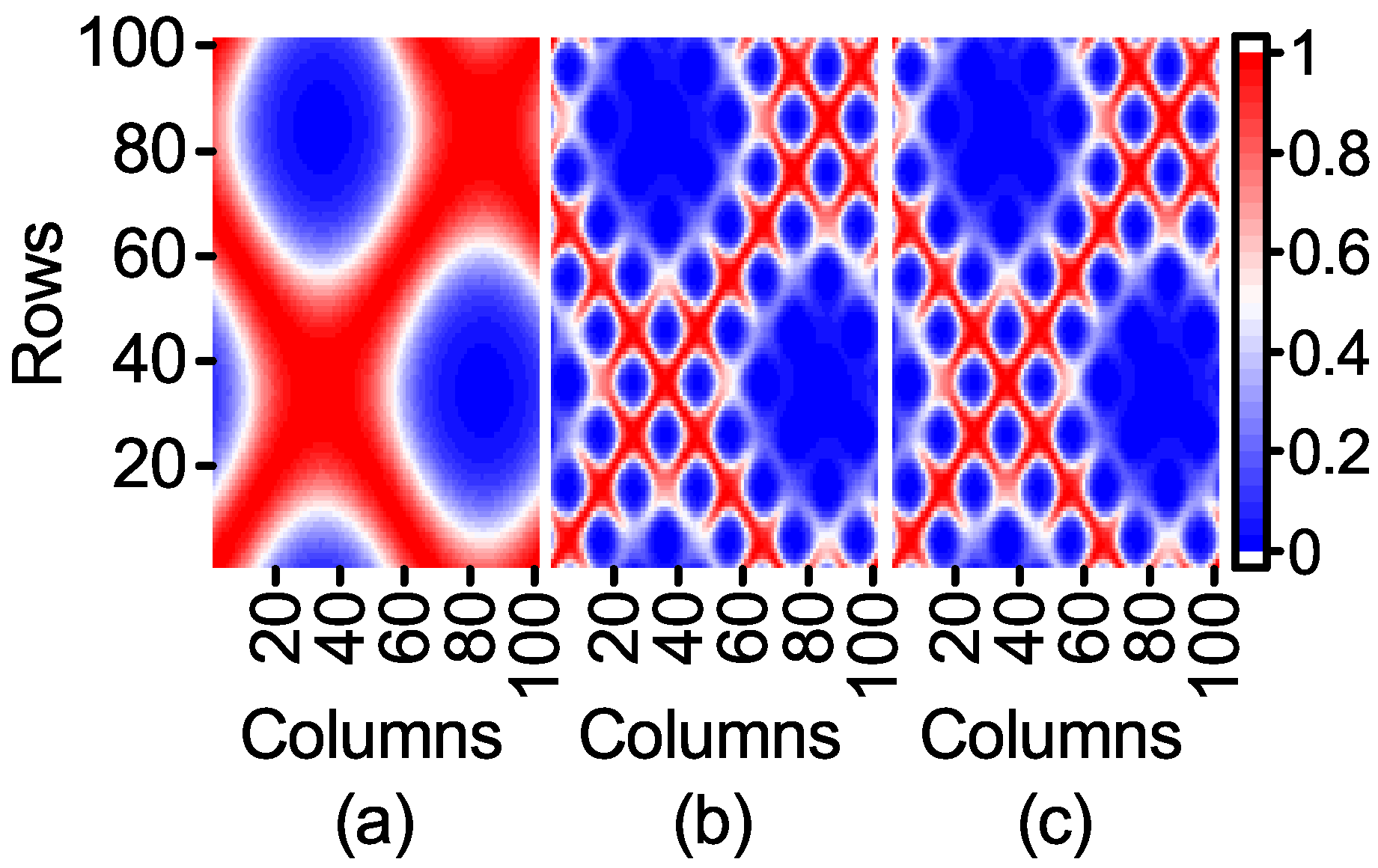
Firstly, the kernel matrix generated by feature weighting and by other methods is compared. In order to facilitate the comparison, when the parameter
is selected, the result consistency of Feature 1 is calculated as the standard of nuclear element calculation, because weighting and normalization will change the value of the feature. The kernel matrix generated by the above method is shown in
Figure 4.
As can be seen from
Figure 4, the feature weighting reduces the influence of Feature 2 on the kernel matrix.
Figure 4a is similar to
Figure 2b. However, the feature weighting preserves the information of Feature 2 compared to the feature selection. It can be deduced from
Figure 4b,c that the normalization method can weaken the influence of Feature 2. However, its influence is still great. As the range of Feature 1 and Feature 2 is essentially the same in normalization, the contributions of Feature 1 and Feature 2 are much the same. When the range of unimportant features is greatly wider than that of important features, the normalization method can largely reduce the influence of unimportant features. On the contrary, the normalization method will increase their influence.
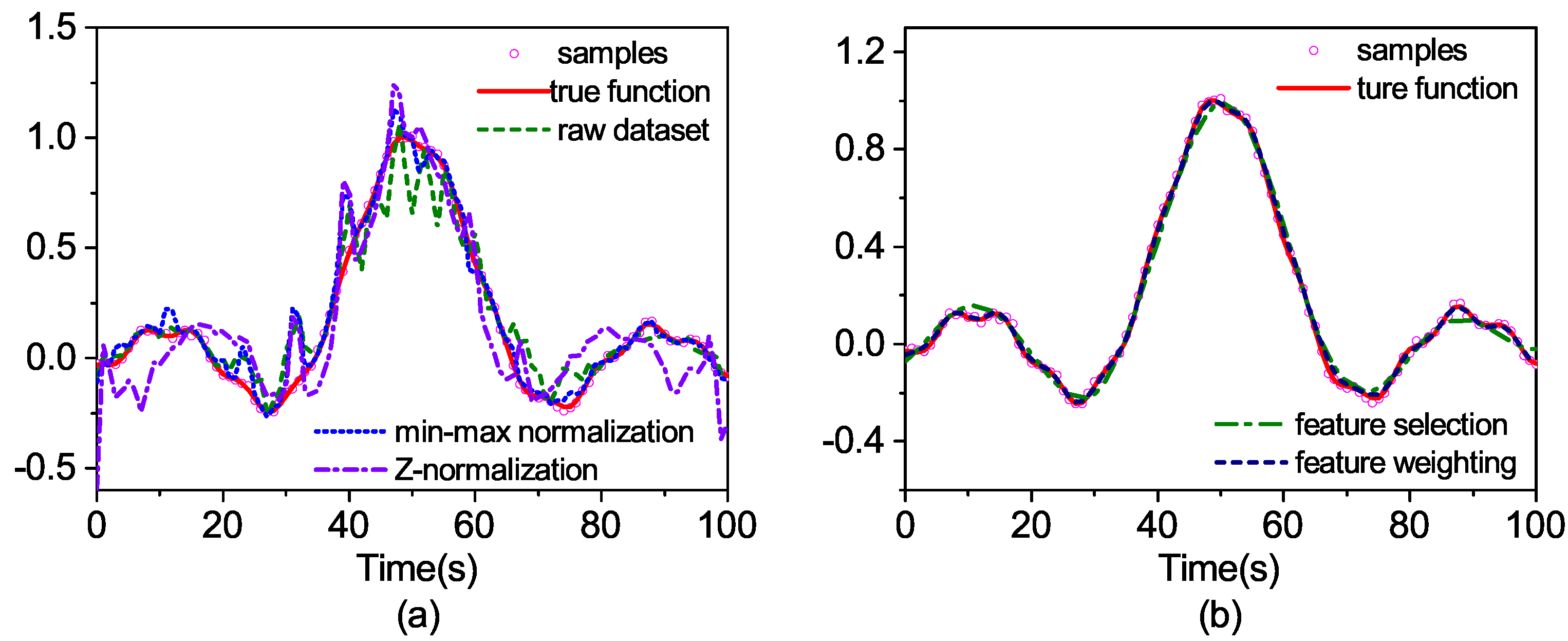
Then, the feature weighting is compared with the raw dataset, the feature selection and the normalization to observe the differences in the generalization ability. The search range of parameters
C and
is
and
, respectively, and
is set to 0.0064. The optimal hyper-parameter is obtained by five-fold cross-validation. The prediction outputs for the test set are shown in
Figure 5.
As can be seen from
Figure 5, the prediction curve with raw data is quite different from the real output and the two prediction curves with normalized data, as well. The feature selection achieves better results. However, under-fitting occurs because of the deletion of Feature 2. The best prediction result is derived from the feature weighting method.
We model the synthetic datasets in
Table 2 to compare the above methods. For the feature selection, all possible feature combinations are tested in order to get the optimal one. It is used to be compared with the feature weighting. The program is repeated 10 times. The optimal combination of weights is shown in
Table 3, and the results are shown in
Table 4, in which bold values indicate the method with the best performance.
Finally, we randomly chose seven UCIbenchmark datasets [
35]. The grid search method is used to select the optimal combination of weights from the set
. The optimal combination of weights is shown in
Table 5, and the results are compared as in
Table 6, in which bold values indicate the method with the best performance.
The Wilcoxon signed rank tests [
36] at the 0.05 significance level are implemented to test the differences between the feature weighting and other data pre-processing techniques to substantiate the indications in
Table 4 and
Table 6. The test results are presented in
Table 7. The prediction results on F1 and F2 using linear and sigmoid kernels were both unacceptable and were not included in this test.
According to
Table 4 and
Table 6, FW-SVR achieves a competitive generalization performance with both synthetic datasets and real datasets. The FW-SVR that uses the Gaussian kernel performs reasonably well on all 11 datasets. Note that the results on F1 and F2 are both unacceptable because of under-fitting for the linear kernel and the sigmoid kernel. The two datasets are not included in the following comparison. As for the linear kernel, three optimal results and three suboptimal results are obtained by FW-SVR. In addition, there are three results that are close to the optimal ones. As for the sigmoid kernel, FW-SVR achieves a competitive generalization performance on synthetic datasets. For example, the mean RMSE o 0.0024 on F4 is better than the value of 0.0120 of the Gaussian kernel. However, FW-SVR is not the optimal choice for the UCI datasets, as shown in
Table 6. In general, the overall results obtained by the Wilcoxon tests presented in
Table 7 show that the FW-SVR achieves the best generalization performance in comparison with the other five data pre-processing methods when the most suitable kernel type is selected. Comparing the five methods, we deduce that the contribution of the feature to the output is taken into account by FW-SVR, which reduces the influence of unimportant features on the kernel space feature.